Minimizing 3T MRI Geometric Distortions for Stereotactic Radiosurgery via Anterior–Posterior Phase Encoding—A Phantom Study

Abstract

To directly address the important issue of MRI geometric distortions in stereotactic radiosurgery (SRS) planning, we performed a phantom study of sequence acquisition optimization. This study analyzed, in particular, the effects of clinically relevant gadolinium (Gd) concentration as filling solution for the phantom, as well as phase encoding reversal direction and flip angle on distortion. We created a rigid geometric grid phantom with 840 fiducial markers for distortion quantification on a 3T MRI scanner. To choose the optimal filling solution, an anthropomorphic RANDO phantom was employed, and 1 mmol/L gadolinium was chosen due to clinical relevance. An automated Python-based software (version 3.7.1) was developed for efficient detection and matching of phantom inserts between MRI and CT scans. A series of MRI acquisition parameter optimizations were systematically evaluated. The standard SRS protocol exhibited the highest average distortion of 1.301 mm. Notably, reversing the phase-encoding direction to anterior–posterior (AP) reduced the mean distortion to 0.725 mm, a 44.27% decrease, while the maximum distortion was reduced by 15.65%. The AP phase sequence maintained acquisition time, SAR, SNR, and CNR within acceptable limits. Additional distortion reduction was achieved by increasing the flip angle from 12° to 18°. In this work, we succeeded in significantly reducing the mean distortion observed in phantom images. As the gadolinium concentration used in the phantom is clinically similar to the gadolinium concentration observed in patients undergoing MRI scans with contrast agents, the achieved distortion reduction is prospectively reproducible in patients.

1. Introduction

Magnetic resonance imaging (MRI) has gained significant attention in radiotherapy (RT) due to its superior soft tissue contrast when compared with computed tomography (CT) [1]. However, the presence of geometric distortions in MRI remains a considerable challenge, particularly in scenarios where strict accuracy is required, such as in stereotactic radiosurgery (SRS) treatment planning, which often requires distortion thresholds of no more than 1 mm [2]. Geometric distortion in MRI can be system- or patient-dependent and is influenced by various causes, including B₀ field inhomogeneity and gradient nonlinearity [3]. Furthermore, the trend toward high magnetic field strength scanners, such as 3T scanners, poses increased distortion concerns [4,5,6].

Currently, many different approaches have been proposed to minimize geometric distortion e.g., [7,8]. Active or passive shimming techniques, which introduce small magnetic fields to increase the homogeneity of B₀, are commonly implemented [9,10]. Pulse sequence choices can also improve the imaging outcome, as low-bandwidth sequences are particularly vulnerable to these inhomogeneities [11]. Parallel imaging methods, such as sensitivity encoding [12], can also be used to minimize the distortions caused by B₀ inhomogeneity.

Regarding other ways to quantify geometric distortion, Liu et al. [13] used the Euclidean distance formula to quantify their 3D distortion values, which could then be optimized by its minimization. While some MRI scanners are equipped with algorithms designed to correct hardware-related distortions, residual geometric distortion often remains [13,14,15,16,17,18,19]. Therefore, the development of more effective correction methods remains a high priority in the MRI research community so as to ensure accurate and reliable MRI image quantification.

The quantification of geometric distortion in a phantom makes its optimization possible. Let us denote the positions of control points, as determined by the phantom’s geometry, using the Cartesian coordinates $\overrightarrow{r}$= (x, y, z), while the primed coordinates $\overrightarrow{r^{\prime }}$= (x″, y″, z″) symbolize their corresponding locations within the distorted image space [20]. The geometric distortion at each control point is the residual vector $\overrightarrow{d}= \overrightarrow{r}- \overrightarrow{r^{\prime }},$ computed after rigid MRI-to-CT registration and centroid detection (Figure S1).

This way, the undistorted image space can be recovered from the distorted image space by adding to it the geometric distortion correction factors at each control point and by using an interpolation method for the remaining points [20].

This work focuses on addressing these distortion concerns by optimizing MRI sequence parameters and quantifying distortion values within the field of view (FOV) of a 3T GE Signa MRI scanner used for SRS treatment planning. Thus, the primary objectives of this work are the following:

• Design and construction of a customized geometric phantom to accurately assess geometric distortion. Its filling solution was determined by testing different options on a preliminary phantom.
• Development of distortion quantification software. This tool automated the detection and matching of phantom inserts between MRI and CT scans.
• Optimization of MRI image acquisition by systematically exploring different acquisition parameters. The aim is to identify the most effective sequence to reduce geometric distortion in the MRI scans. This optimization process takes into account crucial factors, such as acquisition time, SAR, SNR, and CNR, while maintaining distortion levels within acceptable clinical thresholds.

2. Materials and Methods

2.1. Phantom Design for Geometric Distortion Measurement

The phantom is entirely made of rectangular polymethyl methacrylate (PMMA) slabs and a PMMA cylindrical casing from a Jaszczak phantom [21,22], measuring 12 cm (height) by 20 cm (diameter).

The final design of the phantom grid consists of three perpendicular square grids, along with two axial grids at the top and bottom of the phantom. The frontal and superior views of one of the geometric phantom grids are presented in Figure 1. An overview of the phantom design and a photograph of the finalized phantom is shown in Figure 2.

The final layout of the phantom has a total of 840 inserts. In the design of the phantom, care was taken to ensure that the separation between air and liquid contrast media, formed by the acrylic walls and boundaries of the phantom, was greater than 6 mm, since significant susceptibility distortions at the interface would otherwise be apparent [23].

The phantom inserts were manually filled with a Gd 1 mmol/L saline solution (Section 2.2). After phantom filling, the influence of small air bubbles inside some inserts was reduced by careful slice selection during image analysis. Approximately 9% of the inserts (those with ≥50% air volume) were not considered in the image.

2.2. Phantom Filling Solution Tests

Different filling materials were tested to determine the optimal material to use in the final geometric phantom. We tested four solutions: commercial mineral oil, 1 mmol/L of gadoteric acid (Dotarem^®), 4.26 mmol/L of copper sulfate, and 10 mmol/L of nickel chloride. These solutions were chosen as candidates based on their magnetic properties, toxicity and potential similarity to the contrast agents used in patients, and their concentrations were selected based on previous research studies and commercial phantoms e.g., [24,25,26,27,28].

A series of CT and MRI scans were conducted on the head of a male anthropomorphic Alderson RANDO (The Phantom Laboratory^®) phantom [29,30], for which a set of customized acrylic inserts were made. These were filled with the four candidate materials. The phantom is cut in 2.5 cm cross-sectional slices [31], and each cavity of the phantom allowed the insertion of acrylic inserts with 0.103 mL of internal volume [32].

The resulting axial slice images were analyzed to assess the geometric distortions induced by each filler material, using CT as distortion-free baseline images. This comparison first involved a rigid 6-degree registration process, carried out in an Eclipse V.16 (Varian Medical Systems) planning system, with isocenter verification.

The final step consisted of a transformation to ensure that the MRI and CT coordinates were in the same reference system, thus allowing direct comparisons with the central insertion coordinates. Thus, the differences yielded the total distortions for each insert, given by $\sqrt{(x_{CT}-x_{MRI}{)}^2+(y_{CT}-y_{MRI}{)}^2}$.

The acrylic inserts employed are 2.5 cm long, matching the thickness of the slices in the axial direction. For this reason, distortions along the z-axis were not assessed. Additional tests on the solution concentration were performed on a six-well cell culture plate.

2.3. Development of Distortion Quantification Software

An algorithm was developed in Python, using the OpenCV package, to automatically calculate geometric distortions. In this section, its development process is presented and made publicly available (https://github.com/BernardoCampilho/MSc_Thesis_MRI_Distortion; accessed on 29 August 2025). The overall structure of the code can be divided into three parts, as follows:

• Image Registration: The registration results obtained using Eclipse planning system (Section 2.2) were used to derive the final outcomes of the developed software.

Differences in slice thickness and number of slices between MRI and CT scans had to be taken into account to ensure adequate pairing. Thus, in these axial scans, the developed software uses the registration software z-value to assign a corresponding MRI slice number to each CT slice, as follows:

$$\mathrm{S}\mathrm{l}\mathrm{i}\mathrm{c}{\mathrm{e}}_{\mathrm{M}\mathrm{R}\mathrm{I}}=\mathrm{S}\mathrm{l}\mathrm{i}\mathrm{c}{\mathrm{e}}_{\mathrm{C}\mathrm{T}}\times {\displaystyle \frac{\mathrm{S}{\mathrm{T}}_{\mathrm{C}\mathrm{T}}}{\mathrm{S}{\mathrm{T}}_{\mathrm{M}\mathrm{R}\mathrm{I}}}}+{\displaystyle \frac{{\mathrm{z}}_{\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}}{\mathrm{S}{\mathrm{T}}_{\mathrm{M}\mathrm{R}\mathrm{I}}}}$$

(1)

where ST_CT and ST_MRI are the slice thickness values of the CT and MRI scans, respectively. This index pairing was used to enforce slice-wise correspondence.

• Insert Detection: After registration between MRI and CT, the inserts observed in each, as seen on each of the MRI and CT slices, were separately detected after several steps of data pre-processing and filtering.

These included converting DICOM images to 16-bit grayscale PNG format, applying Gaussian blur for noise reduction, and using Otsu’s thresholding to create binary images. Contours were then extracted and filtered based on area, distance from the center of the image, circularity, and intensity thresholds to identify relevant blobs, ensuring accuracy and reducing false positives.

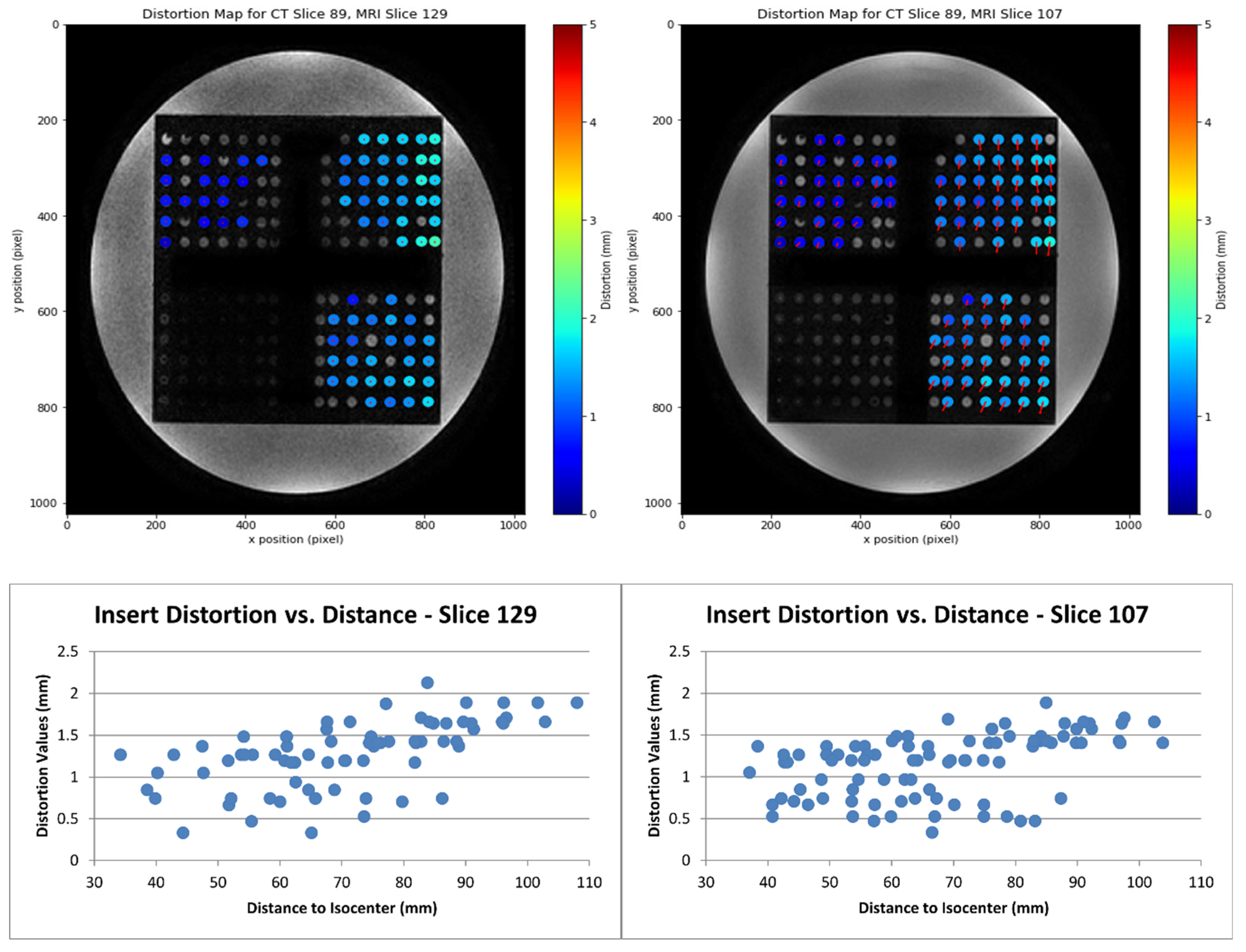
• Distortion Calculation: The geometric distortion was calculated as the distance between each matched insert centroid. The process generated a distortion map, illustrating the magnitude and direction of distortion, with outputs including coordinates, distances to the MR scanner isocenter, and distortion values.

2.4. Phantom Positioning and Image Acquisition

The algorithm was tested on a set of CT and MRI images of the geometric phantom. The MRI images were acquired with a 3D FSPGR sequence (GE Signa HDxt 3.0T scanner, GE Medical Systems, Waukesha, WI, USA; using an 8-channel 3T head coil), with slice thickness of 1 mm, TR of 3000 ms, TE of 83 ms, and an FOV of 240 × 240 mm, with a matrix size of 256 × 256. CT images had a slice thickness of 1.25 mm, a kilovoltage peak (kVp) of 120, and an FOV of 500 × 500 mm, with a matrix size of 512 × 512. On the MRI couch, the phantom was positioned inside the head antenna and centered with isocenter using the duct tape marks. MRI images were acquired with a 3D FSPGR sequence (GE Signa HDxt 3.0T scanner, using an 8-channel 3T head coil), with slice thickness of 1 mm, TR of 3000 ms, TE of 83 ms, and a FOV of 240 × 240 mm, with a matrix size of 256 × 256.

2.5. Optimization of MRI Image Acquisition for SRS Treatment Planning

The MRI acquisition parameters were optimized through a series of experimental tests, listed in

Table 1. 3T MRI image acquisition optimization tests.

Sequence Name	Acquisition Type	Slice Thickness (mm)	TR (ms)	TE (ms)	Number of Excitations	BW (kHz)	Matrix Size (Pixels2)	Flip Angle (°)	FOV (cm)	Resolution (Pixels/mm)	Additional Changes
Protocol	3D	1	5.8	2.1	1	62.5	256 × 256	12	24 × 24	1.1
BWₒₚₜ	3D	0.8	6.5	1.8	1	200	256 × 256	12	24 × 24	1.1
Test 1	3D	0.6	6.9	2.6	1	41.7	256 × 256	12	24 × 24	1.1
Test 2	3D	1	5.8	2.1	1	62.5	256 × 256	18	24 × 24	1.1
Test 3	3D	1	5.8	2.1	1	62.5	256 × 256	12	24 × 24	1.1	Manual shimming
Test 4	3D	1	5.6	1.7	2	200	256 × 256	12	24 × 24	1.1
Test 5	3D	1	5.8	2.1	1	62.5	256 × 256	10	24 × 24	1.1
Test 6	2D	1.9	12	5.8	1	83.3	256 × 256	12	24 × 24	1.1	Multi-echo GE seq.
Test 7	3D	1	5.8	2.1	1	62.5	256 × 256	12	24 × 24	1.1	AP Phase

.

Given the high patient load at our institution and the continuous use of the MRI scanner, the time window for optimization tests was limited. A strategic approach was adopted to carefully select tests that covered a wide range of variables, testing multiple parameters simultaneously.

Table 1: The 3T MRI image acquisition optimization tests. The first row (“Protocol”) shows the parameters for the imaging sequence currently used at our institution in SRS treatment planning (3D FSPGR). Parameters shown in magenta are those evaluated in each test. The scanner automatically optimizes TR and TE values for a given sequence in terms of the other parameters. Here, we focused on optimizing the remaining parameters.

Weighting Factor λ

To quantify the optimal sequence, based on the choice of parameter values in Table 1 and resulting images, a weighting factor (λ) was defined, taking accuracy and clinical feasibility into account. It was defined such that high λ values are optimal and it was normalized by the maximum value across all tests.

The λ Factor (Equation (3)) weighs the acquisition parameters by assigning them one of three priority classes:

• First Priority Class: Acquisition time and the mean distortion (squared weighting).
• Second Priority Class: SNR, CNR, and number of detected inserts (linear weighting in Equation (3)). The SNR was calculated in the usual way for MRI images [33], by dividing the mean pixel intensity μ_signal in the signal region (phantom volume) by the standard deviation of the background σ_background, while the CNR introduces an additional factor by subtracting the mean pixel intensity μ_ROI of a region of interest (detected inserts for each slice), as follows:

$$\mathrm{S}\mathrm{N}\mathrm{R}={\displaystyle \frac{{\mathsf{\mu }}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\mathsf{\sigma }}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}}};\mathrm{C}\mathrm{N}\mathrm{R}={\displaystyle \frac{|{\mathsf{\mu }}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}-{\mathsf{\mu }}_{\mathrm{R}\mathrm{O}\mathrm{I}}|}{{\mathsf{\sigma }}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}}}}$$

(2)

Unlike the first priority class parameters, SNR and CNR are not enough to invalidate the viability of a sequence, except in extreme cases. As for the number of detected inserts, this provides meaningful information, as a sequence in which they are hard to detect may mean, for example, difficulty in detecting metastases of similar size. In this parameter, the number of detected inserts was normalized to the total number of inserts.

• Third Priority Class: SAR and maximum distortion (fractional linear weighting). SAR is an important parameter, but it only becomes a limiting parameter at approximately 2 W/kg [33], and all SAR values achieved were below 0.5 W/kg (

  Table 2. Full color-coded results of sequence parameter tests, including the λ factor. To facilitate visual analysis, results better or worse than the mean by more than half a standard deviation are colored in green and magenta, respectively.

  Sequence Name	Acquisition Time (min)	SAR (W/kg)	SNR	CNR	No. of Detected Inserts	Mean Distortion (mm)	Max Distortion (mm)	λ Factor
  Protocol	4.80	0.29	19.21	5.30	376	1.30	3.38	0.28
  BWopt	5.72	0.27	14.79	4.43	404	0.97	3.06	0.26
  Test 1	5.90	0.26	19.93	5.65	368	1.22	3.36	0.23
  Test 2	4.78	0.47	20.12	7.29	412	1.18	3.32	0.48
  Test 3	4.77	0.29	17.79	4.78	360	1.21	3.33	0.26
  Test 4	18.30	0.30	10.96	2.74	439	0.98	3.13	0.01
  Test 5	4.78	0.25	15.60	4.74	263	1.19	3.29	0.18
  Test 6	3.15	0.04	10.79	5.19	88	1.22	2.36	0.13
  Test 7	4.78	0.29	19.55	5.24	384	0.73	2.85	1.00

  ). Thus, its weight in Equation (3) is defined so that λ = 0 if SAR = 2 W/kg. Regarding the maximum distortion, while it helps to quantify the worst-case scenario, it may also represent an outlier value, so it is considered less important than the mean distortion. Thus, its weighting was implemented such that λ tends to zero as the maximum distortion approaches 10 mm, which is one order of magnitude bigger than the desired threshold.

Thus, the λ weighting factor is defined as follows:

$$\lambda ={\displaystyle \frac{SNR\cdot CNR}{(Time{)}^2\cdot ({\mu }_{dist}{)}^2}}\cdot (1-{\displaystyle \frac{SAR}{2}})\cdot N_{inserts,norm}\cdot (2-{\displaystyle \frac{Ma{x}_{dist}}{5}})$$

(3)

where Time is the image acquisition time, μ_dist is the mean distortion, N_inserts,norm is the normalized number of detected inserts, and Max_dist is the maximum distortion value out of all the detected inserts.

3. Results

3.1. Phantom Filling Solution Tests

This exploratory test allowed us to quantify the distortion effects induced by each filler material. The results indicate that nickel chloride exhibited less pronounced distortion compared with other materials (Figure 3), although the sample size was limited. Our findings also reveal that gadolinium exhibited significant distortion values, making it an ideal filling solution for our study.

In addition to distortion, we considered other crucial factors when choosing the filler material, such as toxicity and similarity to contrasts in patient images. Gadolinium, being a commonly used contrast agent in clinical practice [34,35,36], exhibits high similarity to patient imaging contrasts, making it a favorable choice for our research. Furthermore, it has a relatively low toxicity profile compared with other materials such as nickel chloride, which is known to be toxic [37,38]. This was particularly important in the phantom filling process, as it was undertaken manually.

After choosing gadolinium as the basis for filling the phantom, MRI images of the 6-well cell culture plate obtained with different concentrations of gadolinium (1 and 2 mmol/L) were compared (Figure S2) For each concentration, additional plaques containing the artificial blue colorant FCF (E133) were also tested. This colorant, approved for use in Europe [39], was selected to improve the visualization of the phantom fillings and potential air bubbles.

The results of this test show that mean pixel intensity values obtained with a 1 mmol/L Gd concentration aligned more closely with typical patient values (≈7000 HU). This finding suggests that this concentration is more clinically relevant for medical imaging applications. Moreover, this concentration is also closer to the values set by FDA directives, which recommend a maximum Gd concentration of 0.1 mmol/kg [40].

Given these results, the final solution and concentration chosen for the geometric phantom was 1 mmol/L Gd in 0.9% saline solution, with the addition of FCF blue colorant.

3.2. Distortion Quantification Software

The evolution of the results of the insert detection software for the CT scan is shown in Figure S3. Initially, the software failed to detect a sufficient number of inserts and incorrectly identified air bubbles at the top of the phantom as inserts. To address these issues, the detection parameters were iteratively adjusted. The process for MRI insert detection was similar to that of the CT scan, with minor modifications to the script.

As for the distortion part of the software, the results for two slices are presented in Figure 4. The visualization tool developed within the script can show distortion values and distortion patterns in the image before data analysis is conducted. The distortion can also be separated into its x and y components (Figure S4). The distortion dependence on the distance to the isocenter is again perceptible (Figure 5).

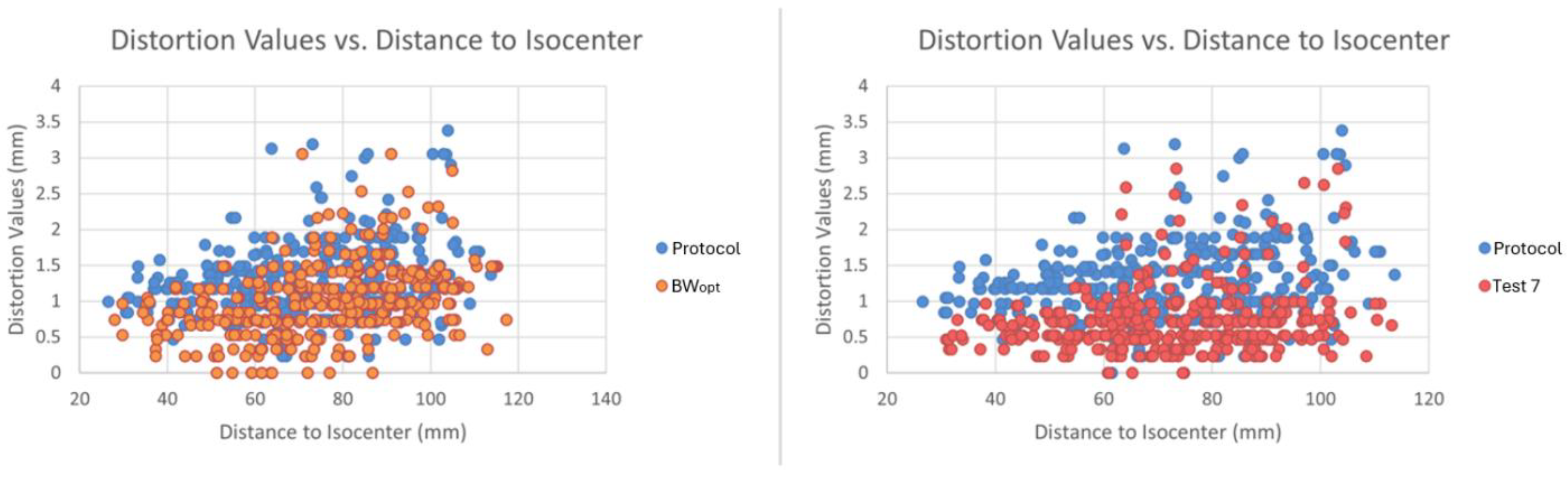
3.3. Optimization of MRI Image Acquisition

The global results for the tested sequences are shown in Table 2, and the distortion results for the detected inserts in each tested sequence are shown in Figure S5. To compare mean distortion values among multiple sequences, a one-way analysis of variance (ANOVA) test was used, and all mean distortion differences were considered significant within a significance level of α = 0.001. Of all of the sequences, the “BW_opt” and “Test 7” sequences showed great potential and will now be analyzed.

Table 2: Full color-coded results of sequence parameter tests, including the λ factor. To facilitate visual analysis, results better or worse than the mean by more than half a standard deviation are colored in green and magenta, respectively.

The “Test 2” sequence, which involved increasing the flip angle from 12° to 18°, showed the highest SNR and CNR, and the second largest λ factor. Although its higher SAR value is not ideal, this is not a limiting factor by itself, given that the value is still within the safety range [33]. This sequence actually performs better than the protocol one overall, with a similar imaging time, but the 9.22% distortion reduction is still not enough to place its mean distortion below 1 mm, as is the case for the “BW_opt” and “Test 7” sequences.

Indeed, the “BW_opt”, “Test 4”, and “Test 7” sequences were the only ones that achieved sub-millimetric mean distortion values (Table 2). Regarding “Test 4”, it had an imaging time of 18.30 min, which is a clinically unfeasible duration, given the current 4.80 min duration of the “Protocol” sequence. Thus, only the “BW_opt” and “Test 7” sequences were considered eligible as candidates for significant improvements over the “Protocol” sequence. Their comparison to the “Protocol” sequence, along with the distortion pattern relative to the distance from the isocenter for both sequences, can be seen in Figure 5.

However, comparing these two sequences in terms of the λ factor shows that the “BW_opt” sequence falls significantly short of the “Test 7” one (0.26 versus 1.00). Indeed, “Test 7” emerges as a clear improvement over the “Protocol” sequence. It is similar in acquisition time, SAR, SNR, CNR, and number of detected inserts while significantly lowering the mean and maximum distortion (by 44.27% and 15.65%, respectively). This test has the phase-encoding direction reversed to AP, rather than the PA direction used in the Protocol sequence.

Reversing the direction of phase encoding direction to AP direction reduced mean (1.301 mm to 0.725 mm, 44.27%) and maximum (reduced 15.65%) distortions, respectively, without any change in the acquisition time. We also found a significant geometric distortion reduction with increasing increased flip angles (12° to 18°), although this implied a higher SAR value, which was still within the safety limits.

4. Discussion

Phantoms used in medical imaging tests can have various characteristics, according to their purpose and design priorities. The phantom developed in this study was a cost-effective alternative to commercial phantoms used for geometric distortion measurements.

Out of the 840 inserts in this phantom, 746 were used, as the rest had significant air bubbles. The random distribution of these air-filled inserts did not compromise their spatial arrangement. The maximum number of inserts detected by the software was 439 for Test 4. This was due to various factors, such as the detection filters (Section 2.3) used to filter out inserts with air bubbles, which also filtered out some of the other inserts.

There was no theoretical a priori reason for the improvement brought upon by the “Test 7” sequence. In fact, while some distortion correction methods involve acquiring two sets of images with reversed phase-encoding directions [41], this sequence did not include the second set of images to avoid doubling the imaging time. Previous clinical studies have also found a difference in distortion when reversing the phase-encoding direction [42,43]. Susceptibility-based artifacts were suggested as the reason for the difference found in Kennis et al. [42].

In the present study, the interaction of the phase-encoding direction with the magnetic susceptibility artifact played a significant role. While gradient non-linearity artifacts are mostly independent of the phase-encoding direction, the susceptibility artifact shifts when the phase-encoding direction is reversed. When the susceptibility artifact aligns with gradient non-linearity, geometric distortion is maximized, and vice versa. This relationship follows the equation Δr ∝ Δχ B₀/G, where Δχ is the volume susceptibility difference between two materials, B₀ is the magnetic field strength, and G is the readout gradient strength [43]. The high susceptibility of gadolinium compared with other inorganic compounds [44], and the reversal of Δχ (and Δr) with a phase-encoding change, could explain the results. Another possibility has to do with metal artifacts (gadolinium is a metal), as they have been shown to depend on the phase-encoding direction in some cases [45].

One limitation of this study is that it was performed using a single MRI scanner (3T GE Signa MRI). While the principles that drove the improvement with AP readout should generalize in principle, as they are physics-based, it is true that factors such as the gradient nonlinearity are dependent on the scanner. Despite rigid MRI-to-CT registration, residual setup uncertainty may also persist, which we attempted to minimize by our registration and centroid-based matching approach.

Therefore, given that both the presented phantom design and open-source Python pipeline are scanner-agnostic, follow-up studies could verify the reproducibility of these results using different scanner models. The script can be easily adapted to other phantoms or scanners by suitably changing parameters such as the image grayscale thresholds, or insert size. We also hope that the $\lambda$ weighting factor introduced in this study can be used as a way to quantify and streamline comparisons between different sequences, even from different scanners.

Due to the fact that this study took into account several imaging parameters when optimizing the sequences, and not only the distortion minimization, we ensured that the resulting optimized sequence is not only the one which presents the lowest mean and maximum distortions, but is also clinically feasible and easily implementable. The clinical translation of these findings is only possible because of the fact that the gadolinium concentrations used were clinically realistic.

In the current reality of many medical physics departments in hospitals, image quality control is often constrained by aging scanners, limited staffing, and increased demands that limit the amount of time that can be devoted to the quality control of images and scanners. The observations in this study support the notion that sequences that were once optimized for stereotactic planning may be outdated despite ongoing vendor maintenance, while a zero-cost protocol adjustment may offer an immediately adoptable improvement for clinical practice.

SRS error budgets accumulate from multiple sources and, as reported in Table 2, the mean and maximum distortions obtained with the Protocol sequence are significantly higher than the acceptable limits published in Paulson et al. [2]. Reducing the mean geometric distortion by 0.6 mm, as was the case with Test 7, would be crucial even if the initial value was already below 1 mm, as there are other sources of uncertainty, particularly in humans, such as delineation uncertainty [46].

5. Conclusions

In this study, we showed that the systematic optimization of MRI acquisition parameters (particularly phase-encoding direction and flip angle) significantly reduced geometric distortions, which is crucial to stereotactic radiosurgery (SRS) planning. The integration of a custom-designed geometric phantom and automated Python-based quantification software enabled precise distortion analysis.

Implementation of a 1 mmol/L gadolinium filling solution added a level of clinic relevance with simulation of closely similar patient imaging scenarios. These improvements validate the potential for optimized MRI protocols to provide submillimetric accuracy, reliably enhancing MRI-guided target delineation in SRS workflows. Future studies can explore whether improvements with reverse encoding direction are specific to an MRI scanner model or represent a generalizable feature of this imaging modality.