PoMQ-ViT: Mixed-Precision Quantization Vision Transformer with Pareto Optimization
Abstract
1. Introduction
1.1. Research Background
1.2. Problem Statement
1.3. Research Objectives
1.4. Scope and Contributions of This Study
- Efficient Vision Transformer
- 2.
- Post Training-Quantization for Vision Transformer
1.5. Structure of the Paper
2. Materials and Methods
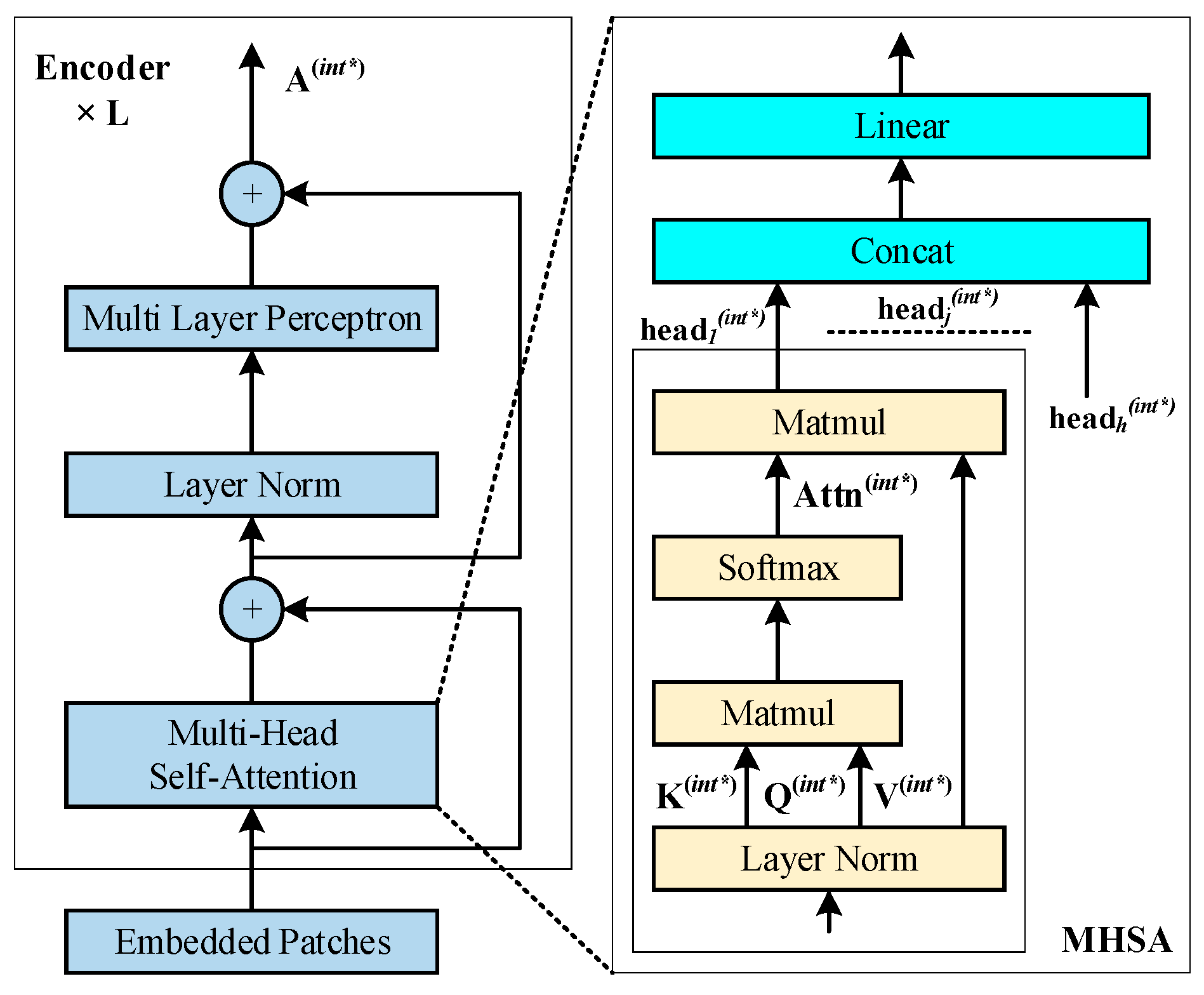
2.1. Standard ViT Computation Flow
2.2. Fully Quantized ViT Computation Flow
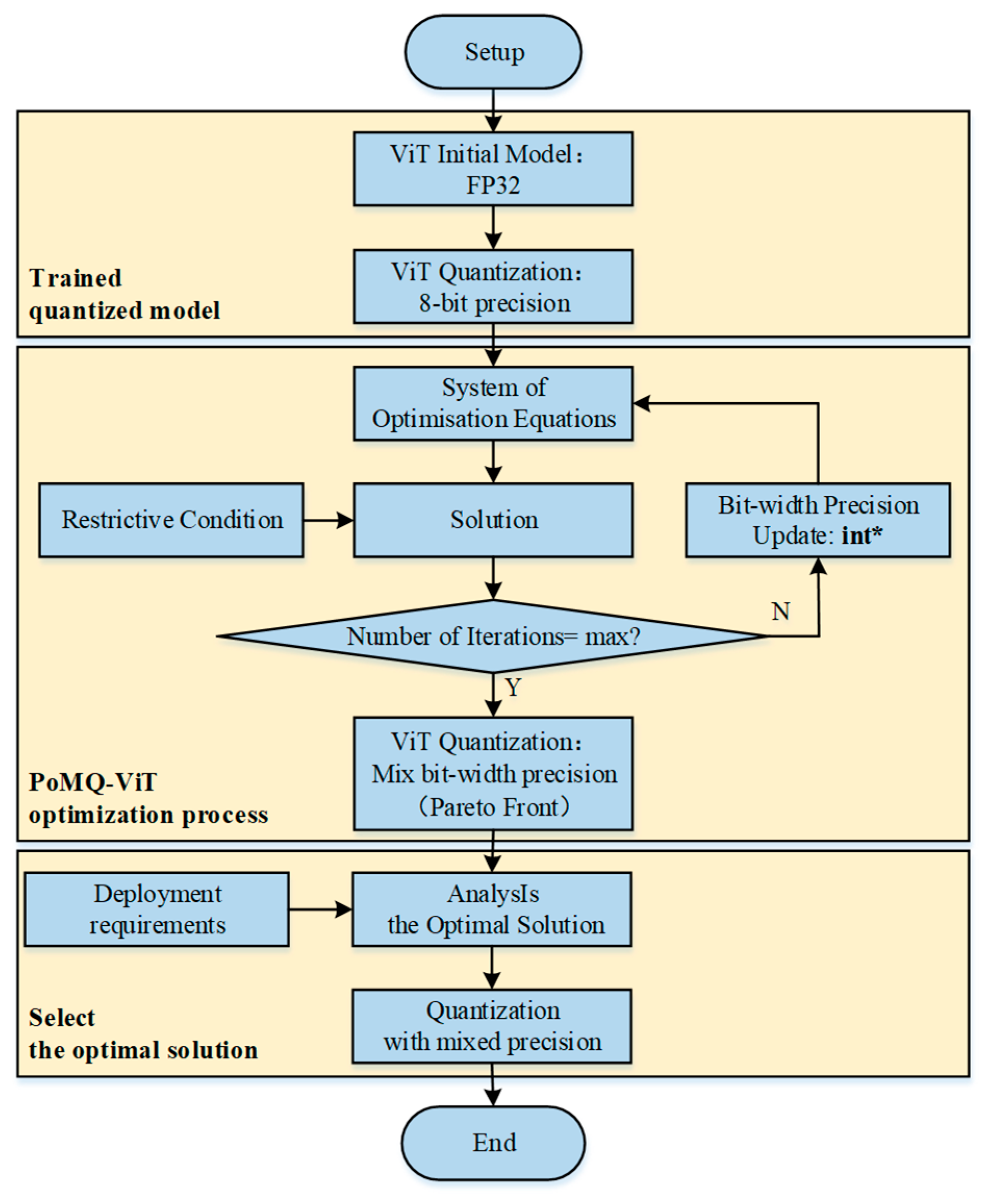
2.3. Methodology
- (1)
- Since the quantization research of FQ-ViT is established on the basis of 8-bit width precision, and it is obvious that 2-bit width precision quantization tends to cause significant precision loss, the selection of our quantization bit width precision is limited to 4-bit and 8-bit. The first constraint equation is that the weights , activation values , and attention values are allowed to have bit-width of either 4-bit or 8-bit.
- (2)
- Owing to the adoption of mixed-precision quantization in our approach, the quantization precision of the weights , activation values , and attention values cannot all be 4-bit, nor can they all be 8-bit.
- (3)
- To ensure the improvement in inference speed with mixed-precision quantization, let denote the inference time of the ViT model in floating-point precision. Then, the inference time constraint for mixed-precision ViT is:
- (4)
- One important purpose of model quantization is to reduce the size of the model, facilitating its deployment on mobile devices, edge devices, or devices with limited storage space. The size of the model after mixed-quantization needs to be considered. We introduce the function to represent the size of the mixed-quantized ViT model, and the function to represent the size of the fully quantized ViT model. Therefore, the constraint on model size is:
2.4. Experimental Setup and Measurement Protocols
- Operating System: Windows 11 Professional (22H2) (Microsoft Corporation, Redmond, WA, USA) with Windows Subsystem for Linux 2 (WSL2) (Microsoft Corporation, Redmond, WA, USA) enabled. This bridges Windows-based workflow advantages with Linux-optimized deep learning toolchains.
- Linux Distribution: Ubuntu 22.04 LTS (Canonical Ltd., London, UK) (within WSL2). Offers a stable open-source environment for deploying frameworks and profiling tools.
- Deep Learning Framework: PyTorch 1.12.1 (Meta Platforms, Inc., Menlo Park, CA, USA), paired with CUDA Toolkit 12.4 (NVIDIA, Santa Clara, CA, USA) (low-level GPU kernel programming) and cuDNN 8.9.2 (NVIDIA, Santa Clara, CA, USA) (optimized deep neural network primitives). These enable efficient model training and inference.
- Latency Profiling Tools: torch.cuda.Event, the Python 3.9.12 timeit (Python Software Foundation, Wilmington, DE, USA) module, and NVIDIA Nsight Systems 2023.3 (NVIDIA, Santa Clara, CA, USA) were employed for latency computation.
- Benchmark Dataset: ImageNet-1K (1.2 M training images, 50 K validation images; 1000 classes) (Princeton University, Princeton, NJ, USA). Serves as a standard for evaluating image classification performance.
- Model Sizes and Configurations: For each architecture, four sizes (tiny, small, base, large) are tested to analyze complexity-performance tradeoffs. Key structural parameters (critical for overhead calculation) are summarized in Table 1.
- Most of the official configurations were adopted in this study, including a learning rate of 1 × 10−5, a weight decay of 1 × 10−3, and the Adam optimizer with its first moment decay rate set to 0.9 and second moment decay rate set to 0.999. The batchsize for the validation set is typically set to a power of 2. In our current experimental environment, a batchsize greater than 50 exceeds the GPU memory capacity, causing an out-of-memory error. Therefore, we set the default batchsize for the validation set to 50.
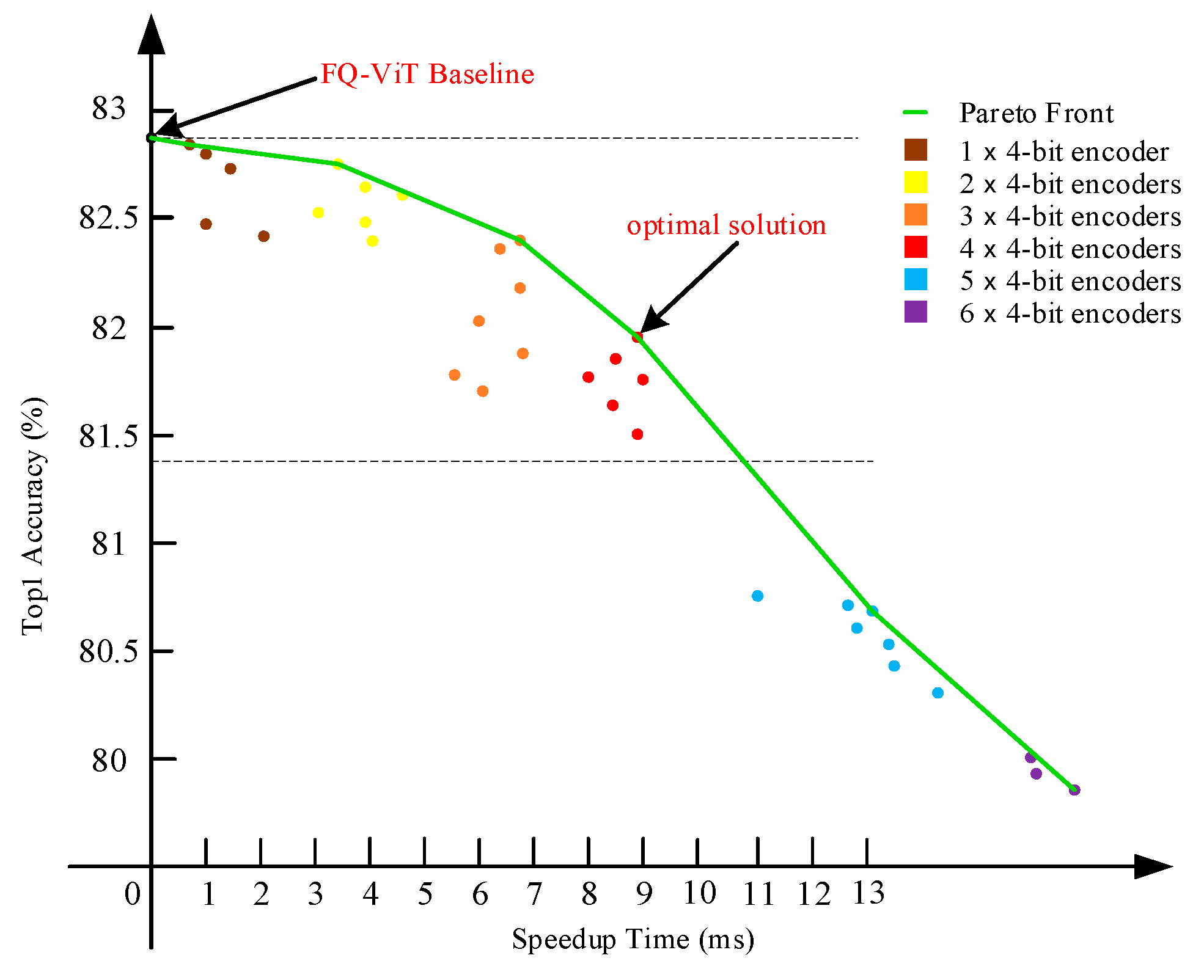
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ViT | Vision Transformer |
| PoMQ-ViT | Mixed-Precision Quantization Vision Transformer with Pareto Optimization |
| FQ-ViT | Post-Training Quantization for Fully Quantized Vision Transformer |
| PTF | the power-of-two factor |
| LIS | log-int-Softmax |
| SA | self-attention |
| FFN | feed-forward network |
| MHSA | multi-head self-attention |
| FP32 | Float Point 32-bit |
| DeiT | Data-efficient Image Transformer |
| Swin | Shifted Window Transformer |
| MinMax | Min-Max Algorithm |
| MatMul | Matrix Multiplication |
| NDS | Non-dominated Sorting |
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Houlsby, N. An image is worth 16x16 words: Transformers for image recognition at scale. Adv. Neural Inf. Process. Syst. 2021, 34. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training data-efficient image transformers distillation through attention. Int. Conf. Mach. Learn. 2021, 139, 10347–10357. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2020; Volume 12346, pp. 213–229. [Google Scholar] [CrossRef]
- Rekavandi, A.M.; Rashidi, S.; Boussaid, F.; Hoefs, S.; Akbas, E. Transformers in small object detection: A benchmark and survey of state-of-the-art. Pattern Recognit. 2023, 141, 109659. [Google Scholar] [CrossRef]
- Beal, J.; Kim, E.; Tzeng, E.; Park, D.H.; Zhai, A.; Kislyuk, D. Toward transformer-based object detection. arXiv 2020, arXiv:2012.09958. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, G.; Liu, Z.; Xiong, Z.; Hu, J. A deep learning algorithm for one-step contour aware nuclei segmentation of histopathology images. In Medical & Biological Engineering & Computing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 57, pp. 2027–2043. [Google Scholar] [CrossRef]
- Yigit, G. Vit-GAN: Image-to-Image Translation with Vision Transformes and Conditional GANS, Authorea Preprints; Springer: Berlin/Heidelberg, Germany, 2023; Available online: https://arxiv.org/abs/2110.09305 (accessed on 14 July 2025).
- Xi, H.; Qin, H.; Xiong, Z.; Zhang, J. Transformer-based conditional generative adversarial networks for image generation. In Proceedings of the International Symposium on Artificial Intelligence Control and Application Technology (AICAT 2022), Hangzhou, China, 6–8 May 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12305, pp. 250–255. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Y.; Guo, J.; Tu, Z.; Han, K.; Hu, H.; Tao, D. A survey on transformer compression. arXiv 2024, arXiv:2402.05964. [Google Scholar] [CrossRef]
- Zhuang, B.; Liu, J.; Pan, Z.; He, H.; Weng, Y.; Shen, C. A survey on efficient training of transformers. arXiv 2023, arXiv:2302.01107. [Google Scholar] [CrossRef]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar] [CrossRef]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized neural networks: Training neural networks with low precision weights and activations. J. Mach. Learn. Res. 2017, 18, 6869–6898. [Google Scholar]
- Liang, Y.; Ge, C.; Tong, Z.; Song, Y.; Wang, J.; Xie, P. Not all patches are what you need: Expediting vision transformers via token reorganizations. Adv. Neural Inf. Process. Syst. 2022, 35, 28096–28108. [Google Scholar]
- Xu, Y.; Zhang, Z.; Zhang, M.; Sheng, K.; Li, K.; Dong, W.; Zhang, L.; Xu, C.; Sun, X. Evo-vit: Slow-fast token evolution for dynamic vision transformer. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 2964–2972. Available online: https://arxiv.org/pdf/2108.01390 (accessed on 14 July 2025).
- Jiao, X.; Yin, Y.; Shang, L.; Jiang, X.; Chen, X.; Li, L.; Wang, F.; Liu, Q. Tinybert: Distilling bert for natural language understanding. arXiv 2019, arXiv:1909.10351. [Google Scholar]
- Wu, K.T.; Zhang, J.; Peng, H.; Liu, M.; Xiao, B.; Fu, J.; Tinyvit, L.Y. Fast Pretraining Distillation for Small Vision Transformers. Lect. Notes Comput. Sci. 2022, 13681. Available online: https://arxiv.org/pdf/2207.10666v1 (accessed on 14 July 2025).
- Yang, Z.; Li, Z.; Zeng, A.; Li, Z.; Yuan, C.; Li, Y. Vitkd: Practical guidelines for vit feature knowledge distillation. arXiv 2022, arXiv:2209.02432. [Google Scholar]
- Yang, H.; Yin, H.; Shen, M.; Molchanov, P.; Li, H.; Kautz, J. Global vision transformer pruning with hessian-aware saliency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18547–18557. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, T.; Sun, P.; Li, Z.; Zhou, S. Fq-vit: Post-training quantization for fully quantized vision transformer. arXiv 2021, arXiv:2111.13824. [Google Scholar]
- Li, Z.; Gu, Q. I-vit: Integer-only quantization for efficient vision transformer inference. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 17065–17075. [Google Scholar] [CrossRef]
- Esser, S.K.; McKinstry, J.L.; Bablani, D.; Appuswamy, R.; Modha, D.S. Learned step size quantization. arXiv 2019, arXiv:1902.08153. [Google Scholar]
- Li, Y.; Gong, R.; Tan, X.; Yang, Y.; Hu, P.; Zhang, Q.; Gu, S. Brecq: Pushing the limit of post-training quantization by block reconstruction. arXiv 2021, arXiv:2102.05426. [Google Scholar] [CrossRef]
- Wang, W.; Xie, E.; Li, X.; Fan, D.-P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 548–558. [Google Scholar] [CrossRef]
- Wang, W.; Xie, E.; Li, X.; Fan, D.-P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pvt v2: Improved baselines with pyramid vision transformer. Comput. Vis. Media 2022, 8, 415–424. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [CrossRef]
- Pan, Z.; Cai, J.; Zhuang, B. Fast vision transformers with hilo attention. Adv. Neural Inf. Process. Syst. 2022, 35, 14541–14554. [Google Scholar]
- Mehta, S.; Rastegari, M. Separable self-attention for mobile vision transformers. arXiv 2022, arXiv:2206.02680. [Google Scholar] [CrossRef]
- Luo, G.; Zhou, Y.; Sun, X.; Wang, Y.; Cao, L.; Wu, Y.; Huang, F.; Ji, R. Towards lightweight transformer via group-wise transformation for vision-and-language tasks. IEEE Trans. Image Process. 2022, 31, 3386–3398. [Google Scholar] [CrossRef]
- Maaz, M.; Shaker, A.; Cholakkal, H.; Khan, S.; Zamir, S.W.; Anwer, R.M.; Shahbaz Khan, F. Edgenext: Efficiently amalgamated cnn-transformer architecture for mobile vision applications. Eur. Conf. Comput. Vis. 2022, 3–20. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Y.; Zhang, J.; Zhang, H.; Wei, Z.; Lin, Z.; Yuille, A. Lite vision transformer with enhanced self-attention. In Proceedings of the IEEE/CVF International Conference on Computer Vision, New Orleans, LA, USA, 18–24 June 2022; pp. 11998–12008. [Google Scholar] [CrossRef]
- He, Y.; Lou, Z.; Zhang, L.; Liu, J.; Wu, W.; Zhou, H.; Zhuang, B. Bivit: Extremely compressed binary vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 5651–5663. Available online: https://arxiv.org/pdf/2211.07091 (accessed on 14 July 2025).
- Li, Z.; Xiao, J.; Yang, L.; Gu, Q. Repq-vit: Scale reparameterization for post-training quantization of vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 17227–17236. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Dong, Z.; Keutzer, K.; Du, L.; Zhang, S. Noisyquant: Noisy bias-enhanced post-training activation quantization for vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 20321–20330. Available online: https://arxiv.org/abs/2211.16056 (accessed on 14 July 2025).
- Nagel, M.; Amjad, R.A.; Van Baalen, M.; Louizos, C.; Blankevoort, T. Up or down? adaptive rounding for post-training quantization. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 7197–7206. Available online: https://proceedings.mlr.press/v119/nagel20a.html (accessed on 14 July 2025).
- Choukroun, Y.; Kravchik, E.; Yang, F.; Kisilev, P. Low-bit quantization of neural networks for efficient inference. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3009–3018. [Google Scholar] [CrossRef]
- Ngatchou, P.; Zarei, A.; El-Sharkawi, A. Pareto multi objective optimization. In Proceedings of the 13th International Conference on, Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005; pp. 84–91. [Google Scholar]
- Bechikh, S.; Datta, R.; Gupta, A. Recent Advances in Evolutionary Multi-Objective Optimization; Springer: Cham, Switzerland, 2017; pp. 31–70. ISBN 978-3-319-42978-6. [Google Scholar]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comp arison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. Available online: https://arxiv.org/abs/2103.14030 (accessed on 14 July 2025).
| Model Size | Encoders | SA Heads | Embedding Dimension |
|---|---|---|---|
| base | 12 | 12 | 768 |
| tiny | 12 | 6 | 192 |
| small | 12 | 3 | 384 |
| large | 24 | 16 | 1024 |
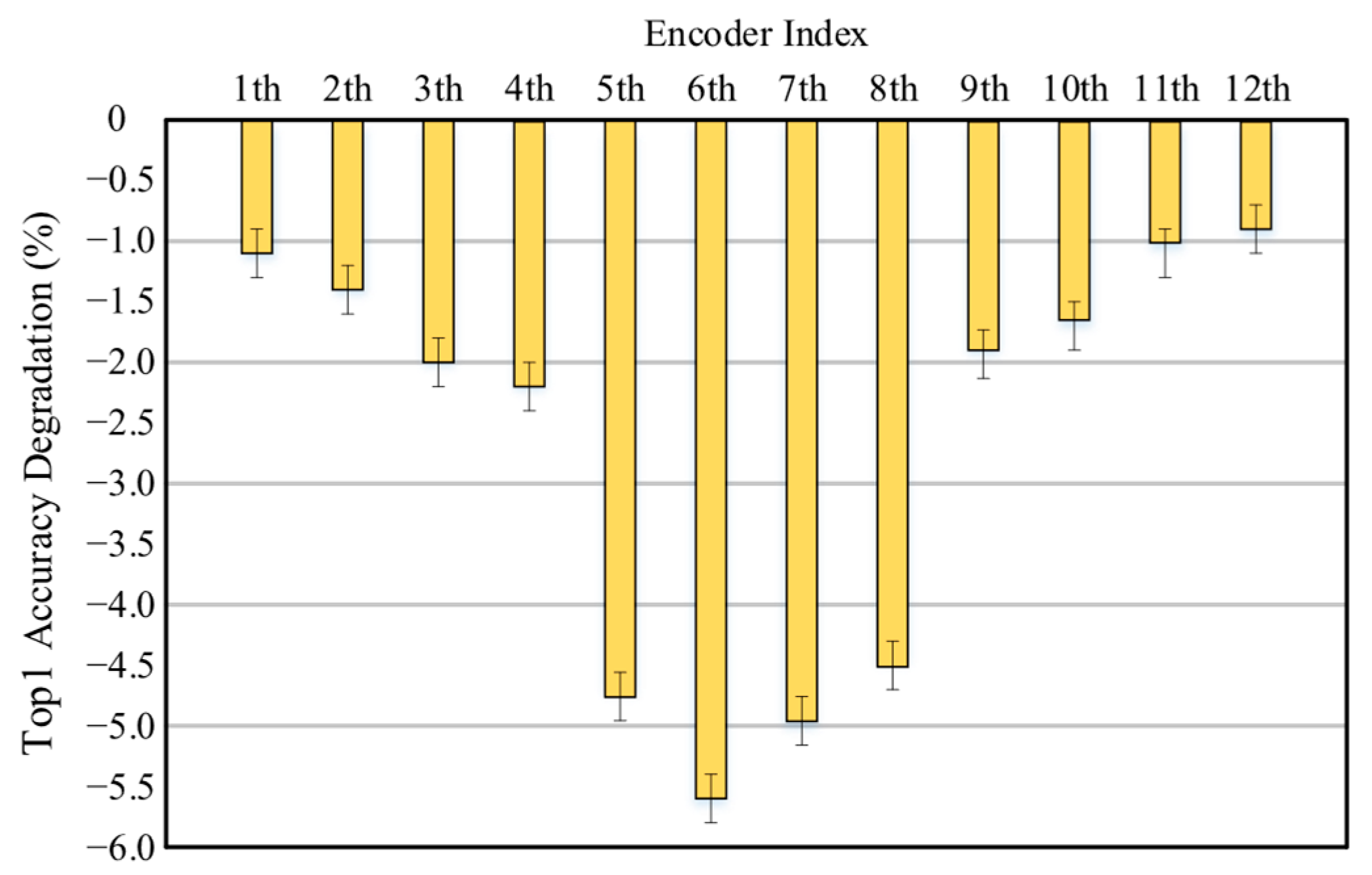
| Encoder | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bit-width | 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 4 | 4 |
| Model | 8-Bit | Top-1 (%) Stochastic | PoMQ | 8-Bit | Time (ms) Stochastic | PoMQ | 8-Bit | Size (M) Stochastic | PoMQ |
|---|---|---|---|---|---|---|---|---|---|
| DeiT_base | 80.662 | 78.231 | 79.764 | 449.394 | 440.56 | 439.267 | 338 | 267 | 267 |
| DeiT_small | 78.36 | 77.23 | 77.326 | 224.797 | 210.64 | 200.998 | 86 | 70 | 70 |
| DeiT_tiny | 70.036 | 68.733 | 68.866 | 139.173 | 110.892 | 101.458 | 22 | 20 | 20 |
| Swin_base | 82.554 | 80.223 | 81.472 | 618.859 | 611.90 | 610.023 | 344 | 272 | 272 |
| Swin_small | 82.172 | 80.568 | 80.86 | 458.221 | 447.776 | 442.395 | 195 | 162 | 162 |
| Swin_tiny | 80.218 | 78.650 | 78.698 | 286.715 | 268.554 | 261.898 | 111 | 94 | 94 |
| ViT_base | 82.860 | 81.840 | 81.993 | 450.467 | 443.568 | 441.479 | 338 | 267 | 267 |
| ViT_large | 85.004 | 83.998 | 84.35 | 1229.861 | 1225.041 | 1223.621 | 1116 | 883 | 883 |
| Iterations | 2 | 5 | 10 | 20 | |
|---|---|---|---|---|---|
| Top-1 (%) | |||||
| DeiT_base | 77.981 | 79.002 | 79.764 | 79.803 | |
| DeiT_small | 75.005 | 76.997 | 77.326 | 77.369 | |
| DeiT_tiny | 65.008 | 67.834 | 68.866 | 69.002 | |
| Swin_base | 80.033 | 81.006 | 81.472 | 81.501 | |
| Swin_small | 79.512 | 80.504 | 80.86 | 80.905 | |
| Swin_tiny | 76.827 | 78.509 | 78.698 | 78.893 | |
| ViT_base | 80.274 | 81.506 | 81.993 | 82.031 | |
| ViT_large | 83.106 | 84.008 | 84.35 | 84.301 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhao, Z. PoMQ-ViT: Mixed-Precision Quantization Vision Transformer with Pareto Optimization. Appl. Sci. 2025, 15, 9856. https://doi.org/10.3390/app15189856
Wu Z, Zhao Z. PoMQ-ViT: Mixed-Precision Quantization Vision Transformer with Pareto Optimization. Applied Sciences. 2025; 15(18):9856. https://doi.org/10.3390/app15189856
Chicago/Turabian StyleWu, Zhiqiang, and Zhong Zhao. 2025. "PoMQ-ViT: Mixed-Precision Quantization Vision Transformer with Pareto Optimization" Applied Sciences 15, no. 18: 9856. https://doi.org/10.3390/app15189856
APA StyleWu, Z., & Zhao, Z. (2025). PoMQ-ViT: Mixed-Precision Quantization Vision Transformer with Pareto Optimization. Applied Sciences, 15(18), 9856. https://doi.org/10.3390/app15189856






