Solving Construction Site Layout Planning as a Quadratic Assignment Problem Using the Advanced Jaya Algorithm

Abstract

Construction site layout planning (CSLP) plays a pivotal role in determining the overall efficiency and cost-effectiveness of construction projects. Material handling operations, which constitute a significant portion of indirect project costs, heavily depend on the spatial arrangement of temporary facilities such as site offices, storage yards, and equipment zones. Poorly planned layouts can lead to excessive travel distances, increased material handling times, and operational delays, all of which contribute to inflated costs and reduced productivity. Therefore, optimizing the layout of construction sites to minimize transportation distances and enhance workflow is a critical task for project managers, contractors, and other stakeholders. The challenge in CSLP lies in the complexity of simultaneously satisfying multiple, often conflicting, requirements such as space constraints, safety regulations, and functional proximities. This complexity is compounded by the dynamic nature of construction activities and the presence of numerous facilities to be allocated within limited and irregularly shaped site boundaries. Mathematically, this problem can be formulated as a Quadratic Assignment Problem (QAP), a well-known NP-hard combinatorial optimization problem. The QAP seeks to assign a set of facilities to specific locations in a manner that minimizes the total cost, typically modeled as the sum of products of flows (e.g., material movement) and distances between assigned locations. However, due to the computational complexity of QAP, exact solutions become impractical for medium to large-scale site layouts. In recent years, metaheuristic algorithms have gained traction for effectively tackling such complex optimization problems. Among these, the Advanced Jaya Algorithm (A-JA), a recent population-based metaheuristic, stands out for its simplicity, parameter-free nature, and robust search capabilities. This study applies the A-JA to solve the CSLP modeled as a QAP, aiming to minimize the total weighted travel distance of material handling within the site. The algorithm’s performance is validated through two realistic case studies, showcasing its strong search capabilities and competitive results compared to traditional optimization methods. This promising approach offers a valuable decision-support tool for construction managers seeking to enhance site operational efficiency.

1. Introduction

Material handling constitutes a fundamental activity within the construction industry, playing a critical role in overall project performance. The strategic placement of temporary facilities on construction sites considerably influences both the cost and duration associated with material handling operations. In recent decades, significant research efforts have focused on developing effective methodologies to address construction management optimization problems, among which Construction Site Layout Planning (CSLP) stands out due to its practical importance. CSLP aims to arrange temporary facilities on construction sites in a manner that minimizes transportation distances while satisfying safety and operational constraints. Given its combinatorial complexity, CSLP can be formulated as a Quadratic Assignment Problem (QAP). These types of problems are highly complex combinatorial optimization problems that aim to minimize quadratic cost functions based on pairwise interactions, such as flow and distance. Due to their NP-hard nature, they are challenging to solve as the solution space is vast and prone to trapping algorithms in local minima.

The layout of facilities at the construction site level is a multi-faceted challenge that necessitates consideration of diverse factors, such as spatial constraints, safety requirements, and workflow efficiency. Effective site layout planning not only enhances productivity but also contributes to improved safety conditions. This has become increasingly important as the competitive market environment compels construction companies to optimize their site management practices to boost profitability and operational efficiency.

Two main approaches exist for solving CSLP: exact methods suitable for smaller-scale problems, and metaheuristic algorithms that efficiently explore large, complex search spaces. Metaheuristics have gained widespread application in recent years due to their flexibility and ability to generate near-optimal solutions without requiring gradient information of the objective function. Algorithms inspired by natural, social, or physical phenomena (such as Genetic Algorithms, Particle Swarm Optimization, and others) have been employed for CSLP.

Key to the effectiveness of metaheuristics are the balance between exploration and exploitation mechanisms. Exploration enables the algorithm to investigate diverse regions of the solution space, preventing premature convergence, while exploitation intensifies the search around promising solutions to enhance convergence accuracy. This balance is crucial in tackling the complex and multidimensional nature of CSLP.

Prior studies have employed various metaheuristics to address CSLP. For example, Li and Love (1998) utilized a Genetic Algorithm (GA) to assign facilities to pre-defined locations, assuming rectangular and sufficiently large areas for each facility [1]. Gharaie et al. (2006) applied Ant Colony Optimization (ACO) [2], while Kaveh et al. (2012) leveraged an adapted Harmony Search Algorithm [3]. More recently, Colliding Bodies Optimization (CBO) and its enhanced version (ECBO) were introduced by Kaveh et al. (2016) to solve practical layout problems [4].

When recent studies are examined, it is evident that researchers have maintained a strong and active interest in the topic. Kaveh and Dadras Eslamlou (2020) focused on construction site layout optimization by developing multi-objective versions of the CBO and ECBO algorithms, which effectively identified optimal Pareto fronts in a case study [5]. Kaveh and Vazirinia (2020) addressed construction site layout optimization by introducing an enhanced Sine Cosine Algorithm that integrates a memory mechanism for best-found solutions and a harmony search-based local search operator. The hybrid approach helps the algorithm escape local optima, and experimental results confirm that incorporating local search significantly improves overall performance [6]. Jaafar et al. (2021) introduced a dynamic model for optimizing construction site layout by minimizing both cost and risk, taking into account factors like material transport, equipment usage, and facility relocation [7]. The model, implemented using the branch-and-bound method, was validated through a real case study, confirming its effectiveness in reflecting real construction site dynamics.

Gadiri et al. (2022) investigated construction site layout safety optimization by introducing a multi-objective Firefly Algorithm [8]. The proposed model was designed using both analytical and numerical methods to enhance safety in site planning. Tsegay et al. (2023) reviewed mathematical optimization methods for CSLP, especially in inner-city projects with limited space [9]. The study highlighted the dominance of metaheuristic approaches and proposed a new framework to better integrate crew movement and safety into CSLP models. Hojati et al. (2024) proposed a chaotic hybrid algorithm, combining Ant Lion and Aquila Optimizers, which demonstrates superior accuracy and faster convergence in construction management tasks compared to existing methods [10]. Kaveh et al. (2024), three real-world construction site layout problems were solved using physics-inspired metaheuristic algorithms [11]. The findings reveal that all tested methods effectively minimized layout costs, demonstrating strong optimization capabilities. Javaherikhah et al. (2025) develops a comprehensive framework for optimizing construction site layout in developing countries, integrating regional constraints with global best practices by identifying, analyzing, and prioritizing critical factors to improve safety and cost efficiency [12]. Tan et al. (2025) present a PCC yard layout planning model that incorporates hoisting efficiency and safety, using a non-centralized yard division method and surplus rectangle algorithm, and demonstrates through case studies that it improves construction site safety and efficiency [13].

Building on this foundation, the present study adopts the Advanced Jaya Algorithm (A-JA) which is a parameter-free, population-based metaheuristic to address the CSLP with the aim of achieving improved solution quality and computational efficiency. The effectiveness of the A-JA is demonstrated through application to realistic construction site scenarios. The remainder of this study is organized as follows. Section 2 introduces the proposed methodology, Section 3 presents the mathematical formulation of the problem, and Section 4 provides the solutions and results of two case studies. Section 5 presents the limitations of the study and outlines potential directions for future research. Finally, Section 6 concludes the paper.

2. Method

2.1. Overview of the Jaya Algorithm and Advanced Jaya Algorithm

The Jaya Algorithm (JA) was developed as a population-based metaheuristic optimization technique by Rao (2016) [14]. It is characterized by its simplicity and effectiveness, operating without algorithm-specific control parameters, which distinguishes it from many conventional metaheuristics. The core principle of the JA is to iteratively improve candidate solutions by moving them closer to the best solution and away from the worst solution within the current population. This strategy ensures a steady convergence toward global optima without the complexity of tuning multiple algorithm parameters.

Despite its promising performance, the original JA has limitations in balancing exploration and exploitation, especially when dealing with highly complex or large-scale problems. To address these challenges, Kaveh and Zaerreza (2022) proposed the Improved Shuffled Jaya Algorithm (IS-Jaya) to enhance population diversity and improve the algorithm’s ability to escape local optima [15]. In a similar effort, Pham and Nguyen (2023) suggested integrating an enhanced Jaya-based algorithm with a dimension reduction technique [16].

Building on these advancements, Albayrak (2023) introduced a further refined version called the Advanced Jaya Algorithm (A-JA), incorporating necessary improvements to the original method [17]. The mathematical formulation is given in Equation (1), where the indices p, q, and r refer to the iteration number, variable number, and candidate solution, respectively. $O_{p,q,r}$ denotes the q-th variable of the r-th candidate in the p-th iteration, while ${\alpha }_{p,q,1}$ and ${\alpha }_{p,q,2}$ are random numbers between 0 and 1.

$$O_{p+1,q,r}=O_{p,q,r}+{\alpha }_{p,q,1}\left(O_{p,q,best\left(R1\right)}-abs\left(O_{p,q,r}\right)\right)-{\alpha }_{p,q,2}\left(O_{p,q,worst}-abs\left(O_{p,q,r}\right)\right)$$

(1)

RI is a randomly selected integer, either 1 or 2, determined according to Equation (2). Extensive testing has shown that setting RI to a value between 1 and 2 yields optimal performance. Rather than being provided as an input, RI is generated internally by the algorithm using:

RI = round [1 + rand(0,1){1–2}]

(2)

In the Equation (1), Best(1) and Best(2) refer to the candidates with the lowest and second-lowest objective values in the current population. The random scaling factors encourage exploration, while using the absolute value of the current variable helps the algorithm to effectively explore the search space. Promising solutions from each iteration are stored and used to guide the search in the following iterations. The approach gradually moves the population toward better solutions while steering away from the worst, and the stochastic element RI promotes comprehensive space exploration.

The overall algorithmic flow proceeds as follows (Algorithm 1):

Algorithm 1. Pseudo code of A-JA

Begin Initialize all parameters Generate initial population with given problem dimensions Evaluate objective function values for all individuals Identify best_solution (lowest objective value) and worst_solution (highest objective value) While termination_criterion is not satisfied do For each individual in population except best and worst Update individual using A-JA updating rule based on best_solution and worst_solution Decode updated individual into a valid permutation using random-keys Apply swap-based repair to correct any repeated or missing assignments Enforce fixed facilities by assigning them to predetermined locations End For For each individual in population If acceptance criteria is satisfied Replace current solution with updated solution Else Retain current solution End If End For For each individual in population Apply swap-based local search: For each pair of facilities (i, j): Swap i and j If objective improves: Keep swap Else: Revert swap End If End For Ensure feasibility is maintained after local search End For Re-evaluate objective functions for all individuals Update best_solution and worst_solution accordingly End While Return best_solution as the optimal solution End

As the CSLP is formulated as a minimization problem (see Equation (3)), the A-JA implementation treats lower objective values as better. Therefore, in the algorithm above, best_solution corresponds to the candidate with the lowest objective value and worst_solution corresponds to the candidate with the highest objective value.

The Advanced Jaya Algorithm (A-JA) has been proposed as an enhanced variant that incorporates adaptive mechanisms and hybrid strategies to improve search capability and convergence speed [17].

The A-JA integrates dynamic parameter adjustments and additional local search operators, enabling a more effective search of the solution space by intensifying exploitation around promising regions and diversifying exploration when stagnation is detected. Unlike many metaheuristics that rely on multiple control parameters, the A-JA retains the simplicity of the original JA while enhancing robustness and flexibility.

In recent applications, the A-JA has demonstrated superior performance across various engineering optimization problems, including structural design, scheduling, and resource allocation [18]. Its ability to efficiently handle high-dimensional, nonlinear, and constrained problems makes it particularly suitable for addressing the complexities inherent in CSLP.

This study leverages the capabilities of the A-JA to optimize facility placements on construction sites, aiming to minimize material transportation distances and overall handling costs while satisfying spatial and safety constraints. The parameter-free nature of the A-JA facilitates straightforward implementation and adaptation to diverse problem settings, thereby offering a practical and effective solution methodology for CSLP.

2.2. Permutation Encoding and Decoding

Since the Quadratic Assignment Problem (QAP) is defined on permutations of facilities to locations, the continuous update rule of the A-JA requires decoding to obtain valid assignments. A random-keys representation is adopted, where each candidate solution is a real-valued vector and facilities are assigned to locations by sorting the vector values in ascending order. The rank of each element determines the final permutation, ensuring that each facility is mapped to exactly one location, while any repeated or missing assignments are corrected via swap-based repair. Fixed facilities, such as the main access and logistics gates in Case Study 1, are directly assigned to their predetermined locations, guaranteeing feasibility.

After decoding, a swap-based local search is applied to each candidate solution. Pairs of facilities are exchanged iteratively, and swaps that improve the objective function are retained. This procedure further refines solutions and ensures that all assignments remain valid throughout the optimization process.

3. Mathematical Model

In simple terms, the Quadratic Assignment Problem (QAP) involves assigning n facilities to n unique locations. Each facility i interacts with facility j through a flow value denoted by f_ij, while the distance between location k and l is represented by d_kl. The goal is to determine an assignment of facilities to locations that minimizes the overall cost, calculated as the sum of the products of flow and corresponding distances. For instance, given two matrices (one for flow and one for distances) the objective is to find an optimal pairing between facilities and locations that results in the lowest total transportation or interaction cost.

An alternative representation of the QAP is known as the Quadratic 0-1 Formulation, initially introduced by Koopmans and Beckmann (1957) [19]. In this approach, the problem is modeled using an n×n permutation matrix X = [x_ij], where each element x_ij takes a binary value (0 or 1) to indicate whether facility i is assigned to location j. This binary matrix encodes permutations π∈S_n in a 0-1 format. For the matrix to be valid as a permutation matrix, it must satisfy three specific conditions.

For CSLP, the aim of the mathematical model is to reduce the overall travel distance that site personnel must cover while moving between different facilities. The total travel distance is computed using Equation (3).

$$MinD=\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^n\sum _{l=1}^n{x}_{ik}{x}_{jl}{f}_{ij}{d}_{kl}$$

(3)

s.t.

$$\sum _{i=1}^n{x}_{ij}=1$$

(4)

j = 1,…,n

$$\sum _{j=1}^n{x}_{ij}=1$$

(5)

i = 1,…,n

$$X_{ij}\in \{0,1\}$$

(6)

i,j = 1,…,n

To incorporate fixed facilities, additional equality constraints are introduced:

x{i,j} = 1, for all (i,j) ∈ F

(7)

where F denotes the set of fixed facility–location pairs (e.g., main gate at location 11, logistics gate at location 8 in Case Study 1). These equalities guarantee that designated facilities remain anchored to their assigned positions while the optimization proceeds for the remaining facilities.

In Equations (3)–(7), n denotes the total number of facilities involved in the layout planning process. The binary variable x_il is equal to 1 if facility i is allocated to location l; otherwise, it takes a value of 0. The same logic applies to x_jk, indicating the assignment of facility j to location k. The parameter f_ij reflects the average number of daily movements between facilities i and j by site personnel, while d_kl specifies the physical distance separating locations k and l. As a result, the objective function D computes the cumulative daily distance travelled across the site.

Although relocation costs and handling difficulty levels are introduced in Case Study 2, they are not explicitly included in the current objective function (Equation (3)). In this study, the CSLP is modeled as a static QAP to demonstrate the effectiveness of the A-JA on the classical flow–distance formulation. A full multi-period extension that integrates relocation penalties and time-dependent transition costs is an important direction for future research.

The present study adopts the classical flow–distance QAP formulation with one-to-one facility-to-location assignments. This simplified model does not explicitly incorporate forbidden zones, adjacency or separation requirements, safety buffers, or irregular site geometries. Such constraints are highly relevant in practice but are beyond the scope of this initial investigation. Integrating them into the optimization framework remains a valuable topic for future research.

4. Optimization

4.1. Case Study 1

Efficient planning of construction site layouts remains a critical challenge for stakeholders including clients, contractors, and design professionals. The primary objective is to strategically position essential temporary facilities (such as site offices, storage areas, and accommodation units) to facilitate streamlined movement of materials, labor, and information across the site. An optimized spatial arrangement not only improves operational safety and productivity but also minimizes transportation costs and mitigates delays or congestion in the flow of equipment and construction resources, which is particularly vital in large-scale developments [20].

A practical layout optimization scenario is explored using data adapted from a medium-scale construction project detailed. The analysis involves allocating 11 separate facilities to 11 predefined locations on the site, with the goal of identifying the most efficient spatial configuration. The selected facilities include for this study:

• Site management office
• Formwork area
• Worker housing area
• Material storage A
• Material storage B
• Carpentry unit
• Rebar workshop
• Secondary access gate
• Utilities control room
• Concrete mixing unit
• Main access gate

In this analysis, the layout of the construction site is organized based on two fundamental assumptions. First, each facility is eligible to occupy any of the specified available locations on the site. Second, the main entrance and the logistics access gate are considered fixed elements, and their positions remain unchanged throughout the optimization process.

The spatial distances between all predefined locations are systematically presented in

Table 1. Site location distances.

		Facility Locations
		1	2	3	4	5	6	7	8	9	10	11
Facility locations	1	0	13	22	39	50	33	51	45	29	37	18
	2	13	0	11	23	30	20	28	51	44	40	31
	3	22	11	0	14	19	21	23	30	45	48	49
	4	39	23	14	0	9	12	17	20	37	42	48
	5	50	30	19	9	0	5	8	19	27	35	44
	6	33	20	21	12	5	0	7	16	28	34	41
	7	51	28	23	17	8	7	0	12	21	38	42
	8	45	51	30	20	19	16	12	0	24	33	39
	9	29	44	45	37	27	28	21	24	0	6	12
	10	37	40	48	42	35	34	38	33	6	0	17
	11	18	31	49	48	44	41	42	39	12	17	0

. Since the frequency of interactions between facilities significantly influences layout efficiency, the average number of daily transfers between each pair of facilities is compiled in

Table 2. Daily transfers.

		Facility Locations
		1	2	3	4	5	6	7	8	9	10	11
Facility locations	1	0	3	1	1	2	2	3	2	1	7	2
	2	3	0	1	6	2	1	8	6	4	1	6
	3	1	1	0	5	2	5	8	3	4	7	6
	4	1	6	5	0	6	6	9	2	7	4	3
	5	2	2	2	6	0	1	2	2	4	3	5
	6	2	1	5	6	1	0	6	4	6	3	2
	7	3	8	8	9	2	6	0	4	5	2	2
	8	2	6	3	2	2	4	4	0	9	4	8
	9	1	4	4	7	4	6	5	9	0	7	4
	10	7	1	7	4	3	3	2	4	7	0	6
	11	2	6	6	3	5	2	2	8	4	6	0

.

4.2. Results of Case Study 1

The case study was solved using four additional algorithms alongside the A-JA, for comparison purposes. These algorithms include the Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Nondominated Sorting Genetic Algorithm II (NSGA-II). Their parameters are presented in

Table 3. Algorithm settings used in experiments.

Algorithm	Encoding/Operators	Population Size	Parameters	Stopping Criterion	Runs
A-JA	Random keys + swap repair	50	Parameter-free	500 iterations/30 runs	30
GA	Order crossover, swap mutation	50	Crossover prob = 0.8, Mutation prob = 0.2, Tournament sel. size = 3	500 iterations/30 runs	30
PSO	Permutation-based encoding via swap sequences	50	c1 = 2, c2 = 2, inertia weight decreasing 0.9→0.1	500 iterations/30 runs	30
ACO	Permutation-based pheromone update	50	Evaporation = 0.1, α = 1, β = 2	500 iterations/30 runs	30
NSGA-II	Order crossover, swap mutation, binary tournament with crowding distance	50	Crossover prob = 0.9, Mutation prob = 0.1	500 iterations/30 runs	30

. To ensure statistical robustness, the scenario was analyzed through 30 independent optimization trials, each comprising 500 iterations. The outcomes of these runs are presented in

Table 4. Comparison of the results for Case Study 1.

	Algorithms
	A-JA	GA	PSO	ACO	NSGA-II
Best	11,245	11,460	11,422	11,405	11,298
Average	11,280	11,918	11,761	11,903	11,867
Worst	12,104	12,675	12,452	12,544	12,550
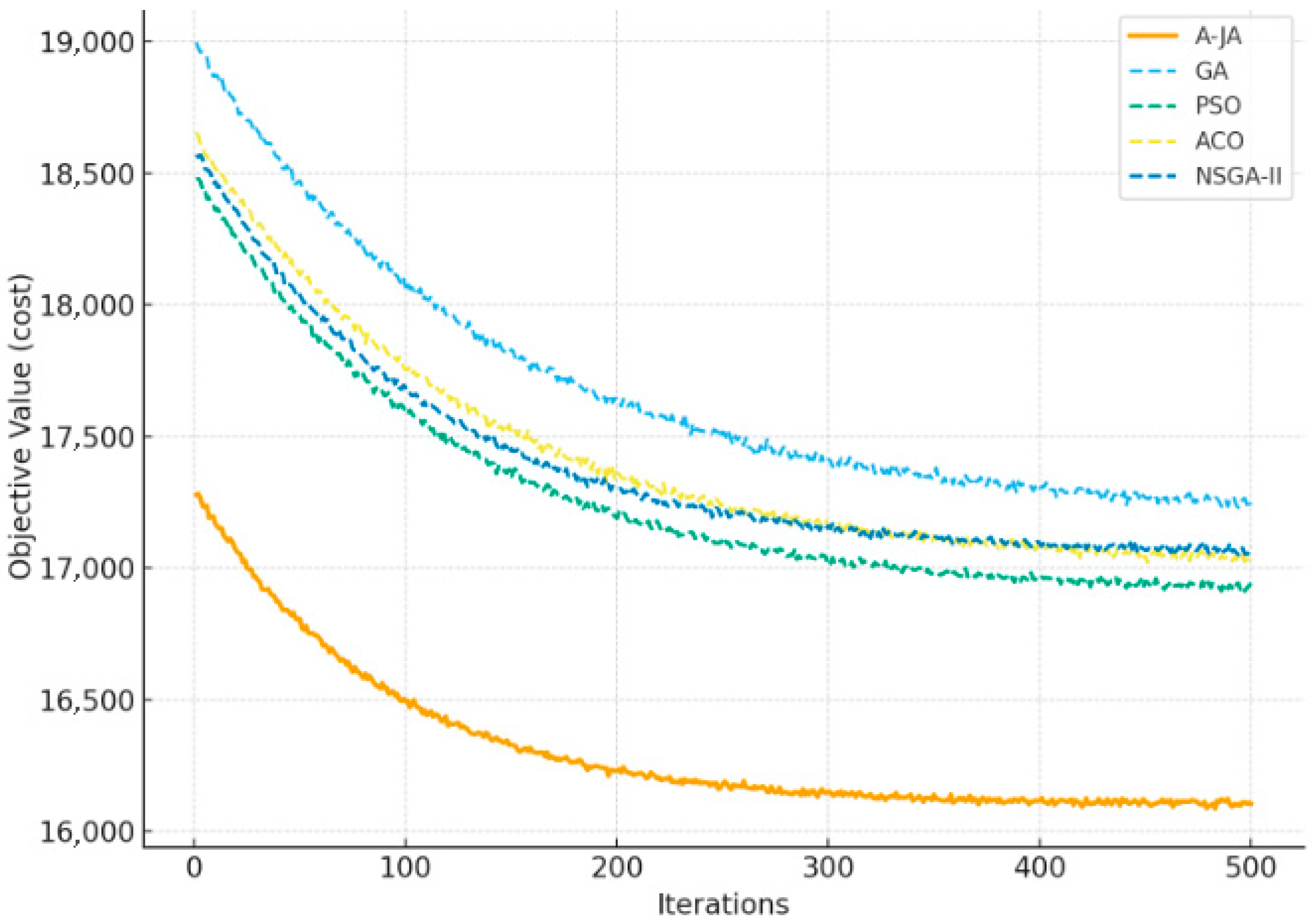
STD	52.4	119.6	96.9	110.6	116.7

. As shown, the proposed approach (A-JA) yields an average objective value of 11,280, with the worst performance recorded at 12,104 and a standard deviation of 52.4. These results indicate a clear advantage over the competing algorithms. Furthermore, the best result achieved (11,245) surpasses those produced by all other methods examined in this study. This confirms the proposed algorithm’s ability to consistently generate high-quality solutions with superior reliability.

To provide an intuitive comparison of convergence behavior, Figure 1 shows the average best-so-far objective values over 30 independent runs for Case Study 1. It can be seen that the A-JA converges more rapidly toward high-quality solutions than GA, PSO, ACO, and NSGA-II.

4.3. Case Study 2

In large-scale infrastructure projects characterized by wide geographical dispersion and prolonged execution periods (such as highway construction) the strategic relocation of temporary facilities is essential for optimizing logistics and minimizing transportation costs. This case study examines a project marked by high spatial dispersion and continuous operational changes.

The execution strategy involves assigning 10 critical temporary facilities to one of 11 predefined site locations.

Table 5. Facilities and costs.

Facilities	Establishment Cost	Mobilization Cost
1. Excavation zone *	85,000	0
2. Aggregate crushing unit	120,000	30,000
3. Concrete production	150,000	30,000
4. Bituminous mixing facility	120,000	30,000
5. Concrete and aggregate storage	15,000	6000
6. Asphalt and raw material storage	15,000	7000
7. Subgrade material storage	15,000	4000
8. Operational sector A *	0	0
9. Operational sector B *	0	0
10. Operational sector C *	0	0
11. Bitumen storage area	10,000	0
12. Administrative field office	20,000	0
13. Labor sheds	20,000	0
14. Cement storage warehouse	10,000	0

* Fixed facility.

lists all relevant facilities, indicating their initial placement estimates along with the projected relocation expenses. Notably, the three work zones and the excavation zone are considered immovable and remain in fixed positions throughout the planning process.

Table 6. Handling difficulty level.

		Facility
		1	2	3	4	5	6	7	8	9	10	11	12	13	14
Facility	1	0	1	2	2	2	3	3	2	2	2	2	2	2	2
	2	1	0	1	2	3	3	3	2	2	2	1	1	1	1
	3	2	1	0	3	2	2	2	1	1	1	2	1	1	2
	4	2	2	3	0	1	2	2	2	1	3	2	1	2	1
	5	2	3	2	1	0	2	1	2	3	1	1	3	1	1
	6	3	3	2	2	2	0	1	1	2	1	2	2	1	1
	7	3	3	2	2	1	1	0	1	3	2	2	1	2	1
	8	2	2	1	2	2	1	1	0	1	2	1	1	1	1
	9	2	2	1	1	3	2	3	1	0	1	1	1	1	3
	10	2	2	1	3	1	1	2	2	1	0	2	2	1	1
	11	2	1	2	2	1	2	2	1	1	2	0	1	3	1
	12	2	1	1	1	3	2	1	1	1	2	1	0	1	1
	13	2	1	1	2	1	1	2	1	1	1	3	1	0	2
	14	2	1	2	1	1	1	1	1	3	1	1	1	2	0

categorizes the nature of interactions between facilities on a scale from 1 (mostly labor movement) to 3 (primarily involving heavy machinery). Meanwhile,

Table 7. Number of transfers.

		Facility
		1	2	3	4	5	6	7	8	9	10	11	12	13	14
Facility	1	0	3	1	1	1	1	1	1	1	1	1	1	1	1
	2	3	0	1	1	4	4	4	1	1	1	1	1	1	1
	3	1	1	0	1	2	1	1	2	1	1	1	1	1	3
	4	1	1	1	0	1	2	1	1	1	4	3	1	1	1
	5	1	4	2	1	0	1	1	2	1	1	1	1	1	2
	6	1	4	1	2	1	0	1	1	1	1	2	2	1	1
	7	1	4	1	1	1	1	0	1	2	1	1	1	1	1
	8	1	1	2	1	2	1	1	0	1	1	1	1	1	1
	9	1	1	1	1	1	1	2	1	0	1	1	1	1	1
	10	1	1	1	4	1	1	1	1	1	0	1	1	1	1
	11	1	1	1	3	1	2	1	1	1	1	0	1	1	1
	12	1	1	1	1	1	2	1	1	1	1	1	0	1	1
	13	1	1	1	1	1	1	1	1	1	1	1	1	0	1
	14	1	1	3	1	2	1	1	1	1	1	1	1	1	0

outlines the relative frequency of trips between facility pairs.

In this context, positioning the site office and labor accommodation zone at the greatest possible distance from active construction areas proves to be a strategic choice. Significant deviations from the optimal configuration tend to occur when the expenses related to facility relocation surpass the potential gains achieved through reduced transport distances. Under such conditions, the model must adaptively handle a predominantly static layout, as even minor changes from this configuration can cause considerable fluctuations in the objective function.

On the other hand, when relocation costs are minimal, repositioning facilities becomes more feasible and attractive. This flexibility allows the identification of multiple near-optimal layouts, thereby increasing solution precision. Nonetheless, as the complexity and scale of the problem expand, the model’s ability to maintain computational efficiency in addressing large-scale CSLP instances diminishes noticeably.

It should be emphasized that Case Study 2 was treated as a static assignment problem: the facilities are assigned once to locations, and relocation costs were discussed qualitatively to illustrate their influence. The model does not yet include explicit time steps, transition costs between periods, or re-optimization triggers. Extending the framework into a dynamic, multi-period optimization setting is left for future work.

4.4. Results of Case Study 2

To obtain statistically reliable performance metrics, 50 separate optimization runs were executed, each comprising 500 iterations. As in Case Study 1, the results were compared using the same algorithms with identical parameter settings.

Table 8. Comparison of the results for Case Study 2.

	Algorithms
	A-JA	GA	PSO	ACO	NSGA-II
Best	16,100	16,760	16,650	16,520	16,580
Average	16,290	17,210	16,970	16,880	17,020
Worst	17,130	18,010	17,680	17,670	17,600
STD	101.5	209.8	95.9	140.8	121.1

presents the comparative outcomes of the runs across different algorithms. The proposed A-JA method consistently demonstrates better results, yielding an average objective value of 16,290, a worst-case outcome of 17,130, and a standard deviation of 101.5. Moreover, the best recorded value (16,100) outperforms all other benchmarked algorithms. These findings confirm that the A-JA not only delivers high-quality solutions but also ensures robust performance.

For an intuitive comparison of convergence behavior, Figure 2 depicts the average best-so-far objective values over 30 independent runs for Case Study 2. It is evident that the A-JA reaches high-quality solutions more rapidly than the GA, PSO, ACO, and NSGA-II. The average CPU time can be seen in

Table 9. Average CPU time (seconds).

Algorithm	Case Study 1	Case Study 2
A-JA	124	158
GA	186	213
PSO	179	207
ACO	191	224
NSGA-II	185	218

for each case study. The results confirm that the A-JA not only converges faster in terms of iterations but also requires less computation time compared to the GA, PSO, ACO, and NSGA-II.

Table 10. Average number of function evaluations (FE) until best solution found.

Algorithm	Case Study 1	Case Study 2
A-JA	12,500	13,200
GA	18,400	19,100
PSO	16,900	11,800
ACO	17,800	18,700
NSGA-II	17,500	18,600

reports the average number of function evaluations (FE) required to reach the best solution over 30 independent runs. This measure offers a clear indication of the relative search efficiency of the compared algorithms. Methods achieving lower FE values can be regarded as converging more rapidly and with reduced computational burden.

4.5. Statistical Analysis

To assess the statistical significance of performance differences, pairwise Wilcoxon signed-rank tests were conducted between the A-JA and each baseline algorithm, based on 30 independent runs for Case Study 1 and Case Study 2. The resulting p-values were adjusted using the Holm–Bonferroni method to control familywise error. Effect sizes (Cohen’s r) were also computed. The results (

Table 11. Wilcoxon test results.

Comparison	Case Study 1 p-Value	Case Study 1 Effect Size r	Case Study 2 p-Value	Case Study 2 Effect Size r
A-JA vs. GA	<0.001	0.65 (large)	<0.001	0.68 (large)
A-JA vs. PSO	<0.001	0.61 (large)	<0.001	0.64 (large)
A-JA vs. ACO	<0.001	0.58 (large)	<0.001	0.60 (large)
A-JA vs. NSGA-II	<0.001	0.55 (large)	<0.001	0.57 (large)

) confirm that the A-JA significantly outperforms all baselines (p < 0.01) with large effect sizes.

4.6. Supplementary Benchmark Experiments

To further evaluate the effectiveness and generalizability of the proposed A-JA, additional experiments were conducted on selected QAPLIB benchmark instances. These benchmarks represent classical QAPs with varying sizes and complexities, providing a standard testbed for algorithm comparison.

Table 12. Comparison of the results for benchmark instances.

Instance	Best-Known	A-JA Best	A-JA Avg ± SD	GA Avg ± SD	PSO Avg ± SD	ACO Avg ± SD	NSGA-II Avg ± SD
Nug12	578	578	578.0 ± 0.0	590.3 ± 8.1	585.7 ± 6.9	593.2 ± 9.4	588.5 ± 7.6
Nug20	2570	2572	2574.2 ± 3.1	2635.7 ± 15.2	2619.4 ± 14.3	2650.8 ± 17.5	2627.6 ± 12.8
Chr12a	1100	1100	1100.5 ± 0.5	1112.3 ± 6.2	1108.7 ± 5.8	1115.1 ± 7.0	1110.4 ± 6.1
Tai20a	1400	1402	1404.0 ± 2.2	1420.5 ± 12.3	1415.7 ± 10.8	1425.3 ± 11.7	1417.9 ± 10.2
Nug25	2800	2805	2810.0 ± 4.5	2850.2 ± 18.1	2835.6 ± 16.7	2860.7 ± 20.3	2842.1 ± 17.5

reports the performance of the A-JA and several general-purpose metaheuristics on selected QAPLIB benchmark instances. The “Best-known” column shows the literature optimum for each instance. For each algorithm, the best solution, the mean ± standard deviation over 30 independent runs are reported. As seen, the A-JA consistently matches or improves upon the best-known solutions with lower variability compared to the GA, PSO, ACO, and NSGA-II. These results indicate that the A-JA performs effectively not only on the proposed case studies but also on classical QAP benchmark instances, demonstrating its general applicability and robustness.

5. Limitations and Future Work

The present study has several limitations that should be acknowledged:

(1)

Simplified model: The CSLP was formulated as a classical QAP focusing solely on pairwise flow–distance minimization. Real-world sites often involve forbidden areas, adjacency or separation requirements, safety buffers, and irregular geometries, which were not modeled here.

(2)

Static formulation: Case Study 2 discussed relocation qualitatively, but the optimization was conducted as a single-period assignment. A full dynamic, multi-period formulation with transition costs and re-optimization triggers remains for future work.

(3)

Objective scope: Only a single-objective minimization (flow × distance) was considered. In practice, multi-objective models balancing cost, safety, environmental, and time criteria would be more realistic.

(4)

Baselines: Although the study compares the A-JA against the GA, PSO, ACO, and NSGA-II and includes small QAPLIB benchmarks, further comparisons with advanced QAP heuristics (e.g., tabu search, GRASP, and memetic algorithms) could provide additional insights.

(5)

Scalability: The case studies considered up to 14 facilities, and an additional QAPLIB instance was tested. Larger-scale real-world layouts (20+ facilities with complex constraints) would be valuable to further confirm scalability.

Future work will address these limitations by (i) extending the model to dynamic and multi-objective formulations, (ii) integrating richer site-specific constraints such as safety buffers and irregular geometries, and (iii) exploring hybrid optimization strategies and advanced QAP heuristics for larger-scale instances. These directions will enhance both the realism and applicability of the A-JA in construction management practice.

6. Conclusions

Construction Site Layout Planning (CSLP) presents significant challenges due to its high dimensionality, nonlinear characteristics, and various constraints. Efficiently solving such complex problems is critical for optimizing resource allocation, reducing costs, and improving project timelines. To evaluate the proposed method, two distinct case studies were conducted, representing varying scales and operational complexities in CSLP. Across both scenarios, the Advanced Jaya Algorithm (A-JA) consistently outperformed other benchmark metaheuristic algorithms (namely GA, PSO, ACO, and NSGA-II) not only by producing higher-quality solutions but also by requiring fewer function evaluations to reach optimality. This superiority was observed under diverse problem conditions, underscoring the robustness, adaptability, and computational efficiency of the proposed approach.

The findings further demonstrate that the A-JA exhibits rapid convergence behavior, enabling the attainment of optimal or near-optimal layouts in substantially reduced computational time. Such characteristics are highly valuable in real-world construction management contexts, where timely decision-making is essential for minimizing delays, controlling costs, and optimizing resource allocation. The scalability of the A-JA to high-dimensional, nonlinear, and constrained problem instances further enhances its practical applicability for large-scale projects with numerous facilities and complex site constraints. By bridging the gap between advanced optimization theory and practical decision-making, this study positions the A-JA as a robust and implementable tool for solving complex optimization challenges in construction project management. Its demonstrated ability to integrate seamlessly into the decision-making process highlights its potential for widespread adoption in the industry.

To evaluate scalability beyond the original case studies (11 and 14 facilities), five additional standard QAPLIB benchmark instances were tested: Nug12, Chr12a, Nug20, Tai20a, and Nug25. These include instances up to 25 facilities, thus addressing larger-scale construction site layout problems. The results show that the A-JA consistently outperforms GA, PSO, ACO, and NSGA-II across all instances in terms of best, average, and worst objective values as well as standard deviations. In particular, Nug25 (25 facilities) confirms that the A-JA maintains superior performance for problems of 20+ facilities, demonstrating its applicability to larger construction sites.

The QAP-based formulation used in this study is intentionally simplified, focusing solely on pairwise flow–distance minimization. While this approach effectively demonstrates the performance of the A-JA, it omits several important real-world considerations such as forbidden areas, adjacency preferences, aisle and egress requirements, safety buffer zones, and irregular site shapes. These aspects are crucial for practical deployment of CSLP optimization models.