A Method for Determining the Soil Shear Strength by Eliminating the Heteroscedasticity and Correlation of the Regression Residual

Abstract

Due to cost and variability of geotechnical test results, the number of samples for geotechnical material parameters in one engineering project is limited, resulting in a certain degree of errors in the calculation of probability distribution, mean, and variance of mechanical parameters of the geotechnical materials. To improve the reliability of geotechnical engineering design, reducing the variance of shear strength is one of the methods. Currently, the least squares method is widely used to regress the shear strength of soil; however, the regression residuals often exhibit heteroscedasticity and correlation, which undermine the validity of the variance estimates of soil shear strength parameters. This study aims to address this issue by applying the generalized least squares method to eliminate the heteroscedasticity and correlation of regression residuals. The results of triaxial consolidated drained (CD) tests on the coarse-grained soil; triaxial unconsolidated undrained(UU), CD, and consolidated undrained (CU) tests on gravelly clay; and triaxial CD tests on sand were analyzed to estimate the mean and variance of their shear strength. The results show that while the mean values of shear strength parameters remain largely unchanged, the generalized least squares method reduces the standard deviation of cohesion by an average of 30.575% and that of the internal friction angle by 14.21%. This reduction in variability enhances the precision of parameter estimation, which is critical for reliability-based design in geotechnical engineering, as it leads to more consistent safety assessments and optimized structural designs. The reliability analysis of an infinitely long slope stability shows that the reliability index of the soil slope calculated by the traditional method is either large or small. The generalized least squares method, which eliminates the heteroscedasticity and correlation of the regression residuals, should be adopted to regress the shear strength of soil.

1. Introduction

The limit state design method based on reliability theory has been widely applied in structural engineering and has become a trend in the development of current geotechnical engineering design methods. However, due to the cost and variability of geotechnical test results, the number of samples of geotechnical parameters in one project is limited, and there are certain calculation errors in the determination of the probability distribution, mean value, and variance of soil shear strength parameters, making it difficult to grasp the parameter variability. Moreover, the variance of the mechanical parameters has a significant impact on the reliability of the structure. Therefore, improving the estimation accuracy of the variance of geotechnical parameters and accurately evaluating the variability of their mechanical parameters is a prerequisite for designing geotechnical engineering based on reliability theory.

In geotechnical engineering, the shear strength of soil is mostly determined by the Mohr–Coulomb strength criterion, with cohesion and friction angle being crucial design parameters. Even for soil under complex stress conditions or with different densities, shear strength can be described by establishing a relationship between cohesion and friction angle with the intermediate principal stress coefficient or density [1,2]. The correctness and discreteness of the cohesion and friction angle used in determining the bearing capacity of the foundation, checking the stability of the soil slope, and designing retaining structures all directly affect the safety and economy of the engineering project.

At present, most current standards adopt the partial factor limit state design method based on reliability theory for structural design. The material properties need to consider adverse variations on their characteristic values. The characteristic value is generally taken as a percentile value of the probability distribution of the material performance. The material strength is generally taken as a lower percentile value of the probability distribution, except for the mean values of the elastic modulus and Poisson’s ratio at the 0.5 percentile value. As is commonly employed internationally, the 0.05 percentile value is taken [3]. If the material strength follows a normal distribution, the standard value ($f_k$) of the material strength is $f_k={\mu }_f-1.645{\sigma }_f$, where ${\mu }_f$ and ${\sigma }_f$ are the mean and standard deviation of the material strength. According to relevant Chinese codes [4,5], the characteristic value for the strength of geotechnical materials can be determined using percentile-based methods. For instance, it may adopt the 0.1 percentile value or the mean of values below the overall mean, as specified in $f_k={\mu }_f-1.28{\sigma }_f$. According to the “Code for Investigation of Geotechnical Engineering” of China [6], the characteristic values of the shear strength of geotechnical materials are calculated as follows: ${\varphi }_k={\gamma }_s{\varphi }_m$ and ${\gamma }_s=1-\left\{1.704/\sqrt{n}+4.678/n^2\right\}\delta$. ${\varphi }_m$ is the mean value of shear strength, and ${\gamma }_s$ is the statistical correction factor. $n$ is the sample size. $\delta$ is the coefficient of variation of shear strength, and $\delta =\sigma /{\varphi }_m$. $\sigma$ is the standard deviation of shear strength. Therefore, the determination of the standard deviation and the mean of shear strength is equally important for engineering applications.

At present, the shear strength of geotechnical materials is usually determined using a fitting regression method, and the most commonly used methods include the moment method, least squares method, point group center method, and optimal slope method [7,8,9,10]. Based on a great deal of sampling and experimentation, the application of the moment method or linear regression, two mathematical statistical methods, to determine shear strength is currently the most commonly used and accurate method [7,9]. However, in general, the sample size of each group of experiments is relatively small, and the moment method is greatly affected by experimental errors and human factors. The least squares linear regression method places the experimental points of each group in the same coordinate system for regression calculation, which not only effectively solves the problem of the sample size but also eliminates the errors contained in the cohesion and friction angle obtained from each group of experiments [7]. Although the linear regression method has the characteristics of a large sample size and a certain level of accuracy, the standard deviation obtained is not a true reflection of the variability of the actual shear strength, which has often been overlooked in previous calculations [7,9].

The shear strength parameters of the soil are estimated using the original least squares linear regression method [10,11]. The estimated values of these parameters are unbiased, but the variance estimates have errors. The main reason is that the regression equation does not meet the adaptation conditions of the least squares method. In other words, the residuals between the measured and predicted values of the regression equation have heteroscedasticity and correlation. Least squares regression requires the residuals to be independent and to follow a normal distribution with a mean of zero and equal variance under different confining pressures. However, the regression results of triaxial tests on soil samples indicate that the residuals in the regression equation have heteroscedasticity and are correlated with each other. The heteroscedasticity and correlation of regression residuals render parameter estimators ineffective as the variances are not constant and interrelated, rendering t-tests and F-tests ineffective. Due to the influence of the variance of each component of the parameter, the fluctuation between the estimated and true values of the parameter increases, which reduces the estimation accuracy, and as a result, the parameter variance estimated using the original least squares method is no longer the minimum variance estimate. Obviously, the variance estimation of the shear strength parameters is slightly larger to some extent, which can lead to a greater fluctuation in the calculation results of geotechnical structures, resulting in a decrease in the accuracy of the calculation in assessing the safety of geotechnical structures. This may also lead to economically inefficient designs of geotechnical structures.

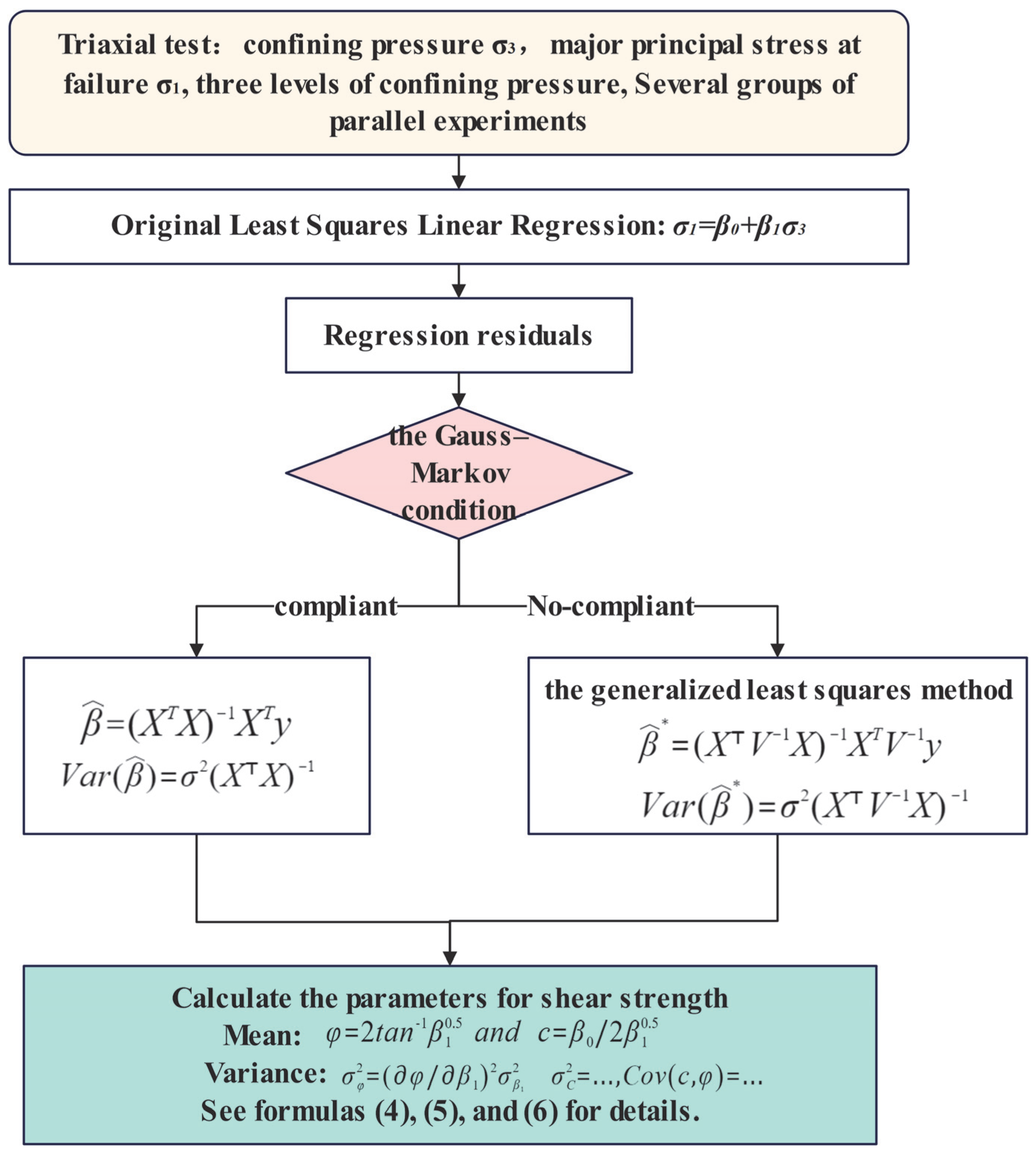
Therefore, to enhance the reliability of safety assessment for geotechnical structures, one approach is to study the precise calculation method of the variance of soil shear strength parameters. In this paper, based on triaxial tests, the cohesion and friction angle of soil are linearly regressed using the classical least squares method. During the process, it was found that the regression residuals did not meet the assumptions of homoscedasticity and uncorrelatedness, which violated the application conditions of the least squares method. To address this issue, the square root matrix of the covariance matrix of the regression residuals was adopted to transform the regression equation, ensuring that it met the application conditions of the least squares method. The research flowchart is shown in Figure 1.

2. Method for Organizing the Shear Strength Parameters of Soil

The regression methods for organizing soil shear strength mainly include the volume stress–shear stress method ($p-q$ method) and major principal stress–minor principal stress method (${\sigma }_1-{\sigma }_3$ method). Chen et al. [7] pointed out that both from theoretical derivation and analysis of the experimental results, it is clear that the shear strength parameter values obtained by these two methods are not the same, and they believe that the result of the ${\sigma }_1-{\sigma }_3$ method is more accurate. Therefore, here we only explain how to organize the shear strength parameters of the soil by the ${\sigma }_1-{\sigma }_3$ method.

The triaxial tests obtained the stress differences $({\sigma }_1-{\sigma }_3)$ at which the specimens failed under various confining pressures ${\sigma }_3$. According to the Mohr–Coulomb strength criterion, the failure line equation is as follows:

$${\sigma }_1=2c\tan \left({\displaystyle \frac{\phi }{2}}+{\displaystyle \frac{\pi }{4}}\right)+{\sigma }_3{\tan }^2\left({\displaystyle \frac{\phi }{2}}+{\displaystyle \frac{\pi }{4}}\right)={\beta }_0+{\beta }_1{\sigma }_3$$

(1)

where ${\sigma }_1$ is the major principal stress at the time of sample failure; ${\sigma }_3$ is the minor principal stress, i.e., the sample confining pressure; $c$ and $\phi$ are the cohesion and friction angle of soil’s shear strength; and ${\beta }_0$ and ${\beta }_1$ are undetermined coefficients. ${\beta }_0=2c\tan \left({\displaystyle \frac{\phi }{2}}+{\displaystyle \frac{\pi }{4}}\right)$, and ${\beta }_1={\tan }^2\left({\displaystyle \frac{\phi }{2}}+{\displaystyle \frac{\pi }{4}}\right)$.

It can be seen that regression Equation (1) cannot directly obtain the $c$ and $\phi$ of soil’s shear strength, but they are determined by the intermediate variables of ${\beta }_0$ and ${\beta }_1$. They are calculated as follows:

$$\phi =2{\tan }^{-1}{\beta }_1^{0.5}-\pi /2, \mathrm{and}c={\displaystyle \frac{{\beta }_0}{2{\beta }_1^{0.5}}}$$

(2)

where ${\beta }_0$ and ${\beta }_1$ are obtained through linear regression of experimental points $({\sigma }_3,{\sigma }_1)$ in Equation (1).

According to Equation (1) and probability theory, the following Equation (3) can be obtained through derivation:

$${\sigma }_{{\sigma }_1}^2={\sigma }_3^2{\sigma }_{{\beta }_1}^2+{\sigma }_{{\beta }_0}^2+2{\sigma }_{3}Cov\left({\beta }_0,{\beta }_1\right)$$

(3)

where ${\sigma }_{{\sigma }_1}$ is the standard deviation of the major principal stress, and ${\sigma }_{{\beta }_0}$ and ${\sigma }_{{\beta }_1}$ are the standard deviations of the regression parameters ${\beta }_0$ and ${\beta }_1$, respectively. $Cov({\beta }_0,{\beta }_1)$ is the covariance of the regression parameters ${\beta }_0$ and ${\beta }_1$.

By performing Taylor expansion on Equation (2) at the mean values of ${\beta }_0$ and ${\beta }_1$ while ignoring second-order and higher-order infinitesimal quantities, the corresponding variance expressions for $\phi$ and $c$ can be expressed as:

$${\sigma }_{\phi }^2={\left(\partial \phi /\partial {\beta }_1\right)}^2{\sigma }_{{\beta }_1}^2$$

(4)

$${\sigma }_c^2={\left(\partial c/\partial {\beta }_0\right)}^2{\sigma }_{{\beta }_0}^2+{\left(\partial c/\partial {\beta }_1\right)}^2{\sigma }_{{\beta }_1}^2+2\left(\partial c/\partial {\beta }_0\right)\left(\partial c/\partial {\beta }_1\right)Cov({\beta }_0,{\beta }_1)$$

(5)

$$Cov(c,\phi )=\left(\partial \phi /\partial {\beta }_1\right)\left(\partial c/\partial {\beta }_1\right){\sigma }_{{\beta }_1}^2+\left(\partial \phi /\partial {\beta }_1\right)\left(\partial c/\partial {\beta }_0\right)Cov({\beta }_0,{\beta }_1)$$

(6)

Based on (4), (5), and (6), the following expression can be obtained:

$${\displaystyle \frac{\partial \phi }{\partial {\beta }_1}}={\displaystyle \frac{1}{({\beta }_1+1){\beta }_1^{0.5}}},{\displaystyle \frac{\partial c}{\partial {\beta }_0}}={\displaystyle \frac{1}{2{\beta }_1^{0.5}}},\mathrm{and}{\displaystyle \frac{\partial c}{\partial {\beta }_1}}={\displaystyle \frac{{\beta }_0}{4{\beta }_1^{1.5}}}$$

(7)

Yu et al. [11] used the orthogonal least squares method to modify the shear strength parameters of the $p-q$ regression method for soil. They derived the revised regression coefficients. It has been theoretically proven that the shear strength parameter values obtained using the modified $p-q$ method are consistent with those obtained using the ${\sigma }_1-{\sigma }_3$ method, and a practical example has also verified that the $c$ and $\phi$ values obtained using these two methods are the same. However, the impacts of the heteroscedasticity and correlation of the regression residuals of the ${\sigma }_1-{\sigma }_3$ method on the regression results were not considered. Chen et al. [9] used the weighted least squares method to organize the shear strength of 64 sets of 320 triaxial consolidated drained (CD) test results for the core wall material of the Xiaolangdi dam. The weighting coefficient used was calculated using the equation $w_i=1/{(\alpha +\beta x_i)}^2$, and the parameters $\alpha$ and $\beta$ were obtained through linear regression of the residuals and independent variables. This is actually equivalent to partially considering the heteroscedasticity of the residuals without fundamentally solving the problem, and no discussion on eliminating the residual correlation has been published [12,13,14,15].

3. Original Least Squares Estimation

Assuming that $y$ is the dependent variable, $x$ is the independent variable that affects $y$, there is a linear relationship between $x$ and $y$, and there are $n$ sets of observed values $(x_i,y_i),i=1,2,3,\dots ,n$, $y$ can be expressed as:

$$y_i={\beta }_0+{\beta }_1{x}_i+e_i,i=1,2,\dots ,n$$

(8)

where $e_i$ is the residual term, which represents the influence of factors other than $x$ on $y$ and the experimental measurement error. ${\beta }_0$ and ${\beta }_1$ are unknown parameters that need to be estimated.

If the residual term $e_i$ satisfies the following conditions: (a) it is expected to be zero, $E(e_i)=0$; (b) equal variance $Var(e_i)={\sigma }^2$; and (c) if there is no correlation ($Cov(e_i,e_j)=0,i\ne j$) between the residuals, then the least squares estimation holds. This is the Gauss–Markov condition [16,17].

The matrix expression of the linear regression model can be expressed as:

$$y=X\beta +e,E(e)=0,Cov(e)={\sigma }^{2}I$$

(9)

where $X=\left[\begin{array}{cccc}1& 1& \dots & 1\\ x_1& x_2& \dots & x_n\end{array}\right]$, $y={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}\right]}^T$, $\beta ={\left[\begin{array}{cc}{\beta }_0& {\beta }_1\end{array}\right]}^T$, and $T$ denotes the transpose of the matrix. $I$ is the identity matrix, and ${\sigma }^2$ is the variance of the entire residual sequence.

The least squares method is used to obtain the estimated value of $\beta$, which minimizes the sum of the squared lengths of the error vector of $e=y-X\beta$, i.e.,

$$Q(\beta )={‖y-X\beta ‖}^2={(y-X\beta )}^T(y-X\beta )$$

(10)

Equation (11) is expanded, the partial derivative is calculated and set to zero, and the parameters to be estimated are calculated as:

$$\beta ={(X^{T}X)}^{-1}{X}^{T}y$$

(11)

By substituting n sets of observation data $\left(x_i,y_i\right)$ into the above Equation (12), the estimated value of $\beta$, i.e., $\widehat{\beta }$, is obtained as:

$$\widehat{\beta }={(X^{T}X)}^{-1}{X}^{T}y$$

(12)

The covariance matrix of the parameter $\widehat{\beta }$ can be expressed as:

$$Cov(\widehat{\beta })={\sigma }^2{\left(X^{T}X\right)}^{-1}$$

(13)

4. Triaxial Tests and Results

Large triaxial consolidation drained (CD) tests were conducted on the coarse-grained soil of the R engineering project, with a total of 11 groups of tests selected based on sample availability and consistency in dry density. Meanwhile, small triaxial consolidation drained (CD), unconsolidated undrained (UU), and consolidated undrained (CU) tests were performed on the gravelly clay of the S engineering project. Due to variations in sample dry density, only 7 to 8 groups with similar densities were used for analysis. Similarly, 6 groups of small triaxial CD tests were conducted on the sand of the T engineering project. The number of test groups for each material was determined to ensure statistical reliability while accounting for practical constraints in sample preparation and testing. The large and small triaxial testing instruments are shown in Figure 2. The sample diameter of the large-scale triaxial test was 300 mm, and the height was 600 mm. The small triaxial apparatus can conduct triaxial tests with two different diameters. For the S project gravelly clay, the CD, UU, and CU tests had a sample diameter of 61.8 mm and a height of 150 mm. For the T project sand triaxial test, the sample diameter was 100 mm, and the height was 200 mm.

Eleven groups of triaxial test data for coarse-grained soil for Project R were used, and the confining pressures of each group were set to six levels. Considering the nonlinearity of the shear strength of the coarse-grained soil, the Mohr–Coulomb shear strength was divided into multiple linear sections. Here, only the shear strength of the low confining pressure section with three levels of confining pressure (100 kPa, 300 kPa, and 500 kPa) is discussed. Eleven groups of triaxial UU, CD, and CU tests were also carried out on the gravelly clay for Project S. However, due to certain differences in the dry density of the samples, seven or eight groups of test data with similar densities were selected for calculation. The confining pressures for each group of tests were 100 kPa, 300 kPa, and 500 kPa. Six groups of CD tests were carried out on sand for Project T, and the confining pressure of each group of tests was also divided into three levels, i.e., 200 kPa, 400 kPa, and 800 kPa. The major principal stress when the samples failed under different confining pressures for each soil material was obtained from the triaxial tests and is shown in

Table 1. The major principal stress at failure during the large and small triaxial tests.

Materials and Tests	Confining Pressure/kPa	The Major Principal Stress at Failure/kPa
		1	2	3	4	5	6	7	8	9	10	11
Coarse-grained soil CD test	100	1208.07	1433.2	1370.69	1295.48	1351.3	1291.34	1333.8	1374.32	1352.26	1379.37	1395.21
	300	2182.25	2532.54	2636.46	2459.26	2413.02	2374.56	2303.87	2375.56	2534.86	2637.45	2821.11
	500	3116.99	3437.18	3534.05	3397.87	3501.24	3520.25	3550.83	3616.59	3396.87	3613.27	3665.85
Gravelly clay UU test	100	600.535	538.425	526.378	628	700.965	701.966	728.844	-	-	-	-
	300	1028.73	1010.78	946.914	966	1127	1063.57	1132.24	-	-	-	-
	500	1319.45	1287.47	1317.51	1366	1456.43	1565	1570.54	-	-	-	-
Gravelly clay CD test	100	486.023	513.984	517.097	488	477.826	487.572	513	415.09	-	-	-
	300	1037.59	1065.96	1010.18	977	1012.55	993.759	997.792	722.93	-	-	-
	500	1576.08	1548.96	1560.59	1497.72	1453.12	1445.52	1464	1343.08	-	-	-
Gravelly clay CU test	100	203.34	461	465	469	434.512	470.72	472.292	-	-	-	-
	300	891.633	992.89	959	887	910.829	889.386	928.74	-	-	-	-
	500	1344	1475.22	1306	1246	1263.65	1320	1400.19	-	-	-	-
Sand CD test	200	816.6	930.9	799.8	759.4	766.9	700	-	-	-	-	-
	400	1756.5	1612.3	1558.2	1551.4	1368	1422				-	-
	800	2999.3	2994.5	2917.7	2710.7	2606.3	2706.5	-	-	-	-	-

.

5. Test for Homogeneity of Variance and Correlation of Residuals in Regression Analysis

Strictly speaking, the homogeneity of the variance and independence of the regression residuals under different confining pressures should be determined through hypothesis testing methods. However, due to article length limitations and because this is not the main focus of this paper, we will not elaborate on it here. A simpler method is to determine the homogeneity of the variance and independence of the residuals by checking whether the principal diagonal elements of the covariance matrix are equal and whether the off-diagonal elements are zero. If all of the diagonal elements of the covariance matrix are equal, the regression residuals have homogeneity of variance; otherwise, they have heteroscedasticity. If the non-diagonal elements of the covariance matrix are not all zero, then the regression residuals are correlated; otherwise, the residuals are uncorrelated.

Based on the results of triaxial tests, the principal stress at the failure points of soil samples under different confining pressures is determined, and n sets of regression data of $({\sigma }_3,{\sigma }_1)$ are generated. Then, the original least squares method is used to regress the relationship between the major and minor principal stresses at the point of failure, and the regression coefficients ${\beta }_0$ and ${\beta }_1$ are obtained. Then, the cohesion and friction angle of the soil are calculated using Equation (2).

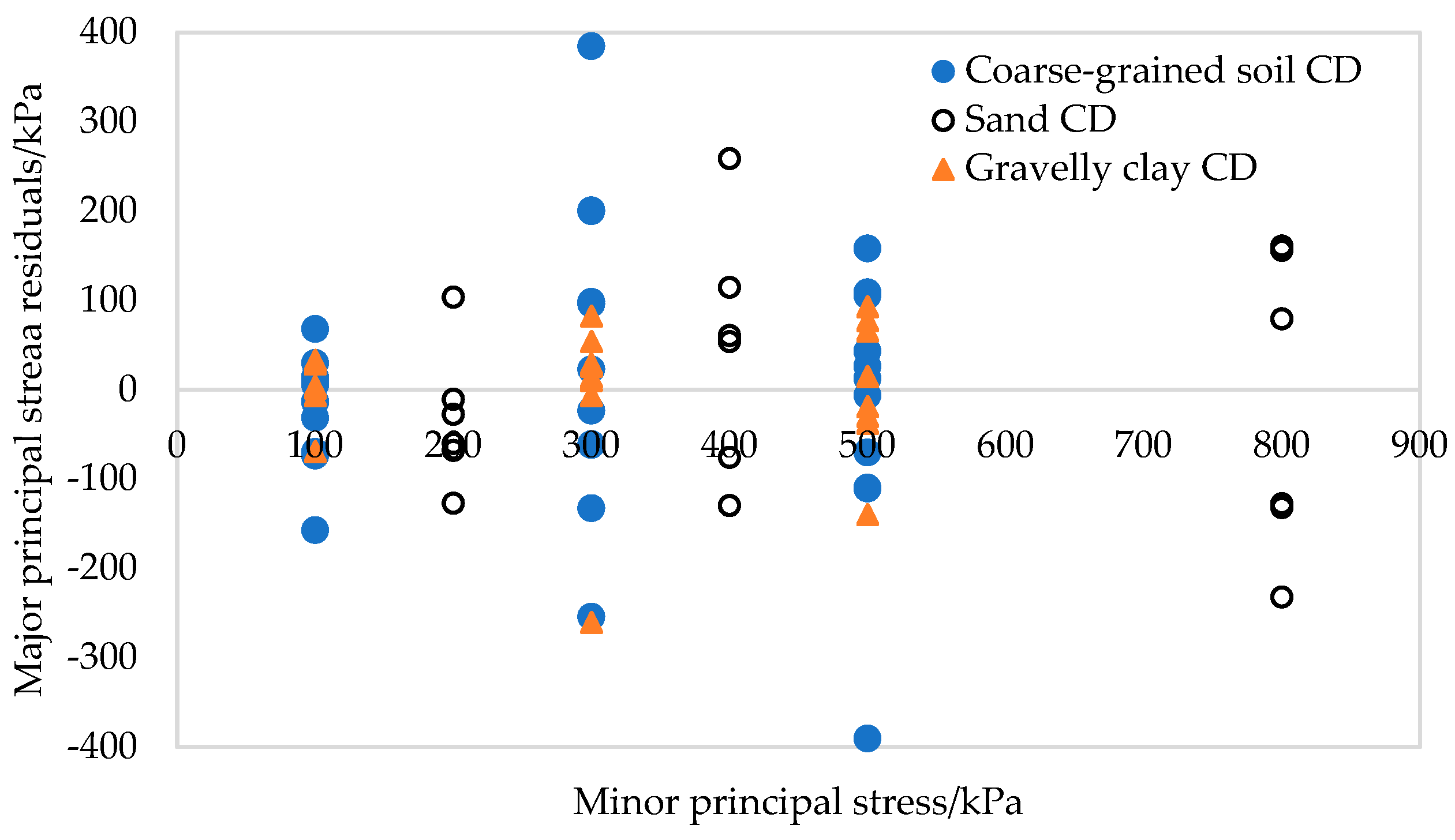
Figure 3 shows the original least squares regression of the triaxial CD tests for the coarse-grained soil of Project R, the gravel clay of Project S, and the sand of Project T. After obtaining the regression equation, the difference between the measured values of the principal stress at failure and the values predicted via the regression equation is calculated and taken as the residual.

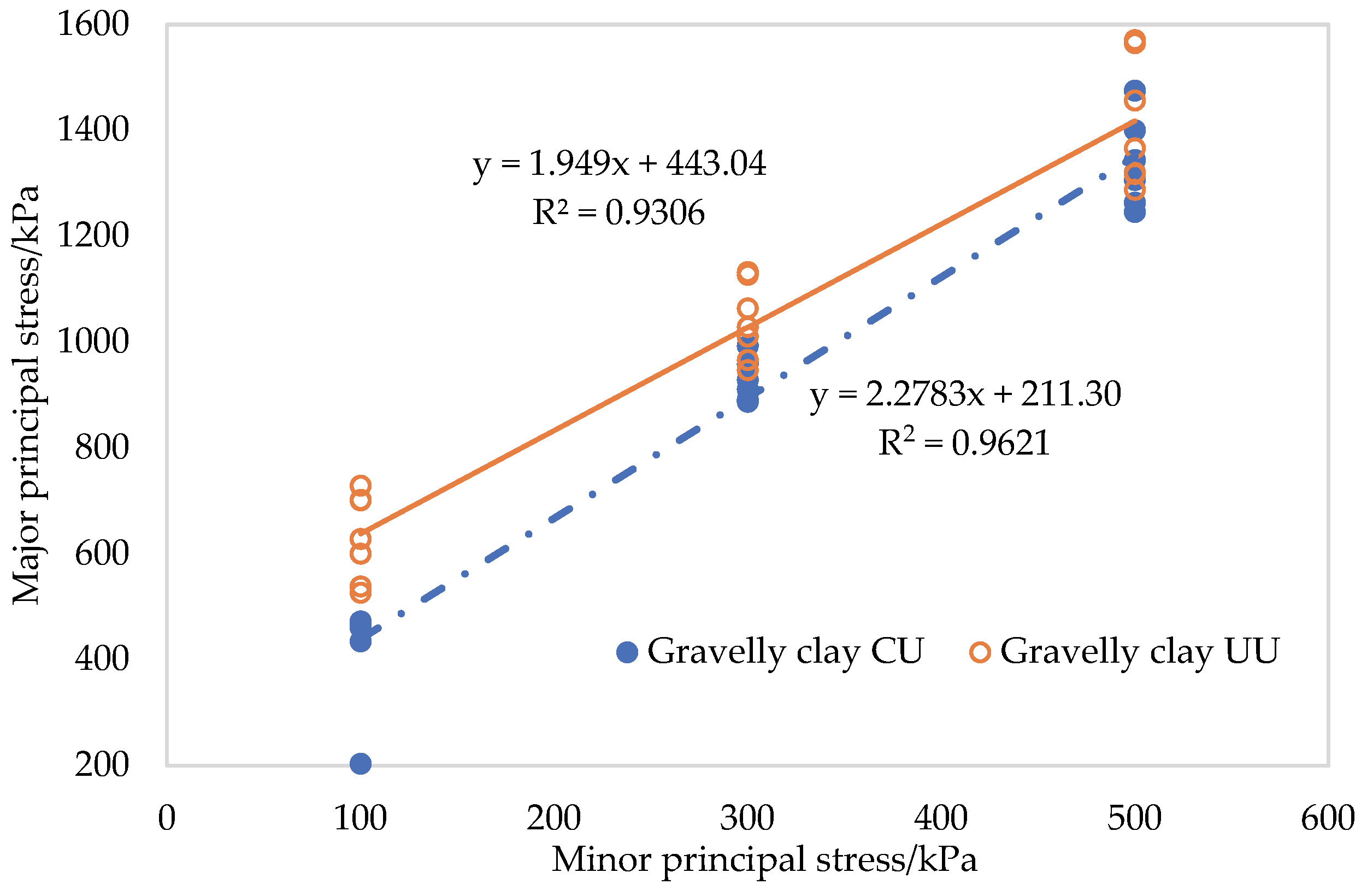
Figure 4 shows the regression residuals in Figure 3. Figure 5 shows the original least squares regression of the triaxial CU and UU tests for the gravel clay of Project S, and Figure 6 shows the regression residuals of the triaxial CU and UU tests for the gravel clay of Project S.

The covariance matrix of the residuals under different confining pressures is calculated for the three types of soil materials and five different tests as follows: sort out the residuals of the same soil material under different confining pressures, treat them as vectors, calculate the variance and covariance of vectors, and form a covariance matrix. For the CD test of the coarse-grained soil, the covariance matrix of the original least squares linear regression residuals can be expressed as:

$$Cov(e_i,e_j)=\left[\begin{array}{ccc}4416.874& 7868.913& 6083.824\\ 7868.913& 29513.526& 15243.505\\ 6083.824& 15243.505& 22708.444\end{array}\right]={\sigma }^{2}V$$

(14)

where ${\sigma }^2=808011.978$.

Based on Equation (15), the following expression can be obtained:

$$V=\left[\begin{array}{ccc}547& 974& 753\\ 974& 3653& 1887\\ 753& 1887& 2810\end{array}\right]\times {10}^{-5}$$

(15)

For the CD test of the gravelly clay, the covariance matrix of the original least squares regression residuals can be expressed as:

$$Cov(e_i,e_j)=\left[\begin{array}{ccc}1080.945& 3119.090& 1978.745\\ 3119.090& 11316.455& 6791.522\\ 1978.745& 6791.522& 5915.705\end{array}\right]={\sigma }^{2}V$$

(16)

where ${\sigma }^2=179093.412$.

Based on (17), the following expression can be obtained:

$$V=\left[\begin{array}{ccc}604& 1742& 1105\\ 1742& 6319& 3792\\ 1105& 3792& 3303\end{array}\right]\times {10}^{-5}$$

(17)

For the UU test of the gravel clay, the covariance matrix of the residual of the original least squares regression can be expressed as:

$$Cov(e_i,e_j)=\left[\begin{array}{ccc}6658.055& 4966.479& 8975.409\\ 4966.479& 5291.741& 6495.849\\ 8975.409& 6495.849& 14272.594\end{array}\right]={\sigma }^{2}V$$

(18)

where ${\sigma }^2=114301.133$.

Based on (19), the following expression can be obtained:

$$V=\left[\begin{array}{ccc}5825& 4345& 7852\\ 4345& 4630& 5683\\ 7852& 5683& 12487\end{array}\right]\times {10}^{-5}$$

(19)

For the UU test of the gravelly clay material, the covariance matrix of the original least squares regression residuals can be expressed as:

$$Cov(e_i,e_j)=\left[\begin{array}{ccc}9730.396& 1323.982& -51.0198\\ 1323.982& 1628.525& 2237.728\\ -51.0198& 2237.728& 6342.379\end{array}\right]={\sigma }^{2}V$$

(20)

where ${\sigma }^2=151057.858$.

Based on (21), the following expression can be obtained:

$$V=\left[\begin{array}{ccc}6442& 876& -34\\ 876& 1078& 1481\\ -34& 1481& 4199\end{array}\right]\times {10}^{-5}$$

(21)

For the CD test of the sand, the covariance matrix of the residuals of the original least squares linear regression can be expressed as:

$$Cov(e_i,e_j)=\left[\begin{array}{ccc}6007.644& 6041.93& 9745.188\\ 6041.93& 19186.862& 20409.064\\ 9745.188& 20409.064& 28520.592\end{array}\right]={\sigma }^{2}V$$

(22)

where ${\sigma }^2=757235.266$.

Based on (23), the following expression can be obtained:

$$V=\left[\begin{array}{ccc}793& 798& 1287\\ 798& 2534& 2695\\ 1105& 2695& 37667\end{array}\right]\times {10}^{-5}$$

(23)

As can be seen from Figure 4 and Figure 6, the distribution of the regression residuals is not the same under different confining pressures. For the same soil material and test, some of the residual points of the confining pressure are relatively concentrated, while others are scattered, indicating that the residuals under different confining pressures do not have homogeneity of variance. Based on the regression covariance matrices of the different types of soil test results, the covariance matrix is full rank, the diagonal elements are unequal, the non-diagonal elements are not zero, and the non-diagonal elements are basically of the same order of magnitude as the diagonal elements, indicating that the residuals not only have heteroscedasticity but also correlation.

The above examples illustrate that for coarse-grained soil, sand, and cohesive soil, for both the effective stress shear strength of the CD test and the total shear strength of the UU and CU tests, when using the original least squares method for soil shear strength parameter regression, the residuals have heteroscedasticity and correlation. If the original least squares method is used to conduct the estimation, its parameters will no longer be valid, and the significance tests of variables and the model predictions will all suffer certain degrees of failure. Therefore, efforts should be made to improve the original least squares regression method to eliminate the heteroscedasticity and the correlation of the regression residuals.

6. Eliminating Residual Variance Heterogeneity and Correlation Using the Generalized Least Squares Method

The linear regression equation of the ${\sigma }_1-{\sigma }_3$ relationship can be expressed as [16,17]:

$$y=X\beta +e,E(e)=0,Cov(e)={\sigma }^{2}V$$

(24)

where $V$ is non-singular and positive definite, and there is a non-singular symmetric matrix $K$, so $K^{T}K=K^{-1}K=V$. Matrix $K$ is the square root matrix of $V$, and $K^T$ and $K^{-1}$ are the transpose matrix and inverse matrix of $K$.

Multiplying both sides of the regression equation $y=X\beta +e$ by $K^{-1}$ at the same time yields $K^{-1}y=K^{-1}X\beta +K^{-1}e$.

$$z=K^{-1}y,B=K^{-1}X,g=K^{-1}e$$

(25)

Thus, the regression variation can be expressed as:

$$z=B\beta +g$$

(26)

After this process, the error of the model has a mean value of zero, i.e., $E(g)=K^{-T}E(e)=0$, and the covariance matrix of $g$ can be expressed as:

$$\begin{gathered} Var(g)=\left\{\left[g-E(g)\right]{\left[g-E(g)\right]}^T\right\}=E\left(g{g}^T\right) \\ =E(K^{-1}e{e}^T{K}^{-1})=K^{-1}E(e{e}^T)K^{-1} \\ ={\sigma }^2{K}^{-1}V{K}^{-1}={\sigma }^2{K}^{-1}KK{K}^{-1} \\ ={\sigma }^{2}I \end{gathered}$$

(27)

Therefore, the element of $g$ has the properties of a mean value of zero, constant variance, and no correlation. The test conditions of the original least squares estimation are satisfied, and the least squares function can be expressed as [16,17]:

$$Q(\beta )=g^{T}g=e^T{V}^{-1}e={(y-X\beta )}^T{V}^{-1}(y-X\beta )$$

(28)

Its canonical Equation (30) can be obtained as:

$$X^T{V}^{-1}X{\widehat{\beta }}^{*}=X^T{V}^{-1}y$$

(29)

The solution of this Equation can be obtained as:

$${\widehat{\beta }}^{*}={\left(X^T{V}^{-1}X\right)}^{-1}{X}^T{V}^{-1}y$$

(30)

The covariance of ${\widehat{\beta }}^{*}$ can be expressed as:

$$\begin{gathered} Var({\widehat{\beta }}^{*})=Var({(X^T{V}^{-1}X)}^{-1}{X}^T{V}^{-1}y)={(X^T{V}^{-1}X)}^{-1}{X}^T{V}^{-1}{\sigma }^{2}V{V}^{-1}X{(X^T{V}^{-1}X)}^{-1} \\ ={\sigma }^2{(X^T{V}^{-1}X)}^{-1} \end{gathered}$$

(31)

7. The Shear Strength Parameters of Soil

The covariance matrix of the regression parameters ${\beta }_0$ and ${\beta }_1$ of the original least squares method is obtained under the Gauss–Markov condition. However, when regressing the ${\sigma }_1-{\sigma }_3$ relationship of the soil triaxial test using the original least squares method, its residual does not meet the Gauss–Markov condition, and its covariance matrix of parameter $\widehat{\beta }$ can be modified as:

$$Cov(\widehat{\beta })={\sigma }^2{\left(X^{T}X\right)}^{-1}{X}^{T}VX{\left(X^{T}X\right)}^{-1}$$

(32)

The friction angle and cohesion of the soil can be calculated using Equation (2) after ${\beta }_0$ and ${\beta }_1$ are calculated using the original and generalized least squares methods according to Equations (13) and (31). Then, the variance and covariance of the friction angle and cohesion are calculated using Equations (4)–(7). The specific calculations are presented in

Table 2. Least squares regression parameters of ${\beta }_0$ and ${\beta }_1$ and their variance.

Materials, Test	Method	${\mathit{\beta }}_0$	${\mathit{\beta }}_1$	$\mathbf{Variance}\mathbf{of}{\mathit{\beta }}_0$	$\mathbf{Variance}\mathbf{of}{\mathit{\beta }}_1$	$\mathbf{Covariance}\mathbf{of}{\mathit{\beta }}_0\mathbf{and}{\mathit{\beta }}_1$	Heteroscedasticity of Residual Variance	Residual Autocorrelation
Coarse-grained soil, CD	original	829.81	5.3559	8361.866	0.0935	−6.657	exists	exists
	generalized	807.24	5.3396	3940.604	0.0923	−4.346	eliminated	eliminated
Gravelly clay, UU	original	443.04	1.949	6206.01	0.0253	2.767	exists	exists
	generalized	448.41	1.977	4220.19	0.0094	0.272	eliminated	eliminated
Gravelly clay, CD	original	234.45	2.497	2132.80	0.0190	1.3909	exists	exists
	generalized	240.55	2.504	429.45	0.0166	−0.6206	eliminated	eliminated
Gravelly clay, CU	original	211.3	2.2783	17,806.65	0.1376	−44.09	exists	exists
	generalized	282.3	2.1453	7198.30	0.0805	−21.37	eliminated	eliminated
Sand, CD	original	156.72	3.352	4026.72	0.0361	2.2829	exists	exists
	generalized	149.42	3.289	3950.93	0.0304	1.6266	eliminated	eliminated

and

Table 3. Soil cohesion and friction angle, and their variance, standard deviation, and coefficient of variation.

$\mathbf{Materials},\mathbf{Test}$	Method	$\mathit{c}$/kPa	Friction Angle (°)	Variance of c	Variance of φ (10−2 Radians)	Covariance of c and φ	Standard Deviation of c	Standard Deviation of φ (°)	Coefficient of Variation of c	Coefficient of Variation of φ
Coarse-grained soil, CD	original	179.28	43.26	464.64	0.0432	−0.204	21.56	1.191	0.120	0.028
	generalized	174.67	43.20	239.94	0.043	−0.167	15.49	1.188	0.089	0.028
Gravelly clay, UU	original	158.67	18.77	757.38	0.15	−0.010	27.52	2.22	0.173	0.118
	generalized	159.46	19.16	541.33	0.05	−0.068	23.27	1.33	0.146	0.070
Gravelly clay, CD	original	74.18	25.35	204.65	0.06	0.0286	14.306	1.429	0.193	0.0564
	generalized	76.00	25.42	52.65	0.05	−0.081	7.256	1.332	0.095	0.0523
Gravelly clay, CU	original	69.995	22.95	2435.1	0.56	−3.378	49.346	4.295	0.705	0.187
	generalized	96.366	21.35	1207.1	0.38	−2.278	34.743	3.528	0.361	0.165
Sand, CD	original	42.800	32.71	293.8	0.06	0.0494	17.14	1.366	0.401	0.042
	generalized	41.197	32.25	295.9	0.05	0.0332	17.20	1.284	0.418	0.040

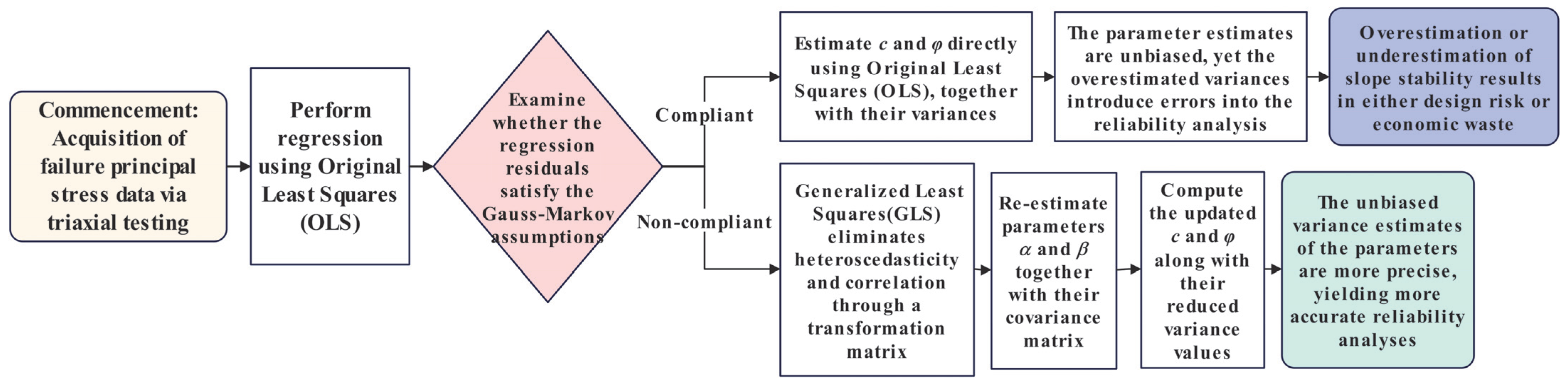
. Table 2 shows the regression parameters and their variance calculation. It can be seen that both the variances of ${\beta }_0$ and ${\beta }_1$ and their covariance between ${\beta }_0$ and ${\beta }_1$ are smaller for the generalized least squares method than the original least squares method, indicating that the generalized least squares method is better than the original least squares method [18]. Based on the above analysis, the comparative differences between the ordinary least squares (OLS) and generalized least squares (GLS) methods are illustrated in Figure 7.

It can be seen from Table 3 that for all three soil materials (i.e., coarse-grained soil, sand, and gravelly clay) and for all of the test types (i.e., UU, CD, and CU triaxial tests and large and small triaxial tests), the means of the soil’s shear strength obtained using the generalized least squares method eliminates the heteroscedasticity and correlation of the residuals, which is not significantly different from that obtained using the original least squares method, but the standard deviation of the shear strength obtained using the generalized least squares method are generally smaller. The generalized least squares method improves the accuracy of the soil shear strength estimation, which is of great significance for accurately determining the safety of geotechnical engineering projects.

There are two points to be noted in the calculation results, as follows:

(a)

As can be seen from Table 3, for the cohesion from the small triaxial CU test on the gravelly clay in the S project, there is a certain difference between the results of the two calculation methods, with a cohesion value of 69.995 kPa obtained using the original least squares method and its corresponding value of 96.366 kPa obtained using the generalized least squares method. This is because the test has a low outlier value at 100 kPa confining pressure (Figure 5). In mathematics, the original least squares method takes the minimum residual error as the objective function, and this low outlier value will inevitably lower the regression intercept of ${\beta }_0$, the original least squares ${\beta }_0=211.3$, and the generalized least squares of ${\beta }_0=282.3$. Therefore, the robust regression of the soil shear strength by the generalized least squares method is better than that of the original least squares method. According to Equation (2), the cohesion of soil is directly proportional to the regression intercept ${\beta }_0$, so the cohesion determined using the original regression least squares method is low.

(b)

As can be seen from Table 3, for the standard deviation of the cohesion of the sand for Project T, there is little difference between the values obtained using the generalized and original least squares regression methods, with values of 17.14 and 17.20 kPa, respectively, but the value obtained from the generalized least squares method is slightly larger. This is because there is little difference between the two methods regarding the regression parameter ${\beta }_0$, with values of 4026.72 and 3950.93 for the generalized and original least squares regression methods, respectively. The variance of the regression parameter ${\beta }_0$ obtained using the generalized least squares method is lower. However, due to the inconsistency between the regression parameters and the variance conversion multiple of the cohesion, the final standard deviation of the cohesion is slightly larger.

Table 4. Percentage reduction in the standard deviation of the cohesion and frictional angle after eliminating the heteroscedasticity and correlation of the regression residual.

Method	Gravelly Clay, UU			Gravelly Clay, CD			Gravelly Clay, CU
	Original	Generalized	Variation/%	Original	Generalized	Variation/%	Original	Generalized	Variation/%
$c$ (kPa)	27.52	23.27	15.4	14.306	7.256	49.3	49.346	34.743	29.6
$\phi$ (°)	2.22	1.33	40.1	1.429	1.332	6.8	4.295	3.528	17.9

and

Table 5. Percentage reduction of the standard deviation of the soil shear strength after eliminating the heteroscedasticity and correlation of the regression residual.

Method	Sand, CD			Coarse-Grained Breccia Soil			Average Decrease
	Original	Generalized	Variation/%	Original	Generalized	Variation/%
$c$ (kPa)	17.14	17.20	−0.4	21.56	15.49	28	30.575
$\phi$ (°)	1.366	1.284	6	1.191	1.188	0.25	14.21

shows the variation in the standard deviation of the Mohr–Coulomb shear strength between the original and generalized least squares methods. It can be seen that except for the 0.4% increase in the standard deviation of the cohesion of the sand, the other standard deviations are reduced. The standard deviation of the cohesion is reduced by 28–49.3% (average of 30.575%), and the standard deviation of the friction angle is reduced by 0.25–40.1% (average of 14.21%). It can be seen that the generalized least squares method eliminates the heteroscedasticity, and the correlation of the residuals has an obvious effect on reducing the standard deviation of the cohesion and frictional angle.

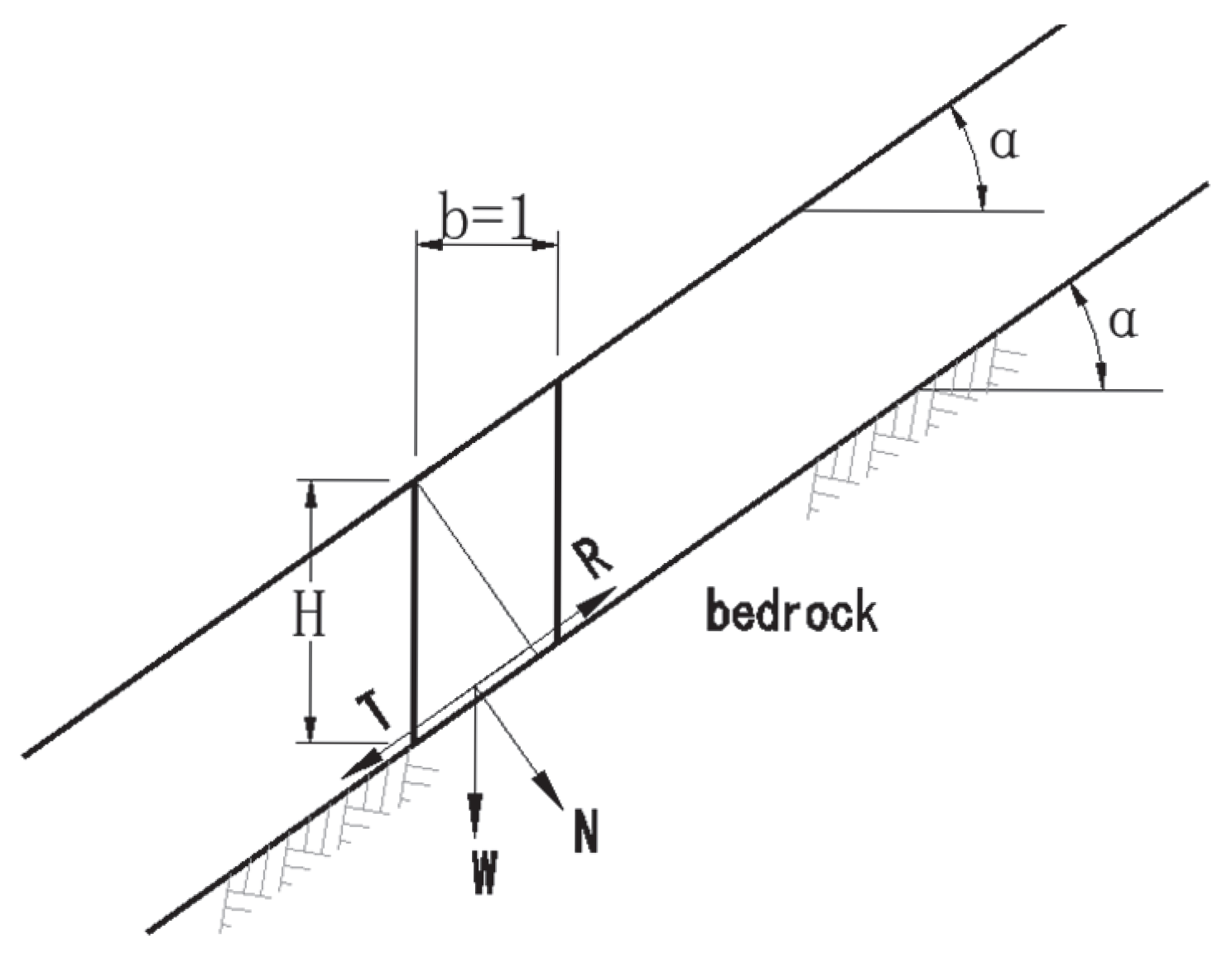
8. The Reliability of Slope Stability Under Different Standard Deviations of Shear Strength

For an infinitely long slope, whose angle with the horizontal plane is $\alpha$, the slope ratio is 1:m, the unit weight of the soil is $\gamma$, the thickness of the soil layer H is equal to 3 m, and the underlying layer is bedrock, the sliding surface slides within the soil layer along the bedrock surface. As shown in Figure 8, the soil layer shear strength and its standard deviation obtained from the literature are used to analyze and compare the reliability index of the slope stability.

The anti-sliding stability safety factor can be expressed as:

$$F={\displaystyle \frac{W\cdot \cos \alpha \cdot \tan \phi +c/\cos \alpha }{W\cdot \sin \alpha }}={\displaystyle \frac{\tan \phi }{\tan \alpha }}+{\displaystyle \frac{c}{\gamma \cdot H\cdot \sin \alpha \cdot \cos \alpha }}$$

(33)

on account of

$$\begin{gathered} m={\displaystyle \frac{1}{\tan \alpha }},2\sin \alpha \cdot \cos \alpha =\sin 2\alpha ={\displaystyle \frac{2\tan \alpha }{{\tan }^2\alpha +1}}={\displaystyle \frac{2/m}{1/m^2+1}}={\displaystyle \frac{2}{m(1/m^2+1)}} \\ F=m\tan \phi +{\displaystyle \frac{cm\left(\frac{1}{m^2}+1\right)}{\gamma H}}=m\tan \phi +{\displaystyle \frac{c(m^2+1)}{\gamma Hm}} \end{gathered}$$

(34)

If ${\displaystyle \frac{(m^2+1)}{\gamma Hm}}=B,f=\tan \phi$.

The safety factor expression has changed to:

$$F=m\cdot f+B\cdot c$$

(35)

The mean and variance of the safety coefficients can be expressed as, respectively:

$${\mu }_F=m{\mu }_f+B{\mu }_c$$

(36)

$$D(F)=m^{2}D(f)+B^{2}D(c)+2mB\cdot Cov(f,c)$$

(37)

$${\sigma }_F=\sqrt{D(F_S)}$$

(38)

In which, ${\mu }_F$, ${\mu }_f$, and ${\mu }_c$ represent the mean of the safety factor, the friction coefficient, and the cohesion, respectively; $D(F)$, $D(f)$, and $D(c)$ represent the variance of the safety factor, the friction coefficient, and the cohesion, respectively; $Cov(f,c)$ is the covariance of the friction coefficient and the cohesion; and ${\sigma }_F$ is the standard deviation of the safety factor.

Since $f=\tan \phi$, the variance and covariance conversion relationship between the friction coefficient and the internal friction angle can be expressed as:

$${\sigma }_f^2={\left({\displaystyle \frac{\partial f}{\partial \phi }}\right)}^2{\sigma }_{\phi }^2={\sec }^2({\mu }_{\phi }){\sigma }_{\phi }^2$$

(39)

$$Cov(f,c)={\sec }^2({\mu }_{\phi }){\sigma }_{\phi }^2$$

(40)

The limit state Equation (42) for slope stability can be expressed as:

$$Z=F-1=0$$

(41)

The corresponding reliability indicator can be expressed as:

$$\beta ={\displaystyle \frac{{\mu }_F-1}{{\sigma }_F}}$$

(42)

Based on the results of the CD tests for coarse-grained soil in Project R, the CD tests for sand in Project T, and the UU tests for gravelly clay in Project S, the soil shear strength parameters obtained through the original and generalized linear regressions were used. Now, assuming that the slope ratios of the infinitely long slopes are 1:1.3, 1:2.0, and 1:2.0, respectively, the reliability indices of the slopes were calculated. Engineering designers generally believe that coarse-grained soils lack fine-grained cohesive soil and thus, the cohesion is unreliable. Therefore, for the coarse-grained soil materials in Project R, their cohesion is not considered. The calculation results are shown in

Table 6. Reliability indexes of slope stability for different soil shear strengths using original and generalized regression methods.

$\mathbf{Types}\mathbf{of}\mathbf{Soil}\mathbf{and}\mathbf{Slope}\mathbf{Ratio}$	Unit Weight /kN m−3	$\mathbf{B}/{10}^{-2}$	Method	Mean Value of $\mathit{c}$	$\mathbf{Mean}\mathbf{Value}\mathbf{of}\mathit{f}$	$\mathbf{Standard}\mathbf{Deviation}\mathbf{of}\mathit{c}$	$\mathbf{Standard}\mathbf{Deviation}\mathbf{of}\mathit{f}$	$\mathbf{Covariance}\mathbf{of}\mathit{c}\mathbf{a}\mathbf{n}\mathbf{d}\mathit{f}$	Mean of Safety Factor	Variance of Safety Factor	Standard Deviation of Safety Factor	Reliability Index
Coarse-grained soil CD, Slope ratio 1:1.3	23	3.63	original	179.28	0.941	21.56	0.029	−0.385	1.223	0.001421	0.0377	6.016
			generalized	174.67	0.939	15.49	0.028	−0.314	1.221	0.001372	0.0370	5.969
Sand CD, Slope ratio 1:2.0	19	4.39	original	42.800	0.642	17.14	0.028	0.070	3.161	0.581	0.762	2.836
			generalized	41.197	0.631	17.20	0.027	0.046	3.069	0.580	0.762	2.716
Gravelly clay UU, Slope ratio 1:2.0	19	4.39	original	158.67	0.340	757.38	0.041	−0.011	6.565	1.462	1.209	4.603
			generalized	159.46	0.347	541.33	0.024	−0.076	6.610	1.030	1.015	5.527

.

It can be seen that the calculated reliability index of the slope stability using the original and generalized linear regression methods for obtaining the soil shear strength parameters is not the same. For the test results of the coarse-grained soil in Project R and the sand in Project T, the reliability index of the soil slope calculated using the generalized linear regression method to obtain the shear strength parameters is smaller than that using the original linear regression method. This indicates that the original linear regression overestimated the shear strength of the soil, and the reliability index was overestimated by 4.418%. Thus, using the original regression algorithm to estimate soil shear strength, the slope stability may lead to an overly risky engineering design.

However, for the S project’s gravelly clay, the opposite is true. That is, using the original least squares method for linear regression, the obtained parameters of the soil’s shear strength are underestimated, leading to an underestimation of the slope stability by 16.718% of the reliability index. This naturally results in certain engineering waste. Therefore, the original least squares method may lead to either overestimation or underestimation of slope reliability, resulting in either unsafe designs or unnecessary conservatism. The reduction in standard deviation achieved by the generalized least squares method directly translates into more stable and predictable reliability indices, enhancing the safety and economic efficiency of geotechnical designs. Thus, the generalized least squares method, which eliminates the heteroscedasticity and correlation of regression residuals, should be adopted for regressing soil shear strength parameters.

9. Conclusions

The shear strength of soil is an important parameter in geotechnical engineering. The selection of the cohesion and friction angle has a direct impact on the bearing capacity of the foundation, the slope stability, and the design of retaining structures. In particular, the design of geotechnical engineering based on reliability theory has become a new trend. However, due to the cost and dispersion of soil test results, there are very few samples of soil parameters in one engineering project, and the calculation errors of the probability distribution, mean, and variance of the parameters are large, making it difficult to grasp the variability of the parameters. The key point is that the variance of soil mechanical parameters has a significant impact on the reliability of the structure. Therefore, it is imperative to improve the estimation accuracy of the variance of the shear strength of the soil.

Currently, the shear strength is usually determined by the moment method or the linear regression method. However, the moment method is greatly affected by experimental errors and human factors. The linear regression method has the advantages of a large sample size and high accuracy. However, the estimated parameter variance of this method is not unbiased. The main reason for this is that the regression residuals have heteroscedasticity and correlation, which do not meet the conditions required for the use of the linear regression least squares method.

In order to eliminate the heteroscedasticity and the correlation of the regression residuals, a generalized least squares regression method for soil shear strength was developed in this study. Based on triaxial CD tests on coarse-grained soil and sand and UU, CD, and CU tests on gravelly clay, the shear strength parameters and their variances are estimated. It was found that the generalized least squares method significantly reduces the variance of shear strength parameters while maintaining comparable mean values. Specifically, the standard deviation of cohesion decreased by an average of 30.575%, and that of the friction angle by 14.21%. This reduction in variability is not merely statistical—it directly improves the reliability of geotechnical designs by reducing uncertainty in safety assessments, thereby supporting more economical and safe engineering decisions.

The analysis of the reliability of the slope stability of an infinitely long slope reveals that the calculation of the reliability index of the slope using the generalized least squares method for the soil shear strength parameters is inconsistent with that of the original method. The reliability index may increase or decrease. In this example, the slope stability reliability index decreased by 4.428% and increased by 16.718% with different parameters. It can be seen that the original least squares method’s regression of the soil shear strength and its variance is not accurate enough, which may lead to deviations in the reliability assessment of geotechnical engineering. Therefore, the generalized least squares method, which eliminates the heteroscedasticity and correlation of the regression residuals, should be used to regress the soil shear strength.

Despite the effectiveness of the generalized least squares (GLS) method in reducing the variance of shear strength parameters, several limitations should be noted. The method requires prior knowledge of the residual covariance structure, which may not be readily available in practical applications and must be estimated from limited data, potentially introducing additional uncertainty. Future research should focus on developing more robust methods for estimating the covariance matrix, especially for small sample sizes, and exploring the applicability of GLS in nonlinear strength models and under complex stress paths. Additionally, the integration of Bayesian methods or machine learning techniques could further enhance the reliability of parameter estimation and provide a more comprehensive uncertainty quantification.