CDR-Solv: Solving the Convection-Diffusion-Reaction Equation with Algebraic Sub-Grid Scale Stabilization Using Python

Abstract

The convection-diffusion-reaction (CDR) equation is a fundamental mathematical model for simulating the transport of pollutants. It is a crucial tool for addressing global environmental challenges. However, most existing computational solutions are proprietary and inaccessible, making the development of open-source educational platforms with advanced stabilization capabilities necessary. This study developed and validated a computational framework that solves CDR equations using algebraic sub-grid scale (ASGS) stabilization. The research addressed the fundamental challenge of spurious oscillations that emerge in standard Galerkin formulations when convective transport significantly exceeds diffusive processes. This is a prevalent issue in transport phenomena modeling. A novel, Python-based educational software platform called CDR-Solv was developed to demonstrate the effectiveness of ASGS stabilization across polynomial degrees ranging from linear to cubic approximations. Numerical experiments with minimal diffusion coefficients showed that numerical instabilities were successfully eliminated while maintaining solution accuracy across various source term configurations. The stabilization parameter, ${\tau }_K$, was instrumental in achieving computational stability without compromising mathematical rigor. Comparative analysis revealed the superior performance of higher-order approximations in capturing boundary layer phenomena and sharp gradient regions. The primary contribution of this study is the development of an open-source educational platform that provides access to advanced stabilization techniques and algorithmic transparency. The CDR-Solv framework also allows for the systematic exploration of the effects of selecting different polynomial degrees on solution quality in transport-dominated regimes.

1. Introduction

The convection-diffusion-reaction (CDR) equation is a fundamental partial differential equation that describes the complex transport of substances, energy, and other physical quantities within diverse engineering systems. It has extensive real-world applications across multiple engineering disciplines. For example, it is used in environmental engineering to model contaminant transport in groundwater and atmospheric pollutant dispersion [1]; in biomedical engineering to analyze drug delivery systems and nutrient transport in biological tissues [2]; and in chemical process engineering to optimize heat and mass transfer in reactor design and separation processes [3]. This work’s computational domain encompasses systematically discretizing complex physical problems into manageable finite element subdomains. This approach leverages computational power to decompose large-scale engineering challenges into thousands or millions of smaller, interconnected subsystems. This finite element approach transforms analytically intractable problems, which are impossible to solve manually due to their mathematical complexity and computational intensity, into numerically solvable systems through computer-aided domain decomposition. This computational framework allows engineers to analyze intricate transport phenomena involving multiple physical scales and complex geometries. It provides solutions where traditional analytical methods fail and manual calculations would require excessive computational effort [4,5,6].

1.1. Equation

The general form of the stationary scalar convection-diffusion-reaction equation is expressed in Equation (1):

$$-k∆u+\mathit{a}\cdot \nabla u+su=f \mathrm{e}\mathrm{n} \mathsf{\Omega },$$

(1)

where $u$ represents the concentration, which is an unknown scalar variable, $\mathit{a}$ is the velocity vector associated with convection, $k$ is the diffusion coefficient, $s$ is the reaction coefficient, and $f$ is the known source term.

1.2. Concepts

Diffusion is the dispersion of particles or energy from areas of high concentration to areas of low concentration due to random molecular motion. In an equation, diffusion is usually represented by a term involving a diffusion coefficient and the second spatial derivative of the quantity being transported.

Convection involves the transport of a substance or energy due to the motion of a fluid’s mass. The convection term in the equation generally includes fluid velocity and the spatial derivative of the transported quantity. The reaction term accounts for the generation or consumption of the transported quantity due to chemical or biological reactions. The reaction term includes a coefficient and the quantity being transported.

1.3. Solution Methods

The convection-diffusion-reaction equation can be solved using analytical or numerical methods. Analytical solutions are exact but generally limited to simplified cases with specific boundary conditions.

Numerical methods approximate solutions by discretizing equations and domains. These methods are necessary when analytical solutions are unavailable or when the geometry or problem is too complex for exact solutions [7].

Some examples of numerical methods are:

• Finite Difference Method (FDM): Approximates derivatives in an equation by using the differences between values of a variable at specific points in space and time [8,9,10];
• Finite Element Method (FEM): Divides the domain into smaller elements and approximates the solution within each element using a set of shape functions [7,11];
• Finite Volume Method (FVM): Divides the domain into control volumes and enforces conservation of the transported quantity within each volume [12];
• Radial Basis Function (RBF) Method: A mesh-free method that approximates solutions using radial basis functions [8].

1.4. Galerkin’s Method

The Galerkin method is a widely used numerical technique for approximating solutions to the convection-diffusion-reaction equation. It belongs to the family of weighted residual methods and forms the basis of the finite element method (FEM). The key idea behind the Galerkin method [8] is to find an approximate solution within a finite-dimensional space by minimizing error when the approximate solution is inserted into the original equation [13].

1.4.1. Variational Formulation

The Galerkin method begins by converting the original differential equation into its variational form. This involves multiplying the equation by a test function and integrating by parts over the domain. This reduces the original problem to first-order derivatives, which is a key feature for using relatively simple approximation spaces.

1.4.2. Approach Space

The Galerkin method approximates solutions using subspaces of finite-dimensional functions [11,14]. This subspace is typically constructed using polynomial-shaped functions. The choice of the approximation space is crucial. Finite element spaces, which are defined by a domain mesh and a set of shape functions on each mesh element, are often used [15,16].

1.4.3. Galerkin Discretization

The variational form of the equation is solved using functions of a finite-dimensional space [14]. This expression is a linear combination of shape functions within the chosen finite-dimensional space.

This method requires the variational form of the equation to be satisfied for all test functions within the same space. This results in a system with an equal number of linearly independent equations and unknowns. These unknowns correspond to the nodal values of the variable $u$ [15].

1.4.4. Error Analysis

Error analysis is important for determining the accuracy of an approximation. Optimal error estimates can be derived for certain Galerkin methods when assumptions are made about the regularity of the exact solution. Factors such as the choice of numerical scheme or irregularities in the mesh can affect the rate of convergence [17,18].

1.4.5. Instability

The Galerkin method can become unstable in problems with dominant convection ($k\ll \left|\mathit{a}\right|$), which can lead to spurious oscillations in the numerical solution.

Several stabilization techniques have been developed to overcome these problems. These techniques modify the Galerkin method to reduce oscillations, thereby improving the stability and accuracy of the numerical solution. Some of these techniques are:

• Galerkin least squares (GLS): Uses a least-squares term in the Galerkin formulation, resulting in a more stable approximation [19,20];
• Discontinuous Galerkin (DG): Allows for discontinuities in the approximation at element boundaries. DG can handle complex flows and high Péclet numbers and is used in the discretization of the hyperbolic convection-diffusion-reaction model [16,21];
• Petrov–Galerkin: Uses different spaces for the trial and test functions, unlike the standard Galerkin method, where they are the same. This approach is often designed to be more robust [13,16];
• Hybridizable Discontinuous Galerkin (HDG): Combines the advantages of discontinuous Galerkin (DG) methods with hybridization techniques that reduce degrees of freedom [17,22].

1.5. Related Works

The numerical solution of convection-diffusion-reaction (CDR) equations has evolved through various methodological approaches. Each approach addresses specific computational challenges and contributes unique innovations to the field. Traditional finite element methods have been refined to overcome the limitations of convection-dominated problems, which are characterized by the Péclet number ($P_e$), defined as $P_e ={\displaystyle \frac{\left|a\right|h}{2k}}$, where $\left|a\right|$ is the magnitude of the convective velocity, $h$ is the characteristic element size, and $k$ is the diffusion coefficient. When $P_e$ exceeds unity ($P_e > 1$), spurious oscillations typically emerge in standard Galerkin formulations, indicating that convective transport significantly dominates diffusive processes [23]. These nonphysical oscillations manifest in regions with steep gradients and boundary layers, compromising solution accuracy. Specialized stabilization techniques are required to ensure numerical stability and preserve the physical meaning of the computed solutions. Realistic convection-diffusion-reaction systems often include nonlinear reaction terms or space-dependent coefficients, which significantly complicate numerical analysis and solution strategies. Studies have shown that nonlinear reaction kinetics in biomedical applications exhibit complex, concentration-dependent behaviors that require sophisticated numerical approaches [24,25]. Space-dependent reaction coefficients naturally arise in heterogeneous porous media applications, where local material properties vary significantly across computational domains. The Galerkin finite element method provides an optimal theoretical framework for handling such complexities through its variational formulation. This formulation enables the systematic treatment of nonlinear terms while maintaining mathematical rigor and computational efficiency for diverse reaction mechanisms and heterogeneous material distributions.

Nadukandi et al. pioneered the development of high-resolution Petrov–Galerkin (HRPG) finite element methods for one-dimensional CDR problems, systematically addressing spurious oscillations through novel stabilization parameters derived from discrete upwinding operations and mass-lumping techniques [26]. Their approach incorporated both streamline upwinding and discontinuity-capturing operators within a nonlinear Petrov–Galerkin formulation using linear elements, demonstrating superior performance compared to established SUPG, CAU, and modified CAU methods by achieving second-order accuracy in smooth regimes while maintaining excellent shock-capturing capabilities. Building upon this foundation, ref. [27] extended the HRPG methodology to multidimensional scenarios, employing lowest-order block finite elements combined with objective characteristic tensors to achieve frame-independent stabilization parameters. Their implementation utilized bilinear block finite elements with temporal discretization through the generalized trapezoidal method, solved via Picard methodology with a convergence tolerance of 1 × 10⁻⁵, demonstrating superior layer resolution compared to existing stabilized methods while effectively handling exponential and parabolic boundary layers. Lima et al. in 2021 [24] contributed to traditional finite element approaches by implementing the Galerkin finite element method with comprehensive error correlation analysis, utilizing linear shape functions over standardized domains and employing MATLAB for numerical computations and visualization. Their methodology addressed nonlinear parabolic partial differential equations without truncating nonlinear terms, achieving exceptional convergence properties with absolute errors ranging from ${10}^{-10}$ to ${10}^{-2}$ depending on mesh refinement, while demonstrating versatility across diverse engineering applications, including neutron diffusion and pollutant transport modeling. These methodologies were limited by complex parameter calibration requirements, and restricted accessibility for educational purposes. The CDR-Solv framework overcomes these limitations with an open-source implementation that requires minimal parameter tuning.

Innovative hybrid and meshless approaches have emerged to address computational limitations of traditional discretization methods. In 2012, Shirzadi et al. [28] developed a superior numerical framework combining meshless local Petrov–Galerkin (MLPG) formulation with specialized finite difference approximations for Caputo fractional derivatives, creating a hybrid weak-form solution strategy for two-dimensional fractional-time CDR equations. Their implementation featured circular subdomains with sophisticated adaptive stepping algorithms and eight-point Legendre–Gauss quadrature formulations, demonstrating capability to handle convection coefficients ranging from $\omega = 0.005$ to $\omega = 15$, substantially exceeding the limitations of strong-form methodologies. Liu et al. in 2021 [29] advanced meshless methodologies by developing the localized method of fundamental solutions (LMFS) for transient CDR equations, combining Crank–Nicolson time-stepping with pseudo-spectral Chebyshev collocation schemes in their CN-CCS-LMFS approach. Their MATLAB implementation utilized the ‘gmres’ and ‘pinv’ functions with specific tolerance settings, transforming dense matrix structures into sparse, banded systems through domain decomposition techniques, enabling large-scale dynamic simulations that were previously computationally prohibitive while maintaining accuracy comparable to traditional methods. In 2011, Theeraek et al. [30] contributed an innovative adaptive finite volume element method that combined cell-centered finite volume discretization with finite element concepts, implementing second-order accuracy through Taylor series expansion along local characteristic lines. Their approach integrated adaptive meshing utilizing an advancing front methodology with weighted residual methods from finite element theory, successfully eliminating spurious oscillations while optimizing computational efficiency through dynamic element size adjustment based on principal stress concepts from solid mechanics theory. These sophisticated methodologies remain limited by complex mathematical formulations and commercial software dependencies. The CDR-Solv study addresses these limitations by providing an open-source Python implementation with simplified ASGS stabilization.

Specialized high-order and spectral methodologies have been developed to achieve superior accuracy with reduced computational requirements. In 2022, Mkhatshwa and Khumalo [31] introduced a novel trivariate spectral collocation approach (TSQLM) for three-dimensional elliptic partial differential equations, employing quasilinearization methods combined with triple Lagrange interpolating polynomials established via Chebyshev–Gauss–Lobatto nodes. Their MATLAB 2015a implementation utilized specialized functions including kron() for Kronecker products and superkron() for multi-matrix operations, achieving exceptional accuracy with absolute errors approaching 10⁻¹⁷ using minimal grid sizes of 15 × 15 × 15, significantly outperforming existing methods that required thousands of discretization points for equivalent precision. Wei et al. in 2022 [32] developed innovative high-order compact (HOC) finite difference methods utilizing fourth-order Padé approximation schemes combined with Taylor series expansion and truncation error remainder correction, achieving fourth-order spatial accuracy and second-order temporal accuracy. Their methodology employed minimal computational stencils of five points for 2D and seven points for 3D problems compared to traditional approaches requiring 9–27-point stencils. It implemented successive over-relaxation iterative methods with PHOEBESolver software v2.x for validation, demonstrating unconditional stability for variable coefficient problems, in which existing HOC methods typically face stability limitations. In 2021, Ullmann et al. [33] contributed specialized reduced basis methodologies by implementing Stochastic Galerkin Reduced Basis (SGRB) and Monte Carlo Reduced Basis (MCRB) approaches for parameter-dependent statistics estimation. Their implementation employed finite element discretization using continuous piecewise linear elements with 225 to 961 degrees of freedom, utilizing polynomial chaos expansions with Legendre polynomials and proper orthogonal decomposition for snapshot-based reduced space generation, demonstrating that approximately 16 reduced basis functions sufficed for accurate statistical estimates while providing computational speedup proportional to Monte Carlo sample sizes. These specialized approaches require complex mathematical expertise and lack algorithmic transparency, which limits educational accessibility. The CDR-Solv framework, however, provides complete algorithmic transparency and educational accessibility while maintaining robust, high-order stabilization capabilities for convection-dominated transport problems.

Surface-based and advanced flux correction methodologies have addressed specialized geometric and physical constraints. Xiao et al. in 2019 [34] developed an adaptive finite element methodology specifically for CDR equations on curved surfaces, combining the Surface Finite Element Method (SFEM) with Streamline Diffusion Method (SDM) for stabilization and Zienkiewicz–Zhu gradient-recovery-based error estimation for adaptive mesh refinement. Their implementation employed piecewise linear finite elements on curved triangular meshes with local Delaunay algorithm refinement strategies, achieving convergence rates between 1.7 and 5.0 while successfully capturing complex solution behaviors, including spiral-type curves and internal layers on spherical and toroidal surfaces. It is worth mentioning the prior work of Zalesak [35], which addressed critical limitations of flux-corrected transport algorithms by developing fully multidimensional flux limiting techniques, implemented through sophisticated finite difference approaches in conservation form. Their vectorized Fortran implementation on a Texas Instruments ASC computer employed leapfrog-trapezoidal transport algorithms with varying spatial accuracy orders from second to eighth order, combining low-order monotonic schemes with high-order schemes through novel six-step procedures that simultaneously considered antidiffusive fluxes in all coordinate directions, effectively eliminating “clipping” phenomena while maintaining sharp discontinuity resolution over 2–4 grid points without numerical oscillations. Analytical and specialized mathematical approaches have provided alternatives to purely numerical methodologies. In 2022, Parhizi et al. [36] diverged from traditional numerical approaches by developing a comprehensive Green’s function-based methodology for arbitrary source terms in CDR equations, employing mathematical transformation approaches through variable substitution and separation of variables techniques to derive eigenvalue-based solutions. Their purely analytical framework eliminated computational instabilities commonly encountered in finite element and finite difference methods, requiring only 7–25 eigenvalues for convergence across different Péclet numbers with computation times of 0.4–3.3 s compared to 4.1 s for conventional numerical methods, while providing superior accuracy and computational speed for complex transport phenomena, including drug delivery systems and contaminant dispersion applications. These approaches are limited by geometry-specific implementations, complex, multi-step algorithms, and restricted applicability to specific source term configurations. The CDR-Solv framework overcomes these limitations by providing consistent ASGS stabilization across arbitrary convection regimes, robust high-order finite element formulations for general geometries, and parameter-free stabilization that eliminates the need for complex calibration procedures while maintaining computational stability in transport-dominated scenarios.

There are a few open-source software alternatives available for solving CDR problems, such as FEniCS [37] and OpenFOAM [38]. While FEniCS and OpenFOAM offer extensive finite element and computational fluid dynamics capabilities, they often necessitate substantial expertise and intricate configurations for CDR issues. The CDR-Solv framework stands out by offering specialized ASGS stabilization, educational accessibility, and simplified implementation tailored specifically for convection-dominated transport phenomena. Its transparent algorithmic structure is designed for research and pedagogical applications in developing computational environments.

1.6. Outline

This paper is organized as follows: Section 1, “Introduction,” presents the convection-diffusion-reaction problem and explains why stabilized finite element methods are necessary in convection-dominated regimes. Section 2, “Materials and Methods,” describes the mathematical formulation of the ASGS stabilization method and its computational implementation with high-order finite elements in Python. Section 3, “Results,” presents the numerical solutions obtained with different polynomial degrees and source term configurations. Section 4, “Discussion,” analyzes the ASGS method’s effectiveness compared to existing approaches and outlines the educational contributions of the open-source CDR-Solv framework. Section 5, “Conclusions,” summarizes the findings on the successful combination of ASGS stabilization and high-order finite elements and identifies areas for future research.

2. Materials and Methods

2.1. Mathematical Models

The stationary scalar convection-diffusion-reaction Equation (2) was used, where $u$ is solved for using numerical methods.

$$\begin{gathered} \mathcal{L}\left(u\right):=-k∆u+\mathit{a}\cdot \nabla u+su=f in \mathsf{\Omega } \\ u=u_D in \partial \mathsf{\Omega }, \end{gathered}$$

(2)

where $u$ is the unknown scalar variable in $\mathsf{\Omega }$, $k$ is the diffusion coefficient, $\mathit{a}$ is the convective velocity field for incompressible flow, $s$ is the reaction coefficient, and $f$ is the known source term. The Dirichlet boundary conditions $u_D$ are known along the boundary $\partial \mathsf{\Omega }$. In addition to Dirichlet boundary conditions, convection-diffusion-reaction problems may require alternative formulations of boundary conditions that are particularly relevant for convection-dominated regimes. Neumann boundary conditions specify the normal flux across the boundary as $\partial u/\partial n = g$, where $g$ is the prescribed flux value. This is essential for modeling regions of inflow and outflow where the concentration gradient is known rather than the concentration itself. Robin boundary conditions, also known as mixed boundary conditions, combine concentration and flux information in the form $\alpha u + \beta (\partial u/\partial n) = \gamma$, where $\alpha$, $\beta$, and $\gamma$ are prescribed coefficients [39]. These boundary conditions are important for convection-dominated problems because they allow for the proper treatment of outflow boundaries, where the solution behavior is primarily governed by convective transport, and they can be easily added to the framework in Equation (2).

Integrating Equation (2) by parts yields the continuous variational form of the problem, which is to find $u\in V=H_0^1\left(\Omega \right)$ such that:

$$\underset{\Omega }{\int }\left(k\nabla \mathrm{u}\cdot \nabla v+v \mathit{a}\cdot \nabla \mathrm{u}+vs\mathrm{u}\right)\mathrm{d}\mathsf{\Omega }=\underset{\mathsf{\Omega }}{\int }vf \mathrm{d}\mathsf{\Omega } \forall v\in V,$$

(3)

By partitioning the domain $\mathsf{\Omega }=\bigcup _i^{n_{el}}{\Omega }_i^e$, we obtain the discretized integral equation that allows us to find $u_h\in V_h$, where $n_{el}$ is the number of elements in the partition, and ${\Omega }_i^e$ is the domain of the element:

$$\sum _{e=1}^{n_{el}}\underset{{\mathsf{\Omega }}^e}{\int }\left(k\nabla u_h\cdot \nabla v_h+v_h \mathit{a}\cdot \nabla u_h+v_{h}s{u}_h\right)\mathrm{d}\mathsf{\Omega }=\sum _{i=1}^{n_{el}}\underset{{\mathsf{\Omega }}^e}{\int }{v}_{h}f \mathrm{d}\mathsf{\Omega } \forall v_h\in {\mathrm{V}}_h,$$

(4)

To numerically calculate the integrals in Equation (4), we approximate the variable $\mathrm{u}$ in the domain ${\mathsf{\Omega }}^e$ with $u_h$ by interpolating with shape functions, given by:

$$u_h=\sum _{m=1}^M{u}_m{N}_m,$$

(5)

where $M$ is the number of nodes in the finite element, $u_m$ is the nodal value of the function $u$ at the node $m$, $N_m$ is the polynomial form of the function such that it equals one at node $m$ and zero at the other nodes in the finite element.

By replacing Equation (5) and using the Galerkin method for $V_h=N_l$, we obtain the standard Galerkin formulation. This formulation can be used to solve the stationary scalar convection-diffusion-reaction equation numerically using a computational algorithm developed in Python:

$$\sum _{e=1}^{n_{el}}\sum _{m=1}^M{u}_m\underset{{\mathsf{\Omega }}^e}{\int }\left(k\nabla N_l\cdot \nabla N_m+N_l \mathit{a}\cdot \nabla N_m+N_{l}s{\mathrm{N}}_{\mathrm{M}}\right)\mathrm{d}\mathsf{\Omega }=\sum _{i=1}^{n_{el}}\underset{{\mathsf{\Omega }}^e}{\int }{N}_{l}f \mathrm{d}\mathsf{\Omega }\forall l=\mathrm{1,2},\dots ,\mathrm{M}.$$

(6)

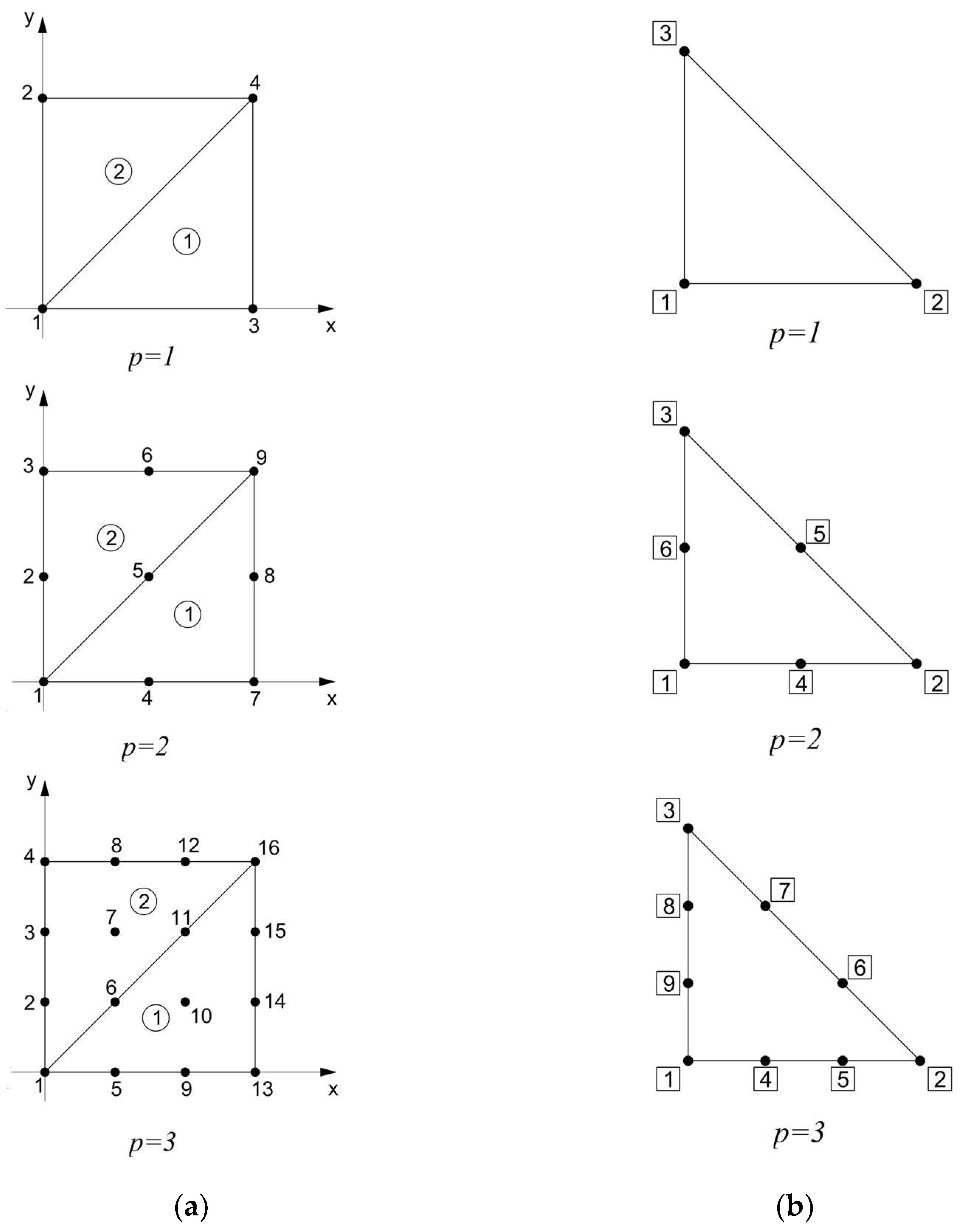
2.2. Shape Functions

Shape functions enable the numerical calculation of the convection-diffusion-reaction equation. In the present case, the functions must be of class $C^0$, i.e., they must be continuous. Continuity depends on how the functions are connected element by element, rather than how they are interpolated within them. Lagrange class elements, the most common in the finite element method, belong to class ${\mathrm{C}}^0$, while Hermite class elements belong to class $C^1$ [15].

The model used contains second derivatives in the convection-diffusion-reaction equation. When weakened with the variational form, the largest derivatives are of first order. Therefore, $C^0$ class shape functions are required to satisfy continuity between elements, and at a minimum, linear shape functions are required to obtain mesh convergence. Test functions must have the same continuity conditions as shape functions to approximate the unknown function $u$ [14,15].

2.3. Regular Mesh

The equation is solved for a rectangular area with sides $lx$ and $ly$. Given the number of elements into which each side of the rectangle is divided and the degree of the polynomial $p$ of the shape functions, a grid is generated in which each intersection corresponds to a node. The nodes are numbered globally from bottom to top and from left to right, including the edges. The total number of nodes, including the edges, is ${\left(np+1\right)}^2$, and the total number of nodes inside the mesh, excluding the edges, is ${\left(np-1\right)}^2$. This corresponds to the number of unknowns because the values of the function at the edges are known, as the Dirichlet conditions are prescribed at the boundary. The total number of triangular elements is $2n^2$.

As in previous studies [32,33], we tested different configurations, including three polynomial degrees ranging from linear to cubic, due to their advantages in exploring high-gradient areas. Figure 1a presents an example of the global node numbering (points with numbers) and triangular element numbering (enclosed numbers) for a single segment on each side of the rectangle and for three polynomial degrees of linear ($p=1$), quadratic ($p = 2$), and cubic ($p = 3$) shape functions.

Figure 1b shows the local numbering of nodes in a triangular element for the three polynomial degrees. Local numbering allows for consistent referencing of nodes forming a triangular element, which is required in the connectivity matrix.

The current CDR-Solv implementation directly supports structured rectangular meshes through the regular mesh generation algorithm. However, users requiring unstructured or complex geometries can adapt the framework by implementing custom Lagrange shape functions (linear, quadratic, or cubic) with minimal modifications to the Python code, particularly in the shape function evaluation modules ($ffT$, $vffydp2DT$ detailed in Section 2.6). Additionally, while the current implementation uses regular structured meshes for instructional purposes, it is recognized that resolving the boundary layer in convection-dominated flows often necessitates unstructured and adaptive mesh refinement strategies, especially anisotropic refinement near steep gradients and boundary layers [40]. The CDR-Solv framework architecture allows for the straightforward implementation of adaptive mesh refinement algorithms by modifying the mesh generation and connectivity matrix functions. However, to maintain the educational focus and algorithmic transparency of this version, adaptive meshing capabilities were excluded from the current implementation and will be included in future releases.

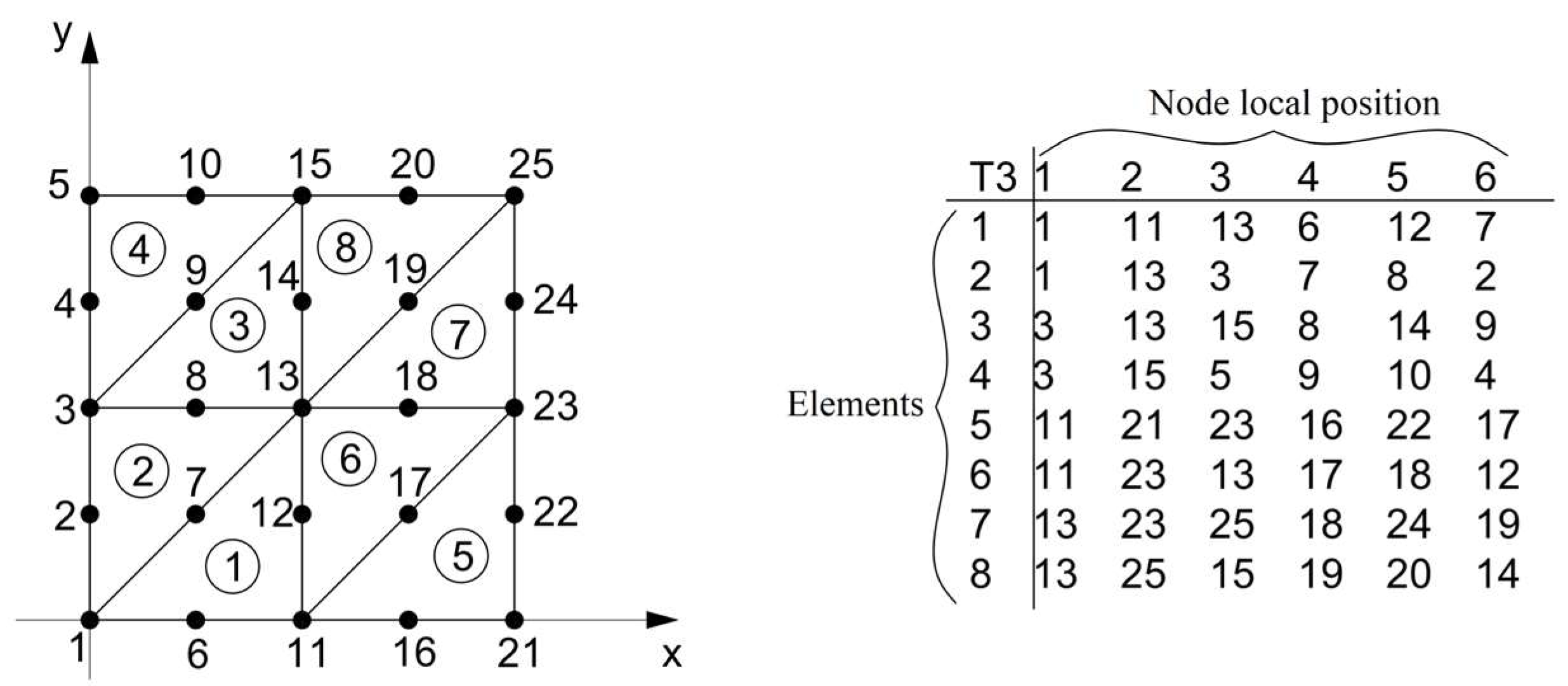
2.4. Connectivity Matrix

The connectivity matrix containing $2n^2$ rows is generated based on the number of elements into which each side of the rectangle is divided and the degree of the polynomial of the shape functions. Each row of the connectivity matrix corresponds to a triangular element. For each triangular element, a list of node numbers is placed based on the global node numbering (see Figure 1a). This list must follow the sequence given by the local node numbering (see Figure 1b).

Figure 2 shows an example of a connectivity matrix with $n = 2$ and $p = 2$. The eight triangular elements are numbered, and the global node numbering and connectivity matrix follow the sequence given by the local node numbering in Figure 1b for $p = 2$.

2.5. Elementary Matrix and Force Vector

The elementary matrix and force vector are generated for each triangular element, considering the parameters defined in the stationary scalar convection-diffusion-reaction equation statement.

In the standard Galerkin formulation, the element matrix of Equation (7) and the force vector of Equation (8) are unstable in the case of dominant convection:

$$\begin{array}{cc}{k}_{lm}^e={\int }_{{\Omega }^e}(k𝛻N_l\cdot 𝛻N_m+N_l\mathit{a}\cdot 𝛻N_m+N_{l}s{N}_m)d\Omega & \forall l,m=\mathrm{1,2},\dots , M\end{array},$$

(7)

$$\begin{array}{cc}{f}_l^e={\int }_{{\Omega }^e}{N}_{l}fd\Omega & \forall l=\mathrm{1,2},\dots , M\end{array},$$

(8)

Applying ASGS stabilization [41,42] yields the stable element matrix (Equation (9)) and the stable force vector (Equation (10)):

$$\begin{gathered} \begin{array}{cc}{k}_{l{m}_{stab}}^e={\int }_{{\Omega }^e}\left[\right(k𝛻N_l\cdot 𝛻N_m+N_l\mathit{a}\cdot 𝛻N_m+N_{l}s{N}_m)& \end{array} \\ +{\tau }_K(-k∆N_l+\mathit{a}\cdot 𝛻N_l+s{N}_l)( -k∆N_m+\mathit{a}\cdot 𝛻N_m+s{N}_m)] d\Omega \\ \forall l,m=1,2,\dots , M, \end{gathered}$$

(9)

$$\begin{array}{cc}{f}_{l_{stab}}^e={\int }_{{\Omega }^e}\left[N_{l}f+{\tau }_K\left(-k∆N_l+\mathit{a}\cdot 𝛻N_l+s{N}_l\right) f \right] d\Omega & \forall l,m=\mathrm{1,2},\dots , M\end{array},$$

(10)

In Equations (9) and (10), the stabilization parameter, ${\tau }_K$, is given by Equation (11):

$$\begin{array}{cc}{\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|\mathit{a}\right|p}{h}}\right)}^{-1} & with c_1=4 and c_2=2\end{array}$$

(11)

2.6. User Interface and Execution

A Python program was developed that allows the user to configure constants, source terms, and Dirichlet boundary conditions via a user interface. The CDR-Solv framework was written in Python 3.8 or higher and requires minimal core dependencies for optimal functionality. These include NumPy v1.21.0 for numerical computations, Matplotlib v3.3.4 for visualization rendering, SciPy v1.5.0 for scientific computing operations, and PyQt5 v 5.12.0 for graphical user interface development. These dependencies can be easily installed using standard Python package managers (pip or conda) or by downloading them directly from their official GitHub repositories. The program then uses Python functions created to obtain the solution, which is displayed as three- and two-dimensional plots.

The functions used are:

• main_cdr.py: This is the main file that contains initialization, the user interface, and all the used functions;
• get_config: This function retrieves all data entered in the user interface and verifies it;
• nodes: This function creates the regular mesh. The first column is the X coordinate, the second column is the Y coordinate, and each row represents a different node. The order of the nodes in this matrix determines the overall node numbering;
• tc3: This function generates the connectivity matrix. As shown in Figure 2, each row represents a triangular element and its component nodes;
• cccnpg: A function that transforms Cartesian coordinates to natural coordinates at a Gauss point;
• kefe2DT: A function that obtains the elemental matrix and force vector, corrected according to ASGS stabilization;
• ffT: A function that generates shape functions and their derivatives at a Gauss point for a given polynomial degree;
• vffydp2DT: Calculates the values of the shape functions and their partial derivatives at all Gauss points for triangular elements and all polynomial degrees;
• gauss2DT: Function to obtain matrices with Gauss weights and points;
• es2: Assembles and solves the system of equations under the entered parameters.

Figure 3 shows the complete algorithmic workflow of the CDR-Solv computational framework. Execution begins with parameter validation and mesh generation, then progresses through shape function preconditioning and Gauss integration point establishment. The core computational phase involves element-by-element assembly. During this phase, the kefe2DT function computes stabilized element matrices while incorporating coordinate transformations via cccnpg and shape function evaluations via ffT. Next, the algorithm applies Dirichlet boundary conditions, assembles the global system, and solves the resulting linear equations. Finally, it generates three-dimensional surface and two-dimensional contour visualizations of the computed solution field.

3. Results

The following figures are screenshots generated with boundary layers. In all examples, $\mathrm{k}=1\times {10}^{-5}$ is used to ensure dominant convection while maintaining $s=0$, $a_x=1, { a}_y=0, lx=1, ly=1$.

3.1. Evolution with Polynomial Degree

Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show an example of the evolution for different polynomial degrees ($p$), with $n = 20$ divisions and a constant source term of $f = 1$ and $u = 0$.

3.2. Other Functions for Source Term

In Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, p = 3, and the previous data are maintained; only the source term is changed.

Figure 9 and Figure 10 show the results with a source term of $f = x + y$.

Figure 12 and Figure 13 show the results with a source term of $f = x²y²$.

Figure 14 and Figure 15 show an example in which the result is known in advance: $u(x,y) = x^2 y^2 {\left(1-x\right)}^2 {\left(1-y\right)}^2$.

3.3. Comparative Validation

Finally, we tested whether the results of CDR-Solv solutions matched those of other available open-source tools. To this end, we considered the FEniCS library, the most complete and well-known solver available, which allows one to solve the CDR problem and implement boundary conditions and ASGS stabilization. To validate the computational framework developed in CDR-Solv, a comparative implementation was constructed using FEniCS version 2019.1.0, Ubuntu 24.04, and Python 3.7.3, which incorporates the NumPy 1.21.0 and Matplotlib 3.3.4 libraries. The validation code uses the same ASGS stabilization methodology with Lagrange finite elements as the original CDR-Solv framework, employing the same stabilization parameter, ${\tau }_K$, and the same physical parameters presented in Section 3.2. The FEniCS implementation uses automatic differentiation for gradient computations and integrates stabilization terms through variational formulation assembly, which enables a direct comparison of the numerical solutions. The code used for using FEniCS to solve the following examples is available at: “https://github.com/erickherreraresearch/CDR-Solv/blob/main/EjemploFEniCS.py (accessed on 21 July 2025)”. The results are presented in

Table 1. Solution validation using FEniCS library.

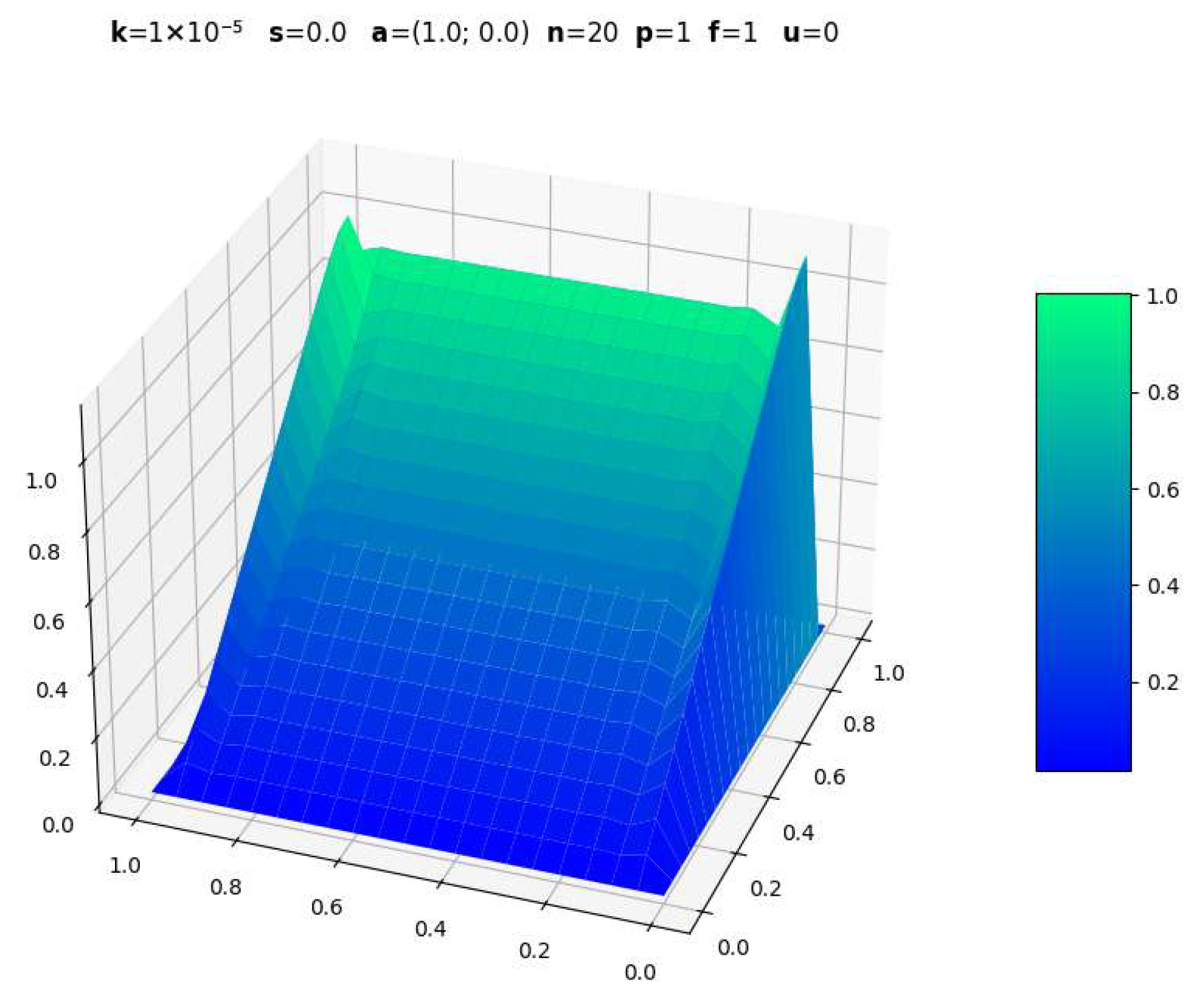
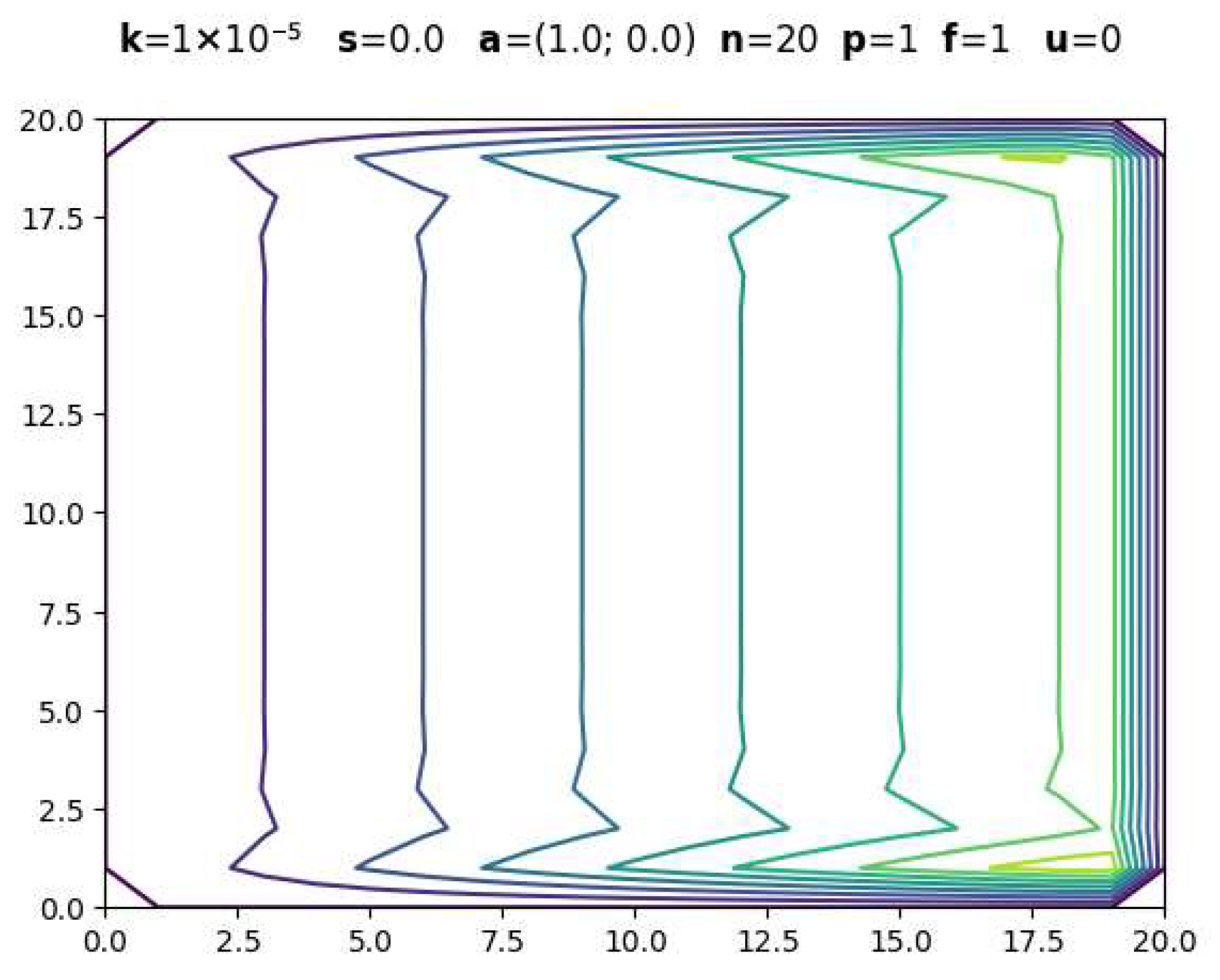
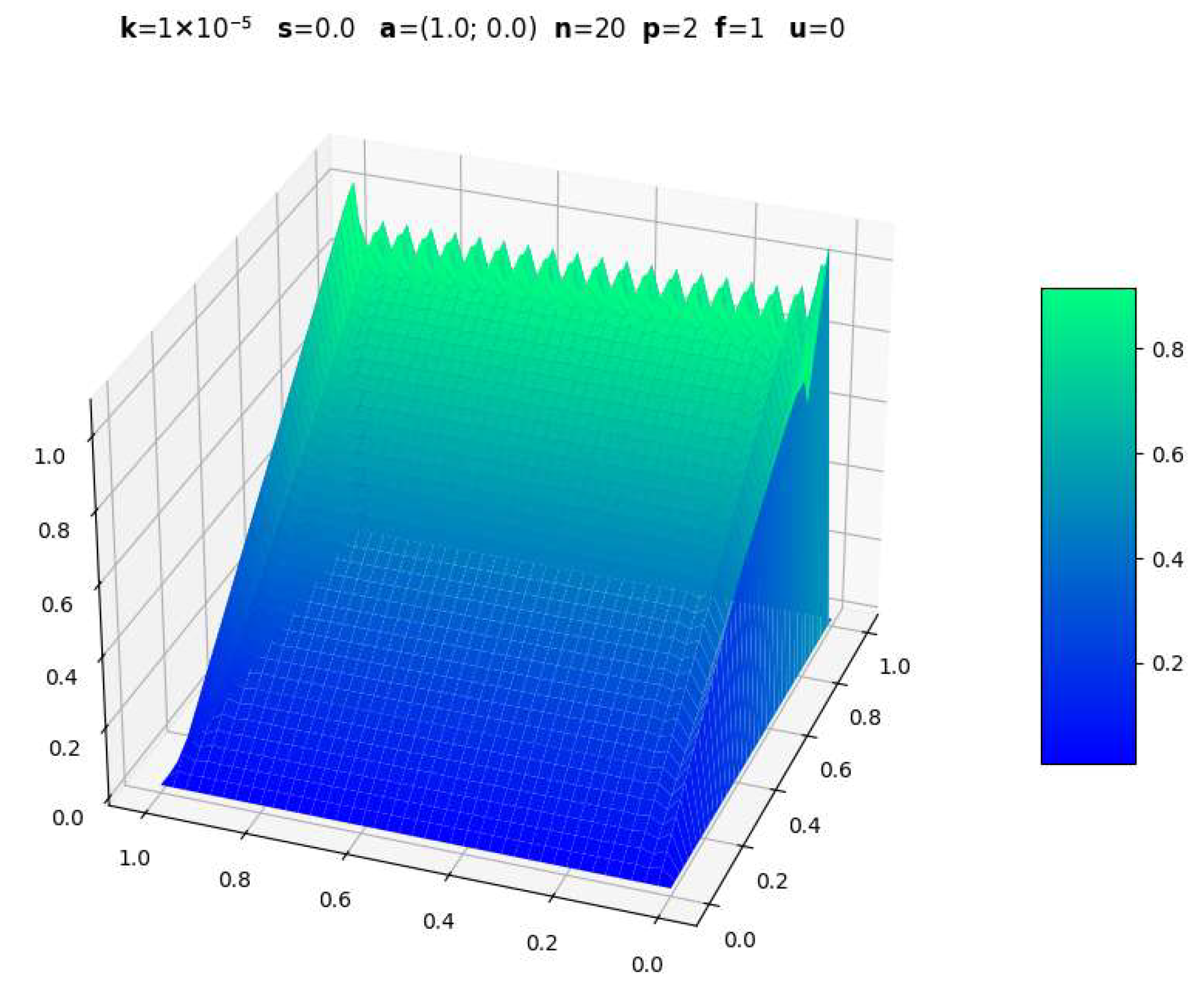
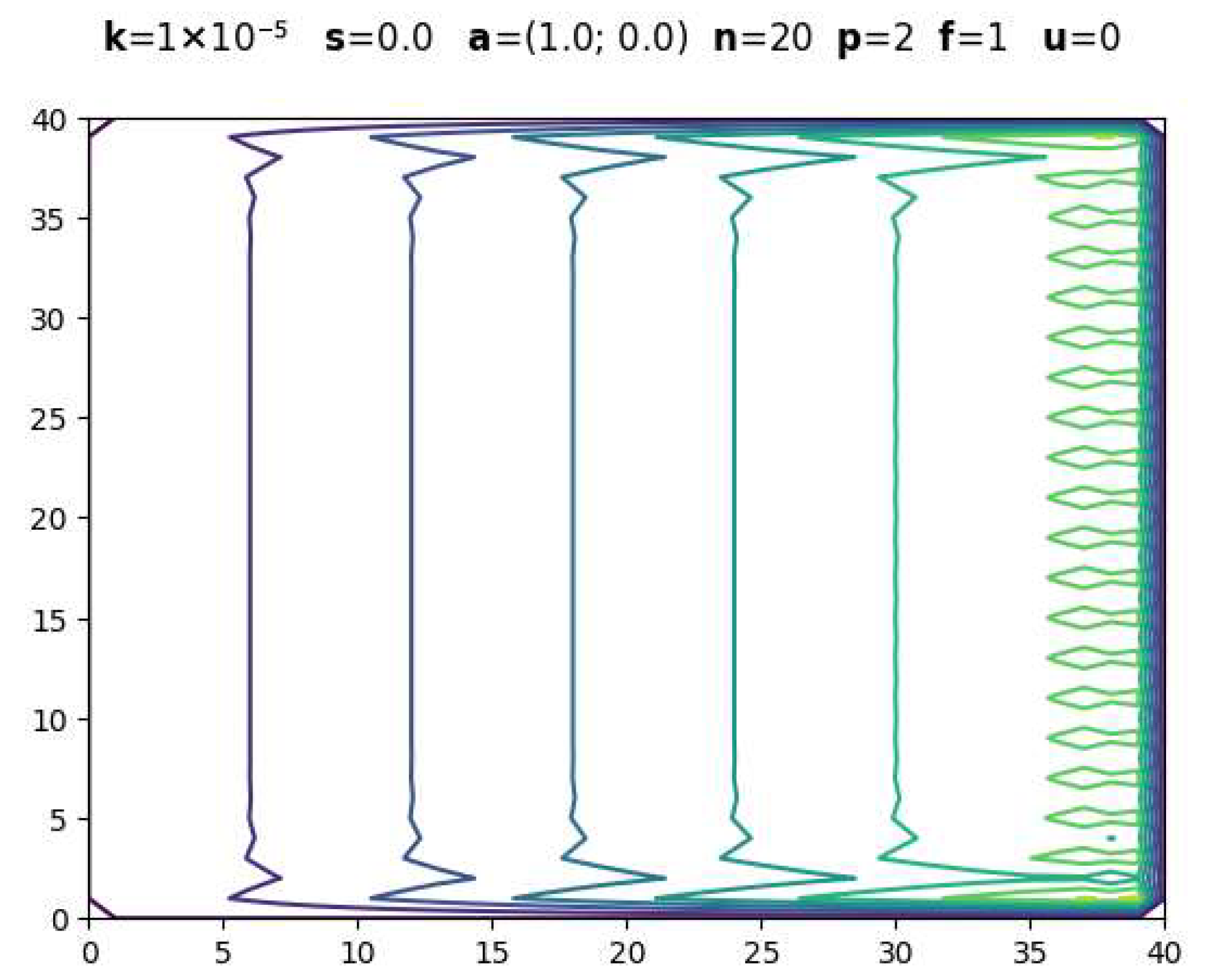
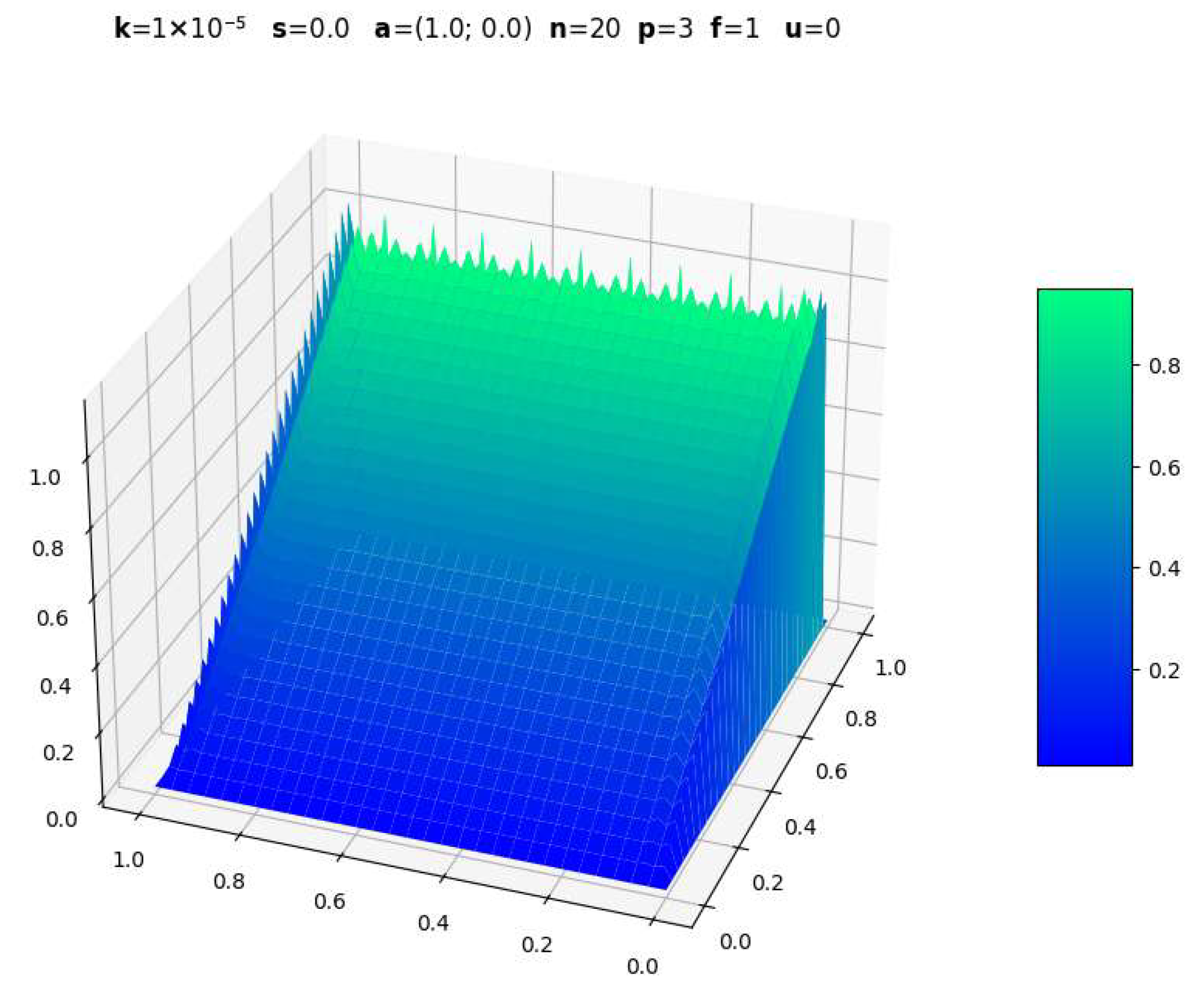
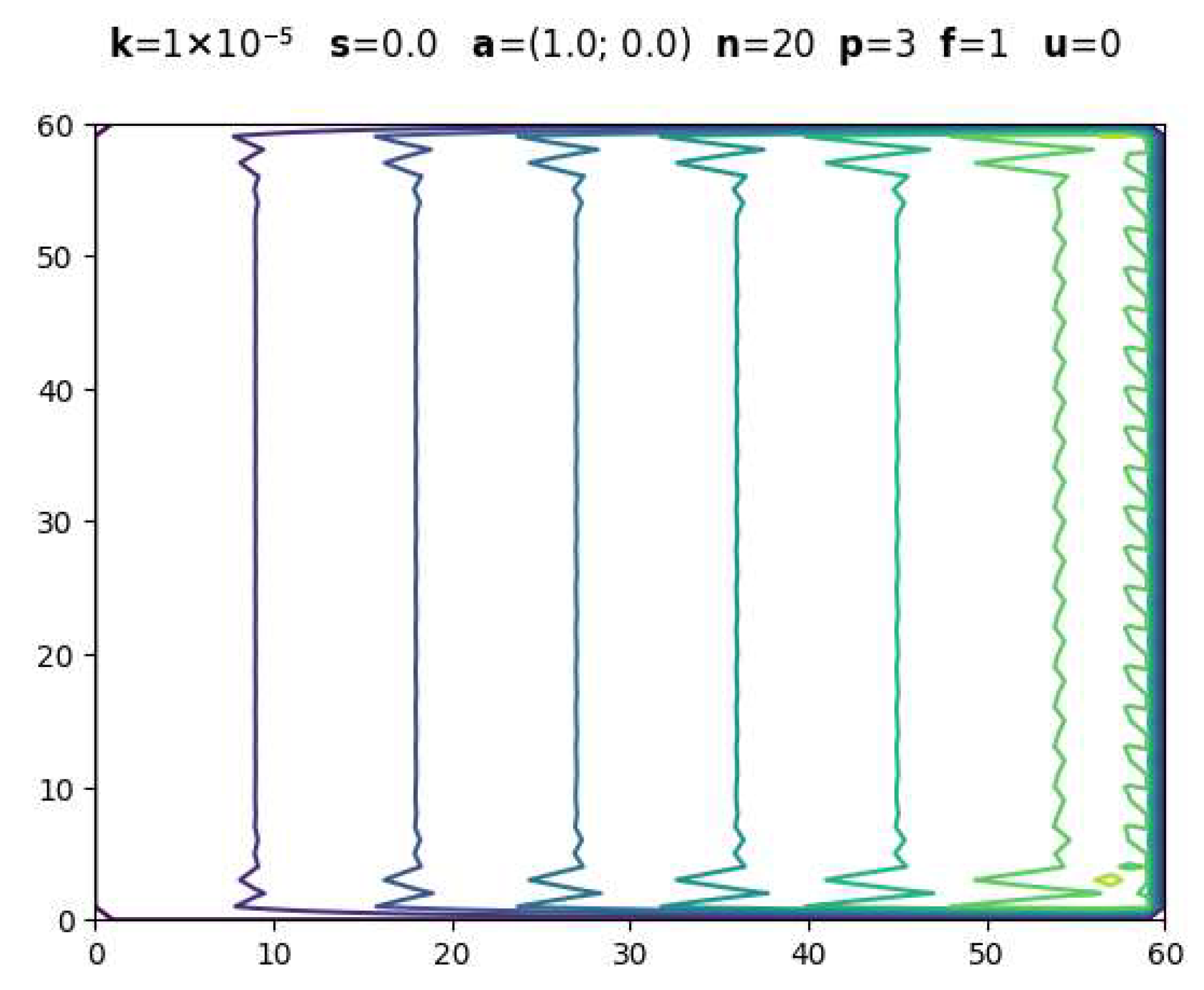
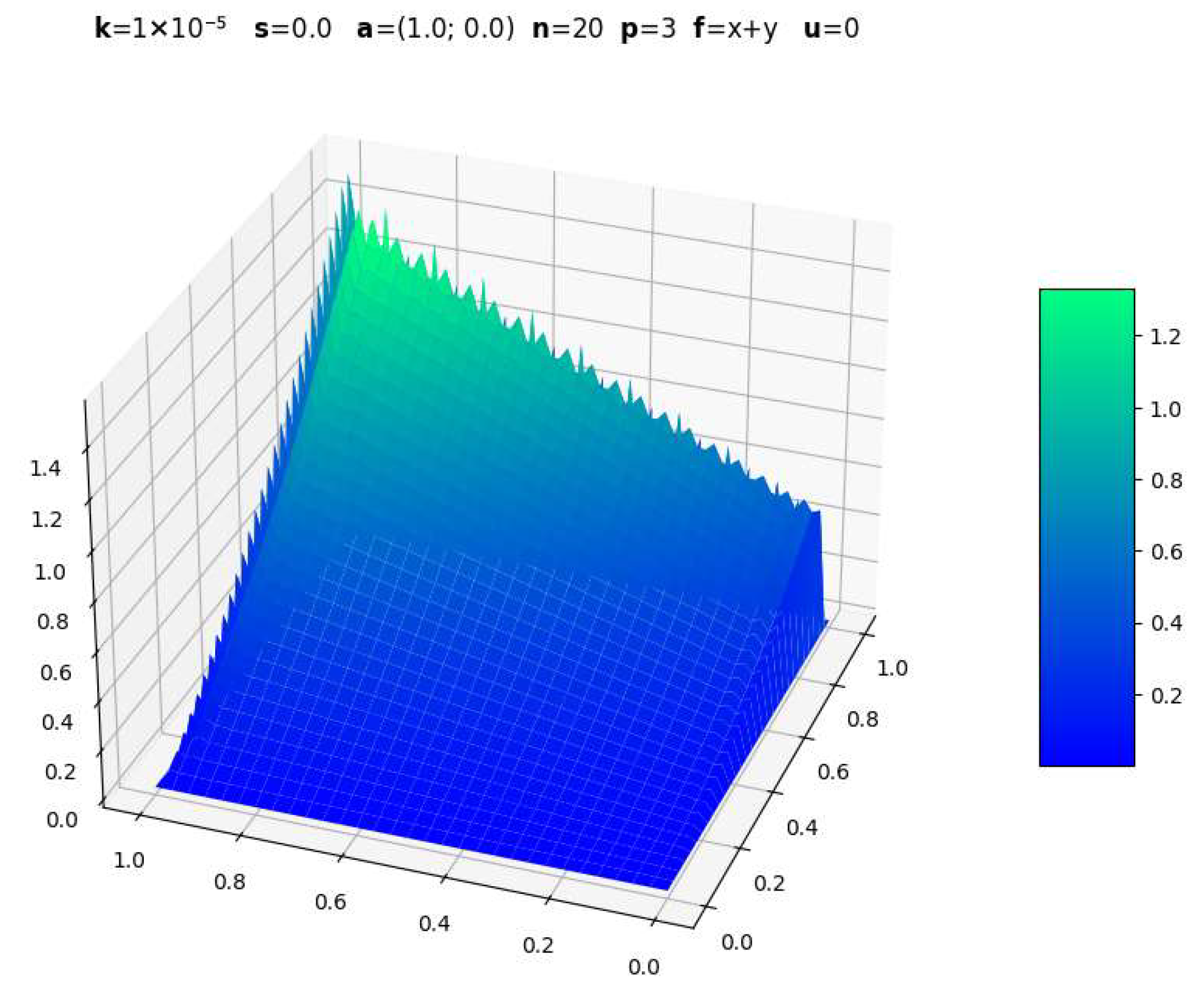
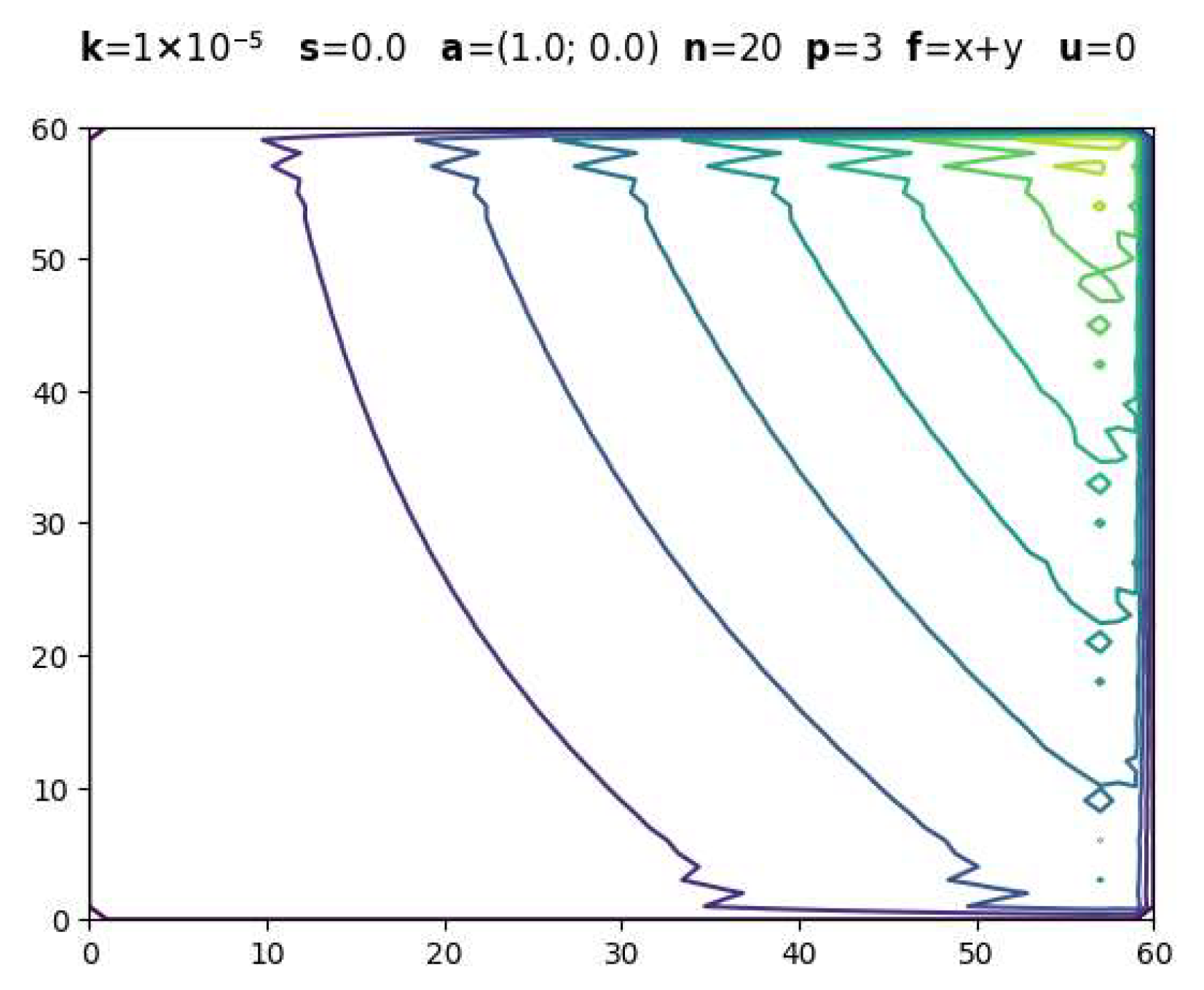
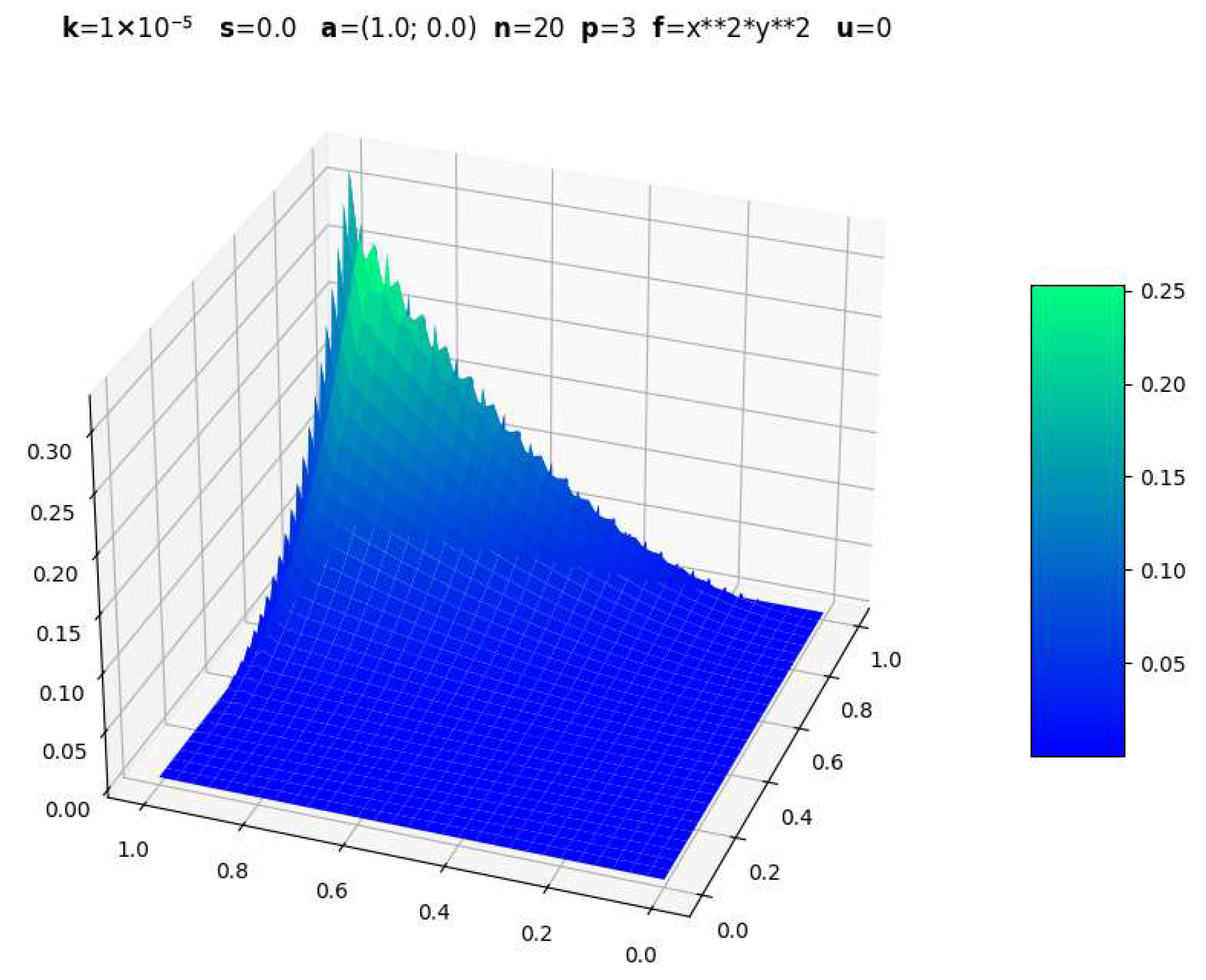
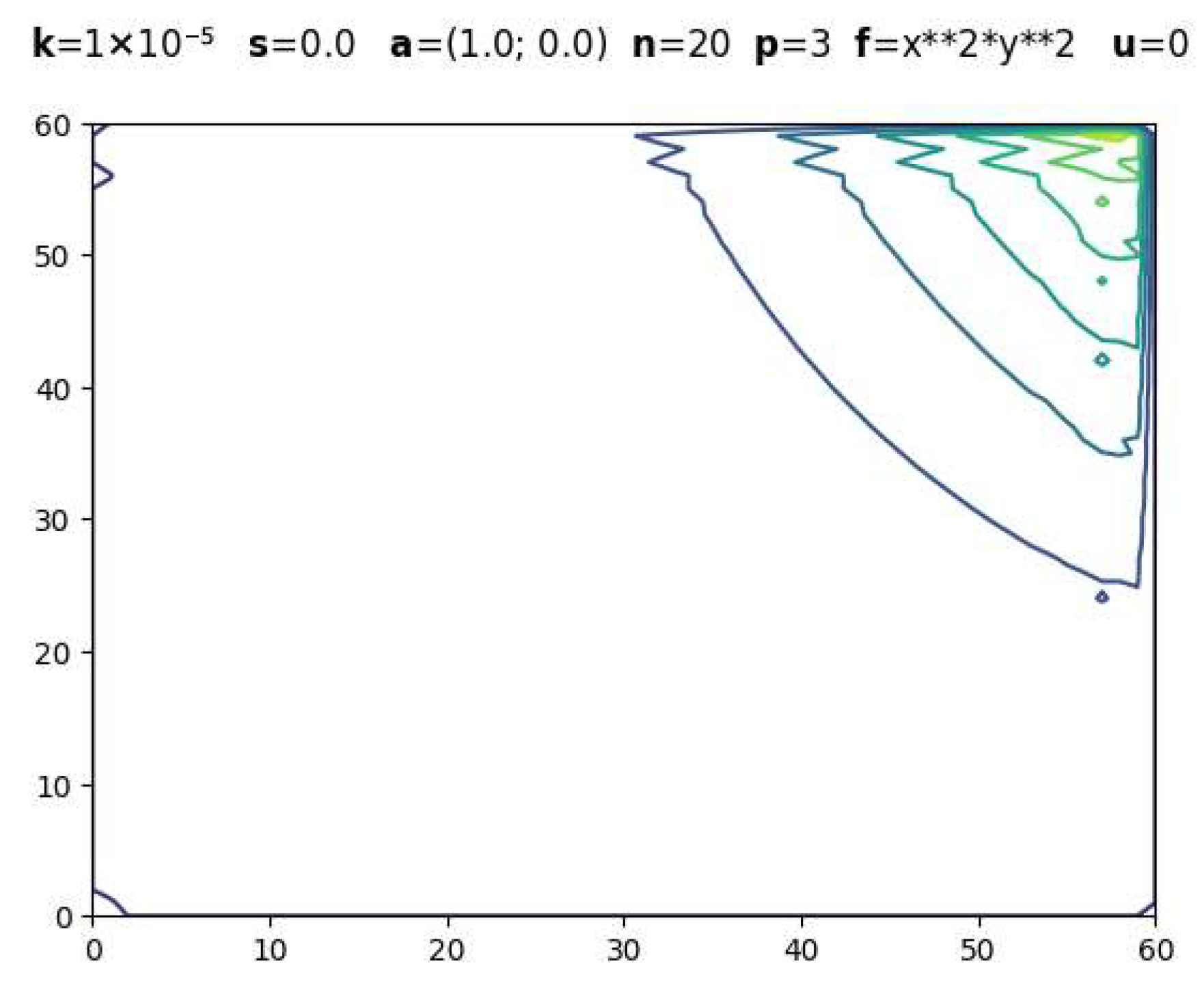
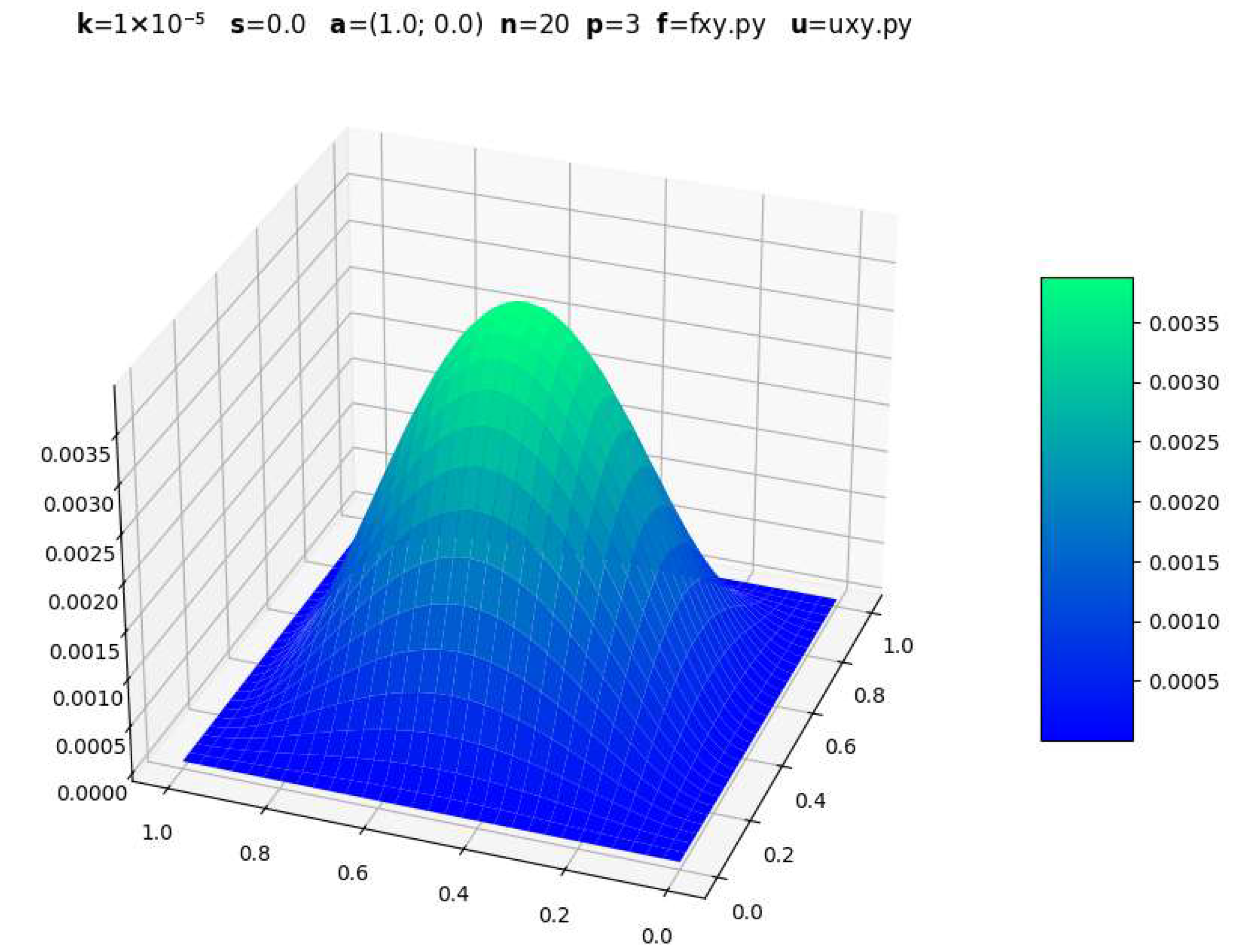
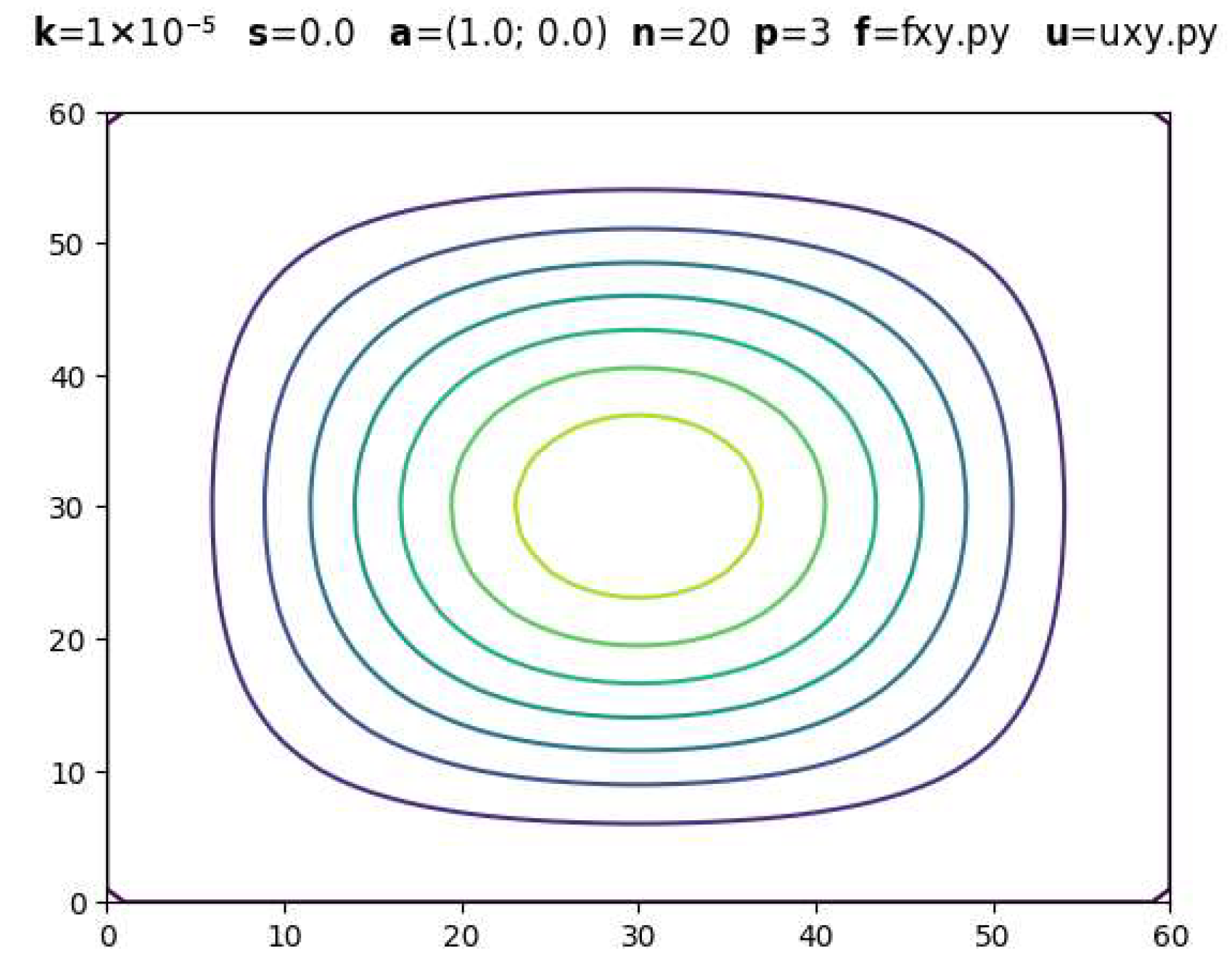
Parameters	CDR-Solv Solution	FEniCS Solution	Average Execution Times *
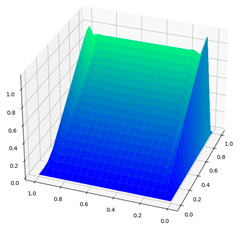$k=1\times {10}^{-5}$ $p=1$ $s=0$ $a=\left(\mathrm{1,0}\right)$ $f=1$ $u=0$ ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|\mathit{a}\right|p}{h}}\right)}^{-1}$			CDR-Solv: 1.0135 FEniCS: 1.0908 Approximate computational complexity: $\mathbf{CDR}\mathbf{\text{-}}\mathbf{Solv} \mathbf{(}\mathbf{GMRES}\mathbf{/}\mathbf{CG}\mathbf{)}\mathbf{\text{:}} \mathrm{from} O\left(n^{1.5}\right)$$\mathrm{to} O\left(n^2\right)$$\mathbf{FEniCS} \mathbf{(}\mathbf{LU}\mathbf{/}\mathbf{Cholesky}\mathbf{)}\text{:} O\left(n^3\right)$
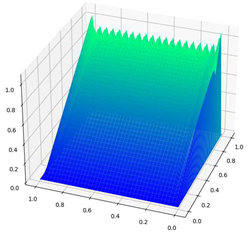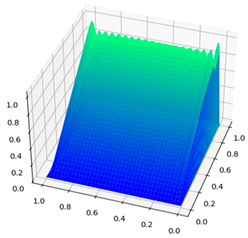$k=1\times {10}^{-5}$ $p=2$ $s=0$ $a=(1,0)$ $f=1$ $u=0$ ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|\mathit{a}\right|p}{h}}\right)}^{-1}$			CDR-Solv: 0.9874 FEniCS: 1.1572 Approximate computational complexity: $\mathrm{CDR}\mathbf{\text{-}}\mathbf{Solv} \mathbf{(}\mathbf{GMRES}\mathbf{/}\mathbf{CG}\mathbf{)}\mathbf{\text{:}} \mathrm{from} O\left(n^{1.5}\right)$$\mathrm{to} O\left(n^2\right)$$\mathbf{FEniCS} \mathbf{(}\mathbf{LU}\mathbf{/}\mathbf{Cholesky}\mathbf{)}\mathbf{\text{:}} O\left(n^3\right)$
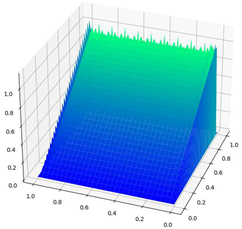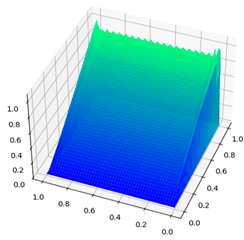$k=1\times {10}^{-5}$ $p=3$ $s=0$ $a=\left(\mathrm{1,0}\right)$ $f=1$ $u=0$ ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|\mathit{a}\right|p}{h}}\right)}^{-1}$			CDR-Solv: 1.1538 FEniCS: 1.2270 Approximate computational complexity: $\mathbf{CDR}\mathbf{\text{-}}\mathbf{Solv} \mathbf{(}\mathbf{GMRES}\mathbf{/}\mathbf{CG}\mathbf{)}\mathbf{\text{:}} \mathrm{from} O\left(n^{1.5}\right)$$\mathrm{to} O\left(n^2\right)$$\mathbf{FEniCS} \mathbf{(}\mathbf{LU}\mathbf{/}\mathbf{Cholesky}\mathbf{)}\mathbf{\text{:}} O\left(n^3\right)$
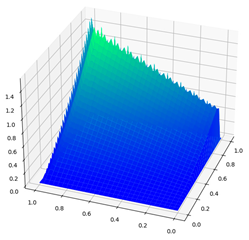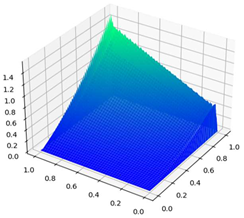$k=1\times {10}^{-5}$ $p=3$ $s=0$ $a=\left(\mathrm{1,0}\right)$ $f=x+y$ $u=0$ ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|\mathit{a}\right|p}{h}}\right)}^{-1}$			CDR-Solv: 1.5529 FEniCS: 2.1067 Approximate computational complexity: $\mathbf{CDR}\mathbf{\text{-}}\mathbf{Solv} \mathbf{(}\mathbf{GMRES}\mathbf{/}\mathbf{CG}\mathbf{)}\mathbf{\text{:}} \mathrm{from} O\left(n^{1.5}\right)$$\mathrm{to} O\left(n^2\right)$$\mathbf{FEniCS} \mathbf{(}\mathbf{LU}\mathbf{/}\mathbf{Cholesky}\mathbf{)}\mathbf{\text{:}} O\left(n^3\right)$

* The average times were obtained by taking the average of ten executions of each example. Section 4 provides more details regarding computer complexity. The computational validation was performed on a system equipped with an AMD Ryzen™ 7 3800X processor (8 cores, 16 threads, 3.9–4.5 GHz, TSMC made in Hsinchu, Taiwan), an NVIDIA RTX 3060 (3584 CUDA cores, 12 GB GDDR6, ASUS made in Hanoi, Vietnam), 16 GB of DDR4 RAM at 3200 MHz, and an NVMe SSD. The average power consumption was approximately 600 W.

.

4. Discussion

The present investigation successfully demonstrated the effectiveness of combining the algebraic sub-grid scale (ASGS) stabilization method with high-order finite elements for solving convection-diffusion-reaction equations in convection-dominated regimes. The computational framework developed in Python provided robust numerical solutions across multiple polynomial degrees and source term configurations, establishing a significant contribution to the field of computational fluid dynamics and transport phenomena modeling.

The numerical experiments conducted with various polynomial degrees ($p = 1, 2, 3$) consistently demonstrated the superior performance of higher-order elements in capturing solution features, particularly in boundary layer regions where convection dominates diffusion ($k = 1\times {10}^{-5}$). The implementation achieved stable solutions across all tested configurations, effectively eliminating the spurious oscillations that typically plague standard Galerkin formulations in convection-dominated problems. The stabilization parameter ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|a\right|p}{h}}\right)}^{-1}$ proved crucial in maintaining numerical stability while preserving solution accuracy, demonstrating the theoretical soundness of the ASGS approach.

When compared to previous investigations detailed in the related works section, the current study distinguished itself through several key aspects. Unlike the meshless approaches of [28,29], which focused on fractional-time and localized fundamental solutions, respectively, the present work employed a stabilized finite element framework that maintains the mathematical rigor of variational formulations while providing computational efficiency through structured mesh implementations. The ASGS method implemented herein offered distinct advantages over the high-resolution Petrov–Galerkin (HRPG) approaches of [26,27], particularly in terms of implementation simplicity, as ASGS does not require complex stabilization parameter calibration for different physical regimes. The spectral accuracy achievements of [31] with their trivariate spectral collocation approach (TSQLM) represented a different paradigm, targeting exceptional precision through minimal grid points but requiring specialized mathematical formulations. In contrast, the CDR-Solv framework prioritized accessibility and educational value through its open-source Python implementation, making advanced stabilization techniques available to a broader scientific community.

Table 2. Advantages and limitations of different proposals.

Name	Technique	Advantages	Limitations
CDR-Solv (Present Study)	ASGS stabilization with Python implementation	Open-source accessibility, educational value, high-order finite elements, robust stabilization, user-friendly interface	Limited to structured meshes, requires Python environment
Nadukandi et al. [26]	High-resolution Petrov–Galerkin (HRPG) with linear elements	Superior shock-capturing, second-order accuracy in smooth regimes	Complex parameter calibration, limited to 1D problems, requires specialized implementation
Liu et al. [29]	Localized Method of Fundamental Solutions (LMFS) with MATLAB	Meshless approach, sparse matrix structure, large-scale capability	Requires MATLAB license, complex mathematical formulation, limited geometric flexibility
Mkhatshwa & Khumalo [31]	Trivariate Spectral Collocation (TSQLM) with MATLAB	Exceptional accuracy (10−17), minimal grid points, spectral convergence	MATLAB dependency, limited to elliptic problems, requires specialized mathematical expertise
Parhizi et al. [36]	Green’s function analytical approach	Pure analytical framework, superior computational speed, exact solutions	Limited to specific source terms, complex mathematical derivations, restricted geometric applications

summarizes the observed advantages and limitations of these proposals.

We selected the open-access tool most similar to our implementation as a validation mechanism. This tool is the FEniCS library, which is available for use on Linux and iOS operating systems but not Windows. Unlike FEniCS, CDR-Solv can be easily implemented on all three operating systems. After running the four examples in Table 1 ten times with each tool, we obtained the average execution times presented in Table 1. Similar results were obtained with both tools (though CDR-Solv presented slightly more resolution). Lower average execution times were obtained with the CDR-Solv tool in all examples, which can be attributed to the computational complexity of the solver used by each tool. Regarding the computational complexity standpoint, the CDR-Solv framework exhibits superior efficiency compared to standard FEniCS configurations. In CDR-Solv, the overall complexity is dominated by the iterative resolution of the linear system using GMRES or Conjugate Gradient (CG), yielding a complexity of at most $O\left(n^{1.5}\right)$ to $O\left(n^2\right)$, depending on mesh quality and preconditioning. This is because both mesh generation and stiffness matrix assembly scale linearly with the number of degrees of freedom $n$. In contrast, FEniCS—when using its default direct solvers such as LU or Cholesky factorization—incurs a worst-case complexity of $O\left(n^3\right)$, due to the dense factorization steps involved in solving the global linear system (symbolic factorization, numeric factorization, and forward and backward substitution). Consequently, for large-scale problems, CDR-Solv achieves faster execution by leveraging the algebraic sub-grid scale (ASGS) stabilization within an iterative framework, making it more computationally tractable in convection-dominated regimes.

The ASGS stabilization method is a significant improvement over traditional approaches because it provides consistent stabilization across different convection regimes without requiring problem-specific parameter tuning. This distinguishes the present work from conventional methods, such as the finite volume element approach, which typically require complex stability analyses and CFL-like restrictions. The ASGS formulation inherently addresses the Gibbs phenomenon and spurious oscillations through its multiscale variational approach. This offers theoretical advantages over ad hoc stabilization techniques while maintaining computational efficiency for problems characterized by boundary layers or sharp gradients.

The educational contributions of the CDR-Solv framework are a significant advancement in computational science pedagogy. The open-source Python implementation provides several advantages, including complete algorithmic transparency, cross-platform compatibility without licensing restrictions, and seamless integration with the Python scientific computing ecosystem. It is also accessible to researchers and students in developing countries, where commercial software licenses may be prohibitively expensive. Its modular code structure features clearly defined functions for mesh generation (nodes, TC3), element matrix assembly (KEFE2DT), and shape function evaluation (FFT, VFFYDp2DT). This structure establishes an educational framework for understanding the fundamentals of finite element implementation. CDR-Solv is particularly valuable in instructional settings for finite element and numerical methods courses. The framework enables students to systematically explore the relationship between polynomial degree selection and solution quality in convection-dominated regimes. It provides hands-on experience with stabilization techniques that are typically limited to theoretical discussion. The software facilitates laboratory exercises in which students can investigate boundary layer phenomena, analyze the effects of different source term configurations, and observe firsthand how ASGS stabilization eliminates spurious oscillations. Additionally, the transparent implementation allows instructors to guide students through the mathematical foundations of finite element assembly processes, from shape function evaluation to global system construction. This bridges the gap between theoretical concepts and practical implementation.

Future research directions encompass critical technical challenges that will expand the capabilities and educational value of CDR-Solv. Extending to three-dimensional geometries requires addressing the computational complexity of tetrahedral element integration and developing efficient storage schemes for higher-dimensional connectivity matrices. Implementing adaptive mesh refinement capabilities presents the technical challenge of developing error estimation algorithms tailored to ASGS-stabilized formulations. Proposed solutions involve residual-based indicators combined with gradient recovery techniques. Integrating Neumann and Robin boundary condition configurations will require modifying the global assembly process to accommodate natural boundary conditions while maintaining stabilization parameter consistency across different boundary types. This will necessitate the development of specialized variational formulations for mixed boundary value problems. However, this is beyond the scope of this work and will be included in future releases.

5. Conclusions

This investigation demonstrated that the ASGS stabilization method combined with high-order finite elements successfully addresses convection-diffusion-reaction equations in convection-dominated regimes ($k = 1\times {10}^{-5}$). Computational validation using polynomial degrees $p = 1, 2, 3$ showed that the CDR-Solv framework consistently achieved slightly faster execution times compared to existing open-source tools, with computational complexity ranging approximately from $O\left(n^{1.5}\right)$ to $O\left(n^2\right)$. Specifically, CDR-Solv demonstrated execution time improvements of 9–26%, depending on problem complexity. The stabilization parameter ${\tau }_K={\left({\displaystyle \frac{c_{1}k{p}^4}{h^2}}+{\displaystyle \frac{c_2\left|a\right|p}{h}}\right)}^{-1}$ effectively eliminated spurious oscillations across all polynomial degrees while maintaining solution accuracy, validating the theoretical foundations of the multiscale variational approach. Extensive numerical experimentation across diverse source term configurations, including constant ($f = 1$), linear ($f = x + y$), polynomial ($f = x^2{y}^2$), and analytical benchmark functions, consistently yielded stable solutions in boundary layer regions where conventional finite element methods typically exhibit instability. The experimental findings revealed that higher-order elements ($p = 3$) outperformed linear approximations when capturing sharp gradient phenomena. These elements achieved superior resolution of steep concentration gradients near outflow boundaries.

The ASGS method successfully maintained computational tractability without requiring complex parameter calibration. This distinguishes the ASGS method from existing methodologies, which often demand specialized mathematical formulations. The framework demonstrated robustness across various physical parameters and offered a simpler implementation than conventional stabilization techniques.

The primary contribution is providing an open-source educational platform offering algorithmic transparency, cross-platform compatibility, and no licensing restrictions. The modular Python implementation allows students and researchers to grasp the fundamentals of finite elements through clearly defined functions for mesh generation, element assembly, and stabilization. This addresses the critical shortage of accessible educational tools for advanced stabilization techniques in computational transport phenomena. These findings underscore the importance of using ASGS stabilization methodology for convection-dominated transport problems and advance practical educational applications.