Abstract
As critical industrial equipment, the operational stability of a centrifugal pump is profoundly affected by hydraulic radial forces acting on the impeller. However, existing research has limitations in systematically characterizing time-varying force patterns, elucidating the correlations between fluid–structure interaction (FSI) and vibration and noise, and developing multi-operating condition analysis methodologies. This study focuses on a horizontal end-suction centrifugal pump, integrating computational fluid dynamics (CFD) simulations to develop a transient radial force dataset covering nine operating conditions ranging from 0.4 Qn to 1.2 Qn. Feature engineering was utilized to extract 23 time-frequency domain features. Through Pearson correlation analysis and agglomerative hierarchical clustering (AHC) algorithms, multi-operating condition classification patterns of hydraulic radial forces were unveiled. Key findings include: (1) the X/Y directional force components exhibit distinct anisotropic correlations with the flow rate; (2) hierarchical clustering based on cosine distance and average linkage divides operating conditions into low, medium, and high flow regimes; (3) feature redundancy elimination requires balancing statistical metrics with physical interpretability. This work proposes an unsupervised learning framework, offering a data-driven approach for the hydraulic optimization of centrifugal pumps and intelligent diagnostics, with engineering significance for improving equipment reliability and operational efficiency.
1. Introduction
Centrifugal pumps serve as critical components in diverse industrial and municipal systems. Specifically, these systems include water supply networks, chemical processing plants, and energy generation facilities [1,2,3]. Recent technological advancements have propelled centrifugal pumps toward high-speed, large-capacity, and high-head operational regimes. Consequently, hydraulic excitation levels have increased, and operational stability has become an increasingly critical design consideration. The operational reliability and efficiency of these pumps are profoundly influenced by hydraulic forces acting on the impeller. Among these forces, radial forces generated within the impeller-volute interaction zone are particularly significant. These radial forces not only induce structural vibrations but also exacerbate deformation and wear in critical components. For instance, these components include bearings, shafts, and seals. Ultimately, this compromises system longevity and safety [4,5,6,7].
The generation mechanism of hydraulic radial forces in centrifugal pumps stems from asymmetric pressure distributions. These distributions arise from impeller-volute interactions. The inherent geometric asymmetry of volute casings creates circumferentially uneven static pressure gradients. This phenomenon becomes particularly pronounced under off-design conditions, especially at extreme flow rates (both below and above the optimal ranges) [8,9,10]. Computational fluid dynamics (CFD) simulations and experimental measurements have quantitatively validated this phenomenon. For example, Zhu et al. [9] systematically illustrated that distinct blade-tongue clearance configurations directly modulate fluid pulsation intensity. In turn, this modulation induces significant unsteady fluctuations in radial forces. Specifically, when blade trailing edges align with the volute tongue region, flow blockage effects arise. This flow disturbance not only aggravates circumferential pressure nonuniformity at the diffuser outlet; it also amplifies transient fluctuations in power consumption, blade loading characteristics, and resultant radial forces. Recent investigations on mixed-flow pumps have further revealed transient and delayed phenomena in radial force evolution. These phenomena, importantly, occur during rapid startup cycles. This observation highlights the complex transient nature of these fluid–structure interactions [5].
Current design methodologies for centrifugal pumps rely heavily on computational fluid dynamics (CFD) to optimize hydraulic geometries. The primary goal is to mitigate impeller radial forces. Extensive research has demonstrated that critical structural parameters significantly influence radial force characteristics, including double volute configurations and impeller geometric features [11,12,13]. For instance, Cao et al. [14] conducted numerical simulations on a large-scale centrifugal dredger pump. Their work achieved a 38% reduction in mean hydraulic radial force through double volute implementation. This modification also decreased pulsation amplitude by 3%. The improvement enhanced operational stability by reducing shaft vibration and fatigue failure risks under design conditions. Similarly, Jia et al. [15] optimized three key blade parameters: outlet angle, pressure surface curvature radius, and maximum thickness. Their parametric study revealed that these geometric adjustments suppress unstable vortex formation. The modifications also weaken rotor-stator interactions. Ultimately, they reduce both the magnitude and fluctuation intensity of impeller radial forces. This corresponds to measurable decreases in vibration amplitudes.
In centrifugal pump systems, hydraulic radial forces from internal unsteady flows correlate with externally measurable vibration/noise signatures. These dynamic features can be captured via strategically deployed sensors. Vibration sensors are mounted on bearings, volute casings, and pump bases. Acoustic sensors are positioned in ambient environments. Vibration monitoring provides crucial spectral information. It reveals impeller radial force characteristics through axial frequencies, blade-passing frequencies, and associated harmonics [16,17].
Acoustic monitoring offers non-contact detection advantages. It proves valuable in high-temperature or corrosive environments. Frequency-domain analysis of noise signals identifies pressure fluctuation patterns. These patterns arise from rotor-stator interactions near the volute tongue region [18,19]. Cheng et al. [20] investigated flow-induced vibration and noise in a marine centrifugal pump (specific speed = 66.7) using integrated methods. Their parametric analysis of volute geometry showed that increasing base circle diameter improves flow uniformity. This modification suppresses pressure fluctuations. In the optimized configuration, vibration amplitudes were reduced by 8.3% at the inlet flange. They were also reduced by 7.9% at the outlet flange and 12.3% at the pump base. Simultaneously, characteristic frequency sound pressure levels exhibited proportional attenuation. This result validates the efficacy of geometric optimization in simultaneously mitigating structural vibration and flow-induced noise.
Unsteady flow characteristics in centrifugal pumps create complex vibration and noise signatures from hydrodynamic excitations. Current research focuses on advanced signal processing for feature extraction and pattern recognition. In frequency-domain analysis, the fast Fourier transform (FFT) acts as the fundamental method for identifying dominant frequency components and energy distribution patterns. A representative application involves detecting blade fractures via characteristic frequency shifts where shaft rotational frequencies exceed blade-passing frequencies in magnitude, establishing a diagnostic indicator [21]. For non-stationary signal processing, advanced methods including the Hilbert–Huang transform (HHT) and wavelet packet decomposition allow joint time-frequency analysis. These techniques prove especially effective in monitoring cavitation progression, as evidenced by quantifiable changes in time-frequency energy distributions during incipient cavitation stages [22,23,24]. Building on these techniques, machine learning algorithms such as support vector machines (SVM) and k-nearest neighbors (KNN) have been successfully implemented for automated classification of vibration/noise feature vectors [10,25,26,27]. Recent advancements demonstrate the growing potential of deep learning architectures in this domain: convolutional neural networks (CNN) exhibit superior performance in spatial feature extraction while long short-term memory networks (LSTM) effectively capture temporal dependencies in operational data. Furthermore, ensemble learning and transfer learning frameworks address key challenges. They improve performance with limited fault data and enhance cross-operational condition generalization [28,29,30,31].
In summary, centrifugal pump design optimization currently depends on CFD-based prediction of transient hydraulic radial forces under various geometric configurations. Concurrently, operation and maintenance strategies focus on operational state identification and fault diagnosis through time-frequency analysis of flow-induced vibration and noise signatures. Nevertheless, three critical research gaps remain: (1) Insufficient systematization in characterizing the time-dependent hydraulic force patterns across varying flow regimes; (2) Limited interpretability of signal analysis-related machine learning methods, impeding fundamental correlations between internal unsteady flow dynamics and external vibro-acoustic responses; (3) Overreliance on single-condition analyses with simplistic statistical approaches [32,33].
To address these limitations, this study develops an unsupervised learning framework. It incorporates 23 multidimensional features for systematic recognition of hydraulic force patterns under multi-operational scenarios. Specifically, this study targets a horizontal end-suction centrifugal pump. It uses CFD simulation and hydraulic radial force acquisition methods consistent with our prior work and builds a transient radial force dataset for 9 conditions (0.4 Qn–1.2 Qn). The study extracts 23 time-frequency features, then applies Pearson correlation analysis and AHC to identify hydraulic radial force multi-condition patterns. This addresses limitations in time-varying force characterization and multi-condition analysis. The motivation for selecting unsupervised learning is that it can discover latent structures and natural groupings in multidimensional feature data. Importantly, it does this without relying on preassigned categories. This capability aligns with the goal of identifying intrinsic force patterns that may not have been characterized previously. The subsequent sections are organized as follows: Section 2 describes data acquisition protocols and experimental configurations. Section 3 presents the feature engineering methodology with cross-correlation analysis. Section 4 applies hierarchical clustering algorithms and interprets the resultant force pattern classifications. Section 5 evaluates the framework’s scientific insights and practical implementation potential in pump design and diagnostics. Concluding remarks and future directions are presented in Section 6.
2. Dataset
Building upon the authors’ prior CFD investigation [34] of a horizontal end-suction centrifugal pump (design parameters: Qn = 12.5 m3/h, Hn = 22.7 m, n = 2900 rpm, handling room-temperature water), a comprehensive dataset of transient hydraulic radial forces on the impeller derived from simulations was established, using the same numerical calculation methods and experimental approaches. Regarding the numerical calculation basis, the CFD simulation framework and impeller transient hydraulic radial force acquisition method align with the authors’ prior work. The CFD framework covers geometric modeling, mesh generation, boundary conditions, and turbulence model settings. Detailed specifications of this numerical model are in Ref. [34], which ensures reliable and consistent calculation of hydrodynamic components herein. To enable the AHC (Agglomerative Hierarchical Clustering) to cover the full flow range, the validated CFD framework retains identical geometric and numerical configurations while expanding the flow regime analysis from 0.8 Qn–1.2 Qn to 0.4 Qn–1.2 Qn, with nine equidistant operating points set at 0.1 Qn increments.
Complementary experimental measurements were conducted following the original test protocol. These measurements aimed to acquire extended pump performance data. Figure 1 comparatively presents the numerically predicted versus experimentally measured characteristics. The analysis covers head (red curves) and hydraulic efficiency (blue curves) across the full operational range. Here, efficiency specifically refers to hydraulic efficiency, where experimental values are derived through ηhe = η/(ηv × ηm), with η representing total efficiency, ηv representing volumetric efficiency, and ηm representing mechanical efficiency. Based on a systematic evaluation of manufacturer-provided engineering datasets, the volumetric-mechanical efficiency coefficient (ηv × ηm) was determined as 80% [34]. Experimental uncertainty bounds are quantified via shaded bands surrounding the measurement curves.
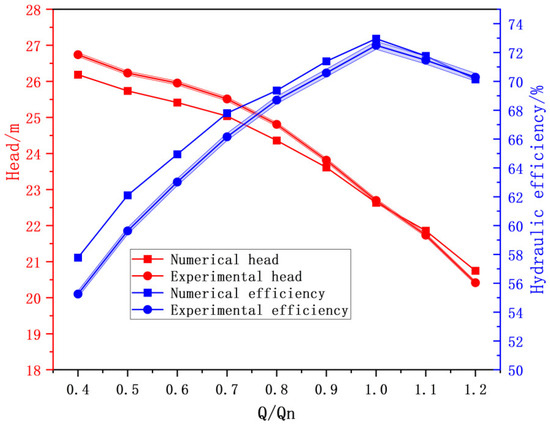
Figure 1.
Comparison of experimental and calculated values of external characteristic parameters.
Throughout the investigated range the numerical predictions show remarkably consistent agreement with experimental trends. At rated flow (1.0 Qn), head and efficiency prediction errors are constrained to 0.064 m (0.28% relative error) and 0.46% absolute deviation, respectively. Deviation magnitudes increase as operational conditions diverge. This effect is most pronounced under low-flow regimes (0.4 Qn–0.7 Qn), where maximum discrepancies reach 0.56 m (2.48%) in head and 2.53% in efficiency. This accuracy degradation arises from intensified unsteady flow phenomena. These include elevated incidence angles, rotor-stator interactions, and boundary layer separation, which occur as impeller inflow velocities deviate from design conditions. Nevertheless, all prediction errors remain within 3% absolute deviation thresholds. This unequivocally confirms the computational model’s validity and reliability for subsequent hydraulic force pattern analyses.
The CFD-derived dataset comprises nine time-series files (Q04.csv to Q12.csv). Each file documents transient hydraulic radial force components in orthogonal X-Y coordinates across distinct flow conditions. As exemplified by the Q04.csv file corresponding to 0.4 Qn operation, the data structure contains three critical parameters: “Flowtime” (temporal index), “ForceTotalX” (instantaneous radial force in the X-direction), and “ForceTotalY” (corresponding Y-direction component), with the temporal resolution ensuring 1° rotational angle increments per data point.
To ensure systematic analysis, we extracted two complete impeller rotation cycles from each dataset. This extraction captured periodic stabilization characteristics. Figure 2 presents the comparative time-domain trajectories of X/Y-direction radial forces across nine representative flow conditions (0.4 Qn–1.2 Qn, with 0.1 Qn increments). The results reveal significant differences in magnitude, fluctuation amplitude, and waveform characteristics between the two orthogonal forces. This demonstrates the inherent complexity of radial forces acting on the centrifugal pump impeller.
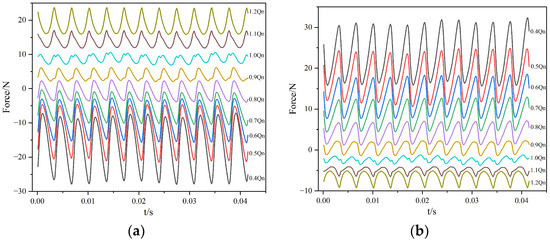
Figure 2.
Time variation in the hydraulic radial force on the impeller: (a) X direction; (b) Y direction.
3. Feature Engineering and Correlation Analysis
3.1. Feature Collection
The dataset undergoes feature engineering processing to establish a foundation for subsequent in-depth analysis. Feature engineering is defined as the systematic extraction of actionable information through raw data preprocessing, transformation, and synthetic feature generation. This methodology enables the development of refined datasets that enhance model training, predictive performance, and result interpretability [35].
As elaborated in Table 1, 24 distinct features are systematically extracted from each time series in the dataset. These features are categorized into time-domain and frequency-domain groups. Time-domain features are further divided into dimensional metrics (e.g., Maximum, Peak to valley value) and dimensionless indicators (e.g., Kurtosis, Peak factor), while frequency-domain features encompass parameters derived from frequency spectrum analysis (e.g., Centroid frequency) and power spectrum characteristics (e.g., Total power). Comprehensive definitions for all features are provided in Table A1 (Appendix A), with mathematical formulations documented in [36,37,38].

Table 1.
Features collected from the original dataset.
To address engineering concerns related to centrifugal pump impeller loading, we incorporate the resultant radial force into the feature set. This force is computed as the vector sum of X- and Y-directional components. The parameter is calculated using the following formula:
where FX and FY represent orthogonal radial force components, and FT quantifies their combined effect. By integrating this domain-specific metric, the feature framework aligns with practical engineering demands for assessing net impeller loading closely monitored operational conditions. The field name of FT is set as “ForceTotalT”.
The feature extraction process and subsequent data analysis/mining procedures are executed on the MATLAB R2022a platform. The complete source code is provided in the Supplementary Materials. A custom auxiliary function, designated as “Getfeatures”, is utilized to perform feature extraction. All derived features are systematically stored within a dedicated data structure labeled “Features”.
This data structure contains nine distinct cell arrays. Each array corresponds to a specific flow condition. Within each cell array, the feature extraction outcomes for FX, FY and FT time series obtained under the respective flow conditions are archived. This organizational framework ensures clear segregation of results by flow regime. It enables efficient data retrieval and facilitates comparative analysis across operational scenarios.
3.2. Normalization Processing
Preliminary analyses reveal that the PS_MPF (maximum power frequency) remains consistently stable at 289.3 Hz across all flow conditions. This value closely approximates the blade passing frequency (BPF) of the investigated centrifugal pump. Specifically, the pump impeller is configured with 6 blades and operates at a rotational speed of 2900 r/min. The blade passing frequency is calculated as (number of blades × rotational speed)/60, i.e., (6 × 2900)/60 = 290 Hz, which is in close agreement with the measured PS_MPF value of 289.3 Hz. This correspondence stems from the hydrodynamic mechanism governing radial force generation on the impeller: the asymmetric pressure distribution in the surrounding flow field creates periodic pressure fluctuations as rotating blades interact with the stationary volute. The dominant frequency of these fluctuations is theoretically determined by the product of the blade count and rotational frequency [39,40].
Given the invariant nature of the maximum power frequency across all operational conditions, this feature is identified as redundant and subsequently excluded from further analytical procedures. To eliminate dimensional bias in the remaining 23 features, a normalization process is applied using the following formula:
where x represents the original feature value under a certain flow rate, xmin and xmax represent the minimum and maximum values of the original feature values under all flow conditions, respectively, and X represents the normalized feature value. This standardization ensures uniform comparability across features while preserving their intrinsic variability patterns-critical for reliable model training and robust comparative analysis.
Firstly, the original time series data of the radial force components FX and FY are obtained through CFD simulation, and the time series data of the total force FT are directly calculated using Equation (1). Then, the features of FX, FY and FT under different flow conditions (0.4 Qn to 1.2 Qn) are extracted and normalized using Equation (2) to generate the normalized feature sets of FX, FY and FT for these flow conditions. Through this systematic processing, normalized feature sets for FX, FY and FT are finalized under varying flow conditions. It is emphasized that during subsequent analyses, all normalized features in the dataset are rigorously partitioned into three distinct subsets, each exclusively corresponding to features derived from FX, FY and FT sources, respectively. Each subset comprises 23 distinct feature categories, with each individual feature represented by nine computed values associated with flow rates ranging from 0.4 Qn to 1.2 Qn.
To further characterize the distribution properties of these normalized values, a normalized variance is calculated using the following formula:
where Xi represents all elements of a normalized feature of a certain total force; where represents the mean value of a normalized feature of a certain total force; and where S2 represents the variance of a normalized feature of a certain total force. the mean value is first calculated for each column of feature values in the normalized feature set, and then the variance of each normalized parameter is computed using Equation (3), with these variances compiled into Table 2. This quantitative assessment enables comprehensive comparative evaluations of feature variability across different operational conditions and data sources (FX, FY and FT), providing valuable insights into data consistency and potential outliers within the feature space.

Table 2.
Variances of each normalized feature value.
As shown in Table 2, the variances of the majority of normalized feature values fall within the range of 0.1 to 0.2. No significant disparities were observed. To obtain detailed quantitative insights, the variances of all normalized features corresponding to FX, FY and FT are further computed to determine their maximum, minimum, and mean values, which are systematically documented in Table 3. Notably, each column in Table 3 represents the aggregated statistical measures derived from the corresponding column in Table 2.

Table 3.
Statistical values of all normalized feature variances.
The results in Table 3 demonstrate that the mean variance across all columns is approximates 0.12, with the difference between the maximum and minimum values and the mean consistently below 0.06. This uniformity validates the feature selection method. It also confirms that feature values remain stable across flow conditions. These results confirm the normalized feature set’s suitability for subsequent analysis. The validation supports their use in further analytical procedures.
Figure 3 illustrates the normalized feature datasets for FX, FY and FT across varying flow conditions. The horizontal axis denotes feature indices, with specific parameter designations corresponding to each index provided in Table 1 or Table 2. The ordinate, ordered from top to bottom, represents nine distinct flow conditions, ranging from 0.4 Qn to 1.2 Qn. This graphical representation facilitates systematic and intuitive examination of the relative variations exhibited by each feature within the time series of X- and Y-directional hydraulic radial forces, as well as their resultant force, across different flow rates.
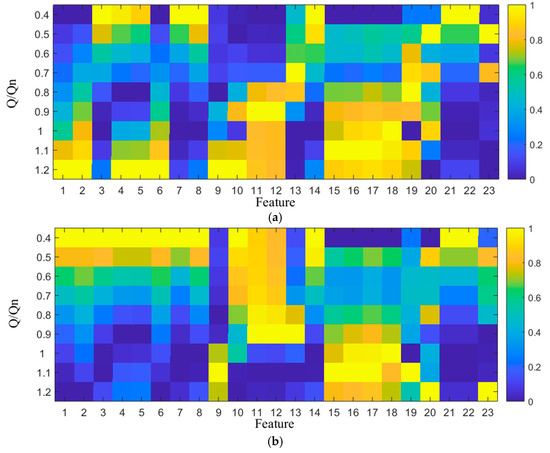
Figure 3.
Normalized feature values: (a) FX; (b) FY; (c) FT.
Visual inspection Figure 3 reveals distinct variation patterns among features. Notably, the first feature defined as the maximum force in the time domain demonstrates contrasting behaviors when extracted from FX and FY time series. Specifically, the FX-derived values exhibit a consistent increase with rising flow rate, while FY-derived values show corresponding reduction. Consequently, the resultant force FT, representing the combined effect of FX and FY, manifests a distribution characterized by higher magnitudes at the extremes of the flow rate range and lower magnitudes in the mid-range.
3.3. Correlation Between Features and Flow Rate
To characterize feature-flow rate interplay, we compute Pearson coefficients between each feature vector and flow rate vector (visualized in Figure 4). Radial forces are also influenced by rotor geometry (e.g., rotor outer diameter, hydraulic channel width), but this section focuses specifically on flow rate correlation to clarify its direct association with feature variations. In this analysis, each column of data in Figure 3 represents a feature vector. The flow rate vector is defined as the column array (0.4:0.1:1.2), which contains the nine normalized flow rates from 0.4 to 1.2.

Figure 4.
Correlation coefficients between each feature and flow rate.
The Pearson correlation coefficient, a statistical metric quantifying the linear association between two variables, is mathematically defined as the ratio of their covariance to the product of their respective standard deviations [41]. This metric quantifies the degree and direction of correlation, as formulated below:
where r is the Pearson correlation coefficient between data samples X and Y; sX and sY are the standard deviations of data samples X and Y, respectively; Cov(X,Y) is the covariance of data samples X and Y:
where xi and yi are the elements of data samples X and Y, respectively.
The Pearson correlation coefficient ranges between −1 and 1. Values approaching 1 indicate strong positive linear correlations between the two variables. Coefficients near −1 represent strong negative linear associations.
Figure 4 reveals clear variations in correlation coefficients across features and flow rates. Pronounced differences exist when comparing features derived from FX, FY and FT sources. The 23 features are systematically categorized into four distinct groups based on their correlation patterns:
- Group 1: This category comprises features extracted from all three sources that exhibit a relatively strong positive correlation with flow rate, as indicated by Pearson correlation coefficients exceeding 0.65. Included here are Kurtosis, Centroid frequency, Mean square frequency, Root mean square frequency, and Frequency variance (corresponding to serial numbers 9, 15, 16, 17, and 18 in Table 1, respectively).
- Group 2: Features in this group demonstrate a pronounced negative correlation with flow rate, with Pearson correlation coefficients below −0.84 across all three sources. This includes Peak to valley value, Variance, Standard deviation, Average value of the amplitudes, Total power, and Mean power (serial numbers 3, 7, 8, 14, 21, and 22 in Table 1, respectively).
- Group 3: Characterized by weak correlations with flow rate, features in this category exhibit Pearson correlation coefficients with absolute values no higher than 0.65 across all sources. These features include Mean frequency, Median frequency, and Ratio of low-frequency to high-frequency power (serial numbers 19, 20, and 23 in Table 1, respectively).
- Group 4: This heterogeneous group contains features where at least one source demonstrates a strong flow rate association (|Pearson coefficient| > 0.65), while correlations derived from different sources show marked discrepancies. This category encompasses the remaining nine features not classified above. For instance, the Maximum value in the time domain (feature number 1) exhibits a Pearson coefficient exceeding 0.97 in FX time series but falls below −0.98 in FY time series, highlighting contrasting correlation behaviors with flow rate.
3.4. Correlation Coefficients Within Features
Adopting the methodological framework established through prior correlation analysis, the Pearson correlation coefficients for all pairwise feature combinations are systematically computed and visualized in Figure 5. Figure 5a–c display heatmaps generated from pairwise correlation analysis of 23 equidimensional feature vectors extracted from FX, FY and FT sources, respectively. Each vector corresponds to a distinct operational feature, encompassing nine discretized radial force measurements collected across hydraulic conditions spanning 0.4 Qn to 1.2 Qn.
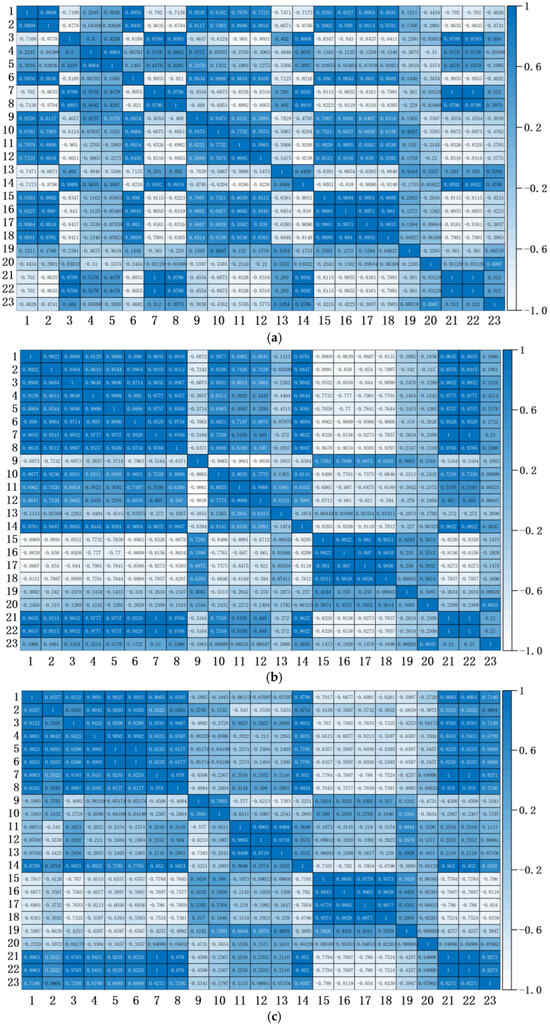
Figure 5.
Correlation coefficients between each feature pairs: (a) FX; (b) FY; (c) FT.
Within the three subgraphs, the diagonal elements consistently exhibit a value of 1, reflecting the inherent perfect autocorrelation of each feature with itself. The correlation matrices show distinct symmetry about the main diagonal: the coefficient between any two features at position (i, j) is identical to that at position (j, i). The correlation coefficients are encoded using a color scale, with darker hues indicating values closer to 1 (strong positive correlation) and lighter hues denoting values approaching −1 (strong negative correlation).
Based on the classification framework established in Section 3.3, four correlation patterns emerge from Figure 5:
Pattern 1: High Positive Correlation Within Groups 1 and 2. Features categorized into Group 1 or Group 2 display robust positive correlations when paired. For instance, Features 9, 15, 16, 17, and 18 (Group 1) demonstrate consistently high correlation coefficients among themselves. Analogously, Features 3, 7, 8, 14, 21, and 22 (Group 2) also show strong internal positive correlations. This pattern arises because features within these groups exhibit monotonic trends (increasing or decreasing) with flow rate, coupled with high inter-feature coherence.
Pattern 2: Negative Correlation Between Groups 1 and 2. A pronounced negative correlation is observed between features from Group 1 and Group 2. For example, Feature 9 (Group 1) shows significant negative coefficients when paired with Features 3, 7, 8, 14, 21, or 22 (Group 2). This anticorrelation stems from opposing trends between the groups: Group 1 features increase with flow rate, while Group 2 features decrease.
Pattern 3: Low Correlation Within Group 3. Features in Group 3 (Features 19, 20, and 23) exhibit minimal correlations among themselves. No significant pairwise associations are detected within this group, reflecting their weak coupling to flow rate variations and limited mutual dependency.
Pattern 4: Heterogeneous Correlation in Group 4. Group 4 features display mixed correlation behaviors across FX, FY and FT sources. While some features (e.g., Features 1 and 2) demonstrate high cross-source correlations (minimum coefficients > 0.83), most exhibit inconsistent associations. This variability indicates divergent predictive utilities across data sources for Group 4 features.
4. Hierarchical Clustering
4.1. Methodology
The inherent data structure and hierarchical relationships of hydraulic radial forces under varying flow conditions are systematically probed via hierarchical clustering analysis applied to three distinct data subsets (FX, FY and FT). Given that categorical assignments of data samples are not predefined, this problem is classified within the unsupervised learning paradigm. In this paradigm, spatially adjacent samples are grouped into homogeneous clusters based on similarity metrics.
A bottom-up agglomerative hierarchical clustering (AHC) algorithm is implemented, wherein data points are iteratively merged via recursive iterations [42]. This methodology has demonstrated efficacy in fluid machinery data analysis; Li et al. [43] highlighted that AHC, especially when combined with advanced technologies such as ensemble learning and improved similarity measurement methods, exhibits excellent performance in capturing complex hierarchical relationships in multi-dimensional data. This process generates a dendrogram, a tree-like diagram that visually represents the clustering hierarchy. The methodology is characterized by the progressive aggregation of the most similar data pairs. Throughout the clustering procedure, comprehensive records of merging sequences and distance metrics are maintained.
The principal procedural steps of AHC are systematically demonstrated in Figure 6, following this operational sequence:
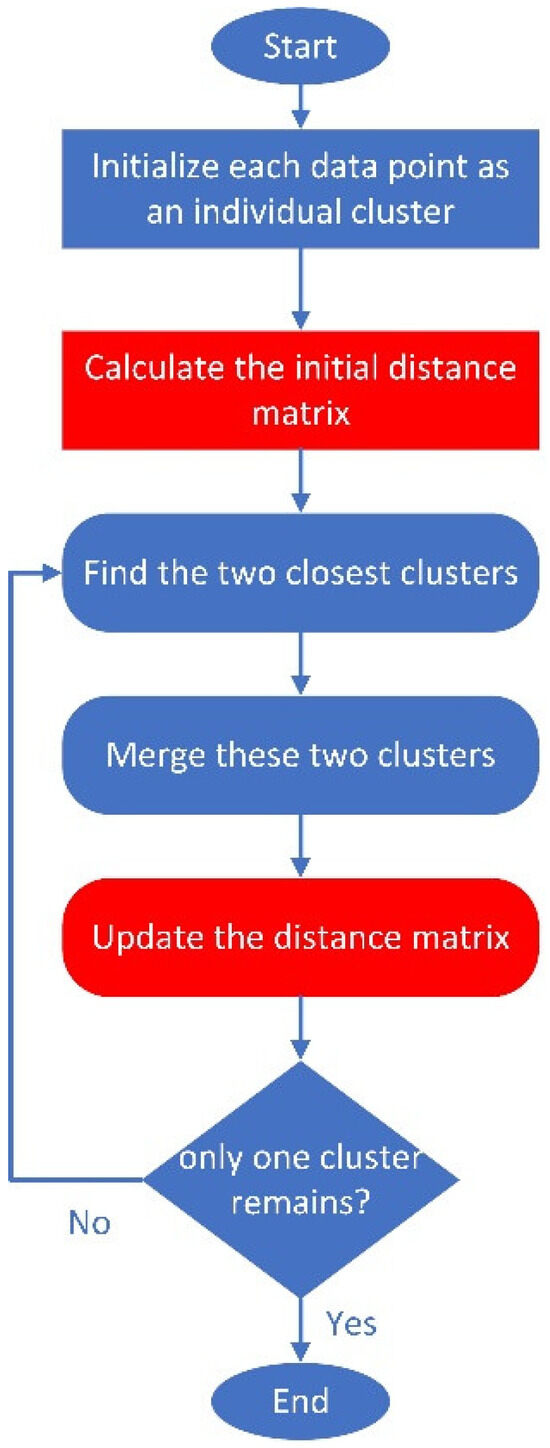
Figure 6.
Flowchart of the agglomerative hierarchical clustering.
- Initialization: Each data point is initially assigned as an individual cluster, establishing a one-to-one correspondence between observations and primary clusters.
- Distance Computation: Inter-cluster distances are systematically computed across all pairwise combinations using predefined similarity metrics.
- Cluster Pair Selection: The most proximate cluster pair is subsequently identified and selected for merging through comparative analysis of the distance matrix.
- Matrix Updating: The distance matrix is dynamically updated following each merging, with recalculated proximity values reflecting the newly formed cluster configuration.
- Iterative Convergence: This algorithmic cycle (Steps 2–4) is iteratively repeated until complete data coalescence is achieved, forming a singular hierarchical cluster.
The clustering process is visualized via a dendrogram constructed from documented merging sequences and linkage distances. This hierarchical topology provides intuitive insights into the progressive aggregation of clusters at varying resolution levels.
4.2. Comparison of Clustering Metrics
The computational foundation of AHC is fundamentally determined by two critical components: (1) the implementation of distance metrics in Step 2, and (2) the dynamic matrix updating mechanism in Step 4. Within this algorithmic framework, pairwise distances between all data points are systematically computed. Three principal measurement methods are used for this computation: Euclidean distance, Manhattan distance, and cosine similarity.
Mathematically, given two multivariate data points X (x1, x2, …, xn) and Y (y1, y2, …, yn), these distance metrics are defined as follows:
- Euclidean Distance: Defined as the L2-norm spatial separation between vectors (Equation (6)).
- Manhattan Distance: Defined through L1-norm vector component summation (Equation (7)).
- Cosine Similarity: Defined via angular deviation measurement in vector space (Equation (8)).
The complete mathematical formalization and computational workflows for these distance computations are explicitly provided in Equations (6)–(8), establishing the computational foundation for subsequent cluster merging operations.
The critical determinant in distance matrix updating is recognized as the selection of linkage strategies. Alternative proximity recalculation methods will produce distinct cluster configurations. This requirement arises from the multi-point composition of merged clusters. In merged clusters, inter-cluster relationships are governed by specific linkage criteria. Three principal linkage strategies are commonly used in hierarchical clustering:
- Single Linkage: Inter-cluster distances are defined as the minimum pairwise distance between any two points across clusters.
- Complete Linkage: Cluster separation is measured by maximum distance values among all cross-cluster data pairs.
- Average Linkage: Cluster proximity is calculated as the arithmetic mean of all inter-point distances between clusters.
These three linkage methodologies are mathematically formalized in Equations (9)–(11), where clusters Ci and Cj represent two distinct data groupings. The complete mathematical representations establish precise computational rules for cluster distance recalculation following each merging operation.
The selection of appropriate distance metrics and linkage strategies is based on a single-variable controlled approach. Under this approach, clustering performance under varying parameter configurations is systematically evaluated. Initially, the linkage strategy is held constant. Three distinct distance metrics (‘Euclidean’, ‘Cityblock’, and ‘cosine’) are applied sequentially to the FX, FY and FT data subsets. Each subset is partitioned into three clusters. Clustering effectiveness is quantitatively evaluated using the mean Silhouette Coefficient, with comparative results presented in Figure 7a.
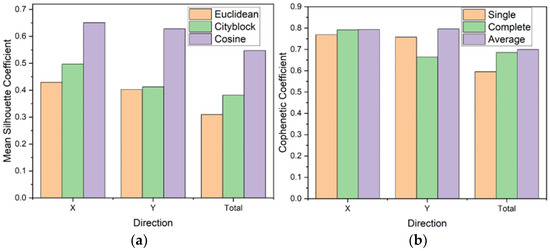
Figure 7.
Comparison of different clustering metrics: (a) distance metric; (b) linkage strategy.
The Silhouette Coefficient, originally proposed by Peter J. Rousseeuw (1987) as a cluster validation index, serves to measure the compactness of data samples relative to their assigned clusters [44]. As shown in Figure 7a, the cosine-based distance metric consistently yields significantly higher mean Silhouette Coefficients across all FX, FY and FT subsets. This is in comparison to Euclidean and Cityblock metrics.
This preference for cosine distance stems from its mathematical advantage. It excels at capturing directional consistency within normalized feature spaces. Despite normalization of all 23 features to the [0, 1] range, cosine similarity inherently emphasizes angular disparities between vectors a critical property for distinguishing clusters defined by relative feature ratios rather than absolute magnitudes. For example, subtle directional differences in some vectors (e.g., [0.2, 0.8, 0.1] versus [0.8, 0.2, 0.1]) are amplified by cosine distance. In contrast, these differences are obscured by Euclidean metrics, which prioritize positional proximity [45,46]. This directional sensitivity enhances the Silhouette Coefficient’s ability to reflect intra-cluster homogeneity. This is particularly true in high-dimensional spaces, where angular relationships encode discriminative features [47].
Subsequently, the distance metric is fixed as ‘cosine’, and three linkage strategies (‘single’, ‘complete’, and ‘average’) are systematically evaluated. The Cophenetic Coefficient is computed for these methods across the FX, FY and FT subsets. Results are shown in Figure 7b. Notably, the Cophenetic Coefficient quantifies the consistency between pairwise distances in the original data and dendrogram merge heights [48]. Figure 7b indicates that the average linkage method produces notably higher Cophenetic Coefficients across all subsets compared to single and complete linkage methods.
The marginally superior performance of average linkage in Cophenetic Coefficient evaluation arises from its statistical robustness. It effectively manages normalized and high-dimensional feature interactions. Despite uniform feature scaling to the [0, 1] range, the 23-dimensional data subsets exhibit complex distance distributions. This is due to inter-feature correlations across varying flow conditions. Single linkage (susceptible to chaining effects from localized noise) and complete linkage (is overly sensitive to residual outliers) both lead to distortions in dendrogram structures. In contrast, average linkage computes mean pairwise distances between clusters. This reduces localized perturbations through statistical smoothing. It also preserves global relationships between flow-regime clusters—relationships that depend on multi-feature synergies [49]. This mechanism ensures that dendrogram merging heights correlate more accurately with original cosine distances. This is a critical requirement in normalized high-dimensional spaces where subtle directional differences define cluster boundaries [50].
Therefore, based on the comparative results presented in Figure 7, the combination of the ‘cosine’ distance metric and the ‘average’ linkage method is determined to be the optimal configuration for this study.
4.3. Clustering Results
The AHC results for the three FX, FY, and FT data subsets are plotted in Figure 8a to 8c, respectively. Each dataset subset utilized for clustering is formatted as a 9 × 23 matrix. Rows of this matrix correspond to flow conditions ranging from 0.4 Qn to 1.2 Qn, and columns represent normalized features. The horizontal axis of each dendrogram denotes the flow operating points. The vertical axis represents the level of heterogeneity level during cluster merging, calculated using the cosine distance metric and average linkage method.
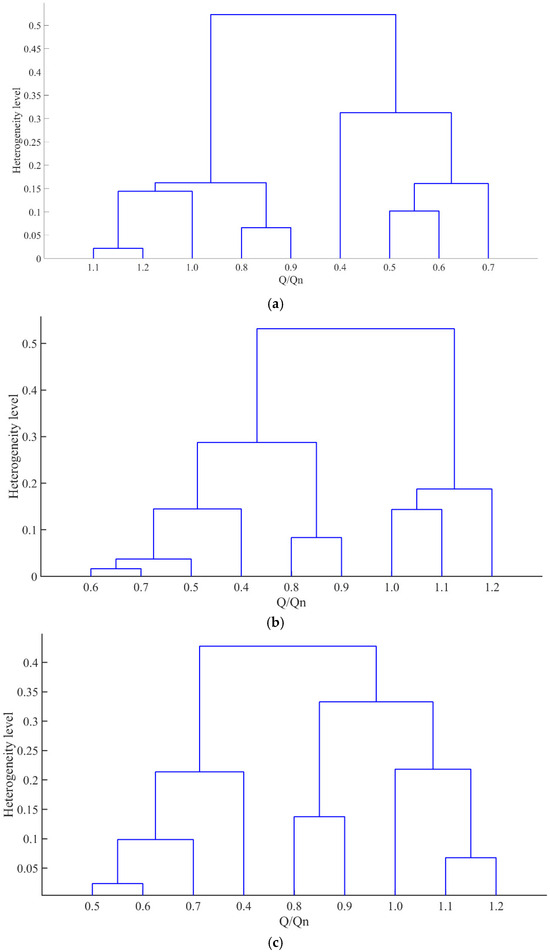
Figure 8.
Clustering results: (a) FX; (b) FY; (c) FT.
From the lowest clustering hierarchy, adjacent flow operating points in Figure 8a–c are consistently aggregated into the same cluster. Subsequently, either a neighboring flow operating point or an adjacent cluster is successively merged with the existing cluster to form higher-level clusters. This hierarchical merging process is repeated. It continues until all clusters are ultimately unified into a single cluster.
For instance, the hierarchical clustering result of the FX subset (Figure 8a) follows a distinctive sequence:
- Initial clusters:
Three base-level clusters are formed, each containing paired flow operating points: (1.1 Qn and 1.2 Qn), (0.8 Qn and 0.9 Qn), and (0.5 Qn and 0.6 Qn).
- 2.
- Secondary-level merging:
- The base-level cluster (1.1 Qn–1.2 Qn) is expanded by merging it with 1.0 Qn to form a secondary-level cluster.
- This secondary-level cluster is then combined with the base-level cluster (0.8 Qn–0.9 Qn) to generate a higher-level cluster.
- 3.
- Parallel merging:
The base-level cluster (0.5 Qn–0.6 Qn) is merged with 0.7 Qn to create another secondary-level cluster, which is further merged with 0.4 Qn to form a distinct higher-level cluster.
- 4.
- Final unification:
The two highest-level clusters are merged into a single cluster. When focusing on the intermediate clustering hierarchy, the nine flow operating conditions are classified into three distinct ranges:
- Lower flow range: 0.4 Qn–0.7 Qn.
- Intermediate flow range: 0.8 Qn–0.9 Qn.
- Higher flow range: 1.0 Qn–1.2 Qn.
While the merging direction of the intermediate flow range and either the lower or higher flow range is dictated by the specific data subset:
- In the FX subset (Figure 8a), the intermediate flow range (0.8 Qn–0.9 Qn) is merged with the higher flow range (1.0 Qn–1.2 Qn).
- In the FY subset (Figure 8b), the intermediate flow range is merged with the lower flow range (0.4 Qn–0.7 Qn).
- In the FT subset derived from the combined effect of FX and FY, the intermediate flow range is ultimately unified with the higher flow range, consistent with the merging pattern observed in the FX subset.
The observed clustering hierarchies are intimately linked to the complex unsteady flow characteristics in centrifugal pumps under varying operating conditions [51,52,53]. This phenomenon can be attributed to the directional dependence of flow instabilities across different force components. Specifically, the merging tendency of the intermediate flow range (0.8 Qn–0.9 Qn) with either the lower (0.4 Qn–0.7 Qn) or higher (1.0 Qn–1.2 Qn) flow ranges depends on the specific force subset being analyzed. In the FX subset, the intermediate range is preferentially merged with the higher flow range. This pattern likely arises from the dominance of high-frequency vortex shedding at elevated flows. Such a mechanism may amplify unsteady forces in the X-direction. Conversely, in the FY subset, the intermediate range is preferentially merged with the lower flow range. This potentially reflects the influence of low-frequency backflow oscillations. These oscillations generate pronounced Y-direction pressure fluctuations at partial flow rates.
Notably, for the FT subset (derived from the resultant forces of FX and FY), the intermediate range is ultimately grouped with the higher flow range. This behavior is consistent with the predominant energy contribution of FX under high-flow conditions. This directional discrepancy underscores how distinct flow instability mechanisms govern clustering patterns in different force components.
4.4. Effect of Feature Reduction on Clustering Quality
While the hierarchical clustering results presented in Figure 8 exhibit discernible regularity and strong interpretability, these properties are derived from the simultaneous use of 23 distinct data features. As demonstrated in Section 3.3 and Section 3.4 through correlation analysis, multiple features are observed to be strongly intercorrelated. From a machine learning perspective, the dataset retains redundant feature information. Eliminating such redundancies is known to reduce computational overhead in practical classification applications.
To mitigate feature redundancy, a Pearson correlation coefficient cutoff of 0.9 was employed to identify redundant feature pairs within the correlation matrices shown in Figure 5a,b. Feature pairs with absolute correlation coefficients exceeding this threshold are systematically filtered. Only one representative feature is retained from each highly correlated pair. The elimination process is algorithmically implemented as follows: the correlation matrix is systematically traversed, and feature pairs exhibiting correlations above the threshold are flagged for redundancy assessment. Specifically, for each feature pair (i, j) where |rij| ≥ 0.9, the latter feature (j) in the pair is marked for removal unless it has already been designated as redundant in prior comparisons. This hierarchical filtering approach ensures that retained features maintain maximal information diversity while minimizing inter-feature collinearity. The procedure is executed in MATLAB using nested loop verification. During iteration indices of redundant features are dynamically recorded in the features_to_remove array during iteration.
The intersection of features marked for removal across the FX, FY, and FT data subsets is algorithmically identified, with the final redundant features identified as 13 distinct entries corresponding to the index set {2, 5, 6, 7, 8, 11, 12, 14, 16, 17, 18, 21, 22}. These features are systematically removed from the original FX, FY, and FT subsets. The refined subsets are then subjected to agglomerative hierarchical clustering. The original protocol outlined in Section 4.3 is used for this clustering, and the resultant dendrograms are presented in Figure 9a–c.
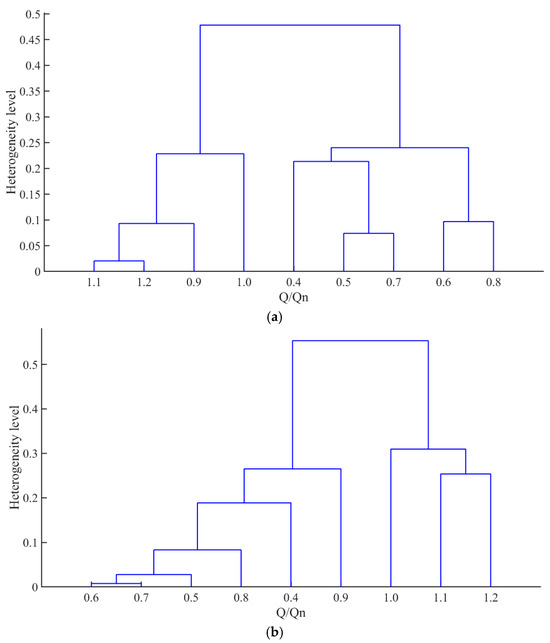
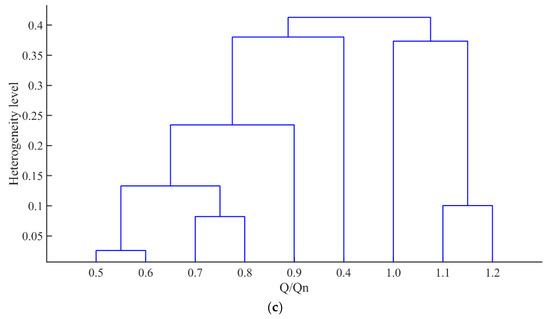
Figure 9.
Clustering results after feature reduction: (a) FX; (b) FY; (c) FT.
A comparative analysis of Figure 8 and Figure 9 reveals distinct clustering patterns induced by the elimination of redundant features. In Figure 9 (following removal of 13 redundant features), cross-flow-rate baseline clusters are observed, as exemplified by the pairing of (0.5 Qn, 0.7 Qn) and (0.6 Qn, 0.8 Qn) into terminal clusters in Figure 9a. These patterns are neither observed in Figure 8 (original 23-feature clustering) nor aligned with established physical principles.
Further differences are evident in higher clustering hierarchies. Taking the FX subset as a case study, the 9 data points in Figure 8a are divided into three interpretable clusters: lower flow range (0.4 Qn–0.7 Qn), intermediate flow range (0.8 Qn–0.9 Qn), and higher flow range (1.0 Qn–1.2 Qn), with the higher flow range cluster exhibiting greater similarity to the intermediate cluster than to the lower flow group. In contrast, Figure 9a exhibits a bifurcated structure: all data points are classified into high flow rates (0.9 Qn–1.2 Qn) and low flow rates (0.4 Qn–0.8 Qn), with the 0.9 Qn data point positioned closer to the terminal (1.1 Qn, 1.2 Qn) cluster than to the 1.0 Qn data point.
While redundant features are known to increase computational overhead. Existing studies also suggest they may introduce noise, exacerbate high-dimensional instability, and potentially obscure intrinsic geometric relationships [54]. However, the comparative analyses here reveal that even conservative redundancy elimination (e.g., using a Pearson correlation coefficient threshold of 0.9) disrupts the intricate physical relationships embedded in the dataset. This disruption ultimately deprives clustering results of physical interpretability. A plausible explanation is that the agglomerative hierarchical clustering algorithm is highly sensitive to feature scale distortion and distance metric deviations. When redundancy elimination is overly applied, the detailed structure of the data is compromised, leading to alterations in clustering patterns [55,56,57].
Based on these findings, caution must be exercised in engineering practice. Specifically, when implementing the proposed feature extraction and hierarchical clustering methodology, the “over-optimization trap” should be avoided. If statistical indicators (e.g., correlation coefficients) are solely relied upon for redundancy reduction, critical features such as those characterizing transient flow patterns under varying operational conditions may be inadvertently discarded. Future research should systematically integrate statistical screening criteria (e.g., correlation thresholds) with domain-specific expertise (e.g., CFD analyses). Features with explicit physical interpretations or dynamic correlations should be prioritized. Additionally, systematic cross-validation through comparative analysis is required. This step ensures the robustness of clustering outcomes across different feature subsets.
5. Implications for Engineering Applications
The research paradigm and scientific findings presented in this study pave the way for advancing centrifugal pump design optimization and operational monitoring systems. By addressing the critical gaps in hydraulic force characterization and leveraging unsupervised learning for multi-operational pattern recognition, this work bridges computational modeling, experimental validation, and data-driven diagnostics. Below, we discuss the implications of this framework for engineering applications. The discussion focuses on two core aspects: hydraulic design improvements and condition-based maintenance strategies.
5.1. Enhanced Hydraulic Design Optimization
Multi-Regime Force Pattern Recognition: The hierarchical clustering results (Section 4.3) systematically classify hydraulic radial forces into distinct operational regimes (e.g., low, intermediate, and high flow ranges). These classifications provide actionable insights for optimizing impeller-volute interactions. For instance, the directional divergence in FX and FY clustering patterns is notable. It highlights the need for asymmetric geometric adjustments in volute casings or blade profiles. Such adjustments aim to mitigate flow instabilities specific to certain flow ranges. Designers can prioritize double volute configurations [14] or blade curvature optimizations [15] for flow regimes exhibiting pronounced force fluctuations.
Feature-Driven Parametric Refinement: The 23-dimensional feature set (Table 1) quantifies characteristics of hydraulic radial forces. It covers both time- and frequency-domain attributes, offering a granular basis for evaluating design modifications. For example, the strong correlation between features like Kurtosis and Centroid Frequency with flow rate (Section 3.3) suggests that suppressing high-frequency pressure pulsations (e.g., via increased base circle diameters or diffuser blade adjustments) could stabilize forces dynamics in high-flow regimes. Similarly, reducing Peak-to-Valley values in low-flow conditions may require boundary layer control strategies to minimize flow separation.
Redundancy-Aware Design Validation: The sensitivity of clustering outcomes to feature reduction (Section 4.4) underscores the importance of retaining physically interpretable features (e.g., the Peak-to-Valley amplitude of radial force fluctuations) during design iterations. Engineers should integrate domain expertise (e.g., CFD-derived flow field analyses) with statistical screening to rigorously avoid inadvertently discarding features. These features are critical to capturing transient force dynamics.
5.2. Intelligent Condition Monitoring and Diagnostics
Multi-Sensor Fusion for Early Fault Detection: The feature engineering framework (Section 3) helps align vibration and dynamic features with internal hydraulic forces, enabling non-intrusive monitoring. By deploying vibration sensors on bearings and acoustic sensors near the volute tongue, operators can extract features like PS_LHR (ratio of low-frequency to high-frequency power) to detect cavitation or impeller imbalance. The directional specificity of FX and FY features further allows precision-localized fault diagnosis (e.g., excessive FY variance may indicate bearing wear due to asymmetric Y-direction loading).
Unsupervised Learning for Adaptive Diagnostics: The hierarchical clustering methodology (Section 4) provides a template for real-time operational state identification without predefined fault labels. In industrial settings, this approach can autonomously segment pump performance into “healthy”, “transitional”, and “fault-prone” clusters based on streaming sensor data.
Interpretable Machine Learning Integration: While deep learning models (e.g., CNNs, LSTMs) offer high accuracy, their “black-box” nature limits practical adoption. This study’s emphasis on feature correlation and clustering interpretability (Section 3.3 and Section 3.4) demonstrates how hybrid frameworks combining physics-based features with unsupervised learning can significantly enhance diagnostic transparency. Engineers can prioritize features with strong flow-rate correlations (e.g., Skewness, Wave Factor) to build explainable fault classifiers. This, in turn, improves stakeholder trust in predictive maintenance systems.
6. Conclusions
To address the challenge of recognizing multi-operating condition patterns of complex, variable hydraulic radial forces in centrifugal pumps, this study proposes an unsupervised learning framework. This framework integrates feature engineering and hierarchical clustering. The primary scientific discoveries and contributions are as follows:
Anisotropic Correlation between Multidimensional Features and Flow Rate: Pearson correlation analysis reveals a strong positive correlation (r > 0.97) between peak X-directional force components and flow rate. In contrast, Y-directional components exhibit a significant negative correlation (r < −0.98). These findings preliminarily reveal the differential excitation mechanisms of the asymmetric flow field on force components in different directions to a certain degree. They might provide a potential basis for further exploring the correlative characteristics of these components.
Clustering Patterns Based on Flow Regime Partitioning: Employing hierarchical clustering with cosine distance and average linkage, nine operating conditions are classified into three modes: low-flow (0.4 Qn–0.7 Qn), transitional-flow (0.8 Qn–0.9 Qn), and high-flow (1.0 Qn–1.2 Qn). These clustering results might be associated, in some way, with the effects of unstable flow phenomena such as vortex shedding and backflow oscillations on force distribution, which could provide a basis for in-depth exploration of flow regime attributes.
Physical Constraints in Feature Redundancy Elimination: Comparative analysis demonstrates that redundancy removal relying solely on statistical correlation (e.g., threshold r > 0.9) compromises the physical interpretability of clustering results. Retaining critical dynamic features through CFD flow field analysis is essential. This provides methodological guidance for engineering feature selection.
Engineering Applicability of the Unsupervised Framework: The proposed method preliminarily validates the feasibility of non-intrusive operating condition identification. This validation relies on a 23-dimensional feature set, which provides a data-driven basis for centrifugal pump design optimization and fault prognosis. While the 23-dimensional radial force feature set may require dimensionality reduction to enhance engineering utility, this work establishes a foundational framework for exploring scalable data-driven tools in centrifugal pump operation and maintenance. It delivers actionable insights for applying unsupervised learning to address practical engineering challenges.
This work innovatively establishes a quantitative link between hydraulic radial forces and multi-operating flow regimes, bridging the gap in systematic characterization of transient force patterns. It provides a theoretical foundation for intelligent maintenance of centrifugal pumps. The proposed unsupervised learning framework further offers a distinct advantage by enabling the systematic identification of hydraulic force patterns across multiple operating conditions. This capability overcomes the limitation of single-operating-condition analysis prevalent in existing studies. The findings thus provide direct actionable support for on-site hydraulic optimization of centrifugal pumps, while also facilitating the development of intelligent condition monitoring systems. Future research may further integrate deep learning methods to enhance cross-condition generalization capabilities.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app151810251/s1. File S1: Analysis of Radial Hydraulic Forces in Centrifugal Pump Operation via Hierarchical Clustering (HC) Algorithms.
Author Contributions
Conceptualization, H.Z.; methodology, H.Z.; software, K.L. and J.H.; validation, T.L. and Y.L.; formal analysis, T.L.; investigation, K.L. and Y.L.; resources, H.Z.; data curation, H.Z.; writing—original draft preparation, H.Z.; writing—review and editing, K.L. and J.H.; visualization, H.Z.; supervision, Q.Z. and L.J.; project administration, H.Z.; funding acquisition, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Natural Science Foundation of Hunan Province, China, grant number 2023JJ50240.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request, the data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Description of each feature.
Table A1.
Description of each feature.
| No. | Parameter Name | Description |
|---|---|---|
| 1 | Maximum | The largest value. |
| 2 | Minimum | The smallest value. |
| 3 | Peak to valley value | A measure of the range of a probability distribution, indicating the difference between the highest and lowest possible values. |
| 4 | Root mean square value | The square root of the average of squared values. |
| 5 | Absolute mean value | The average of absolute values. |
| 6 | Arithmetic mean value | The sum of values divided by the number of values. |
| 7 | Variance | A measure of data dispersion, calculated as the average of the squared differences between each value and the mean. |
| 8 | Standard deviation | The square root of the variance, measuring data dispersion. |
| 9 | Kurtosis | A measure of the peakedness of a probability distribution, which compares the tails of the distribution to a normal distribution. |
| 10 | Skewness | A measure of the asymmetry of a probability distribution, which compares the relative weight of the left and right tail of the distribution. |
| 11 | Peak factor | The ratio of the maximum to the root mean square value, reflecting the extreme degree of the signal. |
| 12 | Pulse factor | The ratio of the maximum to the absolute mean value, reflecting the oscillation degree of the signal. |
| 13 | Wave factor | The ratio of the pulse factor to peak factor. |
| 14 | Average value of the amplitudes | The average value of the amplitudes in frequency domain |
| 15 | Centroid frequency | A measure of the central tendency of the frequency spectrum of a signal, indicating the frequency at which the energy is concentrated. |
| 16 | Mean square frequency | A measure of the average frequency content of a signal, calculated by squaring the frequencies and then averaging them. |
| 17 | Root mean square frequency | A measure of the average frequency content of a signal, calculated by squaring the frequencies and then taking the square root of the mean. |
| 18 | Frequency variance | A weighting measure of the spread of frequencies in a signal or time series, indicating how much the frequencies vary from the centroid frequency. |
| 19 | Mean frequency | The weighting average value of the frequency components in a signal series, indicating the dominant frequency present. |
| 20 | Median frequency | The frequency at which the power spectrum of a signal is halfway between the maximum and minimum frequencies present. |
| 21 | Total power | The sum of the power spectral density across all frequencies, indicating the overall energy content of a signal. |
| 22 | Mean power | The average power spectral density across all frequencies, indicating the average energy content of a signal. |
| 23 | Ratio of low-frequency to high-frequency power | The ratio of the power spectral density at low frequencies to that at high frequencies, indicating the relative energy content across different frequency ranges. |
| 24 | Maximum power frequency | The frequency at which the power spectral density is the highest, indicating the frequency with the most energy content |
References
- Abuan, J.; Honra, J. Numerical investigation and design optimization of centrifugal water pump with splitter blades using response surface method. Designs 2025, 9, 40. [Google Scholar] [CrossRef]
- Xu, S.; Gong, W. Analysis of noise source in a centrifugal pump based on vortex sound theory. Phys. Fluids 2025, 37, 015197. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Bai, L.; Shi, W.; Zhou, L. Assessing energy loss and entropy production in a centrifugal pump with various impeller blade trailing edges. J. Appl. Fluid Mech. 2024, 18, 518–534. [Google Scholar] [CrossRef]
- Ye, D.; Zhai, F.; Luo, Y.; Wu, J.; Chen, J.; Lai, X.; Tian, W. Guide vane angle and reactor coolant pump performance during idling. Ann. Nucl. Energy 2024, 207, 110720. [Google Scholar] [CrossRef]
- Zeng, G.; Chen, W.; Li, J.; Wu, P.; Huang, B.; Wu, D. Numerical study on transient hydraulic excitation force characteristics of a water jet mixed-flow pump during rapid startup period. J. Mech. Sci. Technol. 2023, 37, 5117–5132. [Google Scholar] [CrossRef]
- Song, X.; Shi, Y.; Zheng, K.; Luo, X. Pressure oscillations and radial forces for centrifugal pumps with single- or double-suction impellers. J. Mech. Sci. Technol. 2024, 38, 3009–3025. [Google Scholar] [CrossRef]
- Zhang, H.H.; Deng, C.; Chang, C.P.; You, H.L. Novel dual synergistic sealing ring design for a high-pressure pump—Part I. Seal. Technol. 2022, 2022, 9–17. [Google Scholar] [CrossRef]
- Rao, Z.; Tang, L.; Zhang, H. Double-tongue worm shell structure on plastic centrifugal pump performance study. Appl. Sci. 2023, 13, 8507. [Google Scholar] [CrossRef]
- Zhu, X.; Han, X.; Xie, C.; Zhang, H.; Jiang, E. Numerical investigation of clocking effect on fluctuating characters and radial force within impeller for a centrifugal pump. J. Appl. Fluid Mech. 2025, 18, 549–566. [Google Scholar] [CrossRef]
- Zhao, C.; Chai, K. Simulation study on the flow-induced vibration and noise in marine centrifugal pumps. J. Vib. Control 2024, 30, 2549–2567. [Google Scholar] [CrossRef]
- Ye, C.; Xia, K.; Yan, H.; Cao, S.; Wang, Z.; Tian, Q.; van Esch, B.P.M.; Zheng, Y.; Yang, C. Study on the influence of volute structure on the performance of seawater-pumped storage hydropower plant unit. J. Energy Storage 2024, 90, 111848. [Google Scholar] [CrossRef]
- Kibar, A.; Yigit, K.S. Investigation of double-volute balancing in centrifugal pumps. Meccanica 2024, 59, 1859–1875. [Google Scholar] [CrossRef]
- Nguyen, D.-A.; Roh, M.-S.; Kim, S.; Kim, J.-H. Hydrodynamic and radial force characteristics with design of a single-channel pump for wastewater treatment based on the similarity law. Process Saf. Environ. Prot. 2023, 170, 1137–1150. [Google Scholar] [CrossRef]
- Cao, L.; Wu, T.; Guo, T.; Hu, J.; Cao, J. Numerical analysis on the unsteady radial load on the shaft of a large-scale dredge pump unit. J. Appl. Fluid Mech. 2023, 16, 1005–1016. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, J.; Chen, D.; Tang, Z.; Huang, Q.; Zhou, C.; Ma, Y.; Zhao, Q.; Lin, Z. Impact of key airfoil blade parameters on the internal flow and vibration characteristics of centrifugal pumps. Phys. Fluids 2025, 37, 015134. [Google Scholar] [CrossRef]
- Liang, S.; Li, C.; Yu, W.; Liu, J.; Yv, F.; Dai, Y.; Chen, Z. Analysis and study of transient characteristics of hydrogen circulation pump under different stopping modes. Int. J. Hydrogen Energy 2024, 89, 1040–1048. [Google Scholar] [CrossRef]
- Pu, K.; Huang, B.; Miao, H.; Shi, P.; Wu, D. Quantitative analysis of energy loss and vibration performance in a circulating axial pump. Energy 2022, 243, 122753. [Google Scholar] [CrossRef]
- Lu, J.; Li, L.; Gong, Y.; Liu, X.; Zhang, F.; Zhu, B. Experimental and numerical investigations of the noise induced by cavitation in a centrifugal pump. Iran. J. Sci. Technol. Trans. Mech. Eng. 2024, 48, 1937–1955. [Google Scholar] [CrossRef]
- Zhang, R.; Nan, L.; Chen, D.; Han, W.; Huang, W. Transient flow and noise characteristics of vortex-turbulence-noise interaction in centrifugal pump. Proc. Inst. Mech. Eng. Part A J. Power Energy. 2025, 239, 84–101. [Google Scholar] [CrossRef]
- Cheng, Z.; Ma, Q.; Liu, H.; Dong, L.; Pan, Q. Influence of dynamic and static interference on the internal flow and vibration and noise characteristics of marine centrifugal pump. J. Appl. Fluid Mech. 2023, 16, 1989–2001. [Google Scholar] [CrossRef]
- Mao, Y.-h.; Liu, H.-l.; Wang, Y.; Chen, J.; Liu, F. Experimental study on effects of air injection on cavitation pressure pulsation and vibration in a centrifugal pump with inducer. J. Hydrodyn. 2023, 35, 1168–1178. [Google Scholar] [CrossRef]
- Yu, B.; Kim, Y.; Lee, T.; Cho, Y.; Park, J.; Lee, J.; Park, J. Study on methods using multi-label learning for the classification of compound faults in auxiliary equipment pumps of marine engine systems. Processes 2024, 12, 2161. [Google Scholar] [CrossRef]
- Gong, B.; Zhang, Z.; Feng, C.; Yin, J.; Li, N.; Wang, D. Experimental investigation of characteristics of tip leakage vortex cavitation-induced vibration of a pump. Ann. Nucl. Energy 2023, 192, 109935. [Google Scholar] [CrossRef]
- Ahmad, Z.; Kim, J.-Y.; Kim, J.-M. A technique for centrifugal pump fault detection and identification based on a novel fault-specific mann-whitney test. Sensors 2023, 23, 9090. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Chen, H.; Gu, Q.; Ma, Z. Investigation on performance of a marine centrifugal pump with broken impeller. Mod. Phys. Lett. B 2022, 36, 2250174. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Wu, P.; Huang, B.; Wu, D. Optimization of a centrifugal pump to improve hydraulic efficiency and reduce hydro-induced vibration. Energy 2023, 268, 126677. [Google Scholar] [CrossRef]
- Bai, J.; Che, C.; Liu, X.; Wang, L.; He, Z.; Xie, F.; Dou, B.; Guo, H.; Ma, R.; Zou, H. Fault diagnosis of pumped storage units-a novel data-model hybrid-driven strategy. Processes 2024, 12, 2127. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Y.; Zhou, W.; Zhang, J.; Zhu, J. Optimization of a centrifugal pump with high efficiency and low noise based on fast prediction method and vortex control. Energy 2024, 289, 129835. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, Y.; Zhang, R.; Ye, Z.; Qin, H.; Tao, F.; Li, H.; Zhu, R. Intelligent condition monitoring for the vertical centrifugal pump using multimodal signals and hybrid models. Measurement 2025, 242, 115813. [Google Scholar] [CrossRef]
- Haoqing, J.; Wei, D.; Sucheng, L.; Fan, H. Optimization of centrifugal pump performance and excitation force based on machine learning and enhanced non-dominated sorting genetic algorithm III. Eng. Appl. Artif. Intell. 2025, 143, 110036. [Google Scholar] [CrossRef]
- Yu, B.-M.; Lee, J.-J.; Kim, Y.-J.; Lee, T.-H.; Kim, Y.-K.; Jang, H.-S.; Park, J.; Park, J. A study on fault classification for condition-based maintenance of auxiliary pump in ship’s engine systems using HHT and CNN. J. Appl. Reliab. 2023, 23, 366–374. [Google Scholar] [CrossRef]
- Zhang, N.; Li, D.; Gao, B.; Ni, D.; Li, Z. Unsteady pressure pulsations in pumps—A review. Energies 2023, 16, 150. [Google Scholar] [CrossRef]
- Rapur, J.S.; Tiwari, R.; Aakash, D.; Bordoloi, D.J. Review: Measurement-based monitoring and fault identification in centrifugal pumps. J. Harbin Inst. Technol (New Ser.) 2023, 30, 25–47. [Google Scholar] [CrossRef]
- Zhang, H.; Li, K.; Liu, T.; Liu, Y.; Hu, J.; Zuo, Q.; Jiang, L. Analysis the composition of hydraulic radial force on centrifugal pump impeller: A data-centric approach based on CFD datasets. Appl. Sci. 2025, 15, 7597. [Google Scholar] [CrossRef]
- Long, W.; Lu, Z.; Cui, L. Deep learning-based feature engineering for stock price movement prediction. Knowl.-Based Syst. 2019, 164, 163–173. [Google Scholar] [CrossRef]
- Reddy, T.A.; Henze, G.P. Applied Data Analysis and Modeling for Energy Engineers and Scientists, 2nd ed.; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Privalsky, V. Time Series Analysis in Climatology and Related Sciences, 1st ed.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Yi, K.; Zhang, Q.; Fan, W.; Cao, L.; Wang, S.; Long, G.; Hu, L.; He, H.; Wen, Q.; Xiong, H. A survey on deep learning based time series analysis with frequency transformation. arXiv 2023, arXiv:2302.02173. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, N.; Zheng, F.; Gad, M.; Gao, B. Experimental investigation on the effect of the rotor-stator matching mode on velocity pulsation in the centrifugal pump with a vaned diffuser. Nucl. Eng. Technol. 2025, 57, 103255. [Google Scholar] [CrossRef]
- Du, L.; Zheng, F.; Gao, B.; Gad, M.; Li, D.; Zhang, N. Numerical investigation of rotor and stator matching mode on the complex flow field and pressure pulsation of a vaned centrifugal pump. Energies 2024, 17, 2416. [Google Scholar] [CrossRef]
- Waldmann, P. On the use of the pearson correlation coefficient for model evaluation in genome-wide prediction. Front. Genet. 2019, 10, 899. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Yu, Q.; Liu, X.; Zhou, X.; Song, A. Efficient agglomerative hierarchical clustering. Expert Syst. Appl. 2015, 42, 2785–2797. [Google Scholar] [CrossRef]
- Li, T.; Rezaeipanah, A.; Tag El Din, E.M. An ensemble agglomerative hierarchical clustering algorithm based on clusters clustering technique and the novel similarity measurement. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 3828–3842. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Leskovec, J.; Rajaraman, A.; Ullman, J.D. Mining of Massive Datasets, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Gomaa, W.H.; Fahmy, A.A. A survey of text similarity approaches. Int. J. Comput. Appl. 2013, 68, 13–18. [Google Scholar] [CrossRef]
- Bai, S.; Khosravi, E.; Park, S.J. An mpi-enabled mapreduce framework for molecular dynamics simulation applications. In Proceedings of the 2013 IEEE International Conference on Bioinformatics and Biomedicine, Shanghai, China, 18–21 December 2013; pp. 1–3. [Google Scholar] [CrossRef]
- Farris, J.S. On the cophenetic correlation coefficient. Syst. Biol. 1969, 18, 279–285. [Google Scholar] [CrossRef]
- Seifoddini, H.K. Single linkage versus average linkage clustering in machine cells formation applications. Comput. Ind. Eng. 1989, 16, 419–426. [Google Scholar] [CrossRef]
- Zhu, L.; Jhia Ooi, Z.; Zhang, T.; Brooks, C.S.; Pan, L. Identification of flow regimes in boiling flow with clustering algorithms: An interpretable machine-learning perspective. Appl. Therm. Eng. 2023, 228, 120493. [Google Scholar] [CrossRef]
- Cui, B.; Shi, M. Analysis of unsteady flow characteristics near the cutwater by cutting impeller hub in a high-speed centrifugal pump. J. Mar. Sci. Eng. 2024, 12, 587. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, F.; Xu, Z.; Yuan, S.; Zulu, B.; Hong, Q. Study on fish damage mechanism of the large flow rate centrifugal pump in hydraulic engineering pump station. Phys. Fluids 2024, 36, 115135. [Google Scholar] [CrossRef]
- Tang, X.; Liu, Z.; Zhao, M.; Yang, H.; Jiang, W.; Wang, Y.; Chen, D. Analysis of unsteady flow characteristics of centrifugal pump under part load based on DDES turbulence model. Shock Vib. 2021, 2021, 9970800. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Silva, V.d.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Luxburg, U.v. Clustering stability: An overview. Found. Trends Mach. Learn. 2010, 2, 235–274. [Google Scholar] [CrossRef]
- Kakkavas, G.; Karyotis, V.; Papavassiliou, S. A distance-based agglomerative clustering algorithm for multicast network tomography. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Guyon, I.; Nikravesh, M.; Gunn, S.; Zadeh, L.A. Feature Extraction: Foundations and Applications (Studies in Fuzziness and Soft Computing); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).