Boosting Adversarial Transferability Through Adversarial Attack Enhancer
Abstract
1. Introduction
- We propose Multi-Path Random Restarts (MPRR), a novel random-restart mechanism that simultaneously initializes multiple perturbed starting points at each restart and aggregates gradients across these parallel paths to better guide gradient updates. MPRR can be easily combined with existing gradient-based attacks to improve adversarial transferability.
- We empirically demonstrate that MPRR is effective when the perturbations are sampled from various distributions (Gaussian, uniform, Bernoulli and Poisson); in all cases MPRR yields substantial improvements in attack performance.
- We introduce the Channel Shuffled Attack Method (CSAM), a gradient-based attack that employs channel permutations as a form of data augmentation and leverages MPRR to produce highly transferable adversarial examples. CSAM can be integrated with existing input-transformation techniques to further enhance transferability.
- Extensive experiments on the ImageNet dataset show that integrating MPRR with standard attacks increases average black-box success rates by approximately 22.4–38.2%, and that CSAM outperforms state-of-the-art methods by about 13.8–24.0% on average.
2. Related Work
2.1. Random Restarts
2.2. Adversarial Transferability
2.3. Adversarial Defenses
3. Methodology
3.1. Preliminaries
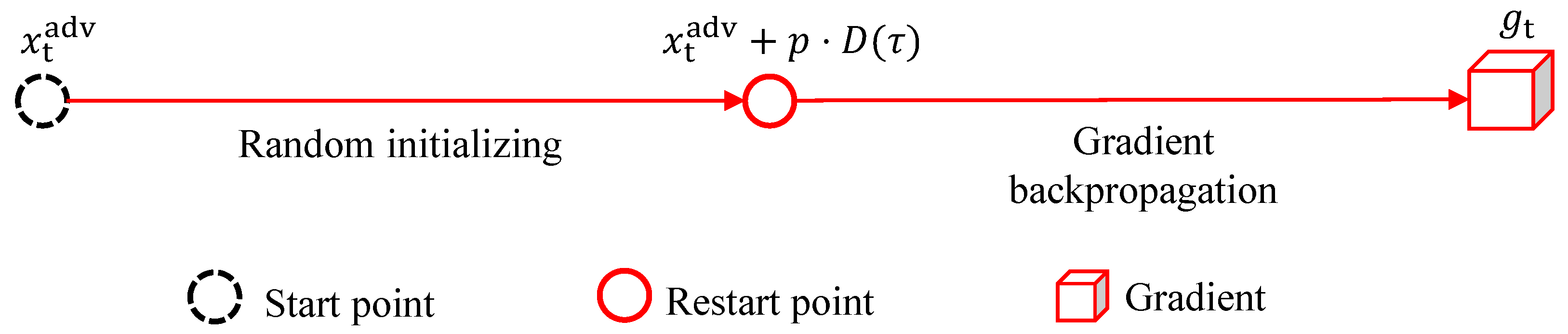
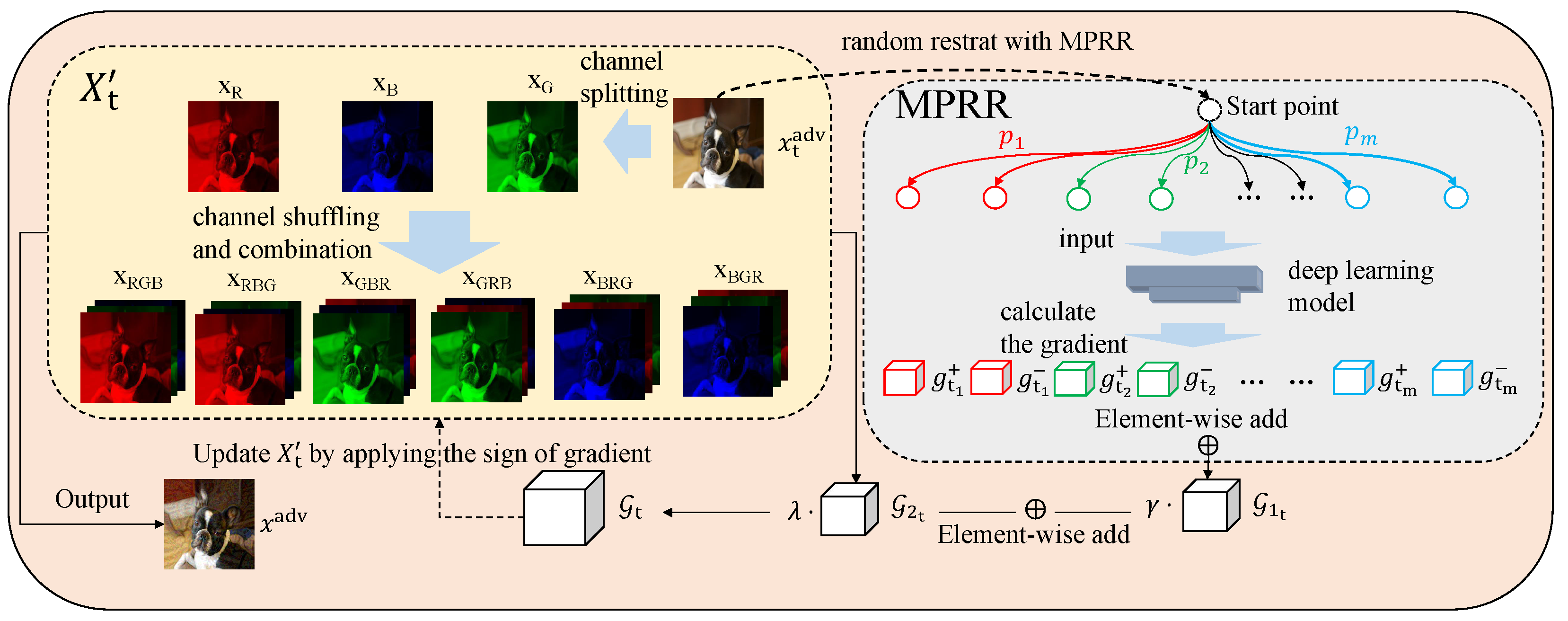
3.2. The Random Multi-Path Restarts
3.3. The Channel Shuffled Attack Method
| Algorithm 1 CSAM |
| Require: A classifier f with loss function L, A benign example x with ground-truth label y, the maximum perturbation , number of iterations T and decay factor Ensure: An adversarial example |
4. Experiments
4.1. Experimental Setups
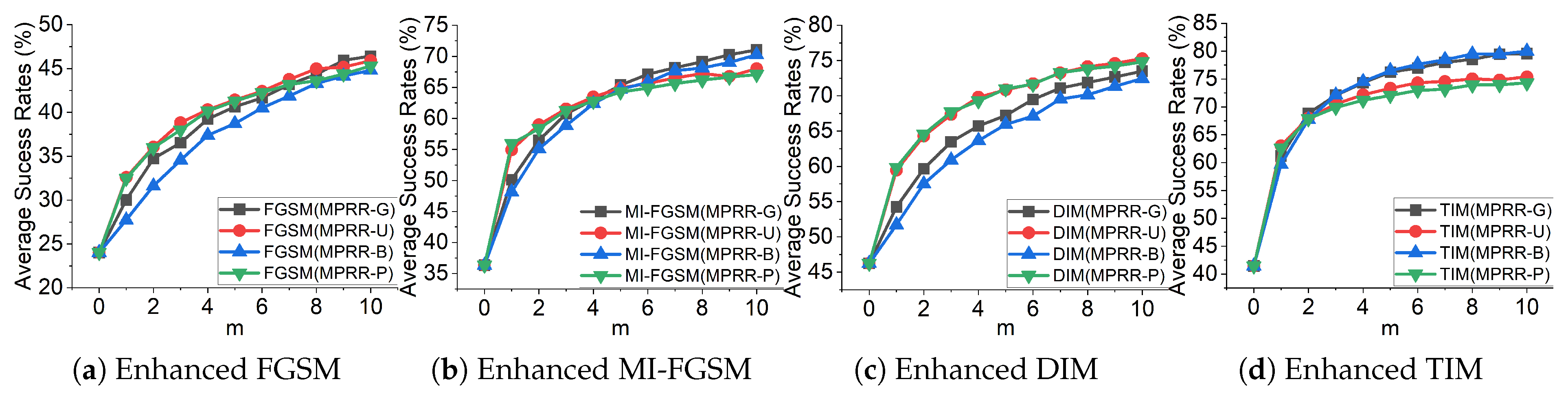
4.2. Evaluation of MPRR
4.3. Evaluation of CSAM
4.3.1. Attacking on Baseline Models
4.3.2. Combined with Transformation-Based Attacks
4.3.3. Attacking on Advanced Defense Models
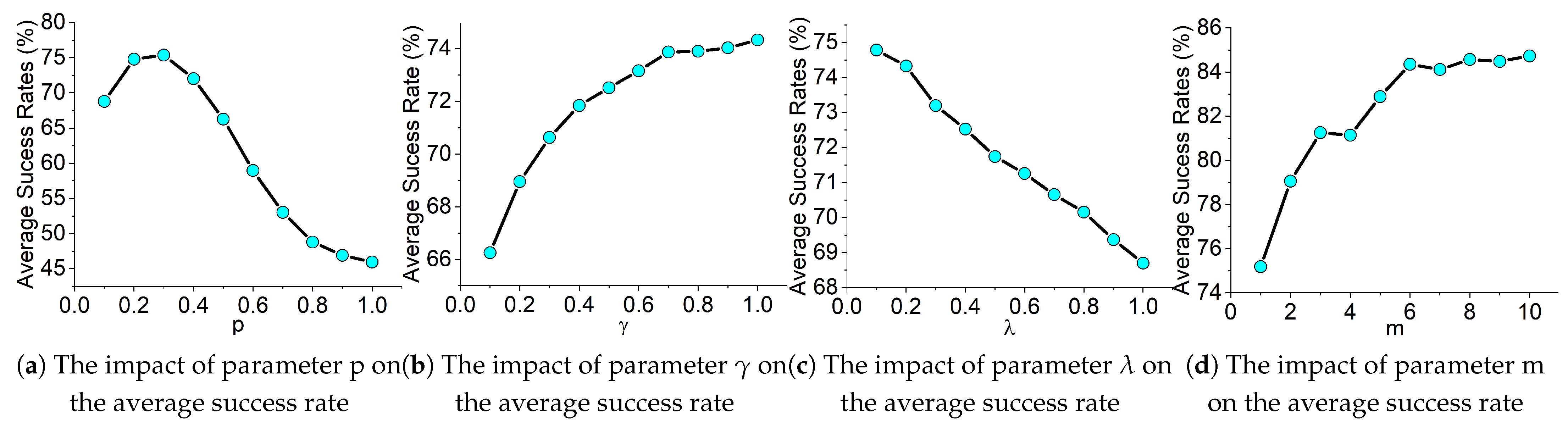
4.4. Ablation Studies of Hyper-Parameters
5. Conclusions
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Mądry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. Stat 2017, 1050, 9. [Google Scholar]
- Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the International Workshop on Artificial Intelligence and Security (AISec), Dallas, TX, USA, 3 November 2017; pp. 15–26. [Google Scholar]
- Cheng, S.; Dong, Y.; Pang, T.; Su, H.; Zhu, J. Improving black-box adversarial attacks with a transfer-based prior. In Proceedings of the NIPS’19: 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; p. 15947. [Google Scholar]
- Li, H.; Xu, X.; Zhang, X.; Yang, S.; Li, B. Qeba: Query-efficient boundary-based blackbox attack. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1221–1230. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9185–9193. [Google Scholar]
- Wang, X.; He, X.; Wang, J.; He, K. Admix: Enhancing the transferability of adversarial attacks. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 16158–16167. [Google Scholar]
- Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving transferability of adversarial examples with input diversity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2730–2739. [Google Scholar]
- Dong, Y.; Pang, T.; Su, H.; Zhu, J. Evading defenses to transferable adversarial examples by translation-invariant attacks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4312–4321. [Google Scholar]
- He, Z.; Duan, Y.; Zhang, W.; Zou, J.; He, Z.; Wang, Y.; Pan, Z. Boosting adversarial attacks with transformed gradient. Comput. Secur. 2022, 118, 102720. [Google Scholar] [CrossRef]
- Lin, J.; Song, C.; He, K.; Wang, L.; Hopcroft, J.E. Nesterov Accelerated Gradient and Scale Invariance for Adversarial Attacks. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zheng, T.; Chen, C.; Ren, K. Distributionally adversarial attack. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 2253–2260. [Google Scholar]
- Croce, F.; Hein, M. Minimally distorted adversarial examples with a fast adaptive boundary attack. In Proceedings of the International Conference on Machine Learning (ICML), Online, 13–18 July 2020; pp. 2196–2205. [Google Scholar]
- Tashiro, Y.; Song, Y.; Ermon, S. Diversity can be transferred: Output diversification for white-and black-box attacks. NeurIPS 2020, 33, 4536–4548. [Google Scholar]
- Mosbach, M.; Andriushchenko, M.; Trost, T.; Hein, M.; Klakow, D. Logit pairing methods can fool gradient-based attacks. arXiv 2018, arXiv:1810.12042. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. Mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Wang, X.; He, K. Enhancing the transferability of adversarial attacks through variance tuning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Virtually, 19–25 June 2021; pp. 1924–1933. [Google Scholar]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial machine learning at scale. arXiv 2016, arXiv:1611.01236. [Google Scholar]
- Tramèr, F.; Boneh, D.; Kurakin, A.; Goodfellow, I.; Papernot, N.; McDaniel, P. Ensemble adversarial training: Attacks and defenses. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Xu, W.; Evans, D.; Qi, Y. Feature squeezing: Detecting adversarial examples in deep neural networks. arXiv 2017, arXiv:1704.01155. [Google Scholar] [CrossRef]
- Liao, F.; Liang, M.; Dong, Y.; Pang, T.; Hu, X.; Zhu, J. Defense against adversarial attacks using high-level representation guided denoiser. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1778–1787. [Google Scholar]
- Xie, C.; Wang, J.; Zhang, Z.; Ren, Z.; Yuille, A. Mitigating Adversarial Effects Through Randomization. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Jia, X.; Wei, X.; Cao, X.; Foroosh, H. Comdefend: An efficient image compression model to defend adversarial examples. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6084–6092. [Google Scholar]
- Cohen, J.; Rosenfeld, E.; Kolter, Z. Certified adversarial robustness via randomized smoothing. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 1310–1320. [Google Scholar]
- Naseer, M.; Khan, S.; Hayat, M.; Khan, F.S.; Porikli, F. A self-supervised approach for adversarial robustness. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 262–271. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
| Model | Attack | Inc-v3 | Inc-v4 | IncRes-v2 | Res-101 | Inc-v3ens3 | Inc-v3ens4 | IncRes-v2ens | Average |
|---|---|---|---|---|---|---|---|---|---|
| Inc-v3 | SIM | 100.0 * | 69.2 | 67.9 | 62.4 | 31.3 | 31.2 | 16.6 | 54.1 |
| AAM | 100.0 * | 80.6 | 77.2 | 70.7 | 36.3 | 34.9 | 18.9 | 59.8 | |
| VTS | 100.0 * | 86.5 | 83.7 | 77.3 | 55.1 | 52.5 | 35.2 | 70.0 | |
| CSAM | 100.0 * | 93.7 | 92.7 | 89.6 | 75.7 | 74.8 | 60.1 | 83.8 | |
| Inc-v4 | SIM | 80.9 | 99.9 * | 73.6 | 69.2 | 47.4 | 44.7 | 29.5 | 63.6 |
| AAM | 88.1 | 99.8 * | 84.3 | 76.8 | 51.6 | 47.8 | 30.5 | 68.4 | |
| VTS | 88.8 | 99.7 * | 84.5 | 78.8 | 64.7 | 61.9 | 47.3 | 75.1 | |
| CSAM | 93.4 | 99.3 * | 91.5 | 88.5 | 81.0 | 79.2 | 68.2 | 85.9 | |
| IncRes-v2 | SIM | 85.1 | 80.8 | 99.0 * | 76.2 | 56.7 | 49.2 | 42.6 | 69.9 |
| AAM | 89.1 | 86.5 | 99.4 * | 82.8 | 63.9 | 55.2 | 45.9 | 74.7 | |
| VTS | 89.6 | 87.8 | 98.9 * | 83.8 | 72.8 | 66.7 | 64.9 | 80.6 | |
| CSAM | 92.7 | 91.9 | 98.5 * | 88.9 | 83.8 | 82.0 | 78.8 | 88.1 | |
| Res-101 | SIM | 74.0 | 69.0 | 69.4 | 99.7 * | 42.5 | 39.3 | 26.1 | 60 |
| AAM | 82.9 | 78.2 | 77.9 | 99.9 * | 49.4 | 44.1 | 28.7 | 65.9 | |
| VTS | 85.1 | 79.7 | 81.2 | 99.8 * | 64.5 | 58.1 | 44.0 | 73.2 | |
| CSAM | 89.6 | 86.1 | 87.7 | 100.0 * | 81.9 | 77.5 | 69.0 | 84.5 |
| Model | Attack | Inc-v3 | Inc-v4 | IncRes-v2 | Res-101 | Inc-v3ens3 | Inc-v3ens4 | IncRes-v2ens | Average |
|---|---|---|---|---|---|---|---|---|---|
| Inc-v3 | TD-SIM | 99.3 * | 83.8 | 79.4 | 75.8 | 64.9 | 61.9 | 45.2 | 72.9 |
| TD-AAM | 99.9 * | 89.6 | 87.4 | 81.2 | 70.5 | 68.1 | 48.9 | 77.9 | |
| TD-VTS | 98.9 * | 88.8 | 86.4 | 82.2 | 78.8 | 76.0 | 65.0 | 82.3 | |
| TD-CSAM | 99.5 * | 93.9 | 92.9 | 89.8 | 89.1 | 87.2 | 79.9 | 90.3 | |
| Inc-v4 | TD-SIM | 86.0 | 98.2 * | 81.8 | 75.3 | 68.1 | 65.5 | 55.2 | 75.7 |
| TD-AAM | 89.6 | 99.0 * | 87.0 | 83.3 | 75.2 | 71.5 | 60.5 | 80.9 | |
| TD-VTS | 89.6 | 98.4 * | 86.6 | 81.3 | 78.4 | 76.1 | 68.8 | 82.7 | |
| TD-CSAM | 94.1 | 99.4 * | 92.0 | 89.2 | 87.4 | 87.0 | 81.0 | 90.0 | |
| IncRes-v2 | TD-SIM | 88.1 | 84.3 | 96.9 * | 81.4 | 77.1 | 72.8 | 70.5 | 81.6 |
| TD-AAM | 91.1 | 89.3 | 97.8 * | 85.7 | 80.6 | 77.5 | 74.9 | 85.3 | |
| TD-VTS | 90.0 | 88.3 | 97.8 * | 85.3 | 82.5 | 82.0 | 80.2 | 86.6 | |
| TD-CSAM | 93.2 | 91.4 | 98.3 * | 90.0 | 90.2 | 88.4 | 88.8 | 91.5 | |
| Res-101 | TD-SIM | 83.7 | 81.7 | 82.7 | 99.0 * | 75.2 | 70.9 | 60.5 | 79.1 |
| TD-AAM | 88.2 | 85.4 | 87.4 | 99.9 * | 79.1 | 75.5 | 67.7 | 83.3 | |
| TD-VTS | 87.2 | 83.2 | 86.8 | 99.0 * | 81.5 | 78.9 | 72.6 | 84.2 | |
| TD-CSAM | 90.6 | 86.2 | 89.7 | 99.6 * | 89.2 | 88.7 | 84.6 | 89.8 |
| ATTACK | HGD | R&P | NIPs-r3 | NRP | RS | Bit-Red | ComDefend | Average |
|---|---|---|---|---|---|---|---|---|
| TD-AAM | 62.7 | 50.9 | 60.8 | 46.1 | 43.9 | 52.1 | 82.5 | 57.0 |
| TD-VTS | 72.2 | 64.2 | 69.6 | 56.9 | 50.5 | 58.4 | 82.1 | 64.8 |
| TD-CSAM | 81.9 | 78.3 | 82.9 | 77.5 | 71.9 | 75.0 | 88.4 | 79.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, W.; Huang, H.; Chen, J. Boosting Adversarial Transferability Through Adversarial Attack Enhancer. Appl. Sci. 2025, 15, 10242. https://doi.org/10.3390/app151810242
Zeng W, Huang H, Chen J. Boosting Adversarial Transferability Through Adversarial Attack Enhancer. Applied Sciences. 2025; 15(18):10242. https://doi.org/10.3390/app151810242
Chicago/Turabian StyleZeng, Wenli, Hong Huang, and Jixin Chen. 2025. "Boosting Adversarial Transferability Through Adversarial Attack Enhancer" Applied Sciences 15, no. 18: 10242. https://doi.org/10.3390/app151810242
APA StyleZeng, W., Huang, H., & Chen, J. (2025). Boosting Adversarial Transferability Through Adversarial Attack Enhancer. Applied Sciences, 15(18), 10242. https://doi.org/10.3390/app151810242






