Client-Oriented Highway Construction Cost Estimation Models Using Machine Learning
Abstract
1. Introduction
2. Literature Review
| First Author | Year | Project Type | Data Source Country | Method | Method Category |
|---|---|---|---|---|---|
| Hegazy [49] | 1998 | Roads | Canada | ANN | ML |
| Adeli [48] | 1998 | Roads | USA | ANN | ML |
| Sodikov [27] | 2005 | Roads | Poland, Thailand | ANN | ML |
| Wilmot [34] | 2005 | Roads | USA | ANN | ML |
| Chou [46] | 2006 | Roads | USA | NLR | ML |
| Chou [3] | 2007 | Roads | USA | ES-(RDBMS) | ES/DM and DVTs |
| Hammad [35] | 2008 | Multiple project types including Roads | Jordan | MLR | ML |
| Bouabaz [63] | 2008 | Bridges | UK | ANN | ML |
| Pewdum [36] | 2009 | Roads | Thailand | ANN | ML |
| Chou [29] | 2009 | Roads | USA | ES using GLM | ML-Expert/DM |
| Petroutsatou [64] | 2010 | Tunnels | Greece | SEM/MLR/ANN | ML and S/MM |
| Kim [50] | 2010 | Roads | South Korea | CBR | ES/DM |
| Fragkakis [65] | 2011 | Bridges (foundations) | Greece | RA | ML |
| Kang [47] | 2011 | Roads | South Korea | CBR/RA | ES/DM and S/MM |
| Chou [30] | 2011 | Roads (Pavements) | Taiwan | MCS | STs |
| Asmar [40] | 2011 | Roads | USA | PERT | S/MM |
| Mahamid [41] | 2011 | Roads | West Bank | MLR | ML |
| Petroutsatou [66] | 2012 | Tunnels | Greece | ANN | ML |
| Rostami [22] | 2013 | Tunnels | Canada, USA | UCA/RA | S/MM |
| Mahamid [43] | 2013 | Roads | Saudi Arabia | MLR | S/MM |
| Kim [42] | 2013 | Roads | South Korea | CBR/AHP | ES/DM |
| He [31] | 2014 | Roads (Pavements) | China | ANN | ML |
| Park [51] | 2014 | Roads | Korea | BIM/GIS | DVTs |
| Antoniou [67] | 2016 | Bridges (overpasses) | Greece | MLR | ML |
| Fragkakis [68] | 2016 | Bridges | Greece | UCA/MLR | S/MM-ML |
| Peško [37] | 2017 | Roads | Serbia | ANN | ML |
| Swei [32] | 2017 | Roads (Pavements) | USA | RA | S/MM |
| Zhang [69] | 2017 | Bridges | USA | MARS | ML |
| Antoniou [5] | 2018 | Bridges (underpasses) | Greece | MLR | ML |
| Aretoulis [38] | 2019 | Roads | Greece | ANN | ML |
| Mahalakshmi [57] | 2019 | Roads | India | ANN | ML |
| Juszczyk [70] | 2019 | Bridges | Poland | SVM | ML |
| Lin [56] | 2019 | Roads | Thailand | ANN/MLR | ML |
| Meharie [58] | 2020 | Roads | Ethiopia | RF/SVM/ANN | ML |
| Juszczyk [71] | 2020 | Bridges | Poland | ANN | ML |
| Wang [62] | 2021 | Roads | China | PCA/PSO/LSSVM | ML and MOAs |
| Petroutsatou [72] | 2021 | Tunnels | Greece | ANN | ML |
| Kovacevic [73] | 2021 | Bridges | Serbia | ANN/RTE/RF/GBM/SVR/GPR | ML |
| Markiz [74] | 2022 | Bridges | Canada | ES/BIM | ES/DM and DVTs |
| Feng [55] | 2022 | Roads | China | RF/SVM | ML |
| Liu [75] | 2022 | Tunnels | China | SVM | ML |
| Meharie [59] | 2022 | Roads | Ethiopia | GBMwithLR/SVM/ANN | ML |
| Mahmoodzadeh [24] | 2022 | Tunnels | Iran/Iraq | GPR | ML |
| Mahmoodzadeh [26] | 2022 | Tunnels | Iran/Iraq | MCS | STs |
| Mahmoodzadeh [25] | 2022 | Tunnels | Iran/Iraq | LR/GPR/SVR/DT | ML |
| Mahmoodzadeh [23] | 2022 | Tunnels | Iran/Iraq | GPR/PSO/GWO/MVO/MFO/SCA/SSO | ML and MOAs |
| Ghadbhan Abed [44] | 2022 | Roads | Iraq | LASSO/K-NN/RF | ML and MOAs |
| Gante [33] | 2022 | Roads (Improvements) | Phillipines | ANN | ML |
| Mohamed [60] | 2022 | Roads | USA | ANN/SVM/RF/EML | ML |
| Warren [52] | 2022 | Roads | USA | ML | ML |
| Hoffmann [61] | 2023 | Roads | Austria | UCA | S/MM |
| Kovacevic [28] | 2023 | Bridges | Serbia | ANN/RT/MGGP/VIKOR | ML-ES/DM |
| Vagdatli [7] | 2023 | Bridges | Greece | DBN | ML |
| Zhang [53] | 2023 | Roads | USA | LASSO/GRNN | ML and MOAs |
| Wang [54] | 2024 | Roads | China | GA-BP | ML |
| Zhou [76] | 2024 | Tunnels | China | SSAE | ML |
| Birhanu Belete [39] | 2024 | Roads | Ethiopia | RA | S/MM |
| Vagdatli [77] | 2024 | Bridges | Greece | DBN | ML |
| Abd [45] | 2024 | Roads | Iraq | ANN | ML |
| Helaly [78] | 2025 | Bridges | USA | ML | ML |
| First Author (Year) [Ref] | Database Size | Dependent Variables | Independent Variable | Comments | Method |
|---|---|---|---|---|---|
| Chou (2007) [3] | Unspecified number of projects from Texas DoT | Project Type (choice of 8), Project length (miles), Shoulder width (ft),Lane width (ft), Lanes (n), Percent trucks, Design speed (mph), Location (choice of 3),Divided highway (yes/no), Characteristics (e.g., Freeway), National Highway System (yes, no), Truck system flag (yes, no), Bridges (n), Bridge deck area (ft2). Dominant bridge material (type) | Construction Cost | Does not present the statistical models that are used for calculation of cost estimate but presents the development of a web-based system for users to input the IV. Does not consider IV related to number of culverts or interchanges or existence of tunnels. | ES-RDBMS (Non-ML) |
| Lin (2019) [56] | 51 rural road projects in Thailand | Road length (km), Lane width (m), Number of lanes per direction, Pavement type, Earthwork quantity, Miscellaneous | Construction Cost | Does not consider IV related to number of culverts or interchanges nor consider existence and size of possible bridges or tunnels. It requires a method of estimating earthwork quantities during the feasibility phase without any design work having been completed. | RA (ML) |
| Mahalakshmi (2019) [57] | 52 road projects in India | Road classification, Topography, Type of pavement (flexible or rigid), C/S of pavement (cutting or embankment), Soil Condition (based on CBR) (%), Contract duration, Length of pavement, lane width, Pavement thickness, No. of cross drains | Construction Cost | Does not consider IV related to number of interchanges nor considers existence and size of possible bridges or tunnels. It requires a method of estimating contract duration, which is challenging during the feasibility phase without the detailed contractual scope having been defined. | ANN (ML) |
| Meharie (2020) [58] | 74 road projects in Ethiopia | Project length, Number of bridges, Inflation rate, Project scope, Terrain type, Project type, Contract duration and Project location. | Construction Cost | Does not consider IV related to number of culverts or interchanges nor consider existence and size of possible tunnels. It requires a method of estimating contract duration, which is challenging during the feasibility phase without the detailed contractual scope having been defined. | RF/SVM/ANN (ML) |
| Wang (2021) [62] | 60 road projects in China | Length (km), Width (m), Earthwork Quantity (m3), Number of bridges (n), Number of interchanges, Number of separated interchanges, Number of tunnels, Pavement form, Landform features and area. | Construction Cost per km | Most similar to our idea but also requires a method of estimating earthwork quantities during the feasibility phase without any design work having been completed. | PCA/ PSO/ LSSVM (ML) |
| Meharie (2022) [59] | 117 road projects in Ethiopia | Number of bridges, Inflation rate, Terrain type and Project type | Construction Cost | Does not consider IV related to number of culverts or interchanges nor consider existence and size of possible tunnels | GBM + LR/SVM/ANN (ML) |
| Mohamed (2022) [60] | 284 USA highway projects | Location, Facility Type (Roads, Bridges, Drainage, and Intelligent Transportation System), Project Scope (New Construction/Expansion, Rehabilitation/Reconstruction, and Resurfacing/Renewal), Highway Type (Rural Interstate, Urban Interstate, Rural Primary, Urban Primary, and Rural Secondary). Length (km), Number of Lanes, Technical Complexity (Non-complex, Moderately Complex, and Most Complex) | Construction Cost | Does not consider IV related to number of culverts or interchanges nor consider existence and size of possible bridges or tunnels | ANN/ SVM/ RF/ EML (ML) |
| Hoffmann (2023) [61] | Unspecified number of projects in Austria | Lane kilometers, Area of bridges and tunnels | Unit prices | Provides expected unit prices per lane km and per square meter of bridge or tunnel. Does not consider number of interchanges nor number of culverts. | UCA (Non-ML) |
3. Methods
3.1. Research Objectives
3.2. Data Collection and Description
- Lm = length of main axis (m);
- Wm = width of main axis (m);
- Am = area of main axis (m2);
- Ls= length of service roads (m);
- Ws = width of service roads (m);
- As = area of service roads (m2);
- Am+s = total road area (main + service) (m2);
- Nic = number of interchanges;
- Ab= area of bridges (m2);
- Aop = area of overpasses (m2);
- Aup = area of underpasses (m2);
- Ast = sum of area of all structures (m2);
- Lt= total length of single bore tunnels (m);
- Nc = number of culverts;
- LR= length of river training (m);
- LRb = length of river bridges (m);
- WRb= length of river bridges (m);
- Ns = number of spans of river bridges;
- ARb = area of river bridges (m2).
3.3. Machine-Learning Approaches
3.3.1. Multilayer Perceptron-Artificial Neural Network (MLP-ANN) Models
3.3.2. Radial Basis Function-Artificial Neural Network (RBF-ANN) Models
3.3.3. Multiple Linear Regression (MLR) Models
3.3.4. Random Forest (RF) Models
3.3.5. Support Vector Regression (SVR) Models
3.3.6. XGBoost Technique
3.3.7. K-Nearest Neighbors (KNN) Algorithm
3.4. Model Evaluation Metrics
3.4.1. Mean Absolute Error (MAE)
3.4.2. R2
3.4.3. MAE % of Mean
3.4.4. Mean Absolute Percentage Error (MAPE)
4. Results
4.1. Models Tested
4.2. Development, Training and Testing of ML Models
- Models a, b:MLPRegressor(hidden_layer_sizes = (3), activation = ‘relu’, max_iter = 3000, learning_rate_init = 0.001, random_state = 42).
- Models c, d, e:Same configuration as above, except hidden_layer_sizes = (10).RBF-ANN
- All models:rbf_model = RBFNetwork(n_centers = 5), rbf_model.fit(X_train_scaled, Y_train),Y_pred_rbf = rbf_model.predict(X_test_scaled)RF:
- All models: RandomForestRegressor(n_estimators = 100, random_state = 42)SVR
- All models: SVR(kernel = ‘rbf’, C = 100, gamma = 1)XGBoost:
- Models a, b:xgb.XGBRegressor(objective =‘reg:squarederror’, colsample_bytree = 0.3, learning_rate = 0.1, max_depth = 5, alpha = 10, n_estimators = 100, random_state = 42)
- Models c, d, e:Same as above, except learning_rate = 0.01, max_depth =KNN:
- All models: KNeighborsRegressor(n_neighbors = 5)
4.3. Model Evaluation Metric Results and Analysis
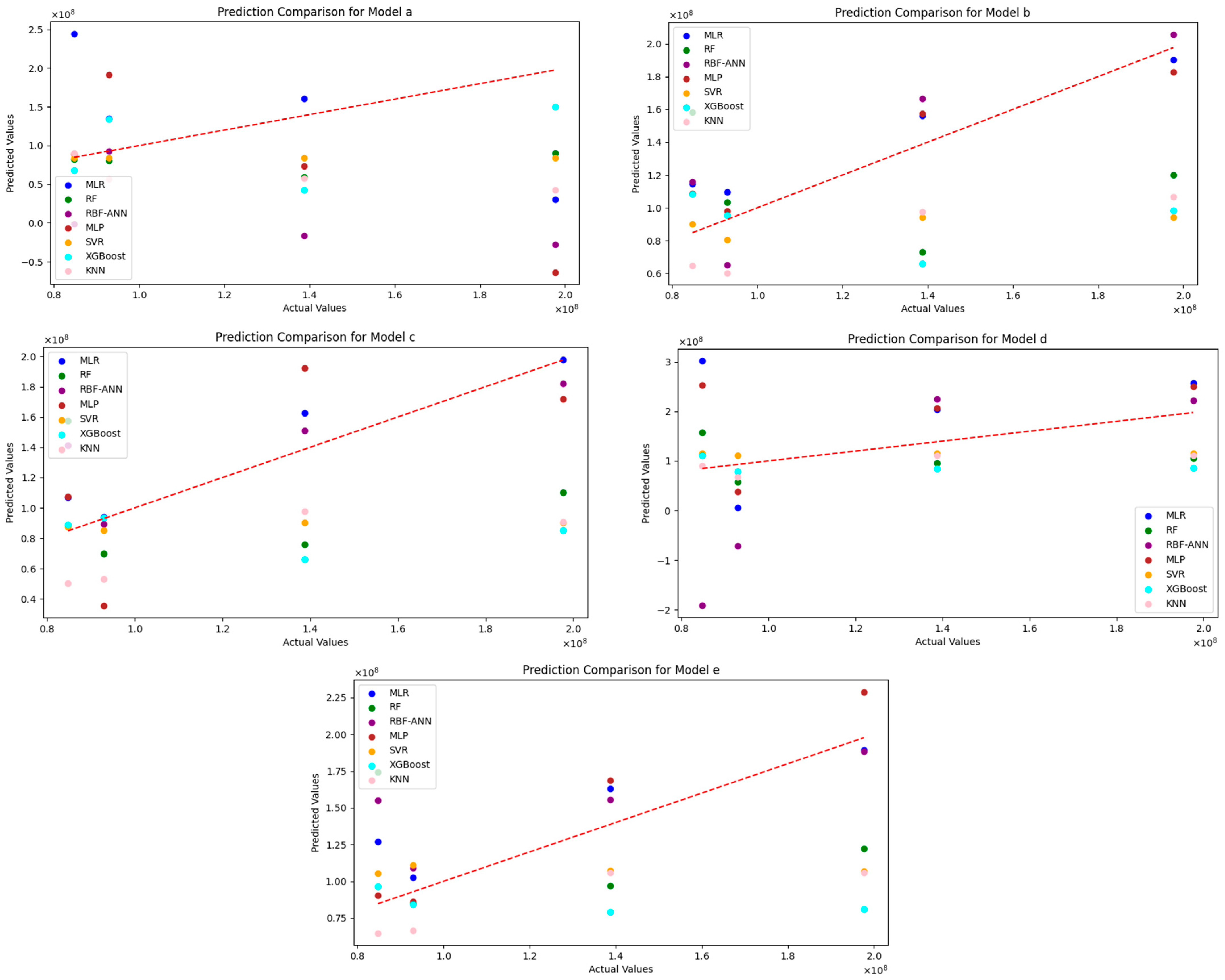
4.3.1. Result Presentation
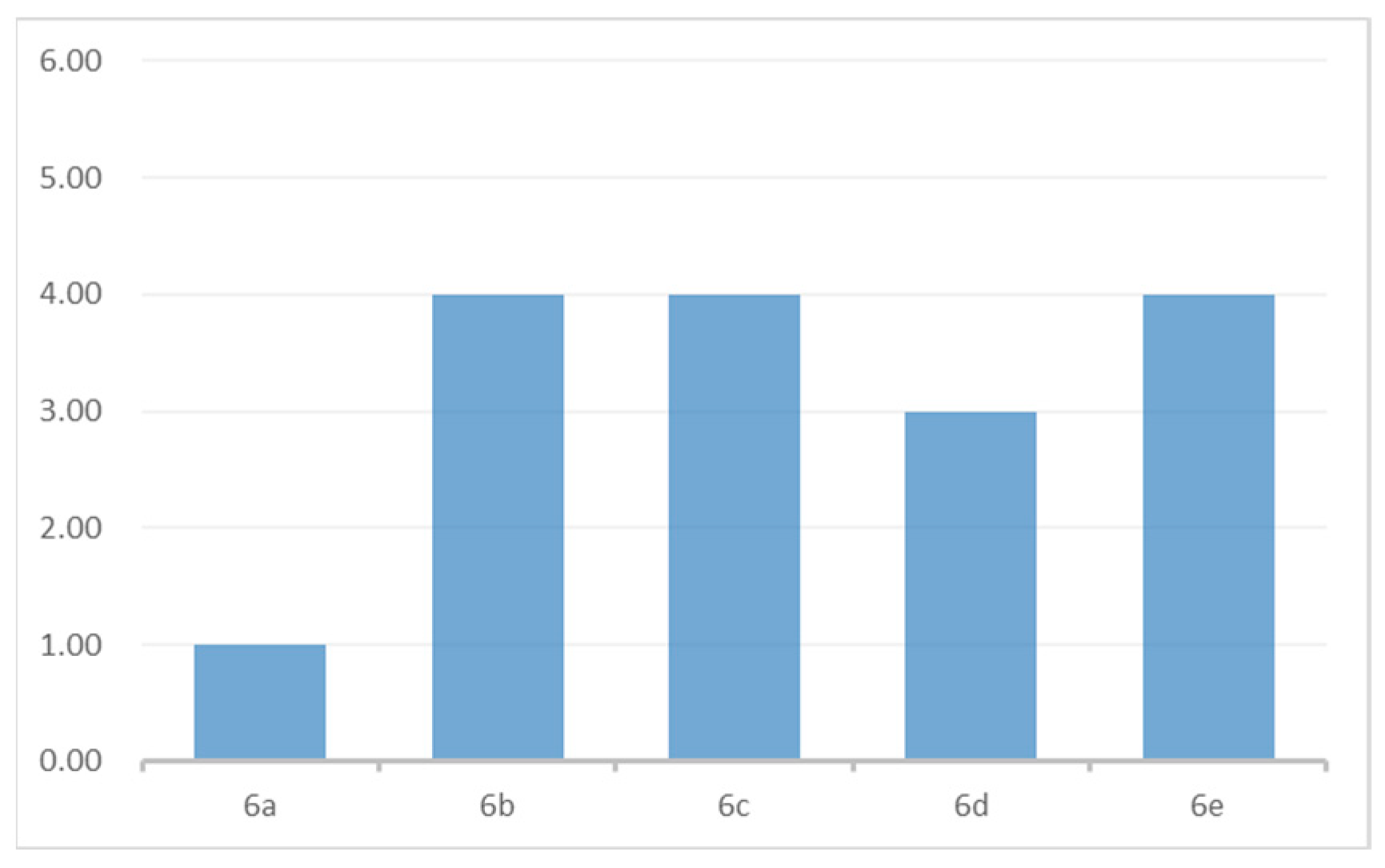
4.3.2. Model Ranking and Acceptance Procedure
- MAE < 30% of the mean Total Cost of the 19 data sample projects.
- R2 > 0.50.
- MAE% < 30.
- MAPE% < 30.
4.3.3. Comparative Evaluation of Accepted Models
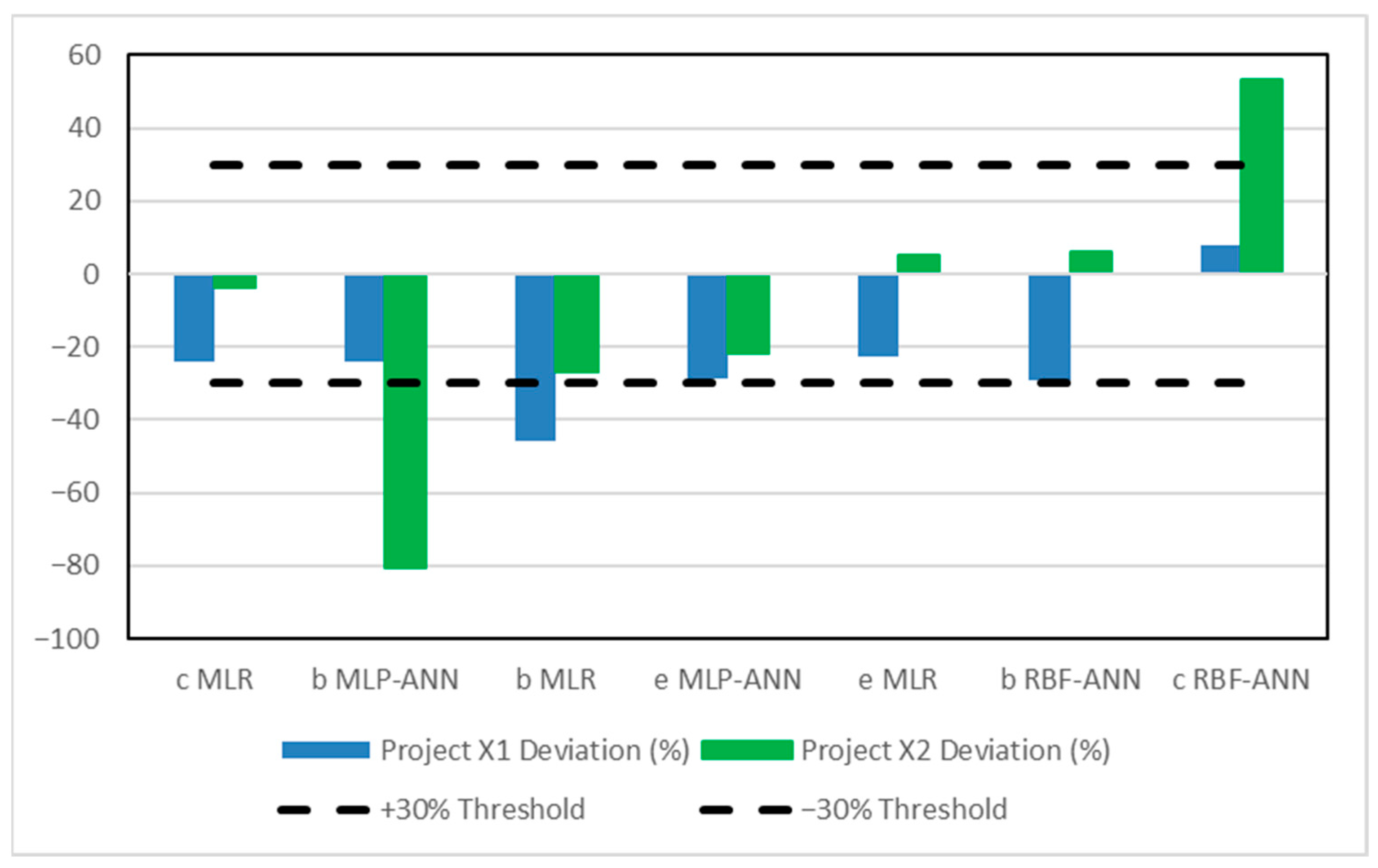
4.4. Cross-Validation of Selected Models Using Independent Project Data
4.5. Model Application Procedure
- Step 1: Estimate inputs: mainline length (Lm), service road length (Ls), number of interchanges (Nic), total area of structures (Ast), single-bore tunnel length (Lt), and number of culverts (Nc).
- Step 2: Standardize variables using the means and standard deviations from Table 11.
- Step 3: Apply coefficients from Equation (6) to obtain the predicted total cost of work items (2024 price level).
- Step 4: Adjust to tender budget: In the Greek context, add 18% for overhead and profit and 9% for contingency. Other countries may adjust according to national procurement rules.
- Step 5: Update prices: When applying the model after 2024 in Greece or across countries, revalue using appropriate harmonized price indices.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Commission: Directorate-General for Mobility and Transport. EU Transport in Figures: Statistical Pocketbook 2021; Publications Office: Luxemburg, 2021. [Google Scholar]
- Barakchi, M.; Torp, O.; Belay, A.M. Cost Estimation Methods for Transport Infrastructure: A Systematic Literature Review. Procedia Eng. 2017, 196, 270–277. [Google Scholar] [CrossRef]
- Chou, J.-S.; O’Connor, J.T. Internet-Based Preliminary Highway Construction Cost Estimating Database. Autom. Constr. 2007, 17, 65–74. [Google Scholar] [CrossRef]
- Bakhshi, P.; Touran, A. An Overview of Budget Contingency Calculation Methods in Construction Industry. Procedia Eng. 2014, 85, 52–60. [Google Scholar] [CrossRef]
- Antoniou, F.; Konstantinidis, D.; Aretoulis, G.; Xenidis, Y. Preliminary Construction Cost Estimates for Motorway Underpass Bridges. Int. J. Constr. Manag. 2017, 18, 321–330. [Google Scholar] [CrossRef]
- Shim, H.S.; Lee, S.H. Developing a Probable Cost Analysis Model for Comparing Bridge Deck Rehabilitation Methods. KSCE J. Civ. Eng. 2016, 20, 68–76. [Google Scholar] [CrossRef]
- Vagdatli, T.; Petroutsatou, K.; Panetsos, P.; Barmpa, Z.; Fragkakis, N. Bayesian Pre-Estimation of Bridge Life-Cycle Costs. In Life-Cycle of Structures and Infrastructure Systems; CRC Press: London, UK, 2023; pp. 3252–3259. [Google Scholar]
- Gadiraju, D.S.; Muthiah, S.R.; Khazanchi, D. A Deep Reinforcement Learning Based Approach for Bridge Health Maintenance. In Proceedings of the 2023 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 13–15 December 2023; pp. 43–48. [Google Scholar]
- Petroutsatou, K.; Vagdatli, T.; Louloudakis, N.; Panetsos, P. Life-Cycle Maintenance Cost Model for Concrete Bridges Using Markovian Deterioration Curves. Buildings 2025, 15, 807. [Google Scholar] [CrossRef]
- Fragkakis, N.; Petroutsatou, K.; Marinelli, M. Preliminary Cost Estimate Model for Road Underpasses. In Proceedings of the Eighth International Conference on Construction in the 21st Century (CITC-8) “Changing the Field: Recent Developments for the Future of Engineering and Construction”, Thessaloniki, Greece, 27 May 2015. [Google Scholar]
- Flyvbjerg, B.; Holm, M.S.; Buhl, S. Underestimating Costs Public Works Projects: Error Or Lie? J. Am. Plan. Assoc. 2002, 68, 279–295. [Google Scholar] [CrossRef]
- Burke, R. Project Management—Tools and Techniques; Burke Publishing: London, UK, 2010. [Google Scholar]
- Association for the Advancement of Cost Engineering AACE. 18R-97: Cost Estimate Classification System—As Applied in Engineering, Procurement, and Construction for the Process Industries; AACE International: Fairmont, WV, USA, 2005. [Google Scholar]
- Heralova, R.S.; Hromada, E.; Johnston, H. Cost Structure of the Highway Projects in the Czech Republic. Procedia Eng. 2014, 85, 222–230. [Google Scholar] [CrossRef]
- Hanioğlu, M.N. A Cost Based Approach to Project Management Planning and Controlling Construction Project Costs; Routledge: New York, NY, USA, 2023. [Google Scholar]
- Gardner, B.J.; Gransberg, D.D.; Jeong, H.D. Reducing Data-Collection Efforts for Conceptual Cost Estimating at a Highway Agency. J. Constr. Eng. Manag. 2016, 142, 04016057. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. BMJ 2009, 339, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Halevi, G.; Moed, H.; Bar-Ilan, J. Suitability of Google Scholar as a Source of Scientific Information and as a Source of Data for Scientific Evaluation—Review of the Literature. J. Inf. 2017, 11, 823–834. [Google Scholar] [CrossRef]
- Pranckutė, R. Web of Science (WoS) and Scopus: The Titans of Bibliographic Information in Today’s Academic World. Publications 2021, 9, 12. [Google Scholar] [CrossRef]
- Bar-Ilan, J. Which H-Index?—A Comparison of WoS, Scopus and Google Scholar. Scientometrics 2008, 74, 257–271. [Google Scholar] [CrossRef]
- Antoniou, F.; Aretoulis, G.; Giannoulakis, D.; Konstantinidis, D. Cost and Material Quantities Prediction Models for the Construction of Underground Metro Stations. Buildings 2023, 13, 382. [Google Scholar] [CrossRef]
- Rostami, J.; Sepehrmanesh, M.; Gharahbagh, E.A.; Mojtabai, N. Planning Level Tunnel Cost Estimation Based on Statistical Analysis of Historical Data. Tunn. Undergr. Space Technol. 2013, 33, 22–33. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Nejati, H.R.; Mohammadi, M.; Hashim Ibrahim, H.; Khishe, M.; Rashidi, S.; Hussein Mohammed, A. Developing Six Hybrid Machine Learning Models Based on Gaussian Process Regression and Meta-Heuristic Optimization Algorithms for Prediction of Duration and Cost of Road Tunnels Construction. Tunn. Undergr. Space Technol. 2022, 130, 104759. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Abdulhamid, S.N.; Ibrahim, H.H.; Ali, H.F.H.; Nejati, H.R.; Rashidi, S. Prediction of Duration and Construction Cost of Road Tunnels Using Gaussian Process Regression. Geomech. Eng. 2022, 28, 65–75. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Nejati, H.R.; Mohammadi, M. Optimized Machine Learning Modelling for Predicting the Construction Cost and Duration of Tunnelling Projects. Autom. Constr. 2022, 139, 104305. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ali, H.F.H.; Salim, S.G.; Abdulhamid, S.N.; Ibrahim, H.H.; Rashidi, S.A. Markov-Based Prediction Model of Tunnel Geology, Construction Time, and Construction Costs. Geomech. Eng. 2022, 28, 421–435. [Google Scholar]
- Sodikov, J. Cost Estimation of Highway Projects in Developing Countries: Artificaila Neural Network Approach. J. East. Asia Soc. Transp. Stud. 2005, 6, 1036–1047. [Google Scholar]
- Kovačević, M.; Antoniou, F. Machine-Learning-Based Consumption Estimation of Prestressed Steel for Prestressed Concrete Bridge Construction. Buildings 2023, 13, 1187. [Google Scholar] [CrossRef]
- Chou, J.-S. Generalized Linear Model-Based Expert System for Estimating the Cost of Transportation Projects. Expert. Syst. Appl. 2009, 36, 4253–4267. [Google Scholar] [CrossRef]
- Chou, J.-S. Cost Simulation in an Item-Based Project Involving Construction Engineering and Management. Int. J. Proj. Manag. 2011, 29, 706–717. [Google Scholar] [CrossRef]
- He, J.; Qi, Z.; Hang, W.; Zhao, C.; King, M. Predicting Freeway Pavement Construction Cost Using a Back-Propagation Neural Network: A Case Study in Henan, China. Balt. J. Road Bridge Eng. 2014, 9, 66–76. [Google Scholar] [CrossRef]
- Swei, O.; Gregory, J.; Kirchain, R. Construction Cost Estimation: A Parametric Approach for Better Estimates of Expected Cost and Variation. Transp. Res. Part. B Methodol. 2017, 101, 295–305. [Google Scholar] [CrossRef]
- Gante, D.V.; Silva, D.L.; Leopoldo, M.P. Forecasting Construction Cost Using Artificial Neural Network for Road Projects in the Department of Public Works and Highways Region XI. In Frontiers in Artificial Intelligence and Applications; IOS Press B.V.: Amsterdan, The Netherlands, 2022; Volume 352, pp. 64–71. [Google Scholar]
- Wilmot, C.G.; Mei, B. Neural Network Modeling of Highway Construction Costs. J. Constr. Eng. Manag. 2005, 131, 765–771. [Google Scholar] [CrossRef]
- Hammad, A.A.A.; Alhaj Ali, S.M.; Sweis, G.J.; Bashir, A. Prediction Model for Construction Cost and Duration in Jordan. Jordan J. Civ. Eng. 2008, 2, 250–266. [Google Scholar]
- Pewdum, W.; Rujirayanyong, T.; Sooksatra, V. Forecasting Final Budget and Duration of Highway Construction Projects. Eng. Constr. Archit. Manag. 2009, 16, 544–557. [Google Scholar] [CrossRef]
- Peško, I.; Mučenski, V.; Šešlija, M.; Radović, N.; Vujkov, A.; Bibić, D.; Krklješ, M. Estimation of Costs and Durations of Construction of Urban Roads Using ANN and SVM. Complexity 2017, 2017, 2450370. [Google Scholar] [CrossRef]
- Aretoulis, G.N. Neural Network Models for Actual Cost Prediction in Greek Public Highway Projects. Int. J. Proj. Organ. Manag. 2019, 11, 41–64. [Google Scholar] [CrossRef]
- Birhanu Belete, S.; Getnet Meharie, M.; Getawa Ayalew, G. Development of a Mathematical Model to Predict the Cost of Ethiopian Roads Authority Road Projects: The Case of Ethiopia. Cogent Eng. 2024, 11, 2297492. [Google Scholar] [CrossRef]
- Asmar, M.E.; Hanna, A.S.; Whited, G.C. New Approach to Developing Conceptual Cost Estimates for Highway Projects. J. Constr. Eng. Manag. 2011, 137, 942–949. [Google Scholar] [CrossRef]
- Mahamid, I. Early Cost Estimating for Road Construction Projects Using Multiple Regression Techniques. Constr. Econ. Build. 2011, 11, 87–101. [Google Scholar] [CrossRef]
- Kim, S. Hybrid Forcasting System Based on Case-Based Reasoning and Analytic Heirarchy Process for Cost Estimation. J. Civ. Eng. Manag. 2013, 19, 86–96. [Google Scholar] [CrossRef]
- Mahamid, I. Conceptual Cost Estimate of Road Construction Projects in Saudi Arabia. Jordan. J. Civ. Eng. 2013, 7, 285–294. [Google Scholar]
- Ghadbhan Abed, Y.; Mohammed Hasan, T.; Nihad Zehawi, R. Cost Prediction for Roads Construction Using Machine Learning Models. Int. J. Electr. Comput. Eng. Syst. 2022, 13, 927–936. [Google Scholar] [CrossRef]
- Abd, A.M.; Kareem, Y.A.; Zehawi, R.N. Prediction and Estimation of Highway Construction Cost Using Machine Learning. Eng. Technol. Appl. Sci. Res. 2024, 14, 17222–17231. [Google Scholar] [CrossRef]
- Chou, J.-S.; Peng, M.; Persad, K.; O’Connor, J. Quantity-Based Approach to Preliminary Cost Estimates for Highway Projects. Transp. Res. Rec. J. Transp. Res. Board 2006, 1946, 22–30. [Google Scholar] [CrossRef]
- Kang, T.K.; Park, W.; Lee, Y.S. Development Of CBR-Based Road Construction Project Cost Estimation System. In Proceedings of the Conference: 28th International Symposium on Automation and Robotics in Construction, Seoul, Republic of Korea, 29 June–2 July 2011; International Association for Automation & Robotics in Construction (IAARC): Oulu, Finland, 2011; pp. 1314–1319. [Google Scholar]
- Adeli, H.; Wu, M. Regularization Neural Network for Construction Cost Estimation. J. Constr. Eng. Manag. 1998, 124, 18–24. [Google Scholar] [CrossRef]
- Hegazy, T.; Ayed, A. Neural Network Model for Parametric Cost Estimation of Highway Projects. J. Constr. Eng. Manag. 1998, 124, 210–218. [Google Scholar] [CrossRef]
- Kim, K.J.; Kim, K. Preliminary Cost Estimation Model Using Case-Based Reasoning and Genetic Algorithms. J. Comput. Civ. Eng. 2010, 24, 499–505. [Google Scholar] [CrossRef]
- Park, T.; Kang, T.; Lee, Y.; Seo, K. Project Cost Estimation of National Road in Preliminary Feasibility Stage Using BIM/GIS Platform. In Proceedings of the Computing in Civil and Building Engineering, Orlando, FL, USA, 23–25 June 2014; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 423–430. [Google Scholar]
- Warren, J.; Allen, D.; Storey, J. Systematic Cost Estimating Tool for the Mississippi Department of Transportation. In Proceedings of the IISE Annual Conference and Expo 2022, Seattle, WA, USA, 21–24 May 2022; Institute of Industrial & Systems Engineers (IISE): Norcross, GA, USA, 2022. [Google Scholar]
- Zhang, Y.; Minchin, R.E.; Flood, I.; Ries, R.J. Preliminary Cost Estimation of Highway Projects Using Statistical Learning Methods. J. Constr. Eng. Manag. 2023, 149, 04023026. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z. Research on the Construction of Highway Engineering Cost Prediction Model Based on GA-BP Algorithm. Lect. Notes Electr. Eng. 2024, 1216, 271–279. [Google Scholar] [CrossRef]
- Feng, F. Cost Prediction of Municipal Road Engineering Based on Optimization of SVM Parameters by RF-WPA Hybrid Algorithm. In Lecture Notes on Data Engineering and Communications Technologies; Springer Nature: Cham, Switzerland, 2022; Volume 138, pp. 86–93. [Google Scholar]
- Lin, W.P.; Techapeeraparnich, W. Model for Predicting Cost of Rural Road Projects in Thailand. IOP Conf. Ser. Mater. Sci. Eng. 2019, 652, 012004. [Google Scholar] [CrossRef]
- Mahalakshmi, G.; Rajasekaran, C. Early Cost Estimation of Highway Projects in India Using Artificial Neural Network. In Sustainable Construction and Building Materials: Select Proceedings of ICSCBM 2018; Springer: Singapore, 2019; pp. 659–672. [Google Scholar]
- Meharie, M.G.; Shaik, N. Predicting Highway Construction Costs: Comparison of the Performance of Random Forest, Neural Network and Support Vector Machine Models. J. Soft Comput. Civ. Eng. 2020, 4, 103–112. [Google Scholar] [CrossRef]
- Meharie, M.G.; Mengesha, W.J.; Gariy, Z.A.; Mutuku, R.N.N. Application of Stacking Ensemble Machine Learning Algorithm in Predicting the Cost of Highway Construction Projects. Eng. Constr. Archit. Manag. 2022, 29, 2836–2853. [Google Scholar] [CrossRef]
- Mohamed, B.; Moselhi, O. Conceptual Estimation of Construction Duration and Cost of Public Highway Projects. J. Inf. Technol. Constr. 2022, 27, 595–618. [Google Scholar] [CrossRef]
- Hoffmann, M.; Donev, V. Reliable Estimation of Investment and Life-Cycle Costs from Road Projects to Single Road Assets. In Life-Cycle of Structures and Infrastructure Systems; CRC Press: London, UK, 2023; pp. 3284–3291. [Google Scholar]
- Wang, X.; Liu, S.; Zhang, L. Highway Cost Prediction Based on LSSVM Optimized by Intial Parameters. Comput. Syst. Sci. Eng. 2021, 36, 259–269. [Google Scholar] [CrossRef]
- Bouabaz, M.; Hamami, M. A Cost Estimation Model for Repair Bridges Based on Artificial Neural Network. Am. J. Appl. Sci. 2008, 5, 334–339. [Google Scholar] [CrossRef]
- Petroutsatou, K.; Lambropoulos, S. Road Tunnels Construction Cost Estimation: A Structural Equation Model Development and Comparison. Oper. Res. 2010, 10, 163–173. [Google Scholar] [CrossRef]
- Fragkakis, N.; Lambropoulos, S.; Tsiambaos, G. Parametric Model for Conceptual Cost Estimation of Concrete Bridge Foundations. J. Infrastruct. Syst. 2011, 17, 66–74. [Google Scholar] [CrossRef]
- Petroutsatou, K.; Georgopoulos, E.; Lambropoulos, S.; Pantouvakis, J.P. Early Cost Estimating of Road Tunnel Construction Using Neural Networks. J. Constr. Eng. Manag. 2012, 138, 679–687. [Google Scholar] [CrossRef]
- Antoniou, F.; Konstantinidis, D.; Aretoulis, G. Analytical Formulation for Early Cost Estimation and Material Consumption of Road Overpass Bridges. Res. J. Appl. Sci. Eng. Technol. 2016, 12, 716–725. [Google Scholar] [CrossRef]
- Fragkakis, N.; Lambropoulos, S.; Pantouvakis, J.-P. A Computer-Aided Conceptual Cost Estimating System for Pre-Stressed Concrete Road Bridges. In Civil and Environmental Engineering: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2016; Volume 2, pp. 563–575. [Google Scholar]
- Zhang, Y.; Minchin, R.E. Forecasting Conceptual Costs of Bridge Projects Using Non-Parametric Regression Analysis. Proc. Int. Struct. Eng. Constr. 2017, 4, 35. [Google Scholar] [CrossRef]
- Juszczyk, M. On the Search of Models for Early Cost Estimates of Bridges: An SVM-Based Approach. Buildings 2019, 10, 2. [Google Scholar] [CrossRef]
- Juszczyk, M. Early Cost Estimates of Bridge Structures Aided by Artificial Neural Networks. In International Scientific Siberian Transport Forum; Springer International Publishing: Cham, Switzerland, 2020; pp. 10–20. [Google Scholar]
- Petroutsatou, K.; Maravas, A.; Saramourtsis, A. A Life Cycle Model for Estimating Road Tunnel Cost. Tunn. Undergr. Space Technol. 2021, 111, 103858. [Google Scholar] [CrossRef]
- Miljan, K.; Ivanišević, N.; Petronijević, P. Construction Cost Estimation of Reinforced and Prestressed Concrete Bridges Using Machine Learning. J. Croat. Assoc. Civ. Eng. 2021, 73, 1–13. [Google Scholar] [CrossRef]
- Markiz, N.; Jrade, A. Integrating an Expert System with BrIMS, Cost Estimation, and Linear Scheduling at Conceptual Design Stage of Bridge Projects. Int. J. Constr. Manag. 2022, 22, 913–928. [Google Scholar] [CrossRef]
- Liu, S.; Hou, D. Construction Cost Prediction of Main Tunnel in Railway Tunnel Based on Support Vector Machine|基于支持向量机的铁路隧道洞身工程造价预测. J. Railw. Eng. Soc. 2022, 39, 108–113. [Google Scholar]
- Zhou, J.-Q.; Liu, Q.-M.; Ma, C.-X.; Li, D. Cost Prediction of Tunnel Construction Based on Interpretative Structural Model and Stacked Autoencoder. Eng. Lett. 2024, 32, 1966–1980. [Google Scholar]
- Vagdatli, T.; Petroutsatou, K.; Panetsos, P.; Barmpa, Z.; Fragkakis, N. Probabilistic Pre-Estimation of Life-Cycle Costs of Road Bridges Using Dynamic Bayesian Networks. Struct. Infrastruct. Eng. 2024, 20, 1–20. [Google Scholar] [CrossRef]
- Helaly, H.; El-Rayes, K.; Ignacio, E.-J.; Joan, H.J. Comparison of Machine-Learning Algorithms for Estimating Cost of Conventional and Accelerated Bridge Construction Methods during Early Design Phase. J. Constr. Eng. Manag. 2025, 151, 04025004. [Google Scholar] [CrossRef]
- Liolios, A.; Kotoulas, D.; Antoniou, F.; Konstantinidis, D. Egnatia Motorway Bridge Management Systems for Design, Construction and Maintenance. In Proceedings of the 3rd International Conference on Bridge Maintenance, Safety and Management—Bridge Maintenance, Safety, Management, Life-Cycle Performance and Cost, Porto, Portugal, 16–19 July 2006; pp. 135–137. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
- Ramchoun, H.; Amine, M.; Idrissi, J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. Int. J. Interact. Multimed. Artif. Intell. 2016, 4, 26. [Google Scholar] [CrossRef]
- Kulkarni, P.S.; Londhe, S.N.; Deo, M.C. Artificial Neural Networks for Construction Management: A Review. J. Soft Comput. Civ. Eng. 2017, 1, 70–88. [Google Scholar] [CrossRef]
- Papadimitriou, V.E.; Aretoulis, G.N. A Final Cost Estimating Model for Building Renovation Projects. Buildings 2024, 14, 1072. [Google Scholar] [CrossRef]
- Kim, G.-H.; Yoon, J.-E.; An, S.-H.; Cho, H.-H.; Kang, K.-I. Neural Network Model Incorporating a Genetic Algorithm in Estimating Construction Costs. Build. Environ. 2004, 39, 1333–1340. [Google Scholar] [CrossRef]
- Bayram, S.; Ocal, M.E.; Laptali Oral, E.; Atis, C.D. Comparison of MultiLayer Perceptron (MLP) and Radial Basis Function (RBF) for Construction Cost Estimation: The Case of Turkey. J. Constr. Eng. Manag. 2015, 22, 480–490. [Google Scholar] [CrossRef]
- Grigoras, A.E.; Aretoulis, G.N.; Antoniou, F.; Karatzas, S. Application of Artificial Neural Networks for the Prediction of Cashflows in Public Road Works. In Financial Evaluation and Risk Management of Infrastructure Projects; IGI Global: Hershey, PA, USA, 2023; pp. 101–130. ISBN 9781668477878. [Google Scholar]
- Broomhead, D.S. Lowe David Multivariabe Functional Interpolation and Adaptive Networks. Complex Syst. 1988, 2, 321–355. [Google Scholar]
- Yu, S.; Zhu, K.; Gao, S. A Hybrid MPSO-BP Structure Adaptive Algorithm for RBFNs. Neural Comput. Appl. 2009, 18, 769–779. [Google Scholar] [CrossRef]
- Galton, F. Regression towards Mediocrity in Hereditary Stature. J. Anthropol. Inst. Great Br. Irel. 1886, 15, 246–263. [Google Scholar] [CrossRef]
- Dang-Trinh, N.; Duc-Thang, P.; Nguyen-Ngoc Cuong, T.; Duc-Hoc, T. Machine Learning Models for Estimating Preliminary Factory Construction Cost: Case Study in Southern Vietnam. Int. J. Constr. Manag. 2023, 23, 2879–2887. [Google Scholar] [CrossRef]
- Kantianis, D.D. Design Morphology Complexity and Conceptual Building Project Cost Forecasting. J. Financ. Manag. Prop. Constr. 2022, 27, 387–414. [Google Scholar] [CrossRef]
- Sharma, S.; Goyal, P.K. Fuzzy Assessment of the Risk Factors Causing Cost Overrun in Construction Industry. Evol. Intell. 2022, 15, 2269–2281. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Almuflih, A.S. Extreme Gradient Boosting-Based Machine Learning Approach for Green Building Cost Prediction. Sustainability 2022, 14, 6651. [Google Scholar] [CrossRef]
- Goel, S.; Oberoi, S.; Vats, A. Construction Cost Estimator: An Effective Approach to Estimate the Cost of Construction in Metropolitan Areas. In Proceedings of the 2021 3rd International Conference on Advances in Computing, Communication Control and Networking (ICAC3N), Greater Noida, India, 17–18 December 2021; pp. 122–127. [Google Scholar]
- Ye, X.; Ding, P.; Jin, D.; Zhou, C.; Li, Y.; Zhang, J. Intelligent Analysis of Construction Costs of Shield Tunneling in Complex Geological Conditions by Machine Learning Method. Mathematics 2023, 11, 1423. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R. News 2002, 2, 18–22. [Google Scholar]
- Smola, A.J.; Schölkopf, B.; Schölkopf, S. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Coffie, G.H.; Cudjoe, S.K.F. Using Extreme Gradient Boosting (XGBoost) Machine Learning to Predict Construction Cost Overruns. Int. J. Constr. Manag. 2024, 24, 1742–1750. [Google Scholar] [CrossRef]
- ForouzeshNejad, A.A.; Arabikhan, F.; Aheleroff, S. Optimizing Project Time and Cost Prediction Using a Hybrid XGBoost and Simulated Annealing Algorithm. Machines 2024, 12, 867. [Google Scholar] [CrossRef]
- Cover, T.M.; Hart, P.E. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Arabiat, A.; Al-Bdour, H.; Bisharah, M. Predicting the Construction Projects Time and Cost Overruns Using K-Nearest Neighbor and Artificial Neural Network: A Case Study from Jordan. Asian J. Civ. Eng. 2023, 24, 2405–2414. [Google Scholar] [CrossRef]
- Gareth, J.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning with Applications in Python; Springer: Cham, Switzerland, 2023. [Google Scholar]
- McKinney, W. Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython; O’Reilly Media, Inc.: Santa Rosa, CA, USA, 2018; ISBN 9781491957660. [Google Scholar]
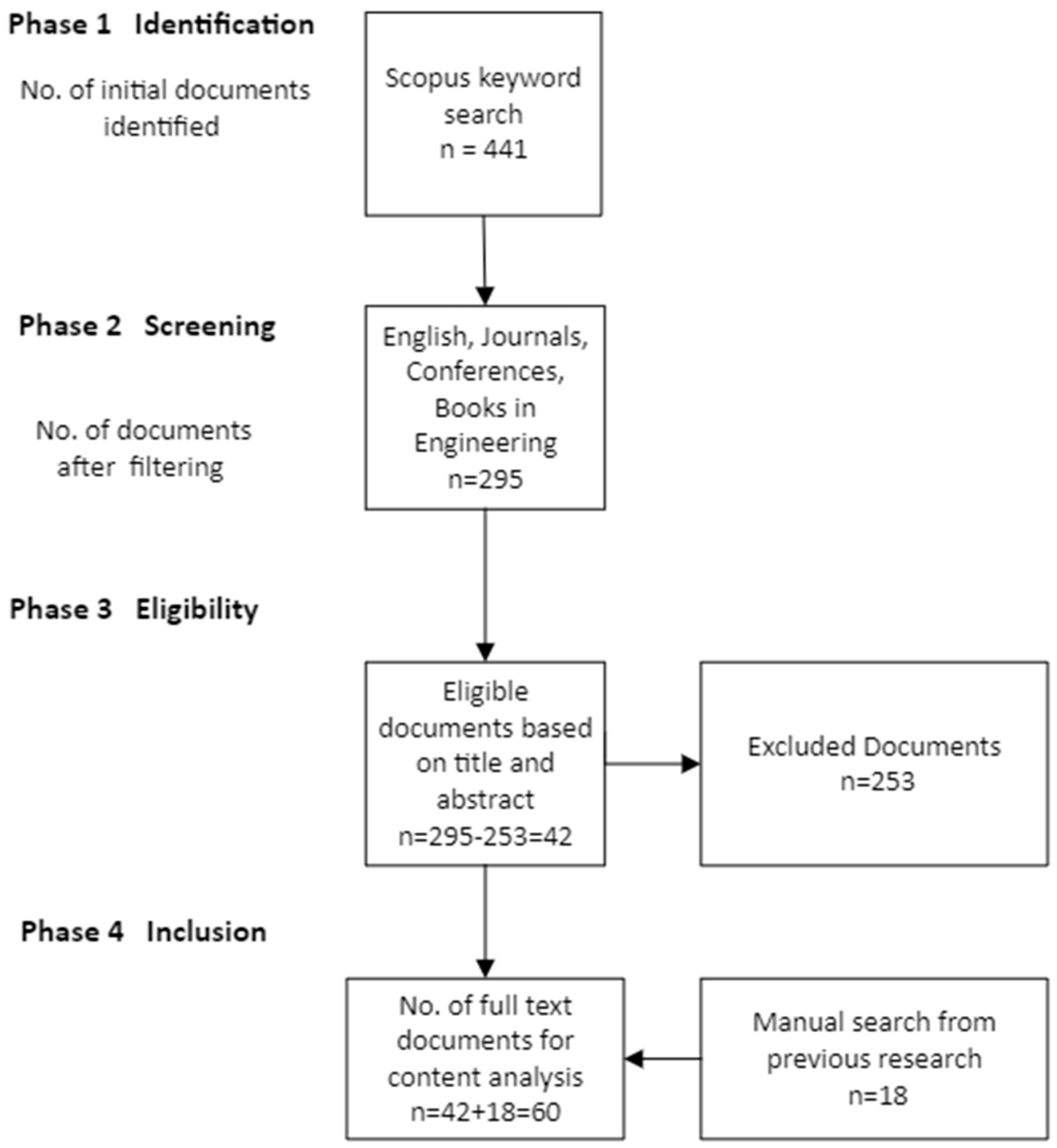


| Variable | N | Minimum | Maximum | Mean | Std. Deviation |
|---|---|---|---|---|---|
| Length of Main Axis (m) | 19 | 1900.00 | 32,610.00 | 14,856.21 | 8435.85 |
| Width of Main Axis (m) | 19 | 22.00 | 27.00 | 24.52 | 0.86 |
| Area of Main Axis (m2) | 19 | 45,600.00 | 811,032.00 | 364,176.64 | 208,449.02 |
| Length of Service Roads (m) | 18 | 63.30 | 59,211.00 | 17,044.84 | 15,327.77 |
| Width of Service Roads (m) | 18 | 4.95 | 7.50 | 6.33 | 0.68 |
| Area of Service Roads (m2) | 19 | 411.45 | 357,302.00 | 107,811.06 | 97,885.08 |
| Total road area (main + service) (m2) | 19 | 125,766.50 | 1,168,334.20 | 466,313.44 | 284,562.64 |
| Number of Interchanges | 14 | 1.00 | 3.00 | 1.57 | 0.65 |
| Area of bridges (m2) | 19 | 420.00 | 34,157.10 | 10,782.17 | 9006.64 |
| Area of underpasses (m2) | 17 | 627.33 | 10,890.00 | 3611.01 | 3129.30 |
| Area of overpasses (m2) | 16 | 540.00 | 25,146.00 | 4004.51 | 6018.26 |
| Sum of area of all structures(m2) | 19 | 3135.91 | 42,477.60 | 17,385.30 | 11,672.47 |
| Total length of single bore tunnels (m) | 7 | 280.00 | 9030.00 | 3637.92 | 3647.64 |
| Number of culverts | 17 | 6 | 90.00 | 46.29 | 24.64 |
| Length of river training(m) | 1 | 900.00 | 900.00 | 900.00 | |
| Length of river bridges(m) | 11 | 27.50 | 507.00 | 258.53 | 167.72 |
| Width of river bridges(m) | 11 | 11.30 | 28.90 | 24.53 | 6.28 |
| Number of spans of river bridges | 11 | 1.00 | 18.00 | 7.73 | 5.24 |
| Area of river bridges (m2) | 11 | 310.75 | 13,178.40 | 6731.06 | 4826.87 |
| Total Cost (€ 2024) | 19 | 14,033,929.00 | 275,847,756.00 | 92,564,860.11 | 67,242,393,739.00 |
| IV | Total Cost (€ 2024) |
|---|---|
| Length of main axis (Lm) | 0.278 |
| Width of main axis (Wm) | −0.125 |
| Area of main axis (Am) | 0.262 |
| Length of service roads (Ls) | −0.067 |
| Width of service roads (Ws) | −0.170 |
| Area of service roads (As) | −0.069 |
| Total road area (main + service)(Am+s) | 0.168 |
| Number of Interchanges (Nic) | 0.018 |
| Area of bridges (Ab) | 0.647 ** |
| Area of underpasses (Aup) | 0.116 |
| Area of overpasses (Aop) | −0.083 |
| Sum of area of all structures (Ast) | 0.490 * |
| Total length of single bore tunnels (Lt) | 0.804 ** |
| Number of Culverts (Nc) | −0.099 |
| Length of river training (LR) | c |
| Length of river bridges (LRb) | 0.272 |
| Width of river bridges (WRb) | −0.045 |
| Number of spans of river bridges (Ns) | 0.467 |
| Area of river bridges (ARb) | 0.161 |
| Model | DV | IV(s) |
|---|---|---|
| a | Total Cost | Lm, Wm, Ls, Ws, Nic, Ab, Aop, Aup, Lt, Nc Lr. Ns Aup |
| b | Total Cost | Lm, Ls, Ast, Lt, Nc |
| c | Total Cost | Lm, Ls, Nic, Ast, Lt, Nc |
| d | Total Cost | Ns, Lt, Ast, Ab |
| e | Total Cost | Lm, Ast, Lt, Ns |
| Total Cost Model | ML Method | MAE | R2 | MAE% | MAPE% |
|---|---|---|---|---|---|
| a | MLP-ANN | 107,201,806.45 | −9.17 | 129.19 | 72.50 |
| a | RBF-ANN | 116,741,876.34 | −9.20 | 140.69 | 81.97 |
| a | MLR | 97,888,659.68 | −5.92 | 117.97 | 83.69 |
| a | RF | 50,499,385.15 | −1.23 | 60.86 | 32.06 |
| a | SVR | 44,239,797.61 | −0.97 | 53.32 | 26.62 |
| a | XGBoost | 50,350,221.57 | −0.67 | 60.68 | 39.33 |
| a | KNN | 69,416,458.68 | −2.96 | 83.66 | 45.55 |
| b | MLP-ANN | 15,590,969.66 | 0.86 | 18.79 | 13.64 |
| b | RBF-ANN | 23,758,675.83 | 0.68 | 28.63 | 22.71 |
| b | MLR | 17,752,384.39 | 0.81 | 21.39 | 17.29 |
| b | RF | 56,918,499.33 | −0.97 | 68.60 | 46.24 |
| b | SVR | 41,372,128.39 | −0.59 | 49.86 | 25.97 |
| b | XGBoost | 49,586,328.22 | −0.95 | 59.76 | 33.33 |
| b | KNN | 46,084,716.58 | −0.41 | 55.54 | 33.51 |
| c | MLP-ANN | 39,790,753.09 | 0.09 | 49.59 | 35.00 |
| c | RBF-ANN | 21,974,168.76 | 0.55 | 26.48 | 21.83 |
| c | MLR | 11,980,640.05 | 0.87 | 14.44 | 11.27 |
| c | RF | 61,522,837.83 | −1.16 | 74.14 | 50.04 |
| c | SVR | 41,475,979.34 | −0.72 | 49.98 | 25.13 |
| c | XGBoost | 47,477,931.22 | −1.23 | 57.22 | 28.70 |
| c | KNN | 55,560,571.41 | −0.97 | 66.69 | 41.76 |
| d | MLP-ANN | 86,098,841.82 | −3.81 | 103.76 | 83.44 |
| d | RBF-ANN | 13,766,993.70 | −12.73 | 165.91 | 144.00 |
| d | MLR | 107,177,935.78 | −6.73 | 129.17 | 106.63 |
| d | RF | 61,008,294.17 | −1.11 | 73.52 | 50.55 |
| d | SVR | 38,771,335.90 | −0.08 | 46.73 | 28.54 |
| d | XGBoost | 51,344,221.21 | −1.01 | 61.88 | 35.21 |
| d | KNN | 35,883,364.00 | −0.09 | 43.24 | 24.04 |
| e | MLP-ANN | 18,300,913.98 | 0.76 | 22.06 | 12.75 |
| e | RBF-ANN | 28,328,341.99 | 0.30 | 34.14 | 29.47 |
| e | MLR | 21,232,975.87 | 0.68 | 25.59 | 20.55 |
| e | RF | 53.607.513.38 | −0.92 | 64.60 | 45.54 |
| e | SVR | 40.234.082.82 | −0.24 | 48.49 | 28.09 |
| e | XGBoost | 49,022,275.21 | −1.14 | 59.08 | 31.17 |
| e | KNN | 42,612,353.80 | −0.31 | 51.35 | 30.40 |
| Score | * MAE | ** R2 | * MAE% | * MAPE% |
|---|---|---|---|---|
| 0 | >27,769,458.03 | ≤0.00 | >30.00 | >30.00 |
| 1 | 22,215,566.43–27,769,458.03 | 0.01–0.49 | 24.01–30.00 | 24.01–30.00 |
| 2 | 16,661,674.83–22,215,566.42 | 0.50–0.59 | 18.01–24.00 | 18.01–24.00 |
| 3 | 11,107,783.22–16,661,674.82 | 0.60–0.69 | 12.01–18.00 | 12.01–18.00 |
| 4 | 5,553,891.62–11,107,783.21 | 0.70–0.79 | 6.01–12.00 | 6.01–12.00 |
| Model | ML Method | MAE | R2 | MAE% | MAPE% | Average | Rank |
|---|---|---|---|---|---|---|---|
| c | MLR | 3.00 | 5.00 | 3.00 | 3.00 | 3.50 | 1.00 |
| b | MLP-ANN | 3.00 | 5.00 | 2.00 | 3.00 | 3.25 | 2.00 |
| b | MLR | 2.00 | 5.00 | 2.00 | 3.00 | 3.00 | 3.00 |
| e | MLP-ANN | 2.00 | 4.00 | 2.00 | 3.00 | 2.75 | 4.00 |
| e | MLR | 2.00 | 3.00 | 1.00 | 2.00 | 2.00 | 5.00 |
| b | RBF-ANN | 1.00 | 3.00 | 1.00 | 2.00 | 1.75 | 6.00 |
| c | RBF-ANN | 2.00 | 2.00 | 1.00 | 2.00 | 1.75 | 6.00 |
| e | RBF-ANN | 0.00 | 1.00 | 0.00 | 1.00 | 0.50 | 9.00 |
| a | SVR | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| b | SVR | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| c | SVR | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| c | XGBoost | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| d | SVR | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| d | KNN | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| e | SVR | 0.00 | 0.00 | 0.00 | 1.00 | 0.25 | 10.00 |
| IV | Project X1 | Project X2 |
|---|---|---|
| Lm | 8500 m | 16,000 m |
| Ls | 11,170 m | 32,000 m |
| Nic | 2 | 3 |
| Ab | 2280 m2 | 1680 m2 |
| Aup | 1500 | 2250 m2 |
| Aop | 0 | 2160 m2 |
| Ast | 3780 m2 | 6090 m2 |
| Lt | 0 | 1200 |
| Nc | 43 | 80 |
| Ns | 0 | 3 |
| Rank | Model | X1 Actual (EUR) | X1 Predicted (EUR) | Deviation | X2 Actual (EUR) | X2 Predicted (EUR) | Deviation | |
|---|---|---|---|---|---|---|---|---|
| 1 | c | MLR | 39,194,023.43 | 29,726,360.79 | −24.16% | 78,571,146.85 | 75,775,227.52 | −3.56% |
| 2 | b | MLP-ANN | 39,194,023.43 | 29,805,189.53 | −23.95% | 78,571,146.85 | 15,243,355.69 | −80.60% |
| 3 | b | MLR | 39,194,023.43 | 21,310,216.12 | −45.63% | 78,571,146.85 | 57,651,670.78 | −26.62% |
| 4 | e | MLP-ANN | 39,194,023.43 | 27,929,433.09 | −28.74% | €78,571,146.85 | 61,418,111.86 | −21.83% |
| 5 | e | MLR | 39,194,023.43 | 30,219,523.12 | −22.90% | 78,571,146.85 | 82,647,440.00 | 5.19% |
| 6 | b | RBF-ANN | 39,194,023.43 | 27,743,288.58 | −29.22% | 78,571,146.85 | 83,457,835.30 | 6.22% |
| 6 | c | RBF-ANN | 39,194,023.43 | 42,265,903.31 | 7.84% | €78,571,146.85 | 120,399,833.00 | 53.24% |
| IV | Units | w | μ | σ |
|---|---|---|---|---|
| Lm | m | 37,916,007.05 | 15,533.13 | 8691.05 |
| Ls | m | −8,296,717.99 | 19,309.72 | 15,105.06 |
| Nic | n | 7,517,364.66 | 1.33 | 0.87 |
| Ast | m2 | 15,446,845.90 | 15,101.14 | 10,538.05 |
| Lt | n | 46,184,784.74 | 804.67 | 2275.03 |
| Nc | n | −8,896,822.25 | 43.40 | 28.32 |
| b | 82,977,372.26 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoniou, F.; Konstantinidis, K. Client-Oriented Highway Construction Cost Estimation Models Using Machine Learning. Appl. Sci. 2025, 15, 10237. https://doi.org/10.3390/app151810237
Antoniou F, Konstantinidis K. Client-Oriented Highway Construction Cost Estimation Models Using Machine Learning. Applied Sciences. 2025; 15(18):10237. https://doi.org/10.3390/app151810237
Chicago/Turabian StyleAntoniou, Fani, and Konstantinos Konstantinidis. 2025. "Client-Oriented Highway Construction Cost Estimation Models Using Machine Learning" Applied Sciences 15, no. 18: 10237. https://doi.org/10.3390/app151810237
APA StyleAntoniou, F., & Konstantinidis, K. (2025). Client-Oriented Highway Construction Cost Estimation Models Using Machine Learning. Applied Sciences, 15(18), 10237. https://doi.org/10.3390/app151810237








