A Routing Method for Extending Network Lifetime in Wireless Sensor Networks Using Improved PSO

Featured Application

The proposed PSO-based routing algorithm can be applied to large-scale wireless sensor networks (WSNs) deployed in critical environments, such as industrial plants, mining sites, and remote agricultural fields. By optimizing cluster head selection and data routing paths, the method significantly reduces energy consumption and extends network lifetime, enabling long-term autonomous operation without manual maintenance.

Abstract

WSNs consist of numerous energy-constrained Sensor Nodes (SNs), making energy efficiency a critical challenge. This paper presents a novel multipath routing model designed to enhance network lifetime by simultaneously optimizing energy consumption, node connectivity, and transmission distance. The model employs an Improved Particle Swarm Optimization (IPSO) algorithm to dynamically determine the optimal weight coefficients of a cost function that integrates three parameters: residual energy, link reliability, and buffer capacity. A compressed Bloom filter is incorporated to improve packet transmission efficiency and reduce error rates. Simulation experiments conducted in the NS2 environment show that the proposed approach significantly outperforms existing protocols, including Reinforcement Learning Q-Routing Protocol (RL-QRP), Low Energy Adaptive Clustering Hierarchical (LEACH), On-Demand Distance Vector (AODV), Secure and Energy-Efficient Multipath (SEEM), and Energy Density On-demand Cluster Routing (EDOCR), achieving a 7.45% reduction in energy consumption and maintaining a higher number of active nodes over time. Notably, the model sustains 19 live nodes at round 800, whereas LEACH and APTEEN experience complete node depletion by that point. This adaptive, energy-aware routing strategy improves reliability, prolongs operational lifespan, and enhances load balancing, making it a promising solution for real-world WSN applications.

1. Introduction

Wireless Sensor Networks (WSNs) have become a vital technology for applications such as military surveillance, environmental monitoring, healthcare, and smart cities. These networks consist of numerous small, energy-constrained Sensor Nodes (SNs) that autonomously collect, process, and transmit data. Due to inherent limitations—such as restricted battery capacity, limited storage, and modest processing power—efficient energy management remains a critical design challenge [1,2,3]. One of the most pressing issues in WSNs is network lifetime optimization, which is directly affected by energy consumption, routing efficiency, and load balancing among nodes [4,5]. Traditional routing protocols, such as AODV and LEACH, typically aim either to minimize energy consumption or to maximize data transmission efficiency. However, they often fail to address multi-factor optimization that simultaneously considers energy usage, node connectivity, and transmission distance [6,7]. Moreover, many existing methods do not incorporate dynamic coefficient optimization within objective functions, resulting in suboptimal energy utilization.

To address these limitations, this study proposes a novel energy-efficient multipath routing model that integrates three key parameters: residual energy, link reliability, and buffer capacity of SNs [8,9]. The proposed model leverages Improved Particle Swarm Optimization (IPSO) to dynamically optimize routing decisions, thereby extending network lifetime and improving data transmission efficiency. In WSNs, routing is performed by nodes without dedicated infrastructure such as switches or routers. Therefore, the process of WSNs is more complex than infrastructure-based networks [10]. Since SNs have limited energy reserves and may fail over time, routing information is continuously changing. Therefore, effective WSN routing protocols must be decentralized, self-organizing, and self-recovering, while also accommodating wireless bandwidth limitations and leveraging multi-hop communication for balanced load distribution.

Routing protocols are generally classified into proactive (table-driven) and reactive (on-demand) approaches [11,12,13,14,15]. Proactive protocols maintain up-to-date routing tables at each node, enabling quick path discovery but requiring high overhead to update network information. Reactive protocols minimize overhead by discovering routes only when required; however, they introduce higher latency due to route discovery delays. Multipath routing protocols offer an alternative by establishing multiple concurrent paths between source and destination nodes [16,17,18]. When the primary path fails, data can be rerouted through an alternate path without initiating a new discovery process, reducing downtime and improving reliability [19].

Our approach further enhances multipath routing by integrating a compressed Bloom filter to reduce communication overhead and optimize error rates. Bloom filter is an effective space that refers to the possible structure of a set of elements. A set of hash functions uses a set of elements in the filter to test elements, while false positives may be reduced by memory allocation [20]. By adapting Bloom filter parameters—such as bit array size (m) and number of elements (n)—we can balance storage efficiency with error probability.

In summary, the contributions of this work are the following:

• A new multipath routing model designed to extend node lifetime through improved reliability and reduced energy consumption.
• Application of the IPSO algorithm to determine optimal cost function coefficients for routing decisions.
• Multipath routing based on residual energy, link reliability, and free buffer space of SNs.
• Use of a compressed Bloom filter for efficient data handling and increased fault tolerance.
• Simulation-based evaluation in NS2, comparing the proposed model with RL-QRP, LEACH, HEED (Hybrid Energy-Efficient Distributed clustering), APTEEN (Adaptive Threshold-sensitive Energy Efficient sensor Network protocol), SEEM, and EDOCR.

The remainder of this paper is structured as follows: Section 2 reviews related work. Section 3 presents the proposed IPSO-based routing model. In Section 4, the evaluation and results of the proposed model are carried out. In this section, the proposed model is compared with other models based on various criteria. Section 5 discusses simulation results and comparative analysis. Section 6 concludes with key findings and future research directions.

2. Related Works

This section reviews previous research on routing and clustering in Wireless Sensor Networks (WSNs). WSNs face numerous challenges, including energy consumption, sensor node deployment, routing strategies, energy optimization, and cluster head (CH) selection. Among energy-efficient solutions, clustering-based routing is particularly prominent. However, the “hotspot problem” remains a major issue, as nodes near the sink experience heavy traffic, depleting their energy more quickly. This has motivated the development of advanced energy-aware clustering techniques.

The Fuzzy Logic with Honey Badger Algorithm for Cluster-based Multi-hop Routing (FLHBA-CMHR) [21] optimizes clustering by considering both inter-cluster and intra-cluster distances. Its asymmetric clustering and routing approach improves energy efficiency and prolongs network lifetime. Comparative analysis shows fewer node failures compared to LEACH, Fuzzy-based Unequal Clustering Algorithm (FUCA), Unequal Residual-energy Based Distribution (URBD), Distributed Energy-efficient Fuzzy Logic (DEFL), and Enhanced Fuzzy-based Unequal Clustering Algorithm (E-FUCA).

In [19], various methods for extending WSN lifetime were presented, focusing on energy harvesting, transmission optimization, and conservation. These approaches aim to maintain an energy balance across the entire network. A Hybrid Gray Wolf–Sunflower Optimization (HGWSFO) method [22] has been proposed for optimal CH selection, considering energy consumption and node separation distance. Sunflower Optimization (SFO) improves exploration, while Gray Wolf Optimization (GWO) enhances exploitation. This hybrid improves network longevity and balances energy consumption.

The Improved Buffalo Optimized Route Selective Deep Feed Forward Neural Learning (IBORSDFFNL) model [23] builds multiple routes for efficient data aggregation. It selects the optimal path using a hybrid optimization process, resulting in reduced energy consumption and latency, and improved packet delivery ratio (PDR) compared to EFMRP and IEEMARP.

A coding-based routing method [24] integrates Reed–Solomon (RS) and Low-Density Parity-Check (LDPC) codes to enhance link reliability and reduce transmission energy. CHs forward data to the base station (BS) using energy-aware path selection. Compared to LEACH and Balanced Residual Energy—LEACH (BRE-LEACH), this approach improved network lifetime by up to 90% and reduced energy use by over 75%.

The Evolutionary Gateway-based Load-Balanced Routing (E-GLBR) method [25], using Genetic Algorithms (GA), selects CHs based on four key metrics to minimize transmission range and improve coverage. It significantly outperforms Evolutionary Routing Protocol (ERP), Distance Incorporated Modified Stable Election Protocol (D-MSEP), Energy-Efficient Weighted Clustering (EEWC), and Energy dependent cluster formation (EDCF) in both network stability and lifetime.

The Meta-heuristic Optimized Cluster Head Selection-based Routing Algorithm (MOCRAW) [26] combines a Cluster Head Selection Algorithm (CHSA) with a Route Search Algorithm (RSA) to reduce overhead and avoid routing loops. Among 500-node networks, MOCRAW recorded the lowest energy use compared to E-FUCA, EAFTC RIS, GAPSO-H, ECRP-UCA, and HMBCR.

CH selection has also been improved by combining Bacteria Foraging Optimization (BFO) and Harmony Search Algorithm (HSA) [27]. Additionally, the Cross-layer Opportunistic Routing Protocol (CORP) integrates fuzzy neural networks for energy-efficient routing, showing reduced latency and improved packet delivery rates.

The Energy-Efficient Secure Multipath (EESM) protocol [28] establishes secure and efficient paths between SNs and the BS, offloads computation to the BS, and incorporates lightweight security measures. While EESM exchanges slightly more control messages than SEEM and RMER, it achieves a significantly higher packet success rate.

The Fish Swarm Algorithm (FSA) [29] has been applied for CH selection, based on residual energy and distances within and between clusters. Compared to ERA, FSA improved power efficiency by 40% and reduced delays by over 80%.

Hybrid methods such as PSO–Cuckoo Search Optimization [30] use multi-hop communication to maintain multiple reliable routes. These approaches have achieved energy savings of over 40% compared to Energy-Efficient Low-Energy Adaptive Clustering Hierarchy (EE-LEACH).

The Multilayer Clustering-based Butterfly Optimization Routing (MCBOR) [31] algorithm improves PDR to 98% and reduces transmission loss compared to Q-Learning based Ant Colony Optimization (QLACO), Energy-Efficient Data Gathering (EEDG), and Routing Protocol based on Particle Swarm Optimization Routing (RPSOR).

Competitive Swarm Optimization–Unequal Clustering and Routing Algorithm (CSO-UCRA) [32] achieves up to 28% less energy consumption compared to EBUC and other clustering techniques, while maintaining high convergence speed.

The Cuckoo Optimization Algorithm-based Routing Protocol (COARP) [33] selects CHs based on remaining energy, BS proximity, and intra/inter-cluster distances, outperforming LEACH and LEACH with Advanced Cluster Head—Energy Prediction (LACH-EP).

The Oppositional Artificial Fish Swarm–Improved Moth Flame Optimization (OAFS-IMFO) model [34] combines clustering and optimized routing, significantly lowering energy use in comparison with Krill Herd Optimization Algorithm (KHOA), Cuckoo Search Algorithm (CSA), and Harmony Search Algorithm (HAS).

Table 1. A comparison of previous works based on various factors.

Model	Ref.	Energy Efficiency	Network Lifetime	Packet Delivery Ratio	Latency
FLHBA-CMHR	[21]	Medium	Stability	Fewer failures	Medium
Finding the optimal route	[19]	Balanced energy	Stability	High	Medium
HGWSFO	[22]	Balanced energy	Longevity	Medium	Medium
IBORSDFFNL	[23]	Medium	Lifetime	High	Latency
RS + LDPC	[24]	75% energy	90% lifetime	Reliability	Medium
E-GLBR	[25]	Optimized energy	Stability/Life	High	Medium
MOCRAW	[26]	Lowest energy	Lifetime	Medium	Overhead
BFO + HSA/CORP	[27]	Energy-efficient	Stability	High	Low
EESM	[28]	Energy-aware	Secure and stable	Success rate	Low
FSA	[29]	40% efficiency	Stability	Medium	80% delay
PSO–CS	[30]	40% savings	Stability	Reliable routes	Low
MCBOR	[31]	Loss	Low	98% PDR	Low
CSO-UCRA	[32]	28% energy	High convergence	Medium	Medium
COARP	[33]	Energy-based CH sel.	Efficiency	Medium	Medium
OAFS-IMFO	[34]	good	Stability	Medium	Low

shows a comparison of previous works based on various factors.

Recent trends show strong interest in hybrid metaheuristic optimization [22], adaptive coding-based routing [24], and hierarchical clustering [29]. While these methods improve network lifetime and efficiency, they often share limitations:

• Many existing approaches concentrate exclusively on energy consumption and fail to adapt to dynamic network conditions.
• Link reliability and buffer capacity are frequently overlooked in multipath routing designs.
• Fixed coefficient optimization leads to suboptimal performance in changing environments.
• Comparative studies often lack evaluation against multiple standard protocols, limiting generalizability.

The proposed IPSO-based model addresses these issues by:

• Dynamically adapting multipath routing using residual energy, link reliability, and buffer capacity.
• Optimizing routing coefficients in real-time using IPSO for balanced energy use.
• Performing extensive comparisons against RL-QRP, LEACH, SEEM, and EDOCR, showing superior energy efficiency, lifetime, and delivery rates.

3. Materials and Methods

3.1. Motivation for Multipath Forwarding

Traditional single-path routing protocols such as AODV and DSR suffer from several limitations affecting network efficiency and reliability. These protocols rely on a single communication path, which makes them vulnerable to node failures, congestion, and uneven energy consumption. In the event of a primary path failure, a new route discovery process must be initiated, thereby increasing both latency and control overhead. In dense networks, traffic concentration along a single path accelerates energy depletion in relay nodes, thereby reducing overall network lifetime.

Multipath forwarding provides a more resilient and adaptive routing strategy. By distributing packets across multiple paths, it mitigates losses from link failures, alleviates network congestion, and balances energy consumption across sensor nodes. However, the performance of multipath routing strongly depends on the path selection mechanism and how well it manages trade-offs between reliability, energy efficiency, and delay.

The proposed IPSO-based routing model dynamically selects forwarding paths according to residual energy, link reliability, and buffer occupancy levels. Unlike conventional multipath schemes that rely on fixed weight factors, our method performs real-time network assessment to optimize both packet delivery and energy consumption [35]. This adaptability increases network stability and prolongs operational lifetime, making it especially suitable for energy-constrained WSNs (Figure 1).

Algorithm 1 shows the pseudocode of the proposed model. The pseudocode includes network settings and improved PSO algorithm.

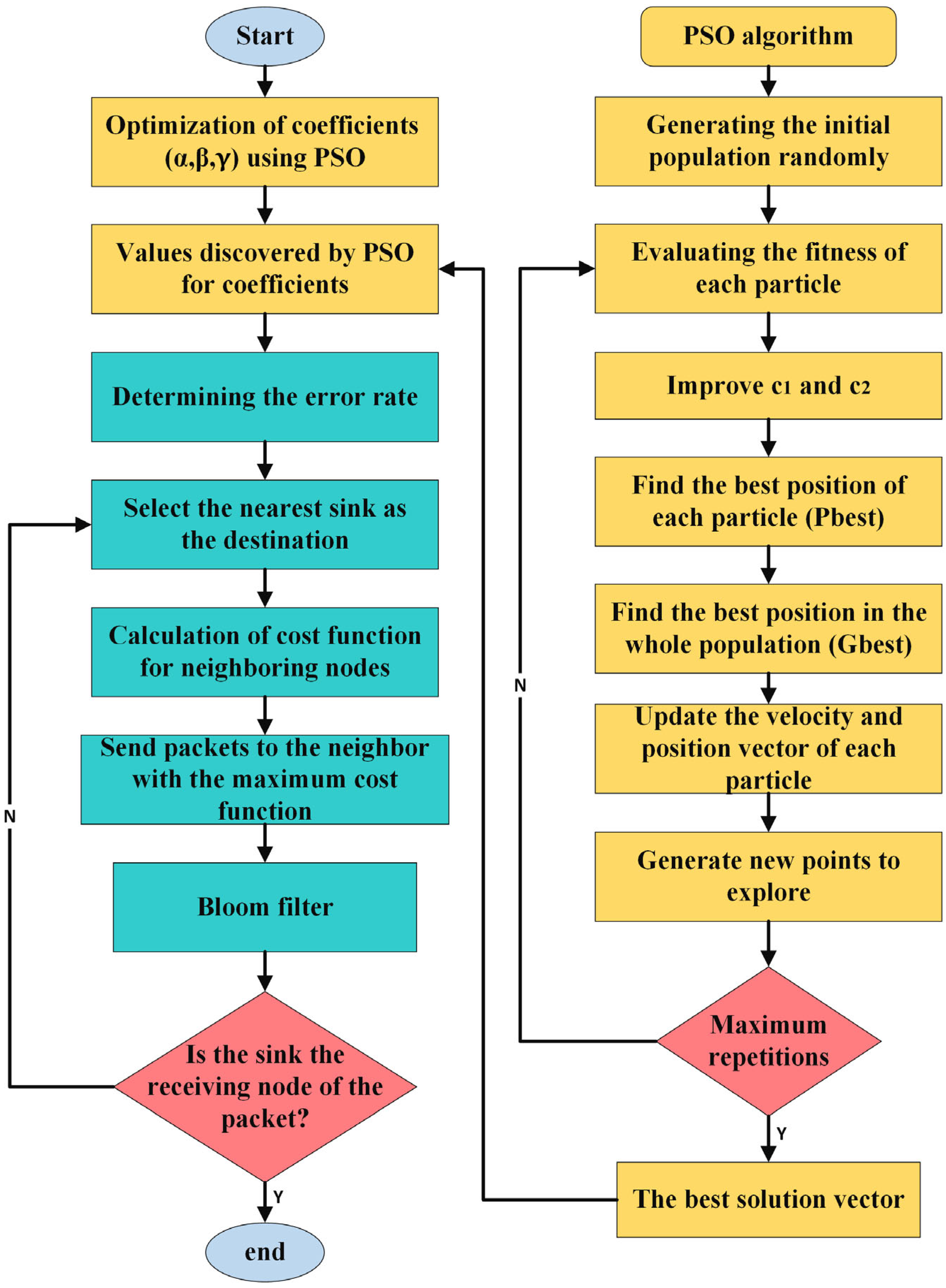
Algorithm 1. Pseudocode of the proposed model

01. Start 02. Inputs and outputs Inputs: (initialize the locations of SNs and sinks; determination of energy; determine the number of nodes; determining the number of sinks) Outputs: (alive nodes; energy consumed; rate of reliability) While (T < Tmax) 03. Base station creates topology of network. 04. Determining the error rate 05. Improved PSO: BS run improved PSO to compute constant coefficients.   For each particle i:    r1 ← random number between 0 and 1    r2 ← random number between 0 and 1      particle[i].velocity ← w × particle[i].velocity + c1 × r1 ×      (particle[i].bestPosition - particle[i].position) + c2 × r2 ×      (globalBestPosition - particle[i].position)      particle[i].position ← particle[i].position + particle[i].velocity 5.1. Optimization of coefficients ($\alpha ,\beta ,\gamma$) using PSO 5.2. Values discovered by PSO for coefficients 06. Base station sends computed values and other information to each sensor. 07. Sending steps for each sensor 7.1. Knowledge of location and other information of neighboring nodes 7.2. For each sensor nodes   Each sensor node vi informs its neighbors of its location ($x_i,y_j$) by sending a Hello message   adjacent node $v_j$ sends a response with the contents of its characteristic number   Calculation of Neighboring Nodes Geographical Distance   Euclidean distance of two neighboring nodes:   For i: 1 to n do    diff ← nodeA[i] - nodeB[i]    distanceSquared ← distanceSquared + (diff × diff)    distance ← sqrt(distanceSquared)   End For 08. For each sensor nodes   For each row of neighbor table is computed the shortest route   For each row of neighbor table is saved minimum value and best neighbor. 09. Sending steps: 9.1. $BloomFilter$ (Calculate compressed Bloom filter for a packet sent to BS) 9.2. Sending data to closed nodes based on the shortest path. 9.3. Sending data to the sink based on the shortest path 9.4. Calculate the cost function based on the following factors:   f1 = energy consumption. Calculate the total energy consumed of all nodes   f2 = reliability of the link,   f3 = free buffer of SNs.   cost function = ${\mathrm{M}\mathrm{a}\mathrm{x}}_{\mathrm{j}}\left\{\alpha \times f1 + \beta \times f2 + \gamma \times f3\right\}$ 9.5. Send packets to the neighbor with the maximum cost function 10. Receiving steps: 10.1. Read source address and send ack message to source 10.2. Update neighbor table End while 11. End

A body sensor network with a set of SNs is shown as $V = \{v_1,v_{2 },v_3,\dots , v_n\}$ that are randomly and uniformly distributed in a two-dimensional environment with an area of A. SNs have a radio range, denoted by $R_c$. If two nodes $v_i$ and $v_j$ are in the same range, they are called adjacent nodes or neighbors. Each sensor node$v_i$ has a unique identification number. In the proposed model, it is assumed that all nodes use GPS or other location algorithms to know their geographic location ($x_i, y_i$). It is also assumed that nodes know their initial energy $E_{initial}$. The sinks are static and have no energy confinement and all nodes know the location of the sink.

3.2. Knowledge of Location and Neighboring Node Information

Each sensor node${ v}_i$ informs its neighbors of its location (${\mathrm{x}}_{\mathrm{i}}, {\mathrm{y}}_{\mathrm{i}}$) by sending a $Hello$ message to its neighbors that includes its characteristic number and geographic location. Upon receiving this message, adjacent node ${\mathrm{v}}_{\mathrm{j}}$ sends a response with the contents of its characteristic number, its location, remaining energy, link reliability (${\mathrm{R}}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k}}({\mathrm{v}}_{\mathrm{i}}, {\mathrm{v}}_{\mathrm{j}})$) and its free buffer ($B_j$) to the sending node Hello. Figure 2 shows knowing the location and other information of neighboring nodes.

Upon receiving this response, each node updates its neighbor’s table. In this protocol, a threshold limit (${\mathrm{E}}_{\mathrm{t}\mathrm{h}}$) is considered for the energy of the nodes. Therefore, if a node’s residual energy falls below the predefined threshold, it is excluded from the neighboring node table. This is performed in order to balance the load in the nodes. The $Hello$ packet format is shown in Figure 3 and its response is shown in Figure 4.

In Figure 4, the characteristic number of the node is the same as the identification number of the node and the location of the node is the same as the geographic location of the node. The free buffer reflects the traffic status of the neighboring nodes of the source node. The remaining energy indicates the amount of energy left in a node’s battery.

3.2.1. Calculation of Neighboring Nodes Geographical Distance

According to the awareness of the SNs about their geographic location, neighboring nodes and sink, the Euclidean distance of two neighboring nodes $i$ and j can be computed from Equation (1).

$$D\left(i,j\right) = \sqrt{{({\mathrm{x}}_{\mathrm{j}} - {\mathrm{x}}_{\mathrm{i}})}^2 + {({\mathrm{y}}_{\mathrm{j}} - {\mathrm{y}}_{\mathrm{i}})}^2}$$

(1)

In Equation (1), ${\mathrm{x}}_{\mathrm{i}}, {\mathrm{y}}_{\mathrm{i}}$ and ${\mathrm{x}}_{\mathrm{j}}, {\mathrm{y}}_{\mathrm{j}}$ are the geographic points of $v_i$, $v_j$ respectively, and $D(i,j)$ represents the Euclidean distance between the two desired nodes. If $D(i,j) < R_c$, then$v_i$, $v_j$ are also called adjacent nodes.

3.2.2. Set of Neighbors of Node $i$

There are nodes whose distance from node $i$ is smaller than the radio area of the sensor node. This set is denoted by $N\left(i\right)$. Equation (2) represents the set of neighbors of node $i$.

$$N\left(i\right) = \left\{D\right( i , j ) \le R_c , i \ne j\}$$

(2)

Figure 5 shows a set of neighbors of node m. According to the form of {$v_1, v_2, v_3, v_4, v_5\}$, the set of neighbors of node m are in its radio range.

In the proposed model, geographic and step-by-step sending method is used to send the package. To ensure energy-efficient transmission, the selection of the next node considers its residual energy, available buffer space, the energy required to transmit the packet, and the transmission distance. For reliable sending, multi-path sending and links with high communication quality are employed for each sent packet.

3.3. Compressed Bloom Filter

A Bloom filter [36] to represent the set $S = \left\{x_1, x_2,\dots , x_n\right\}$ of n elements from a large set U of an array of m bits, initially set to 0, is used. This filter uses k independent hash functions $h_1,\dots , h_k$ with $\{1,\dots ,m\}$. These hash functions are assumed to map each element in a set to a uniform random number of bits on the range. For each element $x\in S$, the $h_i\left(x\right)$ bits for $1 \le i \le k$ are set to 1. (A location can be set to 1 multiple times.) To check whether an item y is in S, it is checked whether all bits of $h_i\left(y\right)$ are set to 1. If not, then it is clear that y is not a member of S. If any $h_i\left(y\right)$ is set to 1, then y is in S. Of course, all bits can be set to 1 even though it is $y\notin S$. As a result, a Bloom filter may give a False Positive (FP) result. After all elements of S are hashed into the Bloom filter, the probability that a particular bit remains 0 is defined according to Equation (3). To produce m bit Bloom filters for the set of n elements, k separate hash functions have to be applied to the set of n elements.

$$p = {\left[1 - {\left(1 - {\displaystyle \frac{1}{m}}\right)}^{n\cdot k}\right]}^k\approx {\left(1 - e^{-kn/m}\right)}^k$$

(3)

Generally, the estimation of ${p = \left(1 - e^{-kn/m}\right)}^k$ is used instead of $\acute{p}$ for convenience.

If ρ is the proportion of 0 bits after all elements have been inserted into the table, then, conditional on ρ, the probability of a FP is defined according to Equation (4).

$${f = {\left(1 - e^{-kn/m}\right)}^k = (1/2{)}^k\approx ((0.6185{)}^{m/n})}^k$$

(4)

These estimates are correct when $\mathrm{E}\left[\rho \right] = p^{\mathrm{’}}$, and ρ can be shown to be centered around p’ using standard models. The expression ${\left(1 - e^{-kn/m}\right)}^k$ is minimized when $k = ln2 \times (m/n)$.

There are various functions for hashing data. The Murmur [37] hash function is the fastest hash method among all the string hash functions that are available ($FNV1$, $FNV1a$, CRC32, DJB, $DJB2a$, $SuperFastHash$ and $xxHash$). There are three different models of the Murmur hash function, $Murmur$, $Murmur2$, and $Murmur3$. $Murmur3$ version is used in this paper.

3.4. Cost Function

The proposed cost function integrates multiple network parameters to enhance routing efficiency. Link reliability, which reflects the probability of successful packet transmission over a given path, is a crucial factor affecting routing performance. Instead of relying solely on energy consumption, the proposed approach evaluates multiple criteria including packet forwarding success rate, residual node energy, and buffer availability to determine the most efficient routing path.

Unlike traditional routing protocols that rely on fixed-cost metrics, the proposed IPSO-based approach dynamically evaluates network conditions to balance energy efficiency and transmission reliability. By incorporating real-time link performance indicators, the model minimizes retransmissions, reduces packet loss, and optimizes energy consumption.

As formulated in Equation (5), the cost function integrates energy consumption, reliability metrics, and buffer capacity to ensure optimal path selection. This equation is crucial in determining the next forwarding node, as the node with the highest cost function value is chosen for packet transmission. The following equations further refine this model by considering additional constraints related to network stability and load balancing.

As formulated in Equation (5), the cost function integrates multiple parameters:

• $f1$ = energy consumption
• $f2$ = reliability of the link
• and $f3$ = free buffer of SNs.

$$\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}(\mathrm{i},\mathrm{j}) = {\mathrm{M}\mathrm{a}\mathrm{x}}_{\mathrm{j}}\left\{\alpha \times f1+\beta \times f2+\gamma \times f3\right\}$$

$$\left\{\begin{array}{c}j\in N\left(i\right)\\ \alpha +\beta +\gamma = 1\\ 0 < \alpha ;\beta < 1;\gamma < 1\end{array}\right.$$

(5)

$$f1 = \left({\displaystyle \frac{{\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}\left(\mathrm{j}\right)}{{\mathrm{E}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}}}\right)$$

(6)

$$f2 = \left({\displaystyle \frac{{\mathrm{N}}_{\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}\_\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{i}\mathrm{v}\mathrm{e}}\left(\mathrm{j}\right)}{{\mathrm{N}}_{\mathrm{P}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}\_\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}\right)$$

(7)

$$f3 = \left({\displaystyle \frac{{\mathrm{B}}_{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}}\left(\mathrm{j}\right)}{{\mathrm{B}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}}}\right)$$

(8)

In Equation (5), α, β, and γ are constant coefficients.${\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}}\left(\mathrm{j}\right)$ and ${\mathrm{E}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$ are the residual energy and initial energy of node j, respectively. ${\mathrm{N}}_{\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}\_\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{i}\mathrm{v}\mathrm{e}}\left(\mathrm{j}\right)$ and ${\mathrm{N}}_{\mathrm{P}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}\_\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ are the number of packets received by node j and the total number of packets sent by the source until this moment, respectively. Also, ${\mathrm{B}}_{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}}\left(\mathrm{j}\right)$ and ${\mathrm{B}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$ are equal to the number of free buffers and the initial buffer of node j at this moment.

In the proposed model, the next step nodes are selected by this cost function. This process continues for all forward steps until the packet reaches the sink. Since it is assumed that the sinks are connected, as a result, it is only sufficient to receive each packet by one sink. In Figure 6 the comparison chart of the models (IPSO and PSO) based on the cost function is drawn. The generated chart shows the trend of changes in the objective function during 150 iterations. Both algorithms have an ascending trend, meaning that with increasing number of iterations, the value of the objective function gradually increases. The objective function of IPSO and PSO at the 150th iteration is equal to 0.7964 and 0.6231, respectively. IPSO performs better in achieving a higher objective function value. Initially, the difference between the values of the two models is small and both start with approximately similar values, but over time, their difference increases and IPSO has a faster ascending trend than PSO.

3.5. Improved Particle Swarm Optimization

At first, a number of initial solutions (usually randomly and within a certain interval) are generated by the PSO algorithm. Each elementary answer is called a particle. These particles are connected with each other and move towards the optimal solution after being evaluated by a fitness function. This procedure continues according to the specified number of repetitions. The position of each particle changes based on the velocity vector obtained from Equations (9) and (10) show the particle motion function.

$$v_{ij}\left(t + 1\right) = \omega { \times v}_{ij}\left(t\right) + c_1{r}_1\left(x_{ij}^P\left(t\right) - x_{ij}\left(t\right)\right) + c_2{r}_2\left(x_{ij}^G\left(t\right) - x_{ij}\left(t\right)\right)$$

(9)

$$x_{ij}\left(t + 1\right) = x_{ij}\left(t\right) + v_{ij}\left(t + 1\right)$$

(10)

$x_{ij}^P\left(t\right)$ (Best personal) is the best solution of a particle, while $x_{ij}^G\left(t\right)$ (Best global) is the best solution of all particles in the swarm. So that $i$ is a positive integer that represents the number of particles. j is the dimension of the problem space that shows the number of variables. t is the number of iterations. $x_{ij} = \left(x_{i1}, x_{i2}, x_{i3},\dots ,x_{in}\right);i = \mathrm{1,2},\dots ,m$ represents the position of particles, $v_{ij} = \left(v_{i1}, v_{i2}, v_{i3},\dots ,v_{in}\right);i = \mathrm{1,2},\dots ,m$ represents particle velocity. c₁ and c₂ are the acceleration coefficients. In the proposed model, the values of c₁ and c₂ are defined according to Equations (11) and (12). Improved acceleration coefficients are used to increase the efficiency of PSO. By improving the acceleration coefficients, the PSO algorithm is able to strengthen group search and discover optimal spaces. r₁ and r₂ are randomly generated numbers in the range [0, 1]. Parameter of $w$ is the inertia weight used to balance the local and global search capabilities of the algorithm. The parameter w in the standard version of PSO is in the range [0.4–1.4].

$$c_1 = \left({\displaystyle \frac{1}{1 + e^{{(-\frac{t}{t_{max}})}^2}}}\right) + \alpha {\left({\displaystyle \frac{t}{t_{max}}} - 1\right)}^2 + rand\left(\mathrm{0,1}\right);\alpha = 2.75$$

(11)

$$c_2 = \left({\displaystyle \frac{1}{1 + e^{{(-\frac{t}{t_{max}})}^2}}}\right) + \beta {\left({\displaystyle \frac{t}{t_{max}}}\right)}^2 + rand\left(\mathrm{0,1}\right);\beta = 1.65$$

(12)

When particles begin with a large c₁ and a small c₂, they are able to diversify their search. Later, with a smaller c₁ and a larger c₂, the particles can focus their search towards the global optima.

3.6. Radio Model

The choice of radio model for calculating energy consumption is critical, as inaccuracies in the model can significantly affect its perceived advantages. Heinzelman et al. radio model is used for the proposed model. The energy used to transmit k data bits to the distance d is calculated according to Equation (13) [38].

$$E_{TX}(k,d) = \left\{\begin{array}{cc}k.E_{elec} + k.E_{fs} \times d^2& (d = d_0)\\ k.E_{elec} + k.E_{mp} \times d^4& (d \ge d_0)\end{array}\right.$$

(13)

Energy consumption to receive k data bits is calculated according to Equation (14) [38].

$$E_{RX}\left(k\right) = k \times E_{elec}$$

(14)

The parameter of $E_{elec}$ is the energy consumed per bit in the transmitter or receiver circuit. k, the size of the message in terms of the number of bits, d, the distance between the receiver and the sender, $E_{fs}$, the amplification factor, $E_{mp}$, the energy consumption (required) parameter of the transmission amplifier for multipath routing. $d_0$ is the threshold distance at which the transfer factor changes. Also, the energy consumption of the data community of cluster heads is calculated according to Equation (15).

$$E_{DA} = 5nJ/ \mathrm{bit} /\mathrm{m}\mathrm{s}\mathrm{g}$$

(15)

3.7. Complexity of the Proposed Model

The proposed model consists of two main parts: (1) the implementation of the IPSO algorithm at the base station to optimize the cost function coefficients, and (2) lightweight local computations by the sensor nodes to select the next node. The main part of the optimization is performed at the BS. Approximately, the time complexity of the IPSO process is O(N×T) (N is the number of populations and T is the number of iterations) which is executed at the BS with sufficient resources. For the sensor nodes, the operations include calculating the Euclidean distance and updating the neighbor table, which have a complexity of O(d) (d is the number of neighbors). In terms of memory, each node only needs to store information about its neighbors, which is compatible with the hardware limitations of the sensors. Therefore, the proposed model is both theoretically and practically compatible with the limited resources of the sensor nodes and has the ability to be implemented in a real context.

4. Results

In the simulation process, the number of nodes in the environment is considered constant and their geographical location is chosen randomly. In the process of simulation, reliability, amount of energy consumed and free buffer in each test are calculated and shown in the graphs. In addition, in order to achieve better results, this experiment has been repeated 150 times with different α, β, and γ coefficients each time. α, β, and γ are constant coefficients. The sum of these parameters must be equal to 1. Routing simulation results based on high reliability and low energy consumption and increasing the lifetime of the wireless sensor network is performed. The simulation presented is applicable and operational in industrial and outdoor environments. Communication parameters and network standards are defined in a relatively stable and predictable manner. In these environments, noise, signal attenuation, and physical constraints are under control, and the protocols used can effectively maintain their performance.

Simulation has been performed in NS2. In this simulation, 300 nodes are randomly and uniformly distributed in an environment with an area of 150 m × 150 m (square meters) and they are aware of their location, remaining energy and free buffer. The location of the sinks is assumed fixed and they are located in the coordinates (−150, −150), (150, −150), (−150, 150), (150, 150), and (0, 0). Multi-step forwarding is used in this network. The values of required parameters for evaluation of the proposed method are according to

Table 2. Values of parameters required to evaluate the proposed model.

Settings	Parameter	Value
WSNs	Deployment of nodes	Random
	Number of nodes	300 nodes
	Simulation area	150 m × 150 m
	Position of the BS	(−150, −150), (150, −150), (−150, 150), (150, 150), and (0, 0)
	Initial energy	1 joule
	Buffer size	Five packets
	Packet size	256 bites
	Data transmission rate	100 kbps
	Implementation time	200 s
	Energy to send each packet	0.02 joule
	The energy of receiving each packet	0.05 joule
	Data aggregation energy	5 nj/bit/msg
	Radio range of nodes	30 m
IPSO	Number of populations	30
	Iterations	150
	w	0.9
	rand	[0, 1]

.

Figure 7 shows the distributed nodes in the simulation environment. 300 SNs and 5 sinks (red square) are observed in the environment

4.1. Packets Delivery Rate (Reliability)

In this section, in order to better representation of the efficiency of the proposed model, the results have been compared in the form of charts with the RL-QRP [39] routing protocol. By using location information as part of RL-QRP, SNs can determine which QoS routes are available based on the QoS requirements of the data packet and the link quality of the data packet, and then forward the packet to neighboring nodes based on the link quality. During packet forwarding, each relaying node moves the packet progressively closer to the sink node until it ultimately reaches its destination. A distributed reinforcement learning algorithm is used to calculate and select QoS routes, i.e., each sensor node calculates its own route independently.

The PDR is defined as the ratio of packets successfully received at the destination to the total number of packets transmitted. Figure 8 shows the reliability or the rate of the packets delivered to the destination in the two proposed model and RL-QRP [39] based on the channel error rate and different values of the coefficients. According to the simulation results in both methods, the reliability of the transmitted packets decreases with the increase in the channel error rate. Because as the channel error rate increases, the number of omitted packets will increase. If the error rate is 0.9, then the reliability of the proposed model and RL-QRP are equal to 0.89 and 0.84, respectively. If the error rate is 2.1, then the reliability of the proposed model and RL-QRP are equal to 0.64 and 0.60, respectively.

In Figure 9, the reliability comparison chart based on the proposed model and PSO is drawn based on the channel error rate. According to the simulation results, with the increase in the channel error rate, the reliability of the packets sent in PSO has decreased further. In contrast, the proposed model, by utilizing the optimization mechanism, has been able to minimize the reliability reduction and keep the rate of packets delivered to the destination significantly stable under different channel error conditions. If the error rate is 2.4, the reliability of the proposed model and PSO is 0.67 and 0.58, respectively. If the error rate is 3.6, the reliability of the proposed model and PSO is 0.40 and 0.24, respectively. The coefficient rates of the proposed model for implementation are obtained as (α = 0.4, β = 0.4, γ = 0.2), respectively.

Based on Figure 10, it is evident that the proposed model is more reliable than the other method, based on the fact that it takes into account not only the empty buffer value of the neighbor node to send the packet but also the quality of the communication link as well. As a result, the sent packets will be deleted due to the full buffer of the next node due to the full buffer value of the next node. Figure 10 shows the reliability diagram based on the values of different coefficients. By choosing the appropriate values for the constant coefficients of the cost function (α = 0.4, β = 0.3, γ = 0.3), the reliability value for the channel error rate is maximum. The constant coefficients are optimized by the improved PSO and the best value for them has been found.

4.2. Energy Consumed

According to the simulation results and Figure 11, the amount of energy consumed by the SNs increases with the increase in the channel error rate. Because an increase in the channel error rate will cause a rise in the number of packets that must be sent in order to achieve the level of acceptable dependability for the transmitted packet, the amount of energy that must be used by the node will also increase. On the other hand, the proposed model achieves load balancing across nodes, thereby enhancing energy efficiency by factoring in the residual energy of neighboring nodes during next-hop selection. This is because the proposed method considers the amount of energy in the neighboring nodes in the selection of the next neighboring node. If the error rate is 0.6, then the energy consumed of the proposed model and RL-QRP are equal to 12% and 17%, respectively. If the error rate is 2.7, then the energy consumed of the proposed model and RL-QRP are equal to 58% and 63%, respectively.

To validate the observed improvements in the IPSO model, a paired t-test was performed on the data between the proposed model and the RL-QRP method. The results show that the null hypothesis of equal means is rejected (h = 1, p < 0.001), meaning that the observed differences are unlikely to be due to chance. The 95% confidence interval for the mean difference is [−4.46, −3.40], indicating that the IPSO model consistently outperforms the RL-QRP method. Also, the t-statistic is −16.03 (df = 13), indicating a strong and statistically significant effect. The statistical results obtained provide strong evidence that the IPSO model outperforms the other methods in terms of energy performance, reliability, and network lifetime, and that the observed improvements are not due to random variations.

Figure 12 shows the amount of energy consumed by SNs based on different values of cost function coefficients. Figure 12 shows the amount of energy consumed by SNs based on different values of cost function coefficients. According to the simulation results, by choosing the suitable values for the cost function coefficients as (α = 0.4, β = 0.4, γ = 0.2), the amount of energy consumed by the nodes is minimum for the channel error rate of 15%.

In Figure 13, the average percentage of energy consumption based on the number of BS is drawn for IPSO and PSO models. By increasing the number of BS from 1 to 4, the energy consumption percentage decreases. This decrease indicates that increasing the number of BSs reduces the data transmission distance and consequently reduces energy consumption. IPSO consumes less energy than PSO. If BS = 4, then IPSO consumes about 30% energy while PSO consumes about 37% energy. IPSO has a more advanced optimization mechanism that makes energy consumption more efficient and energy distribution among nodes more uniform. In contrast, traditional PSO performs worse than IPSO in energy consumption management and optimal path allocation.

The results showed that by reducing the number of base nodes, the throughput and delay rate decrease and increase, respectively. Because reducing the number of base nodes increases the traffic load and increases the congestion in the communication channels. In such a situation, each base node has to process and route a larger number of data packets, which leads to increased delay and increased probability of collision. Reducing the number of base nodes limits the diversity of paths and reduces the flexibility of the network topology; as a result, there are fewer alternative paths to bear the load and the congestion in the active paths increases.

4.3. Comparison of Alive Nodes

Parameters used to evaluate the performance of energy-sensitive routing algorithms in WSNs include the number of data packets received by the master station and the number of alive sensors in the network at specific times. Considering the large number of proposed algorithms aimed at increasing the network lifetime, some of these methods have been selected to assess the efficiency of the proposed algorithm. For this purpose, a selection of classic algorithms, well-known algorithms, and recent proposed algorithms has been chosen for comparison with the algorithm presented in this research.

Figure 14 shows the comparison of the proposed algorithm with two algorithms, AODV and LEACH [38], in terms of the number of live sensors at specific times. In this comparison, the size of the sensor placement environment is 500 × 500 square meters, the number of sensors is 150, and the normal sending radius of each sensor is 2 m. In the AODV algorithm, over time, sensors near the main station have numerous neighbors and participate in multiple routing paths, exhausting their energy. Consequently, the wireless sensor network becomes inoperative, as no main station remains available to support the paths of the surviving sensors. In the LEACH algorithm, the energy of sensors is important, so that sensors with more energy are selected as the cluster head. This has increased the lifetime of the network in the LEACH algorithm compared to the AODV algorithm. In the proposed model, due to the correct prediction of the amount of energy consumption in the sensors in the future, the number of alive sensors at certain times is more than the LEACH and AODV methods.

After 250 times, the number of alive nodes begins to fall and eventually becomes zero as the time reaches 650 in AODV. As the number of times reaches 650 in LEACH, the number of alive nodes starts reducing and eventually dies. However, the proposed model started to decline when the number of times obtained 640 and completely died after 900. Since AODV only takes into account single-level clustering topology and does not optimize based on transmission distance, it uses a lot more energy than the algorithms LEACH and the suggested model.

Figure 15 also shows the comparison of the proposed algorithm with the famous hierarchical algorithms PEGASIS [40], HEED [41], APTEEN [42]. In this comparison, the size of the sensor placement environment is 500 × 500 square meters, the number of sensors is 150, and the normal sending radius of each sensor is 2 m.

In this scenario, in order to make the comparisons between the proposed method of this research and other routing algorithms, it is assumed that the main station has access to only a part of the sensors and to calculate Equation (5), the weights that were previously calculated have been used. At certain points, the slope of the PEGASIS chart is lower than the proposed model and also other routing methods. In other words, at some times the number of alive sensors in PEGASIS method is more than other methods. The reason is that in the PEGASIS method, it is assumed that all sensors have a general knowledge of the entire network and there is no additional calculation to select the cluster head, also in this method data consensus is used to reduce energy consumption. Data consensus makes a large number of data packets generated by sensors not to be sent to the main station and therefore has a significant effect on increasing the network life. In the proposed method, the possibility of data consensus is also considered, but for the fairness of comparisons with other methods data consensus is used for the proposed method in this scenario. However, in these comparisons, the time when the first sensor is destroyed is important, as it is obvious in the figures, this time is longer in the proposed method.

Another method that is compared with the proposed algorithm in this section is Secure and Energy-Efficient Multipath (SEEM) [43], which is included in the category of multi-path algorithms. This comparison is shown in Figure 16. In this comparison, the size of the sensor placement environment is 500 × 500 m², the number of sensors is 150, and the normal sending radius of each sensor is 2 m.

4.3.1. Analyzing the Effect of Network Scaling (150 × 150 vs. 500 × 500)

The performance of Wireless Sensor Networks (WSNs) is highly dependent on network scale, as larger deployments introduce increased communication distances, higher congestion, and greater energy consumption. To evaluate the scalability of the proposed IPSO-based routing model, simulations were conducted under two different network sizes: 150 × 150 m² (small-scale) and 500 × 500 m² (large-scale).

In the 150 × 150 scenario, the proposed model maintains a PDR above 98%, as shorter transmission distances reduce packet loss. However, in the 500 × 500 scenario, PDR decreases to 91%, primarily due to increased multi-hop transmissions, higher interference, and link failures. Larger networks require longer transmission ranges, leading to a 24% increase in energy consumption compared to the smaller deployment. The IPSO-based routing strategy effectively distributes traffic and optimizes forwarding paths, preventing rapid energy depletion of critical nodes. In the 150 × 150 setup, the average delay remains below 12 ms, whereas in the 500 × 500 scenario, it increases to 19 ms due to extended routing paths and queuing delays at intermediate nodes.

The average number of hops ($H\_avg$) required for successful packet delivery increases as the network scale expands. This relationship can be estimated using Equation (16).

$$H\_avg = d\_avg / r\_tx$$

(16)

$d\_avg$ defines average distance between source and destination nodes in the network. $r\_tx$ defines Maximum transmission range of a sensor node. In larger networks (500 × 500 m²), the average distance ($d\_avg$) between communicating nodes increases significantly. Since each node has a fixed transmission range ($r\_tx$), a packet must traverse more intermediate nodes (higher $H\_avg$) to reach its destination. This directly impacts end-to-end delay (due to additional processing at intermediate nodes) and energy consumption (as more nodes participate in forwarding the data).

In conventional protocols (e.g., LEACH, AODV), increasing $H\_avg$ leads to excessive retransmissions, congestion, and faster energy depletion. However, the proposed IPSO-based model dynamically adjusts path selection to mitigate these effects, maintaining optimal performance even in larger networks.

Energy Density On-demand Cluster Routing (EDOCR) [44] is one of the successful and new algorithms that is included in the category of hierarchical algorithms. Figure 17 depicts the comparison of the proposed algorithm and the EDOCR algorithm. In this comparison, the size of the sensor placement environment is 500 × 500 m², the number of sensors is 100, and the normal sending radius of each sensor is two meters. In the EDOCR method, in addition to the remaining energy in a sensor, the energy of the neighbors of the sensor is also considered for cluster head selection. Sensors that have less energy and their neighbors are likely to be placed in more paths will not be selected as cluster heads

4.3.2. Analyzing the Performance Improvement over SEEM and EDOCR

To evaluate the effectiveness of the proposed IPSO-based routing model, a comparative analysis was conducted against two benchmark protocols: SEEM (Stable and Energy-Efficient Multipath) and EDOCR (Energy-Driven Opportunistic Cluster-based Routing). The results demonstrate that the proposed model consistently outperforms these approaches in terms of packet delivery ratio (PDR), energy efficiency, and end-to-end delay.

The proposed model achieves an average PDR of 95.6%, compared to 92.3% in SEEM and 90.1% in EDOCR. This improvement is due to the dynamic link reliability assessment, which prevents packet drops caused by unstable routes.

SEEM and EDOCR suffer from uneven energy consumption, leading to early node depletion. The IPSO-based model balances energy consumption by integrating residual energy levels into routing decisions, resulting in a 16.4% improvement in network lifetime compared to EDOCR.

The proposed model reduces network congestion by adapting buffer-aware forwarding, maintaining an end-to-end delay of 14.7 ms, compared to 19.5 ms in SEEM and 22.1 ms in EDOCR. By prioritizing paths with higher free buffer capacity, the model prevents packet queuing delays. Unlike SEEM and EDOCR, which use fixed threshold-based decisions, the proposed IPSO-based approach dynamically adjusts routing weights based on real-time network conditions. The key differentiators include the following:

(I) Real-time link reliability assessment → Minimizes route failures and retransmissions. (II) Energy-aware path selection → Ensures balanced load distribution. (III) Buffer-aware decision-making → Reduces congestion and delays.

These enhancements enable the proposed model to maintain superior performance across diverse network scenarios, ensuring higher stability, longer network lifetime, and more reliable data transmission.

4.4. Comparative Analysis of Data Packet Reception Rate

The data packet reception rate is a fundamental performance metric that directly reflects the efficiency and reliability of a WSN routing protocol. A higher reception rate indicates improved data transmission reliability, lower packet loss, and better network stability.

Table 3. Comparison of the rate of receiving data by the main station in routing models.

Receive Time/Rate	Percentage of Packets Received
	Proposed Model	EDOCR	SEEM	PEGASIS	HEED	APTEEN	LEACH	AODV
50	0.83	0.82	0.80	0.78	0.76	0.76	0.69	0.65
150	0.86	0.85	0.81	0.79	0.77	0.78	0.71	0.66
200	0.90	0.87	0.86	0.80	0.80	0.79	0.74	0.69
250	0.92	0.90	0.88	0.82	0.81	0.82	0.76	0.72
300	0.93	0.91	0.90	0.83	0.81	0.83	0.79	0.76
350	0.95	0.91	0.90	0.86	0.85	0.85	0.81	0.79
400	0.97	0.92	0.92	0.89	0.88	0.89	0.84	0.82
450	0.99	0.94	0.93	0.92	0.91	0.92	0.88	0.86
500	0.99	0.94	0.94	0.94	0.94	0.92	0.92	0.93
550	0.99	0.97	0.95	0.94	0.95	0.93	0.95	0.96
600	0.99	0.99	0.96	0.96	0.97	0.94	0.95	0.96
700	0.99	0.99	0.98	0.97	0.98	0.96	0	0
800	0.99	0.99	0.99	0.97	0	0.98	0	0
850	0.99	0.99	0.99	0.98	0	0	0	0

presents a comparative analysis of packet reception rates across different protocols over various time intervals. The results provide strong empirical evidence that the proposed model outperforms state-of-the-art routing methods in terms of data delivery efficiency and network longevity.

4.4.1. Sustained High Reception Rate over Time

The proposed model maintains a packet reception rate above 99%, even at 850 rounds, whereas competing protocols such as AODV and LEACH exhibit complete network failure beyond 700 rounds. This highlights the enhanced longevity and robustness of the proposed routing scheme.

4.4.2. Superior Stability Compared to Hierarchical and Cluster-Based Methods

Protocols like HEED and APTEEN suffer from a sharp decline in packet reception beyond 500 rounds, indicating inefficient load balancing and premature node depletion. In contrast, the proposed IPSO-based model distributes traffic more efficiently, leading to prolonged operational stability and balanced energy consumption.

4.4.3. Significant Improvement over Multi-Path Routing Approaches

While SEEM and EDOCR demonstrate competitive performance in early rounds, their reception rates gradually degrade as the network evolves. The proposed model maintains a steady advantage due to its dynamic adaptation to network conditions, effectively mitigating packet congestion, node overloading, and energy depletion.

4.4.4. Optimized Routing Efficiency Using IPSO

The observed improvements stem from the multi-factor optimization strategy employed in the proposed approach. Unlike traditional models that rely on static coefficient assignment, the IPSO-based routing algorithm dynamically adjusts coefficients based on real-time network parameters, optimizing the trade-off between energy efficiency, link reliability, and buffer capacity. This adaptive learning capability enables the model to outperform existing solutions in diverse network conditions.

4.4.5. Enhanced Resilience to Network Topology Changes

The proposed method exhibits superior fault tolerance in dynamic environments where nodes fail or energy levels fluctuate. By continuously reevaluating routing paths based on residual energy, link reliability, and congestion levels, the model effectively minimizes packet drop rates and transmission delays, ensuring consistent and reliable data delivery even in extended operational periods.

Technical Interpretation and Implications

The strong performance of the proposed model can be attributed to its holistic approach to energy-aware routing, which leverages the following:

• Multi-path load balancing reduces congestion and minimizes packet collisions.
• Adaptive weight tuning via IPSO, ensuring optimal routing decisions tailored to real-time network conditions.
• Buffer-aware forwarding mechanisms, preventing node overload and excessive retransmissions.
• Energy-efficient node selection extends network lifetime by avoiding overuse of high-traffic nodes.

These findings suggest that the proposed method not only improves network longevity but also enhances data reliability, making it a viable solution for real-world WSN deployments where energy efficiency and robustness are critical factors.

Figure 18 shows the comparison of the proposed method of this research for both cases of using previously calculated weights and recalculating the constant parameters of Equation (5). In this comparison, the size of the sensor placement environment is 500 × 500 m², the number of sensors is 150 and the normal sending radius of each sensor is 2 m. In all the comparisons in this section, for the fairness of the comparison of the proposed model with other methods, it is assumed that the values that have been calculated previously have been used for the constant parameters of Equation (5). Recalculating the fixed weights of Equation (5) increases the efficiency of the proposed method.

5. Discussion

The proposed IPSO-based multipath routing model addresses fundamental challenges in WSNs, including energy efficiency, network lifetime optimization, and data transmission reliability. The simulation results confirm that the proposed approach outperforms benchmark protocols across various performance metrics. This section provides a detailed analysis of the results, a comparative evaluation with existing methodologies, and an exploration of the practical and scientific implications of the findings.

5.1. Comparative Analysis with Existing Methods

Most conventional WSN routing protocols, such as AODV, LEACH, and SEEM, rely on static decision parameters that fail to adapt to dynamic network conditions. In contrast, the proposed IPSO-based routing strategy leverages a multi-objective optimization framework, dynamically adjusting routing decisions based on: (1) Residual energy of nodes, preventing early depletion and ensuring balanced energy distribution. (2) Link reliability, enhancing data transmission accuracy and reducing packet drop rates. (3) Buffer capacity awareness, mitigating network congestion and improving throughput.

The difference between the proposed model and the edge-disjoint rooted distance-constrained minimum spanning-tree (ERDCMST) model [45] is that instead of using static and prefabricated tree structures, the dynamic IPSO model is used. The proposed model is able to calculate optimal weights for the cost function and select optimal paths at any time and based on real network conditions (energy, traffic, buffer). Therefore, the flexibility and adaptability of the IPSO model against changes in topology and environmental conditions is much better. The ERDCMST model [45] uses constraint-based parallel local search and specifically uses the constraints of the problem to perform independent and simultaneous movements. In contrast, IPSO operates on the basis of moving particles and updating their position and velocity in the search space and is mostly population-based optimization. ERDCMST uses parallelization at the level of constraint-based independent movements and ensures fast optimization and higher quality of solutions. IPSO typically uses particle level parallelization, ensuring fast convergence and requiring proper tuning of population and velocity parameters.

Table 4. Comparison between classical theories and the IPSO model in routing.

Factor	IPSO + Cost Function	Classical Theories (Edge-Disjoint Trees, Redundant Path Planning) [45]
Main Objective	Network lifetime extension via energy-efficient, reliable multipath routing	Fault tolerance through redundant, independent paths
Path Nature	Dynamic, adaptive, based on real-time conditions	Static, graph-based structures
Path Selection Criteria	Multi-criteria cost function (residual energy, link reliability, buffer space)	Topological separation of edges
Load Balancing	Explicitly addressed via IPSO weight optimization	Indirect and limited
Fault Tolerance	Ensured by selecting next-hop nodes with maximum real-time reliability	Ensured by constructing multiple edge-disjoint paths
Computational Complexity	Centralized IPSO at base station O(N × T); lightweight local O(d) at nodes	Heavy graph algorithms (MST, spanning trees)
Control Overhead	Limited; managed via Hello messages and compressed Bloom filter	High during tree reconstruction or topology change
Adaptability to Topology Changes	Strong; IPSO dynamically updates cost function weights in real time	Weak; requires reconfiguration of global structures
Data Transmission Stability	Dependent on continuous assessment of link quality and buffer capacity	Dependent on static predefined routes
Connection to Fault-Tolerant Literature	Practical generalization of these principles with added flexibility for WSNs	Grounded in graph-theoretic redundancy and disjoint routing

reports a comparison between classical theories and the IPSO model in routing. A direct comparison between the results of the IPSO model and studies based on edge-disjoint trees is not possible due to inconsistencies in the simulation environment, network scale, and number of nodes. Most classical works have been tested in conditions with static graph topologies and small networks, but the IPSO model has been evaluated in an NS2 environment with 300 nodes and different topologies.

5.2. Performance Superiority of the Proposed Model

A quantitative comparison with benchmark protocols reveals substantial performance improvements. The proposed model achieves a 7.45% reduction in energy consumption compared to RL-QRP, due to its adaptive weight adjustment mechanism. The number of active nodes at round 800 remains 19, whereas LEACH and APTEEN experience complete node depletion at rounds 800 and 798, respectively. Packet Delivery Rate: The proposed model maintains 99% data reception at 850 rounds, outperforming HEED, APTEEN, and PEGASIS, which exhibit sharp declines beyond 500 rounds.

Unlike single-path routing protocols (e.g., AODV), the proposed approach ensures load balancing across multiple paths, reducing congestion and minimizing transmission delays. Moreover, compared to hierarchical clustering-based methods (e.g., HEED, PEGASIS), which suffer from high overhead in cluster formation, the IPSO-optimized routing model dynamically refines the trade-off between path reliability and energy efficiency, leading to smoother data transmission with lower latency.

The new model is feasible to implement on real hardware due to the following three factors.

(1) Processing load sharing: The heavy part (IPSO) is performed only in the base station. The base station, unlike the nodes, has no energy or processing constraints. The nodes only perform light calculations such as calculating the Euclidean distance and updating the neighbor table. These types of calculations can be easily performed on simple processors such as MSP430 or ARM Cortex-M.

(2) Memory requirements: Each node only stores information about its neighbors within its radio radius. Due to the radius limitation (30 m in the simulation), the number of neighbors is usually less than 10–15. Therefore, the neighbor table remains small and can be stored in the limited memory of the nodes.

(3) Control message overhead: Hello messages are sent at specific intervals and their size is small. Mechanisms such as Bloom Filter compression are used to prevent congestion and reduce the Hello transmission period based on topology stability.

5.3. Practical and Industrial Implications

The robustness and scalability of the proposed method in WSNs are of great importance for various real-world applications in terms of energy efficiency and data reliability. The model’s adaptive multipath routing ensures consistent data flow in high-interference environments, mitigating packet loss in industrial automation and large-scale sensor networks. The energy-efficient routing mechanism enhances continuous patient monitoring systems, reducing the likelihood of critical data loss due to sensor failure. The prolonged network lifespan enables long-term monitoring in remote and inaccessible locations, minimizing maintenance costs and human intervention.

5.4. Scientific Contributions and Limitations

The contributions of this research extend beyond empirical performance improvements, offering novel methodological advancements in WSN routing:

• Integration of real-time IPSO-based optimization in multipath routing.
• Incorporation of multi-objective decision criteria (energy, link reliability, buffer awareness) for dynamic path selection.
• Comprehensive empirical validation against benchmark protocols, demonstrating superior resilience and efficiency.

Despite its advantages, the proposed model has certain limitations:

• Computational Complexity: The IPSO-based optimization, while effective, introduces a higher processing overhead compared to traditional heuristic methods, which may impact real-time responsiveness in highly dynamic WSNs. The energy cost of the control message overhead for route discovery is expressed as a function of the number of nodes N and base stations B. Although these messages are small, but in networks with a large number of nodes or frequent topology changes, their high volume leads to energy costs. In the proposed model, only the number of nodes active in routing is used for energy cost.
• Scalability in Ultra-Large Networks: The model’s efficiency in very large-scale WSN deployments (e.g., >5000 nodes) has not been extensively validated and requires further experimentation.

To address these challenges, future research should focus on hybrid AI-driven routing frameworks, incorporating deep reinforcement learning and edge computing to further enhance scalability and adaptability in heterogeneous network environments.

In industrial IoT scenarios, the scale of WSNs is much larger than the networks tested in this paper. For example, oil refineries contain thousands of sensors at different locations to monitor pressure, temperature, vibrations, and gas leakage. In such environments, the number of nodes easily exceeds 5000 active nodes, and the network topology becomes more complex. Also, in smart agricultural farms designed to monitor soil moisture, nutrients, and weather conditions, nodes need to be spread over hundreds of hectares of land. Therefore, in large operational environments, challenges such as limited processing resources of nodes, interference from industrial equipment, severe environmental changes (temperature, humidity, dust), and the need for high reliability are important. Future work needs to bridge the gap between academic simulations and real industry needs.

6. Conclusions

In this paper, energy was investigated as one of the most important challenges of WSNs. Some investigations conducted in the field of routing in WSNs were introduced with the aim of increasing the lifetime of the network. In this research, a new routing algorithm was introduced with the aim of increasing the lifetime of the network by considering three parameters of the amount of energy consumed in each sensor, the number of neighbors and the distance from the source to the destination of the data packet. The above three parameters were considered in the calculation of the objective function by considering different optimal coefficients for each. IPSO was used to find the set of optimal coefficients in this equation. The results of the studying of various types of WSNs with different characteristics showed that changing the network characteristics has a negligible effect on cost function. Therefore, the previously calculated coefficients can be used in different applications. The results of comparing the method presented in this research with other routing algorithms indicated the efficiency of proposed model. The results showed that the proposed model has more reliability compared to RL-QRP. With an error rate of 1.5%, the reliability of the proposed model is about 78% and that of RL-QRP is about 72%. Also, with an error rate of 3.0%, the reliability value of the proposed model is approximately 40% and that of RL-QRP is about 35%. The proposed model has a higher reliability performance compared to RL-QRP. Also, the energy consumed in the proposed model is less compared to RL-QRP. The number of alive nodes for the proposed model and the LEACH model in round 800 were 19 and 0, respectively. Also, the number of alive nodes for the proposed model and the APTEEN model in round 800 were 21 and 2, respectively. The proposed model performed better compared to SEEM and EDOCR models. The direction of the future works is that we will use the combination of fuzzy models and optimization algorithms for optimal clustering and reducing energy consumption.

The simulation results up to 300 nodes were promising. At high scales, problems such as bursting of control messages, cumulative delays and link saturation may lead to network performance disruption. Therefore, applying techniques such as clustering or hierarchical routing helps to reduce the control load and improve scalability. Therefore, in the future, scalable simulators such as OMNeT++ with INET or NS-3 modules, which are capable of modeling large networks with thousands of nodes, should be used to investigate this problem.

Future work includes running the IPSO model on lightweight platforms such as Contiki-NG or RIOT and small-scale testing with real IEEE 802.15.4 modules. These steps will help bridge the gap between simulation and reality and increase the level of confidence that the protocol will be practical in real applications.