Optoelectronic Properties of Hydrogen-Terminated Silicon Nanowires via Aliphatic C8 Moieties: Impact of C–C Bond Order from First Principles
Abstract
1. Introduction
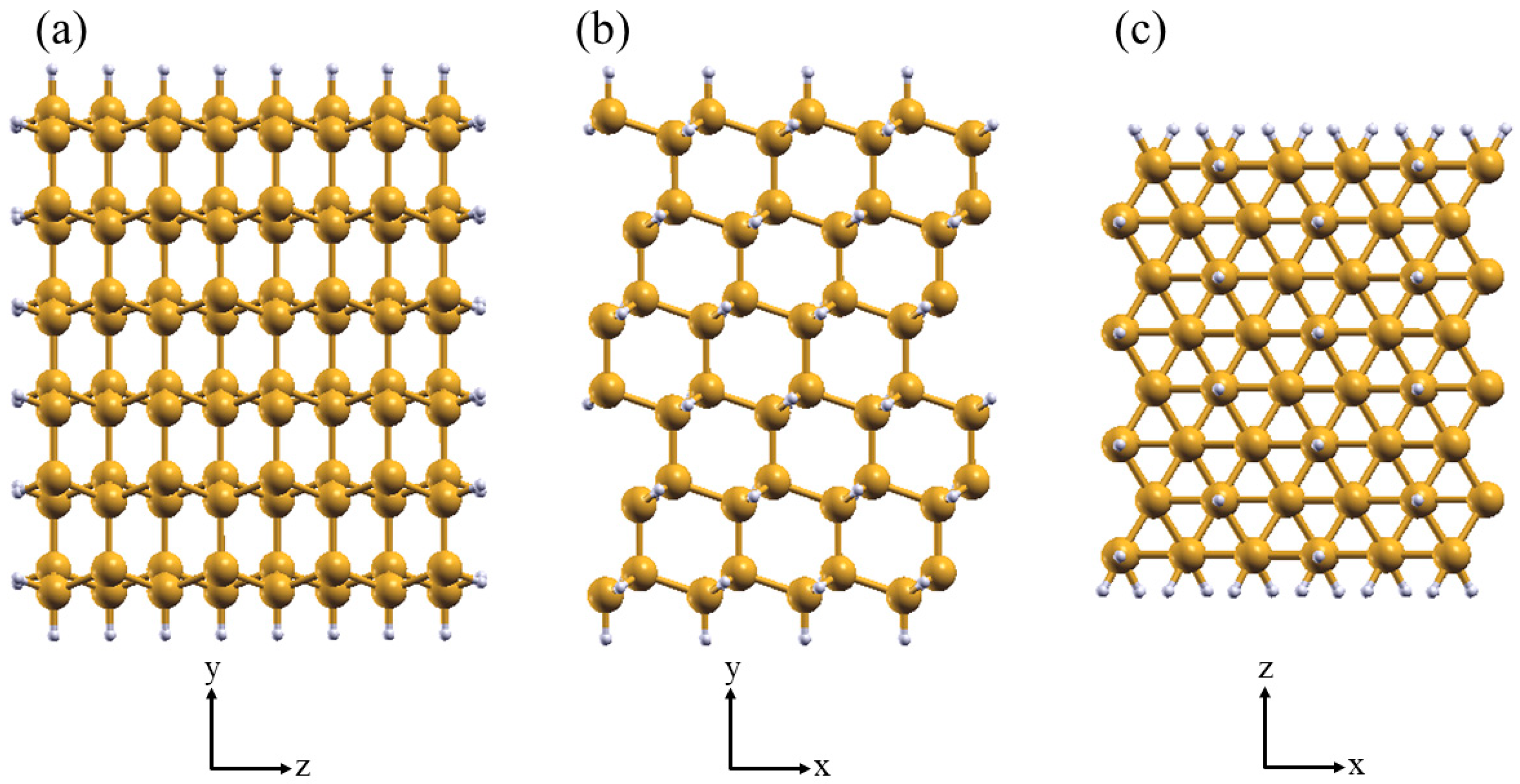
2. Methods
3. Results
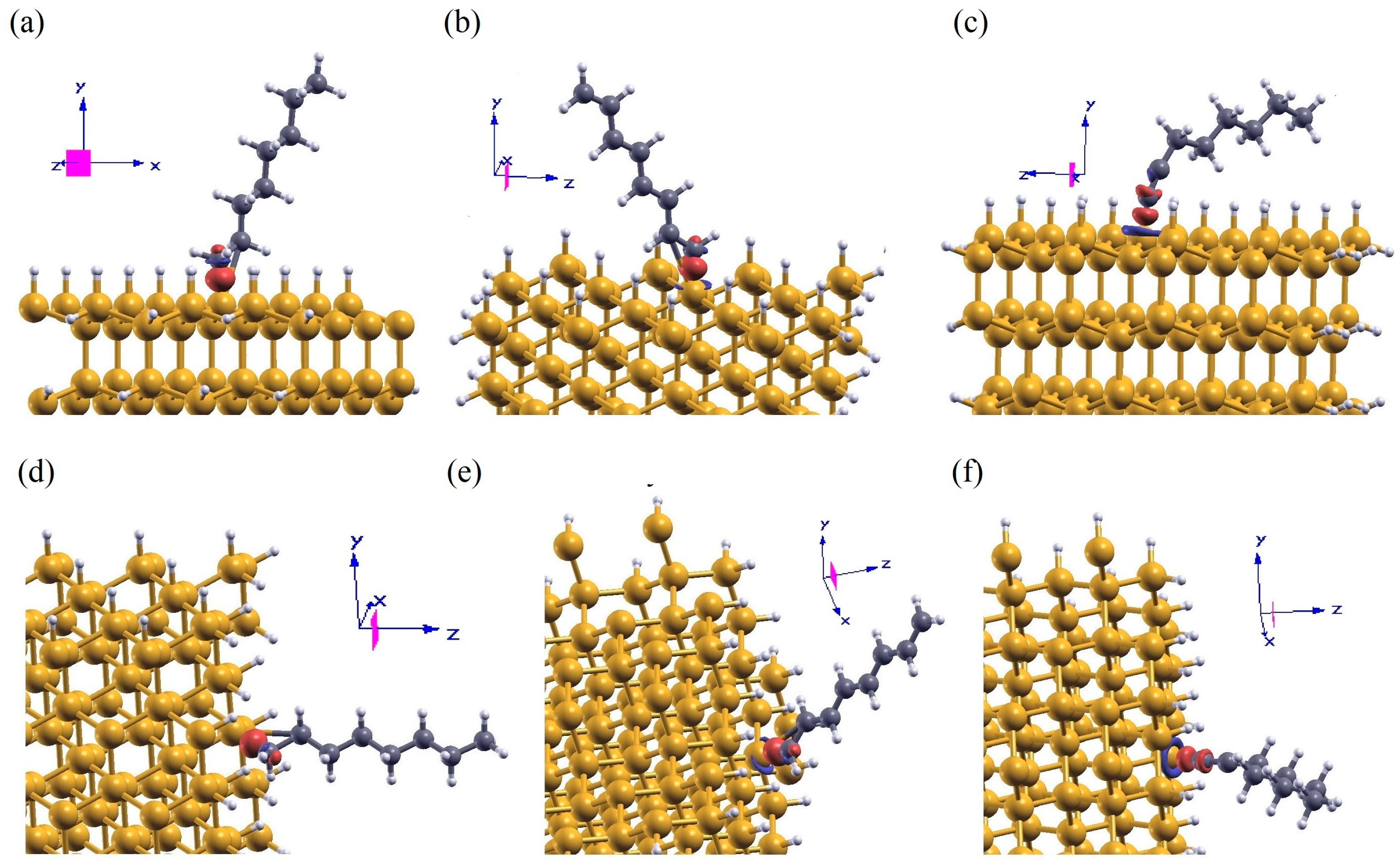
3.1. Structural Properties of Aliphatic Moieties Chemisorbed on SiNW:H
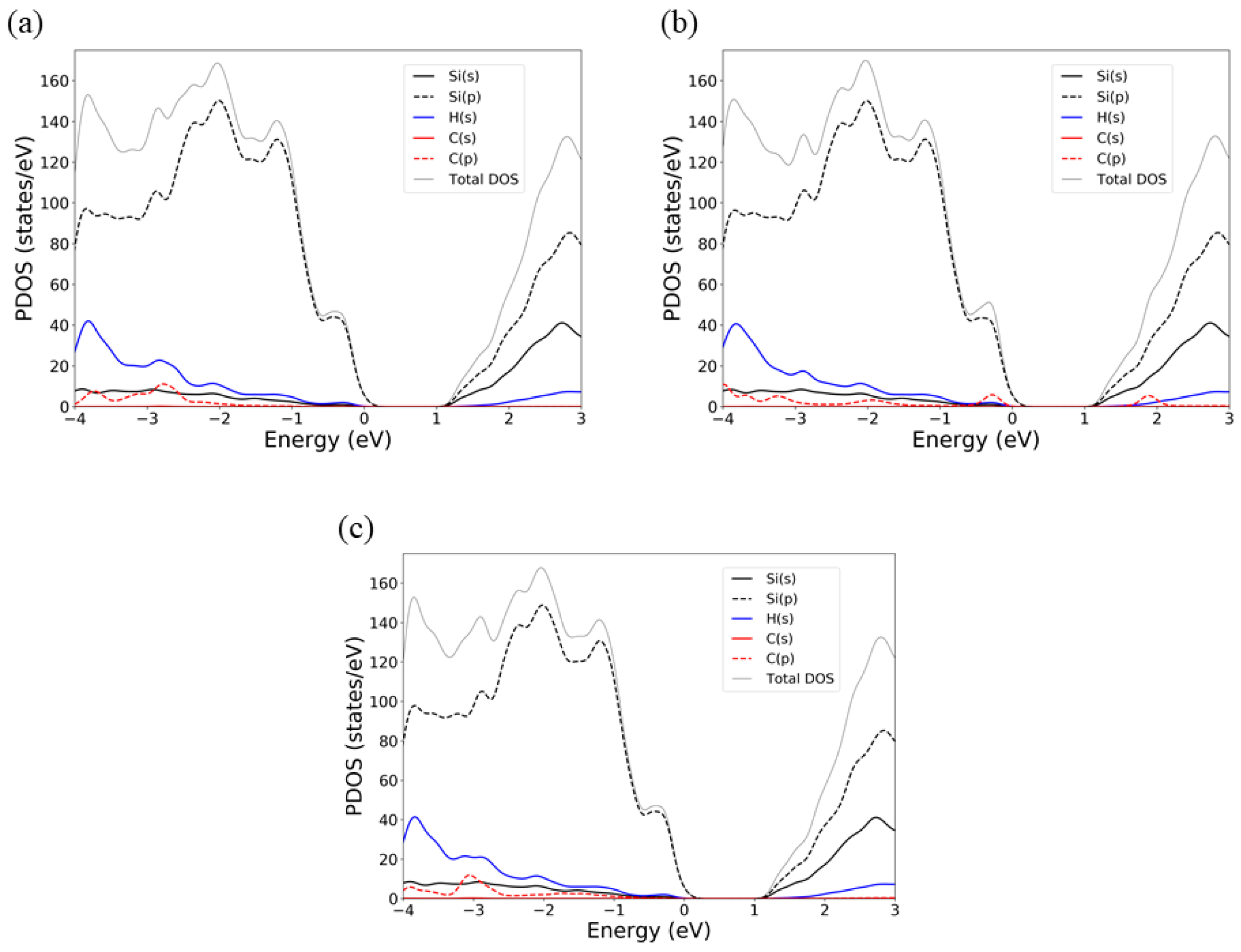
3.2. Electronic Properties of Aliphatic Moieties Chemisorbed on SiNW:H
3.3. Charge Transfer of Aliphatic Moieties Chemisorbed on SiNW:H
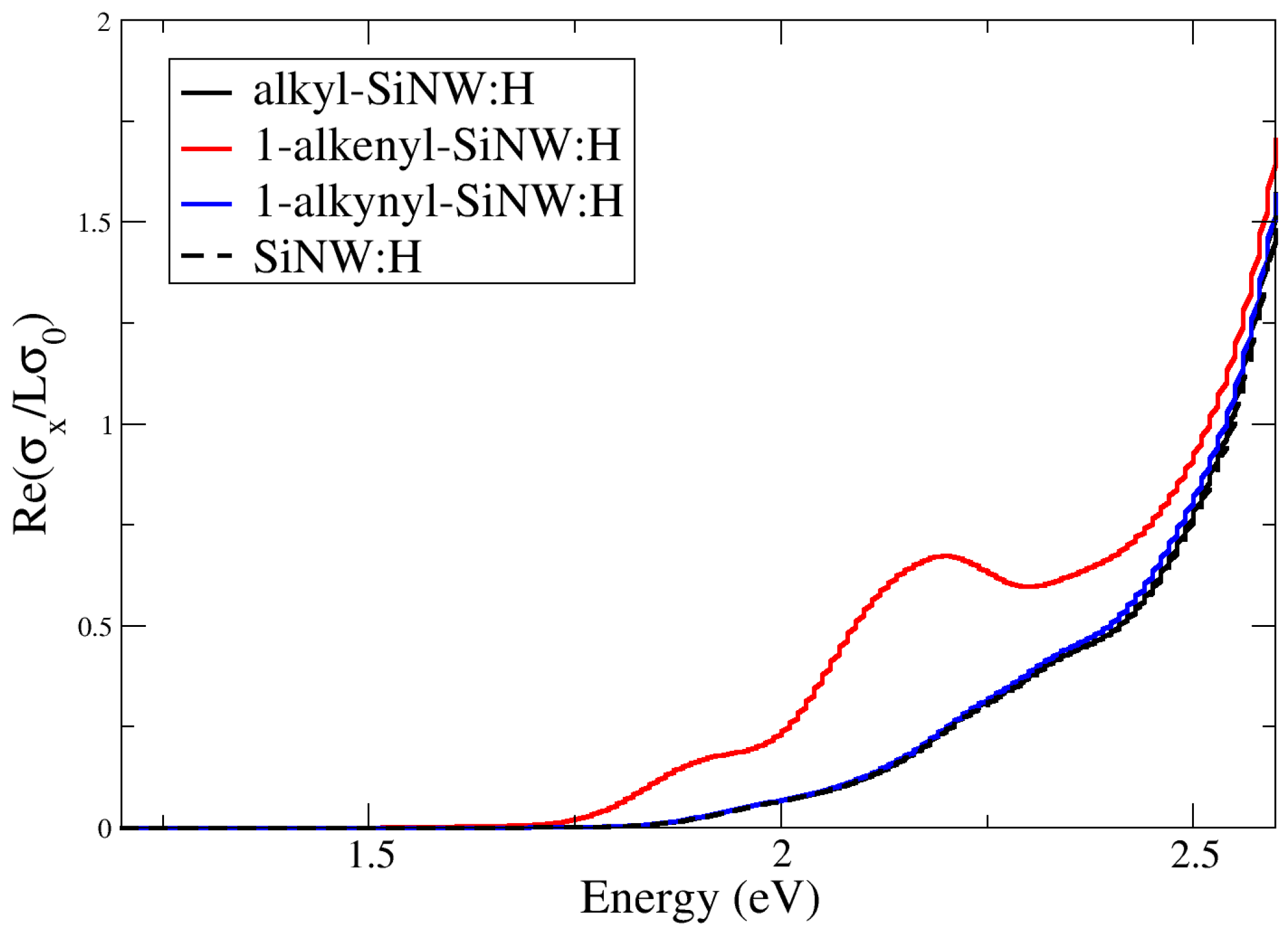
3.4. Optical Properties of Aliphatic Moieties Chemisorbed on SiNW:H
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BDE | Bond Dissociation Energy |
| HOMO | Highest Occupied Molecular Orbital |
| LUMO | Lowest Unoccupied Molecular Orbital |
| SiNW | Silicon NanoWire |
| SiNW:H | H-terminated Silicon NanoWire |
| DFT | Density Functional Theory |
| PBE | Perdew, Burke and Enzerholf exchange-correlation |
| GGA | Generalized Gradient Approximation |
| PDOS | Projected Density of States |
| VBM | Valence Band Maximum |
| CBM | Conduction Band Minimum |
| ZPE | Zero-Point Energy |
References
- Long, Y.-Z.; Yu, M.; Sun, B.; Gu, C.-Z.; Fan, Z. Recent Advances in Large-Scale Assembly of Semiconducting Inorganic Nanowires and Nanofibers for Electronics, Sensors and Photovoltaics. Chem. Soc. Rev. 2012, 41, 4560. [Google Scholar] [CrossRef]
- Zhou, W.; Dai, X.; Fu, T.-M.; Xie, C.; Liu, J.; Lieber, C.M. Long Term Stability of Nanowire Nanoelectronics in Physiological Environments. Nano Lett. 2014, 14, 1614–1619. [Google Scholar] [CrossRef]
- Shalabny, A.; Buonocore, F.; Celino, M.; Shalev, G.; Zhang, L.; Wu, W.; Li, P.; Arbiol, J.; Bashouti, M.Y. Semiconductivity Transition in Silicon Nanowires by Hole Transport Layer. Nano Lett. 2020, 20, 8369–8374. [Google Scholar] [CrossRef]
- Laajimi, R.; Laajimi, K.; Rahmani, M. High-Precision Machine Learning Analysis of Photoluminescence and I-V Measurements in SiNWs-Based Schottky Diodes. J. Lumin. 2025, 286, 121379. [Google Scholar] [CrossRef]
- Puglisi, R.A.; Di Franco, S.; La Magna, A.; Buongiorno, C.; Garozzo, C. Mannino Giovanni Molecular Doping Applied to Si Nanowires Array Based Solar Cells. Sol. Energy Mater. Sol. Cells 2014, 132, 118–122. [Google Scholar] [CrossRef]
- Sahoo, M.K.; Kale, P. Integration of Silicon Nanowires in Solar Cell Structure for Efficiency Enhancement: A Review. J. Mater. 2019, 5, 34–48. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, W.; Kang, W.; Ye, Y.; Pan, Q.; Zhang, X.; Ke, Y.; Wang, C.; Qui, Z.; Tang, Y. A Review on Silicon Nanowire Based Anodes for Next-Generation High-Performance Lithium-Ion Batteries from a Material-Based Perspective. Sustain. Energy Fuels 2020, 4, 1577–1594. [Google Scholar] [CrossRef]
- Kato, S.; Kurokawa, Y.; Gotoh, K.; Soga, T. Silicon Nanowire Heterojunction Solar Cells with an Al2O3 Passivation Film Fabricated by Atomic Layer Deposition. Nanoscale Res. Lett. 2019, 14, 99. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Chandran, K.S.R. A Critical Review of Silicon Nanowire Electrodes and Their Energy Storage Capacities in Li-Ion Cells. RSC Adv. 2023, 13, 3947–3957. [Google Scholar] [CrossRef]
- Farid, G.; Amade-Rovira, R.; Ma, Y.; Ospina, R.; Serafin, J.; Chaitoglou, S.; Majumdar, S.; Poveda, A.; Bertran-Serra, E. Improving Lithium-Ion Battery Performance through Patterned Growth of Carbon Nanotubes over Vertically Aligned Silicon Nanowires. J. Energy Storage 2024, 101, 113830. [Google Scholar] [CrossRef]
- Coffinier, Y.; Boukherroub, R. Chapter 3. Surface Modification of Silicon Nanowires for Biosensing. In Semiconducting Silicon Nanowires for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 25–68. [Google Scholar] [CrossRef]
- Izuan, J.; Rashid, A.; Abdullah, J.; Yusof, N.A.; Hajian, R. The Development of Silicon Nanowire as Sensing Material and Its Applications. J. Nanomater. 2013, 2013, 328093. [Google Scholar] [CrossRef]
- Keribi, M.; Nafie, N.; Boujmil, M.F.; Bouaicha, M. Response Modulation of Silicon Nanowires-Based Sensor to Carbon Number in Petroleum Vapor Detection. Fuel 2021, 304, 121260. [Google Scholar] [CrossRef]
- Ahoulou, S.; Perret, E.; Nedelec, J.-M. Functionalization and Characterization of Silicon Nanowires for Sensing Applications: A Review. Nanomaterials 2021, 11, 999. [Google Scholar] [CrossRef]
- Aradi, B.; Ramos, L.E.; Deák, P.; Köhler, T.; Bechstedt, F.; Zhang, R.Q.; Frauenheim, T. Theoretical Study of the Chemical Gap Tuning in Silicon Nanowires. Phys. Rev. B 2007, 76, 035305. [Google Scholar] [CrossRef]
- Schmidt, V.; Wittemann, J.V.; Senz, S.; Gösele, U. Silicon Nanowires: A Review on Aspects of Their Growth and Their Electrical Properties. Adv. Mater. 2009, 21, 2681–2702. [Google Scholar] [CrossRef]
- Priolo, F.; Gregorkiewicz, T.; Galli, M.; Krauss, T.F. Silicon Nanostructures for Photonics and Photovoltaics. Nat. Nanotechnol. 2014, 9, 19–32. [Google Scholar] [CrossRef]
- Ninno, D.; Iadonisi, G.; Buonocore, F. Carrier Localization and Photoluminescence in Porous Silicon. Solid State Commun. 1999, 112, 521–525. [Google Scholar] [CrossRef]
- Bashouti, M.Y.; Stelzner, T.; Berger, A.; Christiansen, S.; Haick, H. Chemical Passivation of Silicon Nanowires with C1−C6 Alkyl Chains through Covalent Si−C Bonds. J. Phys. Chem. C 2008, 112, 19168–19172. [Google Scholar] [CrossRef]
- Banerjee, D.; Benavides, J.A.; Guo, X.; Cloutier, S.G. Tailored Interfaces of the Bulk Silicon Nanowire/TiO2 Heterojunction Promoting Enhanced Photovoltaic Performances. ACS Omega 2018, 3, 5064–5070. [Google Scholar] [CrossRef]
- Bashouti, M.Y.; Sardashti, K.; Schmitt, S.W.; Pietsch, M.; Ristein, J.; Haick, H.; Christiansen, S.H. Oxide-Free Hybrid Silicon Nanowires: From Fundamentals to Applied Nanotechnology. Prog. Surf. Sci. 2013, 88, 39–60. [Google Scholar] [CrossRef]
- Veerbeek, J.; Huskens, J. Applications of Monolayer-Functionalized H-Terminated Silicon Surfaces: A Review. Small Methods 2017, 1, 1700072. [Google Scholar] [CrossRef]
- Bashouti, M.Y.; Stelzner, T.; Christiansen, S.; Haick, H. Covalent Attachment of Alkyl Functionality to 50 Nm Silicon Nanowires through a Chlorination/Alkylation Process. J. Phys. Chem. C 2009, 113, 14823–14828. [Google Scholar] [CrossRef]
- Abu Much, R.; Natarajan, P.; Shalabny, A.; Sadhujan, S.; Harilal, S.; Y. Bashouti, M. Heterojunction-Based Hybrid Silicon Nanowires Solar Cell. In Solar Cells; Nayeripour, M., Mansouri, M., Waffenschmidt, E., Eds.; IntechOpen: Rijeka, Croatia, 2020; ISBN 978-1-78984-125-1. [Google Scholar]
- Akbari-Saatlu, M.; Procek, M.; Mattsson, C.; Thungström, G.; Nilsson, H.-E.; Xiong, W.; Xu, B.; Li, Y.; Radamson, H.H. Silicon Nanowires for Gas Sensing: A Review. Nanomaterials 2020, 10, 2215. [Google Scholar] [CrossRef]
- Ng, M.-F.; Sim, L.Y.; Da, H.; Jin, H.; Lim, K.H.; Yang, S.-W. Modulation of the Work Function of Silicon Nanowire by Chemical Surface Passivation: A DFT Study. Theor. Chem. Acc. 2010, 127, 689–695. [Google Scholar] [CrossRef]
- Ma, D.; Chen, J.; Li, J.; Ji, X.; Shi, J.-W. A Review on Passivation Engineering for Improving Photocatalytic Hydrogen Evolution Performance. J. Mater. Chem. A 2024, 12, 12293–12324. [Google Scholar] [CrossRef]
- Natan, A.; Kroni, L.; Haick, H.; Tung, R.T. Electrostatic Properties of Ideal and Non-Ideal Polar Organic Monolayers: Implications for Electronic Devices. Adv. Mater. 2007, 19, 4103–4117. [Google Scholar] [CrossRef]
- Bashouti, M.Y.; Tung, R.T.; Haick, H. Tuning the Electrical Properties of Si Nanowire Field-Effect Transistors by Molecular Engineering. Small 2009, 5, 2761–2769. [Google Scholar] [CrossRef] [PubMed]
- Yoshitake, M. Work Function and Band Alignment of Electrode Materials: The Art of Interface Potential for Electronic Devices, Solar 452 Cells, and Batteries (NIMS Monographs), 1st ed.; (English Edition); Springer: Berlin/Heidelberg, Germany, 2021; pp. 97–112. [Google Scholar]
- Njema, G.G.; Kibet, J.K.; Ngari, S.M. A Review of Interface Engineering Characteristics for High Performance Perovskite Solar Cells. Meas. Energy 2024, 2, 100005. [Google Scholar] [CrossRef]
- Yu, X.; Shen, X.; Mu, X.; Zhang, J.; Sun, B.; Zeng, L.; Yang, L.; Wu, Y.; He, H.; Yang, D. High Efficiency Organic/Silicon-Nanowire Hybrid Solar Cells: Significance of Strong Inversion Layer. Sci. Rep. 2015, 5, 17371. [Google Scholar] [CrossRef] [PubMed]
- Raman, S.; Ravi, S.A.; Sindhuja, M. Advances in Silicon Nanowire Applications in Energy Generation, Storage, Sensing, and Electronics: A Review. Nanothecnology 2023, 34, 182001. [Google Scholar] [CrossRef] [PubMed]
- Buonocore, F.; Marchio, S.; Giusepponi, S.; Celino, M. Computational Insights into the Energetics of Single C2–C10 Aliphatic Moieties Adsorbed on the Hydrogenated Silicon (111) Surface. Langmuir 2025, 41, 9706–9715. [Google Scholar] [CrossRef]
- Ferrucci, B.; Buonocore, F.; Giusepponi, S.; Shalabny, A.; Bashouti, M.Y.; Celino, M. Ab Initio Study of Octane Moiety Adsorption on H- and Cl-Functionalized Silicon Nanowires. Nanomaterials 2022, 12, 1590. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Inhomogeneous Electron Gas 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B Condens. Matter 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Elge Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef]
- Buonocore, F.; Lisi, N.; Pulci, O. Electronic and Optical Properties of Metal Decorated Nitrogen-Doped Vacancy Defects in Graphene. J. Phys. Condens. Matter 2019, 31, 235302. [Google Scholar] [CrossRef] [PubMed]
- Marchio, S.; Buonocore, F.; Giusepponi, S.; Celino, M. Density Functional Theory Study of Silicon Nanowires Functionalized by Grafting Organic Molecules. Mater. Cloud Arch. 2025, 101. [Google Scholar] [CrossRef]
- Rino, J.P.; Ebbsjö, I.; Branicio, P.S.; Kalia, R.K.; Nakano, A.; Shimojo, F.; Vashishta, P. Short- and Intermediate-Range Structural Correlations in Amorphous Silicon Carbide: A Molecular Dynamics Study. Phys. Rev. B 2004, 70, 045207. [Google Scholar] [CrossRef]
- Fox, M.A.; Whitesell, J.K. Organic Chemistry; Jones & Bartlett Learning: Sudbury, MA, USA, 2004. [Google Scholar]
- Haziri, V.; Phal, S.; Boily, J.-F.; Berisha, A.; Tesfalidet, S. Oxygen Interactions with Covalently Grafted 2D Nanometric Carboxyphenyl Thin Films—An Experimental and DFT Study. Coatings 2022, 12, 49. [Google Scholar] [CrossRef]
- Jing, Z.; Whitten, J.L. Ab Initio Studies of H Chemisorption on Si(100) Surface. Phys. Rev. B 1992, 46, 9544. [Google Scholar] [CrossRef]
- Bruno, M.; Palummo, M.; Marini, A.; Del Sole, R.; Ossicini, S. From Si Nanowires to Porous Silicon: The Role of Excitonic Effects. Phys. Rev. Lett. 2007, 98, 036807. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Dvorak, M.; Wu, Z. Hybrid Functionals with Fixed Mixing Parameter Perform No Better than PBE for Fundamental Band Gaps of Nanoscale Materials. Phys. Rev. B 2016, 94, 195429. [Google Scholar] [CrossRef]
- Capelle, K. A Bird’s-Eye View of Density-Functional Theory. Braz. J. Phys. 2006, 36, 1318–1343. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Koshi, N.A.; Lee, S.-C. Customizing PBE Exchange-Correlation Functionals: A Comprehensive Approach for Band Gap Prediction in Diverse Semiconductors. Phys. Chem. Chem. Phys. 2024, 26, 26443–26452. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Bihlmayer, G.; Björkman, T.; Blaha, P.; Blügel, S.; Blum, V.; Caliste, D.; Castelli, I.E.; Clark, S.J.; Dal Corso, A.; et al. Reproducibility in Density Functional Theory Calculations of Solids. Science 2016, 351, aad3000. [Google Scholar] [CrossRef] [PubMed]
- Bashouti, M.Y.; Garzuzi, C.A.; De La Mata, M.; Arbiol, J.; Ristein, J.; Haick, H.; Christiansen, S. Role of Silicon Nanowire Diameter for Alkyl (Chain Lengths C1–C18) Passivation Efficiency through Si–C Bonds. Langmuir 2015, 31, 2430–2437. [Google Scholar] [CrossRef] [PubMed]
- Rogozhina, E.V.; Eckhoff, D.A.; Gratton, E.; Braun, P.V. Carboxyl Functionalization of Ultrasmall Luminescent Silicon Nanoparticles through Thermal Hydrosilylation. J. Mater. Chem. 2006, 16, 1421. [Google Scholar] [CrossRef]
- Molteni, E.; Cappellini, G.; Cardia, R.; Onida, G.; Mula, G. Eumelanin Adsorption on Silicon: Optical Properties of Si(001)-Adsorbed Eumelanin Tetrameric Protomolecules. J. Phys. Chem. C 2020, 124, 9376–9384. [Google Scholar] [CrossRef]
- He, L.; Jiang, C.; Wang, H.; Lai, D. Si Nanowires Organic Semiconductor Hybrid Heterojunction Solar Cells Toward 10% Efficiency. ACS Appl. Mater. Interfaces 2012, 4, 1704–1708. [Google Scholar] [CrossRef]
- Shen, X.; Ma, B.; Chen, L.; Zhao, J. High Efficiency Conjugated Polymer/Si Hybrid Solar Cells with Tetramethylammonium Hydroxide Treatment. RSC Adv. 2017, 7, 688–693. [Google Scholar] [CrossRef]
- Cullis, A.G.; Canham, L.T.; Calcott, P.D.J. The Structural and Luminescence Properties of Porous Silicon. J. Appl. Phys. 1997, 82, 909–965. [Google Scholar] [CrossRef]
- Iannone, F.; Ambrosino, F.; Bracco, G.; De Rosa, M.; Funel, A.; Guarnieri, G.; Migliori, S.; Palombi, F.; Ponti, G.; Santomauro, G.; et al. CRESCO ENEA HPC Clusters: A Working Example of a Multifabric GPFS Spectrum Scale Layout. In Proceedings of the 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; pp. 1051–1052. [Google Scholar]
- Mariano, A.; D’Amato, G.; Ambrosino, F.; Aprea, G.; Buonocore, F.; Celino, M.; Colavincenzo, A.; Fina, M.; Funel, A.; Giusepponi, S.; et al. Fast Access to Remote Objects 2.0 a Renewed Gateway to ENEAGRID Distributed Computing Resources. Future Gener. Comput. Syst. 2019, 94, 920–928. [Google Scholar] [CrossRef]

| NW Structure | θ(C1C8) | θ(C1C2) | d(C1C2) | d(C1Si) | BDE |
|---|---|---|---|---|---|
| alkyl-SiNW:H (111) | 36.43 | 60.87 | 1.53 | 1.91 | 602.82 |
| 1-alkenyl-SiNW:H (111) | 35.19 | 55.13 | 1.36 | 1.87 | 712.99 |
| 1-alkynyl-SiNW:H (111) | 66.50 | 22.34 | 1.23 | 1.82 | 814.55 |
| alkyl-SiNW:H (110) | 3.54 | 32.77 | 1.53 | 1.91 | 600.08 |
| 1-alkenyl-SiNW:H (110) | 34.84 | 47.78 | 1.36 | 1.86 | 712.00 |
| 1-alkynyl-SiNW:H (110) | 56.12 | 28.55 | 1.23 | 1.82 | 820.83 |
| Moiety | HOMO | LUMO | HOMO-LUMO Gap |
|---|---|---|---|
| alkyl C8 | −2.75 | 2.70 | 5.45 |
| 1-alkenyl C8 | −0.30 | 1.90 | 2.20 |
| 1-alkynyl C8 | −1.45 | 3.10 | 4.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buonocore, F.; Ferrucci, B.; Marchio, S.; Giusepponi, S.; Sadhujan, S.; Abu-Hilu, M.; Bashouti, M.Y.; Celino, M. Optoelectronic Properties of Hydrogen-Terminated Silicon Nanowires via Aliphatic C8 Moieties: Impact of C–C Bond Order from First Principles. Appl. Sci. 2025, 15, 10235. https://doi.org/10.3390/app151810235
Buonocore F, Ferrucci B, Marchio S, Giusepponi S, Sadhujan S, Abu-Hilu M, Bashouti MY, Celino M. Optoelectronic Properties of Hydrogen-Terminated Silicon Nanowires via Aliphatic C8 Moieties: Impact of C–C Bond Order from First Principles. Applied Sciences. 2025; 15(18):10235. https://doi.org/10.3390/app151810235
Chicago/Turabian StyleBuonocore, Francesco, Barbara Ferrucci, Sara Marchio, Simone Giusepponi, Sumesh Sadhujan, Musa Abu-Hilu, Muhammad Y. Bashouti, and Massimo Celino. 2025. "Optoelectronic Properties of Hydrogen-Terminated Silicon Nanowires via Aliphatic C8 Moieties: Impact of C–C Bond Order from First Principles" Applied Sciences 15, no. 18: 10235. https://doi.org/10.3390/app151810235
APA StyleBuonocore, F., Ferrucci, B., Marchio, S., Giusepponi, S., Sadhujan, S., Abu-Hilu, M., Bashouti, M. Y., & Celino, M. (2025). Optoelectronic Properties of Hydrogen-Terminated Silicon Nanowires via Aliphatic C8 Moieties: Impact of C–C Bond Order from First Principles. Applied Sciences, 15(18), 10235. https://doi.org/10.3390/app151810235







