Parameter Variance of the Duncan Formula for Nonlinear Shear Strength of Coarse-Grained Soil

Abstract

The reliability analysis of slope stability is significantly influenced by the variance of the soil’s shear strength. Currently, the shear strength of coarse-grained soil is commonly determined using the Duncan formula, which establishes a relationship between the shear strength and confining pressure. Specifically, the parameters of the Duncan formula are estimated based on available test data using least squares regression, which mitigates the limitations associated with small sample sizes and significant errors in the classic grouped data method. However, hypothesis testing in mathematical statistics reveals that the residuals from the classic least squares estimation exhibit heteroscedasticity and correlation, violating the fundamental assumptions required for least squares regression. Consequently, parameter estimates obtained through classic least squares regression have large variances, leading to unreliable statistical inferences. To address this issue, we propose a generalized least squares method that eliminates the heteroscedasticity and correlation of the residuals. Triaxial test data for five different coarse-grained soils are analyzed using the proposed method. The results show that the mean values of the estimated parameters of the Duncan formula are close to those obtained using the classic method, while their variances are significantly reduced, demonstrating the effectiveness of the proposed approach. The reliability analysis of the anti-sliding stability of an infinitely long slope shows that the strength parameters estimated by the classical least squares method tend to underestimate the stability of the slope due to the large variance. Therefore, the Duncan nonlinear shear strength parameters of coarse-grained soils should be estimated using the generalized least squares method that eliminates the heteroscedasticity and correlation of the regression residuals.

1. Introduction

Based on the reliability theory, the limit state design method has become a development trend in current geotechnical engineering design methods. Its core design concept is to regard various uncertainties of geotechnical structures as random variables, such as material strengths, loads, and calculation models, and to measure the reliability of structural safety using probability methods. Finally, the failure probability of the structure is controlled within an acceptable level. Studying the reliability of geotechnical structures’ safety, the mean and variance of the shear strength of geotechnical materials as input data have a significant impact on the results. However, the cost of geotechnical tests is high, and the dispersion of test results is large. In an engineering project, the number of geotechnical samples is limited. Therefore, the mechanical parameters of geotechnical materials are generally obtained by statistically analyzing the parameters of geotechnical samples with similar properties from multiple engineering projects. In this way, for the design of a specific project, the probability distribution of the parameters and the accuracy of the expectation and variance are relatively low, which affects the reliability calculation results. Therefore, improving the statistical accuracy of geotechnical engineering mechanical parameters and accurately evaluating their variability is the prerequisite for designing geotechnical engineering based on the reliability theory.

Coarse-grained soil has the advantages of easy accessibility, low cost, and high permeability and is therefore widely utilized in engineering projects such as roads, earth–rock fill dams, land reclamation, and high-fill airports. Since its shear strength directly affects engineering safety and investment, the strength parameters are key parameters [1]. Currently, the shear strength of soil is mostly calculated using the Mohr–Coulomb formula. However, numerous tests on coarse-grained soils have shown that in a wide range of confining pressures, its shear strength no longer remains linear. Based on the Duncan–Chang stress–strain model, a formula for the shear strength of coarse-grained soil was proposed by Duncan to replace the original linear Mohr–Coulomb strength formula. This has been widely applied in the analysis of high earth–rock dams [2,3,4,5,6,7].

Additionally, the design value of the shear strength is obtained by dividing the characteristic value by the partial coefficient in civil engineering. The guidelines for determining the characteristic value of soil shear strength vary among different standards. For instance, the Design Code for Rolled Earth-Rock Fill Dams [8,9] (SL274-2020, NB/T10872-2021) stipulate that the average value of the sample values with a strength less than the overall average of the shear strength is taken as the characteristic value, i.e., the 0.25th percentile of the probability distribution. These specifications also define the required number of test groups: for fine-grained soils, at least 11 groups are required, and each group contains 4–6 confining pressure levels. For coarse-grained soil, NB/T10872-2021 mandates a minimum of six test groups, whereas SL274-2020 requires at least eleven groups for both fine-grained soils and coarse-grained soils [8]. The Unified Standard for Reliability Design of Hydraulic Engineering Structures [10] recommends using the 0.1 quantile of the probability distribution as the characteristic value for the strength of geotechnical materials and artificial foundations. In addition, the Code for Investigation of Geotechnical Engineering [11] specifies that the characteristic value of a geotechnical parameter should be based on the one-sided confidence limit of the confidence interval for the mean value of the parameter matrix, which is derived using the statistical interval estimation theory. By simplifying this approach, the relationship between the standard value ${\varphi }_k$ and the mean value ${\varphi }_m$ can be expressed as

$${\varphi }_k={\gamma }_s{\varphi }_m,{\gamma }_s=1\pm \left({\displaystyle \frac{1.704}{n^{1/2}}}+{\displaystyle \frac{4.678}{n^2}}\right)\delta$$

(1)

where $\delta$ is the coefficient of variation, which is the ratio of the standard deviation to the mean. n is the number of groups.

Obviously, both the mean value and the variance are directly incorporated into the calculation of the characteristic value of shear strength. Therefore, for engineering applications, the mean value and variance (or standard deviation) of the soil’s shear strength are equally important [12].

2. Nonlinear Shear Strength of Coarse-Grained Soil

The shear strength of soil is generally described by the Mohr–Coulomb theory:

$${\tau }_f={\sigma }_n\tan \phi +c\mathrm{or} {\sigma }_1={\sigma }_3{\tan }^2(\phi /2+{45}^{°})+2c\tan (\phi /2+{45}^{°})$$

(2)

where ${\tau }_f$ is the shear strength of the soil, ${\sigma }_n$ is the normal stress on the shear plane, $c$ and $\phi$ are the cohesion and friction angle of the soil, and ${\sigma }_1$ and ${\sigma }_3$ are the major and minor principal stresses at the limit equilibrium failure point in the triaxial test.

Typically, the parameters $c$ and $\phi$ are assumed to be constants. However, for coarse-grained soil, the shear strength exhibits strong nonlinearity; hence, it is necessary to define these parameters within a limited confining pressure range. In contrast to the linear relationship observed under low confining pressure conditions, under high confining pressure conditions, the strength envelope deviates from a straight line. To characterize the shear strength of coarse-grained soil across a wide confining pressure range, the following approaches have been employed in engineering practices. The first method involves a segmented description, in which different values of $c$ and $\phi$ are used for low (typically 100–800 kPa) and high confining pressure conditions. Another approach directly models the curved envelope of the shear strength, such as the Demeler formula ${\tau }_f=A{\sigma }^m$ and the Duncan formula

$$\phi ={\phi }_0-\Delta \phi \lg \left({\sigma }_3/P_a\right)$$

(3)

where $A$ and $m$ are the shear strength coefficient and exponent, ${\phi }_0$ is the friction angle when the confining pressure is equal to the standard atmosphere, and $\Delta \phi$ is the decrease in the friction angle when the confining pressure ${\sigma }_3$ increases by 10 times. According to the experimental data of the triaxial test, the friction angle is expressed as

$$\phi ={\sin }^{-1}\left({\displaystyle \frac{{\sigma }_1-{\sigma }_3}{{\sigma }_1+{\sigma }_3}}\right)$$

(4)

There are two methods for determining nonlinear strength parameters. In the first method, the strength parameters ${\phi }_0$ and $\Delta \phi$ are determined based on the test groups, and then average the values that are less than the overall average, i.e., the minimum average values are determined. In the second method, the minimum average values, which average the values that are less than the overall average of $({\sigma }_1-{\sigma }_3)$ and $({\sigma }_1+{\sigma }_3)$ under each confining pressure, are determined firstly, and then the friction angle is calculated based on Equation (4). Finally, the strength parameters are determined based on the Duncan formula. The parameters derived using these two methods differ, and both methods suffer from an insufficient number of grouped samples, leading to large errors and a low accuracy for intermediate transition variables. To address this issue, all test data should be utilized, and the least squares method should be used to directly estimate the nonlinear strength parameters [13,14].

The linear regression for estimating Duncan’s nonlinear shear strength parameters of coarse-grained soil:

$$\phi ={\phi }_0-\Delta \phi \lg \left({\displaystyle \frac{{\sigma }_3}{P_a}}\right)$$

(5)

where $\lg ({\sigma }_3/P_a)$ is the independent variable, which is a non-random variable; $\phi$ is the dependent variable, which is a random variable; ${\phi }_0$ and $-\Delta \phi$ are the parameters to be determined.

The prerequisite of this method is that the regression residuals meet the requirements of classic least squares estimation [15,16].

3. Triaxial Tests Data

Triaxial tests were conducted on the coarse-grained soil of Zone I and Zone II of Project A, the coarse-grained soil of Zone I and Zone II of Project B, and the gravelly clay materials of Project C. The differences in the major and minor principal stresses when the specimens failed under different confining pressures were obtained for five types of soil materials from several sets of parallel tests. The failure stresses of the materials in Zone I of Project A under different confining pressures are shown in

Table 1. The difference in principal stress during the triaxial test of the coarse-grained soil in Zone I of Project A.

Confining Pressure /kPa	$\mathbf{The} \mathbf{Stress} \mathbf{Difference} \mathbf{at} \mathbf{Failure} \mathbf{of} \mathbf{the} \mathbf{Triaxial} \mathbf{Specimen} ({\mathit{\sigma }}_1-{\mathit{\sigma }}_3)$/ kPa
	Parallel Test 1	Parallel Test 2	Parallel Test 3	Parallel Test 4	Parallel Test 5	Parallel Test 6	Parallel Test 7	Parallel Test 8	Parallel Test 9	Parallel Test 10	Parallel Test 11	Parallel Test 12
100	979.24	908.26	968.75	958.37	1008.00	1368.90	934.15	1378.89	1080	1060	1008	955
300	1863.85	1711.81	1818.61	1920.27	1908.00	1968.48	1614.03	1928.32	2039	1867	1872	2016
500	2651.12	2459.99	2859.49	2711.49	2742.65	2748.72	2625.07	2660.23	2767	2591	2624	2645
900	2914.24	3043.51	4001.88	3860.73	4018.00	4056.18	3917.43	4103.32	4021	4050	4091	3965
1500	4977.72	5025.87	6116.27	6011.95	5988.61	6018.22	5929.32	5975.73	5982	6301	5825	5965
2500	8640.77	8712.00	9214.46	8920.52	9360.46	9541.40	8687.61	9245.17	9101	9199	8969	9146

, and the friction angles can be determined based on the failure stresses of each parallel test under different confining pressures, as shown in

Table 2. The friction angles of the coarse-grained soil in Zone I of Project A at different confining pressures.

Confining Pressure /kPa	$\mathbf{The} \mathbf{Friction} \mathbf{Angle}/°$
	Parallel Test 1	Parallel Test 2	Parallel Test 3	Parallel Test 4	Parallel Test 5	Parallel Test 6	Parallel Test 7	Parallel Test 8	Parallel Test 9	Parallel Test 10	Parallel Test 11	Parallel Test 12
100	56.140	55.038	55.984	55.827	56.557	60.753	55.453	60.848	57.538	57.274	56.557	55.775
300	49.155	47.771	48.757	49.635	49.532	50.032	46.803	49.702	50.592	49.182	49.225	50.412
500	46.561	45.315	47.808	46.934	47.122	47.159	46.398	46.618	47.268	46.181	46.391	46.523
900	38.183	38.930	43.611	43.002	43.679	43.839	43.249	44.034	43.691	43.813	43.983	43.454
1500	38.605	38.771	42.138	41.844	41.778	41.862	41.608	41.741	41.759	42.645	41.304	41.710
2500	39.305	39.446	40.409	39.853	40.679	41.007	39.398	40.467	40.197	40.381	39.946	40.281

. The test results of other projects are not listed due to the limitations of the article’s length. It can be seen from these tables that a total of 12 sets of triaxial tests were conducted on the coarse-grained soil of Zone I of Project A, with six levels of confining pressure for each set test, which are 100, 300, 500, 900, 1500, and 2500 kPa, respectively.

4. Classic Least Squares Estimation

The linear regression model is as follows:

$${\left(\phi \right)}_i={\phi }_0-\Delta \phi {\left[\lg \left({\sigma }_3/P_a\right)\right]}_i+e_i,(i=1,2,\dots ,n)$$

(6)

where $e_i$ is the residual term or the error term, which represents the influences of factors other than $\left[\lg \left({\sigma }_3/P_a\right)\right]$ on the friction angle ($\phi$) and the measurement error.

If the residual term $e_i(i=1,2,\dots ,n)$ satisfies the following three conditions, then the least squares regression is valid: (a) The mathematical expectation is $E(e_i)=0$; (b) the residuals under different confining pressures have equal variances, that is, $Var(e_i)={\sigma }^2$,$(i=1,2,\dots ,m)$, where m is the number of levels of confining pressure; and (c) the residuals under different confining pressures are uncorrelated, that is, $Cov(e_i,e_j)=0$, $i\ne j$. The above is the Gauss–Markov hypothesis.

The least squares method finds estimates of ${\phi }_0$ and $-\Delta \phi$ that minimize the square of the length of the residual vector $e={\left(\phi \right)}_i-\left\{{\phi }_0-\Delta \phi {[\lg ({\sigma }_3/P_a)]}_i\right\}$, i.e.,${‖{\left(\phi \right)}_i-\left\{{\phi }_0-\Delta \phi {\left[\lg \left({\sigma }_3/P_a\right)\right]}_i\right\}‖}^2$.

By expanding this formula and taking partial derivatives with respect to ${\phi }_0$ and $-\Delta \phi$, and then setting them equal to zero, ${\phi }_0$ and $-\Delta \phi$ can be obtained.

$$\begin{gathered} {\left[\lg \left({\sigma }_3/P_a\right)\right]}_i=x_i, {\left(\phi \right)}_i=y_i, {\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{x}_i}=\overline{x}, {\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{y}_i}=\overline{y} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\Delta \phi ={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}}{{{\displaystyle {\sum }_{i=1}^n(x_i-\overline{x})}}^2}} \\ \hspace{1em}{\phi }_0=\overline{y}+\Delta \phi \overline{x} \end{gathered}$$

(7)

By substituting n sets of observation data $\left({\left[\lg \left({\sigma }_3/P_a\right)\right]}_i,{\left(\phi \right)}_i\right)$ into the above equation, we can obtain estimated values of ${\phi }_0$ and $-\Delta \phi$.

5. Homogeneity of Variance and Correlation Test of the Residuals of the Duncan Formula Estimated via Least Squares Regression

Currently, the prerequisite of the least squares method is generally not tested when determining the shear strength parameters of soil. Chen et al. [13,17,18] noticed the heteroscedasticity of the regression residuals and proposed that the weighted least squares method be applied to improve the regression. The weighting coefficient is $w_i=1/{\left(\alpha +\beta x_i\right)}^2$, and $\alpha$ and $\beta$ are obtained via linear regression of the residuals and independent variables. This approach partially eliminates the heteroscedasticity of the residuals, but it does not fundamentally solve the problem. In the regression method recommended by the specification, i.e., $q={\displaystyle \frac{{\sigma }_1-{\sigma }_3}{2}}$, the independent variable $p={\displaystyle \frac{{\sigma }_1+{\sigma }_3}{2}}$ is also a random variable. Based on this characteristic, Yu et al. [19] proposed that the orthogonal least squares method be applied to correct the shear strength estimated based on the regression using $p-q$. The above methods only involve regressions of the parameters of the Mohr–Coulomb formula. To the best of our knowledge, the heteroscedasticity and correlation of the residuals in the regression of the nonlinear shear strength of coarse-grained soil has not been studied.

5.1. Regression Residuals and the Covariance Matrix

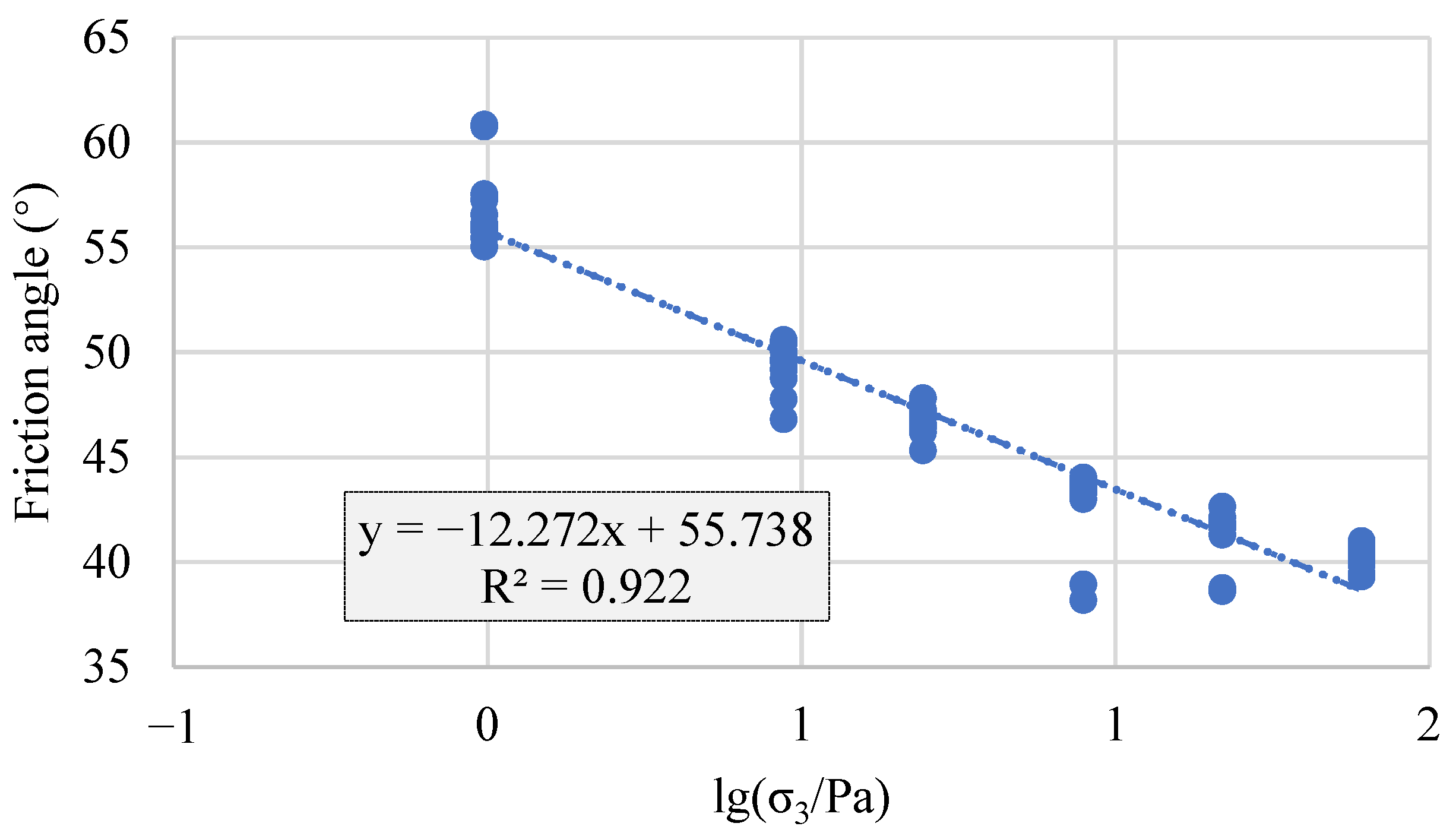
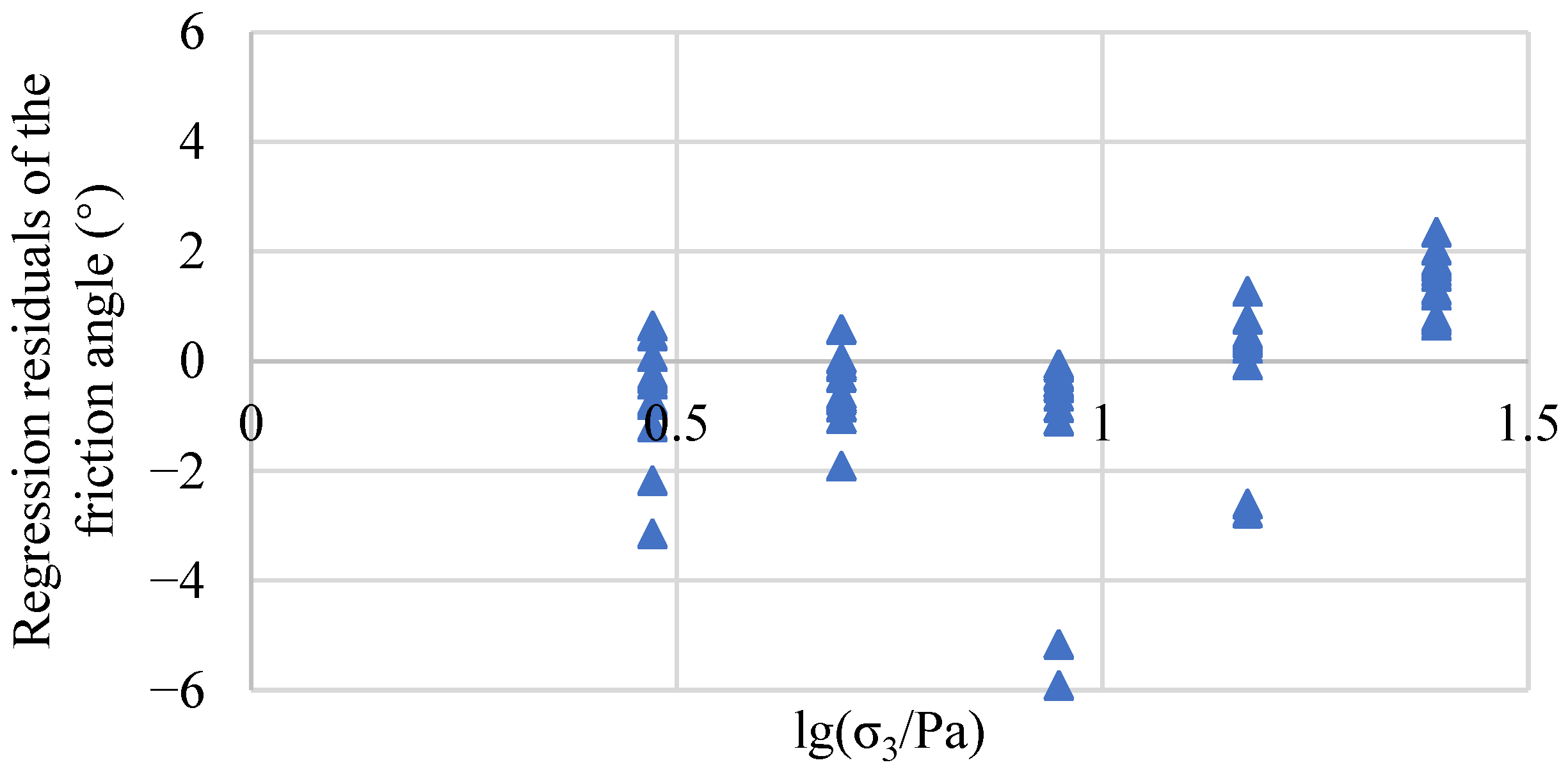
Based on the test results for several coarse-grained soils, the nonlinear shear strength was determined to examine the heteroscedasticity and correlation of the residuals in the nonlinear strength regression. Specifically, in the triaxial test on coarse-grained soil from Zone I of Project A, the regression equation is shown in Figure 1, and the regression residuals are shown in Figure 2. As can be seen from Figure 2, the distribution of the residuals varies across the different confining pressures; the distribution of residuals is not the same when the confining pressure is different, indicating that the variance of residuals will also be different when the distribution is different. To determine whether the residuals under the six confining pressures are correlated, it is necessary to test the covariance matrix of the residuals. The residual covariance matrix was calculated as follows:

$$Cov(e_i,e_j)=\left[\begin{array}{cccccc}3.685& 0.969& 0.331& 1.591& 0.82& 0.688\\ 0.969& 1.147& 0.308& 0.747& 0.438& 0.353\\ 0.331& 0.308& 0.402& 0.641& 0.432& 0.188\\ 1.591& 0.747& 0.641& 4.02& 2.432& 0.754\\ 0.82& 0.438& 0.432& 2.432& 1.607& 0.468\\ 0.688& 0.353& 0.188& 0.754& 0.468& 0.286\end{array}\right]$$

(8)

It can be seen that the main diagonal elements of the residual covariance matrix are not equal, and the non-diagonal elements are not zero. Based on this, it can be reasonably concluded that the residuals have heteroscedasticity and correlation. However, in order to more accurately determine whether the regression residuals satisfy homoscedasticity and independence, a hypothesis test is required.

First, the Kolmogorov–Smirnov (K-S) method was applied to test whether the residuals as a whole satisfy the assumption of a normal distribution. Next, assuming that the ratio of the variances of the regression residuals at each confining pressure level follows the F-distribution, the sample variance at each confining pressure was calculated to test whether the residual variances were consistent across different confining pressures under a certain probability level. This step corresponds to the variance homogeneity test. Finally, the correlation of the regression residuals under different confining pressure levels was examined.

5.2. K-S Test for Normal Distribution of Regression Residuals

(1) The null hypothesis is $H_0:F(x)=F_0(x)$ and the alternative hypothesis is $H_1:F(x)\ne F_0(x)$, where $F_0(x)$ is the given normal distribution function. (2) The test statistic $D_n=\sup \left|F_n(x)-F(x)\right|$ is selected as the principal variable. When the null hypothesis is true, the test statistic is $D_n=\sup \left|F_n(x)-F_0(x)\right|$. At the significance level $\mathsf{\alpha }$, if $\sqrt{n}{D}_n>k$, then the null hypothesis is rejected, where $k$ is an appropriate constant. Kolmogorov derived the limiting distribution of $\sqrt{n}{D}_n$ and tabulated it. (3) The rejection region is determined. For a given significance level $\mathsf{\alpha }$ that satisfies $P(\sqrt{n}{D}_n>t_{\alpha })=\alpha$, the quantile $t_{\alpha }$ is the critical value, and the rejection region is $\left[t_{\alpha },+\infty \right)$.

Table 3. Least squares regression residuals and the residual variances.

Confining Pressure (kPa)	Friction Angle Residual (°)												Variance
100	0.332	−0.77	0.175	0.019	0.749	4.945	−0.356	5.04	1.73	1.466	0.749	−0.033	3.685
300	−0.798	−2.182	−1.196	−0.318	−0.421	0.079	−3.15	−0.251	0.639	−0.771	−0.728	0.459	1.147
500	−0.669	−1.916	0.578	−0.296	−0.108	−0.071	−0.833	−0.612	0.038	−1.05	−0.84	−0.707	0.402
900	−5.914	−5.168	−0.487	−1.096	−0.419	−0.259	−0.848	−0.064	−0.406	−0.285	−0.114	−0.644	4.02
1500	−2.77	−2.604	0.763	0.469	0.403	0.487	0.233	0.366	0.384	1.27	−0.071	0.335	1.607
2500	0.653	0.794	1.757	1.2	2.026	2.355	0.746	1.814	1.544	1.728	1.293	1.629	0.286

presents the regression residuals for the coarse-grained granite from Zone I of Project A under various confining pressure conditions. The mean and standard deviation of all of the residuals are 2.6659 $\times$ 10⁻⁴ and 1.6573. For a significance level of 0.01, $P(\sqrt{n}{D}_n>t_{0.01})=0.01$ and $t=1.63$, which is taken as an approximate value of $t_{0.01}$. Then, the rejection region is $\left[1.63,+\infty \right)$. $D_n=\max (d_{01},d_{02})=0.1782$.

Because $\sqrt{n}{D}_n=\sqrt{72}\times 0.1782=1.5119$, and it falls outside the rejection region $\left[1.63,+\infty \right)$, we accept the hypothesis that the regression residuals of the shear strength are normally distributed.

5.3. Homogeneity Test of Regression Residuals Under Different Confining Pressure Conditions

Theoretical studies have shown that the F-test is sensitive to deviations from the homogeneity of variance, making it suitable for testing the variance of residuals under different confining pressures. The null hypothesis H₀ and alternative hypothesis H₁ are

$H_0:{\sigma }_1^2={\sigma }_2^2=\dots ={\sigma }_k^2$ and $H_1:{\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_k^2$ and are not all equal.

Determine the rejection region.

Let $\alpha =0.05$,

$$P\left(F\le F_{1-{\displaystyle \frac{\alpha }{2}}}\left(n_1-1,n_2-1\right)\right)={\displaystyle \frac{\alpha }{2}}, P\left(F\ge F_{{\displaystyle \frac{\alpha }{2}}}\left(n_1-1,n_2-1\right)\right)={\displaystyle \frac{\alpha }{2}}$$

(9)

$$P\left({\displaystyle \frac{S_1^2}{S_2^2}}\le F_{0.975}\left(11,11\right)\right)=0.025,$$

$$F_{0.975}\left(11,11\right)={\displaystyle \frac{1}{F_{0.025}\left(11,11\right)}}={\displaystyle \frac{1}{3.48}}=0.287356,$$

and

$$F_{0.025}\left(11,11\right)=3.48.$$

Then, the rejection region is $\left(0,0.2874\right]$ and $\left[3.48,+\infty \right)$.

Table 4. Ratio of variance of least squares regression residuals under different confining pressures.

Confining Pressure (kPa)	100	300	500	900	1500	2500
100	1	-	-	-	-	-
300	0.311/$\surd$	1	-	-	-	-
500	0.109/$\times$	0.351/$\surd$	1	-	-	-
900	1.091/$\surd$	3.503/$\times$	9.991/$\times$	1	-	-
1500	0.436/$\surd$	1.4/$\surd$	3.994/$\times$	0.4/$\surd$	1	-
2500	0.078/$\times$	0.249/$\times$	0.71/$\surd$	0.071/$\times$	0.178/$\times$	1

Note: $\surd$ denotes acceptance of the null hypothesis, $\times$ denotes rejection of the null hypothesis.

shows the sample variance ratios of the regression residuals under various confining pressures and whether they are in the rejection region. $\surd$ indicates that the variance ratio is in the acceptance region and the null hypothesis is accepted, while $\times$ indicates that the variance ratio is in the rejection region and the null hypothesis is not accepted.

It can be seen that, except for the diagonal elements where the variance ratio is equal to one, seven of the sample variance ratios of the residuals under different confining pressures are in the acceptance region and eight are in the rejection region. Therefore, the variance homogeneity hypothesis is not accepted.

5.4. Residual Independence Test Under Different Confining Pressure Conditions

Assuming that the regression residuals under different confining pressures are two different random variables U and V, the independence test is equivalent to testing their correlation coefficient $\rho$. The null hypothesis $H_0$ and alternative hypothesis H₁ are $H_0:\rho =0$, and $H_1:\rho \ne 0$. The sample correlation coefficient $R$ is used as the point estimator of $\rho$. $R$ is shown in

Table 5. Calculation of $R$.

Confining Pressure (kPa)	100	300	500	900	1500	2500
100	1	-	-	-	-	-
300	0.471	1	-	-	-	-
500	0.272	0.453	1	-	-	-
900	0.413	0.348	0.504	1	-	-
1500	0.337	0.323	0.537	0.957	1	-
2500	0.67	0.616	0.555	0.704	0.69	1

.

$$R={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n\left(U_i-\overline{U}\right)\left(V_i-\overline{V}\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(U_i-\overline{U}\right)}^2}}\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(V_i-\overline{V}\right)}^2}}}}$$

(10)

When $H_0$ is true,

$$t={\displaystyle \frac{R}{\sqrt{1-R^2}}}\sqrt{n-2}$$

(11)

It follows a t-distribution with degrees of freedom of $n-2$. t can be found in

Table 6. Calculation of t.

Confining Pressure (kPa)	100	300	500	900	1500	2500
100	-	-	-	-	-	-
300	1.688/$\surd$	-	-	-	-	-
500	0.894/$\surd$	1.607/$\surd$	-	-	-	-
900	1.434/$\surd$	1.174/$\surd$	1.845/$\times$	-	-	-
1500	1.132/$\surd$	1.079/$\surd$	2.013/$\times$	10.432/$\times$	-	-
2500	2.854/$\surd$	2.473/$\times$	2.11/$\surd$	3.135/$\times$	3.015/$\times$	-

Note: $\surd$ denotes acceptance of the null hypothesis, $\times$ denotes rejection of the null hypothesis.

. Given a significance level $\alpha$,

$$P\left(\left|t\right|\ge t_{{\displaystyle \frac{\alpha }{2}}}(n-2)\right)=\alpha$$

(12)

If the observed value of t satisfies $\left|t\right|\ge t_{{\displaystyle \frac{\alpha }{2}}}(n-2)$, then the null hypothesis $H_0$ is rejected.

When $\alpha =0.1$,

$P(\left|t\right|\ge t_{0.05}(10))=0.1$, and $t_{0.05}(10)=1.812$.

The rejection regions are (0, −1.812] and [1.812, +$\mathrm{\infty })$.

It can be seen that seven of the above t values are within the rejection region. Therefore, the independence hypothesis of the residuals under each confining pressure is rejected.

The regression residual analysis of the nonlinear shear strength based on the Duncan formula for the coarse-grained soils from three engineering projects (Projects A, B, and C) indicates that the diagonal elements of the covariance matrix of the least squares regression residuals for the nonlinear shear strength friction angle are not equal, and the non-diagonal elements are not zero. Although the probability distribution of the residuals passes the normality test, the residuals under different confining pressures do not exhibit homogeneity of variance and irrelevance. This confirms the occurrence of residual heteroscedasticity and correlation across the different confining pressures.

6. Elimination of Residual Variance Heteroscedasticity and Autocorrelation

If the residuals exhibit heteroscedasticity and correlation, the regression equation no longer meets the prerequisites of least squares regression. In this case, if the least squares method is used, although the estimated values of the parameters are unbiased, the variances of the parameters could deviate from the actual value. A solution is to replace the regression variables. The linear regression equation can be expressed as

$$y=X\beta +e,E(e)=0,Cov(e)={\sigma }^{2}V$$

(13)

where $X=\left[\begin{array}{cccc}1& 1& \dots & 1\\ x_1& x_2& \dots & x_n\end{array}\right]$, $y={\left[\begin{array}{cccc}{\phi }_1& {\phi }_2& \dots & {\phi }_n\end{array}\right]}^T$. $\beta =\left[\begin{array}{cc}{\phi }_0& -\Delta \phi \end{array}\right]$, $x_1=\lg \left({\sigma }_3^1/P_a\right)$,…$x_i=\lg \left({\sigma }_3^i/P_a\right)$,…, and $x_n=\lg \left({\sigma }_3^n/P_a\right)$, ${\sigma }_3^i$ and ${\phi }_i$ are the confining pressure and friction angle of the $\mathrm{i}$th test. The symbol ‘ denotes the matrix transposition. $V$ is the covariance matrix of the residual vector under different confining pressures. ${\sigma }^2$ is the variance of the residual vector.

It can be seen that the covariance matrix of the residual is not an identity matrix. $V$ is a nonsingular and positive definite, and there exists a nonsingular symmetric matrix $K$, such that $K^{\prime }K=K^{-1}K=V$; that is, the matrix $K$ is the square root matrix of $V$.

By defining new variables [15,16], namely,

$$z=K^{-1}y, B=K^{-1}X, \mathrm{and} g=K^{-1}e$$

(14)

The regression equation $y=X\beta +\epsilon$ becomes $K^{-1}y=K^{-1}X\beta +K^{-1}e$, i.e., it can be rewritten as

$$z=B\beta +g$$

(15)

After this transformation, the model residuals have a zero mean, i.e., $E\left(g\right)=K^{-1}E\left(e\right)=0$, and the covariance matrix of $g$ can be expressed as

$$\begin{array}{cc}\hfill Var(g)& =\left\{\left[g-E(g)\right]{\left[g-E(g)\right]}^{\prime }\right\}=E(g{g}^{\prime })\hfill \\ & =E\left(K^{-1}e{e}^{\prime }{K}^{-1}\right)=K^{-1}E\left(e{e}^{\prime }\right)K^{-1}\hfill \\ & =E\left(K^{-1}e{e}^{\prime }{K}^{-1}\right)=K^{-1}E\left(e{e}^{\prime }\right)K^{-1}\hfill \\ & ={\sigma }^2{K}^{-1}V{K}^{-1}={\sigma }^2{K}^{-1}KK{K}^{-1}\hfill \\ & ={\sigma }^{2}I\hfill \end{array}$$

Therefore, $g$ has a zero mean, constant variance, and uncorrelated variance. Equation (14) satisfies the general assumptions of the classic least squares estimation, and the least squares function can be expressed as

$$Q\left(\beta \right)=g^{\prime }g=e^{\prime }{V}^{-1}e=(y-X\beta {)}^{\prime }{V}^{-1}(y-X\beta )$$

The canonical equation for least squares can be expressed as

$$X^{\prime }{V}^{-1}X{\widehat{\beta }}^{*}=X^{\prime }{V}^{-1}y$$

The solution to the equation can be expressed as

$${\widehat{\beta }}^{*}={\left(X^{\prime }{V}^{-1}X\right)}^{-1}{X}^{\prime }{V}^{-1}y$$

(16)

The triaxial test data for five types of coarse-grained soils used in three engineering projects (A, B, and C) were used to perform a classic least squares regression and regression after eliminating the heteroscedasticity and correlation of the residual. After obtaining the regression equation, the covariance matrix of the parameters was calculated. The regression parameters, its variance, and covariance are shown in

Table 7. Regression parameters, its variance, and covariance of the Duncan formula for nonlinear shear strength of coarse-grained soils.

Project	Regression Method	${\mathit{\phi }}_0$ $\mathbf{Mean}$	$\mathbf{\Delta }\mathit{\phi }$ $\mathbf{Mean}$	${\mathit{\phi }}_0$ Variance	$\mathbf{\Delta }\mathit{\phi }$ $\mathbf{Variance}$	${\mathit{\phi }}_0$$\mathbf{and} \mathbf{\Delta }\mathit{\phi }$ Covariance
Coarse-grained soil from Zone I of Project A	Classic least squares method	55.738	12.272	2.054	2.510	−1.954
	Generalized least squares method	54.321	10.227	0.748	0.266	−0.402
Coarse-grained soil from Zone II of Project A	Classic least squares method	50.309	11.680	1.854	2.265	−1.763
	Generalized least squares method	50.709	11.720	0.569	0.309	−0.312
Coarse-grained soil from Zone II of Project B	Classic least squares method	54.234	12.033	1.939	2.369	−1.844
	Generalized least squares method	54.004	12.131	1.137	1.884	−1.396
Coarse-grained soil from Zone II of Project B	Classic least squares method	53.190	13.415	2.477	3.026	−2.355
	Generalized least squares method	52.824	12.415	1.504	1.807	−1.499
Gravel clay from Project C	Classic least squares method	39.977	12.374	2.200	2.685	−2.090
	Generalized least squares method	41.750	11.180	2.181	1.152	0.920

Note: The generalized least squares method can eliminate heteroscedasticity and correlation of the residual. Intermediate variables are used to ensure that the regression meets the prerequisites of the least squares method.

.

It can be seen that, for each coarse-grained soil, the regression parameters obtained using the two methods are similar, yet the variances of the parameters are reduced when the proposed method is applied.

For example, for the coarse-grained material from Zone II of Project A, the regression equation from the classic least squares method and the covariance matrix between ${\phi }_0$ and $\Delta \phi$ can be given as

$$\phi =50.309-11.680\lg \left({\sigma }_3/P_a\right)$$

(17)

$$\mathrm{and} Cov({\phi }_0,\Delta \phi )=\left[\begin{array}{cc}1.854& -1.763\\ -1.763& 2.265\end{array}\right]$$

(18)

After eliminating the residual heteroscedasticity and correlation, the regression equation and covariance matrix can be expressed as

$$\phi =50.709-11.721\lg \left({\sigma }_3/P_a\right)$$

(19)

$$\mathrm{and} Cov({\phi }_0,\Delta \phi )=\left[\begin{array}{cc}0.569& -0.312\\ -0.312& 0.309\end{array}\right]$$

(20)

It can be seen that, after eliminating the heteroscedasticity and correlation of the regression residual, the parameters themselves do not change much; the parameter variance is reduced significantly, providing more accurate estimates of the shear strength parameters of the coarse-grained soil.

7. The Change in the Reliability of the Slope Stability Caused by the Variation in the Standard Deviation of the Nonlinear Shear Strength

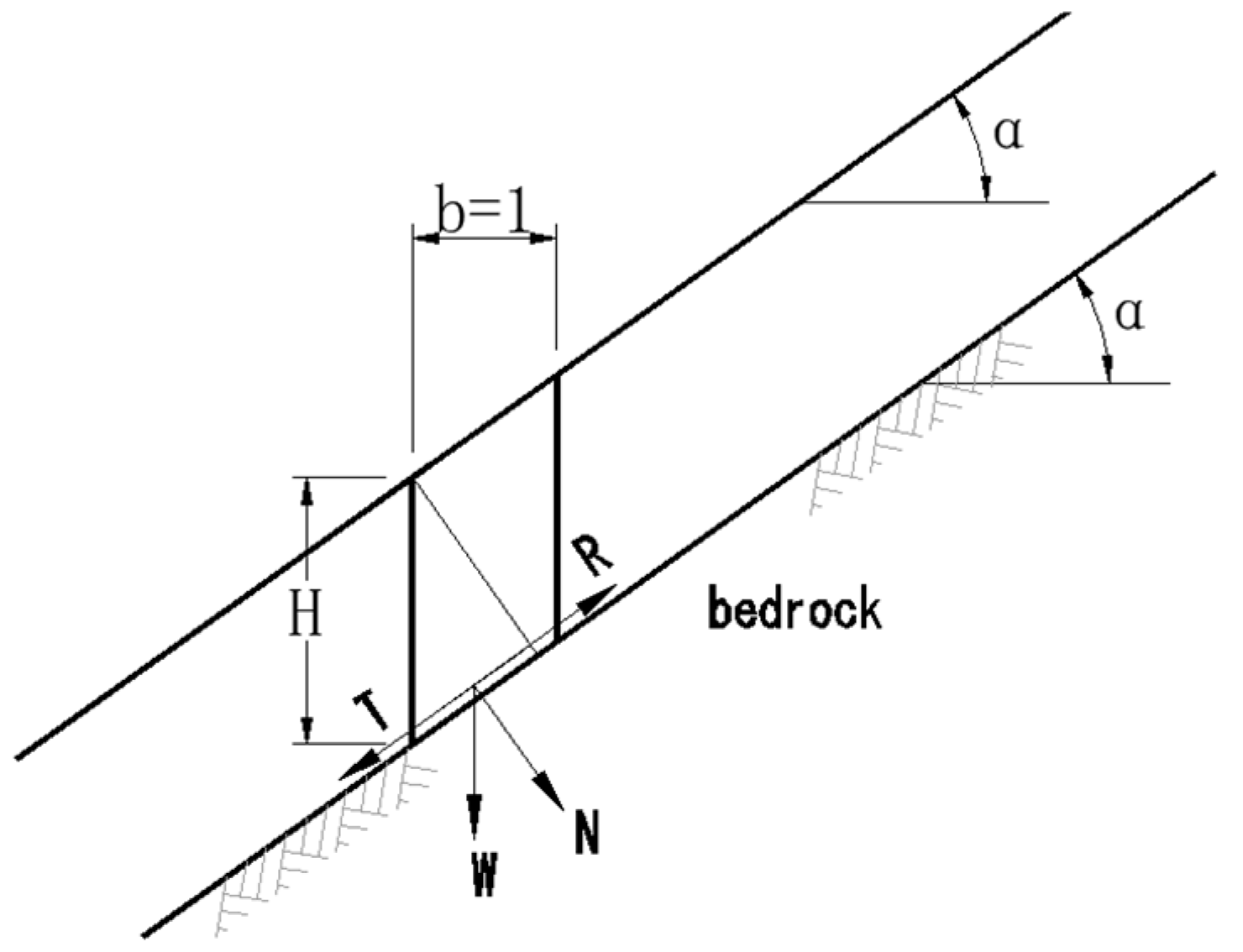
The angle between an infinitely long slope and the horizontal plane is $\alpha$; that is, the slope ratio is 1:m, the unit weight of the soil is $\gamma$, and the thickness of the soil layer (H) is an equal 8 m, with the underlying layer being bedrock. The sliding surface slides within the soil layer along the bedrock surface, as shown in Figure 3. The friction angle of the soil adopts the nonlinear shear strength and its standard deviation calculated in this paper for the coarse-grained soil from Zone I and Zone II of Project A, the coarse-grained soil from Zone I and Zone II of Project B, and the gravelly clay materials in Project C. The reliability index for the stability of the soil slope against sliding is analyzed and compared.

The slope stability safety factor can be expressed as

$$F={\displaystyle \frac{W\cdot \cos \alpha \cdot \tan \phi }{W\cdot \sin \alpha }}={\displaystyle \frac{\tan \phi }{\tan \alpha }}$$

(21)

Let $m={\displaystyle \frac{1}{\tan \alpha }}$, $f=\tan \phi$, and $f$ is friction coefficient. The slope stability safety factor formula has changed to

$$F=mf$$

(22)

The mean and variance of the slope stability safety coefficients can be expressed as, respectively,

$${\mu }_F=m{\mu }_f, {\sigma }_F^2=m^2{\sigma }_f^2, {\sigma }_F=\sqrt{{\sigma }_F^2}$$

(23)

in which ${\mu }_F$, ${\sigma }_F^2$, and ${\sigma }_F$ are the mean, variance, and standard deviation of the slope stability safety coefficient, respectively; ${\mu }_f$ and ${\sigma }_f^2$ are the mean and variance of the friction coefficient.

Because $f=\tan \phi$, the relationship between the variance of friction coefficient and the variance of the friction angle can be expressed as

$${\sigma }_f^2={\left({\displaystyle \frac{\partial f}{\partial \phi }}\right)}^2{\sigma }_{\phi }^2={\sec }^2({\mu }_{\phi }){\sigma }_{\phi }^2$$

(24)

In which ${\sigma }_{\phi }^2$ is the variance of friction angle.

Because $\phi ={\phi }_0-\Delta \phi \lg \left({\displaystyle \frac{{\sigma }_3}{p_a}}\right)$, ${\sigma }_{\phi }^2$ can be obtained

$${\sigma }_{\phi }^2={\sigma }_{\phi 0}^2+{\sigma }_{\Delta \phi }^2{\left[\lg \left({\displaystyle \frac{{\sigma }_3}{p_a}}\right)\right]}^2-a\lg \left({\displaystyle \frac{{\sigma }_3}{p_a}}\right)Cov({\phi }_0,\Delta \phi )$$

(25)

In which ${\sigma }_{\phi 0}^2$ and ${\sigma }_{\Delta \phi }^2$ are the variance of ${\phi }_0$ and $\Delta \phi$; $Cov({\phi }_0,\Delta \phi )$ is the covariance between ${\phi }_0$ and $\Delta \phi$.

The limit state equation for the stability of the soil slope can be expressed as

$$Z=F-1=0$$

(26)

The corresponding reliability indicator can be expressed as

$$\beta ={\displaystyle \frac{{\mu }_F-1}{{\sigma }_F}}$$

(27)

By calculating the reliability of the anti-sliding stability of an infinitely long soil slope, it can be seen that the mean and variance of the Duncan nonlinear shear strength obtained using the generalized least squares method have generally improved the stability reliability index. This indicates that the Duncan nonlinear shear strength obtained using the classical least squares method significantly underestimates the stability safety of the soil slope. This is consistent with the fact that the variance of the Duncan nonlinear strength obtained by the generalized method is smaller than that of the classical method.

8. Conclusions

The shear strength of coarse-grained soil has strong nonlinearity and is commonly determined using the Duncan formula. However, the classic grouped data method for estimating these parameters has the limitations of small sample sizes and large errors. When the classic least squares method is applied to estimate the Duncan nonlinear shear strength parameters based on triaxial test data, it has been found that the residual exhibited heteroscedasticity and correlation, which violates the prerequisites of the least squares method. In this study, we introduced a generalized least squares method to eliminate these issues. By analyzing triaxial test data from five types of coarse-grained soils used in three engineering projects, it was found that the mean values of the nonlinear shear strength parameters remained relatively unchanged compared to those obtained using the classic least squares method, whereas the variance was significantly reduced, with reductions ranging from 51.3% to 89.0% (Table 7), demonstrating the effectiveness of the proposed method. These improvements enable a more accurate characterization of the nonlinear shear strength of coarse-grained soils, enhancing the precision of geotechnical calculations. When calculating the anti-sliding stability of an infinitely long soil slope, it was found that the reliability indices obtained by using the generalized least squares method for Duncan’s nonlinear strength calculation have all improved, showing an increase of 22.5% to 95.6% (

Table 8. Calculation of the reliability index for the anti-sliding stability of an infinitely long slope.

$\mathbf{Project}$	Unit Weight kN/m3	Slope Ratio	Regression Method	$\mathbf{Variance} \mathbf{of} \mathbf{Friction} \mathbf{Angle} {\mathit{\sigma }}_{\mathit{\phi }}^2$	$\mathbf{Variance} \mathbf{of} \mathbf{Friction} \mathbf{Coefficient} {\mathit{\sigma }}_{\mathit{f}}^2$	Mean of Friction Coefficient	Mean of Safety Coefficient	Variance of Safety Coefficient	Standard Deviation of Safety Coefficient	Reliability Index
Coarse-grained soil from Zone I of Project A	21.2	1:1.3	Classic	2.638	0.0425	1.379	1.793	0.072	0.268	2.957
			Generalized	0.863	0.0132	1.323	1.720	0.022	0.149	4.822
Coarse-grained soil from Zone II of Project A	20.8	1:1.4	Classic	2.394	0.0305	1.137	1.592	0.060	0.244	2.421
			Generalized	0.663	0.0086	1.153	1.614	0.017	0.130	4.737
Coarse-grained soil from Zone II of Project B	20.8	1:1.4	Classic	2.504	0.0376	1.305	1.827	0.074	0.271	3.048
			Generalized	1.566	0.0233	1.294	1.811	0.046	0.214	3.800
Coarse-grained soil from Zone II of Project B	20.8	1:1.4	Classic	3.198	0.0455	1.248	1.748	0.089	0.298	2.505
			Generalized	1.961	0.0276	1.238	1.734	0.054	0.233	3.155
Gravel clay from Project C	17.5	1:1.8	Classic	2.628	0.0240	0.804	1.446	0.078	0.279	1.600
			Generalized	2.014	0.0195	0.859	1.547	0.063	0.251	2.178

). This indicates that the Duncan nonlinear shear strength estimated by the classical least squares method will underestimate the anti-sliding stability of the soil slope. Therefore, the Duncan nonlinear strength parameters obtained by the generalized least squares method are superior, which is of great significance for improving the accuracy of the calculation results of geotechnical structures.

Given that the analysis and validation in this study are based on triaxial test data from five types of coarse-grained soils obtained from three specific engineering projects, future research should focus on applying and validating this methodology to a broader range of geotechnical materials, including coarse grained soils and gravelly and rockfill materials, to establish a more comprehensive understanding of its applicability. Furthermore, exploring the integration of this advanced statistical method with emerging computational techniques, such as machine learning algorithms, could lead to the development of hybrid models that not only account for data uncertainty accurately but also adapt to complex, nonlinear soil behavior more efficiently. Such directions would significantly enhance the practical impact and theoretical foundation of reliability-based design in geotechnical engineering.