Benchmarking Overlapped Subarrays in Direct Radiating Arrays for GEO Broadband Satellite Communication Systems
Abstract
1. Introduction
2. Materials and Methods
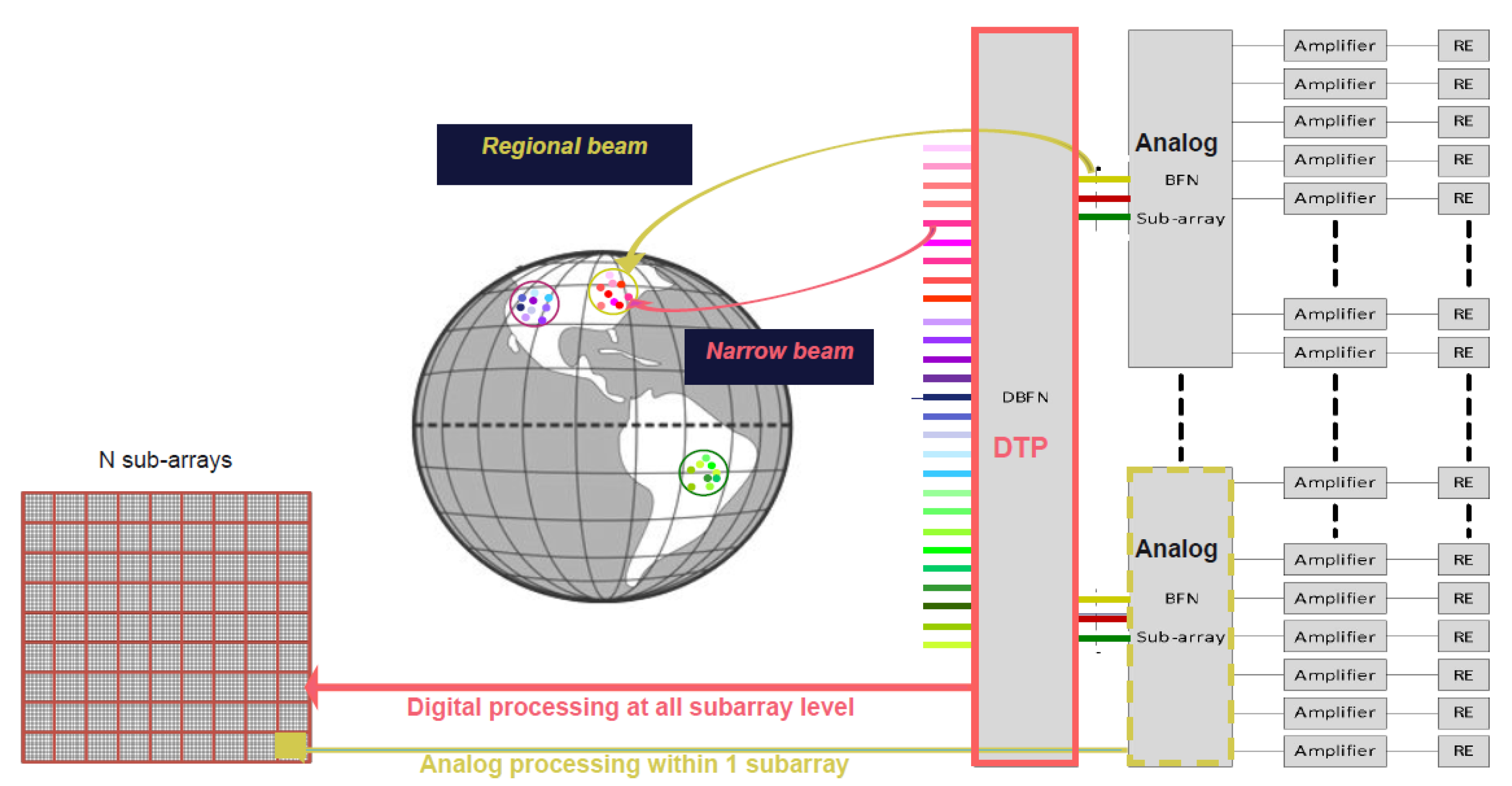
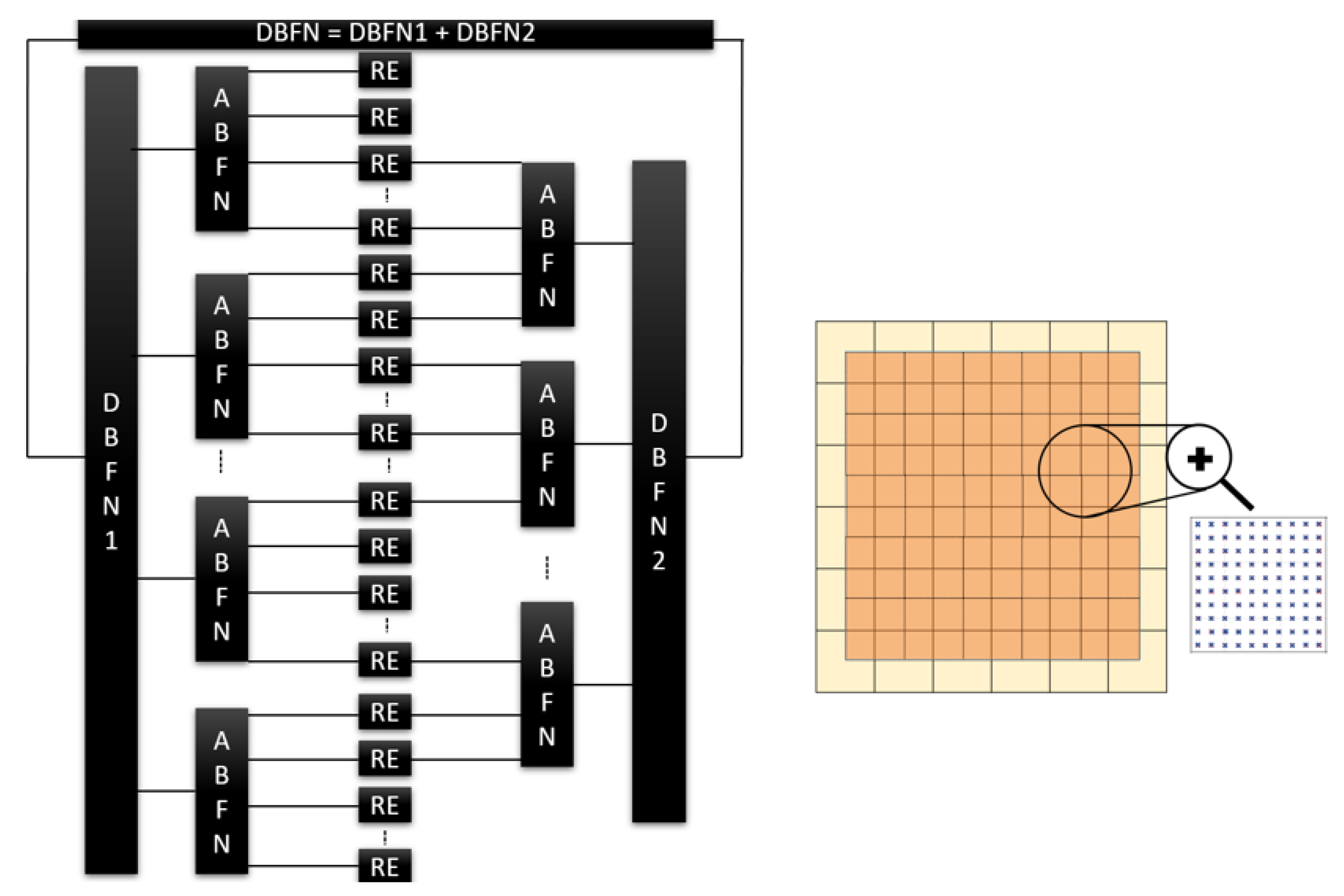
2.1. Overview of Hybrid DRA Configurations for GEO Broadband Communications
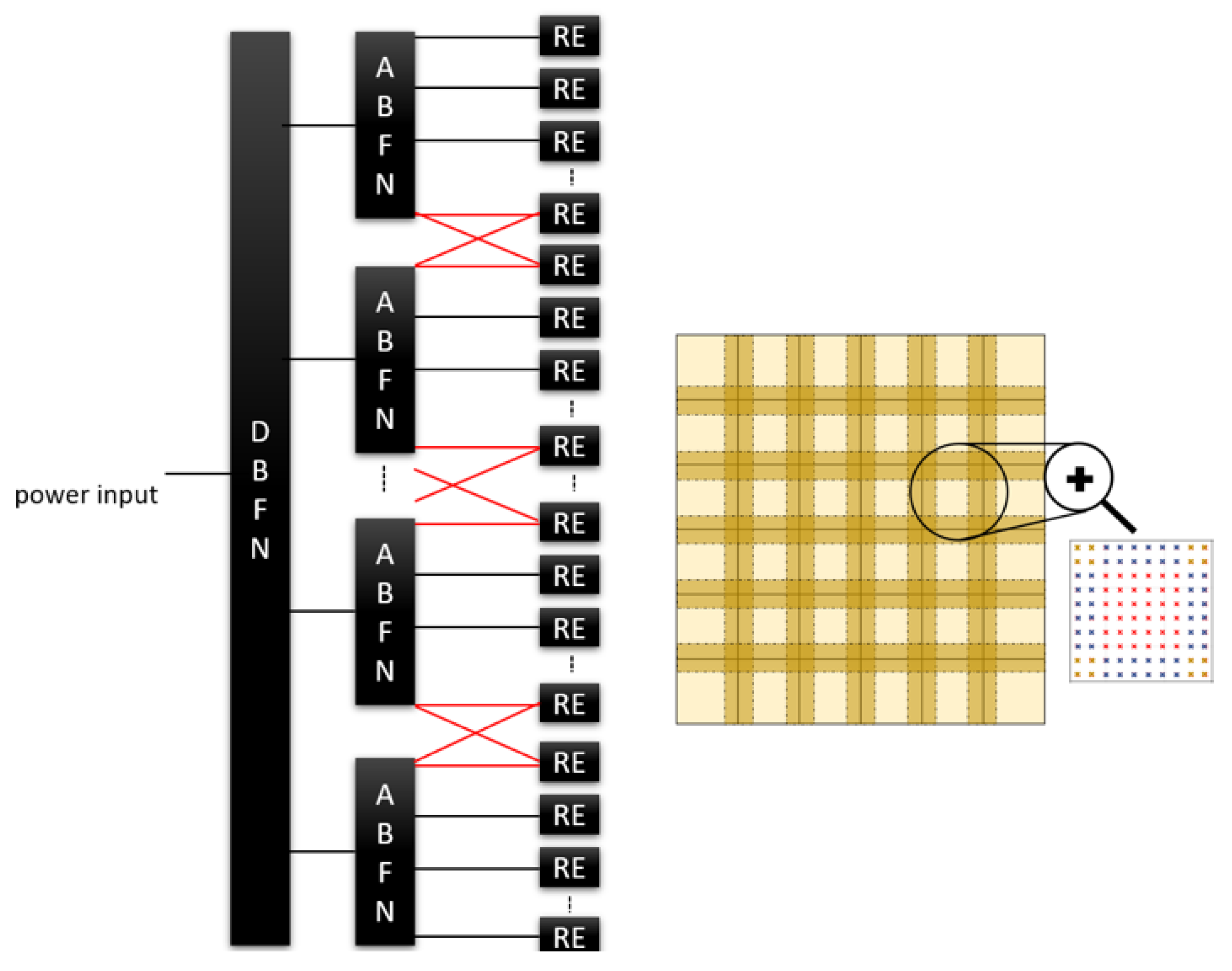
2.2. Existing Hybrid Beamformed Overlapped DRAs for On-Board Satellite Communications
3. Results
3.1. Antenna Characteristics
3.1.1. Radiation Patterns
- The NO and OS architectures produce grating lobes at the same positions.
- The grating lobes of the OA architecture largely overlap with the even grating lobes of the NO architecture. However, at the odd grating lobe position of the NO (and OS) architecture(s) the OA architecture produces a null. This is due to the grating lobe suppression. At the even grating lobe level, which also includes the main lobe as the 0th-order one, the gain is increased by 0.5 dB compared to the NO configuration.
- The grating lobes of the OS architecture are overall at lower levels. This is a known feature for this class of architectures [19].
- For overlapped architecture scanned with a fixed non-adaptive taper at the ABFN, the grating lobes cannot be totally suppressed. Although a null could be enforced at the grating lobe position along a given scanning direction, the multibeam generation context prevents nulling control for every single beam. Indeed, such an operation is implemented on-board the DTP and is unaffordable for thousands of beams generated simultaneously. In this frame, a reduction in or partial suppression of the grating lobes is targeted.

3.1.2. Amplitude and Phase Distribution
3.2. Regional Coverage Area
- The scan loss within the coverage is limited; i.e., a high gain is maintained for all spot beams within one of the regional coverages.
- The interference within the area is low; i.e., there are no high-level grating lobes within the regional area.
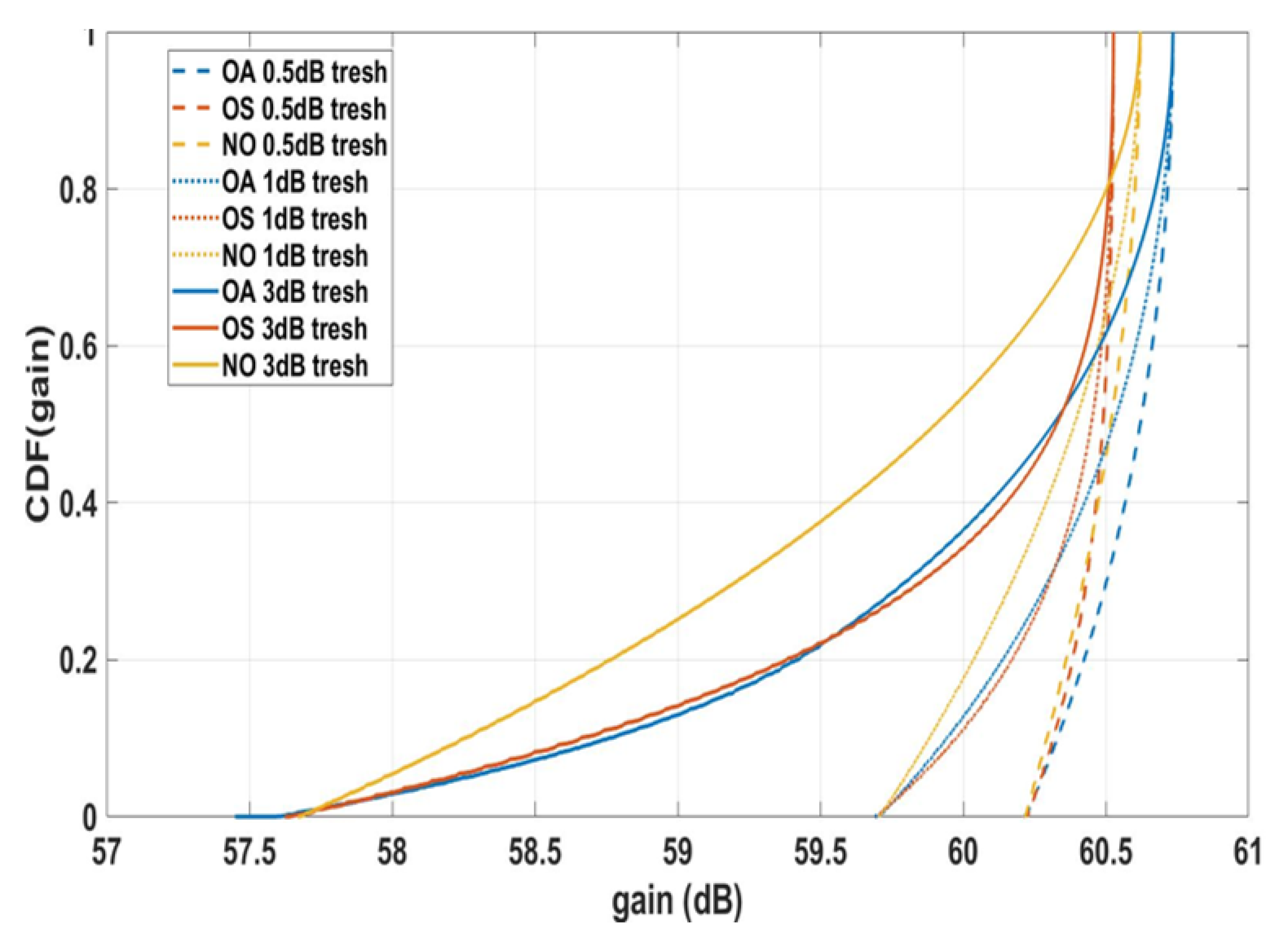
3.2.1. Scanning Performance
3.2.2. Grating Lobes
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| RF | Radio Frequency |
| LEO | Low Earth Orbit |
| MEO | Medium Earth Orbit |
| GEO | Geostationary Orbit |
| DRAs | Direct Radiating Arrays |
| DBFN | Digital Beamforming Network |
| ABFN | Analogue Beamforming Network |
| HBFN | Hybrid Beamforming Network |
| HAD | Hybrid Analog–Digital |
| AFR | Array-Fed Reflector |
| SSPA | Solid-State Power Amplifier |
| DTP | Digital Transparent Processor |
| FFT | Fast Fourier Transform |
| FOV | Field Of View |
| RE | Radiating Element |
| OS | Oversized Subarrays |
| OA | Overlapped Arrays |
| NO | Non-Overlapped Arrays |
| SL(L) | Side Lobe (Levels) |
| GL | Grating Lobe |
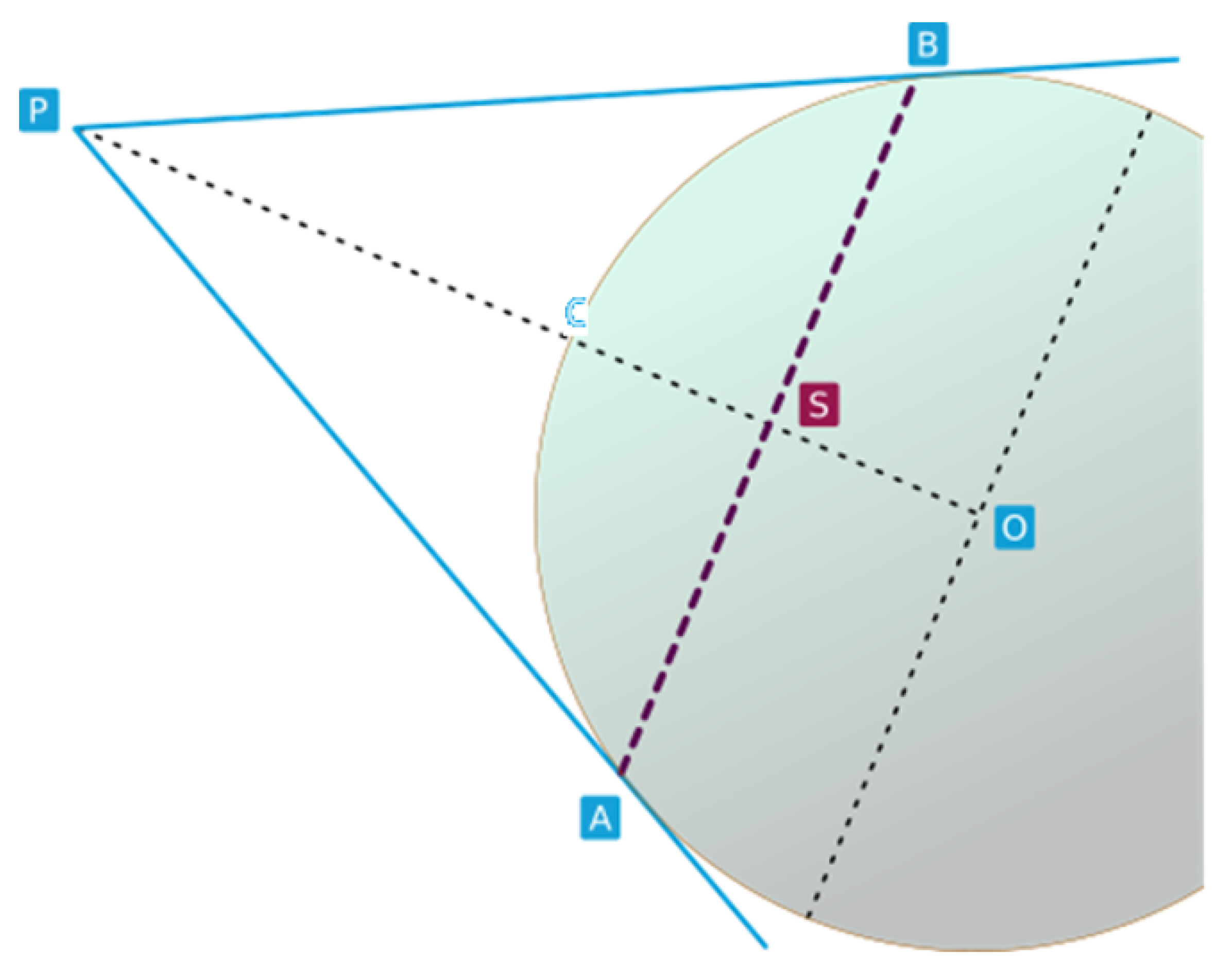
Appendix A. Measurement Set-Up

References
- Maral, G.; Bousquet, M.; Zhili, S. Satellite Communications Systems: Systems, Techniques and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Schuss, J.J.; Upton, J.; Myers, B.; Sikina, T.; Rohwer, A.; Makridakas, P.; Francois, R.; Wardle, L.; Smith, R. The IRIDIUM main mission antenna concept. IEEE Trans. Antennas Propag. 1999, 47, 416–424. [Google Scholar] [CrossRef]
- Metzen, P.L. Globalstar satellite phased array antennas. In Proceedings of the 2000 IEEE International Conference on Phased Array Systems and Technology, Dana Point, CA, USA, 21–25 May 2000. [Google Scholar]
- Cailloce, Y.; Caille, G.; Albert, I.; Lopez, J.M. A Ka-band direct radiating array providing multiple beams for a satellite multimedia mission. In Proceedings of the 2000 IEEE International Conference on Phased Array Systems and Technology, Dana Point, CA, USA, 21–25 May 2000. [Google Scholar]
- Dawkins, A.W.J.; Gulloch, W.J.; Morris, D.J.; Patel, H.K.; Thaker, R.C.; Stirland, S.S. Development of a Direct Radiating Arrays for Future Ku Band TELECOM Applications. In Proceedings of the Second European Conference on Antennas and Propagation, EuCAP 2007, Edinburgh, UK, 11–16 November 2007. [Google Scholar]
- Baldominos, A.; Mengali, A.; Fonseca, N.J.; Goussetis, G. Evaluation of array fed reflector architectures for broadband satellite missions. In Proceedings of the 2021 International Symposium on Antennas and Propagation, ISAP 2021, Taipei, Taiwan, 19–22 October 2021. [Google Scholar]
- Imaz-Lueje, B.; Prado, D.R.; Arrebola, M.; Pino, M.R. Reflectarray antennas: A smart solution for new generation satellite mega-constellations in space communications. Sci. Rep. 2020, 10, 2155. [Google Scholar] [CrossRef] [PubMed]
- Martinez-de-Rioja, D.; Martinez-de-Rioja, E.; Rodriguez-Vaqueiro, Y.; Encinar, J.A.; Pino, A. Multibeam reflectarrays in Ka-band for efficient antenna farms onboard broadband communication satellites. Sensors 2020, 21, 207. [Google Scholar] [CrossRef] [PubMed]
- Kaifas, T.N. State of the Art and Innovations needed for Direct Radiating Arrays to place Very High Throughput Satellite Communications into Technology Reach. In Proceedings of the IEEE 5th International Conference on Communications, Information, Electronic and Energy Systems (CIEES), Veliko Tarnovo, Bulgaria, 20–22 November 2024; pp. 1–6. [Google Scholar]
- Angeletti, P.; Toso, G.; Petrolati, D. A Reconfigurable Multibeam Antenna System. European Patent EP 3 654 544 A1, 13 November 2018. [Google Scholar]
- Stirland, S.J.; Craig, A.D. Phased arrays for satellite communications: Recent developments at Astrium LTD. In Proceedings of the IET Second European Conference on Antennas and Propagation (EuCAP), Edinburgh, UK, 11–16 November 2007; pp. 1–5. [Google Scholar]
- Palacios, J.; González-Prelcic, N.; Mosquera, C.; Shimizu, T.; Wang, C.H. A hybrid beamforming design for massive MIMO LEO satellite communications. Front. Space Technol. 2021, 2, 696464. [Google Scholar] [CrossRef]
- De Gaudenzi, R.; Angeletti, P.; Petrolati, D.; Re, E. Future technologies for very high throughput satellite systems. Wiley Int. J. Satell. Commun. Netw. 2020, 38, 141–161. [Google Scholar] [CrossRef]
- Alhaj, N.A.; Jamlos, M.F.; Manap, S.A.; Abdelsalam, S.; Bakhit, A.A.; Mamat, R.; Gismalla, M.S.M.; Hamdan, M. Integration of hybrid networks, AI, ultra massive-MIMO, THz frequency, and FBMC modulation toward 6G requirements: A review. IEEE Access 2023, 12, 483–513. [Google Scholar] [CrossRef]
- Toso, G.; Mangenot, C.; Roederer, A.G. Sparse and thinned arrays for multiple beam satellite applications. In Proceedings of the IET Second European Conference on Antennas and Propagation (EuCAP), Edinburgh, UK, 11–16 November 2007; pp. 1–4. [Google Scholar]
- Mailloux, R.J.; Santarelli, S.G.; Roberts, T.M.; Luu, D. Irregular Polyomino-Shaped Subarrays for Space-Based Active Arrays. Int. J. Antennas Propag. 2009, 2009, 956524. [Google Scholar] [CrossRef]
- Angeletti, P.; Toso, G.; Petrolati, D. Beam-Forming Network for an Array Antenna and Array Antenna Comprising the Same. U.S. Patent 9,374,145, 26 November 2012. [Google Scholar]
- Pellet, M.; Goussetis, G.; Legay, H.; Mota, J.; Cortazar, B.; Toso, G. A new antenna array architecture with hybrid beamforming for broadband satellite communications. In Proceedings of the IEEE 17th European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023. [Google Scholar]
- Tugend, V.; Thain, A. Hybrid beamforming with reduced grating lobes for satellite applications. In Proceedings of the IEEE 12th European Conference on Antennas and Propagation (EuCAP), London, UK, 9–13 April 2018; pp. 1–5. [Google Scholar]
- Li, X.; Wang, B. Coherence optimised subarray partition for hybrid MIMO phased array radar. IET Microwaves Antennas Propag. 2021, 15, 1441–1457. [Google Scholar] [CrossRef]
- Alieldin, A.; Huang, Y.; Saad, W.M. Optimum partitioning of a phased-MIMO radar array antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2287–2290. [Google Scholar] [CrossRef]
- Herd, J.S.; Duffy, S.M.; Steyskal, H. Design considerations and results for an overlapped subarray radar antenna. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; pp. 1087–1092. [Google Scholar]
- Wang, H.; Fang, D.; Chow, Y.L. Grating lobe reduction in a phased array of limited scanning. IEEE Trans. Antennas Propag. 2008, 56, 1581–1586. [Google Scholar] [CrossRef]
- Lopez, P.; Rodriguez, J.A.; Ares, F.; Moreno, E. Subarray weighting for the difference patterns of monopulse antennas: Joint optimization of subarray configurations and weights. IEEE Trans. Antennas Propag. 2001, 49, 1606–1608. [Google Scholar] [CrossRef]
- Haupt, R. Reducing grating lobes due to subarray amplitude tapering. IEEE Trans. Antennas Propag. 2003, 33, 846–850. [Google Scholar]
- Ye, X.; Yu, Z.; Xiao, D. Grating lobe suppression for wideband large-spacing beam scanning array using subarray null adjustable method. IEEE Antennas Wirel. Propag. Lett. 2022, 22, 347–351. [Google Scholar] [CrossRef]
- Coleman, J.O. Nonseparable Nth-band filters as overlapping-subarray tapers. In Proceedings of the IEEE RadarCon (RADAR), Kansas City, MO, USA, 23–27 May 2011; pp. 141–146. [Google Scholar]
- Griesbach, J.D. Optimal taper design for overlapped subarray formation. In Proceedings of the IEEE Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 2247–2251. [Google Scholar]
- Mailloux, R.J. Phased Array Antenna Handbook; Artech House: New York, NY, USA, 2017. [Google Scholar]
- Pellet, M.; Goussetis, G.; Mota, J.; Legay, H.; Vidal, F. Multibeam coverage optimization for broadband satellites with hybrid beamforming direct radiating arrays. In Proceedings of the IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Portland, OR, USA, 23–28 July 2023; pp. 1541–1542. [Google Scholar]
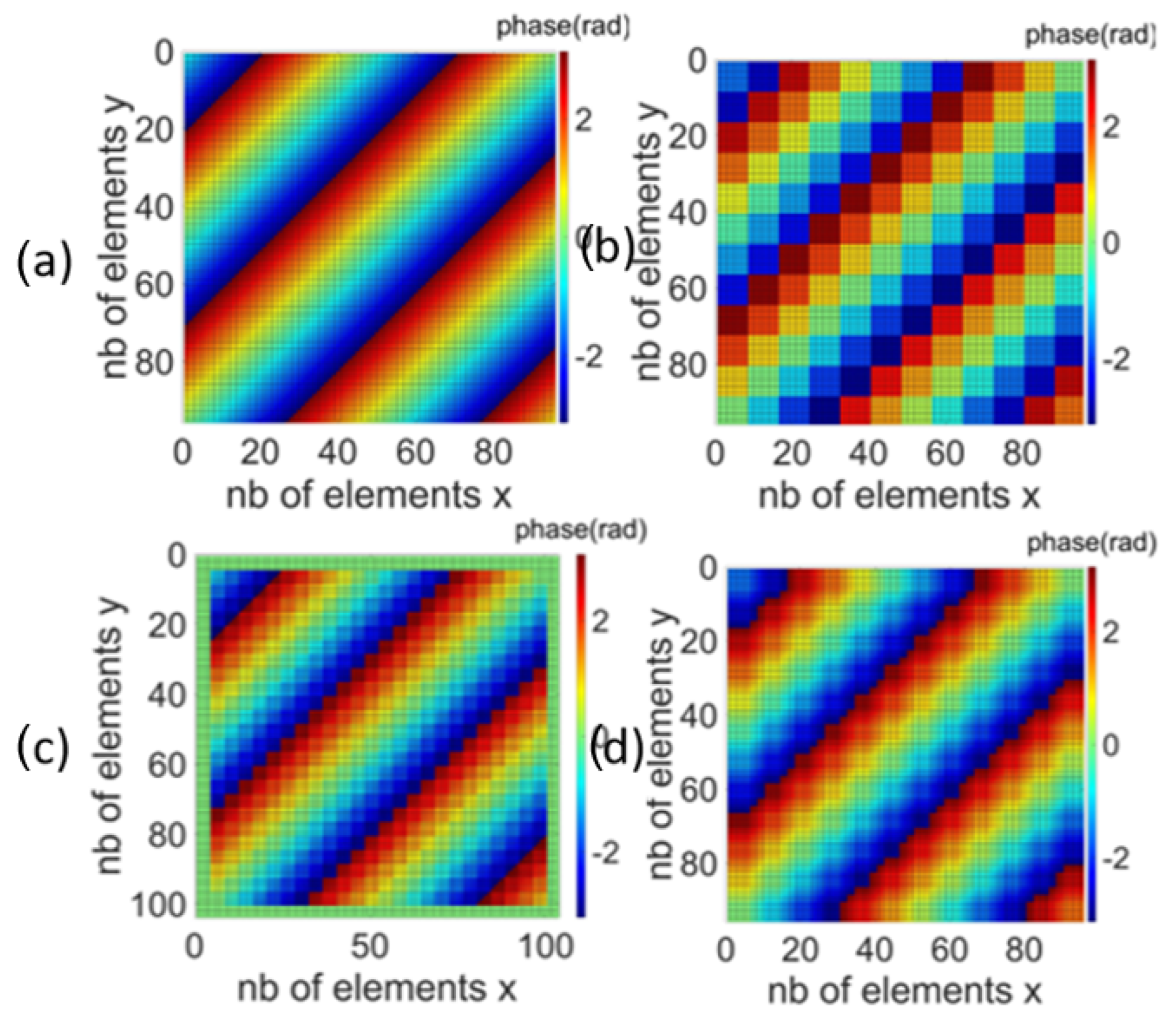
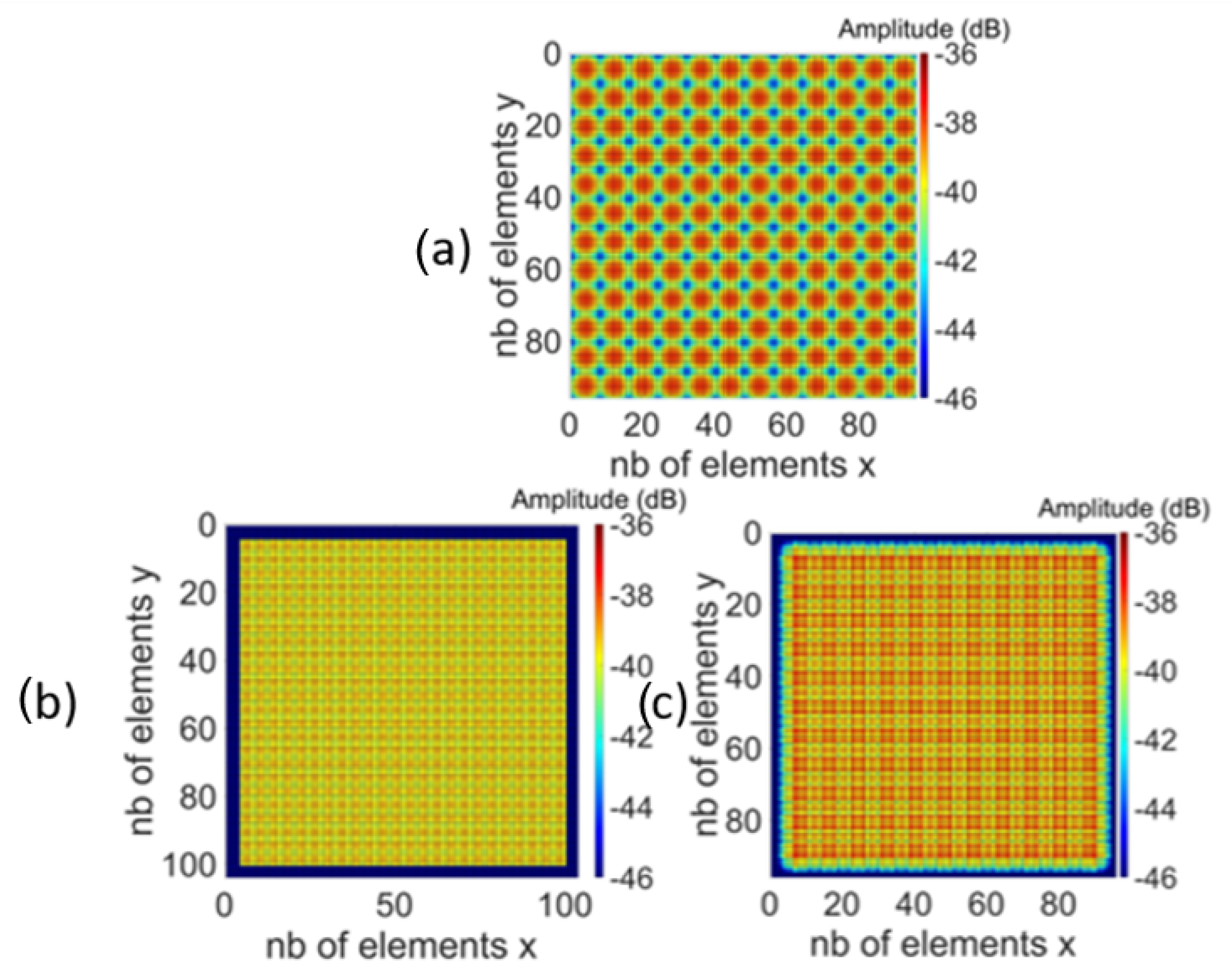


| Architecture | Number of Subarrays | Phase Steps |
|---|---|---|
| NO | 144 | 144 |
| OA | 313 | 576 |
| OS | 144 | 1156 |
| Architecture | Total Radiating Aperture | Number of Subarrays | Number of REs per Subarray | Digital Controls |
|---|---|---|---|---|
| NO | 9216 | 144 | ||
| OS | 9216 | 144 | ||
| OA | 9216 | 145 |
| Architecture | Number of RE | Digital Controls | GL Level | Gain Improvement | Scanning Improvement |
|---|---|---|---|---|---|
| NO | 9216 | 144 | ref | +0 | ref |
| OS | 9216 | 144 | −inf to 0 | +0.35 dB | 28% |
| OA | 9216 | 145 | −inf for odd GL, +0.5 dB for even GL | +0.5 dB | 31% |
| Architecture | Scanning Improvement | Hardware Cost and Manufacturing Trade-Offs |
|---|---|---|
| NO | ref | ref |
| OS | 28% | 3 types of power dividers, connecting each element carefully depending on its position |
| OA | 31% | thicker array, more connections across the overlapped and non-overlapped devices |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellet, M.; Legay, H.; Goussetis, G.; Mota, J.; Toso, G.; Angeletti, P. Benchmarking Overlapped Subarrays in Direct Radiating Arrays for GEO Broadband Satellite Communication Systems. Appl. Sci. 2025, 15, 10216. https://doi.org/10.3390/app151810216
Pellet M, Legay H, Goussetis G, Mota J, Toso G, Angeletti P. Benchmarking Overlapped Subarrays in Direct Radiating Arrays for GEO Broadband Satellite Communication Systems. Applied Sciences. 2025; 15(18):10216. https://doi.org/10.3390/app151810216
Chicago/Turabian StylePellet, Margaux, Hervé Legay, George Goussetis, Joao Mota, Giovanni Toso, and Piero Angeletti. 2025. "Benchmarking Overlapped Subarrays in Direct Radiating Arrays for GEO Broadband Satellite Communication Systems" Applied Sciences 15, no. 18: 10216. https://doi.org/10.3390/app151810216
APA StylePellet, M., Legay, H., Goussetis, G., Mota, J., Toso, G., & Angeletti, P. (2025). Benchmarking Overlapped Subarrays in Direct Radiating Arrays for GEO Broadband Satellite Communication Systems. Applied Sciences, 15(18), 10216. https://doi.org/10.3390/app151810216








