Integration of ANN and RSM to Optimize the Sawing Process of Wood by Circular Saw Blades
Abstract
1. Introduction
2. Materials and Methods
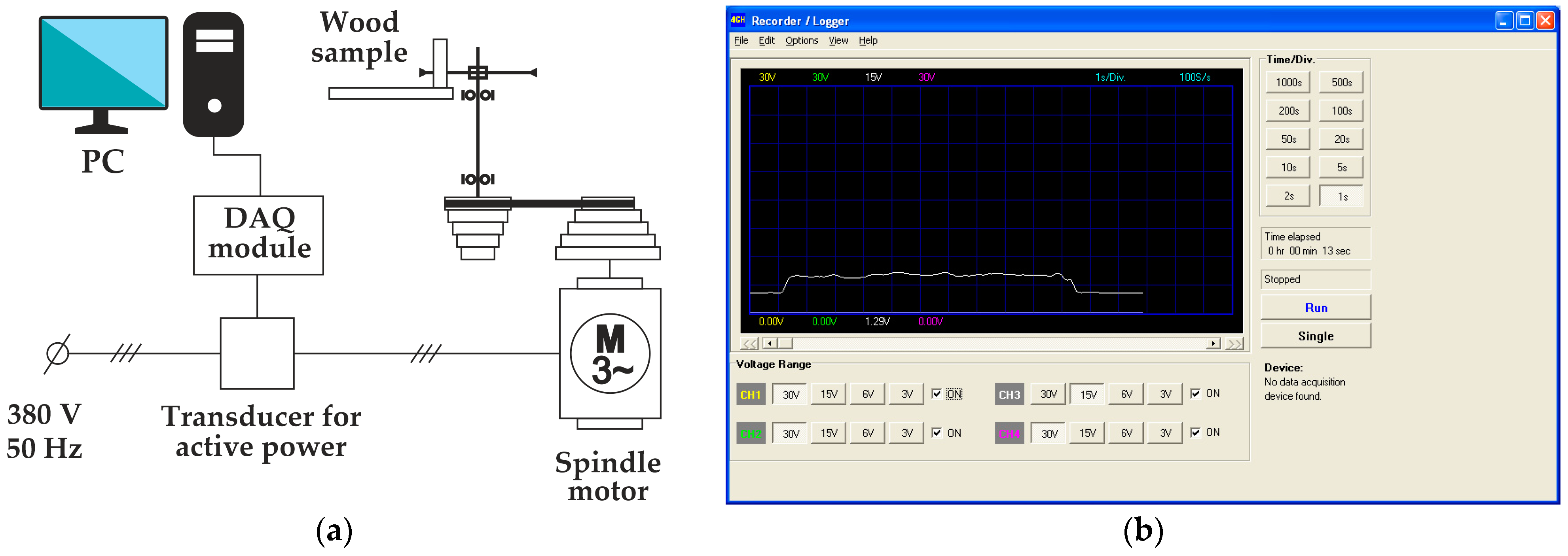
2.1. Experimental Part
2.2. Data Modeling
2.2.1. Artificial Neural Network Modeling
2.2.2. Response Surface Methodology
3. Results and Discussion
3.1. Experimental Data
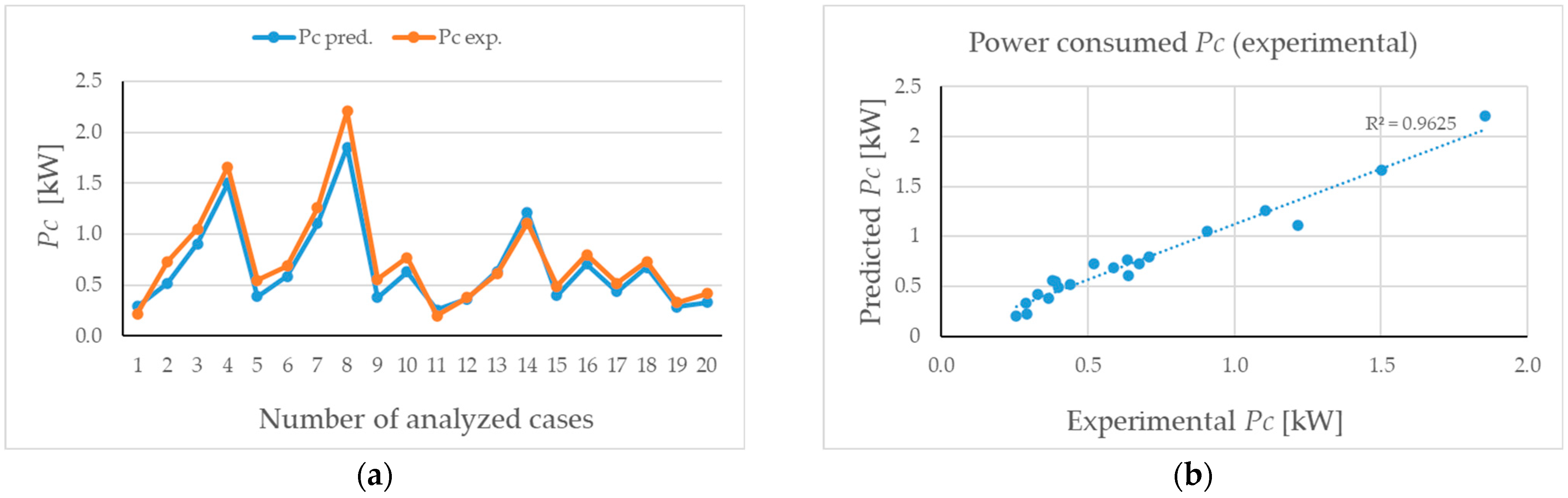
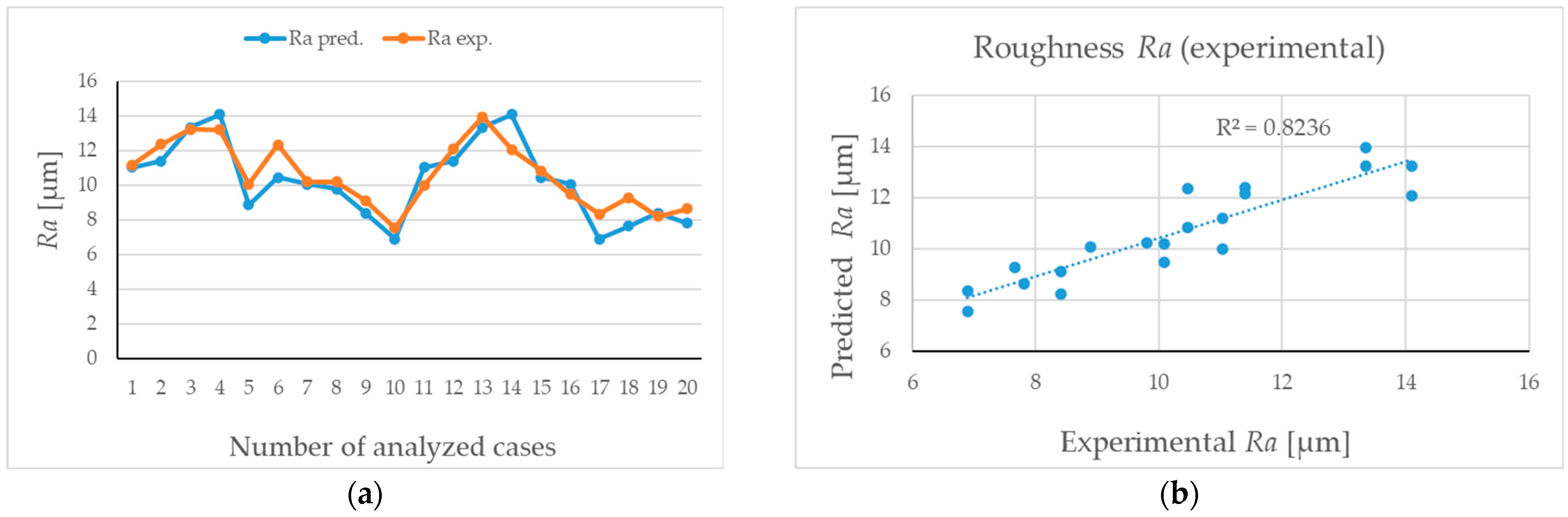
3.2. Models Based on the Artificial Neural Network Modeling Technique
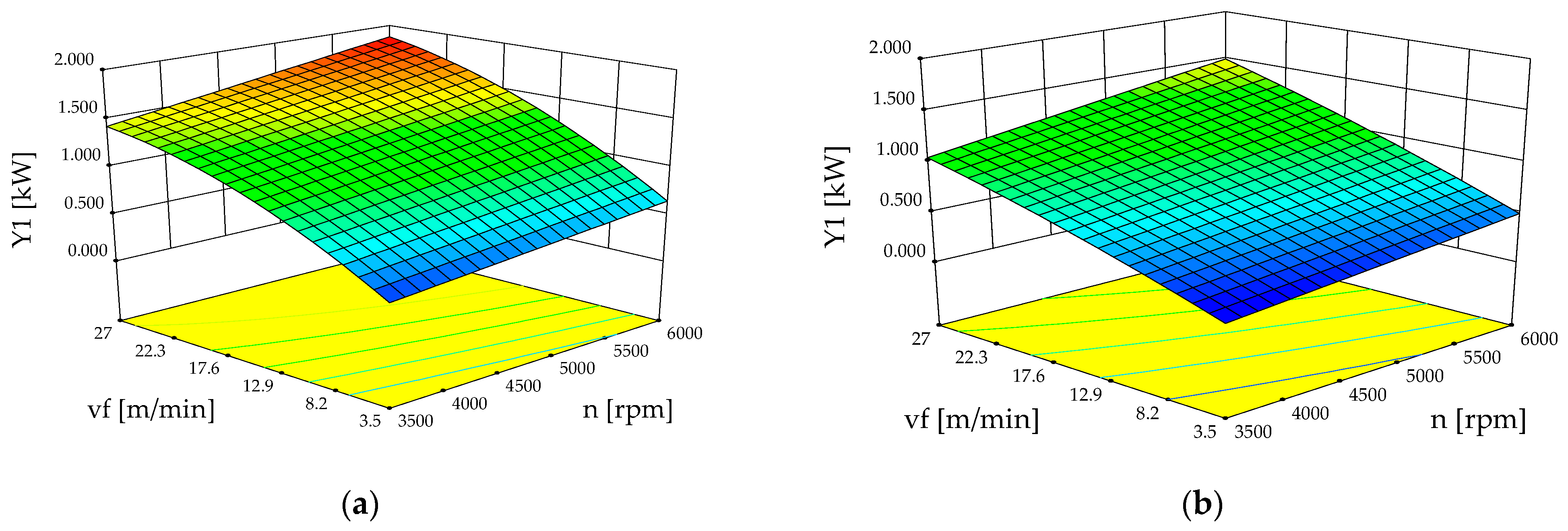
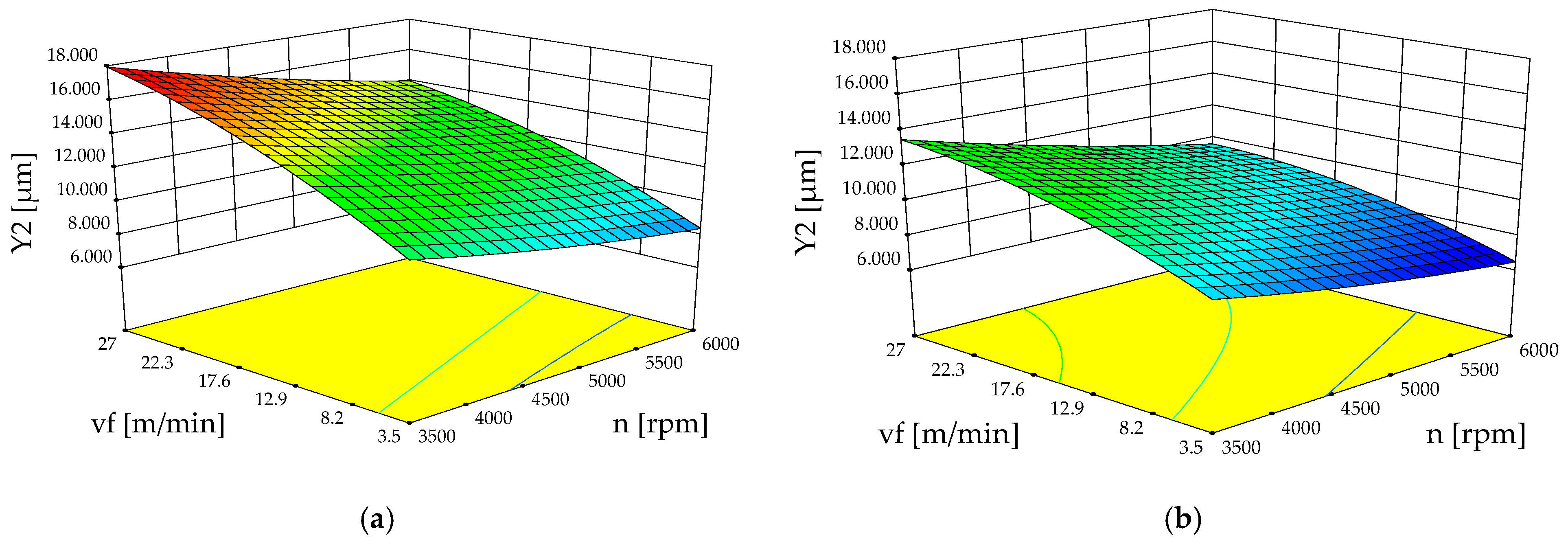
3.3. Influence of Factors and Optimization Study
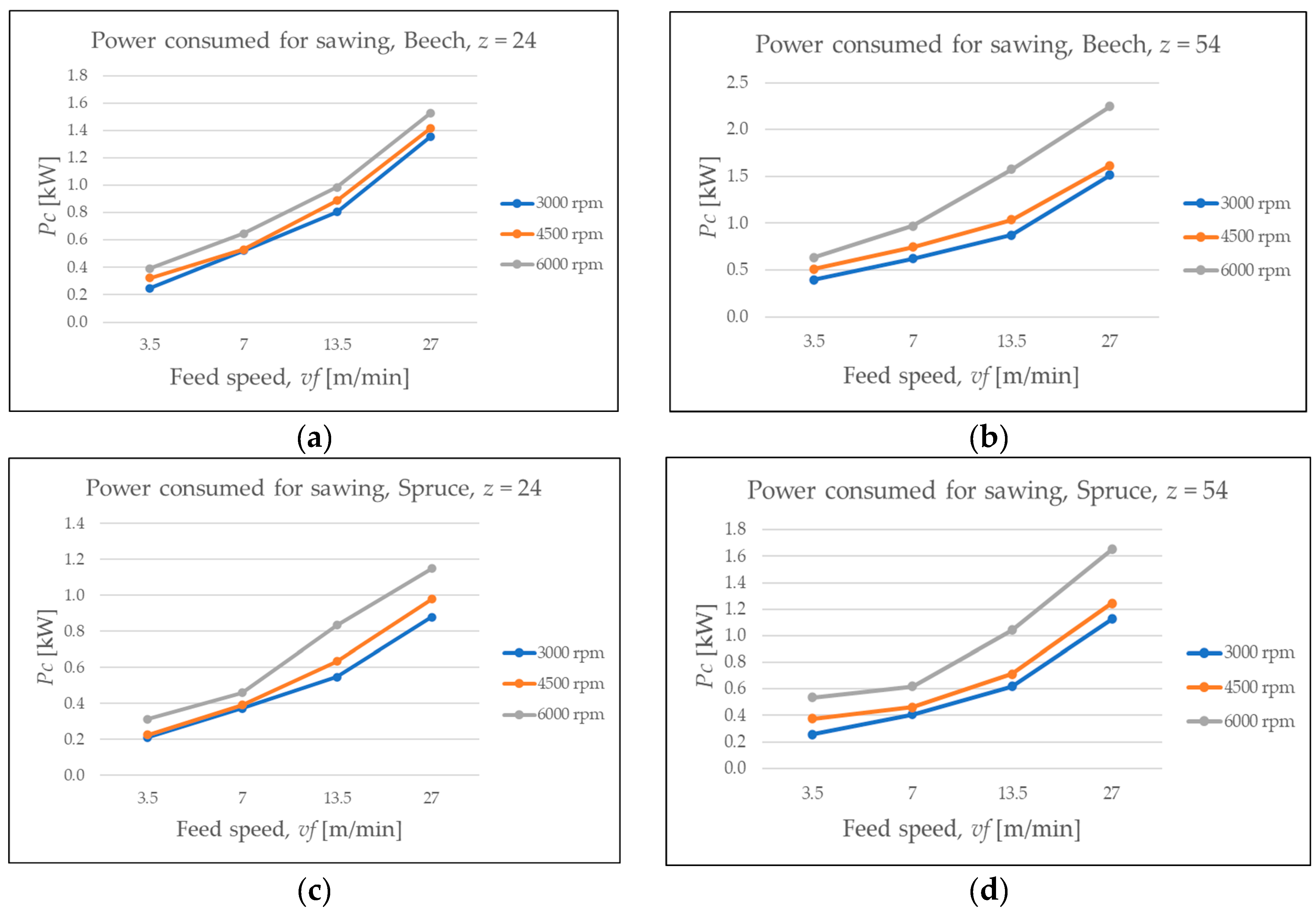
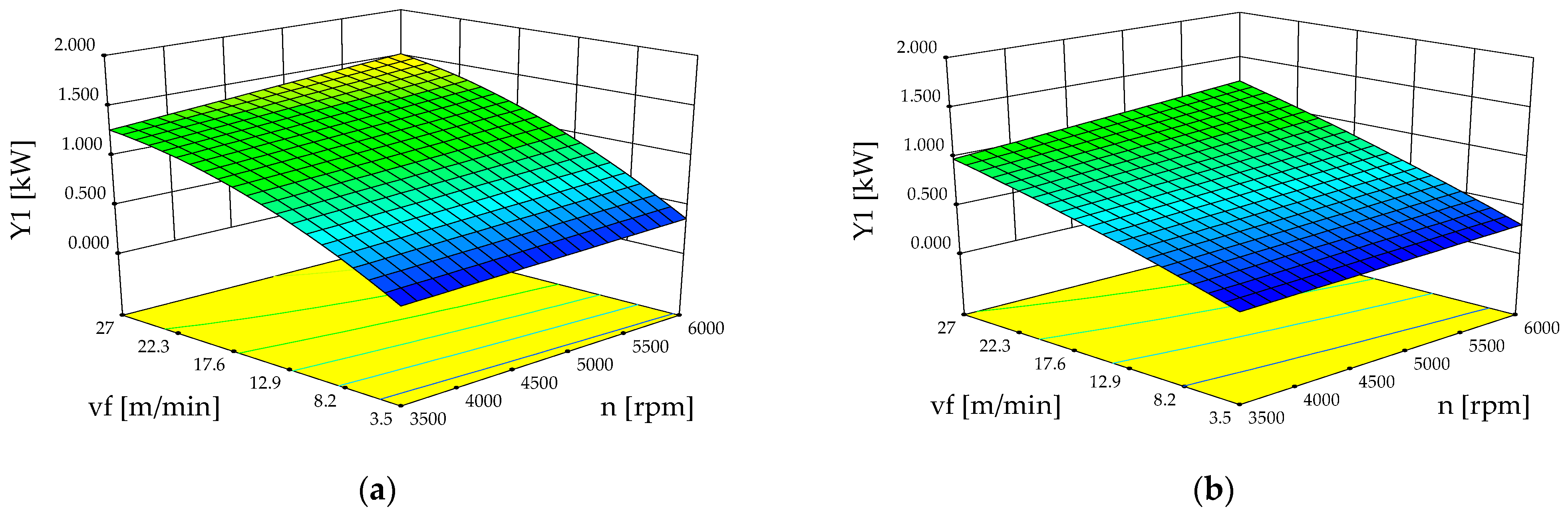
3.3.1. Cutting Power
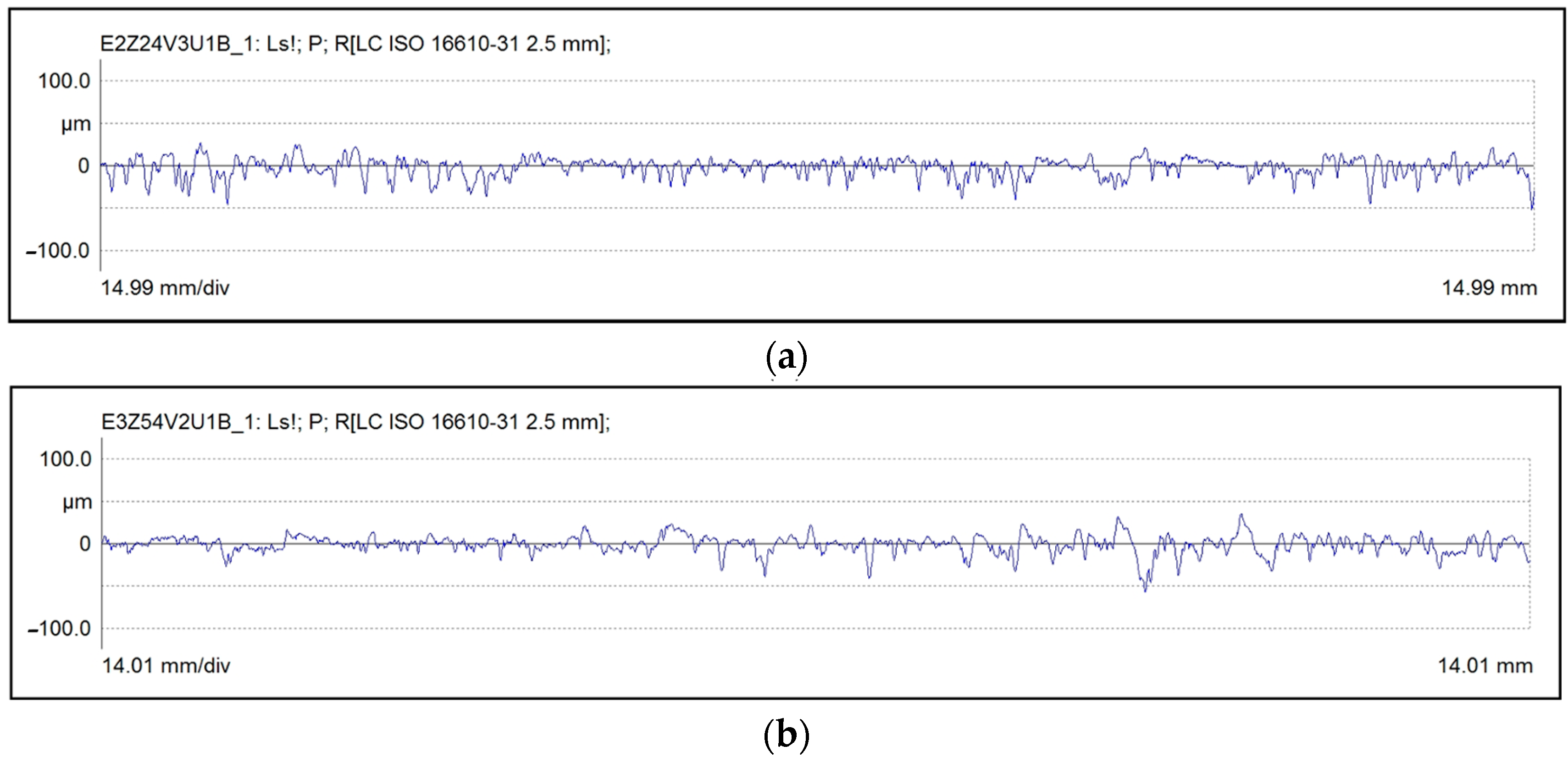
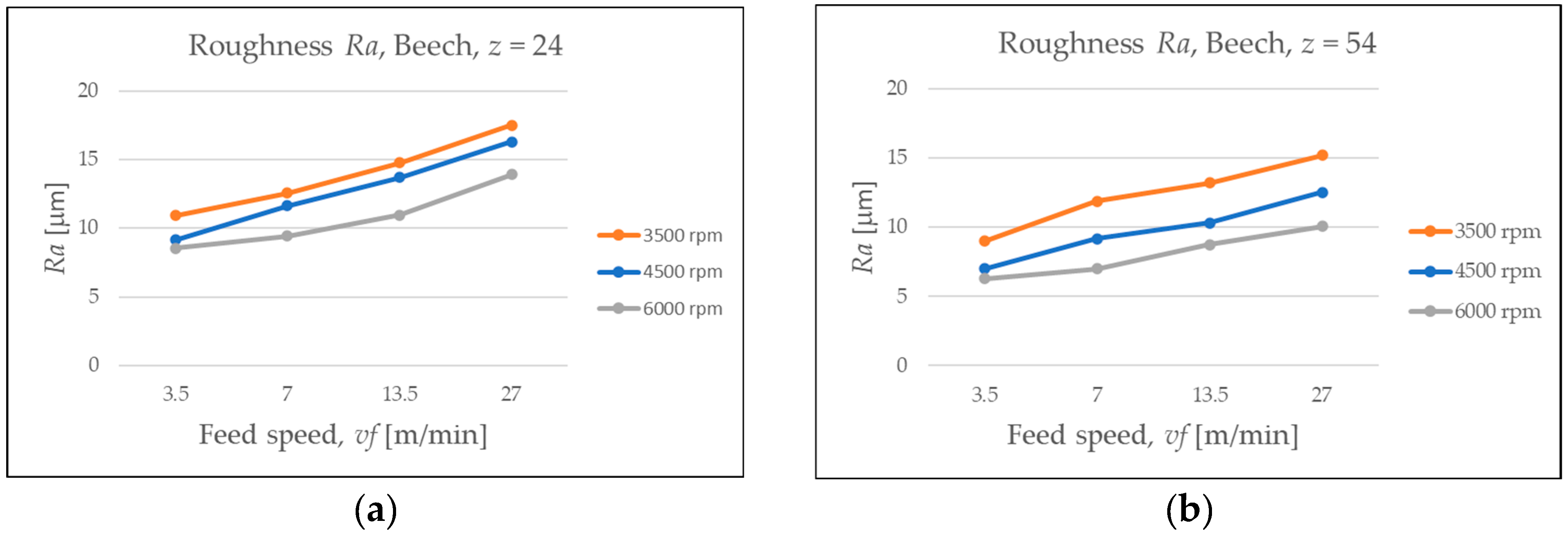
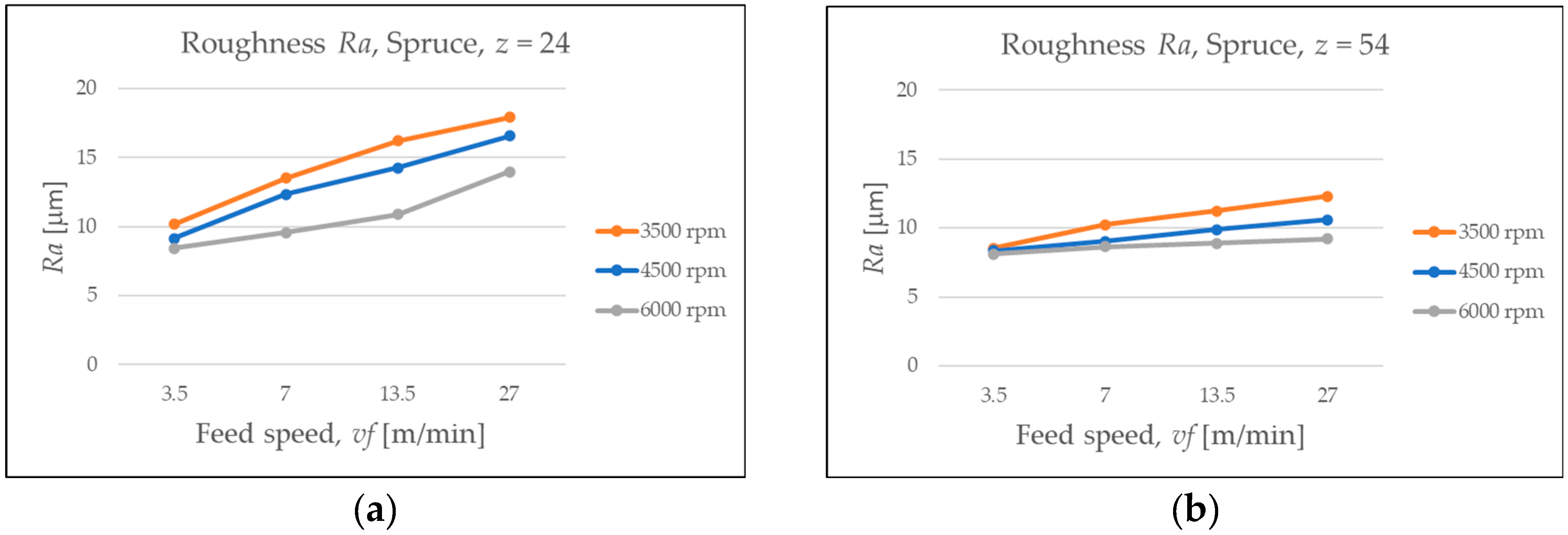
3.3.2. Roughness
4. Conclusions
- The feed speed is the most important factor that affects both the cutting power and surface roughness.
- The wood species affects only the cutting power. The surface roughness was not significantly influenced by the analyzed wood species.
- The blade rotational speed affects both the cutting power and the surface roughness.
- The tool type (number of cutting teeth and other blade geometries) affects both the cutting power and surface roughness. However, it is not clear if this is due to the difference between the numbers of teeth or to the geometric differences of the teeth. Further research is needed to clarify this uncertainty.
- Optimal cutting conditions (for both analyzed species) require a high rotational speed (6000 rpm) and a low feed speed (3.5 m/min) for a circular blade with z = 24 teeth. On the other hand, when a circular saw blade with z = 54 teeth is used, a rotational speed of 4500 rpm and a low feed speed (3.5 m/min) for the spruce and a moderate feed speed (7 m/min) is recommended by the optimization algorithm.
- The designed ANN models were developed and validated based on the experimental data. Both models are characterized by the high values of the performance indicators. Therefore, the models could be considered a reliable tool that could be used to predict the cutting power (Pc) and the surface roughness based on the Ra parameter either for practical or for research purposes. Moreover, both models could be integrated with other statistical techniques, like the Taguchi method, genetic algorithms, and the Monte Carlo method, to optimize the wood machining process in terms of energy consumption, surface quality, and raw material yield. As a limitation of ANN models, it could be stated that the number of cutting teeth and tooth geometry were not studied as individual independent variable. However, this issue could be studied in a further study. Moreover, in a further study, more wood species with different anatomical structures will be analyzed, and other parameters that better describe the surface roughness will be considered.
- As a general limitation of this study, it can be mentioned that circular blades with different numbers of teeth, but with identical geometry, were not considered during the experiments due to the fact that they were not available from the seller.
- From an industrial practice point of view, this study offers the possibility of choosing optimal processing regimes, including the type of saw blade to use. Thus, the computational model is able to “calculate” machining regimes that generate a certain surface quality at maximum productivity, under the conditions of using a certain tool, with a certain power consumption. These regimes may be more oriented towards superior surface quality and/or low energy consumption, or may be more oriented towards high productivity. In industrial conditions, minimum feed is not always justified due to loss of productivity. However, depending on the goal pursued, the management can take the appropriate decision. Models that take into account other factors, such as productivity and tool wear, among other factors, can be developed based on this study.
- Also, certain information can be useful to circular saw manufacturers, such as those related to spindle speeds. Further technical and economic studies are needed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pahlitzsch, V.G.; Friebe, E. On the Behaviour of Circular Sawblades during Cutting—Part II: Effect of the Cutting Conditions on the Quality of Sawn Wood Surfaces. Holz Als Roh-Und Werkst. 1971, 29, 265–269. (In German) [Google Scholar] [CrossRef]
- Hutton, S.G.; Lee, V.; Kirbach, E. Effect of tooth front bevel angle on cutting accuracy and chip formation for circular rip saws. Holz Als Roh Und Werkst. 1992, 50, 313–316. [Google Scholar] [CrossRef]
- Moraes de Souza, E.; Moreira da Silva, J.R.; Lima, J.T.; Napoli, A.; Raad, T.J.; Gontijo, T. Specific cutting energy consumption in a circular saw for Eucalyptus stands VM01 and MN463. Cerne Lavras 2011, 17, 109–115. [Google Scholar] [CrossRef][Green Version]
- Wasielewski, R.; Orlowski, K.A.; Szyszkowski, S. Economical Wood Sawing with Circular Saw Blades of a New Design. Drv. Ind. 2012, 63, 27–32. [Google Scholar] [CrossRef]
- Cristóvão, L.; Ekevad, M.; Grönlund, A. Industrial Sawing of Pinus sylvestris L. Power Consumption. BioResources 2013, 8, 6044–6053. [Google Scholar] [CrossRef]
- Kminiak, R. Effect of the saw blade construction on the surface quality when transverse sawing spruce lumber on crosscut miter saw. Acta Fac. Xylologiae Zvolen. 2014, 56, 87–96. [Google Scholar]
- Kminiak, R.; Gašparík, M.; Kvietková, M. The Dependence of Surface Quality on Tool Wear of Circular Saw Blades during Transversal Sawing of Beech Wood. BioResources 2015, 10, 7123–7135. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Z.; Peng, X.; Li, B. The influences of circular saws with sawteeth of mic-zero-degree radial clearance angles on surface roughness in wood rip sawing. Ann. For. Sci. 2017, 74, 37. [Google Scholar] [CrossRef]
- Andrade, A.C.A.; Silva, J.R.M.; Moulin, J.C.; Oliveira, M.B.; Souza, M.T.; Lima, L.C. Quality of machined surfaces and specific cutting energy in wood of two African mahogany species. Sci. For. 2018, 46, 532–539. [Google Scholar] [CrossRef]
- Fragassa, C.; Lucisano, G.; Marinkovic, D.; Campana, G.A. Practical Guideline in the Design and use of Woodworking Tools. FME Trans. 2019, 47, 487–495. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. Optimal power consumption and surface quality in the circular sawing process of Douglas-fir wood. Eur. J. Wood Wood Prod. 2019, 77, 609–617. [Google Scholar] [CrossRef]
- Krilek, J.; Ťavodová, M.; Kováč, J.; Tichý, B. Impact of Irregular Tooth Pitch of Circular Saw Blades on Power for Wood Cross-Cutting. Drv. Ind. 2020, 71, 3–11. [Google Scholar] [CrossRef]
- Kováč, J.; Harvánek, P.; Krilek, J.; Kuvik, T.; Melicherčík, J. Analysis of Cutting Conditions in the Process of Cross-cutting Wood by Circular Saws. BioResources 2021, 16, 1029–1041. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. Cutting power and surface quality in sawing kiln-dried, green, and frozen hem-fir wood. Wood Sci. Technol. 2021, 55, 505–519. [Google Scholar] [CrossRef]
- Pałubicki, B.; Hlásková, L.; Frömel-Frybort, S.; Rogozinski, T. Feed Force and Sawdust Geometry in Particleboard Sawing. Materials 2021, 14, 945. [Google Scholar] [CrossRef]
- Kvietková, M.S.; Gašparík, M. Surface irregularities of oak wood after transversal cutting with a circular saw. Wood Res. 2021, 66, 1032–1045. [Google Scholar] [CrossRef]
- Đukić, I.; Merhar, M.; Jovanović, J.; Herceg, D. Analysis of Circular Saw Tooth Marks Profile on Material Machined Surface After Filtering with Fast Fourier Transform (FFT). Drv. Ind. 2022, 73, 151–162. [Google Scholar] [CrossRef]
- Svoren, J.; Našcák, L.; Barcík, Š.; Koleda, P.; Stehlík, Š. Influence of Circular Saw Blade Design on Reducing Energy Consumption of a Circular Saw in the Cutting Process. Appl. Sci. 2022, 12, 1276. [Google Scholar] [CrossRef]
- Fekiac, J.; Svoren, J.; Gáborík, J.; Nemec, M. Reducing the Energy Consumption of Circular Saws in the Cutting Process of Plywood. Coatings 2022, 12, 55. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, F.; Li, X.; Wang, Y.; Zhang, T.; Guo, X. Optimization of oak sawing parameters based on energy consumption and surface roughness. Mater. Und Werkst. 2024, 55, 1346–1356. [Google Scholar] [CrossRef]
- Garrido, N.; Martins, J.; Davim, J.P.; Carvalho, L. Influence of machining parameters on edge quality of particleboards: Modeling and optimization. Int. J. Adv. Manuf. Technol. 2024, 133, 5463–5482. [Google Scholar] [CrossRef]
- Buldum, B.B.; Şik, A.; Akdağli, A.; Biçer, M.B.; Aldaş, K.; Özkul, I. ANN surface roughness prediction of AZ91D magnesium alloys in the turning process. Mater. Test. 2017, 59, 916–920. [Google Scholar] [CrossRef]
- Varatharajulu, M.; Jayaprakash, G.; Baskar, N.; Saravanan, A. Genetic algorithm assisted artificial neural network for the estimation of drilling parameters of magnesium AZ91 in vertical milling machine. Surf. Rev. Lett. 2020, 27, 1950221. [Google Scholar] [CrossRef]
- Kulisz, M.; Zagorski, I.; Jozwik, J.; Korpysa, J. Research, modelling and prediction of the influence of technological parameters on the selected 3D roughness parameters, as well as temperature, shape and geometry of chips in milling AZ91D alloy. Materials 2022, 15, 4277. [Google Scholar] [CrossRef]
- Pai, V.M.S.; Udaya, G.D.; Bhat, K.; Thakur, D.; Bhaskara, A. Meta-heuristic algorithm-based optimization studies in cryogenic and conventional milling of magnesium alloy AZ91. Results Eng. 2025, 27, 106256. [Google Scholar] [CrossRef]
- Ren, X.; Fan, J.; Pan, R.; Sun, K. Modeling and process parameter optimization of laser cutting based on artificial neural network and intelligent optimization algorithm. Int. J. Adv. Manuf. Technol. 2023, 127, 1177–1188. [Google Scholar] [CrossRef]
- Song, H.; Ren, G.; Dan, J.; Li, J.; Xiao, J.; Xu, J. Experimental Study of the Cutting Force During Laser-Assisted Machining of Fused Silica Based on Artificial Neural Network and Response Surface Methodology. Silicon 2019, 11, 1903–1916. [Google Scholar] [CrossRef]
- Naresh, C.; Sameer, M.D.; Bose, P.S.C. Comparative Analysis of RSM, ANN and ANFIS Techniques in Optimization of Process Parameters in Laser Assisted Turning of NITINOL Shape Memory Alloy. Lasers Manuf. Mater. Process. 2024, 11, 371–401. [Google Scholar] [CrossRef]
- Meddour, I.; Yallese, M.A.; Bensouilah, H.; Khellaf, A.; Elbah, M. Prediction of surface roughness and cutting forces using RSM, ANN, and NSGA-II in finish turning of AISI 4140 hardened steel with mixed ceramic tool. Int. J. Adv. Manuf. Technol. 2018, 97, 1931–1949. [Google Scholar] [CrossRef]
- Bedelean, B.; Ispas, M.; Răcășan, S. Optimizing Wood Composite Drilling with Artificial Neural Network and Response Surface Methodology. Forests 2024, 15, 1600. [Google Scholar] [CrossRef]
- Bedelean, B.; Ispas, M.; Răcășan, S. Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels. Forests 2023, 14, 2254. [Google Scholar] [CrossRef]
- EN IEC 60688:2024; Electrical Measuring Transducers for Converting AC and DC Electrical Quantities to Analogue or Digital Signals. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2021.
- ISO 16610-31:2016; Geometrical Product Specifications (GPS)—Filtration Part 31: Robust Profile Filters: Gaussian Regression Filters. ISO: Geneva, Switzerland, 2016.
- Gurău, L. The Roughness of Sanded Wood Surfaces. Ph.D. Thesis, Forest Products Research Centre, Buckinghamshire Chilterns University College, Buckinghamshire, UK, 2004. [Google Scholar]
- Tan, P.L.; Sharif, S.; Sudin, I. Roughness Models for Sanded Wood Surfaces. Wood Sci. Technol. 2012, 46, 129–142. [Google Scholar] [CrossRef]
- ISO 21920-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- NeuralWare. NeuralWorks Predict. The Complete Solution for Neural Data Modeling. User Guide; NeuralWare Inc.: Carnagie, PA, USA, 2009; pp. 10–22. [Google Scholar]
- Watanabe, K.; Korai, H.; Matsushita, Y.; Hayashi, T. Predicting internal bond strength of particleboard under outdoor exposure based on climate data: Comparison of multiple linear regression and artificial neural network. J. Wood Sci. 2015, 61, 151–158. [Google Scholar] [CrossRef]




| Numeric Factor | Level | ||||
|---|---|---|---|---|---|
| −α * | −1 | 0 | +1 | +α * | |
| Blade rotation speed (X1), rpm | 3500 | 3500 | 4750 | 6000 | 6000 |
| Feed speed (X2), m/min | 3.5 | 3.5 | 15.25 | 27 | 27 |
| Categoric Factor | Level 1 | Level 2 | |||
| Wood species (X3) | Beech (−1) | Spruce (+1) | |||
| Tool type (different number of teeth and blade geometries) (X4) | z24 (−1) | z54 (+1) | |||
| Combination | Factors | Responses | ||||
|---|---|---|---|---|---|---|
| Blade Rotation Speed (X1), rpm | Feed Speed (X2), m/min | Wood Species (X3) | Tool Type (Number of Cutting Teeth and Blade Geometries) (X4) | Cutting Power, kW, (Y1) | Arithmetical Mean Deviation (Ra), (Y2) μm | |
| 1. | 6000 (+1) | 3.5 (−1) | Spruce (+1) | z24 (−1) | 0.29 | 8.41 |
| 2. | 3500 (−1) | 27 (+1) | Spruce (+1) | z24 (−1) | 1.02 | 17.32 |
| 3. | 4750 (0) | 27 (+1) | Beech (−1) | z54 (+1) | 1.65 | 11.27 |
| 4. | 3500 (−1) | 3.5 (−1) | Spruce (+1) | z24 (−1) | 0.26 | 11.04 |
| 5. | 3500 (−1) | 15.25 (0) | Beech (−1) | z24 (−1) | 0.91 | 16.00 |
| 6. | 4750 (0) | 15.25 (0) | Beech (−1) | z54 (+1) | 1.25 | 9.94 |
| 7. | 3500 (−1) | 27 (+1) | Beech (−1) | z54 (+1) | 1.45 | 13.65 |
| 8. | 6000 (+1) | 27 (+1) | Spruce (−1) | z24 (−1) | 1.22 | 14.10 |
| 9. | 4750 (0) | 3.5 (−1) | Beech (−1) | z54 (+1) | 0.51 | 7.62 |
| 10. | 4750 (0) | 15.25 (0) | Spruce (+1) | z54 (+1) | 0.81 | 9.94 |
| 11. | 6000 (+1) | 27 (+1) | Spruce (+1) | z54 (+1) | 1.50 | 9.80 |
| 12. | 6000 (+1) | 15.25 (0) | Spruce (+1) | z54 (+1) | 1.09 | 8.61 |
| 13. | 6000 (+1) | 3.5 (−1) | Beech (−1) | z24 (−1) | 0.38 | 8.41 |
| 14. | 6000 (+1) | 27 (+1) | Beech (−1) | z24 (−1) | 1.50 | 14.10 |
| 15. | 6000 (+1) | 15.25 (0) | Beech (−1) | z54 (+1) | 1.51 | 8.61 |
| 16. | 4750 (0) | 3.5 (−1) | Spruce (+1) | z54 (+1) | 0.34 | 7.62 |
| 17. | 3500 (−1) | 15.25 (0) | Spruce (+1) | z24 (−1) | 0.64 | 16.00 |
| 18. | 4750 (0) | 15.25 (0) | Beech (−1) | z24 (−1) | 1.01 | 13.40 |
| 19. | 3500 (−1) | 3.5 (−1) | Beech (−1) | z24 (−1) | 0.29 | 11.04 |
| 20. | 4750 (0) | 27 (+1) | Spruce (+1) | z24 (−1) | 1.12 | 16.10 |
| 21. | 3500 (−1) | 15.25 (0) | Spruce (+1) | z54 (+1) | 0.67 | 12.13 |
| 22. | 4750 (0) | 15.25 (0) | Spruce (+1) | z24 (−1) | 0.73 | 13.40 |
| 23. | 6000 (+1) | 15.25 (0) | Beech (−1) | z24 (−1) | 1.17 | 11.50 |
| 24. | 4750 (0) | 27 (+1) | Spruce (+1) | z54 (+1) | 1.24 | 11.27 |
| 25. | 6000 (+1) | 27 (+1) | Beech (−1) | z54 (+1) | 1.86 | 9.80 |
| 26. | 4750 (0) | 3.5 (−1) | Spruce (+1) | z24 (−1) | 0.27 | 9.37 |
| 27. | 4750 (0) | 3.5 (−1) | Beech (−1) | z24 (−1) | 0.32 | 9.37 |
| 28. | 3500 (−1) | 3.5 (−1) | Beech (−1) | z54 (+1) | 0.39 | 8.89 |
| 29. | 4750 (0) | 27 (+1) | Beech (−1) | z24 (−1) | 1.38 | 16.10 |
| 30. | 6000 (+1) | 3.5 (−1) | Beech (−1) | z54 (+1) | 0.63 | 6.90 |
| 31. | 3500 (−1) | 27 (+1) | Spruce (+1) | z54 (+1) | 1.08 | 13.65 |
| 32. | 6000 (+1) | 15.25 (0) | Spruce (+1) | z24 (−1) | 0.84 | 11.50 |
| 33. | 6000 (+1) | 3.5 (−1) | Spruce (+1) | z54 (+1) | 0.44 | 6.90 |
| 34. | 3500 (−1) | 27 (+1) | Beech (−) | z24 (−1) | 1.30 | 17.32 |
| 35. | 3500 (−1) | 15.25 (0) | Beech (−) | z54 (+1) | 1.00 | 12.13 |
| 36. | 3500 (−1) | 3.5 (−1) | Spruce (+1) | z54 (+1) | 0.30 | 8.89 |
| Dependent Variable | Number of Neurons in the Layers of ANN Models | Coefficient of Correlation (R) | Validation Phase | ||||
|---|---|---|---|---|---|---|---|
| Input | Hidden | Outlet | Training Phase | Testing Phase | RMSE | MAPE | |
| Cutting power, kW | 4 | 6 | 1 | 0.987 | 0.986 | 0.13 | 19.78 |
| Roughness (Ra), μm | 4 | 5 | 1 | 0.985 | 0.933 | 1.00 | 8.59 |
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 7.50 | 11 | 0.68 | 433.46 | <0.0001 | Significant |
| Rotation speed (X1) | 0.41 | 1 | 0.41 | 257.93 | <0.0001 | Significant |
| Feed speed (X2) | 5.90 | 1 | 5.90 | 3753.17 | <0.0001 | Significant |
| Species (X3) | 0.36 | 1 | 0.36 | 227.97 | <0.0001 | Significant |
| Tool type (X4) | 0.26 | 1 | 0.26 | 167.65 | <0.0001 | Significant |
| X1X2 | 0.033 | 1 | 0.033 | 21.16 | 0.0001 | Significant |
| X1X4 | 0.056 | 1 | 0.058 | 36.82 | <0.0001 | Significant |
| X2X3 | 0.074 | 1 | 0.074 | 46.78 | <0.0001 | Significant |
| X2X4 | 0.0074 | 1 | 0.0074 | 4.74 | 0.0396 | Significant |
| X3X4 | 0.021 | 1 | 0.021 | 13.33 | 0.0013 | Significant |
| 0.090 | 1 | 0.090 | 57.44 | <0.0001 | Significant | |
| 0.038 | 1 | 0.033 | 20.78 | 0.0001 | Significant | |
| R2 | 0.98 | |||||
| “Source” | “Sum of Squares” | “df” | “Mean Square” | “F-Value” | “p-Value Prob > F” | Observation |
|---|---|---|---|---|---|---|
| Model | 320.00 | 7 | 45.71 | 373.61 | <0.0001 | Significant |
| Rotation speed (X1) | 64.67 | 1 | 64.67 | 528.51 | <0.0001 | Significant |
| Feed speed (X2) | 150.12 | 1 | 150.12 | 1226.91 | <0.0001 | Significant |
| Species (X3) | - | - | - | - | - | Not significant |
| Tool type (X4) | 89.89 | 1 | 89.89 | 734.65 | <0.0001 | Significant |
| X1X2 | 1.49 | 1 | 1.49 | 12.15 | 0.0016 | Significant |
| X2X4 | 9.13 | 1 | 9.13 | 74.58 | <0.0001 | Not significant |
| 0.49 | 1 | 0.49 | 4.01 | 0.0549 | Not significant | |
| 4.22 | 1 | 4.22 | 34.48 | <0.0001 | Significant | |
| R2 | 0.98 | |||||
| Independent Variables | Goal Settings | Minimum Value | Maximum Value | Level of Factor Importance | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rotation speed (X1), [rpm] | In range | 3500 | 6000 | 3 | ||||||
| Feed speed (X2), [m/min] | 3.5 | 27 | 3 | |||||||
| Species (X3) | Beech | Spruce | 3 | |||||||
| Tool type (X4) | z24 | z54 | 3 | |||||||
| Dependent variables | ||||||||||
| Cutting power (Y1), [kW] | Minimize | 0.25 | 1.85 | 3 | ||||||
| Roughness (Y2), [μm] | 6.89 | 17.31 | 3 | |||||||
| Optimal solutions | ||||||||||
| % | X2 | X3 | X4 | Cutting power [kW] | Roughness, [μm] | D | ||||
| Y1 | ER1,% | Y2 | ER2, % | |||||||
| 6000 | 3.5 | Beech | z24 | 0.364 | 0.56 | 35.71 | 8.41 | 9.13 | 7.88 | 0.893 |
| 4500 | 7 | Beech | z54 | 0.740 | 0.78 | 5.12 | 8.80 | 9.18 | 4.13 | 0.883 |
| 6000 | 3.5 | Spruce | z24 | 0.306 | 0.33 | 7.27 | 8.41 | 8.22 | 2.31 | 0.910 |
| 4500 | 3.5 | Spruce | z54 | 0.331 | 0.42 | 21.19 | 7.85 | 8.65 | 9.24 | 0.930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ispas, M.; Răcășan, S.; Bedelean, B.; Angelescu, A.-M. Integration of ANN and RSM to Optimize the Sawing Process of Wood by Circular Saw Blades. Appl. Sci. 2025, 15, 10206. https://doi.org/10.3390/app151810206
Ispas M, Răcășan S, Bedelean B, Angelescu A-M. Integration of ANN and RSM to Optimize the Sawing Process of Wood by Circular Saw Blades. Applied Sciences. 2025; 15(18):10206. https://doi.org/10.3390/app151810206
Chicago/Turabian StyleIspas, Mihai, Sergiu Răcășan, Bogdan Bedelean, and Ana-Maria Angelescu. 2025. "Integration of ANN and RSM to Optimize the Sawing Process of Wood by Circular Saw Blades" Applied Sciences 15, no. 18: 10206. https://doi.org/10.3390/app151810206
APA StyleIspas, M., Răcășan, S., Bedelean, B., & Angelescu, A.-M. (2025). Integration of ANN and RSM to Optimize the Sawing Process of Wood by Circular Saw Blades. Applied Sciences, 15(18), 10206. https://doi.org/10.3390/app151810206







