IPP and PRT Depolarizing Spaces for the Study of Depolarizing Samples: A Review
Abstract
1. Introduction
2. Methodology of Depolarizing Spaces
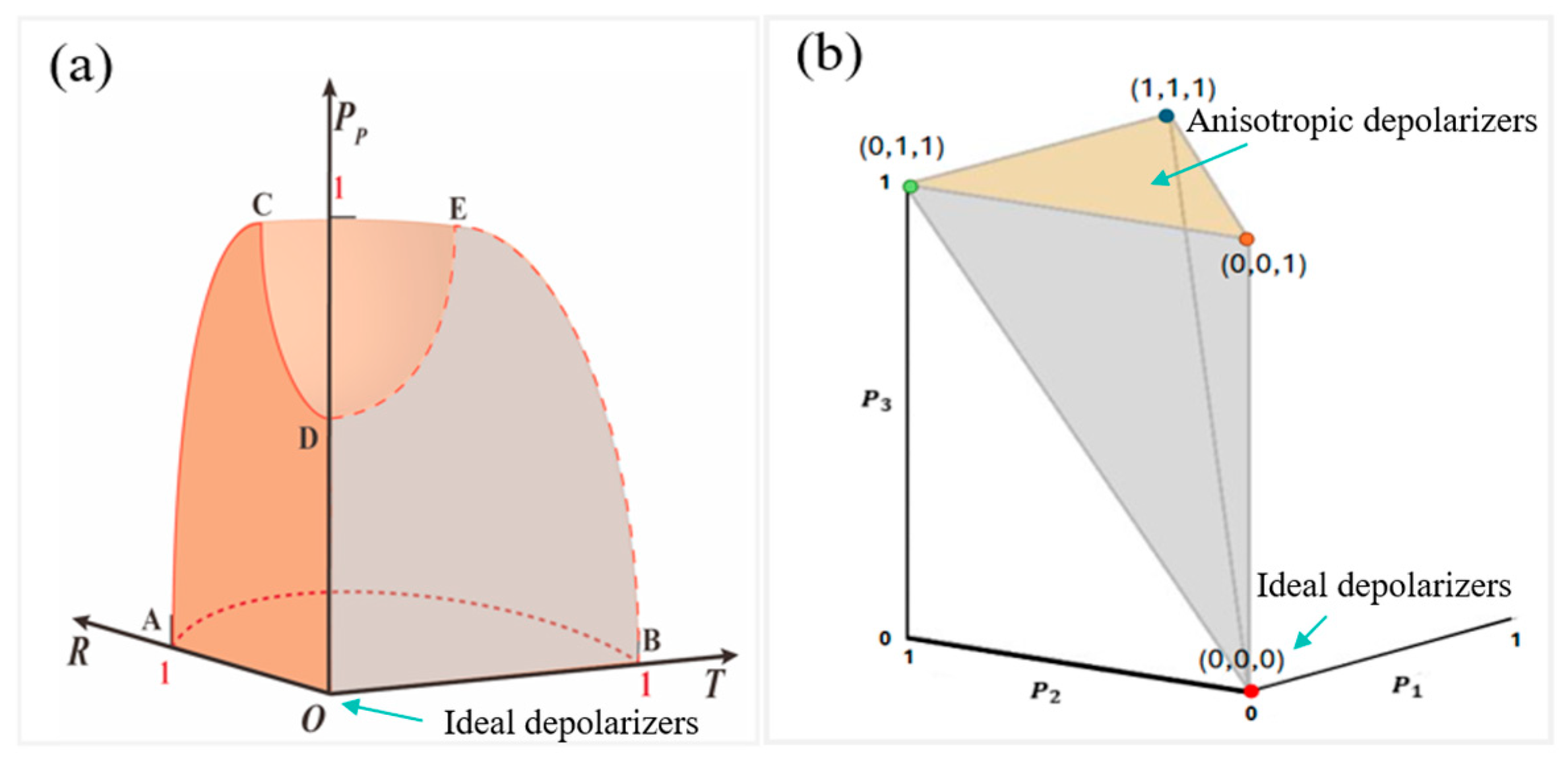
2.1. The PRT Space
2.2. The IPP Space
2.3. Characteristic Decomposition of MMs
3. Discriminating Between Anisotropic and Isotropic Depolarization Origins by the IPP Space
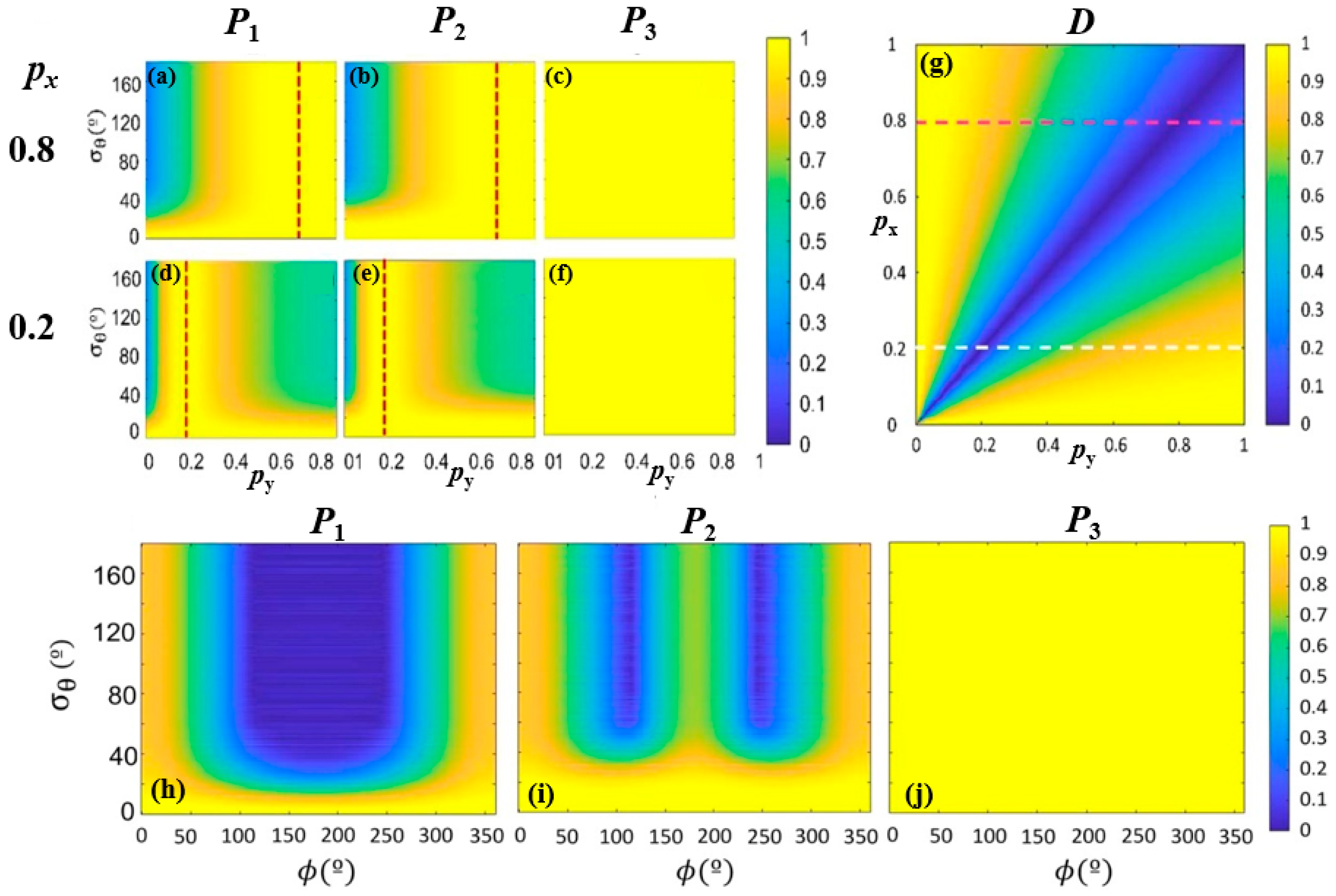
3.1. Anisotropic Origin Behavior Presented by IPP Channels
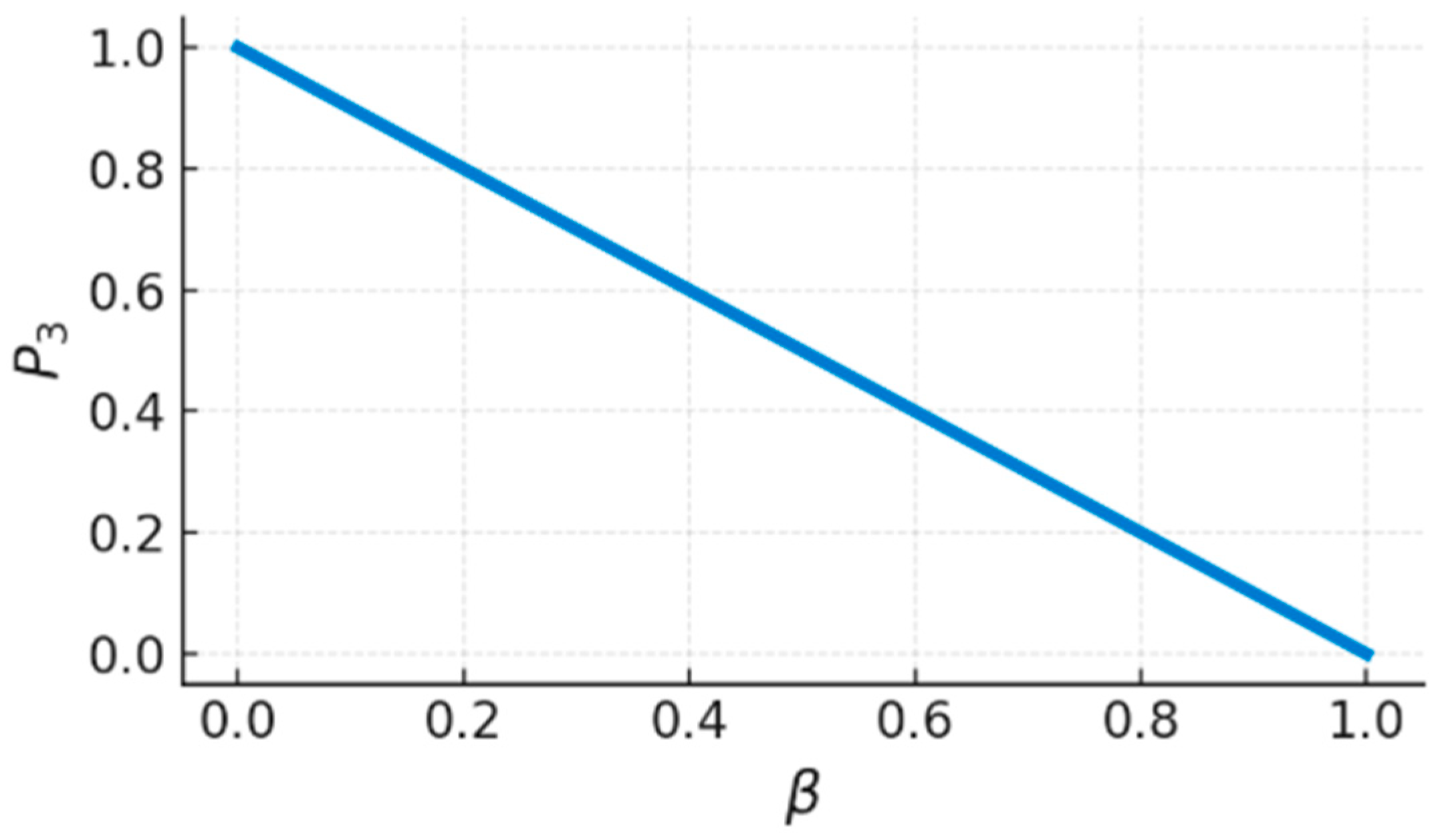
3.2. Isotropic Depolarization Behavior Presented by IPP
4. Combining IPP and PRT Spaces for the Characterization of Anisotropic Depolarizers
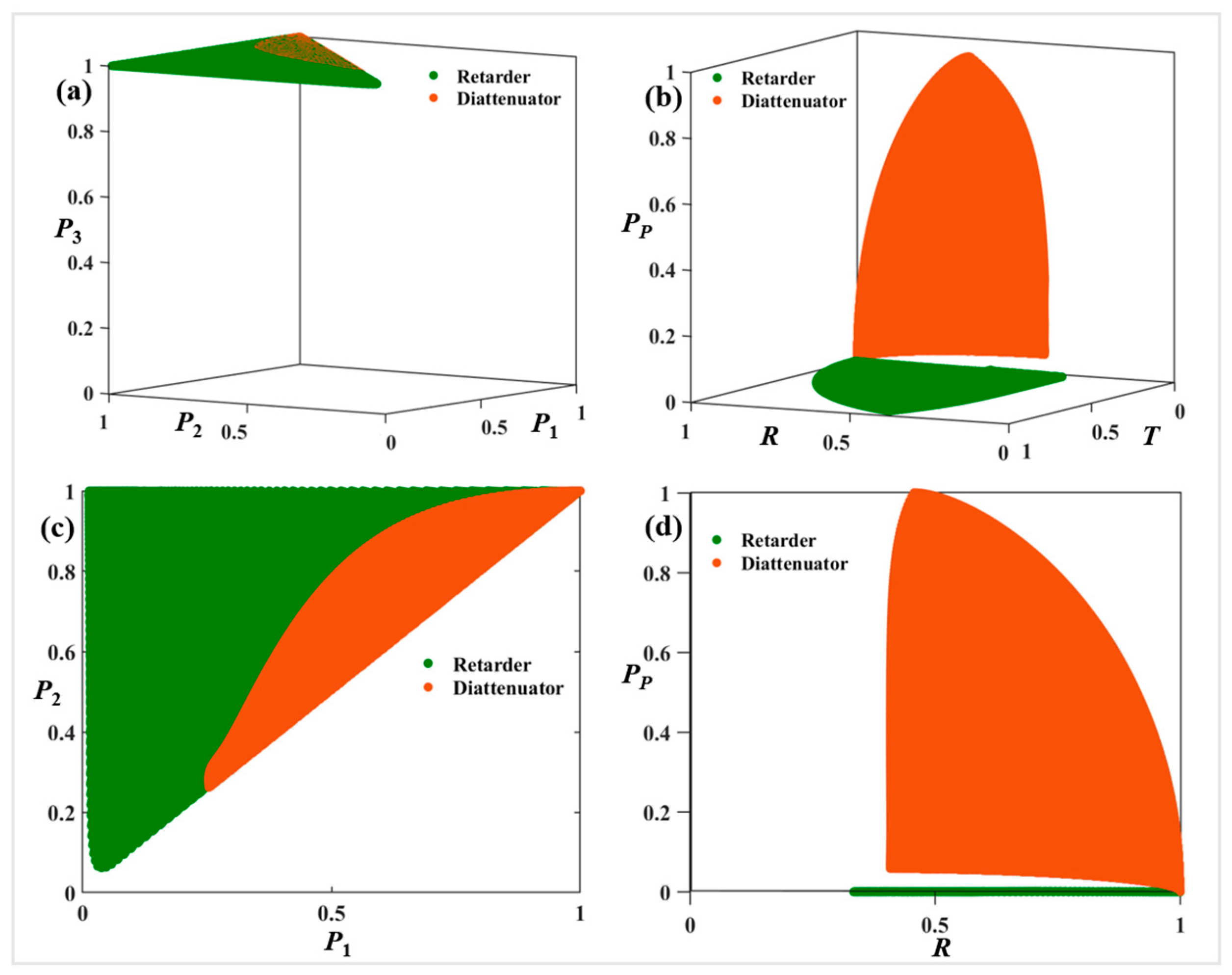
4.1. Retarder-Based and Diattenuator-Based Depolarizer Discrimination
4.2. Characterization of Anisotropic Depolarizers According to Their Inherent Structural Characteristics
4.3. Physical Parameter Characterization from PRT Space Polarimetric Observables
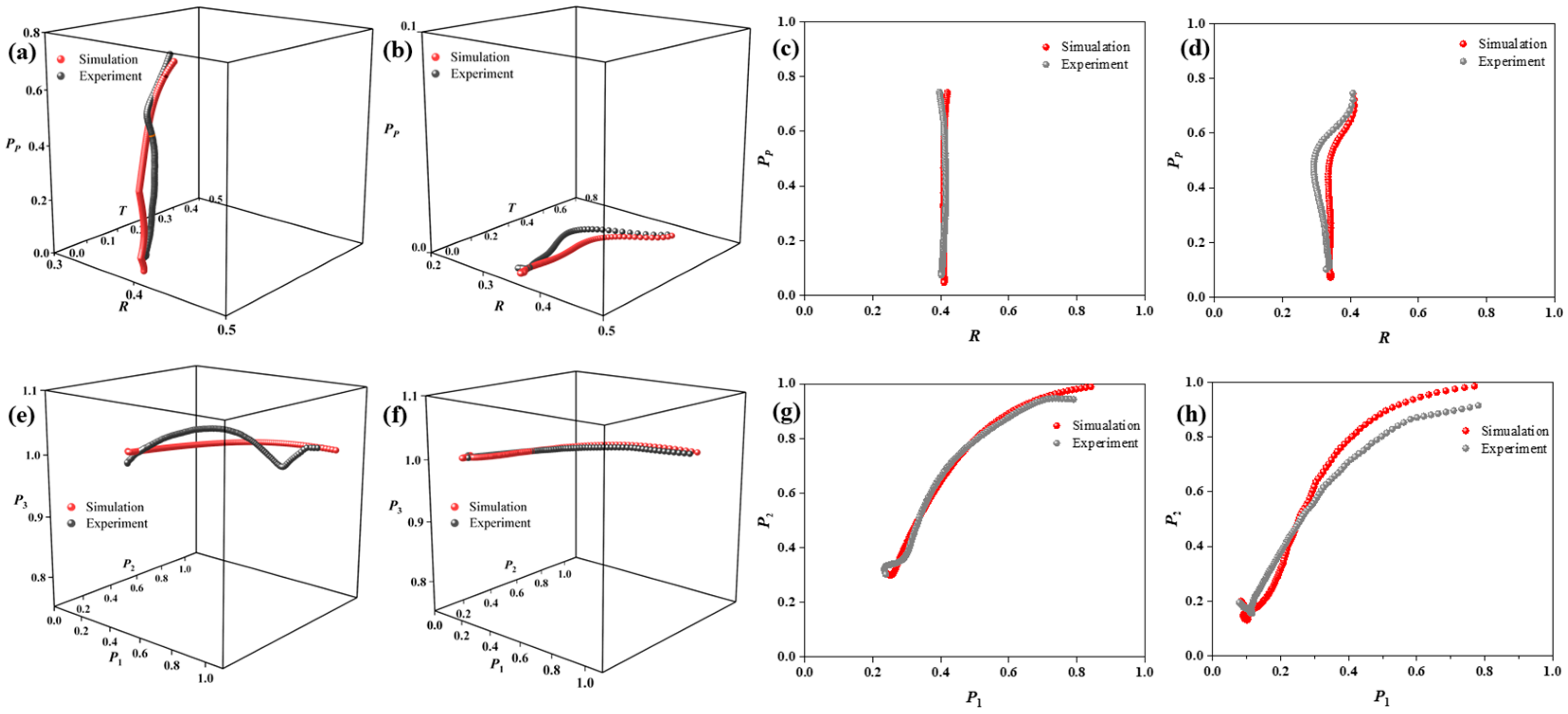
5. Experimental Validation
5.1. Experimental Results for the P3 = 1 Case
5.2. Experimental Results for the P3 < 1 Case
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brosseau, C. Fundamentals of Polarized Light: A Statistical Optics Approach; John Wiley: Hoboken, NJ, USA, 1998. [Google Scholar][Green Version]
- Tyo, J.; Goldstein, D.L.; David, B.C.; Joseph, A.S. Review of passive imaging polarimetry for remote sensing applications. Appl. Opt. 2006, 45, 5453–5469. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light. Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef] [PubMed]
- He, C.; He, H.; Chang, J.; Dong, Y.; Liu, S.; Zeng, N. Characterizing microstructures of cancerous tissues using multispectral transformed Mueller matrix polarization parameters. Biomed. Opt. Express 2015, 17, 2934–2945. [Google Scholar] [CrossRef]
- Dubreuil, M.; Tissier, F.; Rivet, S.; Le, G. Linear diattenuation imaging of biological tissues with near infrared Mueller scanning microscopy. Biomed. Opt. Express 2021, 12, 41–54. [Google Scholar] [CrossRef]
- Menzel, M.; Axer, M.; Amunts, K.; De Raedt, H.; Michielsen, K. Diattenuation imaging reveals different brain tissue properties. Sci. Rep. 2019, 9, 1939. [Google Scholar] [CrossRef] [PubMed]
- Novák, J.; Iliyan, G.; Johannes, H. Monte Carlo methods for volumetric light transport simulation. Comput. Graph. Forum 2018, 37, 551–576. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, X.; He, H.; Ma, H. GPU acceleration of Monte Carlo simulations for polarized photon scattering in anisotropic turbid media. Appl. Opt. 2016, 55, 7468–7476. [Google Scholar] [CrossRef]
- Luo, K.; Fu, Q.; Liu, X.; Zhao, R. Study of polarization transmission characteristics in nonspherical media. Opt. Lasers Eng. 2024, 174, 107970. [Google Scholar] [CrossRef]
- Huang, B.; Liu, T.; Hu, H. Underwater image recovery considering polarization effects of objects. Opt. Express 2016, 24, 9826–9838. [Google Scholar] [CrossRef]
- Nadal, F.; Bréon, F.M. Parameterization of surface polarized reflectance derived from POLDER spaceborne measurements. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1709–1718. [Google Scholar] [CrossRef]
- Li, P.; Lee, H.; Chandel, S.; Lotz, C.; Dembski, S.; Ossikovski, R.; Ma, H.; Novikova, T. Analysis of tissue microstructure with Mueller microscopy: Logarithmic decomposition and Monte Carlo modelling. J. Biomed. Opt. 2020, 25, 015002. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modelling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Keijzer, M.; Jacques, S.L.; Prahl, S.A. Light distributions in artery tissue: Monte Carlo simulations for finite-diameter laser beams Lasers. Surg. Endosc. 1989, 9, 148–154. [Google Scholar] [CrossRef]
- Marshall, N.; Powell, S.; Cronin, T. Polarisation signals a new currency for communication. J. Exp. Biol. 2019, 222, 134213. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, J.; Ren, L. Polarimetric dehazing method for visibility improvement based on visible and infrared image fusion. Appl. Opt. 2016, 55, 8221–8226. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Ren, L.; Ju, H.; Qu, E.; Wang, Y. Visibility enhancement of hazy images based on a universal polarimetric imaging method. J. Appl. Phys. 2014, 116, 173107–173113. [Google Scholar] [CrossRef]
- Liang, J.; Ren Li Ju, H.; Zhang, W.; Qu, E. Polarimetric dehazing method for dense haze removal based on distribution analysis of angle of polarization. Opt. Express 2015, 23, 26146–26157. [Google Scholar] [CrossRef]
- Thilak, V.; Voelz, D.; Creusere, C. Polarization-Based Index of Refraction and Reflection Angle Estimation for Remote Sensing Applications. Appl. Opt. 2007, 46, 7527–7536. [Google Scholar] [CrossRef] [PubMed]
- Agnoil, G.; Cacciari, M.; Garutti, C.; Lenzi, P. Ship detection performance using simulated dual-polarization radarsat constellation mission data. Int. J. Remote Sens. 2015, 36, 1705–1727. [Google Scholar]
- Wang, Y.; Ainsworth, T.; Lee, J. Assessment of System Polarization Quality for Polarimetric SAR Imagery and Target Decomposition. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1755–1771. [Google Scholar] [CrossRef]
- Karouzos, M. Cloudy with a chance of depolarization. Nat. Astron. 2021, 5, 224. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Han, P.L.; Zhang, S.; Shao, X.P. Near-infrared monocular 3D computational polarization imaging of surfaces exhibiting nonuniform reflectance. Opt. Express 2021, 29, 15616–15630. [Google Scholar] [CrossRef]
- Ballesta-Garcia, M.; Peña-Gutiérrez, S.; Rodríguez-Aramendía, A.; García-Gómez, P.; Rodrigo, N.; Bobi, A.R. Analysis of the performance of a polarized LiDAR imager in fog. Opt. Express 2022, 30, 41524–41540. [Google Scholar] [CrossRef] [PubMed]
- Estévez, I.; Oliveira, F.; Braga-Fernandes, P.; Oliveira, M.; Rebouta, L.; IVasilevskiy, M. Urban objects classification using Mueller matrix polarimetry and machine learning. Opt. Express 2022, 30, 28385–28400. [Google Scholar] [CrossRef]
- Maldzius, R.; Lozovski, T.; Sidaravicius, J. Influence of environmental relative humidity on the polarization behaviour of paper and paper-dielectric structures. Cellulose 2020, 27, 10303–10312. [Google Scholar] [CrossRef]
- Lizana, A.; Foldyna1, M.; Stchakovsky, M.; Georges, B.; Nicolas, D.; Garcia-Caurel, E. Enhanced sensitivity to dielectric function and thickness of absorbing thin films by combining total internal reflection ellipsometry with standard ellipsometry and reflectometry. J. Phys. D Appl. Phys. 2013, 46, 105501. [Google Scholar] [CrossRef]
- Nabok, A.; Tsargorodskaya, A. The method of total internal reflection ellipsometry for thin film characterisation and sensing. Thin Solid Film. 2008, 516, 8993–9001. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Ouyang, M.; Zhu, Q.; Fu, Y. Tunable Circular Polarization Detection and Full Stokes Measurement Structure. IEEE Photonics J. 2021, 13, 5800109. [Google Scholar] [CrossRef]
- Ivanov, D.; Dremin, V.; Borisova, E.; Bykov, A.; Novikova, T.; Meglinski, I.; Ossikovski, R. Polarization and depolarization metrics as optical markers in support to histopathology of ex vivo colon tissue. Biomed. Opt. Express 2021, 12, 4560–4572. [Google Scholar] [CrossRef]
- Pierangelo, A.; Benali, A.; Antonelli, M.-R.; Novikova, T.; Validire, P.; Gayet, B. Ex-vivo characterization of human colon cancer by Mueller polarimetric imaging. Opt. Express 2011, 19, 1582. [Google Scholar] [CrossRef]
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J. Biomed. Opt. 2014, 19, 076013. [Google Scholar] [CrossRef] [PubMed]
- Tariq, A.; Li, P.; Chen, D.; Lv, D.; Ma, H. Physically realizable space for the purity-depolarization plane for polarized light scattering media. Phys. Rev. Lett. 2017, 119, 033202. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Chipman, R. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Garcia-Caurel, E.; Garnatje, T.; Durfort, M.; Escalera, J.C.; Vidal, J.; Gil, J.J.; Campos, J.; Lizana, A. Depolarizing metrics for plant samples imaging. PLoS ONE 2019, 14, e0213909. [Google Scholar] [CrossRef]
- Li, D. Polarizance-Reflection-Transformation representation space for sensing and distinguishing pure systems. IEEE Sens. J. 2025, 24, 14763–14769. [Google Scholar] [CrossRef]
- Gil, J.J.; Ossikovski, R. Polarized Light and the Mueller Matrix Approach; CRC Press: New York, NY, USA, 2022. [Google Scholar]
- Rodríguez, C.; Van Eeckhout, A.; Ferrer, L.; Garcia-Caurel, E.; Gonz’alez-Arnay, E.; Campos, J. Polarimetric data-based model for tissue recognition. Biomed. Opt. Express 2021, 12, 4852. [Google Scholar] [CrossRef]
- He, C.; Chang, J.; Salter, S.; Shen, Y.; Dai, B.; Li, P.; Ma, H.; Booth, M. Revealing complex optical phenomena through vectorial metrics. Adv. Photonics 2022, 4, 026001. [Google Scholar] [CrossRef]
- Aiello, A.; Woerdman, J. Physical Bounds to the Entropy-Depolarization Relation in Random Light Scattering. Phys. Rev. Lett. 2005, 94, 090406. [Google Scholar] [CrossRef]
- Ossikovski, R.; Vizet, J. Eigenvalue-based depolarization metric spaces for Mueller matrices. J. Opt. Soc. Am. A 2019, 36, 1173–1186. [Google Scholar] [CrossRef]
- Tariq, A.; He, H.; Li, P.; Ma, H. Purity-depolarization relations and the components of purity of a Mueller matrix. Opt. Express 2019, 27, 22645–22662. [Google Scholar] [CrossRef]
- Eeckhout, A.; Lizana, E.; Gil, J.; Ossikovski, R.; Campos, J. Synthesis and characterization of depolarizing samples based on the indices of polarimetric purity. Opt. Lett. 2017, 42, 4155–4158. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Qi, P.; Zhu, Z.; Xu, J.; Liu, T.; Hu, H. Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media? Remote Sens. 2022, 14, 4148. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Lizana, A.; Garcia-Caurel, E.; Gil, J.J.; Sansa, A.; Rodríguez, C. Polarimetric imaging of biological tissues based on the indices of polarimetric purity. J. Biophotonics 2018, 11, e201700189. [Google Scholar] [CrossRef]
- Rodríguez, C.; Van Eeckhout, A.; Garcia-Caurel, E.; Lizana, A.; Campos, J. Automatic pseudo-coloring approaches to improve visual perception and contrast in polarimetric images of biological tissues. Sci. Rep. 2022, 12, 18479. [Google Scholar] [CrossRef]
- Li, D.; Montes, I.; Canabal-Carbia, M.; Estévez, I.; Guo, Z.; Campos, J.; Lizana, A. Enhanced characterization of depolarizing samples using indices of polarization purity and polarizance–reflection–transformation spaces. Adv. Photon. Nexus 2025, 4, 016009. [Google Scholar] [CrossRef]
- Ossikovski, R.; Martino, A.; Guyot, S. Forward and reverse product decompositions of depolarizing Mueller matrices. Opt. Lett. 2007, 32, 689–691. [Google Scholar] [CrossRef] [PubMed]
- Ossikovski, R. Analysis of depolarizing Mueller matrices through a symmetric decomposition. J. Opt. Soc. Am. A 2009, 26, 1109–1118. [Google Scholar] [CrossRef]
- Canabal-Carbia, M.; Estévez, I.; Nabadda, E.; Garcia-Caurel, E.; Gil, J.; Ossikovski, R.; Márquez, A.; Moreno, I.; Campos, J.; Lizana, A. Connecting the microscopic depolarizing origin of samples with macroscopic measures of the Indices of Polarimetric Purity. Opt. Lasers Eng. 2024, 172, 107830. [Google Scholar] [CrossRef]
- Canabal-Carbia, M.; Estévez, I.; González-Arnay, E.; Montes-Gonzalez, I.; Gil, J.; Garcia-Caurel, E.; Ossikovski, R.; Moreno, I.; Campos, J.; Lizana, A. Revealing hidden bioimaging information by isotropic depolarization filtering. Opt. Laser Technol. 2025, 188, 112956. [Google Scholar] [CrossRef]
- Gil, J.J. Polarimetric characterization of light and media: Physical quantities involved in polarimetric phenomena. Eur. Phys. J. Appl. Phys. 2007, 40, 1–47. [Google Scholar] [CrossRef]
- San José, I.; Gil, J.J. Invariant indices of polarimetric purity: Generalized indices of purity for n × n covariance matrices. Opt. Commun. 2011, 284, 38–47. [Google Scholar] [CrossRef]
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ossikovski, R.; Arteaga, O.; Garcia-Caurel, E.; Hingerl, K. Model for the depolarizing retarder in Mueller matrix polarimetry. J. Opt. Soc. Am A 2022, 39, 873. [Google Scholar] [CrossRef]
- Gil, J.J. On optimal filtering of measured Mueller matrices. Appl. Opt. 2016, 55, 5449. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J. Components of purity of a three-dimensional polarization state. J. Opt. Soc. Am A 2016, 33, 40. [Google Scholar] [CrossRef] [PubMed]
| Diattenuator-Based Depolarizers | Retarder-Based Depolarizers | ||
|---|---|---|---|
| Mean absolute error | 0.0128 | Mean absolute error | 0.0172 |
| P1 | P2 | P3 | |
|---|---|---|---|
| Radial polarizer | 0.163 | 0.876 | 1 |
| Q plate | 0.288 | 0.727 | 1 |
| P1 ± σP1 | P2 ± σP2 | P3 ± σP3 | |
|---|---|---|---|
| Silver diffuse reflector | 0.05 ± 0.02 | 0.11 ± 0.03 | 0.20 ± 0.04 |
| White paper | 0.05 ± 0.02 | 0.14 ± 0.04 | 0.29 ± 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Montes-Gonzalez, I.; Estevez, I.; Canabal-Carbia, M.; López-Coronado, O.; Mao, Y.; Eeckhout, A.V.; Moreno, I.; Campos, J.; Guo, Z.; et al. IPP and PRT Depolarizing Spaces for the Study of Depolarizing Samples: A Review. Appl. Sci. 2025, 15, 10205. https://doi.org/10.3390/app151810205
Li D, Montes-Gonzalez I, Estevez I, Canabal-Carbia M, López-Coronado O, Mao Y, Eeckhout AV, Moreno I, Campos J, Guo Z, et al. IPP and PRT Depolarizing Spaces for the Study of Depolarizing Samples: A Review. Applied Sciences. 2025; 15(18):10205. https://doi.org/10.3390/app151810205
Chicago/Turabian StyleLi, Dekui, Ivan Montes-Gonzalez, Irene Estevez, Mónica Canabal-Carbia, Octavi López-Coronado, Yuxuan Mao, Albert Van Eeckhout, Ignacio Moreno, Juan Campos, Zhongyi Guo, and et al. 2025. "IPP and PRT Depolarizing Spaces for the Study of Depolarizing Samples: A Review" Applied Sciences 15, no. 18: 10205. https://doi.org/10.3390/app151810205
APA StyleLi, D., Montes-Gonzalez, I., Estevez, I., Canabal-Carbia, M., López-Coronado, O., Mao, Y., Eeckhout, A. V., Moreno, I., Campos, J., Guo, Z., Tan, Y., & Lizana, A. (2025). IPP and PRT Depolarizing Spaces for the Study of Depolarizing Samples: A Review. Applied Sciences, 15(18), 10205. https://doi.org/10.3390/app151810205





