Friction Coefficient Tests for Designs of Belt Conveyor Drive Systems
Abstract
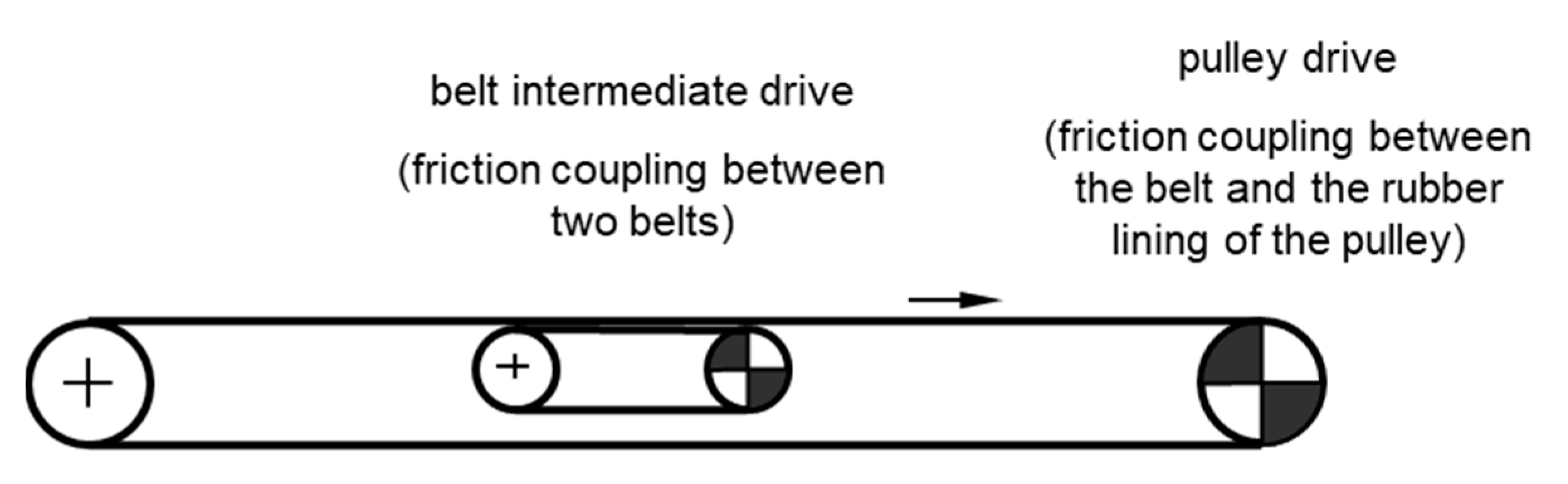
1. Introduction
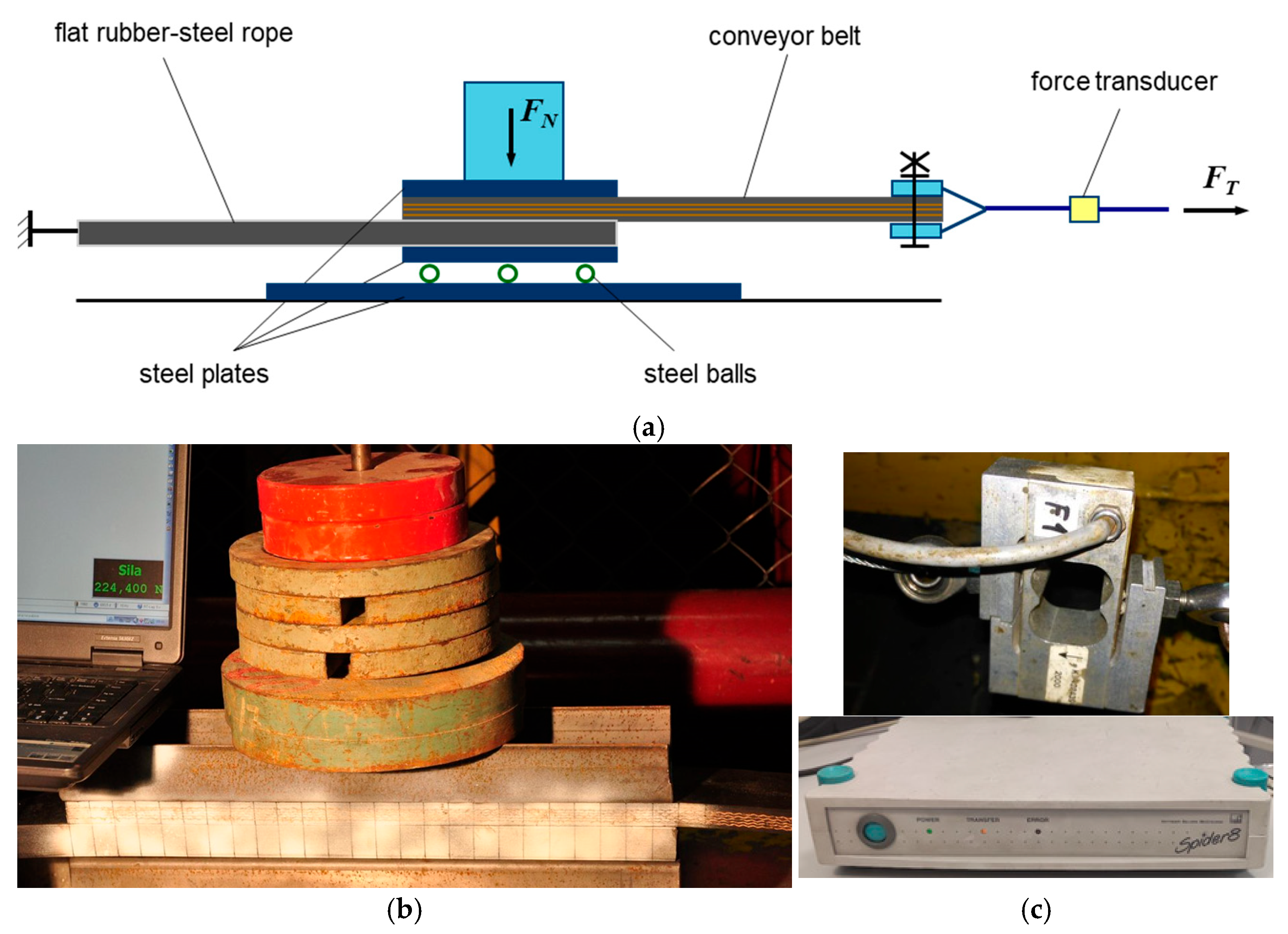
2. Materials and Methods
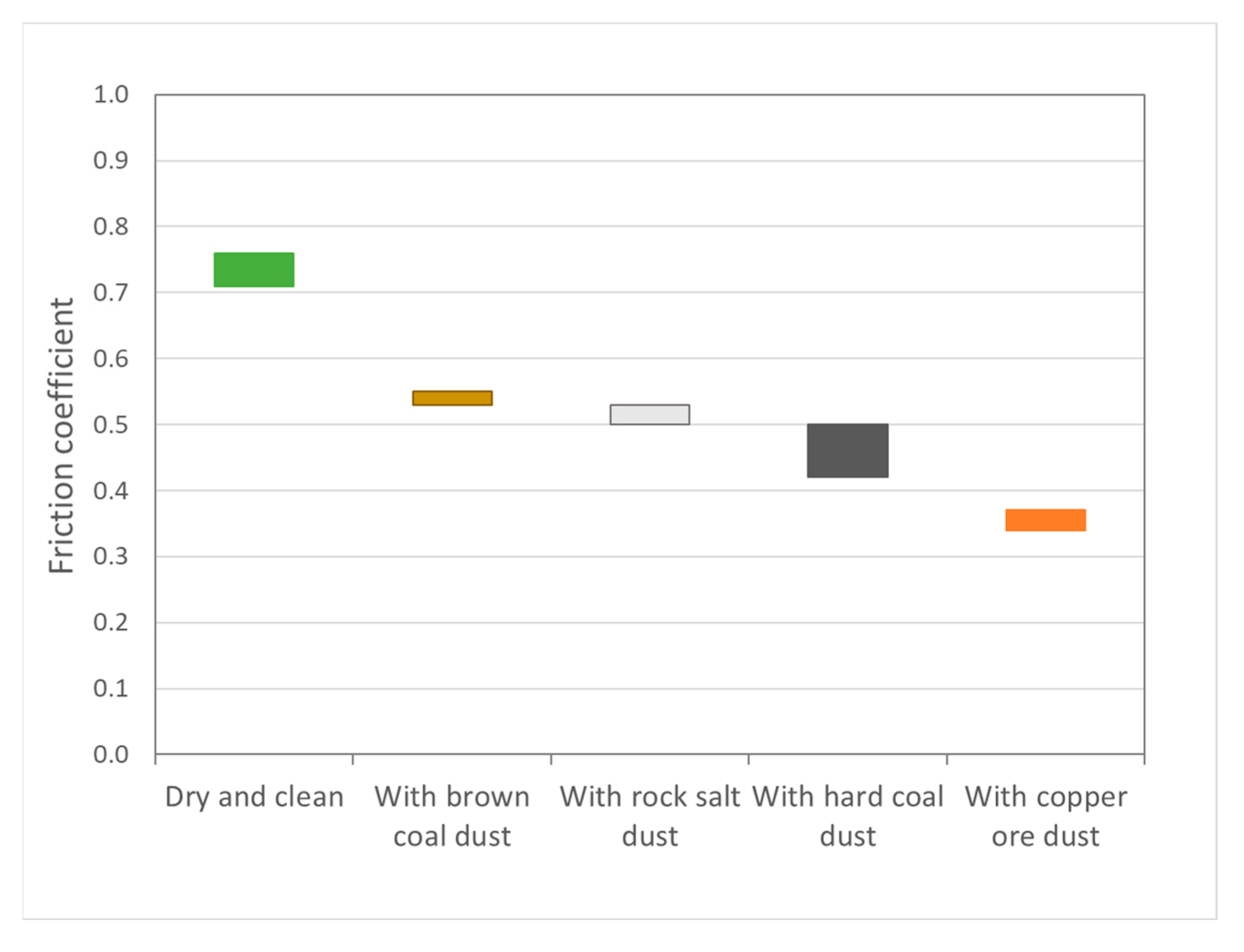
- dry and clean—before the examination, the friction surfaces of the rope and of the conveyor belt were cleaned with fuller’s earth along the length of the frictional engagement zone;
- with copper ore dust—the friction surfaces were covered with dolomite rock dust (a thin layer of dust having a fraction of 0 ÷ 0.5 mm) (Figure 4a);
- with hard coal dust—the friction surfaces were covered with hard coal dust (a thin layer of dust having a fraction of 0 ÷ 0.5 mm);
- wet and clean—the friction surfaces were cleaned and wetted with water (Figure 4b).
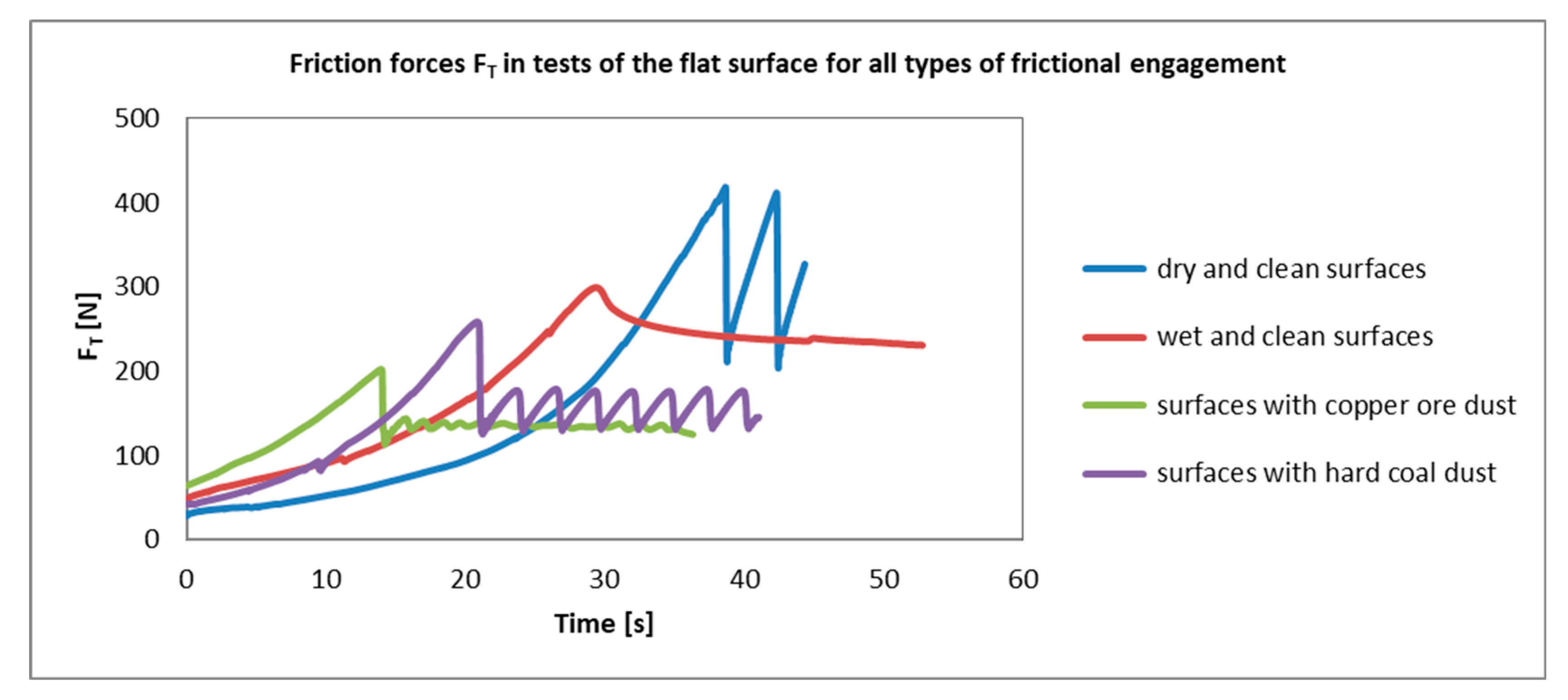
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Euler, M.L. Remarques sur l’effect du frottement dans l’equilibre. Mem. Acad. Sci. 1762, 18, 265. [Google Scholar]
- Gładysiewicz, L. Belt conveyors. In Theory and Calculations; Wrocław University of Science and Technology Publishing House: Wrocław, Poland, 2003; ISBN 83-7085-737-X. (In Polish) [Google Scholar]
- Gładysiewicz, L.; Woźniak, D. The effective belt tension in short conveyor belt drives. Min. Sci. 2014, 21, 65–75. (In Polish) [Google Scholar]
- Feng, Y.; Zhang, M.; Li, G.; Meng, G. Dynamic characteristic analysis and startup optimization design of an intermediate drive belt conveyor with non-uniform load. Sci. Prog. 2019, 103, 0036850419881089. [Google Scholar] [CrossRef] [PubMed]
- Bortnowski, P.; Gładysiewicz, A.; Gładysiewicz, L.; Król, R.; Ozdoba, M. Conveyor Intermediate TT Drive with Power Transmission at the Return Belt. Energies 2022, 15, 6062. [Google Scholar] [CrossRef]
- Schallamach, A. How does rubber slide? Wear 1971, 17, 301–312. [Google Scholar] [CrossRef]
- Wu, Y.; Leamy, M.J.; Varenberg, M. Schallamach waves in rolling: Belt drives. Tribol. Int. 2018, 119, 354–358. [Google Scholar] [CrossRef]
- Wieleba, W. The Analysis of Tribological Processes Proceeding in PTFE Composites Sliding Against Steel. In Prace Naukowe Instytutu Konstrukcji i Eksploatacji Maszyn Politechniki Wrocławskiej; Oficyna Wydawnicza Politechniki Wrocławskiej: Wrocław, Poland, 2002. (In Polish) [Google Scholar]
- Grosch, K.A. The relation between the friction and visco-elastic properties of rubber. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1963, 274, 21–39. [Google Scholar]
- Golden, J.M. A molecular theory of adhesive rubber friction. J. Phys. A Math. Gen. 1975, 8, 966. [Google Scholar] [CrossRef]
- Persson, B.N.J. On the theory of rubber friction. Surf. Sci. 1998, 401, 445–454. [Google Scholar] [CrossRef]
- Smith, R.H. Analyzing Friction in the Design of Rubber Products and Their Paired Surfaces; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Głąb, P.; Bieliński, D.; Maciejewska, K. An attempt to analyze the stick-slip effect for elastomers. Tribologia 2004, 4, 43–49. (In Polish) [Google Scholar]
- Bieliński, D. Tribology of Elastomers and Rubber from the Perspective of Materials Engineering; Wydawnictwo Naukowe Instytutu Technologii Eksploatacji-PIB: Radom, Poland, 2009; ISBN 978-83-7204-752-6. (In Polish) [Google Scholar]
- Furmanik, K. Vibrations excited by dry friction. Theory, experiment, simulation. In Rozprawy Monografie; AGH Uczelniane Wydawnictwa Naukowo-Dydaktyczne: Kraków, Poland, 2006; p. 157. ISSN 0867-6631. (In Polish) [Google Scholar]
- Roth, F.L.; Driscoll, R.L.; Holt, W.L. Frictional properties of rubber. Rubber Chem. Technol. 1943, 16, 155–177. [Google Scholar] [CrossRef]
- Grosch, A. The speed and temperature dependence of rubber friction and its bearing on the skid resistance of tires. Phys. Tire Tract. 1974, 143–165. [Google Scholar]
- Barquins, M.; Roberts, A.D. Rubber friction variation with rate and temperature: Some new observations. J. Phys. D Appl. Phys. 1986, 19, 547–563. [Google Scholar] [CrossRef]
- Persson, B.N.J. Sliding friction. Surf. Sci. Rep. 1999, 33, 83–119. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Albohr, O.; Creton, C.; Peveri, V. Contact area between a viscoelastic solid and a hard, randomly rough, substrate. J. Chem. Phys. 2004, 120, 8779–8793. [Google Scholar] [CrossRef] [PubMed]
- Klüppel, M.; Heinrich, G. Rubber friction on self-affine road tracks. Rubber Chem. Technol. 2000, 73, 578–606. [Google Scholar] [CrossRef]
- Le Gal, A.; Yang, X.; Klüppel, M. Evaluation of sliding friction and contact mechanics of elastomers based on dynamic-mechanical analysis. J. Chem. Phys. 2005, 123, 14704. [Google Scholar] [CrossRef]
- Kong-Hui, G.; Ye, Z.; Shih-Ken, C.; Lin, W. Experimental Research on Friction of Vehicle Tire Rubber. Front. Mech. Eng. 2006, 1, 14–20. [Google Scholar] [CrossRef]
- Vieira, T.; Ferreira, R.; Kuchiishi, A.; Bernucci, L.; Sinatora, A. Evaluation of friction mechanisms and wear rates on rubber tire materials by low-cost laboratory tests. Wear 2015, 328, 556–562. [Google Scholar] [CrossRef]
- Riehm, P.; Unrau, H.; Gauterin, F. A model based method to determine rubber friction data based on rubber sample measurements. Tribol. Int. 2018, 127, 37–46. [Google Scholar] [CrossRef]
- Löwer, J.; Wagner, P.; Unrau, H.J.; Bederna, C.; Gauterin, F. Physical Model of Tire-Road Contact Under Wet Conditions. Tribol. Lett. 2020, 68, 25. [Google Scholar] [CrossRef]
- Hatanaka, S.; Ogawa, Y.; Okubo, H.; Hanzawa, K.; Kajiki, R.; Yamaguchi, K.; Nakano, K. Correlation between friction and wear of rubber: An experimental approach based on the disconnections of Stribeck curves. Wear 2024, 562–563, 205623. [Google Scholar] [CrossRef]
- Kondori, M.S.; Taheri, S. Linear friction tester design and validation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 236, 856–866. [Google Scholar] [CrossRef]
- Čepon, G.; Manin, L.; Boltežar, M. Experimental identification of the contact parameters between a V-ribbed belt and a pulley. Mech. Mach. Theor. 2010, 45, 1424–1433. [Google Scholar] [CrossRef]
- Hrabovský, L.; Nenička, P.; Fries, J. Laboratory Machine Verification of Force Transmission Provided by Friction Acting on the Drive Drum of a Conveyor Belt. Machines 2023, 11, 544. [Google Scholar] [CrossRef]
- Kasza, P.; Kulinowski, P.; Zarzycki, J. The Influence of an Operating Conditions on the Friction Coefficient in Transportation Machines Drives. New Trends Prod. Eng. 2020, 3, 294–302. [Google Scholar] [CrossRef]
- Persson, B.N.J. Conveyor Belt Drive Physics. Tribol. Lett. 2020, 68, 17. [Google Scholar] [CrossRef]
- Kułacz, J. The Effect of Grooving One Surface of A Rubber-Rubber Friction Pair on Sliding Friction. Master’s Thesis, Wrocław University of Science and Technology, Wrocław, Poland, 2013. not published. [Google Scholar]
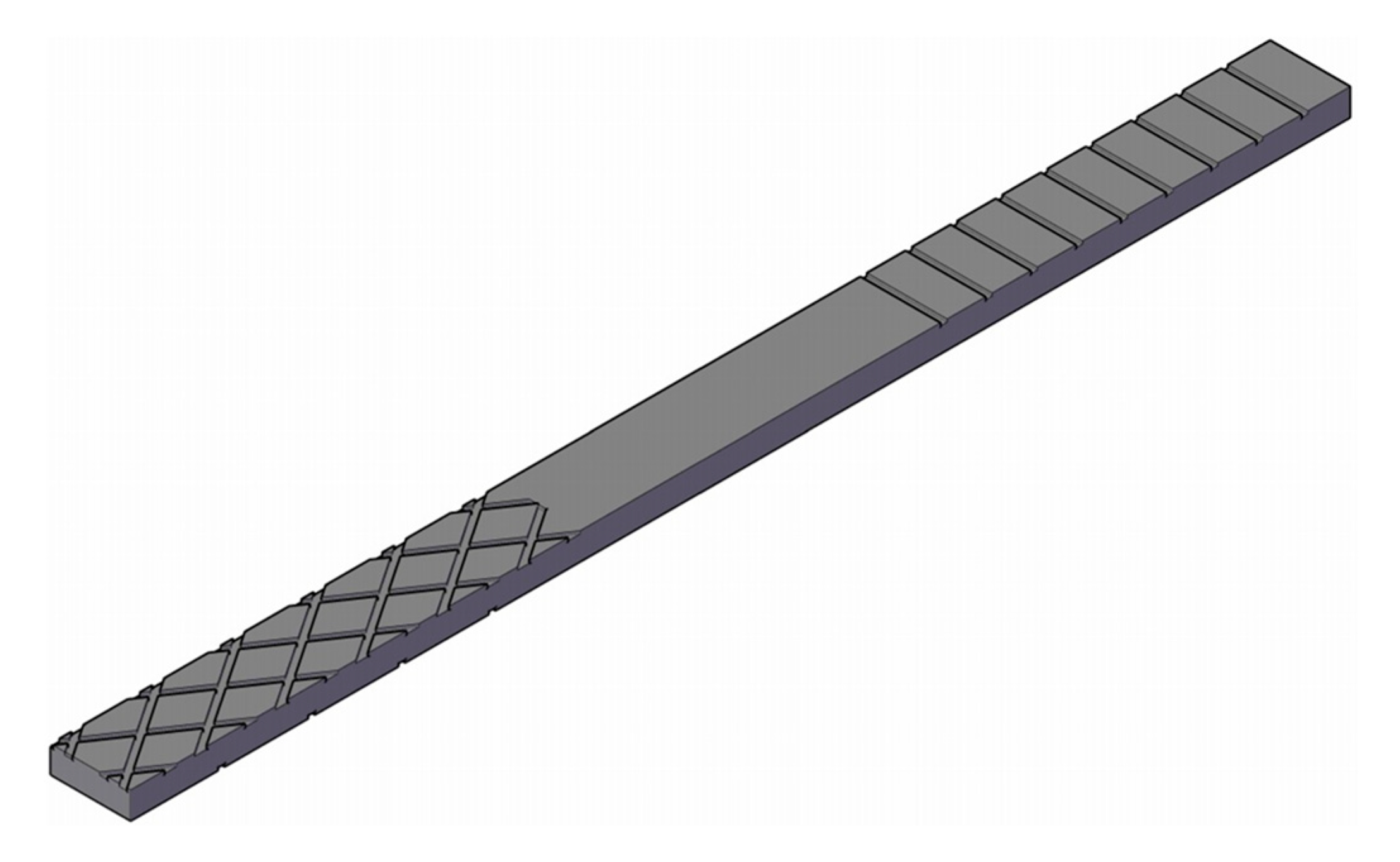





| Surface Type | Contact Zone Width [mm] | Contact Zone Length [mm] | Surface Area of Grooves [mm2] | Surface Area of the Contact Zone [mm2] |
|---|---|---|---|---|
| Flat surface (no grooves) | 88 | 500 | - | 44,000 |
| Surface with transverse grooves | 88 | 500 | 6336 | 37,664 |
| Surface with grooves in “diamond” pattern | 88 | 500 | 12,347 | 31,653 |
| Frictional Engagement Conditions | Dry and Clean | Wet and Clean | with Copper Ore Dust | with Hard Coal Dust | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal force FN [N] | 328 | 415 | 505 | 594 | 328 | 415 | 505 | 594 | 328 | 415 | 505 | 594 | 328 | 415 | 505 | 594 |
| Specimen surfaces | Flat surface | |||||||||||||||
| Max frictional force FT [N] | 222 | 321 | 390 | 418 | 192 | 227 | 265 | 299 | 111 | 137 | 170 | 188 | 172 | 193 | 233 | 258 |
| Static coefficient of friction | 0.68 | 0.77 | 0.77 | 0.70 | 0.58 | 0.55 | 0.53 | 0.50 | 0.34 | 0.33 | 0.34 | 0.32 | 0.52 | 0.46 | 0.46 | 0.43 |
| Specimen surfaces | Surface with transverse grooves | |||||||||||||||
| Max frictional force FT [N] | 212 | 308 | 328 | 394 | 208 | 243 | 295 | 349 | 118 | 143 | 178 | 210 | 171 | 196 | 221 | 253 |
| Static coefficient of friction | 0.65 | 0.74 | 0.65 | 0.66 | 0.64 | 0.58 | 0.59 | 0.59 | 0.36 | 0.34 | 0.35 | 0.35 | 0.52 | 0.47 | 0.44 | 0.43 |
| Specimen surfaces | Surface with “diamond” grooves | |||||||||||||||
| Max frictional force FT [N] | 248 | 294 | 358 | 434 | 254 | 281 | 329 | 427 | 120 | 150 | 173 | 216 | 163 | 182 | 216 | 246 |
| Static coefficient of friction | 0.76 | 0.71 | 0.71 | 0.73 | 0.77 | 0.68 | 0.65 | 0.72 | 0.37 | 0.36 | 0.34 | 0.36 | 0.50 | 0.44 | 0.43 | 0.41 |
| Frictional Engagement Conditions | with Brown Coal Dust | with Rock Salt Dust | ||||||
|---|---|---|---|---|---|---|---|---|
| Normal force FN [N] | 328 | 415 | 505 | 594 | 328 | 415 | 505 | 594 |
| Specimen surfaces | Surface with “diamond” grooves | |||||||
| Max frictional force FT [N] | 180 | 223 | 272 | 317 | 174 | 215 | 256 | 294 |
| Static coefficient of friction | 0.55 | 0.54 | 0.54 | 0.53 | 0.53 | 0.52 | 0.51 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woźniak, D. Friction Coefficient Tests for Designs of Belt Conveyor Drive Systems. Appl. Sci. 2025, 15, 10204. https://doi.org/10.3390/app151810204
Woźniak D. Friction Coefficient Tests for Designs of Belt Conveyor Drive Systems. Applied Sciences. 2025; 15(18):10204. https://doi.org/10.3390/app151810204
Chicago/Turabian StyleWoźniak, Dariusz. 2025. "Friction Coefficient Tests for Designs of Belt Conveyor Drive Systems" Applied Sciences 15, no. 18: 10204. https://doi.org/10.3390/app151810204
APA StyleWoźniak, D. (2025). Friction Coefficient Tests for Designs of Belt Conveyor Drive Systems. Applied Sciences, 15(18), 10204. https://doi.org/10.3390/app151810204






