Abstract
In this paper, the electromagnetohydrodynamic (EMHD) flow and heat transfer of a fluid are analytically investigated. The flow and heat transfer occur in a horizontal channel filled with a porous medium, where the permeabilities of the upper and lower halves of the channel are different. The lower half of the channel is saturated with a hybrid nanofluid, while the upper half is saturated with a nanofluid. The base fluids of the nanofluid and the hybrid nanofluid are different. The channel walls are impermeable. The channel is subjected to external magnetic and electric fields. The problem is analyzed under the inductionless approximation. By introducing dimensionless variables and physical parameters that characterize the flow and heat transfer, the governing equations are transformed into their dimensionless forms. These equations are solved analytically, and the velocity and temperature distributions of the fluid in the channel are obtained. The distributions are graphically illustrated for the case in which the upper half of the channel contains the Al2O3/oil nanofluid and the lower half contains the Cu–TiO2/water hybrid nanofluid, considering various values of the Hartmann number, the external electric load factor, the porosity factor, and the nanoparticle volume fractions. The numerical values of the dimensionless shear stresses and Nusselt numbers at the channel walls are presented in a table. The analysis of the results indicates that an increase in the Hartmann number leads to higher temperatures within the channel. The findings also demonstrate that, in this case, the flow velocities are lower and the temperatures decrease, while the shear stresses and Nusselt numbers at the channel walls are higher compared to those observed for pure fluid (oil and water) flow through the channel. This indicates the advantage of employing the model investigated here over the classical model (water and oil) in engineering practice.
1. Introduction
The idea of enhancing the thermal conductivity of a fluid by dispersing solid particles within it has been present in scientific circles for a long time. Maxwell [1] even provided a relation for estimating the thermal conductivity of such a suspension as early as 1873. At the time, this idea was not implemented in engineering practice due to underdeveloped technology, which also led to a decline in interest in this research. With the advancement of material technology that enabled the formation of solid particles on the nanometer scale, Eastman and Choi, together with their collaborators, revisited this research and published their results in [2], where they introduced suspensions called nanofluids with significantly improved heat transfer characteristics compared to conventional heat transfer fluids.
Since the publication of [2], research in this area has become highly relevant and continues to gain momentum. Increasing attention is being given to studies of flow and heat transfer in nanofluids, as well as hybrid nanofluids fluids that contain more than one type of nanoparticle in various environments. Many researchers are engaged in this field and the literature contains numerous results, a small portion of which are highlighted here.
Jovanović et al. [3] investigated the instability of classical Rayleigh–Bénard convection through direct numerical simulation on a coarse grid for the dimensionless Navier–Stokes equations in the stream function–vorticity form and the energy equation. Umavathi [4] studied the stability of nanofluid flow in a porous medium, considering thermal conductivity and viscosity as functions of nanoparticle volume fraction, with wall temperature varying in time. Aaiza et al. [5] investigated magnetohydrodynamic (MHD) nanofluid flow and mixed convection in a vertical porous channel. Lima et al. [6] analyzed MHD flow and heat transfer of two immiscible fluids in an inclined channel between parallel plates, taking into account various effects. Sharma and Manjeet [7] studied MHD nanofluid flow and convective heat transfer in a porous medium between two horizontal plates, where the upper plate is porous and the lower one is impermeable. Hayat and Nadeem [8] examined the effects of thermal radiation, heat generation, and chemical reaction on the flow and heat transfer of a hybrid nanofluid over a horizontally stretching and rotating plate about a vertical axis. Elmaboud [9] investigated MHD flow and heat transfer in a vertical half-wavy channel, with an electroconductive nanofluid in the left half and a clear, viscous, non-conductive fluid in the right half.
Raju and Ojjela [10] simultaneously studied the flow and heat transfer of a viscous and Jeffrey nanofluid in a horizontal porous channel under the influence of an induced magnetic field, Brownian motion, and thermophoresis. Dogonchi et al. [11] analyzed natural convective heat transfer of a nanofluid in a porous medium between a hot inner rectangular cylinder and a cold outer circular cylinder under an inclined homogeneous magnetic field. Xu and Sun [12] analyzed fully developed convective flow of a hybrid nanofluid in a vertical microchannel, while Slimani et al. [13] examined MHD flow and natural convective heat transfer of a hybrid nanofluid in a truncated conical annulus saturated with a porous medium. Umavathi and Sheremet [14] examined mixed convection in a vertical channel composed of three regions of equal width: a viscous fluid in the central region and nanofluids in the outer porous regions, solving the problem via the perturbation method.
Zainal et al. [15] studied MHD flow and heat transfer of a hybrid nanofluid over a permeable moving surface, including the effect of thermal radiation. Kumar et al. [16] investigated MHD flow and heat transfer of a nanofluid over a rotating disk, forming boundary layer equations that include thermophoresis, Brownian motion, Arrhenius activation energy, and chemical reaction. Nikodijević et al. [17] studied unsteady fluid flow and heat transfer in a horizontal porous channel under an external homogeneous magnetic field inclined relative to the flow direction. Manjeet and Sharma [18] examined flow and thermal convection of two immiscible fluids, one of which is a nanofluid, in a horizontal channel under a transverse magnetic field.
Umavathi and Chamkha [19] studied double-diffusive free and forced convection of a nanofluid in a vertical channel and developed a new mathematical model. Kumar and Ray [20] investigated MHD flow of a hybrid nanofluid over a rotating disk influenced by Hall current and a convectively heated surface, with special attention to the effect of nanoparticle shape factor. Rikitu et al. [21] studied unsteady mixed convective flow and heat transfer with radiation of a nanofluid with variable physical properties in a porous microchannel using convective boundary conditions.
Das et al. [22] investigated the effect of Hall current and thermal radiation on unsteady MHD flow of a nanofluid (Ag-EG) through a vertical porous channel. Bhatti et al. [23] analyzed MHD flow and heat transfer between vertical parallel plates, with gold and magnesium oxide nanoparticles in a sodium alginate base fluid. Petrović et al. [24,25] investigated EMHD flow and heat transfer of two immiscible fluids—a viscous fluid and a nanofluid—in porous channels, both horizontal and vertical, with channel walls maintained at constant but different temperatures. Yadav et al. [26] examined thermal characteristics, entropy generation, velocity profile, and Bejan number for incompressible micropolar and Newtonian fluids in a channel, with special focus on the effects of thermal radiation and magnetic fields. Singh et al. [27] investigated MHD flow and heat transfer of a hybrid nanofluid in a porous medium in an asymmetric channel, considering energy dissipation and Hall currents. Raju and Satish [28] theoretically examined the slip factor effect on MHD flow and heat transfer of two liquid ionized gases within a channel between horizontal plates with Hall currents. Devi and Srinivas [29] used the regular perturbation method to study oscillatory MHD flow and heat transfer of two immiscible fluids in a porous medium in a compliant-walled channel. Aaiza et al. [30] analyzed the effects of radiation and entropy generation on unsteady MHD convective flow of an Ag–H2O nanofluid in a vertical channel, with special attention to the influence of spherical nanoparticle size on velocity and temperature profiles.
In [31], Petrović et al. studied EMHD flow and heat transfer of a Casson nanofluid (Fe3O4–blood) through a porous medium in a channel bounded by horizontal plates maintained at constant but different temperatures. Devi et al. [32] studied MHD flow and heat transfer of immiscible fluids Al2O3–water and Cu–water in a wavy porous channel with permeable walls. Rao and Deka [33] analyzed 2D MHD flow and heat transfer of a hybrid nanofluid (Ag + Al2O3/H2O) induced by a stretching sheet in a porous medium, accounting for thermal radiation, viscous dissipation, and Joule heating. Khalil et al. [34] examined MHD flow and heat transfer of a hybrid nanofluid in a porous medium along an elastic permeable plate, considering temperature-dependent viscosity and thermal conductivity. Ouaf and Abouzeid [35] studied peristaltic flow of a nanofluid (CuO-blood) with thermal radiation, chemical reaction effects, and viscosity dependent on radius and axial coordinate in a non-Darcy porous medium.
Sahao et al. [36] investigated entropy generation, thermophoresis, and viscous dissipation effects on radiative MHD mixed convective flow of a hybrid nanofluid on an inclined, permeable, and moving flat surface. Hussein et al. [37] numerically studied MHD flow and heat transfer of a ternary hybrid nanofluid (Cu-Al-Ti/H2O) over a shrinking/stretching cylinder, considering variable wall temperature and the effects of velocity slip, suction, and curvature. In the work of Othman et al. [38], a numerical solution was determined for the flow and heat transfer of a hybrid nanofluid in an MHD boundary layer over a permeable collecting surface with a heat sink/source and thermal radiation. To enhance heat transfer efficiency and critical heat flux in evaporation and boiling tests with capillary feeding, several studies have investigated nanofluid and porous medium configurations. Wu et al. [39] designed mini-groove geometries and optimized the porous wick distribution. Awan et al. [40] established upper bounds for the remainder term in Boole’s Quadrature Rule involving convex mappings, leveraging their convexity and boundedness properties. Choudhary et al. [41] analyzed MHD flow and heat transfer of a tetra-hybrid nanofluid past a stretching surface, accounting for thermal radiation, heat generation, and slip conditions. Hussain et al. [42] developed a mathematical model of MHD ternary nanofluids in a Darcy–Forchheimer porous medium under linear and nonlinear thermal radiation, examining the resulting velocity, temperature, and concentration fields.
Despite the large number of studies on nanofluids, the available literature contains few works that examine the flow and heat transfer of immiscible nanofluids, as also noted by Umavathi and Sheremet in their 2020 paper [19]. The authors observed that even fewer works address the flow and heat transfer of immiscible nanofluids under the simultaneous influence of external electric and magnetic fields. Two-layer flows of nanofluids and hybrid nanofluids in porous media under electromagnetic fields are of significant interest due to their relevance in heat exchangers, metallurgy, chemical processes, nuclear reactor cooling, fusion management, environmental engineering, and biopharmaceutical applications. Although Umavathi and Sheremet [19] addressed related phenomena five years ago, this topic remains highly relevant, as most studies focus on Newtonian fluids, nanofluids, or hybrid nanofluids in single-layer flows. In contrast, investigations of two-layer flows combining a nanofluid and a hybrid nanofluid, particularly in porous media under simultaneous magnetic and electric fields, are lacking. To address this gap, the present study analytically examines EMHD flow and heat transfer in a horizontal channel with upper and lower halves modeled as porous Darcy media of different permeabilities. Exact solutions for velocity, temperature, wall shear stresses, and Nusselt numbers are derived for general nanofluid–hybrid nanofluid combinations, with continuity of velocity, temperature, stress, and heat flux imposed at the interface. Results for specific fluids and parameter values are also provided, offering benchmarks for validation in future research.
2. Mathematical Model
The problem considered here is described in the last paragraph of the introduction and the physical configuration is presented in Figure 1. The upper wall of the channel is at a constant temperature and the lower one is at a constant temperature The distance between the walls of the channel is constant and is 2h (m). The pressure gradient is in the direction of the flow and is constant. The magnetic induction of the external magnetic field is (T) and the strength of the external electric field is (V/m). An incompressible fluid and a fully developed stationary flow are considered.
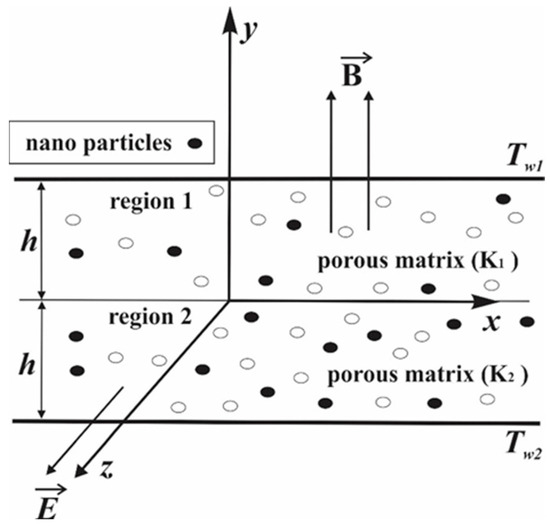
Figure 1.
Physical model.
The upper half of the channel with nanofluid will be considered region 1 and the lower half of the channel with hybrid nanofluid will be considered region 2. The coordinate system is chosen so that the x-axis is the fluid flow direction and is located on the dividing surface and the y-axis is perpendicular to the channel walls.
The momentum equation and the energy equation for the described problem then have the following forms [24]:
where:
The corresponding boundary and surface conditions are as follows:
In Equations (1), (2), and (4), the symbols used are as follows: p (Pa), u (m/s), T (K)—pressure, velocity, and temperature of the fluid, respectively; K(m2)—permeability of the porous medium; (Pas)—dynamic viscosity, (S/m)—electrical conductivity, and (W/(Km))—thermal conductivity of the fluid; subscripts and refer to regions 1 and 2, and subscripts nf and hnf refer to nanofluid and hybrid nanofluid.
The physical characteristics of nanofluid and hybrid nanofluid are given by the following equations [21]:
in which the used labels are as follows: (-)—volume fraction of solid nanoparticles in the nanofluid; —volume fraction of solid nanoparticles in the hybrid nanofluid; the subscripts and correspond to the base fluid and nanoparticles of the nanofluid and the subscripts correspond to the base fluid and solid nanoparticles in the hybrid nanofluid.
Equations (1) and (2) with conditions (4) represent the mathematical model of the described problem of fluid flow and heat transfer. For analytical research, it is necessary to solve them.
3. Solution of the Problem
Equations (1) and (2) are transformed to dimensionless form by introducing dimensionless quantities in the following form:
Using dimensionless quantities (6) and expressions for the physical characteristics of nanofluid and hybrid nanofluid (5), Equations (1) and (2) are transformed into dimensionless forms:
For Region 1:
where:
and the mark * has been omitted, which will continue to be done, for the sake of simpler notations.
For Region 2:
where, in addition to the marks (9), the following marks were also used:
Boundary conditions and conditions on the dividing surface (4) have the following forms:
Equations (7), (8), (10), and (11) and conditions (13) practically represent the mathematical model of the considered problem in dimensionless form. Solving these equations, we find that the velocity and temperature distributions are given by the expressions:
For Region 1:
where:
For Region 2:
where:
and are integration constants.
By using boundary conditions and conditions on the dividing surface (13), we find that the integration constants are given in the following form:
where, again for shorter records, the following notations were used:
Analytical expressions for distributions of dimensionless fluid velocity and temperature in both channel regions were determined. They depend on several physical parameters, which makes it possible to analyze the influence of each of them on fluid flow and heat transfer in the channel.
Dimensionless skin friction on the top and bottom walls of the channel are respectively given by the following expressions:
The local Nusselt numbers on the channel walls, top and bottom, are respectively given by the following relations:
4. Model Verification
For the verification of the model used here, the case considered is the one analyzed by Malashetty et al. [43], where the channel is horizontal. To enable a comparison of results, the same parameter values as those used in the aforementioned study are adopted here: .
The results for the dimensionless velocity distributions obtained in this study and those from the referenced work are presented in Figure 2. It should be noted that the characteristic velocity used in this study is five times greater than the characteristic velocity used by Malashetty et al. [43]. From the figure, it can be observed that the dimensionless velocity distributions obtained in both studies show good agreement. The maximum difference between them is less than 2%, which is entirely acceptable. This deviation arises because an exact method was used to solve the differential equations in this study, while an analytical approximate method based on regular perturbation was employed in the referenced work.
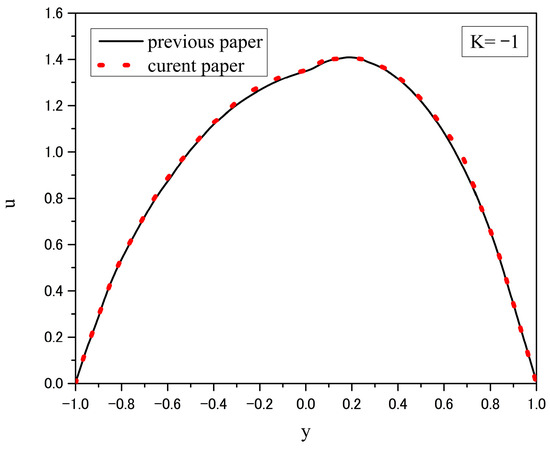
Figure 2.
Velocity comparison.
5. Results and Discussion
In Section 3, analytical expressions were derived for the distributions of dimensionless velocity and temperature within the channel, as well as for the dimensionless shear stresses and local Nusselt numbers at the channel walls. These expressions are formulated as functions of the physical parameters governing the problem.
In order to assess the effect of these parameters on the flow and heat transfer, this section considers the case where the upper layer is a nanofluid with oil as the base fluid and aluminum oxide nanoparticles, while the lower layer is a hybrid nanofluid with water as the base fluid and copper and titanium dioxide nanoparticles. The physical properties of the base fluids and the nanoparticles are given in Table 1. To facilitate a simpler analysis of the influence of the introduced physical factors on the flow and heat transfer in the channel, part of the obtained results for the velocity and temperature distributions is shown in graphical form in the following figures, while the values of the dimensionless shear stresses and local Nusselt numbers on the channel walls are presented in Table 2.

Table 1.
Physical properties of water, oil, copper, aluminum oxide, and titanium dioxide

Table 2.
Values of shear stresses and Nusselt numbers on the channel walls.
Figure 3 and Figure 4 show the distributions of dimensionless velocity and temperature, respectively, for different values of the Hartmann number. The values of the other parameters are held constant and are provided in the figures. By varying the Hartmann number, the influence of the applied magnetic field on the velocity and temperature distributions in the channel is analyzed.
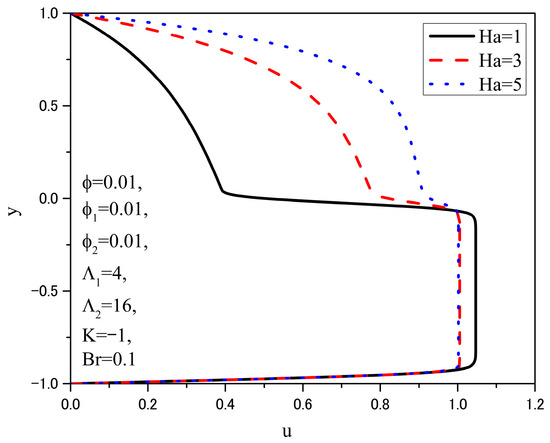
Figure 3.
Velocity distributions u(y) for different Ha.
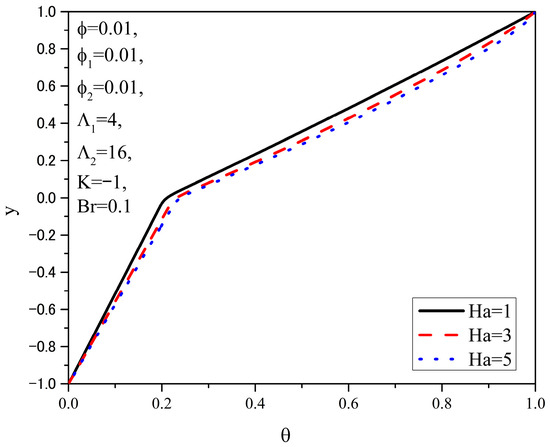
Figure 4.
Temperature distributions θ(y) for different Ha.
From Figure 3, it can be observed that increasing the Hartmann number leads to an increase in the fluid velocity in the upper layer and a decrease in velocity in the lower layer. Due to the combined effect of the applied electric and magnetic fields, an electromagnetic force—Lorentz force—arises, acting on the fluids in the channel.
This electromagnetic force is composed of two components. The first arises from the combined influence of the electric and magnetic fields and may act either as a driving or a resistive force, depending on the orientation of the electric field, i.e., the sign of the factor K. The second component of this force originates from the interaction between the magnetic field and the fluid velocity and acts as a resistive force opposing the fluid motion. In this case, K = −1, so the first component acts as a driving force. In the upper layer, this driving force is dominant and leads to the acceleration of the fluid in that layer. In the lower layer, the resistive component Lorentz force is dominant, resulting in a deceleration of the fluid in that layer. Thus, as the Hartmann number increases, the intensity of the Lorentz force also rises. In the upper half of the channel, this force acts as a driving force, accelerating the flow, whereas in the lower half, it acts as a resistive force, decelerating the fluid motion in that region.
From the same figure, it can be observed that the velocities in the upper layer are lower than those in the lower layer. The reason for this velocity distribution lies in the significantly higher viscosity of the fluid in the upper layer compared to the viscosity of the fluid in the lower layer. From the given results, it can be seen that their ratio is 79.2.
From Figure 4, it can be seen that as the Hartmann number increases, the temperature of the fluid rises in both layers of the channel. The cause of this temperature increase is the enhanced Joule heating, primarily through conduction, and the fact that heat is transferred from the upper wall to the fluid for all considered Hartmann number values.
Figure 5 and Figure 6 depict the distributions of dimensionless velocity and dimensionless temperature of the fluid in the channel, respectively, for various values of the factor K, while all other parameters are held constant as indicated in the figures.
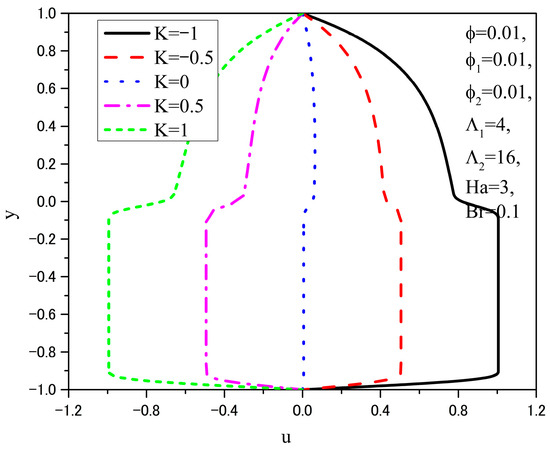
Figure 5.
Velocity distributions u(y) for different K.
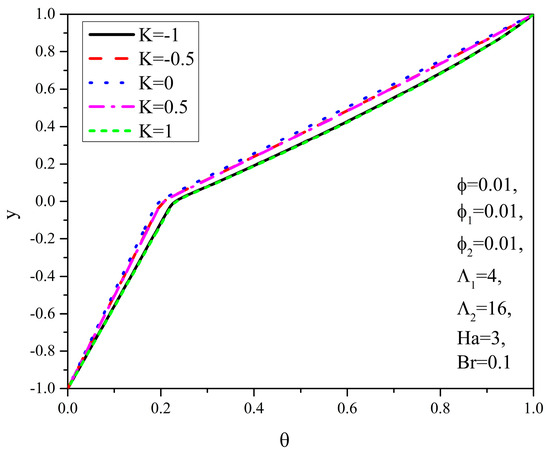
Figure 6.
Temperature distributions θ(y) for different K.
From Figure 5, it can be observed that for K = 0, i.e., when no electric field is applied and all other parameters have the values given in the figure, the velocity of the fluid in the upper layer is low and directed along the x-axis, while the hybrid nanofluid in the lower layer remains at rest. For K = −1 and K = −0.5, the fluid velocity is in the positive x-direction, while for K = 1 and K = 0.5, it is in the negative x-direction. Reversing the sign of factor K, corresponding to a change in the applied electric field direction, reverses the Lorentz force and the flow direction, while increasing |K| enhances the velocity in both layers. The fluid velocities in the upper layer are lower than those of the hybrid nanofluid in the lower layer due to the reason already explained in the analysis of the effect of the Hartmann number.
Figure 6 shows that higher absolute values of the factor K correspond to increased fluid temperatures in both layers, and for equal values of ∣K∣, the temperatures are nearly identical. The increase in fluid temperature is caused by increased Joule heating. In the lower fluid layer, heat transfer occurs primarily by conduction. Heat is transferred from the upper wall to the fluid.
Figure 7 and Figure 8 show the graphs of the dimensionless velocity and dimensionless temperature distributions, respectively, for different values of the porosity factor of the porous medium in the upper half of the channel, while the values of the other parameters are kept constant and provided in the figures.
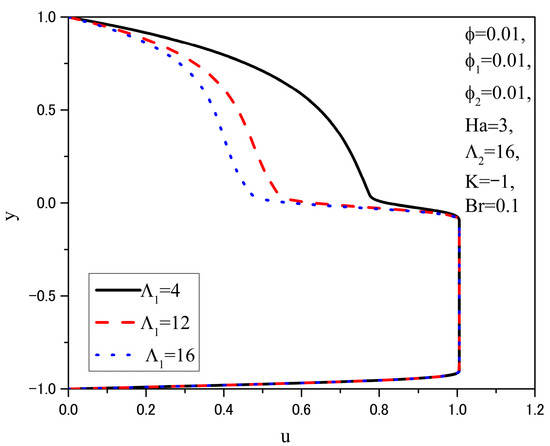
Figure 7.
Velocity distributions u(y) for different Λ1.
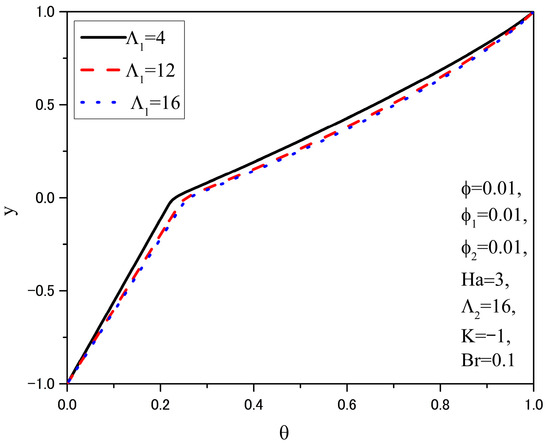
Figure 8.
Temperature distributions θ(y) for different Λ1.
From Figure 7, it can be observed that higher values of the porosity factor, i.e., lower permeability of the porous medium in the upper half of the channel, correspond to lower velocities of the nanofluid. The reason for the reduction in nanofluid velocity in this case is the increased resistance force of the porous medium as the porosity factor increases. In the lower layer, changes in the velocity of the hybrid nanofluid occur only in a small region near the fluid interface due to the velocity continuity conditions on that interface.
From Figure 8, it can be observed that higher values of the porosity factor of the porous medium in the upper half of the channel lead to higher temperatures of the nanofluid. Due to the increased resistance force, additional energy is required to overcome it, which is converted into thermal energy—Darcy dissipation—resulting in a rise in the nanofluid temperature. Due to the temperature continuity condition at the fluid interface, the temperature of the hybrid nanofluid also increases. Heat transfer in the hybrid nanofluid occurs mainly through conduction, and the direction of heat transfer is from the upper wall of the channel to the nanofluid, as in the previous cases.
Figure 9 and Figure 10 show the dimensionless velocity and temperature distributions, respectively, for channels with either pure fluids (oil in the upper half, water in the lower) or a nanofluid in the upper half and a hybrid nanofluid in the lower half with specified volume fractions.
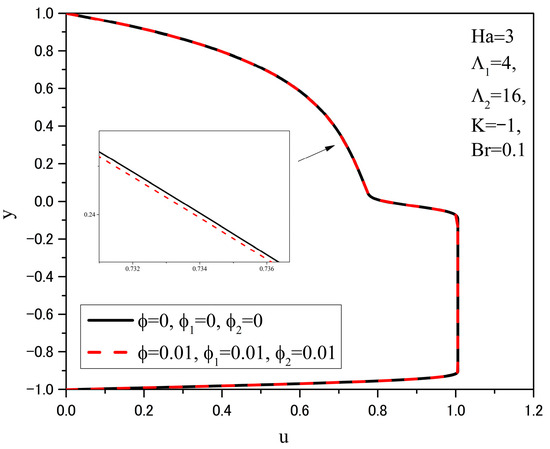
Figure 9.
Velocity distributions u(y) for different ϕ.
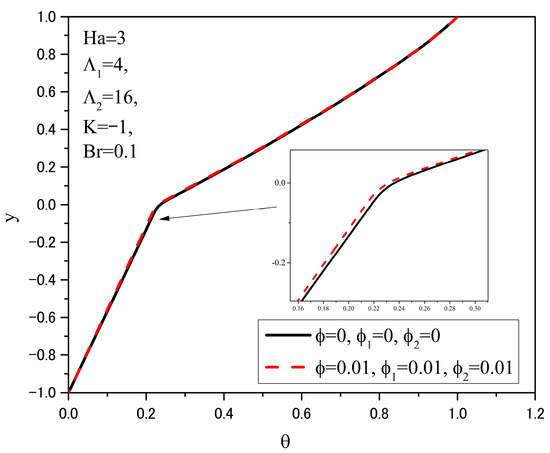
Figure 10.
Temperature distributions θ(y) for different ϕ.
When the upper half of the channel contains the nanofluid Al2O3/oil and the lower half contains the hybrid nanofluid Cu-TiO2/water with nanoparticle volume fractions of 0.01, the fluid velocity in the channel is lower than the velocity when the upper half contains pure oil and the lower half contains pure water, as observed in Figure 9. This velocity reduction is due to the increased density and dynamic viscosity of both the nanofluid and the hybrid nanofluid.
From Figure 10, it can be seen that the temperature in the channel is lower when nanofluid and hybrid nanofluid flow through it, compared to when pure fluids (oil and water) flow. This temperature reduction is a result of the enhanced thermal conductivity of the nanofluid and hybrid nanofluid relative to the base fluids. Thus, the use of commercial fluids enhanced with nanoparticles increases their thermal conductivity, providing an advantage for the model studied here compared to the model with pure commercial fluids, particularly for practical engineering applications.
Table 2 presents the values of the dimensionless shear stresses on the channel walls and the Nusselt numbers on those walls. In this table, the values of these quantities are given for fixed values of the parameters, except when they are varied individually.
From Table 2, it can be observed that with an increase in the Hartmann number, as well as with an increase in the external electric load factor, the shear stresses on both the upper and lower channel walls increase, while the Nusselt numbers decrease on the upper wall and increase on the lower wall. An increase in the porosity factor of the medium in the upper half of the channel decreases the shear stress on the upper wall but does not affect the shear stress on the lower wall. An increase in this factor also decreases the Nusselt number on the upper wall and increases it on the lower wall. An increase in the Brinkman number does not affect the shear stresses but does influence the Nusselt numbers. On the upper wall, it first decreases and then increases the Nusselt number, while on the lower wall, it causes an increase. Both the shear stresses and Nusselt numbers on the channel walls are higher when nanofluid and hybrid nanofluid flow through the channel compared to the corresponding values when pure fluids are flowing.
6. Conclusions
In this study, EMHD flow and heat transfer of fluid in a horizontal channel were investigated. The channel walls are impermeable and maintained at constant but different temperatures. The magnetic Reynolds number is small, and the problem is analyzed under the assumption of negligible magnetic induction (low-induction approximation). The upper and lower halves of the channel are filled by different porous media, with a nanofluid flowing through the upper half and a hybrid nanofluid through the lower half, without mixing. The velocity and temperature distributions within the channel, as well as the shear stresses and Nusselt numbers at the channel walls, were determined as functions of the relevant physical parameters. For the case in which the upper half contains Al2O3/oil nanofluid and the lower half contains Cu-TiO2/water hybrid nanofluid, the velocity and temperature distributions are presented graphically, and the dimensionless shear stresses and Nusselt numbers are given in a table and analyzed. The following conclusions were drawn from this analysis:
- For K = −1, increasing the Hartmann number increases the velocity in the upper layer and decreases it in the lower layer, raises the temperature in both layers of the channel, increases the shear stress values, and increases the Nusselt number on the lower wall while decreasing it on the upper wall.
- Increasing the absolute value of the factor K increases the velocity in both layers, raises the temperature, and increases the shear stress values. The Nusselt number increases on the lower wall and decreases on the upper wall.
- With an increase in the porosity factor of the medium in the upper half of the channel, the velocity in the upper half decreases, the temperature in the channel increases, the shear stress on the upper wall decreases while remaining unchanged on the lower wall, and the Nusselt number decreases on the upper wall and increases on the lower wall.
- When nanofluid and hybrid nanofluid flow through the channel, the velocities are lower, the temperatures are lower, and the shear stresses and Nusselt numbers are higher compared to the case when pure fluids (oil and water) flow through the channel.
This work opens perspectives for further research. Possible directions include studies on multi-hybrid nanofluids (ternary, quaternary, quinary, etc.), multi-layer fluid flows, inclined channels, non-Darcy porous media, inclined magnetic fields, alternative boundary conditions, and other related investigations.
Author Contributions
Conceptualization, Ž.M.S.; Validation, M.M.K.; Investigation, M.D.N.Đ., J.D.P., Ž.M.S. and D.D.N.; Writing—original draft, D.D.N.; Writing—review & editing, M.D.N.Đ.; Visualization, J.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maxwell, J.A. Treatise on Electricity and Magnetism; University of Oxford, at the Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. MRS Online Proc. Libr. 1996, 457, 3–11. [Google Scholar] [CrossRef]
- Jovanović, M.M.; Nikodijević, J.D.; Nikodijević, M.D. Rayleigh-Bénard convection instability in the presence of spatial temperature modulation on both plates. Int. J. Non-Linear Mech. 2015, 73, 69–74. [Google Scholar] [CrossRef]
- Umavathi, J.C. Rayleigh-Benard convection subject to time dependent wall temperature in a porous medium layer saturated by a nanofluid. Mechanica 2015, 50, 981–994. [Google Scholar] [CrossRef]
- Aaiza, G.; Khan, I.; Shafie, S. Energy Transfer in Mixed Convection MHD Flow of Nanofluid Contaning Different Shapes of Nanoparticles in a Channel Filled with Saturated Porous Medium. Nanoscale Res. Lett. 2015, 10, 490. [Google Scholar] [CrossRef] [PubMed]
- Lima, J.A.; Assad, G.E.; Paiva, H.S. A simple approach to analyze the fully developed two-phase magnetoconvection type flows in inclined parallel-plate channels. Lat. Am. Appl. Res. 2016, 46, 93–98. [Google Scholar] [CrossRef]
- Sharma, M.K.; Boora, M. Nanofluid Flow and Heat Convection in a Channel Filled with Porous Medium. J. Int. Acad. Phys. Sci. 2017, 21, 167–188. [Google Scholar]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag-CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2. [Google Scholar] [CrossRef]
- Elmaboud, Y.A. Two layers of immiscible fluids in a vertical semi-corrugated channel with heat transfer: Impact of nanoparticles. Results Phys. 2018, 9, 1643–1655. [Google Scholar] [CrossRef]
- Raju, A.; Ojjela, O. Effects of the induced magnetic field, thermophoresis and Brownian motion on mixed convective Jeffrey nanofluid flow through a porous channel. Eng. Rep. 2019, 1, e12053. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Sheremet, M.A.; Ganji, D.D.; Pop, I. Free convection of copper-water nanofluid in a porous gap between hot rectangular cylinder and cold circular cylinder under the effect of inclined magnetic field. J. Therm. Anal. Calorim. 2019, 135, 1171–1184. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Q. Generalized Hybrid Nanofluid with the Application of Fully Developed Mixed Convection Flow in a Vertical Microchannel. Commun. Theor. Phys. 2019, 71, 903–911. [Google Scholar] [CrossRef]
- Slimani, R.; Aissa, A.; Mebarek-Ondina, F.; Khan, U.; Sahnoun, M.; Chamkha, A.J.; Medebber, M.A. Natural convection analysis flow of Al2O3-Cu/water hybrid nanofluid in a porous conical enclosure subjected to the magnetic field. Eur. Phys. J. Appl. Phys. 2020, 92, 10904. [Google Scholar] [CrossRef]
- Umavati, J.C.; Sheremet, M.A. Heat transfer of viscous fluid in a vertical channel sandwiched between nanofluid porous zones. J. Therm. Anal. Calorim. 2020, 144, 1389–1399. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 858–879. [Google Scholar] [CrossRef]
- Kumar, R.; Bhattacharyya, A.; Seth, G.S.; Chamkha, A.J. Transportation of magnetite nanofluid flow and heat transfer over a rotating porous disk with Arrhenius activation energy: Fourth order Noumerov’s metod. Chin. J. Phys. 2020, 69, 172–185. [Google Scholar] [CrossRef]
- Nikodijevic, M.; Stamenkovic, Z.; Petrovic, J.D.; Kocic, M. Unsteady Fluid Flow and Heat Transfer Through a Porous Medium in a Horizontal Channel with an Inclined Channel with an Inclined Magnetic Field. Trans. FAMENA 2020, 44, 31–46. [Google Scholar] [CrossRef]
- Manjeet, A.; Sharma, M.K. MHD fow and heat convection in a channel filled with two immiscible newtonian and nanofluid fluids. JP J. Heat Mass Trans. 2020, 21, 1–21. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Chamkha, A.J. Thermo-Solutal convection of a Nanofluid Utilizing Fourier’s-Type Compass Conditions. J. Nanofluids 2021, 9, 362–374. [Google Scholar] [CrossRef]
- Kumar, A.; Ray, R.K. Shape effect of nanoparticles and entropy generation analysis for magnetohydrodynamic flow of (Al2O3-Cu/H2O) hybrid nanomaterial under the influence of Hall current. Indian J. Phys. 2022, 96, 3817–3830. [Google Scholar] [CrossRef]
- Rikitu, B.H.; Makinde, O.D.; Enyadene, L.G. Unsteady mixed convection of a radiating and reacting nanofluid with variable properties in a porous medium microchannel. Arch. Appl. Mech. 2022, 92, 99–119. [Google Scholar] [CrossRef]
- Das, S.; Banu, A.S.; Jana, R.N.; Makinde, O.D. Hall Current’s Impact on Ionized Ethylene Glycol Containing Metal Nanoparticles Flowing Through Vertical Permeable Channel. J. Nanofluids 2022, 11, 453–467. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Beg, O.A.; Ellahi, R.; Doranehgard, M.H.; Rabiei, F. Electro/magnetohzdrodznamic hybrid nanofluid flow with gold and magnesium oxide nanoparticles through vertical parallel plates. J. Magn. Magn. Mater. 2022, 564, 2. [Google Scholar] [CrossRef]
- Petrović, J.D.; Stamenković, Z.M.; Bogdanović Jovanović, J.B.; Nikodijević, M.D.; Kocić, M.M.; Nikodijević, D.D. Electro-Magnetoconvection of Conductive Immiscible Pure fluid and Nanofluid. Trans. FAMENA 2022, 46, 13–28. [Google Scholar] [CrossRef]
- Petrović, J.D.; Stamenković, Z.M.; Kocić, M.M.; Nikodijević-Đorđević, M.D.; Bogdanovic Jovanović, J.B.; Nikodijević, D.D. MHD flow and mixed convection of a viscous fluid and a nanofluid through a porous medium in a vertical channel. Therm. Sci. 2023, 27, 1453–1463. [Google Scholar] [CrossRef]
- Yadav, P.K.; Kumar, A.; Filippov, A.N. Analysis of Entropy Production of Immiscible Microploar and Newtonian Fluids Flow through a Channel: Effect of Thermal Radiation and Magnetic Field. Colloid J. 2023, 85, 95–113. [Google Scholar] [CrossRef]
- Kummar Singh, J.; Seth, G.S.; Hussain, S.M. Thermal performance of hydromagnetic nanofluid flow within an asymmetric channel with arbitrarily conductive walls filled with Darcy-Brinkman porous medium. J. Magn. Magn. Mater. 2023, 582, 171034. [Google Scholar] [CrossRef]
- Raju, T.L.; Satish, P. Slip regime MHD 2-liquid plasma heat transfer flow with Hall curcents between parallel plates. Int. J. Appl. Mech. Eng. 2023, 28, 65–85. [Google Scholar] [CrossRef]
- Devi, M.P.; Srinivas, S. Heat transfer effects on the oscillatory MHD flow in a porous channel with two immiscible fluids. Nonlinear Anal. Model. Control, 2023; 1–19, Online First. [Google Scholar]
- Gul, A.; Khan, I.; Shafie, S. Radiation and heat generation effects in magnetohydrodynamic mixed convection flow of nanofluids. Therm. Sci. 2018, 22, 51–62. [Google Scholar] [CrossRef]
- Petrović, J.D.; Nikodijević-Đorđević, M.D.; Kocić, M.M. Electromagnetic hydrodynamic flow and heat transfer of a Casson nanofluid Fe3O4-blood in a porous medium. Therm. Sci. 2023, 27, 4461–4472. [Google Scholar] [CrossRef]
- Devi, M.P.; Goyal, K.; Srinivas, S.; Satyanarayana, B. Effects of different nanoparticles on the two immiscible liquids flow in an inclined channel with Joule heating and viscous dissipation. Gulf J. Math. 2024, 16, 278–290. [Google Scholar] [CrossRef]
- Rao, S.; Deka, P.N. Numerical Analysiis od MHD Hybrid Nanofluid Flow a Porous Stretching Sheet with Thermal Radiation. Int. J. Appl. Comput. Math. 2024, 10, 3. [Google Scholar] [CrossRef]
- Khamlil, S.; Zasmin, H.; Abbas, T.; Muhammad, T. Analaysis of thermal conductivity variation in magneto-hybrid nanofluids flow through porous medium with variable viscosity and slip boundary. Case Stud. Therm. Eng. 2024, 57, 104314. [Google Scholar] [CrossRef]
- Ouaf, M.E.; Abouzeid, M.Y. Chemically reacted lood CuO nanofluid flow through a non-Darcy porous media with radially varying viscosity. Sci. Rep. 2024, 14, 1650. [Google Scholar] [CrossRef]
- Sahao, C.S.; Swain, B.K.; Das, M.; Dash, G.C. Entropy generation and porosity effects on MHD hybrid nanofluid mixed convective flow over an inclined plate in the presence of thermophoresis and heat flux. J. Braz. Soc. Mech. Sci. Eng. 2025, 7, 108. [Google Scholar] [CrossRef]
- Hussein, U.N.; Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics (MHD) flow of ternary nanofluid and heat transfer past a permeable cylinder with velocity slip. Chin. J. Phys. 2025, 93, 328–339. [Google Scholar] [CrossRef]
- Othman, M.N.; Jedi, A.; Bakar, N.A.A. MHD Flow and Heat Transfer of Hybrid Nanofluid over an Exponentially Shrinking Surface with Heat Source/Sink. Appl. Sci. 2021, 11, 8199. [Google Scholar] [CrossRef]
- Wu, J.; Lin, J.; Yan, Y.; You, Z.; Su, Z.; Long, J. Grooved-porous composite wick structures for highly efficient capillary-fed boiling heat transfer. Appl. Therm. Eng. 2024, 256, 124029. [Google Scholar] [CrossRef]
- Javed, M.Z.; Awan, M.U.; Bin-Mohsin, B.; Treanta, S. Upper Bounds for the Remainder Term in Boole’s Quadrature Rule and Applications to Numerical Analysis. Mathematic 2024, 12, 2920. [Google Scholar] [CrossRef]
- Choudhary, P.; Loganathan, K.; Jat, K.; Arunachalam, K.P.; Eswaramoorthi, S. Thermal and velocity slip impacts on MHD tetra-hybrid nanofluids flow over a porous stretching surface. Discov. Appl. Sci. 2025, 7, 720. [Google Scholar] [CrossRef]
- Hussain, M.; Hanif, Z.; Hussain, M.; Amer, I.; Mansor, M. Nonlinear radiative MHD flow of ternary nanofluid with Darcy-Forchheimer porous media: Entropy generation analysis. J. Therm. Anal. Calorim. 2025, 150, 3577–3601. [Google Scholar] [CrossRef]
- Malashetty, M.S.; Umavathi, J.C.; Kumar, J.P. Two-fluid Magnetoconvection Flow in an Inclined Channel. Int. J. Trans. Phenom. 2001, 3, 73–84. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).