Potential Evaluation of Cross-Seasonal Heat Storage of Coal Mine Underground Reservoir: A Case Study Based on Multiphysics Coupling Numerical Simulation Method
Abstract
1. Introduction
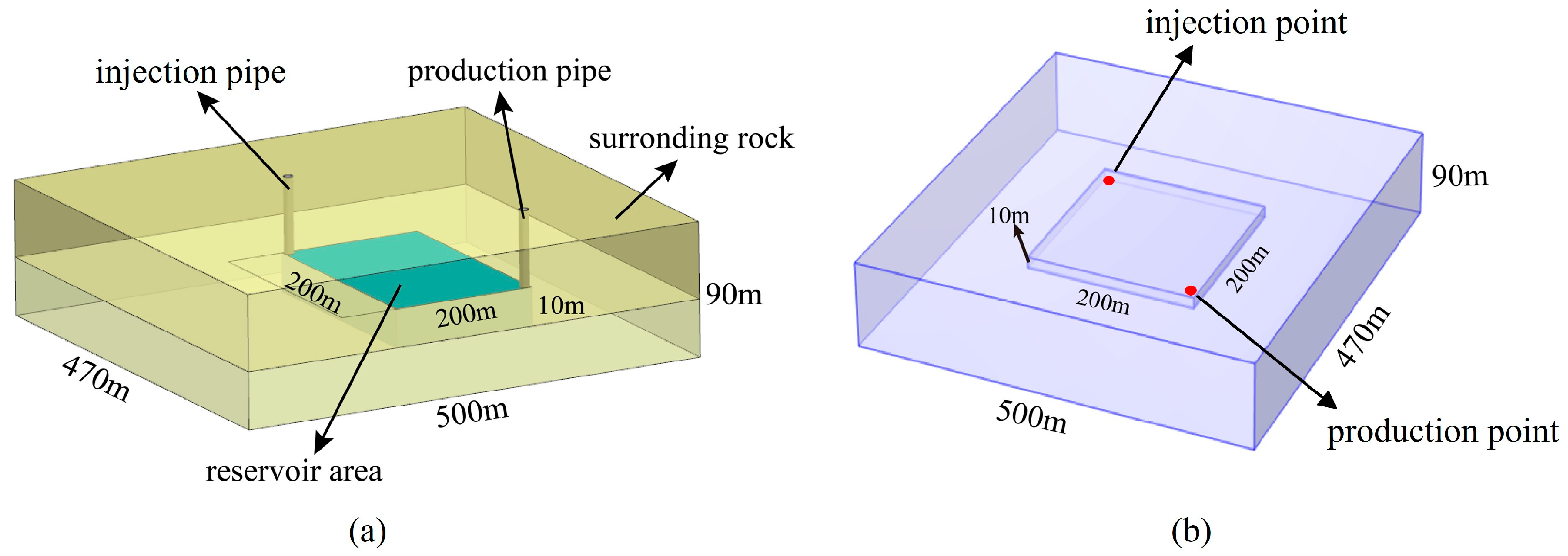
2. Problem Setup
2.1. Conceptual Model of CMUR-ESS
2.2. Governing Equations of CMUR-ESS
2.2.1. Governing Equations for the Fluid Flow
2.2.2. Governing Equations for Heat Transfer
2.3. Boundary and Initial Conditions
2.4. Model Parameters
2.5. Simulation Scheme and Simulation Software
3. Results and Analysis
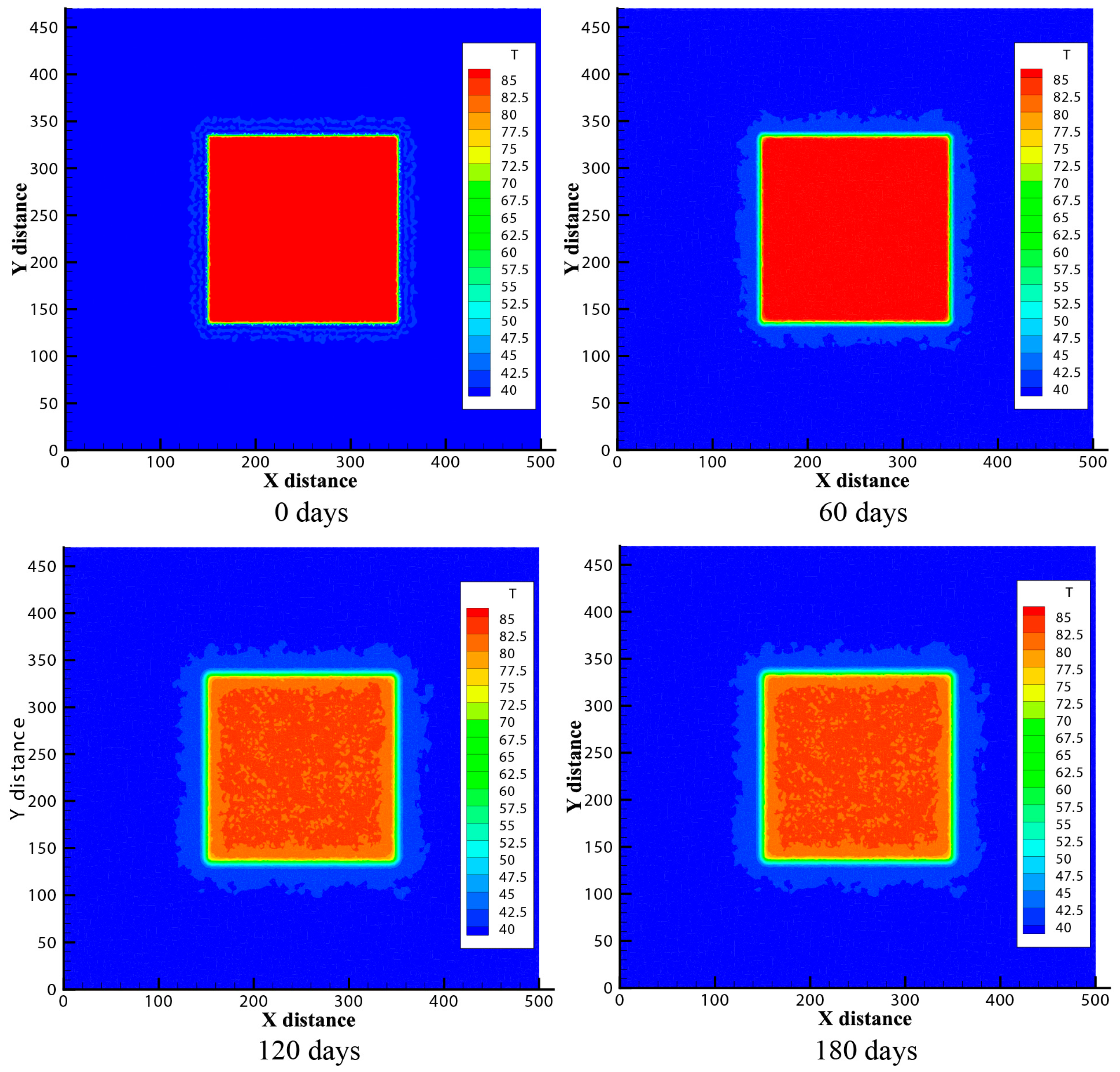
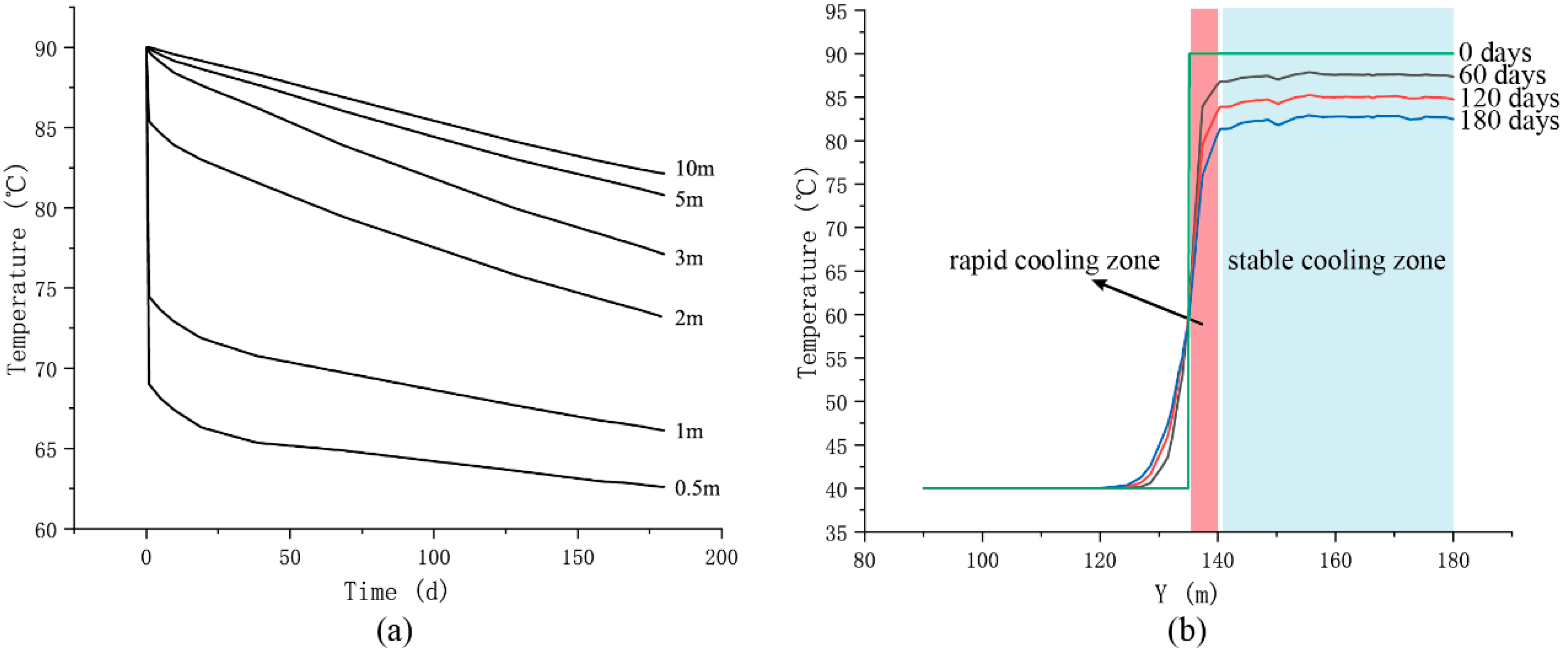
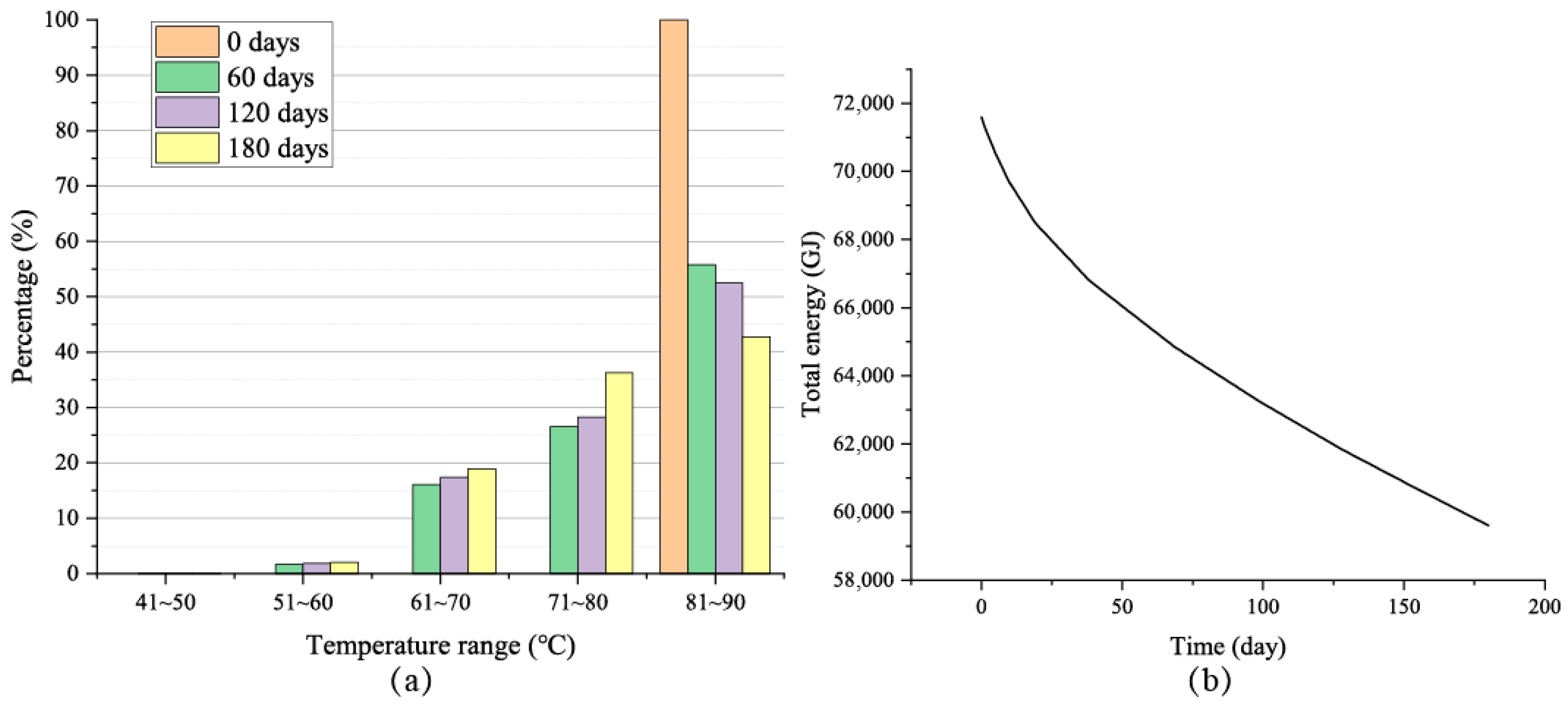
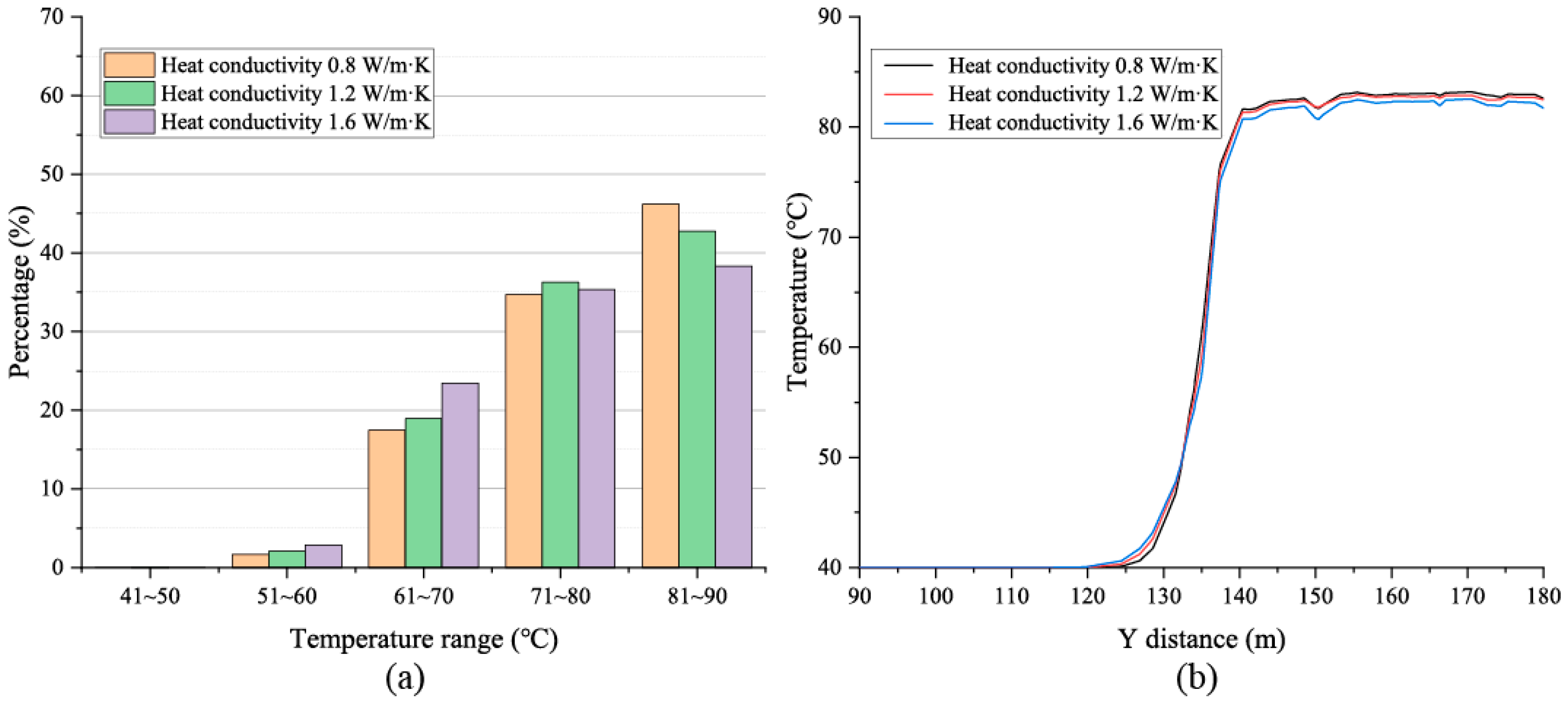
3.1. Temperature Distribution and Evolution of Fluid During Heat Storage Stage
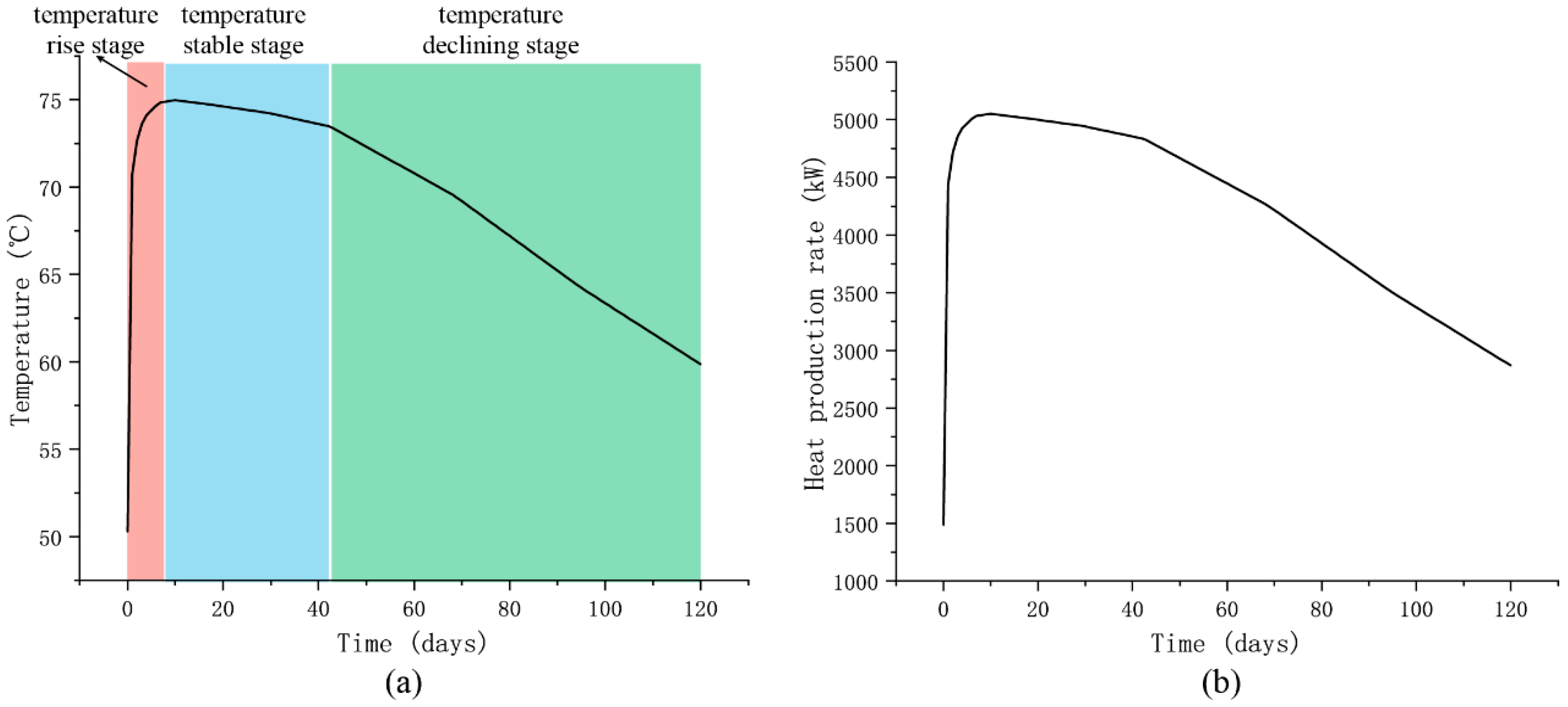
3.2. Output Temperature Analysis During Heat Production Stage
4. Discussion
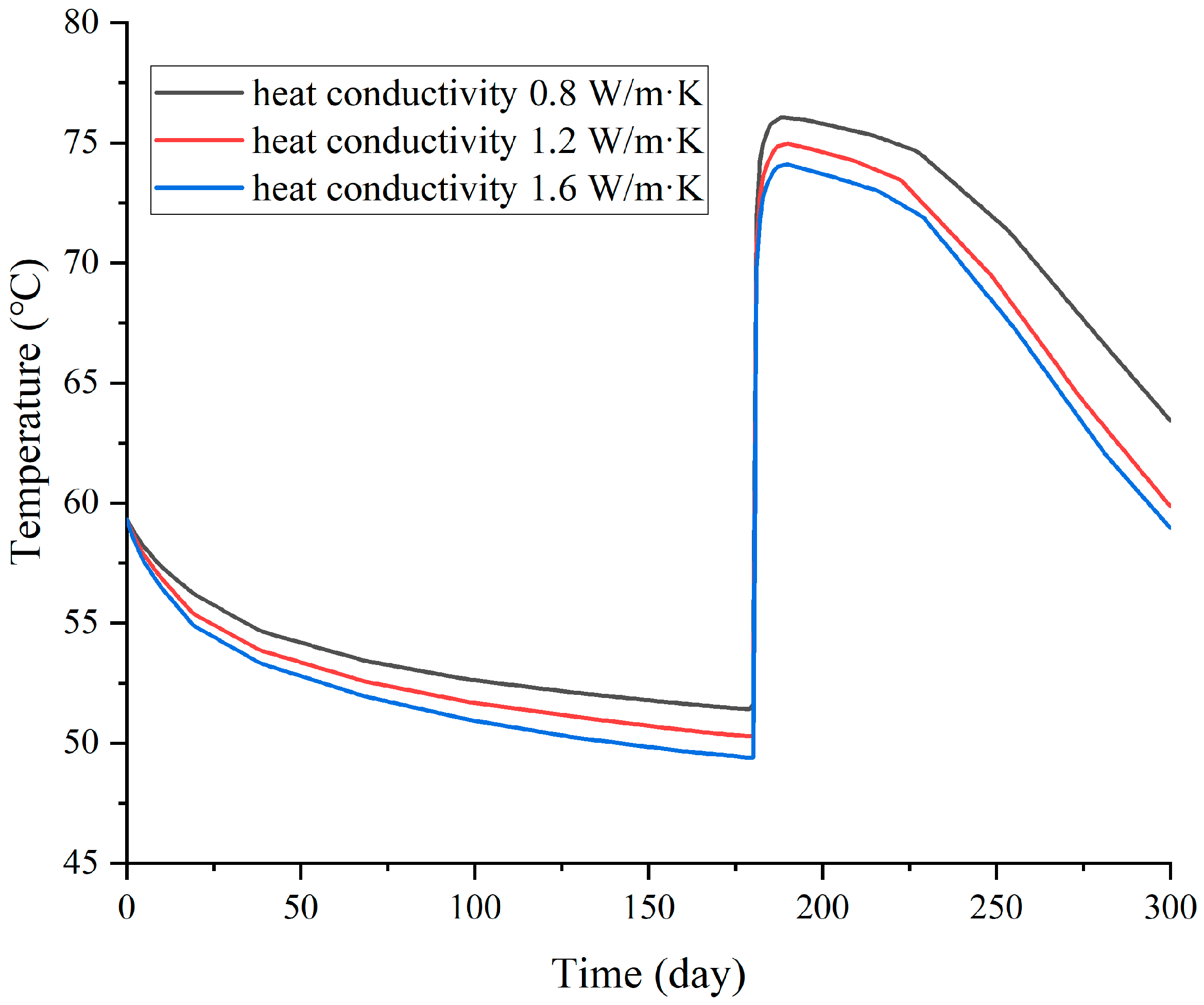
4.1. Influence of Surrounding Rock Thermal Conductivity
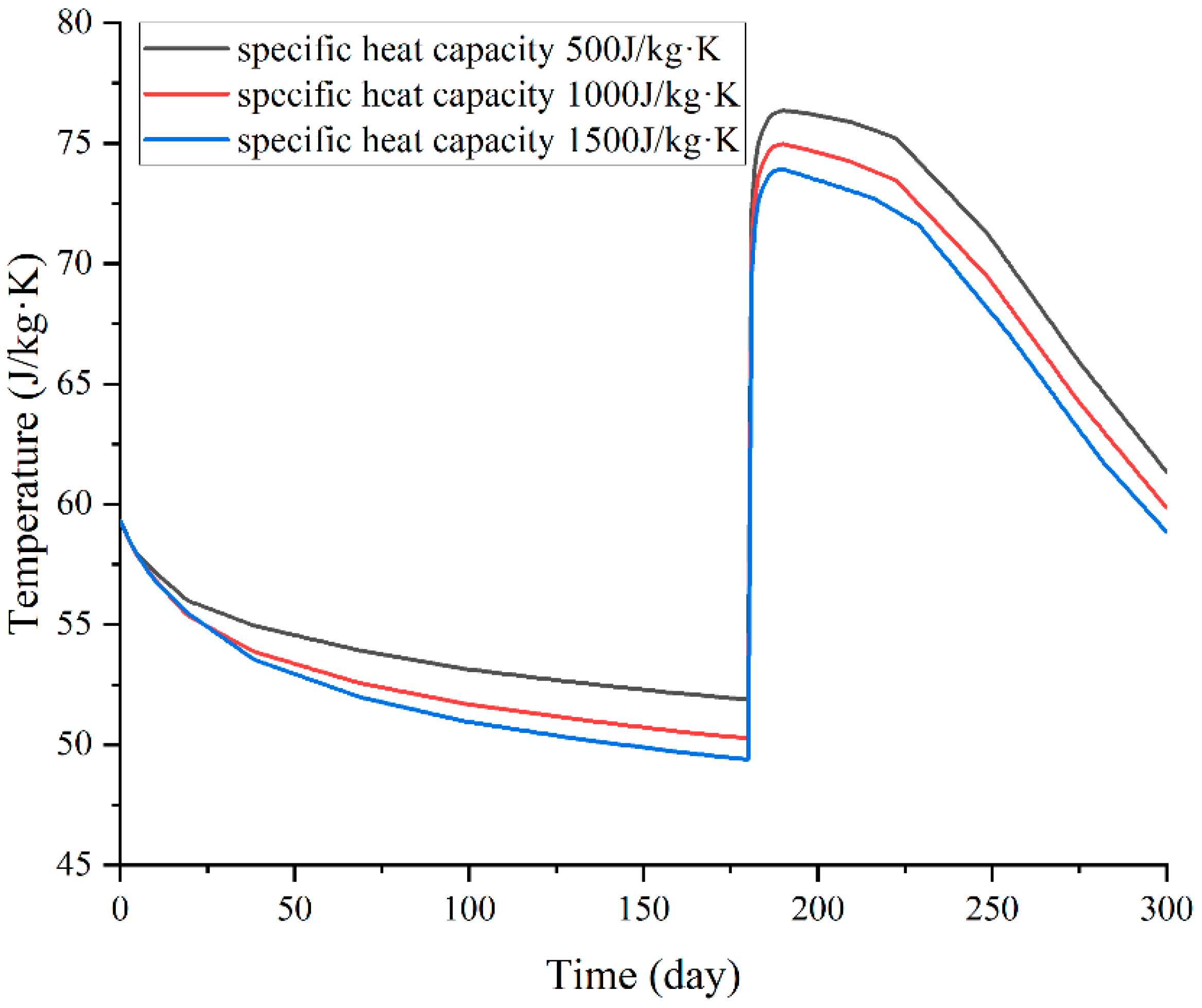
4.2. Surrounding Rock-Specific Heat Capacity
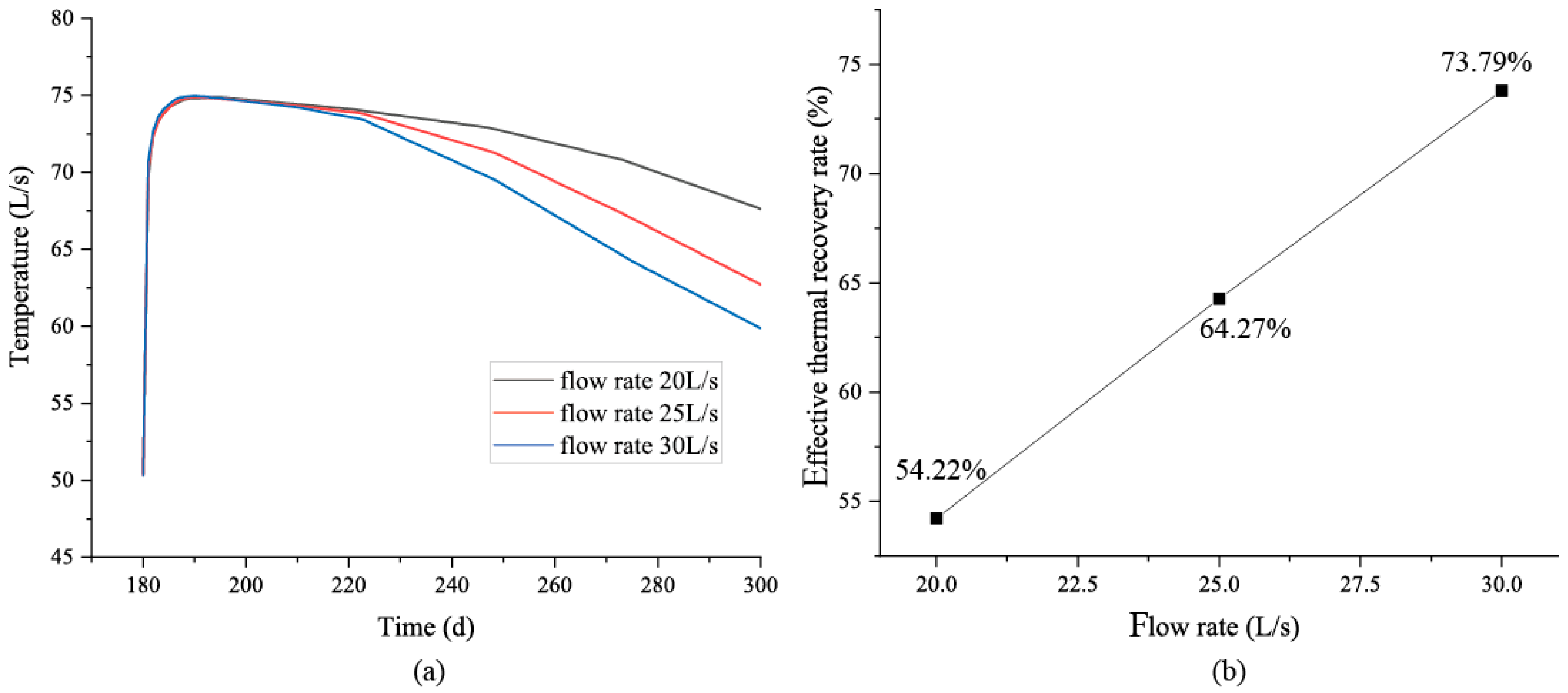
4.3. Pumping Flow Rate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, C.Q.; Wang, B.; Zhao, Y.X.; Xue, L.M. Waste mine to emerging wealth: Innovative solutions for abandoned underground coal mine reutilization on a waste management level. J Clean Prod. 2020, 252, 119748. [Google Scholar] [CrossRef]
- Duchane, D.V. Geothermal energy from hot dry rock: A renew able energy technology moving towards practical implementation. Renew. Energy 1996, 9, 1246–1249. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Xia, F.; Xing, Z.; Wang, L. Impacts of underground reservoir site selection and water storage on the groundwater flow system in a mining Area—A case study of daliuta mine. Water 2022, 14, 3282. [Google Scholar] [CrossRef]
- Pan, L.; Wang, F.; Miao, X. Concurrent mining during construction and water-filling of a goaf groundwater reservoir in a coal mine. Mine Water Environ. 2018, 37, 760–772. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Q.; Wang, T.; Li, Y. Drivers of groundwater storage dynamics in China’s Ordos mining region: Integrating natural and anthropogenic influences. Chin. Geogr. Sci. 2025, 35, 412–427. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Liu, R.; Zhao, H. Creep behavior and permeability evolution of coal pillar dam for underground water reservoir. Int. J. Coal Sci. Technol. 2023, 10, 78–92. [Google Scholar] [CrossRef]
- Menéndez, J.; Loredo, J.S.S. Use of coal mines facilities in northern Spain for the production of sustainable energy. Int. J. Environ. Sci. 2017, 2, 324–328. [Google Scholar]
- Andersson, J. Improving the efficiency of district heating and cooling using a geothermal technology: Underground thermal energy storage (UTES). Renew. Energy Rev. 2021, 15, 45–60. [Google Scholar]
- Smith, L.P.; Johnson, M.K. Modelling the energy production of a borehole thermal energy storage (BTES) system. Geotherm. Energy J. 2020, 8, 112–125. [Google Scholar]
- Lu, J.; Huang, G.; Gao, H.; Li, X.; Zhang, D.; Yin, G. Mechanical Properties of Layered Composite Coal–Rock Subjected to True Triaxial Stress. Rock Mech. Rock Eng. 2020, 53, 4117–4138. [Google Scholar] [CrossRef]
- Su, Z.; Yang, L.; Wang, H.; Liu, S.; Song, J.; Jin, X. Solar-assisted combined cooling and power system integrating energy storage and desulfurization for coal-fired power plants. Therm. Sci. Eng. Prog. 2023, 45, 102110. [Google Scholar] [CrossRef]
- Zhao, H.; Tu, S.; Liu, X.; Ma, J.; Tang, L. Energy-efficient heat resistance and cooling technology for high-temperature working faces with multiple heat sources in deep mines. Int. J. Coal Sci. Technol. 2023, 10, 45–61. [Google Scholar] [CrossRef]
- Saadat, A.; Shojaosadati, S.A. A review of underground energy storage in abandoned mines: Technical insights and case studies. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 41, 820–837. [Google Scholar]
- Holmslykke, H.; Weibel, R.; Olsen, D.; Anthonsen, K.L. Geochemical reactions upon injection of heated formation water in a Danish geothermal reservoir. ACS Earth Space Chem. 2023, 7, 1486–1498. [Google Scholar] [CrossRef]
- Menéndez, J.; Schmidt, F.; Konietzky, H.; Bernardo Sánchez, A.; Loredo, J. Empirical Analysis and Geomechanical Modelling of an Underground Water Reservoir for Hydroelectric Power Plants. Appl. Sci. 2020, 10, 5853. [Google Scholar] [CrossRef]
- Menéndez, J.; Loredo, J. Thermal energy recovery from flooded coal mines in northern Spain: A numerical model-based assessment. Renew. Energy 2019, 143, 1386–1396. [Google Scholar]
- Chudy, K. Mine Water as Geothermal Resource in Nowa Ruda Region (SW Poland). Water 2022, 14, 136. [Google Scholar] [CrossRef]
- Menéndez, J.; Loredo, J. Energy from closed mines: Underground energy storage and geothermal applications. Renew. Sustain. Energy Rev. 2019, 108, 498–512. [Google Scholar] [CrossRef]
- Menéndez, J.; Ordónez, A.; Fernández-Oro, J.M.; Loredo, J.; Díaz-Aguado, M.B. Feasibility analysis of using mine water from abandoned coal mines in Spain for heating and cooling of buildings. Renew. Energy 2020, 146, 1166–1176. [Google Scholar] [CrossRef]
- Ren, G. Water absorption characteristics of sand-mudstone composite lithology model in low/ultra permeability reservoirs. J. Oil Gas Technol. 2020, 42, 40251. [Google Scholar] [CrossRef]
- Smye, K.; Banerji, D.A.; Eastwood, R.; McDaid, G.; Hennings, P. Lithology and reservoir properties of the Delaware Mountain Group and implications for saltwater disposal and induced seismicity. J. Sediment. Res. 2021, 91, 587–601. [Google Scholar]
- Zhang, H.; Ye, Q.; Huan, J.; Zhang, C.; Chen, R. Identification of complex lithofacies based on compositional indicators: A case study of deep-water low-permeability gas reservoir in Baodao Sag, South China Sea. Mar. Geol. Front. 2024, 40, 87–95. [Google Scholar]
- Zhang, K.; Li, H.; Han, J.; Jiang, B.; Gao, J. Understanding of mineral change mechanisms in coal mine groundwater reservoir and their influences on effluent water quality: An experimental study. Int. J. Coal Sci. Technol. 2021, 8, 154–167. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Y. Convergence of solutions for Brinkman equations and Darcy equations interacting in porous media. J. Comput. Math. 2022, 40, 753–772. [Google Scholar]
- Gao, X.-W.; Ding, J.-X.; Liu, H.-Y. Finite line method and its application in coupled heat transfer between fluid-solid domains. Acta Phys. Sin. 2022, 71, 190201. [Google Scholar] [CrossRef]
- Esfe, M.H.; Bahiraei, M.; Hajbarati, H. A comprehensive review on convective heat transfer of nanofluids in porous media: Energy-related and thermohydraulic characteristics. Appl. Therm. Eng. 2020, 175, 115487. [Google Scholar]
- Chaurasia, A.S. Computational Fluid Dynamics and COMSOL Multiphysics: A Step-by-Step Approach for Chemical Engineers; Apple Academic Press: Burlington, ON, USA, 2021. [Google Scholar]
- Zeng, Z.; Shen, W.; Wang, M.; Li, Z.; Wang, X.; Ding, J. Numerical simulation of multi-field coupling in geothermal reservoir heat extraction of enhanced geothermal systems. J. Pet. Explor. Prod. Technol. 2024, 14, 1631–1642. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Zhang, S. Thermal performance and analysis of high-temperature aquifer thermal energy storage based on a practical project. J. Energy Storage 2024, 75, 109702. [Google Scholar]
- Huang, Y.; Li, S.; Zhang, W. Numerical modeling of the high-temperature thermal energy storage system in deep aquifers. Energy 2023, 282, 128875. [Google Scholar]
- Yuan, T.; Li, Y.; Wang, S.; Li, J.; Wang, J.; Chen, J. Energy storage mechanism and modeling method of underground aquifer to meet the demand of large-capacity new energy consumption. Appl. Therm. Eng. 2024, 246, 122966. [Google Scholar] [CrossRef]

| Parameter Name (Unit) | Parameter Value |
|---|---|
| Surrounding rocks density (kg/m3) | 1940 |
| Surrounding rocks permeability (m2) | 1 × 10−16 |
| Surrounding rocks porosity | 0.05 |
| Thermal conductivity of surrounding rocks (W/m·K) | 1.2 |
| Heat capacity of surrounding rocks (J/kg·K) | 9.7 |
| Water density (kg/m3) | 1000 |
| Dynamic viscosity of water (Pa·s) | 1.01 × 10−3 |
| Thermal conductivity of water (W/m·K) | 0.59 |
| Heat capacity of water (J/kg·K) | 4185 |
| Initial water temperature (K) | 363.15 |
| Initial rock temperature (K) | 313.15 |
| Rock Specific Heat Capacity (J/kg·K) | Rock Thermal Conductivity (W/m·K) | Flow Rate (L/s) | |
|---|---|---|---|
| Base case | 970 | 1.2 | 30 |
| Case 1 | 500 | 1.2 | 30 |
| Case 2 | 1500 | 1.2 | 30 |
| Case 3 | 970 | 0.8 | 30 |
| Case 4 | 970 | 1.6 | 30 |
| Case 5 | 970 | 1.2 | 20 |
| Case 6 | 970 | 1.2 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Tang, J.; Hu, Z.; Guo, Q.; Zhang, H.; Zhang, K.; Kang, S.; He, X. Potential Evaluation of Cross-Seasonal Heat Storage of Coal Mine Underground Reservoir: A Case Study Based on Multiphysics Coupling Numerical Simulation Method. Appl. Sci. 2025, 15, 10070. https://doi.org/10.3390/app151810070
Wang Z, Tang J, Hu Z, Guo Q, Zhang H, Zhang K, Kang S, He X. Potential Evaluation of Cross-Seasonal Heat Storage of Coal Mine Underground Reservoir: A Case Study Based on Multiphysics Coupling Numerical Simulation Method. Applied Sciences. 2025; 15(18):10070. https://doi.org/10.3390/app151810070
Chicago/Turabian StyleWang, Zhenyu, Jiawei Tang, Zixu Hu, Qiang Guo, Haiqin Zhang, Kangning Zhang, Siwei Kang, and Xiaolin He. 2025. "Potential Evaluation of Cross-Seasonal Heat Storage of Coal Mine Underground Reservoir: A Case Study Based on Multiphysics Coupling Numerical Simulation Method" Applied Sciences 15, no. 18: 10070. https://doi.org/10.3390/app151810070
APA StyleWang, Z., Tang, J., Hu, Z., Guo, Q., Zhang, H., Zhang, K., Kang, S., & He, X. (2025). Potential Evaluation of Cross-Seasonal Heat Storage of Coal Mine Underground Reservoir: A Case Study Based on Multiphysics Coupling Numerical Simulation Method. Applied Sciences, 15(18), 10070. https://doi.org/10.3390/app151810070





