Research on Identification and Localization of Flanges on LNG Ships Based on Improved YOLOv8s Models
Abstract
1. Introduction
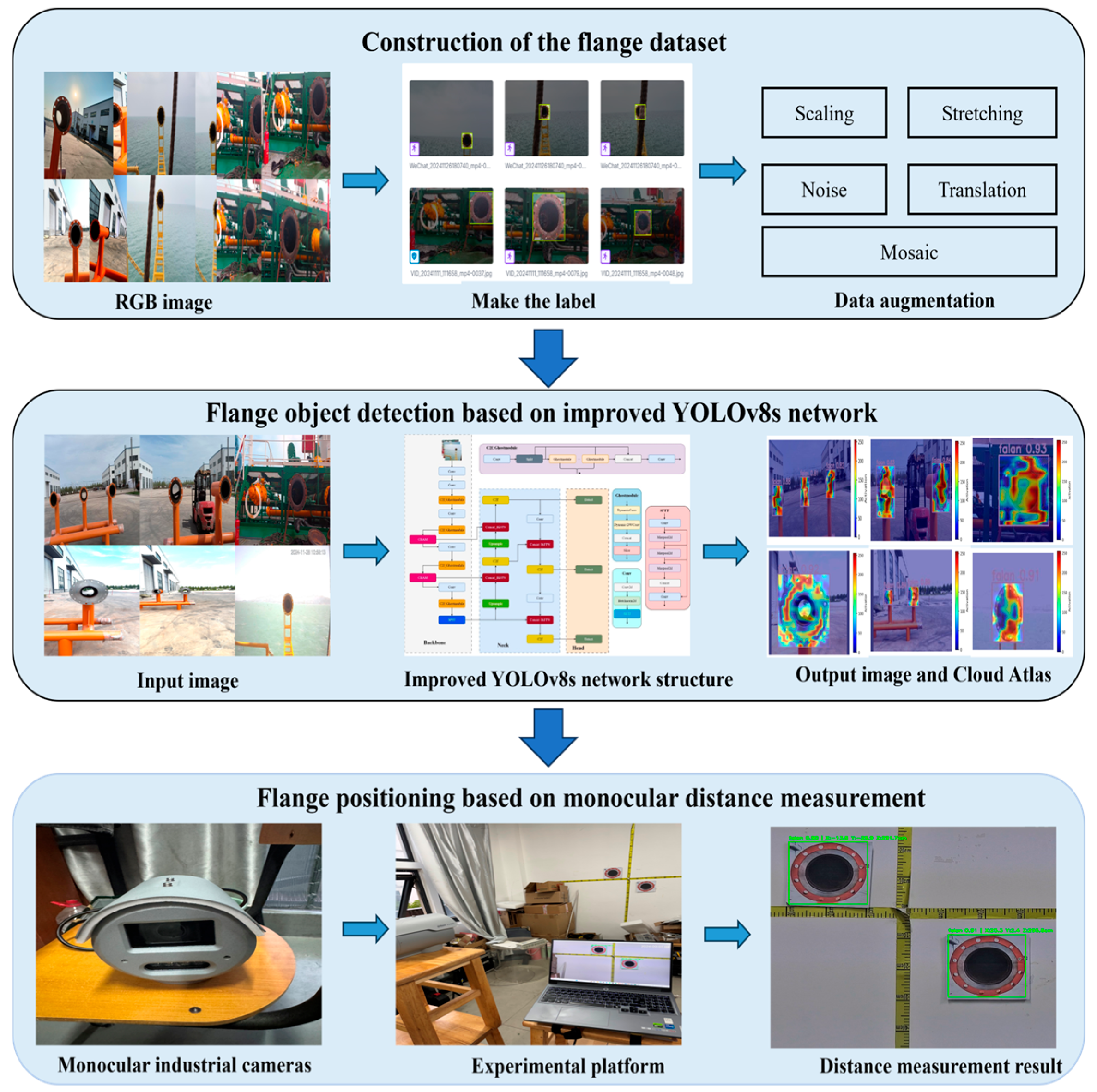
- Capturing flange images, constructing a dataset, labeling the dataset with Roboflow software, training the model to learn, and turning on multiple data enhancements to expand the diversity of the dataset.
- Introducing the Ghost module, which is a combination of dynamic convolution and dynamic depth-separable convolution. It replaces the Bottleneck in the C2f component of the backbone. This reduces the number of model parameters and improves the diversity and accuracy of feature extraction.
- The CBAM attention mechanism is located in the middle two layers of the backbone, which enhances the feature expression ability of the middle layer; improves model generalization and recognition accuracy; and at the same time, avoids defects such as the excessive parameter volume caused by the overall addition, which leads to information redundancy and overfitting of the model.
- Introducing a weighted BiFPN to replace the PAN-FPN structure in the neck for bi-directional enhancement of multiple features, reducing redundant connections and maintaining high efficiency of target feature fusion while having low computational costs.
- Adopting a monocular ranging algorithm based on the target pixel width to realize acquisition of the three-dimensional coordinates of the target. This approach mitigates the risk of difficulty in distance recognition due to the shooting angle and improves the accuracy of ranging.
2. Related Work
2.1. Flange Data Acquisition
2.2. Constructing and Processing the Dataset
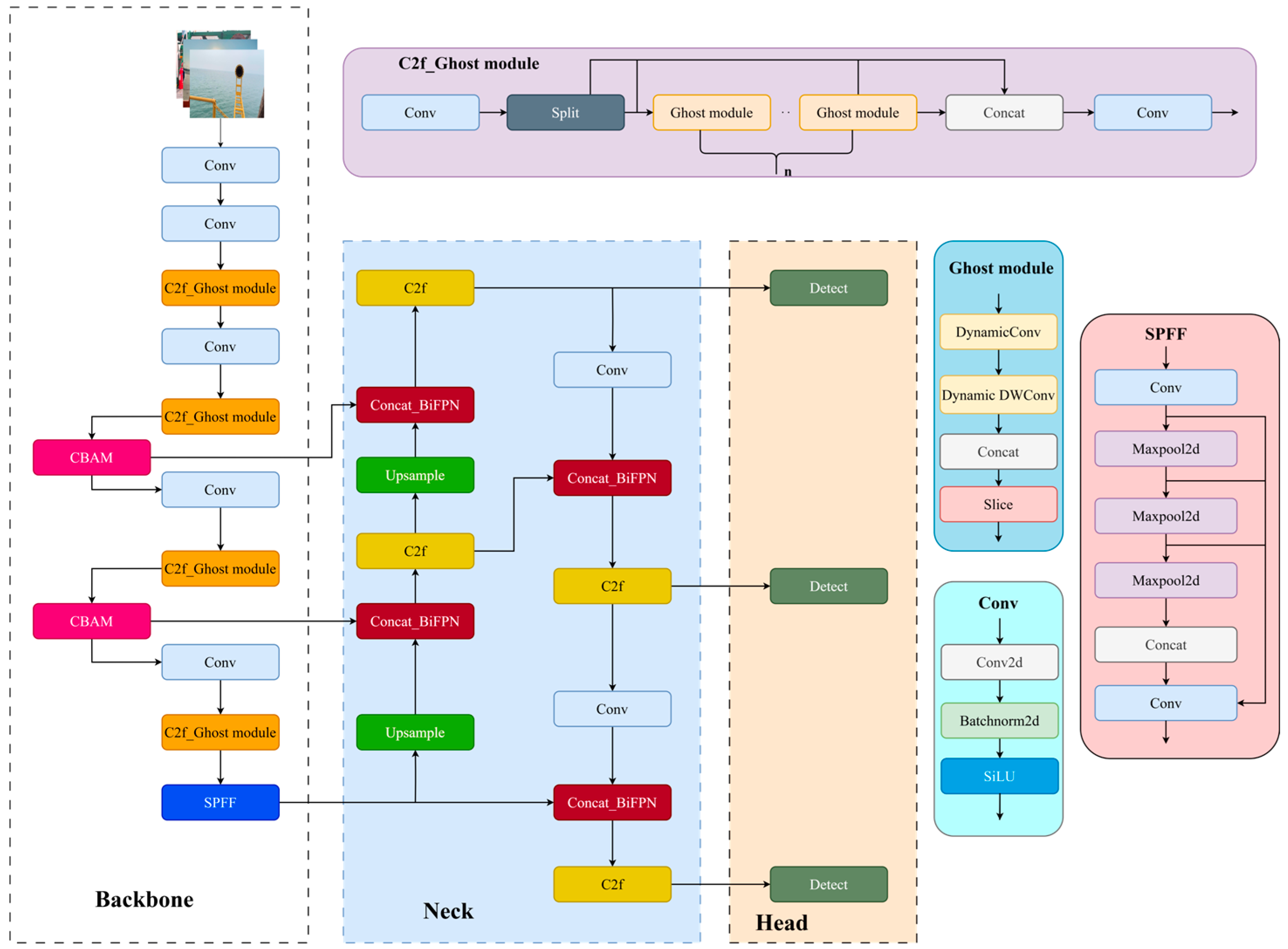
2.3. Improving the YOLOv8s Model
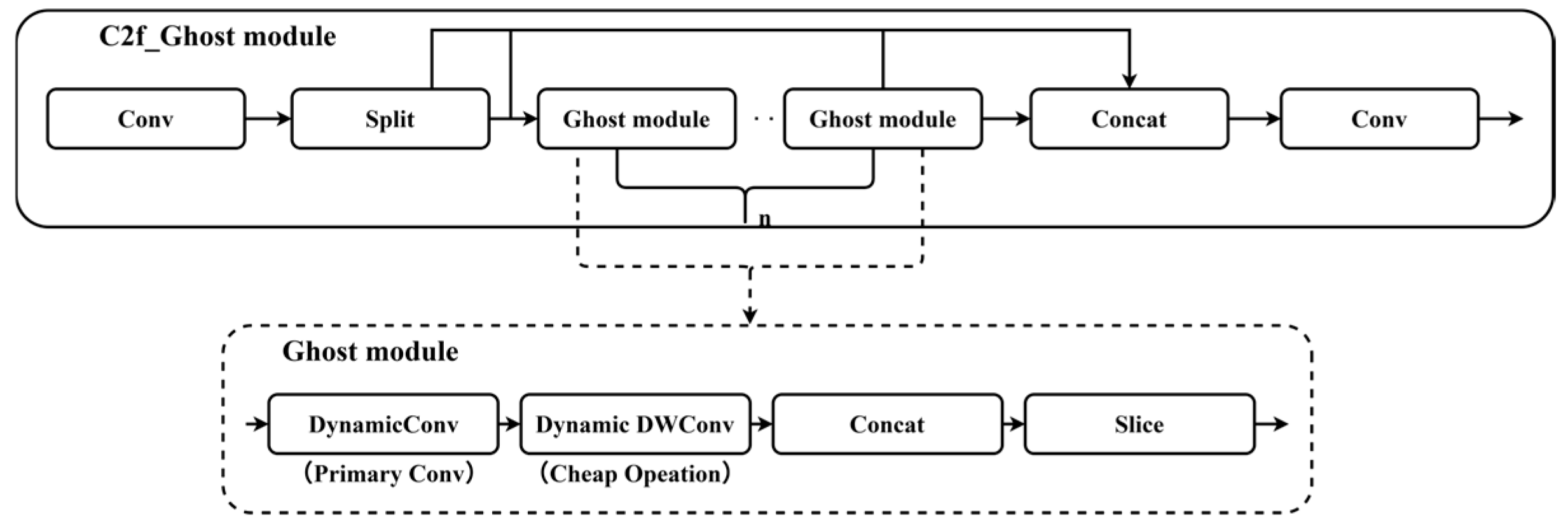
2.4. C2f_Ghost Module
2.5. Introducing CBAM
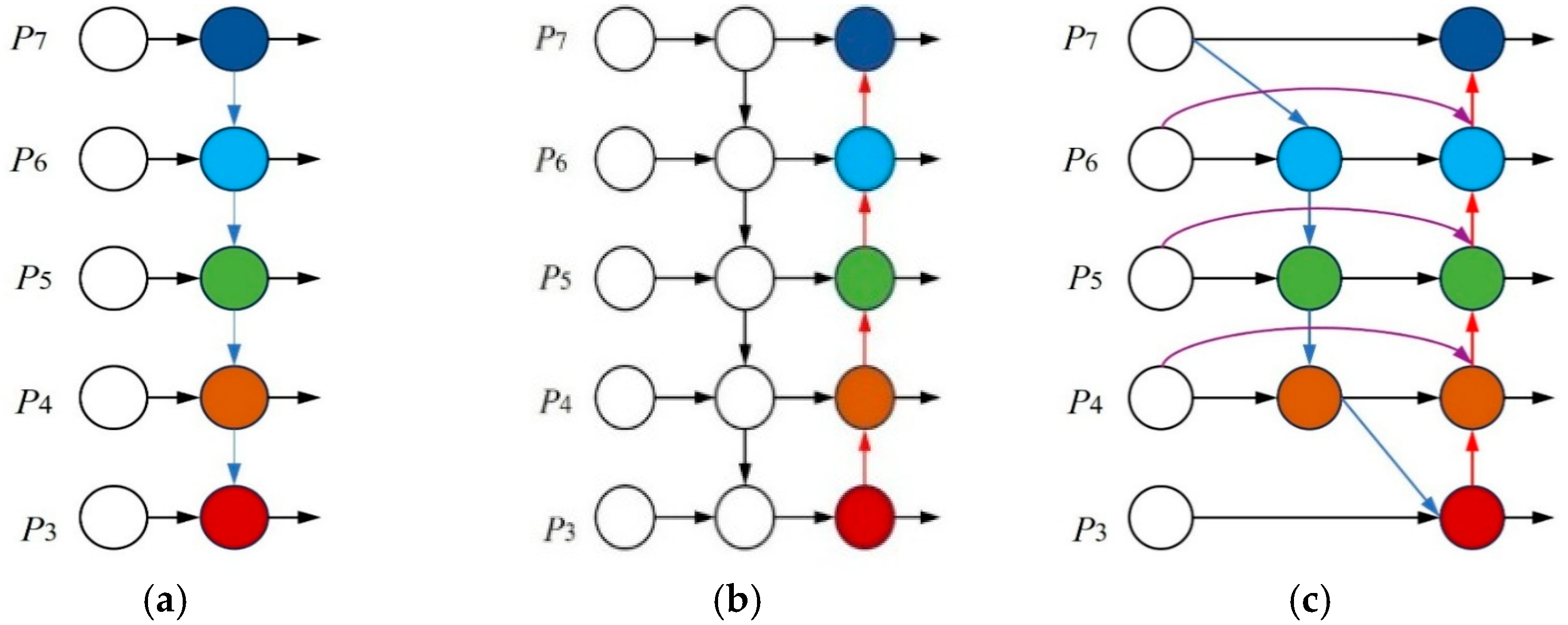
2.6. Introducing Concat_BiFPN
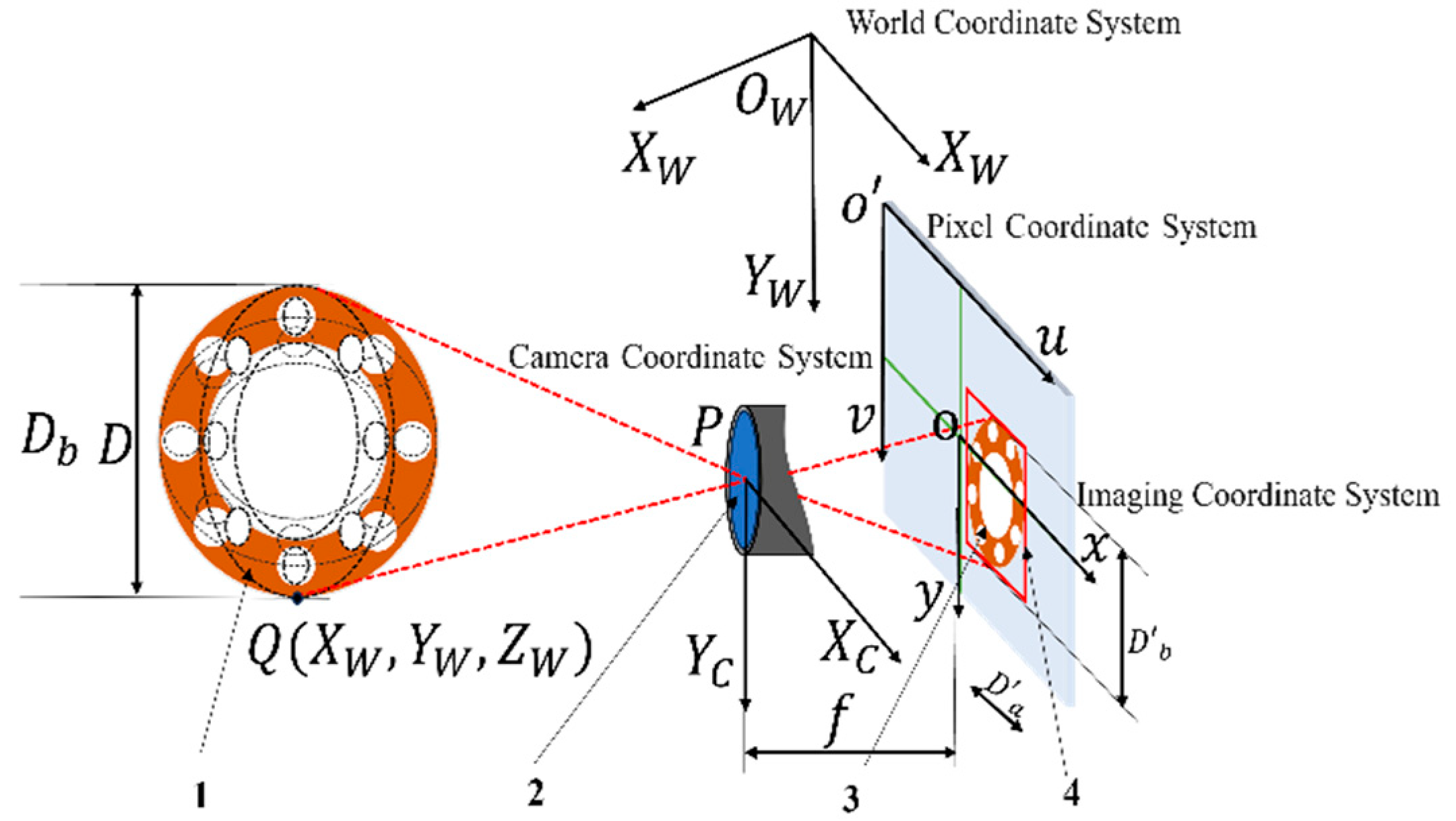
2.7. Monocular Ranging and Localization Models
2.8. Error Analysis and Uncertainty Discussion
- System parameter errors: The calibration residuals of the camera’s focal length () and principal point , along with the manufacturing and measurement tolerances of the flange’s actual diameter (), are directly incorporated into the calculation formula as systematic errors. These affect the accuracy of the distance () and the scaling factor ().
- Random detection error: Pixel-level positioning jitter in YOLO model bounding boxes constitutes the primary source of random error. This error directly impacts measurements of pixel width () and center coordinates, with its influence significantly increasing as the distance (d) increases. It is the main cause of coordinate errors in and .
- Model assumption error: The practical situation where the camera’s optical axis is not perfectly parallel to the target plane slightly violates the parallel assumption in the core derivation, leading to systematic underestimation of distance (). Additionally, residual errors from lens distortion correction introduce nonlinear coordinate transformation deviations.
3. Experiments
3.1. Experimental Parameter Settings
3.2. Evaluation Metrics
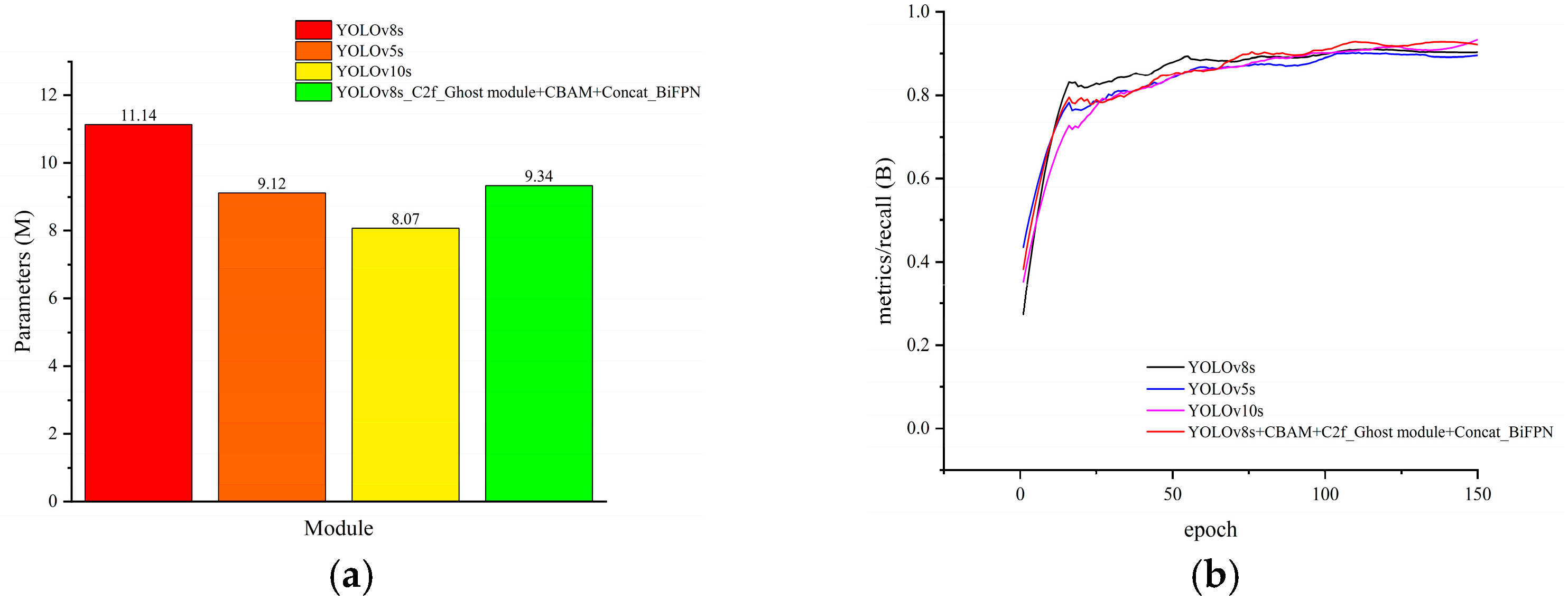
3.3. Ablation Experiments
3.4. Model Comparison Experiments
3.5. Visualizing the Results
3.6. Ranging and Localization Model Experiment
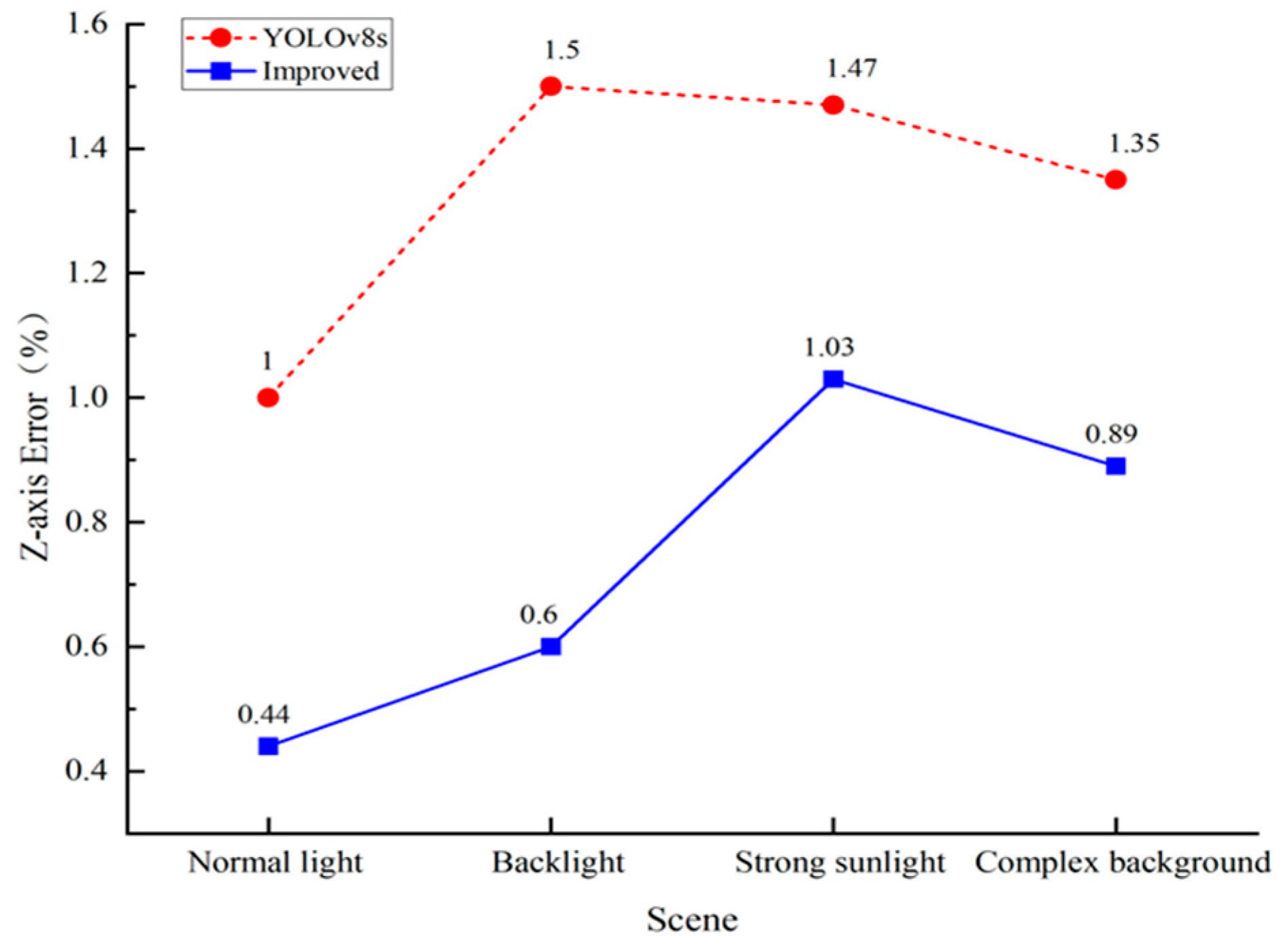
3.7. Model Generalizability Validation Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Lin, M.; Ma, F.; Liu, H.; Yang, Z.; Zhang, G.; Yang, Y.; Guan, C.; Liang, Y.; Wang, Y.; et al. Progress, Challenges and Countermeasures of China’s Natural Gas Industry under the Carbon Neutral Target. Pet. Explor. Dev. 2024, 51, 418–435. [Google Scholar] [CrossRef]
- Song, K.; Liu, Q.; Du, Y.; Liu, X. Analysis of the development status and prospect of China’s gas industry under the “dual-carbon target”. Shandong Chem. Ind. 2022, 51, 97–99. [Google Scholar]
- Gao, Y.; Wang, B.; Hu, M.; Gao, Y.; Hu, A. Review of China’s natural gas development in 2023 and outlook for 2024. Nat. Gas Ind. 2024, 44, 166–177. [Google Scholar]
- Sun, C.; Zhang, J. Analysis of the development status and prospect of LNG industry. Tianjin Sci. Technol. 2017, 44, 94–96. [Google Scholar]
- Cai, J.; Mao, Z.; Li, J.; Wu, X. A review of deep learning based target detection algorithms and applications. Netw. Secur. Technol. Appl. 2023, 11, 41–45. [Google Scholar]
- Ming, Z.Q.; Zhu, M.; Wang, X.; Cheng, J.; Gao, C.; Yang, Y.; Wei, X. Deep learning-based person re-identification methods: Asurvey and outlook of recent works. Image Vision. Comput. 2022, 119, 104394. [Google Scholar] [CrossRef]
- Wei, W.Y.; Yang, W.; Zuo, E.; Qian, Y.; Wang, L. Person re-identification based on deep learning An overview. J. Vis. Commun. Image Represent. 2022, 82, 103418. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, J.; Liao, W.; Guo, Y.; Li, T. Detection of Corrosion Areas in Power Equipment Based on Improved YOLOv5s Algorithm with CBAM Attention Mechanism. In 6GN for Future Wireless Networks. 6GN 2023; Li, J., Zhang, B., Ying, Y., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Cham, Switzerland, 2024; Volume 553. [Google Scholar] [CrossRef]
- Zhu, Y.S.; Wang, X.; Tang, C.H.; Liu, C.Y. Improved RAD-YOLOv8s deep learning algorithm for personnel detection in deep mining workings of mines. J. Real-Time Image Process. 2025, 22, 121. [Google Scholar] [CrossRef]
- Miao, Z.; Zhou, H.; Wang, Q.; Xu, H.; Wang, M.; Zhang, L.; Bai, Y. Improved mine fire detection algorithm for YOLOv8n. Min. Res. Dev. 2025, 45, 200–206. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Cao, J.; Ma, Y.; Zhang, Y.; Liu, X. Lightweight ship target detection algorithm based on improved YOLOv5s. J. Real-Time Image Process. 2024, 21, 3. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J. A lightweight YOLOv8 based on attention mechanism for mango pest and disease detection. J. Real-Time Image Process. 2024, 21, 136. [Google Scholar] [CrossRef]
- Wang, J.B.; Wu, Y.X. Safety helmet wearing detection algorithmof improved YOLOv4-tiny. Comput. Eng. Appl. 2023, 59, 183–190. [Google Scholar] [CrossRef]
- Luo, Y.; Ci, Y.; Jiang, S.; Wei, X. A novel lightweight real-time traffic sign detection method based on an embedded device and YOLOv8. J. Real-Time Image Process. 2024, 21, 24. [Google Scholar] [CrossRef]
- Han, J.; Yuan, J.W.X.; Lu, Y. Pedestrian visualpositioning algorithm for underground roadway based on deep learning. J. Comput. Appl. 2019, 39, 688. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, Q.; Zhang, C.; Tang, Y.; Qian, F. Monocular depth estimation based on deep learning: An overview. Sci. China Technol. Sci. 2020, 63, 1612–1627. [Google Scholar] [CrossRef]
- Shen, C.; Zhao, X.; Liu, Z.; Gao, T.; Xu, J. Joint vehicle detection and distance prediction via monocular depth estimation. IET Intell. Transp. Syst. 2020, 14, 753–763. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, P.; Cao, Z.; Bu, G.; Hao, Y. A Monocular Vision Ranging Method Related to Neural Networks. In Advances and Trends in Artificial Intelligence. Theory and Applications; Fujita, H., Wang, Y., Xiao, Y., Moonis, A., Eds.; IEA/AIE 2023; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2023; Volume 13925. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X. Monocular meta-imaging camera sees depth. Light Sci. Appl. 2025, 14, 5. [Google Scholar] [CrossRef]
- Liu, Q.; Pan, M.; Li, Y. Design of vehicle monocular ranging system based on FPGA. Chin. J. Liq. Cryst. Disp. 2014, 29, 422–428. [Google Scholar]
- Yuan, K.; Huang, Y.; Guo, L.; Chen, H.; Chen, J. Human feedback enhanced autonomous intelligent systems: A perspective from intelligent driving. Auton. Intell. Syst. 2024, 4, 9. [Google Scholar] [CrossRef]
- Chen, H.; Lin, M.; Xue, L.; Gao, T.; Zhu, H. Research on location method based on monocular vision. J. Phys. Conf. Ser. 2021, 1961, 012063. [Google Scholar] [CrossRef]
- Yang, F.; Wang, M.; Tan, T.; Lu, X.; Hu, R. Improved algorithm for monocular ranging of infrared imaging of power equipment based on target pixel width recognition. J. Electrotechnol. 2023, 38, 2244–2254. [Google Scholar] [CrossRef]
- Zeng, S.; Geng, G.; Zou, L.; Zhou, M. Real spatial terrain reconstruction of first person point- of-view sketches. Opt. Precis. Eng. 2020, 28, 1861–1871. [Google Scholar]
- Kim, S.M.; Lee, J.S. A comprehensive review on Compton camera image reconstruction: From principles to AI innovations. Biomed. Eng. Lett. 2024, 14, 1175–1193. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Zhang, Z.; Dai, M. Monocular vision system for distance measurement based on feature points. Opt. Precis. Eng. 2011, 19, 1110–1117. [Google Scholar] [CrossRef]
- Vince, J. Coordinate Systems. In Foundation Mathematics for Computer Science; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]










| Method | C2f_Ghost Module | CBAM | Concat_BiFPN | mAP@0.5 (%) | mAP@0.5:0.95 (%) | Parameters (M) | Recall (%) | GPU Memory (MB) |
|---|---|---|---|---|---|---|---|---|
| A | 96.9 | 68.9 | 11.14 | 92.9 | 120.39 | |||
| B | √ | 96.8 | 80.7 | 9.43 | 93.7 | 119.88 | ||
| C | √ | 96.1 | 80.5 | 11.22 | 93.7 | 120.70 | ||
| D | √ | 96.1 | 71 | 11.14 | 94.9 | 121.54 | ||
| E | √ | √ | 96.4 | 82.6 | 9.34 | 93.7 | 119.52 | |
| F | √ | √ | 96.2 | 81.5 | 9.43 | 94.2 | 119.88 | |
| G | √ | √ | 95.4 | 80 | 11.22 | 92.6 | 122.11 | |
| H | √ | √ | √ | 97.5 | 82.3 | 9.34 | 94.1 | 119.53 |
| Method | mAP@0.5 (%) | mAP@0.5:0.95 (%) | Parameters (M) | Recall (%) | FPS (RTX4060) | GPU Memory (MB) |
|---|---|---|---|---|---|---|
| A | 96.98 ± 0.49 | 74.76 ± 3.90 | 11.14 | 93.22 ± 0.91 | 123.70 | 120.39 |
| H | 96.68 ± 0.68 | 80.24 ± 1.43 | 9.51 | 92.84 ± 1.45 | 129.85 | 119.53 |
| Model | mAP@0.5 (%) | mAP@0.5:0.95 (%) | Parameters (M) | Recall (%) | GPU Memory (MB) |
|---|---|---|---|---|---|
| YOLOv8s | 96.9 | 68.9 | 11.14 | 92.9 | 120.39 |
| YOLOv5s | 96.4 | 65.7 | 9.12 | 92.2 | 107.78 |
| YOLOv10s | 97 | 78 | 8.07 | 93.3 | 108.10 |
| Improved YOLOv8s | 97.5 | 82.3 | 9.34 | 94.1 | 119.53 |
| Number | X-Axis | Y-Axis | Z-Axis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Measured | Inaccuracy | Measured | Inaccuracy | Measured | Inaccuracy | |||
| 1 | 20.0 | 20.6 | 3.00% | −20.0 | −19.2 | 4.00% | 300.0 | 300.5 | 0.17% |
| 2 | 30.0 | 30.8 | 2.67% | −30.0 | −28.4 | 5.33% | 320.0 | 321.2 | 0.37% |
| 3 | 40.0 | 41.1 | 2.75% | −40.0 | −41.9 | 4.75% | 340.0 | 337.8 | 0.65% |
| 4 | 50.0 | 51.4 | 2.80% | −50.0 | −52.3 | 4.60% | 360.0 | 357.2 | 0.78% |
| 5 | 60.0 | 62.3 | 3.83% | −60.0 | −61.9 | 3.17% | 380.0 | 383.5 | 0.92% |
| 6 | −20.0 | −20.9 | 4.50% | 20.0 | 19.8 | 1.00% | 400.0 | 404.3 | 1.08% |
| 7 | −30.0 | −31.2 | 4.00% | 30.0 | 30.9 | 3.00% | 420.0 | 415.2 | 1.14% |
| 8 | −40.0 | −42.1 | 5.25% | 40.0 | 41.3 | 3.25% | 440.0 | 445.7 | 1.30% |
| 9 | −50.0 | −48.7 | 2.60% | 50.0 | 51.2 | 2.40% | 460.0 | 466.2 | 1.35% |
| 10 | −60.0 | −62.6 | 4.33% | 60.0 | 62.1 | 3.50% | 480.0 | 487.3 | 1.52% |
| Average error ± std | 3.57% ± 0.87% | 3.50% ± 1.26% | 0.93% ± 0.44% | ||||||
| Number | X-Axis | Y-Axis | Z-Axis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Actual | Measured | Inaccuracy | Measured | Inaccuracy | Actual | Measured | Inaccuracy | ||
| 1 | 20.0 | 19.8 | 1.00% | −20.0 | −20.7 | 3.50% | 300.0 | 300.4 | 0.13% |
| 2 | 30.0 | 30.4 | 1.33% | −30.0 | −29.2 | 2.67% | 320.0 | 320.9 | 0.28% |
| 3 | 40.0 | 40.7 | 1.75% | −40.0 | −41.8 | 4.50% | 340.0 | 338.2 | 0.53% |
| 4 | 50.0 | 51.2 | 2.40% | −50.0 | −52.2 | 4.40% | 360.0 | 362.4 | 0.67% |
| 5 | 60.0 | 61.5 | 2.50% | −60.0 | −61.5 | 2.50% | 380.0 | 376.3 | 0.97% |
| 6 | −20.0 | −20.5 | 2.50% | 20.0 | 20.4 | 2.00% | 400.0 | 403.8 | 0.95% |
| 7 | −30.0 | −30.9 | 3.00% | 30.0 | 30.7 | 2.33% | 420.0 | 423.5 | 0.83% |
| 8 | −40.0 | −41.3 | 3.25% | 40.0 | 39.2 | 2.00% | 440.0 | 435.6 | 1.00% |
| 9 | −50.0 | −51.7 | 3.40% | 50.0 | 50.8 | 1.60% | 460.0 | 456 | 0.87% |
| 10 | −60.0 | −61.9 | 3.17% | 60.0 | 61.3 | 2.17% | 480.0 | 484.3 | 0.89% |
| Average error ± std | 2.43% ± 0.83 | 2.77% ± 1.02% | 0.71% ± 0.31% | ||||||
| Scene | Actual (cm) | Measured (YOLOv8s) | Measured (Improved) | Error (%) YOLOv8s | Error (%) Improved |
|---|---|---|---|---|---|
| Normal light | 500 | 495 | 497.8 | 1.0 | 0.44 |
| Backlight | 600 | 591 | 596.4 | 1.5 | 0.6 |
| Strong sunlight | 700 | 689.7 | 692.8 | 1.47 | 1.03 |
| Complex background | 650 | 641.2 | 644.2 | 1.35 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Feng, W.; Lin, R.; Wang, W.; Liu, G.; Xu, L. Research on Identification and Localization of Flanges on LNG Ships Based on Improved YOLOv8s Models. Appl. Sci. 2025, 15, 10051. https://doi.org/10.3390/app151810051
Song S, Feng W, Lin R, Wang W, Liu G, Xu L. Research on Identification and Localization of Flanges on LNG Ships Based on Improved YOLOv8s Models. Applied Sciences. 2025; 15(18):10051. https://doi.org/10.3390/app151810051
Chicago/Turabian StyleSong, Songling, Wuwei Feng, Rongsheng Lin, Wei Wang, Guicai Liu, and Lin Xu. 2025. "Research on Identification and Localization of Flanges on LNG Ships Based on Improved YOLOv8s Models" Applied Sciences 15, no. 18: 10051. https://doi.org/10.3390/app151810051
APA StyleSong, S., Feng, W., Lin, R., Wang, W., Liu, G., & Xu, L. (2025). Research on Identification and Localization of Flanges on LNG Ships Based on Improved YOLOv8s Models. Applied Sciences, 15(18), 10051. https://doi.org/10.3390/app151810051






