AutoProPos: An Extension of Prototype Scattering and Positive Sampling Clustering for an Unknown Number of Clusters

Abstract

Parametric deep clustering delivers strong image representations and partitions via modern contrastive and non-contrastive training, but it assumes a known number of clusters, K, which is often unrealistic in real datasets. Conversely, non-parametric methods estimate K but typically rely on weaker autoencoder features. We bridge this gap with AutoProPos, which extends the state-of-the-art ProPos and makes it non-parametric through a lightweight clustering supervisor (CLS). CLS alternates with ProPos and performs model selection over K in a reduced latent subspace using the average silhouette and the Silhouette Uniformity Index (SUI), with the latter encouraging uniform cluster distributions. Across image clustering benchmarks, AutoProPos is competitive with or superior to non-parametric deep clustering: 92.0% ACCon STL-10 (+11% vs. the best non-parametric baseline) and 77.0% ACC on ImageNet-50; against parametric deep clustering, it is also competitive and can even surpass them, as on ImageNet-Dogs, where it improves from 78.1% (ProPos) to 83.3% ACC. CLS estimates K during training with a small overhead (≤2 h on a single GPU), turning ProPos into a competitive non-parametric image-clustering method without sacrificing accuracy or compute.

1. Introduction

Deep clustering is a rapidly evolving field within deep learning, and it is particularly impactful in computer vision due to its performance nearing that of supervised frameworks, notably supervised classification [1,2]. We use deep clusteringto denote methods that train at least one neural component with a clustering-dependent objective, either (i) end-to-end schemes that update a deep encoder jointly with in-loop cluster assignments (the assigner may be classical, such as the spherical k-means [3] used in ProPos [4], or neural), or (ii) multi-stage schemes that keep a pretrained encoder fixed and train a neural clustering head on its features (such as [2]). Deep clustering methods excel in grouping high-dimensional and complex data into clusters based on similarity without prior knowledge of labels. By leveraging deep neural networks for representation learning, deep clustering discovers meaningful patterns, enhancing performance and applicability in scenarios where manual labeling is impractical.

One of the most straightforward categories for deep clustering is into two families: parametric methods and non-parametric methods. Parametric methods involve fixing the number of clusters, K, before training, which can lead to issues like overclustering or underclustering when the true number of clusters is unknown, thus degrading the clustering quality [5,6]. In contrast, non-parametric methods dynamically adjust the number of clusters during training, aligning more closely with real-world scenarios.

In this context, state-of-the-art (SOTA) models like DeepDPM [6] and DIVA [7] have demonstrated the effectiveness of using an alternating framework to train a feature extractor and clustering model alternately. Indeed, this approach significantly enhances performance by iteratively refining both representation and clustering. Thus, these models represent a significant step forward in the development of non-parametric deep clustering techniques.

The quality of deep clustering is closely tied to the representation learning techniques used. While DeepDPM and DIVA perform well on metrics, they rely on traditional self-supervised techniques such as autoencoders with reconstruction for DeepDPM, VAEs for DIVA, and clustering loss for both. Consequently, for large-scale and complex datasets like ImageNet-50 [8], they use a two-step approach through which their models are built on top of the self-supervised model MOCO [9], which uses a contrastive learning framework to generate robust data representations. This separation, however, loses the advantages of an end-to-end approach. Therefore, integrating a more performant framework for representation learning that can alternatively learn the number of clusters remains a challenge to be addressed.

To address these limitations, we propose AutoProPos, an extension of the SOTA deep parametric clustering model ProPos [4]. Like ProPos, AutoProPos belongs to the end-to-end family. AutoProPos includes our Clustering Supervisor Module (CLS) in an alternating framework to dynamically adjust the number of clusters, K, needed for ProPos training, making it non-parametric. Unlike previous works grounded in the Dirichlet process mixture (DPM) field, our CLS employs a model selection framework. This framework involves running a parametric clustering model over a range of specified K values and selecting the best clustering configuration using an unsupervised metric. Model selection-based frameworks determine the optimal number of clusters K for various classical parametric algorithms such as spherical k-means [3], KMeans [10], and spectral clustering [11], making the K prediction adaptable to different data manifolds. ProPos, in our case, produces a uniform representation on a unit hypersphere, a spherical approach rarely explored by DPM-based clustering works (for example [12]). A common disadvantage of both model selection-based frameworks and DPM-based clustering works is their potential computational expense for high-dimensional data. In CLS, we tackle this issue by remapping ProPos’s latent space using autoencoders into a lower-dimensional space and training on a subset of the dataset, as further explained in Section 4.1. Thus, our method is efficient and scalable.

Finally, our CLS module selects the optimal K for the directional latent data produced by ProPos based on the silhouette score and our novel index, the Silhouette Uniformity Index (SUI), designed to find the optimal cluster configuration for balanced datasets.

Our contributions can be summarized as follows: (1) We developed the Clustering Supervisor Module or CLS, a scalable module that automatically determines the optimal number of clusters during ProPos training. (2) We introduced the Silhouette Uniformity Index or SUI, a novel metric to evaluate the number of clusters in balanced datasets. (3) Our approach achieved SOTA and competitive results across various datasets against both parametric and non-parametric deep clustering models.

2. Related Works

2.1. Parametric Deep Clustering

Parametric deep clustering has significantly evolved. Early models like DEC [13] and IDEC [14] pioneered the use of deep neural networks for feature representation and cluster assignment. Subsequently, advanced methods like DeepCluster [15] and JULE [16] further enhanced clustering through iterative processes. SCAN [5] included self-labeling to iteratively improve labels through self-supervised learning, and SPICE [1] addressed stability by adding semantic pseudo-labeled feedback. ProPos [4] improves upon BYOL [17] through a mixture of non-contrastive and contrastive learning, creating uniform data representations globally, as well as through local clusters. Newer models such as TSP [18] and TEMI [2] depend greatly on fine-tuning vision transformer pre-trained models from large-scale datasets (e.g., ImageNet-1K [19]) to achieve significant improvements in clustering accuracy. However, their dependence on extensive pretraining limits their flexibility and adaptability.

2.2. Nonparametric Deep Clustering

Deep clustering without initial K. These models do not require the number of clusters K to be specified to start their training. Furthermore, they dynamically infer it during the training process, making them nonparametric. They incorporate a feature extractor, often a variational auto-encoder (VAE) or a deep neural network, and a clustering module that predicts the data cluster assignments, both of which are trained on unsupervised tasks. Some models refine the feature learning using the inferred clusters. Examples include the following: VAE-nCRP [20], which employs a nested Chinese Restaurant Process; AdapVAE [21]; DCC [22]; DNB [23]; and DeepDPM [6], which uses Dirichlet Process Mixture Models. VSB-DVM [24] and DIVA [7] integrate Bayesian nonparametric methods with VAEs.

Deep clustering transitioning to non-parametric. These models start from a parametric deep clustering network that requires a preset number of clusters, K, and then adjust K during training by attaching an unsupervised control module. We found no related work except Deep Plug-and-Play Clustering with Unknown Number of Clusters [25], which embeds a split–merge block into the clustering network: it augments the K-way head with auxiliary binary heads to split clusters when within-cluster dissimilarity is high and to merge the most similar pairs, using Jensen–Shannon–based criteria; during training, cluster weights are duplicated or averaged when splitting or merging so that K stabilizes at convergence. In contrast, AutoProPos extends ProPos [4] with a lightweight clustering supervisor (CLS) that decouples K-selection from representation learning and performs model selection over K in a reduced autoencoder latent subspace using cosine silhouette together with SUI; CLS alternates with the ProPos loop, returns only the updated K, and preserves ProPos’s spherical k-means assignments and EM-style training (discussed in Section 3).

Evolutionary multi-objective automatic clustering. Another line of work addresses unknown K by jointly optimizing cluster assignments and the number of clusters under multiple objectives, often adding topology-aware encodings and ensemble consensus to improve robustness when K is not given. Representative methods include a hierarchical topology-based cluster representation for scalable multi-objective clustering [26] and an EMO framework enhanced with quality metrics and ensemble selection [27]. In contrast to these joint-optimization pipelines, AutoProPos decouples representation learning and K-selection: ProPos learns spherical features, while CLS performs lightweight model selection over K.

3. Preliminaries: ProPos

As previously introduced, ProPos [4] is a parametric deep clustering model for image clusterization that learns its latent representation using a non-contrastive and prototype scattering framework. The model employs k-means clustering and introduces two new loss functions named Prototype Scattering Loss (PSL) and Positive Sampling Alignment (PSA) to improve the separation of these representations. This section gives a brief overview of its framework, explaining the architecture, novel loss functions, and training methodology.

3.1. ProPos Architecture

ProPos [4] involves three principal encoders: the online network $f(.)$, the target network $f^{\prime }(.)$, and the predictor network $g(.)$. The online network and the predictor weights are updated directly through the backpropagation of the computed loss defined in Section 3.2 and Section 3.3. As stated by the original ProPos authors, the design follows a BYOL-style online–target–predictor scheme [17]: the online and target networks produce instance representations, and the predictor aligns the online representation with the target one to mitigate representational collapse. The parameters of the target network are updated through a moving average of the parameters from the online network, formulated as follows:

$${\theta }_{\mathrm{target}}=m{\theta }_{\mathrm{target}}+(1-m){\theta }_{\mathrm{online}}$$

(1)

where $m\in [0,1]$ is the momentum hyperparameter, and $\theta$ denotes the networks’ parameters.

3.2. Prototype Scattering Loss (PSL)

By partitioning the target network’s representations into K clusters, we can compute its and the online network’s respective cluster centers, also called prototypes by the authors [4]. The PSL loss is subsequently defined as follows:

$${\mathcal{L}}_{\mathrm{psl}}\approx {\displaystyle \frac{1}{K}}\sum _{k=1}^K-{\displaystyle \frac{{\mu }_k^T{\mu }_k^{\prime }}{\tau }}+{\displaystyle \frac{1}{K}}\sum _{k=1}^{K}log\sum _{j\ne k}exp\left({\displaystyle \frac{{\mu }_k^T{\mu }_j}{\tau }}\right)$$

(2)

Here, the networks’ respective prototypes, ${\mu }_k$ and ${\mu }_k^{\prime }$, are computed within a mini-batch, B, as follows:

$${\mu }_k={\displaystyle \frac{{\sum }_{x\in B}p\left(k\right|x)f\left(x\right)}{{∥{\sum }_{x\in B}p\left(k\right|x)f\left(x\right)∥}_2}},$$

(3)

$${\mu }_k^{\prime }={\displaystyle \frac{{\sum }_{x\in B}p\left(k\right|x)f^{\prime }\left(x\right)}{{∥{\sum }_{x\in B}p\left(k\right|x)f^{\prime }\left(x\right)∥}_2}},$$

(4)

where $p\left(k\right|x)$ is the cluster assignment posterior probability. It is important to note that PSL is computed after a warmup epoch because the learned representations, and thus the cluster centers, may not be well defined during the early stages of training. During this initial period, only PSA is computed.

${\mathcal{L}}_{\mathrm{psl}}$ can be viewed as two distinct components, prototypical alignment, denoted by the first term, and prototypical uniformity, represented in the second term. Prototypical alignment stabilizes an update of the prototypes by enforcing alignment among the two views, and prototypical uniformity enforces a uniform distribution over each prototype set on the unit hypersphere, which maximizes the inter-cluster distance.

3.3. Positive Sampling Alignment (PSA)

PSA aims to improve within-cluster compactness by aligning neighboring examples around one augmented view with another view. By sampling neighboring examples from a Gaussian distribution using the reparameterization trick, the following is obtained:

$$v=f\left(x\right)+\sigma ϵ,ϵ\sim \mathcal{N}(0,\mathbf{I})$$

(5)

where $\mathbf{I}$ denotes the identity matrix. This method extends the instance alignment by considering neighboring samples:

$${\mathcal{L}}_{\mathrm{psa}}={∥g\left(v\right)-f^{\prime }\left(x^{+}\right)∥}_2^2={∥g(f\left(x\right)+\sigma ϵ)-f^{\prime }\left(x^{+}\right)∥}_2^2$$

(6)

By ensuring that neighboring examples are from the same cluster, PSA avoids class collision issues [28] and enhances within-cluster compactness.

3.4. Training ProPos

ProPos is optimized using an expectation–maximization (EM) framework with the following steps.

In the E-step, $p\left(k\right|x)$ is estimated for PSL on the projected dataset via the target network using spherical k-means clustering. This $p\left(k\right|x)$ is updated every r epochs (with $r=1$ in our paper).

In the M-step, to compute PSL and PSA, two augmented views of images in the mini-batch are passed into the online and target networks. PSL and PSA losses are then combined to form the objective function:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{psa}}+{\lambda }_{\mathrm{psl}}{\mathcal{L}}_{\mathrm{psl}}$$

(7)

where ${\lambda }_{\mathrm{psl}}$ balances the two loss components. The different networks are then updated, and the whole process is repeated until the maximum number of epochs is reached.

ProPos remains a parametric deep clustering model: it assumes a fixed K and does not explicitly regulate cluster distribution uniformity during training. Section 4 introduces AutoProPos, which augments ProPos with a lightweight clustering supervisor (CLS) that alternates with the ProPos loop to select K using a cosine silhouette computed in a reduced latent subspace and to promote uniform cluster distributions via the Silhouette Uniformity Index (SUI); the final assignments remain those of ProPos’ spherical k-means.

4. Our Method: AutoProPos

The AutoProPos framework combines the strengths of ProPos [4] with our newly developed Clustering Supervisor Module (CLS) to enable dynamic clustering without knowing the cluster counts, K, in advance. This section starts with an overview of the entire framework (Section 4.1), showing how ProPos and CLS work together to refine latent space representations and dynamically adjust K. The CLS module is then presented (Section 4.2), explaining its role in analyzing ProPos latent representations to determine the optimal number of clusters. This includes using the well-known average silhouette score as a metric for assessing clustering quality (Section 4.2.1) and our novel metric, the Silhouette Uniformity Index (Section 4.2.3), designed to select a set of balanced clusters. Finally, we describe the iterative process of the CLS (Section 4.2.4), involving the training of autoencoders, computing the previously presented metrics, and inferring the number of clusters using our Mean K and Max K strategies. The implementation is available at: https://github.com/Cyrilkt/AutoProPos, accessed on 15 July 2025.

4.1. Framework Overview

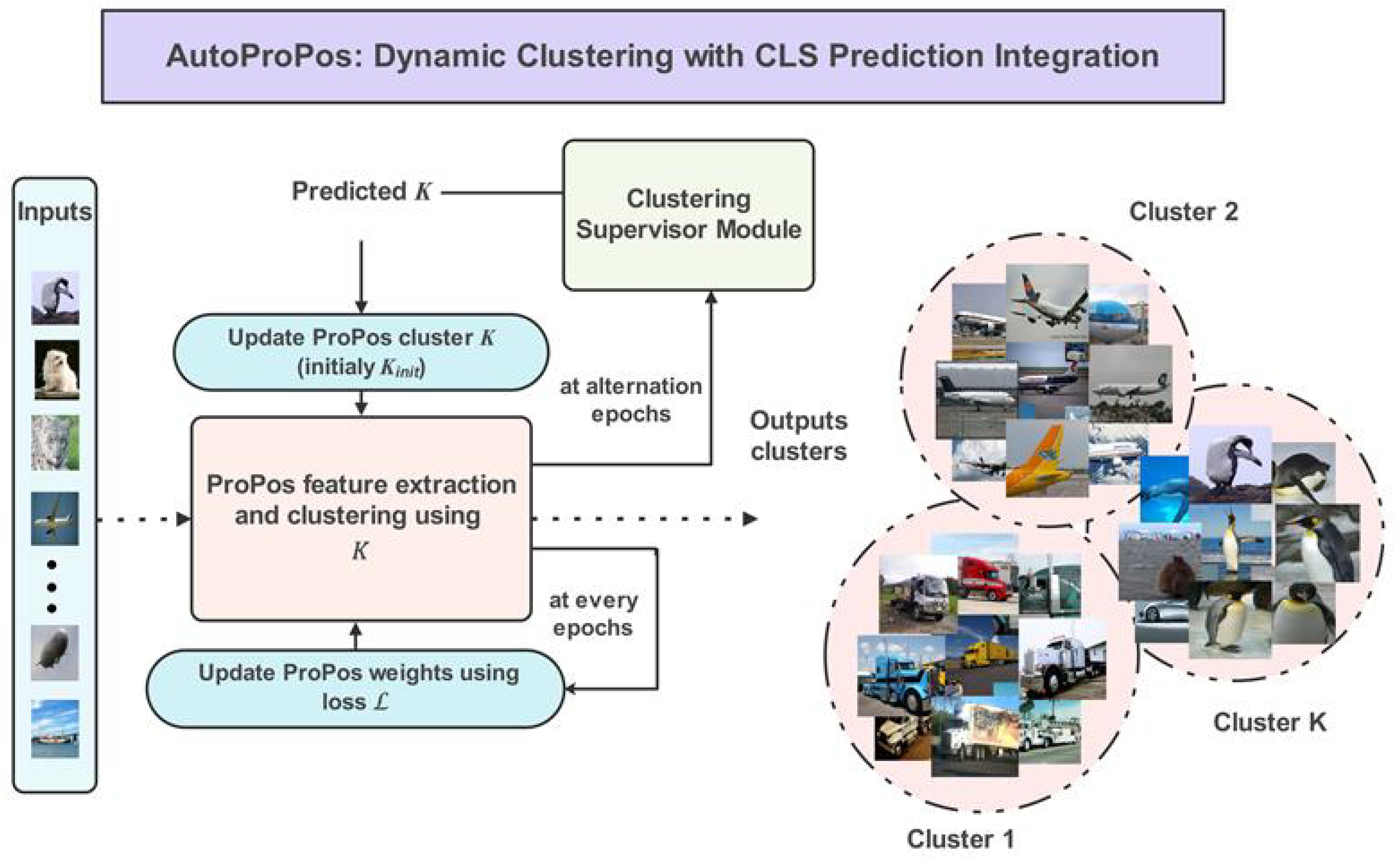
Figure 1 outlines the training pipeline of the AutoProPos framework, demonstrating the sequence of operations from initial setup to the refinement stages. In AutoProPos, we first train ProPos [4] by using an initial estimate of the number of clusters, $K_{\mathrm{init}}$, to refine the latent space representations based on this cluster count. During alternation epochs, the training dataset is projected through the target network to generate latent representations. Our Clustering Supervisor Module (CLS) analyzes these representations and provides the new K to ProPos, continuing the training with this updated count. This iterative training process is repeated until we determine that the cluster count has stabilized. Unlike SOTA non-parametric deep clustering works [6,7], which alternate between training an autoencoder and a clustering module, where the clustering module also aims to infer the final assignment of data to clusters. Our implementation of CLS solely aims to determine the number of clusters. The final sample-to-cluster assignments used to optimize ProPos remain those produced via the spherical k-means E-step (Section 3.4). This focus allows us to use a subset of the data while inferring K using CLS, significantly reducing its computation cost and maintaining training duration for AutoProPos similar to ProPos.

4.2. Clustering Supervisor Module (CLS)

4.2.1. Average Silhouette Score

The average silhouette score, $\overline{S}$, quantifies how well each object has been classified in its cluster compared to other clusters. Like the silhouette score s, it ranges from −1 to 1, where a high $\overline{S}$ value indicates a tight and well-separated cluster structure, while a low $\overline{S}$ means that the clusters are less distinctive with potential overlap between adjacent clusters. The silhouette score can be written as follows:

$$s={\displaystyle \frac{b-a}{max(a,b)}}$$

(8)

where a is the mean intra-cluster distance, defined as follows:

$$a={\displaystyle \frac{1}{|C_i|}}\sum _{y\in C_i}d(y,z)\mathrm{for}z\in C_i$$

(9)

and b is the mean nearest-cluster distance to the next closest cluster, defined as follows:

$$b=\underset{C_j\ne C_i}{min}{\displaystyle \frac{1}{|C_j|}}\sum _{y\in C_j}d(y,z)\mathrm{for}z\in C_i$$

(10)

Here, $C_i$ is the data belonging to cluster i, and the distance function $d(.,.)$ being used is the well-known cosine similarity distance. The average silhouette score is then calculated as follows:

$$\overline{S}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{s}_i$$

(11)

where n is the number of clustered data points.

4.2.2. Internal CVIs Beyond Silhouette

A wide range of internal cluster validity indices (CVIs) has been proposed in the literature (e.g., measures trading off separation and compactness, density-based criteria, or prototype-stability scores). Among the most widely used are Calinski–Harabasz (CH) [29], which favors partitions with strong between-cluster separation relative to within-cluster compactness, and Davies–Bouldin (DB) [30], which penalizes large within-cluster scatter and weak inter-cluster separation. These indices are frequently used as general-purpose, partition-level criteria in automatic clustering.

Scope of this work. AutoProPos employs only silhouette, together with our Silhouette Uniformity Index (SUI). We do not implement or evaluate CH, DB, or other CVIs in this study. Our choice is driven by the fact that SUI operates on per-sample silhouette scores to penalize non-uniform clusters, whereas CH/DB are partition-level summaries; directly substituting them would change the CLS design and its Max-K/Mean-K selection rule.

4.2.3. Silhouette Uniformity Index (SUI)

Our proposed metric, SUI, is as follows. We define $P_i$ as the probability mass function computed from the normalized and shifted silhouette score samples in the i-th cluster. Given the silhouette scores grouped by clusters, $P_i$ is calculated by shifting the scores to ensure that they are positive and then normalizing them to form proper probability distributions. Finally, the scores within each cluster are ordered in descending order. The normalized score for a cluster is given as follows:

$${\tilde{s}}_{ij}={\displaystyle \frac{s_{ij}+C+ϵ}{{\sum }_k(s_{ik}+C+ϵ)}}$$

(12)

where $s_{ij}$ is the silhouette score for the j-th sample in the i-th cluster, C is a constant corresponding to the minimum silhouette score across the set of clusters, and $ϵ$ is a small constant to ensure a normalized score that is defined and non-null (further discussion on $ϵ$ in Supplementary Section S4.2). The probability mass function $P_i\left(k\right)$ can be defined for four cases, as follows:

$$P_i\left(k\right)=\left\{\begin{array}{cc}max\left({\tilde{s}}_{ij}\right)\hfill & \mathrm{if}k=0\hfill \\ {\tilde{s}}_{ij}\hfill & \mathrm{if}0<k\le B_i\hfill \\ P_i(k+1)\le P_i\left(k\right)\hfill & \mathrm{if}0<k\le B_i\hfill \\ 0\hfill & \mathrm{if}{B}_i<k\le N_{\mathrm{data}}\hfill \end{array}\right.$$

(13)

where $B_i$ is the number of data points belonging to cluster i, and $N_{\mathrm{data}}$ is the total number of samples in the largest cluster.

The SUI is then calculated using the generalized Jensen–Shannon formula [31], where the mixture of distributions of the n cluster probability mass functions M is defined as follows:

$$M:=\sum _{i=1}^n{\displaystyle \frac{1}{n}}{P}_i$$

(14)

and the entropy $H\left(P_i\right)$ is given as follows:

$$H\left(P_i\right)=-\sum _k{P}_i\left(k\right)log{P}_i\left(k\right)$$

(15)

$$\mathrm{SUI}=H\left(M\right)-\sum _{i=1}^n{\displaystyle \frac{1}{n}}H\left(P_i\right)$$

(16)

Due to Jensen–Shannon properties, SUI ranges from 0 to 1, with 0 indicating perfect similarity between our probabilities $P_i$ and 1 indicating a complete lack of uniformity. Based on our definition of these probabilities, SUI assesses proportion and silhouette similarities across clusters. SUI quantifies the similarity between each cluster’s silhouette–value distribution and the prototype distribution obtained by averaging across clusters; a higher SUI indicates homogeneous silhouette profiles and discourages the concentration of assignments in a single cluster. Thus, it aims to assess the best cluster configuration for datasets with balanced numbers of data points and evenly distributed clusters.

4.2.4. Description of the Framework

As detailed in Algorithm A1 (referenced at the end of the paper), the CLS framework involves an iterative process of training N autoencoders, computing the average silhouette score and SUI, and selecting the optimal number of clusters using our Mean K and Max K approach.

Firstly, N autoencoders are trained on the ProPos latent projections of a subset of the dataset, D. Our autoencoders are trained by sampling a ratio r of ProPos latent features to be masked and training the autoencoders to reconstruct the entire latent data. This approach, inspired by MAE [32], provides an easy-to-compute but effective self-supervisory task. Unlike MAE, which applies mean squared error to images in the pixel space, we use a cosine dissimilarity loss on the reconstructed and original ProPos latent components.

Once the autoencoders are trained, the latent representations are clustered using spherical k-means over a specified range of K values, denoted as $[K_{min},K_{max}]$. This range reflects prior beliefs about the interval where the true number of clusters might belong. We show in Supplementary Section S4.2 that the number of clusters inferred using AutoProPos is stable even for a large cluster candidate interval.

For each encoder i, we pick the top $n_{\mathrm{candidate}}$ sets of clusters based on the criterion of having the highest average silhouette score. Among these top candidates, we select the best-fitted $K_i$ by choosing the set that has the lowest SUI score.

$$K_i=K_{j\in n_{\mathrm{candidate}}}$$

$$j=\arg \underset{j}{\min }{\mathrm{SUI}}_j$$

(17)

where $n_{\mathrm{candidate}}\in [1,K_{max}-K_{min}]$.

The optimal number of clusters, K, is then selected using two strategies:

• Max K: during the first alternation, we select the maximum K from the top $n_{\mathrm{MaxK}}$ candidates identified based on their SUI scores:

  $$K=\underset{i\in n_{\mathrm{MaxK}}}{max}{K}_i$$

  (18)

  where $n_{\mathrm{MaxK}}\in [1,N]$.
• Mean K: for subsequent alternations, we calculate the mean K from the top $n_{\mathrm{MeanK}}$ candidates, also selected based on their SUI scores:

  $$K={\displaystyle \frac{1}{n_{\mathrm{MeanK}}}}\sum _{i=1}^{n_{\mathrm{MeanK}}}{K}_i$$

  (19)

  where $n_{\mathrm{MeanK}}\in [1,N]$. The resulting K is then rounded to the nearest integer.

The Max K strategy is used during the first alternation because it occurs in the early training epochs of ProPos, where the generated latent representation is still not well advanced, leading to an underestimation of K. Choosing the maximum K among the sets of $K_i$ helps reduce this problem. Conversely, the Mean K strategy is used in subsequent alternations to make the predicted K more robust to the stochasticity in latent spaces produced via autoencoders. We also use SUI scores to select the $n_{\mathrm{MeanK}}$ or $n_{\mathrm{MaxK}}$ latent space candidates that have the best uniform clusterization, thereby representing a balanced data distribution most accurately.

5. Experimental Setup

5.1. Datasets

To evaluate the effectiveness of AutoProPos, we conducted experiments on seven benchmark datasets: MNIST [33], Fashion-MNIST [34], STL10 [35], CIFAR-20 [36], ImageNet-10 [37], ImageNet-Dogs [37], and ImageNet-50 [8], with, respectively, 10 classes for MNIST, Fashion-MNIST, STL10, ImageNet-10, 20 classes for CIFAR-20, 15 classes for ImageNet-Dogs, and 50 classes for ImageNet-50.

For image preprocessing, we keep CIFAR-20 images at 32 × 32 pixels, with MNIST and Fashion-MNIST images at 28 × 28 pixels, and we resize STL10, ImageNet-10, ImageNet-Dogs, and ImageNet-50 images up to 224 × 224 pixels. The dataset characteristics (number of classes K, dataset sizes, resolution, and splits) are summarized in Supplementary Section S1 for readability.

5.2. Backbones

Strictly following Murugesan et al. [4], we use ResNet-34 [38] as the backbone for training ProPos in AutoProPos on the STL10, ImageNet-Dogs, and ImageNet-10 datasets. We also train ImageNet-50 using this backbone. We replace the first convolution layer of kernel size 7 × 7 and stride 2 with a convolution layer of kernel size 3 × 3 and stride 1, and we remove the first max-pooling layer to compensate for the small image size in CIFAR-20.

For a smaller resolution like that of MNIST and Fashion-MNIST, we design a lighter version of ResNet-18 [38] by removing the last eight convolutional layers. Similar to the training of CIFAR-20, we also replace the first convolution layer using the same strategy. We present the AutoProPos architecture and training configurations in Supplementary Sections S2 and S3, respectively.

5.3. Implementation & Availability

We implement AutoProPos in PyTorch (v2.1.2, CUDA 12.1). We reuse the official ProPos implementation [4], including spherical k-means with cosine distance, without modification; our additions are the Clustering Supervisor Module (CLS) and its K-selection policy. AutoProPos operates by alternation between ProPos training and CLS evaluation. The complete alternation schedule and dataset-specific settings are provided in Supplementary S3.2. The code and the exact configuration files, including training scripts, will be released upon publication. Additional implementation detail is provided in Supplementary Sections S2 and S3.

6. Results

We present AutoProPos’s performance in comparison to that of previous parametric and non-parametric methods, as well as an ablation study under multiple training configurations.

6.1. Classical and Deep Non-Parametric Methods

As depicted in

Table 1. AutoProPos performance (mean ± std) over five runs on four benchmark datasets against non-parametric clustering methods. Best results are in bold, and second best are underlined.

Method	ARI	NMI	ACC	ARI	NMI	ACC
	MNIST			Fashion-MNIST
GMM [39]	0.19 ± 0.02	0.30 ± 0.02	0.60 ± 0.01	0.35 ± 0.05	0.51 ± 0.01	0.49 ± 0.02
DEC [13]	-	-	0.84 ± 0.00	0.45 ± 0.01	0.53 ± 0.02	0.60 ± 0.04
GMVAE [40]	0.57 ± 0.04	0.79 ± 0.03	0.82 ± 0.04	0.44 ± 0.02	0.57 ± 0.01	0.61 ± 0.01
DPMM+memoVB [41]	0.13 ± 0.01	0.39 ± 0.01	0.63 ± 0.02	0.23 ± 0.03	0.48 ± 0.01	0.57 ± 0.01
VSB-DVM [24]	0.66 ± 0.07	0.75 ± 0.04	0.86 ± 0.01	0.41 ± 0.01	0.57 ± 0.01	0.64 ± 0.03
DDPM [42]	0.61 ± 0.03	0.72 ± 0.01	0.91 ± 0.01	0.48 ± 0.01	0.56 ± 0.02	0.63 ± 0.02
DeepDPM [6]	0.91 ± 0.02	0.90 ± 0.01	0.93 ± 0.02	0.52 ± 0.01	0.68 ± 0.01	0.63 ± 0.01
DIVA [7]	0.73 ± 0.04	0.80 ± 0.04	0.94 ± 0.01	0.57 ± 0.04	0.83 ± 0.01	0.72 ± 0.01
Deep Plug and Play (SCAN) [25]	-	-	-	-	-	-
AutoProPos (ours)	0.92 ± 0.00	0.92 ± 0.00	0.96 ± 0.00	0.63 ± 0.04	0.73 ± 0.03	0.74 ± 0.03
	STL10			ImageNet-50
GMM [39]	0.47 ± 0.01	0.60 ± 0.03	0.58 ± 0.03	0.32 ± 0.02	0.68 ± 0.00	0.60 ± 0.01
DEC [13]	0.46 ± 0.02	0.66 ± 0.03	0.80 ± 0.01	0.49 ± 0.01	0.70 ± 0.01	0.63 ± 0.01
GMVAE [40]	0.58 ± 0.04	0.76 ± 0.02	0.79 ± 0.04	0.47 ± 0.04	0.69 ± 0.01	0.62 ± 0.02
DPMM+memoVB [41]	0.51 ± 0.05	0.72 ± 0.02	0.64 ± 0.05	0.14 ± 0.00	0.65 ± 0.00	0.57 ± 0.00
VSB-DVM [24]	0.46 ± 0.01	0.62 ± 0.01	0.52 ± 0.03	0.39 ± 0.01	0.65 ± 0.01	0.49 ± 0.02
DDPM [42]	0.39 ± 0.02	0.57 ± 0.02	0.72 ± 0.01	0.50 ± 0.01	0.64 ± 0.01	0.63 ± 0.02
DeepDPM [6]	0.70 ± 0.01	0.79 ± 0.01	0.81 ± 0.02	0.55 ± 0.02	0.79 ± 0.02	0.66 ± 0.01
DIVA [7]	0.87 ± 0.01	0.95 ± 0.00	0.72 ± 0.01	0.88 ± 0.02	0.97 ± 0.01	0.69 ± 0.02
Deep Plug and Play (SCAN) [25]	0.59	0.65	0.75	0.62 ± 0.02	0.80 ± 0.01	0.73 ± 0.01
AutoProPos (ours)	0.85 ± 0.01	0.84 ± 0.00	0.92 ± 0.01	0.67 ± 0.01	0.80 ± 0.01	0.77 ± 0.01

, we evaluate AutoProPos against nine non-parametric clustering methods, which we categorized into two distinct groups: deep clustering models transitioning to non-parametric, and models that do not follow this transition. The evaluation was conducted using three well-known metrics: Normalized Mutual Information (NMI), the Adjusted Rand Index (ARI), and clustering accuracy (ACC), as defined in Supplementary Section S1.

The different methods were tested on four datasets: MNIST, Fashion-MNIST, STL-10, and ImageNet-50. We note that the performance metrics for all models, except for Deep Plug and Play [25], were obtained from DIVA [7]. For Deep Plug and Play, we used the highest results reported in its paper, which utilized SCAN [5] as a baseline.

To ensure a fair comparison between AutoProPos and the other methods, we adhered to the train–test splits, ran our model five times for each dataset, and reported the average and standard deviation on the test set. For STL-10, we utilized both the labeled training set and the unlabeled set for training. Due to the lack of an implementation repository from Deep Plug and Play, we report its performance for STL-10 without providing the mean ± standard deviation.

As shown in Table 1, AutoProPos demonstrates competitive performance against SOTA methods. On MNIST, it outperforms the second-best model by 2% in the tested metrics. For Fashion-MNIST, it achieves the highest ACC of 0.74. On STL-10 and ImageNet-50, it maintains the second-best NMI and ARI scores while surpassing the next-best model in ACC by 11% and 7%, respectively.

Additionally,

Table 2. Inferred K values for different methods and datasets (ground-truth: MNIST = 10, Fashion-MNIST = 10, ImageNet-50 = 50, STL-10 = 10). Bold highlights the best result, underline the second-best.

Method	Inferred K
	MNIST	Fashion-MNIST	ImageNet-50	STL-10
DBSCAN [43]	9.00 ± 0.00	4.00 ± 0.00	16.00	-
DPM Sampler[44]	11.30 ± 0.82	12.40 ± 0.97	72.00 ± 2.60	-
moVB [41]	14.00 ± 1.00	16.90 ± 2.30	46.20 ± 1.30	-
DeepDPM [6]	10.00 ± 0.00	10.20 ± 0.79	55.30 ± 1.50	-
Deep Plug and Play (SCAN) [25]	-	-	50.60 ± 1.70	10.30 ± 0.90
AutoProPos (Ours)	10.00 ± 0.00	9.20 ± 1.10	56.40 ± 0.89	10.00 ± 0.00

presents the inferred number of clusters K by our method and compares it with five known methods for the presented datasets. AutoProPos infers the exact K value for MNIST and STL-10 and comes close for Fashion-MNIST and ImageNet-50. Although DeepDPM and Deep Plug and Play (SCAN) offer the closest predictions for the latter two datasets, AutoProPos outperforms them overall in clustering performance.

6.2. Deep Clustering Transitioning to Non-Parametric and Parametric Methods

In

Table 3. Comparison of parametric and deep clustering transitioning to non-parametric methods on three benchmark datasets. The best results are indicated in bold, and the second best are underlined. The best performance of AutoProPos and ProPos over 5 runs is displayed.

Method	CIFAR-20			ImageNet-10			ImageNet-Dogs
	NMI	ARI	ACC	NMI	ARI	ACC	NMI	ARI	ACC
DCCM [45]	28.5	17.3	32.7	60.8	55.5	71.0	32.1	18.2	38.3
PICA [46]	29.6	15.9	32.2	78.2	73.3	85.0	33.6	17.9	32.4
SCAN [5]	48.6	33.3	50.7	-	-	-	-	-	-
NMM [47]	48.4	31.6	47.7	-	-	-	-	-	-
CC [48]	43.1	26.6	42.9	85.9	82.2	89.3	44.5	27.4	42.9
MiCE [49]	43.6	28.0	44.0	-	-	-	42.3	28.6	43.9
GCC [50]	47.2	30.5	47.2	84.2	82.2	90.1	49.0	36.2	52.6
TCL [51]	52.9	35.7	53.1	87.5	83.7	89.5	62.3	51.6	64.4
TCC [52]	47.9	31.2	49.1	84.8	82.5	89.7	55.4	41.7	59.5
MoCo [53]	39.0	24.2	39.7	-	-	-	34.7	19.7	33.8
SimSiam [54]	52.2	32.7	48.5	83.1	83.3	92.1	58.3	50.1	67.4
BYOL [17]	55.9	39.3	56.9	86.6	87.2	93.9	63.5	54.8	69.4
IDFD [55]	42.6	26.4	42.5	89.8	90.1	95.4	54.6	41.3	59.1
PCL [56]	52.8	36.3	52.6	84.1	82.2	90.7	44.0	29.9	41.2
SPICE [1]	53.8	38.7	56.7	90.2	91.2	95.9	67.5	52.6	62.7
ProPos [4]	60.6	45.1	61.4	91.6	92.6	96.6	75.2	69.2	78.1
Deep Plug and Play (SCAN) [25]	45.2	28.1	43.8	88.6	87.1	91.2	-	-	-
AutoProPos (ours)	61.0	46.1	61.5	90.9	91.9	96.3	76.3	72.4	83.3

, AutoProPos is compared to sixteen parametric deep clustering methods across previously established metrics. Deep Plug and Play is also included in the comparison due to its methodological proximity to AutoProPos. Consequently, the table is divided into two groups: parametric deep clustering methods and models transitioning to non-parametric. We excluded the clustering methods TSP [18] and TEMI [2] from our comparison due to their use of pretrained models on large datasets, giving them an unfair advantage over our method.

We evaluate model performance on three datasets: CIFAR-20, ImageNet-10, and ImageNet-Dogs. Following previous studies (e.g., [1,4]), the training and test sets are merged during the training and evaluation phases of AutoProPos. NMI, ARI, and ACC results for all presented methods, except for ProPos on ImageNet-10 and ImageNet-Dogs, are sourced from ProPos [4], SPICE [1], and Deep Plug and Play [25]. For fair comparisons, ProPos was retrained on ImageNet-10 and ImageNet-Dogs with an input size of 224 × 224 × 3, using Supplementary Sections S2 and S3 configurations. Both ProPos and AutoProPos were run five times, and the best performance was selected.

Despite parametric methods offering the advantage of knowing the ground truth K, AutoProPos demonstrates competitive performance on the tested datasets. AutoProPos achieves better performance than previous methods on CIFAR-20 and ImageNet-Dogs. On ImageNet-10, it closely matches ProPos, with a 0.3% gap in ACC.

6.3. Ablation Study

Here, we present further analyses of AutoProPos to highlight its key components and demonstrate robustness while maintaining training time similar to ProPos [4].

Table 4. AutoProPos performance (mean ± std) with different ablations of the Clustering Supervisor Module components. Bold highlights the best result in each column.

Method	ACC	Inferred K
No autoencoder	0.36 ± 0.03	26.00 ± 0.71
Training one Autoencoder	0.69 ± 0.04	11.00 ± 2.24
Max avg Silhouette Score	0.61 ± 0.15	14.80 ± 7.12
Min Silhouette Similarity Index	0.24 ± 0.05	2.50 ± 0.58
Only Max K strategy	0.62 ± 0.04	16.75 ± 4.11
Only Mean K strategy	0.73 ± 0.04	9.00 ± 0.00
AutoProPos (full method)	0.74 ± 0.03	9.20 ± 1.10

shows the performance of AutoProPos on the Fashion-MNIST dataset with the previously described training configuration. For each ablation, we present the mean and standard deviation of five runs.

We compared the CLS prediction on the ProPos latent space with the prediction obtained by first projecting it using an autoencoder. The latter produced more accurate K values, demonstrating the autoencoder’s ability to map the ProPos latent space towards a representation analyzable via CLS. However, it also produced a high prediction standard deviation, likely due to the stochasticity of the latent representation induced during autoencoder training. We mitigated this in the full method by training multiple encoders and using the Mean K strategy.

We also analyzed the prediction of K using only the average silhouette score and only the SUI score with a one-encoder training setup. We found that, alone, they overestimated and underestimated the K value, respectively. Their combination, as depicted in the full method, provided better results. The average silhouette score helps select well-defined cluster configurations, while the SUI index regulates the final configuration choice.

Finally, as shown in Table 4, using only the Mean K strategy already produces good results; adding the initial Max K step in the full method further improves the overall performance and robustness.

Table 5. AutoProPos performance for various initial K ($K_{\mathrm{init}}$).

ImageNet-10
${\mathit{K}}_{\mathbf{init}}$	NMI	ACC	ARI	Inferred $\mathit{K}$
2	0.89 ± 0.01	0.95 ± 0.01	0.89 ± 0.02	10 ± 0.00
50	0.89 ± 0.01	0.95 ± 0.01	0.89 ± 0.02	10 ± 0.00
100	0.90 ± 0.01	0.95 ± 0.01	0.90 ± 0.02	10 ± 0.00
200	0.88 ± 0.02	0.94 ± 0.03	0.88 ± 0.03	10 ± 0.00

demonstrates AutoProPos’s robustness to the initial number of clusters $K_{\mathrm{init}}$. We trained the model on ImageNet-10 with both underclustering and overclustering $K_{\mathrm{init}}$, and observed stable results across the tested metrics.

Finally,

Table 6. Comparison of training time (in hours) between AutoProPos and ProPos.

Datasets	MNIST	Fashion-MNIST	STL10	CIFAR-20	ImageNet-10	ImageNet-Dogs	ImageNet-50
ProPos [4]	2.86	1.46	33.43	6.59	5.58	7.52	11.35
AutoProPos (ours)	3.83 (+0.96)	2.28 (+0.82)	33.6 (+0.17)	7.66 (+1.07)	6.29 (+0.72)	8.98 (+1.46)	13.29 (+1.94)

compares the training times of AutoProPos and ProPos, both trained on 4× NVIDIA RTX A5000 (24 GB) under Ubuntu 22.04 with PyTorch 2.1.2 (CUDA 12.1); notably, the CLS module uses a single GPU. We report that training AutoProPos only added a maximum of 2 h to the training time on the tested datasets.

Further insights, including extended ablation results, hyperparameter studies, and t-SNE visualizations of the latent space evolution, which further demonstrate the robustness and usefulness of our approach, are available in Supplementary Section S4.

7. Conclusions

We introduced AutoProPos, an extension of the parametric deep clustering model ProPos that integrates a lightweight Clustering Supervisor Module (CLS) to adjust the number of clusters during training. By combining advanced representation learning with a model-selection framework based on the average silhouette and our Silhouette Uniformity Index (SUI), AutoProPos achieves state-of-the-art performance against both parametric and non-parametric methods across extensive experiments. These results highlight AutoProPos’s ability to enhance clustering accuracy and adaptability, showing how a strong parametric backbone can be made effectively non-parametric during training with minimal engineering overhead.

• Summary of improvements. Across benchmarks, AutoProPos delivers consistent gains reported in the main text; for example, it achieves +11 ACC points on STL-10 versus the best non-parametric baseline, and +5.2 on ImageNet-Dogs versus ProPos, while inferring the correct K on MNIST and STL-10 and near-correct on ImageNet-50 with ≤2 h of additional training on a single GPU.
• Implications. By making ProPos non-parametric during training, the CLS supports class discovery and dataset bootstrapping when the number of classes is unknown, with low computational and implementation overhead. Because the selection rule operates on unit-normalized embeddings under cosine geometry, the module is compatible with other backbones that share this geometry and can be used as a drop-in component.
• Limitations and future directions. A systematic comparison of alternative CVIs (including CH [29] and DB [30]), as well as adaptations of our uniformity penalty and selection rule, represents a natural continuation of this work. While our ablation study demonstrates the benefit of combining SUI with the average silhouette, future research will also examine alternative model selection criteria as substitutes for the silhouette score. Another important extension is to evaluate AutoProPos under strong class imbalance and in streaming scenarios. Beyond images, the CLS is modality-agnostic and can be applied to unit-normalized embeddings with cosine geometry; testing AutoProPos on non-image modalities and larger, real-world datasets will further validate its generality and robustness.