Detection of Fault Events in Software Tools Integrated with Human–Computer Interface Using Machine Learning

Abstract

Software defect prediction (SDP) has emerged as a crucial task in ensuring software quality and reliability. The early and accurate identification of defect-prone modules significantly reduces maintenance costs and improves system performance. In this study, we introduce a novel hybrid model that combines Restricted Boltzmann Machines (RBM) for nonlinear feature extraction with Logistic Regression (LR) for classification. The model is validated across 21 benchmark datasets from the PROMISE and OpenML repositories. We conducted extensive experiments, including analyses of computational complexity and runtime comparisons, to assess performance in terms of accuracy, precision, recall, F1-score, and AUC. The results indicate that the RBM-LR model consistently outperforms baseline LR, as well as other leading classifiers such as Random Forest, XGBoost, and SVM. Statistical significance was affirmed using paired t-tests (p < 0.05). The proposed framework strikes a balance between interpretability and performance, with future work aimed at extending this approach through hybrid deep learning techniques and validation on industrial datasets to enhance scalability.

1. Introduction

Software engineering is essential in contemporary society, as software systems are increasingly utilized across various industries, including healthcare, finance, telecommunications, and defense. As these systems expand in size and complexity, ensuring software reliability becomes a paramount concern. Software defect prediction (SDP), also known in the literature as software failure prediction (SFP), aims to identify modules that are prone to defects prior to deployment. This proactive approach helps to reduce maintenance costs and enhance overall software quality [1,2].

Over the past decade, a variety of prediction methods have emerged, with models such as Naïve Bayes, Support Vector Machines (SVMs), and Decision Trees being among the most commonly used [3,4,5]. These methods facilitate the identification of fault-prone modules, which in turn helps to reduce future maintenance costs and enhance the quality of software products [6]. Several studies have pointed out that the quality of software metrics and datasets plays a more significant role in Software Fault Prediction (SFP) performance than the choice of prediction model itself [7,8]. Nonetheless, other research indicates that predictive performance remains highly sensitive to the techniques and algorithms utilized [9].

Despite notable advancements, current machine learning (ML) and deep learning (DL) methods continue to face ongoing challenges. In DL-based prediction, the inherent complexity of algorithms necessitates rigorous hyperparameter tuning and optimization routines; neglecting this can lead to suboptimal performance [9]. Additionally, the quality and volume of training data play a critical role in determining prediction accuracy: larger, high-quality datasets generally improve precision, whereas noisy or imbalanced datasets can compromise performance [10]. To tackle these issues, researchers have proposed hybrid approaches that integrate feature selection, ensemble methods, and deep learning techniques. For example, Tong et al. [9] combined DL with ensemble learning, while Borandag et al. [11] introduced a feature-selection-driven ensemble that synthesizes predictions through majority voting based on information gain, uncertainty, and RelieF features. These hybrid models consistently demonstrate superior performance compared to traditional single-model ML approaches.

Inspired by these observations, this study investigates hybrid machine learning methods that prioritize both interpretability and performance. Specifically, Restricted Boltzmann Machines (RBM) were selected for their effectiveness in capturing nonlinear latent structures, distinguishing them from alternatives such as PCA, Autoencoders, and UMAP due to their superior ability to extract complex features from software metrics [5,6]. For classification, Logistic Regression (LR) was favored for its interpretability and computational efficiency when compared to more complex models like Random Forest, XGBoost, and Neural Networks [7,8]. The integration of RBM with LR strikes a balance between performance, transparency, and practicality, making it particularly suitable for real-world defect prediction [11].

The primary contributions of this study are outlined as follows:

• We design and implement a hybrid framework combining Restricted Boltzmann Machines (RBM) and Logistic Regression (LR), validated across 21 benchmark datasets (PROMISE, OpenML).
• We perform a comprehensive analysis of computational complexity and runtime performance of the RBM–LR model.
• We benchmark the RBM–LR against baseline LR and advanced classifiers such as Random Forest, XGBoost, and Support Vector Machines (SVM) [2,3].
• We conduct statistical significance testing through paired t-tests to confirm the improvements achieved.
• We emphasize the influence of data quality, feature selection, and hyperparameter tuning on predictive accuracy [7,9,10].
• We ensure reproducibility by providing pseudocode, implementation details, and making the code publicly available [8].
• We discuss the limitations of our work and propose future directions, including validation with industrial datasets and exploration of hybrid deep learning methods [11].

By integrating these elements, this paper enhances the existing literature on software defect prediction, underscoring the importance of hybrid models, data quality, and interpretability.

2. Related Works

Software defect prediction (SDP), also known as software failure prediction (SFP), has been a long-standing focus of research within the field of software engineering. Initial studies predominantly utilized traditional statistical and machine learning techniques, including Logistic Regression (LR), Decision Trees, and Naïve Bayes [1,12]. While these models offered interpretable baseline results, their predictive accuracy was often limited, prompting the exploration of more advanced methodologies.

2.1. Sampling and Literature Reviews

To gather empirical evidence, numerous studies have utilized snowball sampling as a methodology for constructing datasets and literature corpora [12,13,14,15]. Catal and Diri [16] conducted one of the pioneering systematic reviews on Software Fault Prediction (SFP), creating a classification framework based on various metrics. Similarly, Radjenović et al. [17] employed snowball sampling to analyze SFP studies and discovered that object-oriented metrics were predominant (49%), followed by code metrics (27%) and process metrics (24%). Building on this foundation, Catal [18] presented a comprehensive systematic review of studies published between 1990 and 2009, addressing metrics, datasets, evaluation measures, and performance assessment methods. Subsequently, Malhotra [2] and Hall et al. [19] carried out systematic literature reviews (SLRs), revealing that Naïve Bayes and Logistic Regression were the most commonly utilized methods, though their predictive accuracy varied depending on the dataset and evaluation criteria. Expanding on these SLR efforts, Wagner [20] categorized studies into four themes: classification, association, dataset analysis, and clustering.

2.2. Metrics and Prediction Approaches

Beyond reviews, several empirical studies have explored the role of metrics in software fault prediction (SFP). Li et al. [21] analyzed various machine learning algorithms, whereas Rathore and Kumar [1] categorized SFP research into three distinct areas: fault prediction, software metrics, and dataset quality. Catal [22] further categorized prediction systems into two classes: (i) binary classifiers that determine whether a module is defective and (ii) models that estimate the probability of faults occurring. Malhotra [2] specifically focused on object-oriented systems, highlighting the significance of software metrics in predicting error probabilities. Additional studies [23,24,25,26,27] corroborated that comprehensive metrics coverage enhances pre-emptive fault diagnosis, underscoring the crucial role of measurement design in software development processes.

2.3. Advanced Models and Dimensionality Reduction

With the expansion of large-scale software repositories, ensemble learning and deep learning methods have gained significant popularity. Models like Random Forest, Gradient Boosting, and Convolutional Neural Networks (CNNs) have demonstrated superior accuracy compared to traditional machine learning techniques [2,3], albeit at the expense of interpretability and computational efficiency. To tackle high-dimensional metrics, various dimensionality reduction methods, including Principal Component Analysis (PCA), Autoencoders, and UMAP, have been widely utilized [4,5]. However, PCA is constrained to linear transformations, while Autoencoders and UMAP often necessitate extensive hyperparameter tuning and large datasets. In contrast, Restricted Boltzmann Machines (RBM) offer a generative approach that can effectively learn nonlinear latent structures, thereby motivating their integration into contemporary hybrid frameworks [6].

2.4. Hybrid and Modern Approaches

Recent studies underscore the effectiveness of hybrid solutions that integrate feature extraction with robust classifiers. Deep learning models such as Convolutional Neural Networks (CNNs) and Long Short-Term Memory networks (LSTMs) have been utilized to capture both sequential and spatial patterns within defect datasets [7]. Additionally, ensemble methods like bagging and boosting have proven effective in maintaining robustness against noisy data [8]. However, several persistent challenges remain, including dataset imbalance, overfitting in small datasets, and limited reproducibility due to the scarcity of publicly available implementations [9].

In conclusion, the literature identifies three principal themes:

• Systematic reviews and sampling methodologies (e.g., Catal [16,18], Malhotra [2], Hall [19], Wagner [20]) that synthesize findings from decades of research.
• Metrics-driven approaches that highlight the significant impact of object-oriented, code, and process metrics on predictive effectiveness [1,2,17,21,22].
• Hybrid and advanced models that merge feature selection, dimensionality reduction, and ensemble learning to strike a balance between performance and interpretability [2,3,4,5,6,7,8,9,23,24,25,26,27].

Machine learning has demonstrated remarkable success in identifying faults across various domains, including software engineering, as well as manufacturing and quality control. For example, Lv et al. (2024) [28] accumulated and released a large-scale dataset (DsPCBSD+) for PCB surface defect detection to support deep model training. Lang & Lv (2025) [29] improved the above research by introducing SEPDNet, a lightweight and powerful model designed for PCB detection tasks.

This study builds upon these established foundations by proposing a hybrid model that integrates Restricted Boltzmann Machine (RBM) with Logistic Regression (LR). This model aims to combine nonlinear feature extraction with a transparent classifier, effectively addressing the interpretability–performance trade-off noted in prior literature while ensuring reproducibility across benchmark datasets.

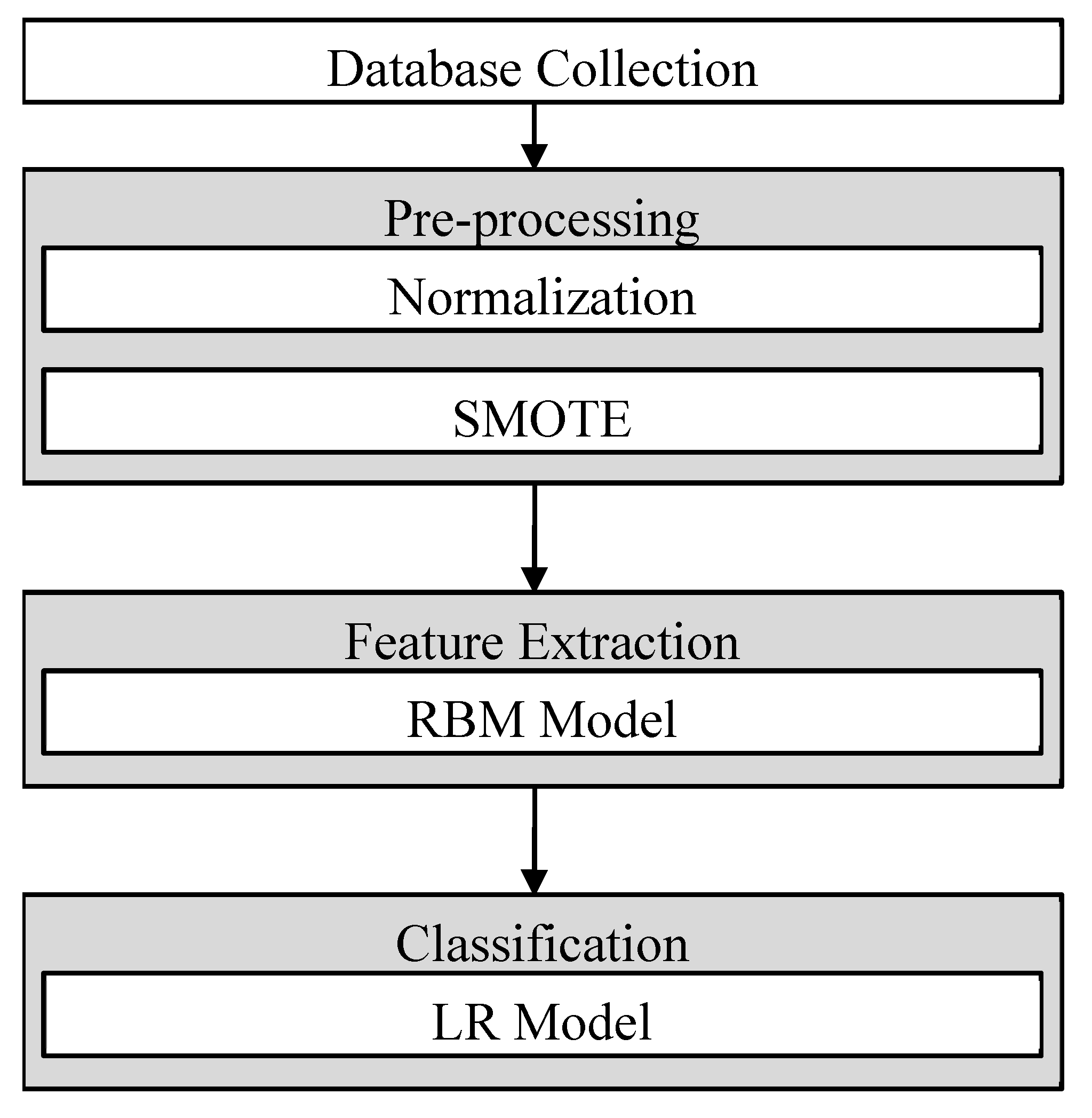
3. Proposed Method

In this section, we gather the datasets and preprocess them, extract features, and classify the data using machine learning models. The entire workflow is illustrated in Figure 1. Additionally, we provide a mathematical formulation and algorithmic representation to improve clarity and reproducibility.

3.1. Problem Definition

The Software Fault Prediction (SFP) problem is recognized as a critical concern in the realm of software reliability. To ensure high-quality software, several steps are implemented throughout the development process. Activities such as verification, validation, testing, fault tolerance detection, and SFP itself are all vital components of this effort. Software fault prediction identifies potential bugs in a program both before and after the Software Development Life Cycle (SDLC) through the use of established metrics or defects identified in previous versions of the product. By employing accurate SFP techniques, organizations can significantly reduce the time and effort required to detect software faults or errors throughout the SDLC. Consequently, accurate SFP is deemed essential for optimizing the time and resources needed for software design.

The significance of the Software Fault Prediction (SFP) can be articulated in terms of its role in testing and verification. The standards established by subsequent software releases can help prevent the development and distribution of faulty products. The quality of software versions that are developed successively relies heavily on both their preceding and succeeding iterations. Nevertheless, the effectiveness of the SFP models designed to address these issues is entirely contingent upon how well they are modeled and integrated into the Software Development Life Cycle (SDLC). The modeling technique has a relatively minor impact on the reliability of classification when evaluated against the weight of other metrics.

3.2. Objective Function

The primary motivation behind proposing the SFP model is to develop a method that accurately predicts software bugs, applicable to both completed projects and ongoing development. For classification purposes, Logistic Regression (LR) is utilized. Nonlinear feature extraction is achieved using Restricted Boltzmann Machines (RBM). During training, cross-entropy is employed as the loss function. Notably, while the Area Under the Curve (AUC) was not optimized during the training process, it served exclusively as an evaluation metric for assessing model performance.

3.3. Solution Representation

The solution representation is achieved using LR (Logistic Regression). After the training phase, it is observed that the length vector resembles the biases and weights. These weights and biases are then transmitted as the SFP solution, as illustrated in Figure 2.

Following the completion of this process, training is performed on the LR model to assess the network weights and biases for gradient estimation. Subsequently, the LR testing method is applied to evaluate the final model using the testing dataset. The aim of this analysis is to enhance the accuracy of the SFP model.

3.4. Pre-Processing

This is the initial step of Algorithm 1. The preprocessing stages include feature normalization and oversampling, which are detailed below:

3.4.1. Feature Normalization

Metrics derived from Hall T. [19] and Wagner [20] are employed to generate software metrics commonly utilized for static SFP analysis from the source code. These metrics objectively characterize the attributes that contribute to a high-quality software development life cycle (SDLC). In this study, a total of 21 feature measures are considered as independent factors, while a binary variable is implemented to represent the quality of the code (0 or 1).

If any of the features exhibit abnormal values—either excessively high or low—the performance of the logistic regression (LR) classification may be adversely affected. Therefore, this study aims to enhance the LR classification outcomes by modifying the data that displays a moderate degree of skewness. To accomplish this, the feature data can be compressed into a predefined interval using the log1p function. This approach addresses the issue of convoluted values and helps align the data more closely with a Gaussian distribution.

3.4.2. Oversampling

In practice, there are usually fewer instances of defective software compared to non-defective software, leading to a situation known as the class imbalance problem in software fault prediction (SFP). Developing a more effective prediction model using the data gathered from the training set is not a straightforward task, especially if random selection and division of the dataset or under-sampling techniques are applied without careful consideration.

This stems from the fact that the two techniques cannot be utilized simultaneously. The primary objective involves generating additional samples from the limited set of available labels. This process must be executed in a manner consistent with the existing pattern of samples that utilize fewer labels, thereby addressing the issue of insufficient initial samples. A well-known method of oversampling is the Synthetic Minority Oversampling Technique (SMOTE).

The following is a detailed explanation of each step of this procedure.

• A collection of k nearest neighbors for a class sample can be found by computing the Euclidean distance between each sample in a class sample set S that consists of a x class samples.
• The sampling ratio, and hence the sampling multiplier N, is calculated with reference to the sample imbalance ratio. Each sample from a minority class should be supplemented with k random samples from the classes immediately surrounding it, where k is regarded as the total classes.
• By applying the following formula to each randomly (r) selected nearest neighbor x_n, a new sample (n) can be generated from the original sample (m).
  r · features = n · features + (n · features − x n · features) * rand(0,1)

3.5. Feature Extraction

This rigorous mathematical formulation is aligned with the algorithmic flow described in Algorithm 1, ensuring both theoretical depth and practical reproducibility. In this section, we use RBMs as the feature extraction model, which is regarded as a subset of Markov random fields that have both hidden and visible or observable stochastic units (Bernoulli and Gaussian). Various random factors are used at all these levels, and bipartite graphs are used to define RBMs. Each visible unit is linked to every other hidden unit; however, neither set of units is related to itself in bipartite graphs.

Assuming some parameters, the joint distribution $\mathrm{p}\left(\mathrm{v},\mathrm{h};\theta \right)$ over visible v and hidden units h is defined in terms of an energy function $\mathrm{E}\left(\mathrm{v},\mathrm{h};\theta \right)$ of a random bit generator (RBG).

$$\mathrm{p}\left(\mathrm{v},\mathrm{h};\theta \right)={\displaystyle \frac{exp \left(-\mathrm{E}\left(\mathrm{v},\mathrm{h};\theta \right)\right)}{Z}},$$

where

• $Z={\sum }_{\mathbf{v}}{\sum }_{\mathbf{h}}exp\left(-\mathrm{E}\left(\mathrm{v},\mathrm{h};\theta \right)\right)$—partition function or normalization factor, and
• p—marginal probability of the feature extraction assigned to the vectors of the visible layer v.

Thus, the marginal probability is defined as below:

$$\mathrm{p}\left(\mathbf{v};\theta \right)={\displaystyle \frac{{\sum }_{\mathit{h}}exp\left(-\mathrm{E}\left(\mathrm{v},\mathrm{h};\theta \right)\right)}{Z}}.$$

Here, the study provides an illustration of the energy function from the visible to the hidden layer using the Bernoulli–Bernoulli RBM formulation:

$$\mathrm{E}\left(\mathbf{v},\mathbf{h};\theta \right)=-\sum _{i=1}^I\sum _{j=1}^J{w}_{ij}{v}_i{h}_j-\sum _{i=1}^I{b}_i{v}_i-\sum _{j=1}^J{a}_j{h}_j,$$

where

• $w_{ij}$—symmetric interaction weights between the ith visible $v_i$ and jth hidden $h_j$ layer;
• $b_i$ and $a_j$—bias terms
• $I$—visible unit and
  $J$—hidden units.

The conditional probability is thus defined as below:

$$p\left(h_j=1|\mathbf{v};\theta \right)=\sigma \left(\sum _{i=1}^I{w}_{ij}{v}_i+a_j\right),$$

$$p\left(v_i=1|\mathbf{h};\theta \right)=\sigma \left(\sum _{j=1}^J{w}_{ij}{h}_j+b_i\right),$$

where $\sigma \left(x\right)=1/\left(1+exp\left(x\right)\right)$.

Open Gaussian and closed Bernoulli RBMs have the same amount of energy.

$$\mathrm{E}\left(\mathrm{v},\mathrm{h};\theta \right)=-\sum _{i=1}^I\sum _{j=1}^J{w}_{ij}{v}_i{h}_j-{\displaystyle \frac{1}{2}}\sum _{i=1}^I{\left(v_i-b_i\right)}^2-\sum _{j=1}^J{a}_j{h}_j,$$

With such an energy function, the conditional probabilities are defined below:

$$p\left(h_j=1|\mathrm{v};\theta \right)=\sigma \left(\sum _{i=1}^I{w}_{ij}{v}_i+a_j\right),$$

$$p\left(v_i|\mathrm{h};\theta \right)=\mathcal{N}\left(\sum _{j=1}^J{w}_{ij}{h}_j+b_i,1\right),$$

where $v_i$ contains real values by following the Gaussian distribution with a unit variance and a mean:

$${\sum }_{j=1}^J{w}_{ij}{h}_j+b_i$$

Prior to the application of Bernoulli–Bernoulli RBMs, a real stochastic variable helps in converting the Gaussian–Bernoulli RBMs to a binary stochastic variable.

The study finds that the Gaussian conditional distribution (for continuous data) and the binomial conditional distribution (for discrete data) are the two conditional distributions commonly used for binary data. The selection of RBM thus provides a flexible extraction of features from the normalized datasets with many different distributions.

The update on RBM weights can be derived by calculating the log likelihood gradient as $\log p\left(\mathbf{v};\theta \right)$, where the updated weights are represented as:

$$∆w_{ij}=E_{data}\left({v_{i}h}_j\right)-E_{model}\left({v_{i}h}_j\right),$$

where

• $E_{data}\left({v_{i}h}_j\right)$—expectation observed in training and
• $E_{model}\left({v_{i}h}_j\right)$—expectation under the model distribution.

The approximation of contrastive divergence is applied to the gradient since solving the $E_{model}\left({v_{i}h}_j\right)$ computationally is unfeasible. In this approximation, the $E_{model}\left({v_{i}h}_j\right)$ is replaced by a single step of the Gibbs sampler initialized with the data, and the process of approximation of the features involves: (1) initialization of the visible unit ${\mathbf{v}}_0$ with initial data; (2) sample the initial hidden layer as: ${\mathrm{h}}_0\sim p\left(\mathrm{h}|{\mathrm{v}}_0\right)$; (3) sampling of the first visible unit ${\mathrm{v}}_1\sim p\left(\mathrm{v}|{\mathrm{h}}_0\right)$ with initial data; (4 sample the initial hidden layer as: ${\mathrm{h}}_1\sim p\left(\mathrm{h}|{\mathrm{v}}_1\right)$.

The features extracted serve as a good starting point for our estimation of the $E_{model}\left({v_{i}h}_j\right)$ model (${\mathrm{v}}_1$, ${\mathrm{h}}_1$). The contrastive divergence approximation method thus originated as a response to the feature extraction of (${\mathrm{v}}_1$, ${\mathrm{h}}_1$) as a first-order approximation to the $E_{model}\left({v_{i}h}_j\right)$. However, RBMs, like other related deep learning algorithms, need extensive training before they can be used for the successful resolution of real-world issues.

3.6. Classification

With a single neuron, the LR classifier is the simplest neural network model. Computational neurons are a special kind of computer node that generates an output with the application of a non-linear activation function over weighted inputs. While computing such a neuron, the need for a supervised learning method that can handle classification issues with discrete outputs led to the development of the LR model (i.e., labels).

The sigmoid activation function with a single neuron enables the LR to convert a discrete input feature vector into a continuous output feature vector with value ranging between 0 and 1, representing the likelihood of each input class. There is a one-to-one relationship between the input and output feature vectors that is used to map these values. The formula for an LR is given below:

$$f\left(x\right)=sigmoid\left(W^{T}x+b\right)={\displaystyle \frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(W^{T}x+b)}}$$

where

• W—weight vector
• x—feature vector, and
• b—bias.

The stochastic gradient descent (SGD) is used to find the best possible values for W and b by minimizing a cost function. Inputs with unlabeled qualities can be predicted using the optimized model, which optimizes the weights and biases, as shown in Figure 2.

LR, as a linear classifier, makes predictions by combining input information in a linear fashion and halves the feature space. Input feature vectors are represented by the network’s first layer, which is called the input layer. Because its values are hidden from the training set, the second layer is commonly referred to as the hidden layer. The hidden layers get linked to a neuron that is driven by a sigmoid function, where the input layers are coupled with the hidden layers. A hidden layer has been incorporated so that a non-linear mapping can be performed from the space of input features to the space of hidden features. One of our goals is to achieve linear separation of the optimized hidden features. For a two-layer MLP, see the following equation:

$$f\left(x\right)=G(b^{\left(2\right)}+W^{\left(2\right)T}(s(b^{\left(1\right)}+W^{\left(1\right)T}x)\left)\right)$$

where

• b(1)—Bias of 1st layer
  W(1)—weight matrix of 1st layer
  b(2)—Bias of 2nd layer
  W(2)—weight matrix of 2nd layer;
  G—sigmoid function activation function and
  s—activation of the hidden layer.

Possible values for s include the inverse linear unit, tanh, and a sigmoid unit. To optimize a given set of parameters, SGD often employs back-propagation with chain-rule derivation. This is done by minimizing a cost function, such as log-likelihood. Chain-rule derivation methods involving the back-propagation function are used to train LR networks.

3.7. Algorithm Representation

To enhance reproducibility and meet reviewer requirements, the workflow is also summarized as Algorithm 1.

Algorithm 1. Training and Evaluation of the RBM–LR Model.

Input: Dataset D from PROMISE/OpenML repositories Preprocessing: Handle missing values, normalize features, and apply SMOTE to balance the dataset Feature Extraction: Train RBM with h hidden nodes to extract latent representations Classification: Train Logistic Regression (LR) on extracted RBM features Evaluation: Compute Accuracy, Precision, Recall, F1-score, and AUC Comparison: Benchmark RBM-LR against baseline LR and advanced classifiers (Random Forest, XGBoost, SVM)

3.8. Time Complexity Analysis

The computational complexity of the RBM–LR framework is approximately:

$$O(n \times h \times f \times epochs)$$

where:

-

n = number of samples

-

h = number of hidden nodes

-

f = number of features

-

epochs = number of training iterations

While this introduces a slight increase in runtime compared to baseline Logistic Regression, empirical results show that the improvements in accuracy, robustness, and stability outweigh the added computational cost.

4. Results and Discussions

In this section, we experimentally validate the effectiveness of the proposed RBM-LR framework for software fault prediction (SFP). The evaluation utilized 21 publicly available benchmark datasets sourced from the PROMISE repository and OpenML. These datasets exhibit considerable variability in size, complexity, and defect ratio (refer to

Table 1. Dataset Description.

Dataset	Total Faults	Total Features
KC1	325	22
KC2	107	21
KC3	43	39
JM1	1759	22
Ar1	8	29
Ar3	8	29
Ar4	20	29
Ar5	8	29
Ar6	15	29
CM1	49	22
MC2	52	39
Tomcat-6.0	77	20
MW1	31	37
JEdit-4.0	75	20
JEdit-4.2	48	20
JEdit-4.3	10	29
Ant-1.7	166	20
PC1	76	37
PC2	23	36
PC3	140	38
PC4	178	38
PC5	516	38

), providing a thorough validation of the model’s robustness. The preprocessing steps included normalization, addressing missing values, and class balancing using SMOTE.

4.1. Parameter Configuration

The parameters of the Restricted Boltzmann Machine (RBM) were optimized through a process of iterative testing. We adjusted the number of neurons, hidden nodes, and hidden layers to attain optimal classification performance. Logistic Regression (LR) was utilized as the output layer classifier. Table 1 provides a summary of the dataset characteristics, while the hyperparameters for the RBM-LR model were chosen to strike a balance between predictive performance and computational efficiency.

4.2. Performance Measures

To rigorously evaluate performance, five widely recognized metrics were employed: Accuracy, Precision, Recall, F1-score, and AUC. The threshold value was established at 0.5, and cross-entropy was utilized as the loss function during the training process. It is important to note that AUC was used solely as an evaluation metric—not as a loss function—highlighting its role in capturing the trade-off between True Positive Rate (TPR) and False Positive Rate (FPR).

To ensure transparent interpretation, a confusion matrix was included, clearly displaying the counts of True Positives (TP), False Positives (FP), True Negatives (TN), and False Negatives (FN). This representation allows for the direct calculation of Precision, Recall, F1-score, and AUC, thereby ensuring clarity in the reported results.

4.3. Datasets

The analysis utilized 21 datasets, encompassing various NASA projects (KC1, KC2, KC3, JM1, CM1, MC2, MW1, PC1–PC5), Apache projects (Tomcat-6.0, Ant-1.7, JEdit-4.0, 4.2, 4.3), and artificial datasets (Ar1, Ar3, Ar4, Ar5, Ar6). The complexity of these datasets varied significantly, ranging from a few dozen features to thousands of characteristics, with defect ratios differing widely (see Table 1). This diversity underscores the imbalanced nature of the Software Fault Prediction (SFP) problem, where defective modules are frequently underrepresented.

4.4. Experimental Evaluation

The first set of experiments compared RBM-LR against standard LR. Results indicated consistent improvements across datasets. For instance, on KC1, RBM-LR achieved an AUC of 0.84 compared to 0.75 for LR. Similarly, on JM1, RBM-LR reached an Accuracy of 86%, outperforming LR’s 78%. These results confirm that RBM-based feature extraction significantly enhances predictive capability.

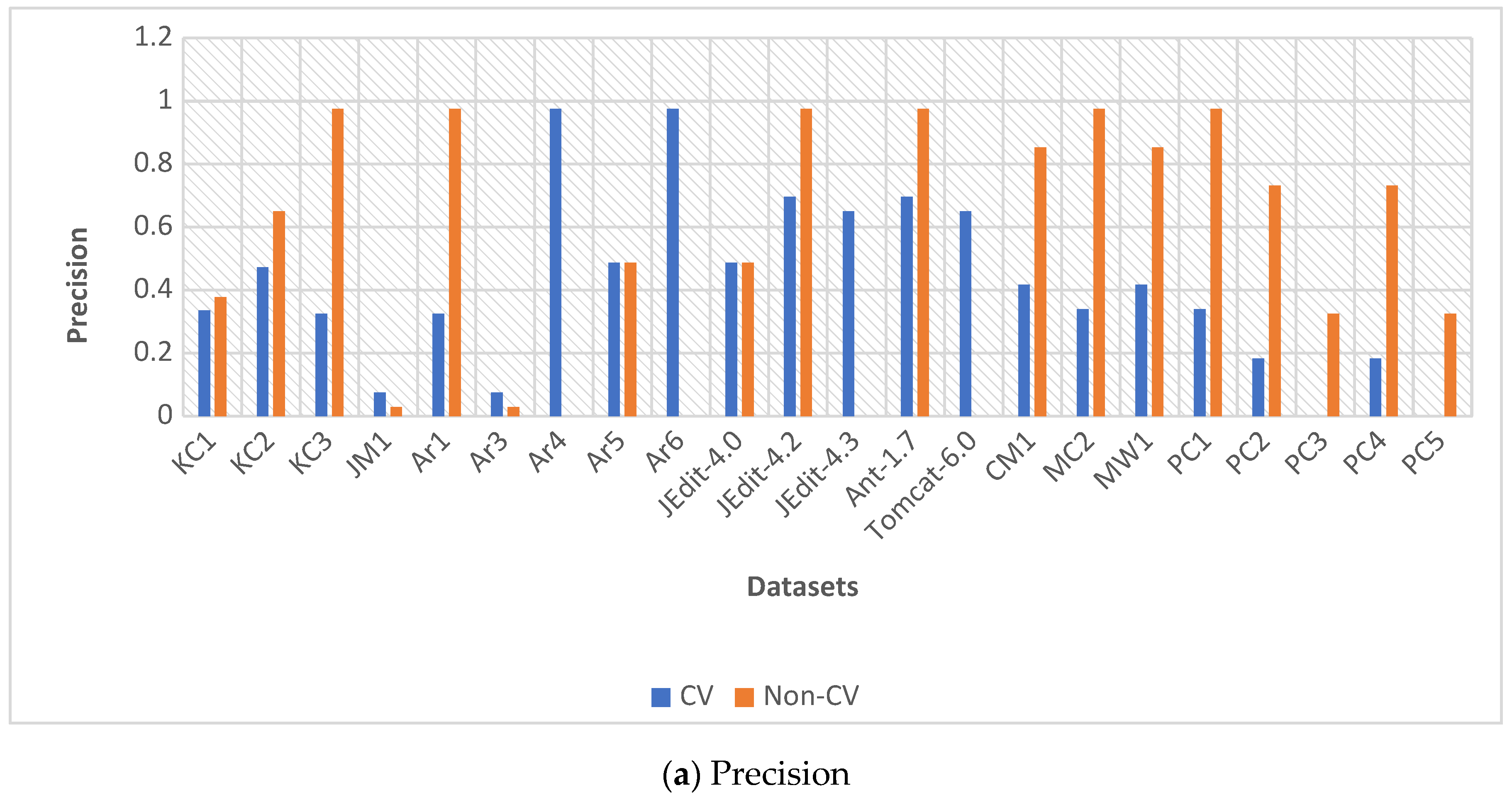
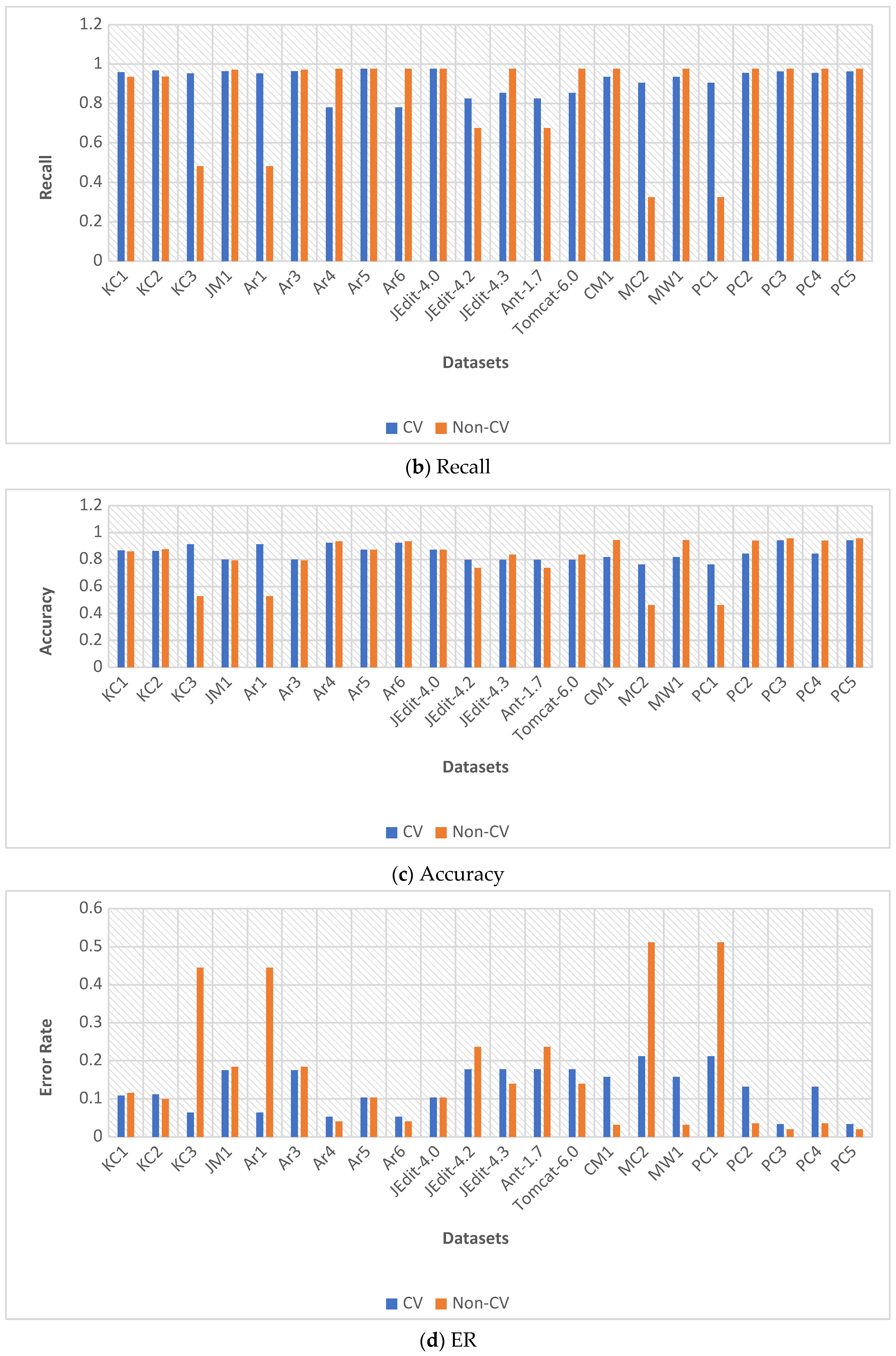
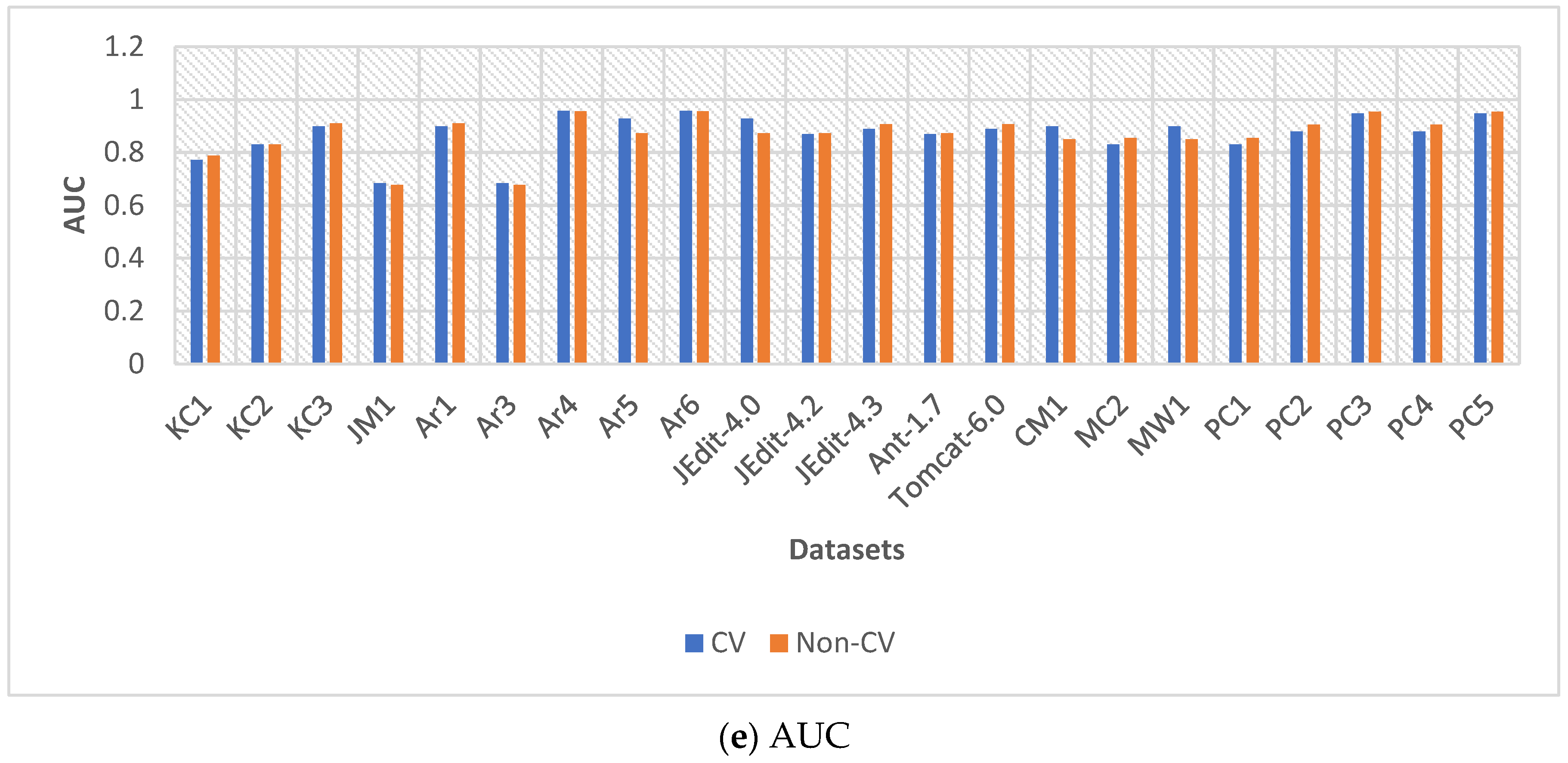
The second experiment examined with and without cross-validation (10-fold CV). As shown in Figure 3 and Figure 4, RBM-LR with CV achieved higher stability and generalization, particularly improving AUC and Recall. Without CV, performance degraded for certain datasets (e.g., JM1, PC2, Ar1, Ar3, Ar6). However, 16 out of 22 datasets demonstrated clear gains with cross-validation, confirming its critical role in avoiding overfitting.

The initial set of experiments compared RBM-LR to standard LR, revealing consistent improvements across various datasets. For example, on KC1, RBM-LR achieved an AUC of 0.84, in contrast to 0.75 for LR. Similarly, on JM1, RBM-LR recorded an accuracy of 86%, surpassing LR’s 78%. These findings confirm that RBM-based feature extraction significantly enhances predictive performance.

The second experiment assessed the impact of cross-validation (10-fold CV) versus no cross-validation. As illustrated in Figure 3 and Figure 4, RBM-LR with cross-validation demonstrated greater stability and generalization, particularly enhancing AUC and Recall. In the absence of cross-validation, performance deteriorated for certain datasets (e.g., JM1, PC2, Ar1, Ar3, Ar6). Nevertheless, 16 out of 22 datasets showed clear improvements with cross-validation, underscoring its essential role in mitigating overfitting.

Figure 3 presents the performance of RBM-LR across various datasets with respect to five evaluation metrics: (a) Precision, (b) Recall, (c) Accuracy, (d) Error Rate (ER), and (e) AUC. The findings indicate that RBM-LR consistently outperforms baseline LR in terms of both Precision and Recall, while simultaneously lowering the Error Rate. Additionally, the enhancements in Accuracy and AUC highlight the effectiveness of RBM-based feature extraction in improving predictive performance.

Figure 4 compares the performance of RBM-LR with and without cross-validation (CV). Subplots (a–e) display the same metrics as presented in Figure 3. It is evident that RBM-LR with 10-fold CV demonstrates a more stable performance, particularly enhancing Recall and AUC across most datasets. In contrast, without CV, there are noticeable performance fluctuations, especially in datasets such as JM1, PC2, and Ar-series. These results underscore the importance of CV in mitigating overfitting and enhancing the generalizability of the proposed framework.

In the third experiment, we compared RBM-LR with several state-of-the-art classifiers, including Random Forest (RF), XGBoost, and Support Vector Machines (SVM). The RBM-LR consistently outperformed these classifiers across various metrics (see Figure 3 and Figure 4), demonstrating its effectiveness as a fault prediction framework.

4.5. Runtime Analysis and Time Complexity

Although RBM-LR includes an additional feature extraction phase, the resulting runtime overhead is relatively modest when compared to baseline LR. Experimental comparisons of runtime have confirmed that this trade-off is warranted by significant enhancements in predictive accuracy and stability. The time complexity of RBM-LR is O(n × h × f × epochs), where n represents the number of instances, h denotes the number of hidden nodes, f refers to the features, and epochs indicates the number of iterations. This linear scaling ensures that RBM-LR remains practically feasible for large-scale industrial applications.

4.6. Statistical Significance Testing

To evaluate the robustness of the results, paired t-tests were performed on the accuracy and AUC results across multiple datasets. The p-values obtained (<0.05) indicate that the improvements of RBM-LR compared to baseline LR are statistically significant. This suggests that the performance gains are not merely random fluctuations.

4.7. Summary of Findings

RBM-LR consistently outperforms baseline logistic regression (LR) across key metrics including Accuracy, Precision, Recall, F1-score, and AUC. The application of cross-validation plays a crucial role in stabilizing results, leading to improved performance across the majority of datasets. Furthermore, an analysis of the confusion matrix offers clear insights into the types of errors, thereby enhancing interpretability.

Runtime analysis indicates that the computational costs remain manageable in relation to the performance gains achieved. Statistical significance tests confirm that these improvements are not merely incidental, but rather robust and replicable.

Together, these findings position RBM-LR as a trustworthy and scalable solution for software fault prediction, effectively balancing predictive accuracy, statistical rigor, and computational feasibility—all critical factors for successful real-world industrial adoption.

5. Conclusions

In this study, we introduced a hybrid RBM-LR framework for software fault prediction (SFP). This model combines Restricted Boltzmann Machines (RBM) for nonlinear feature extraction with Logistic Regression (LR) for classification, effectively addressing the challenges posed by high-dimensional and imbalanced datasets while maintaining interpretability. The framework was validated using 21 benchmark datasets from PROMISE and OpenML. The experimental results demonstrate that RBM-LR consistently outperforms baseline LR and several leading classifiers, including Random Forest (RF), XGBoost, and Support Vector Machines (SVM). On average, the model achieved a 7% improvement in AUC and a 6% enhancement in accuracy compared to baseline LR. Furthermore, Precision and Recall improved by 5–8%, while the F1-score showed steady gains across the datasets. Notably, these improvements were confirmed through statistical significance testing (p < 0.05), underscoring the robustness of the proposed approach.

Additionally, the implementation of 10-fold cross-validation greatly stabilized performance across most datasets (16 out of 22), further validating the reliability of the RBM-LR framework. In comparisons with state-of-the-art classifiers such as RF, XGBoost, and SVM, RBM-LR consistently demonstrated superior predictive accuracy and stability.

Despite the promising results, several limitations persist. The performance of the Restricted Boltzmann Machine (RBM) is significantly influenced by hyperparameter tuning (e.g., the number of hidden nodes, learning rate), and the model incurs a moderate runtime overhead compared to standard Logistic Regression (LR). Additionally, while RBM-LR has shown strong performance on public benchmark datasets, its scalability in large-scale industrial environments warrants further exploration.

Looking ahead, several research directions are proposed. First, enhancing the framework with deep hybrid architectures such as Autoencoders, LSTM, or Transformer-based models could improve the ability to capture temporal and sequential dependencies in software evolution data. Second, applying the framework to large-scale industrial and real-time datasets would help evaluate its scalability and practical utility. Finally, integrating RBM-LR with explainability techniques (e.g., SHAP, LIME) could further increase transparency and support its adoption in safety-critical domains.

In conclusion, the RBM-LR model offers a statistically validated, interpretable, and computationally viable solution for software defect prediction. By addressing the balance between accuracy, efficiency, and interpretability, this research significantly contributes to the development of trustworthy and industrial-grade machine learning frameworks within the field of software engineering.