CFD-Driven Enhancement for Supersonic Aircraft Variable Geometry Inlet

Featured Application

Extended speed and Altitude Range supersonic jets.

Abstract

High-speed propulsion systems require supersonic inlets for operation; however, these inlets lose efficiency when the flight speed range is wide. Fixed-geometry inlets designed for particular conditions encounter operational difficulties when running at supercritical speeds, including shockwave instabilities and pressure reduction, limiting their operational speed and altitude range. Increasing inlet flexibility is a critical requirement for aerospace systems that need multivariable propulsion capabilities for civilian and military operations. This study, based on a supersonic inlet whose design flight Mach number is 2.2, determines its operational performance when operating at a speed of Mach 3 and then investigates modifications for expanding its operational boundaries with variable geometry components. This study used computational fluid dynamics in ANSYS Fluent with the k-ω SST turbulence model for airflow analysis. The methodology starts with Mach 2.2 baseline validation before proceeding to the Mach 3 investigation at different upward cowl-lip deflection angles ranging from 5° to 16°. This study conducted tests with a bleed slot and a 6 mm semi-conical bump to practically diminish unstart occurrences and treatment of shock–boundary-layer interactions. The results showed that a lip deflection angle of 15° upward delivers maximum operational efficiency on Mach 3 in terms of compression efficiency, flow deceleration, and flow uniformity at the inlet exit, as it generates an exit Mach number of 1.9, identical to that of the unmodified baseline operating at Mach 2.2, while a 5° deflection upward has shown the best values for total pressure recovery. Bleed slot implementation with the bump shape decreased unstart effects at a backpressure 30 times bigger than ambient pressure and produced stable flow despite a total pressure recovery drop of 8.5%. At Mach 3, with 15 km altitude, these modifications allow the system to operate with similar effectiveness as the baseline design at lower speeds. This study introduces a method for modifying a fixed-geometry inlet and extending its limitations, offering a pathway for adaptable supersonic inlets. The findings contribute to propulsion systems design by introducing a simple method for applying geometrical variations with less mechanical complexity compared to traditional variable geometry inlets. They change the entire throat area, supporting the design of supersonic vehicles and sustainable supersonic travel.

1. Introduction

Aerospace technology advances with a focus on both supersonic and hypersonic propulsion systems. Supersonic propulsion operates through specific functions of turbojet and ramjet engine components, as well as combined-cycle engine operations [1]. These systems hold enormous importance for achieving extended supersonic operations in civil aviation and military platforms for aircraft such as the XB-70 Valkyrie and SR-71 [2]. In addition, these systems are critical to civilian supersonic jets such as the Tu-144, Concorde, and future high-speed travel jets such as NASA’s X-59 QueSST and Boom Overture, aiming to overcome historical limitations of noise and efficiency [3]. The aircraft’s performance and safety, along with reliability, depend directly on the way the engines are integrated within the aircraft structure [4]. The design of supersonic inlets ensures airflow stability under all situations, including different incidence angles, alongside starting phases and noise-control conditions. The design works as a component of comprehensive technological efforts to achieve design efficiency and reliable system performance [5]. Supersonic inlet designers face a key challenge to control airflow during its transition from supersonic to subsonic speeds. Shockwaves appear in sequences to achieve deceleration in airflow, which creates total-pressure losses during this process [6]. The position and intensity of shockwaves need precise control to decrease pressure losses while maximizing the usable air delivered to the engine system. Supersonic inlets must stay stable as they handle changes in flight conditions, encompassing Mach number variations, alongside altitude and angle of attack modifications. Aircraft operation faces potential danger from unstable airflow, which includes inlet buzz oscillations that may result in engine surges [7,8]. The engine`s performance will drop significantly with increasing Mach number and altitude due to compressibility effects and density drop, both of which will lead to a pressure drop [9,10].

The inlet design should ensure efficient performance throughout all the flight phases. Inlet design for a wide range of speed aircraft will be a challenge, reaching efficient operation throughout all the flight phases, as different flight speeds require different geometrical shapes and scales, which limits the range of efficient operation. Variable-geometry engine inlet in supersonic aircraft applications is designed to adjust the inlet geometry for different flight conditions to reach high efficiency and to ensure maximized engine performance along all the flight phases [11,12]. The variable geometry inlet is critical for ensuring suitable airflow to the engine. A variable geometry inlet will adjust its geometry to suit different flight conditions, which helps in achieving high efficiency by matching geometry with the flow characteristics. It offers advantages over other fixed geometries in terms of flow uniformity, pressure, and speed. The design and control of these inlets often involve complex systems to manage airflow and shockwave positioning, ensuring stable and efficient engine operation [13,14].

The supersonic inlet design developed by Das & Prasad for Mach 2.2 operation [15] shows degradation in operational effectiveness at higher speeds, as it was optimized for Mach 2.2 conditions. Operational efficiency degrades at Mach 3, as the original design utilizes a fixed 4° downward cowl lip intended for Mach 2.2, ensuring shockwave stabilization and maximum total pressure recovery. Raising the speed with cowl-lip downward deflection results in higher-speed flow and unstable shock structures at Mach 3. Speed limits prohibit the inlet’s operational boundaries through variable-geometry mechanisms. This study enables the inlet to have a wider operational speed range through modifying the baseline design that combines shockwave alignment with high-speed total-pressure recovery capabilities while ensuring simplicity of structure.

2. Simulation and Enhancements Methodology

2.1. Background

The methodology employed in this study involves a systematic computational fluid dynamics (CFD) analysis of a two-dimensional variable geometry supersonic aircraft inlet. The primary objective is to optimize the inlet performance at a higher Mach number by modifying the deflection angle of the inlet upper cowl lip. The baseline design for this study was derived from a referenced inlet geometry [15] originally optimized for operation at Mach 2.2. The methodology follows a structured approach, beginning with validation of the reference design results, followed by performance assessment at Mach 3, and concluding with the optimization of the inlet lip deflection angle to enhance total pressure recovery while avoiding inlet unstart conditions at a higher Mach number, which enables the extension of the inlet operational speed.

2.2. Geometrical Details of the Inlet

The reference inlet design features a two-ramp compression surface and a rectangular exit. The initial reference design was intended for operation at Mach 2.2 and incorporated a 4° downward deflection angle of the upper inlet lip as the optimized performance at that speed, as determined in other researchers’ studies from the reference. This study investigates the effect of modifying this deflection angle for operation at Mach 3. The variation of the deflection angle of the lip will allow the inlet to operate over a wider range of speeds.

The geometrical dimensions of the inlet, derived from the reference study, were maintained to ensure consistency in shock formation and flow characteristics. This study focuses solely on the cowl-lip deflection as a means of optimizing inlet performance. The detailed geometrical dimensions are illustrated in Figure 1.

2.3. Meshing

The mesh was generated in ANSYS 2022 R1 Meshing using mapped face meshing with manual edge sizing. A structured meshing procedure was used for grid creation to achieve precise control in mesh topology, along with flow-feature alignment. Sufficient refinement of the mesh has been applied to display important flow characteristics, especially near the walls, which include shock formations and boundary-layer interactions. The mesh quality parameters were observed at the critical areas near the throat and the walls. The quality parameters, such as orthogonal quality, had a value range of 0.8~1, and the mesh skewness had a value range of 0.26~0.0000000013.

Figure 2 illustrates the mesh configuration, including detailed boundary-layer meshing with 523,115 total cells combined with 15 boundary layers on the wall. The first layer height is 0.027 mm, with a growth ratio of 1.2.

2.4. Computational Method

This study was conducted using CFD simulations, which employed the Reynolds-averaged Navier–Stokes (RANS) equations to reconstruct the compressible flow field. The precise determination of turbulent flow requires the implementation of the k-ω SST (Shear Stress Transport) model. This study utilizes $\mathrm{k}-\mathsf{\omega }$ model formulations to achieve accurate boundary-layer calculations. High-speed compressible flows significantly benefit from using this model as a part of the present study. The finite volume method applied a numerical formulation to develop the solution. The RANS equations of continuity and momentum are expressed in Equations (1) and (2), and the modeled energy equation is expressed in Equation (3).

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{i}}}}\left(\rho {\mathrm{u}}_{\mathrm{i}}\right)=0$$

(1)

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{j}}}}\left(\rho {\mathrm{u}}_{\mathrm{i}}{\mathrm{u}}_{\mathrm{j}}\right)=-{\displaystyle \frac{\mathsf{\partial }\mathrm{p}}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{i}}}}+{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{j}}}}\left[\mathsf{\mu }\left({\displaystyle \frac{\mathsf{\partial }{\mathrm{u}}_{\mathrm{i}}}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{j}}}}+{\displaystyle \frac{\mathsf{\partial }{\mathrm{u}}_{\mathrm{j}}}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{i}}}}-{\displaystyle \frac{2}{3}}{\mathsf{\delta }}_{\mathrm{i}\mathrm{j}}{\displaystyle \frac{\mathsf{\partial }{\mathrm{u}}_{\mathrm{k}}}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{k}}}}\right)\right]+{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{\mathrm{x}}_{\mathrm{j}}}}\left(-\rho \overline{{\mathrm{u}}_{\mathrm{i}}^{\prime }{\mathrm{u}}_{\mathrm{j}}^{\prime }}\right)$$

(2)

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{\mathrm{x}}_i}}\left[u_i\left(\rho E+p\right)\right]={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{X}_j}}\left[\left(k+{\displaystyle \frac{C_p{\mu }_t}{{Pr}_t}}\right){\displaystyle \frac{\mathsf{\partial }T}{{\mathsf{\partial }X}_j}}+u_i{\left({\tau }_{ij}\right)}_{eff}\right]+S_h$$

(3)

where ${\mathrm{u}}_{\mathrm{i}}$, $\rho ,$ and $\mathrm{p}$ denote the velocity component in the i-th direction, the fluid density, and the pressure, respectively. ${\delta }_{\mathrm{i}\mathrm{j}}$ is the Kronecker delta function. k, is the thermal conductivity, E is the total energy, and ${\left({\tau }_{ij}\right)}_{eff}$ is the deviatoric stress tensor. The term $-\rho \overline{{\mathrm{u}}_{\mathrm{i}}^{\prime }{\mathrm{u}}_{\mathrm{j}}^{\prime }}$ corresponds to the Reynolds stress, which is modeled using the $\mathrm{k}-\mathsf{\omega }$ shear-stress transport (SST) turbulence model to provide closure for Equation (2). The turbulent viscosity is computed by $\mathrm{k}-\mathsf{\omega }$ SST closure, which enables efficient near-wall turbulence resolution with reliable performance in free-shear flow conditions [16]. The model finds broad acceptance in compressible aerodynamic applications, which justify its use for the current CFD simulations [17].

2.5. Computational Setup

In this study, the mass, momentum, and energy conservation governing equations have been solved with the ANSYS Fluent density-based solver, which is appropriate when solving compressible and supersonic flow conditions. It incorporated a fully coupled approach to concurrently resolve the flow equations with a Rhie–Chow distance-based flux formulation to manage the pressure–velocity coupling to improve numerical stability. All flow variables were spatially discretized using a second-order upwind scheme, including the density, the momentum, the energy, and the turbulence quantities, whereas pressure in this case was discretized based on a second-order scheme. The least squares cell-based technique was employed to perform gradient calculations. Turbulent conditions were solved by the k-omega SST turbulence model, which was thus selected for its capability in evaluating supersonic inlet performance [18]. The pseudo-time option was enabled to facilitate a steady-state solution. The overall convergence was considered achieved when all scaled residuals in all the equations fell below ${10}^{-5}$.

A C-shaped pressure far-field boundary is used to simulate supersonic flow correctly and produce proper shock wave development in the computational domain, as seen in Figure 3. The inlet walls were defined as adiabatic, while the outlet boundary featured a pressure outlet with no backpressure in the initial stage. While steady-state conditions were adopted for this study, tests were executed at a 10 km altitude, since they correspond to atmospheric properties at that altitude. The pressure far-field boundary conditions have a pressure setting of 26,500 Pa, a temperature of 223 K, and a flight Mach number of Ma 2.2 and Ma 3 in different conditions. While the walls were defined as adiabatic and the backpressure value at the pressure outlet is equivalent to the far-field pressure value, which is 26,500 Pa in the initial condition.

2.6. Performance Assessment for Higher Speed Flight

This study proceeded with the assessment of the reference inlet at a higher flight Mach number of 3. The goal was to determine the best lip deflection angle at Mach 3. The lip deflection variation will allow the inlet to operate at higher flight speeds.

A simulation at Mach 3 will be applied to the geometry that comes with a 4° downward deflection, which was originally designed to operate at Mach 2.2. This geometry will be further compared with the final selected geometry to assess performance gain and also to confirm its unsuitability for operation at that speed. However, deflecting the lip downward narrows the inlet entry height, which will cause flow acceleration, as mentioned in the referenced study. Figure 4 illustrates a graphical representation of the inlet cowl-lip deflection. Figure 4a illustrates the 4° downward cowl-lip deflection desired for Mach 2.2 operation, while Figure 4b illustrates the upward lip deflection desired for higher speed operation.

Given that a downward deflection is unsuitable at Mach 3, this study focuses on modifying the inlet cowl lip with upward deflection for flow deceleration, compression, and performance enhancement. Increasing the deflection angle upwards was hypothesized to reduce the Mach number inside the inlet and improve total pressure recovery. A series of simulations were conducted with progressive upward deflection angles to investigate the best angle for Mach 3 operation. The tested angles were 5°, 10°, 11°, 12°, 13°, 14°, 15°, and 16° upward.

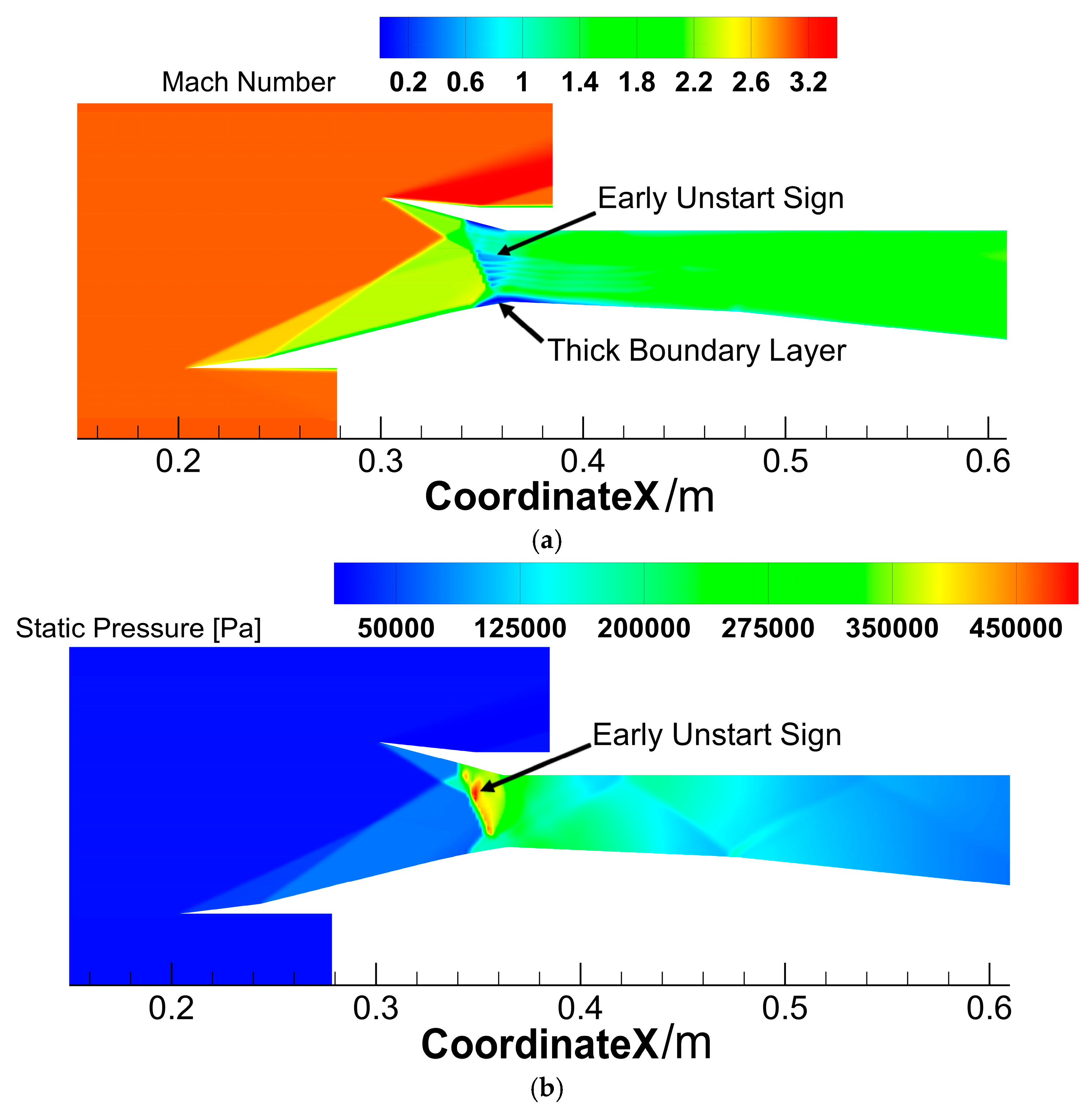
This study investigated these configuration designs through operational tests at Mach 3 and an altitude of 10 km, with a static pressure of 26,500 Pa and a temperature of 223 K applied as the pressure far-field boundary conditions. The test results should reveal better performance outcomes as the deflection angle increases, as improved alignment of shockwaves at Mach 3 helps both improve total pressure recovery and maintain controlled internal Mach numbers. An undesirable flow phenomenon, such as inlet unstart, occurs when deflection exceeds an established threshold. Under unstart conditions, strong shocks in flow paths caused spillage of the airflow and deteriorated performance results. Performance metrics for evaluating each deflection angle consisted of monitoring static pressure, total pressure, and Mach number measurements at the diffuser exit. The selected parameters measured the efficiency of compression shock wave behavior and the stability of inlet flow. Figure 5 displays an example of different upward deflection angles applied to the upper lip for examination purposes. The upward slope of the green section measures a higher deflection point compared to the downward slope of the red section, which displays a lower deflection point.

2.7. Further Enhancements

After the best geometry was determined, more enhancements were applied to both the inlet design and operational conditions to apply one of the off-design conditions, ensuring efficient operation in severe conditions and attempting to maximize the inlet compression efficiency. These points are going to be explained in the next three subsections.

2.7.1. Applying Backpressure

As mentioned above, the simulations used to determine the best deflection angle did not apply backpressure under design conditions. However, under off-design conditions, backpressure was introduced. Applying a high backpressure value during Mach 3 operation led to excessive unstart; however, one of the previous designs for the same inlet indicated few signs of unstart at Mach 2.2. The solution implemented to address this phenomenon will be discussed in the next subsection.

2.7.2. Implementation of Bleed Slot

It was found that the unstart happened because of shock–boundary-layer interaction. For treatment, a pressure outlet was applied at the separated region while setting the static pressure to 20,000 pa, and another simulation was conducted with diffuser outlet pressure to be 30 times bigger than the ambient pressure to ensure that the inlet would be operating safely without being at risk of unstart during the severe off design conditions. In addition, in this case, the operational altitude was raised to 15 km to match the higher speed operation, with a pressure of 12,111 Pa and a temperature of 216 K. Figure 6 illustrates the position of the applied bleed outlet at the separated flow region.

2.7.3. Bump Implementation

After the determination of the best cowl-lip deflection angle for the operation at Mach 3, and while considering the application of a high backpressure value, an additional approach was taken toward maximizing the inlet`s compression efficiency and minimizing the unstart signs. The utilization of a bump located at the bottom cowl lip was investigated to assess the significance of adding this bump. This bump design has been applied in other studies [19,20]. Several other research studies show that bump structure, together with design shapes, affects measurements produce meaningful changes to the inlet flow patterns. Two-dimensional inlet bump sizes of 2 mm and 4 mm decreased spillage of supersonic flow while maximizing the total pressure recovery efficiency to 96.26% for the 2 mm bump diameter. The 4 mm semi-conical bump installed in 3D inlets prevented flow separation and managed shockwaves that significantly boosted the total pressure recovery near the ramp surface, particularly when inlet throttling was active. However, these experiments and simulations were performed at the speed of Mach 2.2 and 0° upper lip deflection, and for the current case, the flight Mach number was increased to 3, while the upper lip deflection angle was also changed. The effect of adding the bump to the inlet geometry was investigated at the new inlet layout, which is variable, operating at a higher Mach number and different cowl-lip deflection angle compared to both designs, the one in the original referenced geometry and the one applying the bump. Figure 7 illustrates a graphical representation of the bump geometrical shape; the bump shape is highlighted in red.

2.8. Mesh Independence Examination

To validate the numerical approach employed accordingly, a mesh independence analysis was performed using a set of three mesh sets, with coarse, fine, and dense meshes. The total number of cells was 348,743, 523,115, and 627,594, respectively.

The comparison of Mach number values at the inlet exit is illustrated in Figure 8, which indicates that the coarse mesh did not capture the flow speed correctly near the walls. In addition, the flow speed is generally captured as a higher speed, as it shows a higher Mach number along the curve and a slight shift in the curve position to the left. This means that in the coarse mesh layout, the flow peak Mach number is shifted downward, toward the bottom wall of the diffuser; on the other hand, the fine and dense mesh produced mostly identical values, with their Mach number curves closely aligned, with minor deviations.

Regarding the qualitative examination, which is illustrated in the Mach contours in Figure 9, similar results were observed, as the coarse mesh shows less sharply defined shockwaves within the inlet, which might affect shock reflection and shock–boundary-layer interaction or shock–shock interaction in the simulations. In contrast, the fine mesh shows the shocks more clearly, ensuring accurate flow capture. The dense mesh showed similar results compared to the fine mesh, while showing slightly sharper shocks in the Mach contours, but this difference is negligible. In general, the fine mesh resolution is sufficient to capture the external and internal flow characteristics and thus is adopted for the subsequent simulations.

An additional overview of mesh independence was also explored by analyzing the boundary layer using the y+ values. Distributions of y+ over the upper and bottom walls were also compared in Figure 10 under coarse, fine, and dense meshes. The y+ metric is essential to the accuracy of turbulence modeling, especially when using the k-omega SST model, where the y+ value must be near 1 to capture the viscous sublayer. The coarser mesh has most of its y+ values greater than 1.0, which indicates lower quality near-wall flow capture. On the other hand, fine and dense meshes occupied better values and were close to each other in most areas, as it corresponded to the requirements stipulated by the model. Although the dense mesh presents slightly smaller y+ values, the fine mesh attains a similar boundary layer resolution with very little difference. This confirms that the fine mesh is sufficient to resolve the near-wall flow physics without excessive computational load. The y+ values were monitored most closely at the critical area near the throat, where flow separation and critical phenomena are expected to occur, as shown in Figure 10.

3. Methodological Validation

The fundamental procedure in computational fluid dynamics research requires validation to establish the accuracy and reliability of numerical models. A validated computational setup must have the ability to mirror other researchers’ experimental or numerical results, which demonstrates that mesh resolution and turbulence modeling, together with boundary conditions, appropriately represent the physical processes. The validation of Mach 2.2 flow conditions using other researchers’ data creates a verified foundation for optimizing the inlet system. The validation process connects original findings with previous knowledge, thus building trust in the newly proposed modifications.

3.1. Qualitative Validation

The validation conducted in this study involved repeating two simulations. The researchers at Das & Prasad [15,16,17,18,19,20,21] replicated two essential cases, which were retested at 0° cowl deflection for simulating flow patterns and shock structures of unoptimized inlet designs. Additionally, in this study, the model included the reference design for Mach 2.2 with a 4° downward cowl-lip deflection, which displayed controlled shock interactions, together with minimal flow separation. Every element of the computational domain was aligned to the reference geometry to achieve consistency.

The experiments conducted by Das & Prasad were carried out in a blowdown supersonic wind tunnel at Birla Institute of Technology, Mesra, having a 50 mm × 100 mm rectangular test section. The tunnel was set at a speed of Mach 2.2, and the pressure of the settling chamber was ${3\times 10}^5 \mathrm{N}/{\mathrm{m}}^2$, with a Reynolds number of the order of $3\times {10}^7/\mathrm{m}$. The model of the rectangular mixed-compression intake, which was designed at Mach 2.2, was produced by the wire-cut EDM method, in order to achieve high precision with a tolerance of 0.01 mm. Static pressure along the ramp centerline was measured using 20 ports with a diameter of 0.8 mm that were connected to a 32-channel electronic pressure-scanner, and exit total pressures were measured using a custom 5-tube pitot rake on the plug. The work used shock structures, schlieren photography, and oil-streak techniques (titanium dioxide/oleic acid/lubricant mixture) on the inside surfaces to capture separation areas. The visualization sidewalls were constructed of Plexiglas in order to allow some optical access. Data acquisition on the pressure was made by using LabVIEW, along with NIDAQ hardware [21].

Das & Prasad established that a 0° cowl-lip deflection produces flow spillage at the inlet entrance because the compression zone is inadequate, as shown in Figure 11a. The mismatched shock angle produces this phenomenon, which triggers airflow to avoid entering the inlet.

The initial design from the reference paper at 0° deflection will serve as the baseline throughout this section because it features substantial flow spillage. The Mach contour in Figure 11b indicates that substantial spillage occurs near the inlet opening, which is comparable to the reference study simulation shown in Figure 11a. When supersonic air flows near the cowl lip, it diverges, which negatively affects mass capture performance, while showing that the simulation conducted matches the reference result.

On the other hand, the shockwave alignment improves significantly when the cowl-lip deflection reaches 4° downward. As Figure 12a shows, oblique shock waves from the compression ramps reflect to create a stable terminal shock close to the throat in the experimental method.

For a 4° downward deflection, the shockwave configuration can be seen in the Mach contour illustrated in Figure 12b, which captures oblique shocks generated by the compression ramps, reflecting at the cowl tip to form a terminal shock near the throat, along with the shock–boundary-layer interaction near the throat. This matches the reference’s shock structure, as showcased in Figure 12a.

3.2. Quantitative Validation

The computational method validation occurred through comparison of a 4° downward cowl-lip deflection case at Mach 2.2 operation against the numerical findings available in Das & Prasad’s study [15,16,17,18,19,20,21]. The evaluation included an assessment of total pressure recovery at the inlet exit, combined with Mach number values and distribution, as well as the examination of static pressure values and their uniformity.

3.2.1. Comparison of Total Pressure Recovery

The pressure recovery measured by Das & Prasad amounted to 97% at Mach 2.2 for a 4° downward cowl-lip deflection under free flow conditions, matching quite closely the 96.4% total pressure recovery derived through the validation simulations performed in this study, as displayed in

Table 1. Comparison for quantitative validation at the inlet exit.

Parameter	Current Study	Das & Prasad’s	Deviation
Total Pressure Recovery	96.4%	97%	−1.006%
Peak Exit Mach Number	1.9–2.0	1.98	±0.02%
Sustainable backpressure	~7	7	~0%

. The minor discrepancy of 1.006% likely arises from differences in numerical discretization, mesh resolution, and solver implementation.

3.2.2. Mach Number Distribution

The simulation performed in this study for the 4° downward deflection showed a peak exit Mach number of 1.98, aligning with Das & Prasad’s simulation data, reporting Mach numbers between 1.9 and 2.0 at the exit. The computational Mach contour in Figure 12a also replicates the shock structure observed in their experiment, as illustrated in Figure 12b, confirming the accurate capture of oblique and terminal shocks.

3.3. Conclusion of Validation Study

The results discussed verified that the computational methods operated correctly by successfully showing similar findings from the referenced study. The computational results at zero-degree deflection validated the reference data by showing how flow spillage and unstart occurred due to shock mismatch (Figure 11). During the 4° deflection test, oblique shock waves stabilized within the throat area, creating 96.4% total pressure recovery with balanced flow (Figure 12). The validation outcomes proved the findings in Das & Prasad’s original study while creating dependable conditions to optimize Mach 3 performance by using adaptive geometrical designs.

4. Performance Enhancement

4.1. Investigation of Lip Deflection

After the validity of the computational setup was confirmed in the previous chapter, this chapter will investigate the results and discuss the modification. The purpose of this investigation is to identify the best deflected lip position for achieving Mach 3 capability while expanding operational speed capabilities. A series of simulations was executed after Mach 2.2 operation validation to identify the best lip deflection angle for Mach 3 operation. Establishing the correct direction of angle adjustment began the first operational phase. A series of tests utilizing different upward deflection angles enabled the determination of the most suitable geometry for Mach 3 operation, with 5°, 10°, 11°, 12°, 13°, 14°, 15°, and 16° deflection angles. Higher upward deflection angles yielded better inlet performance, which resulted in a lower Mach number inside the duct and higher static pressure measurement. Figure 13 presents a comparison of Mach number values at the inlet exit along the vertical axis for 5°, 10°, 14°, 15°, and 16° of upward deflection.

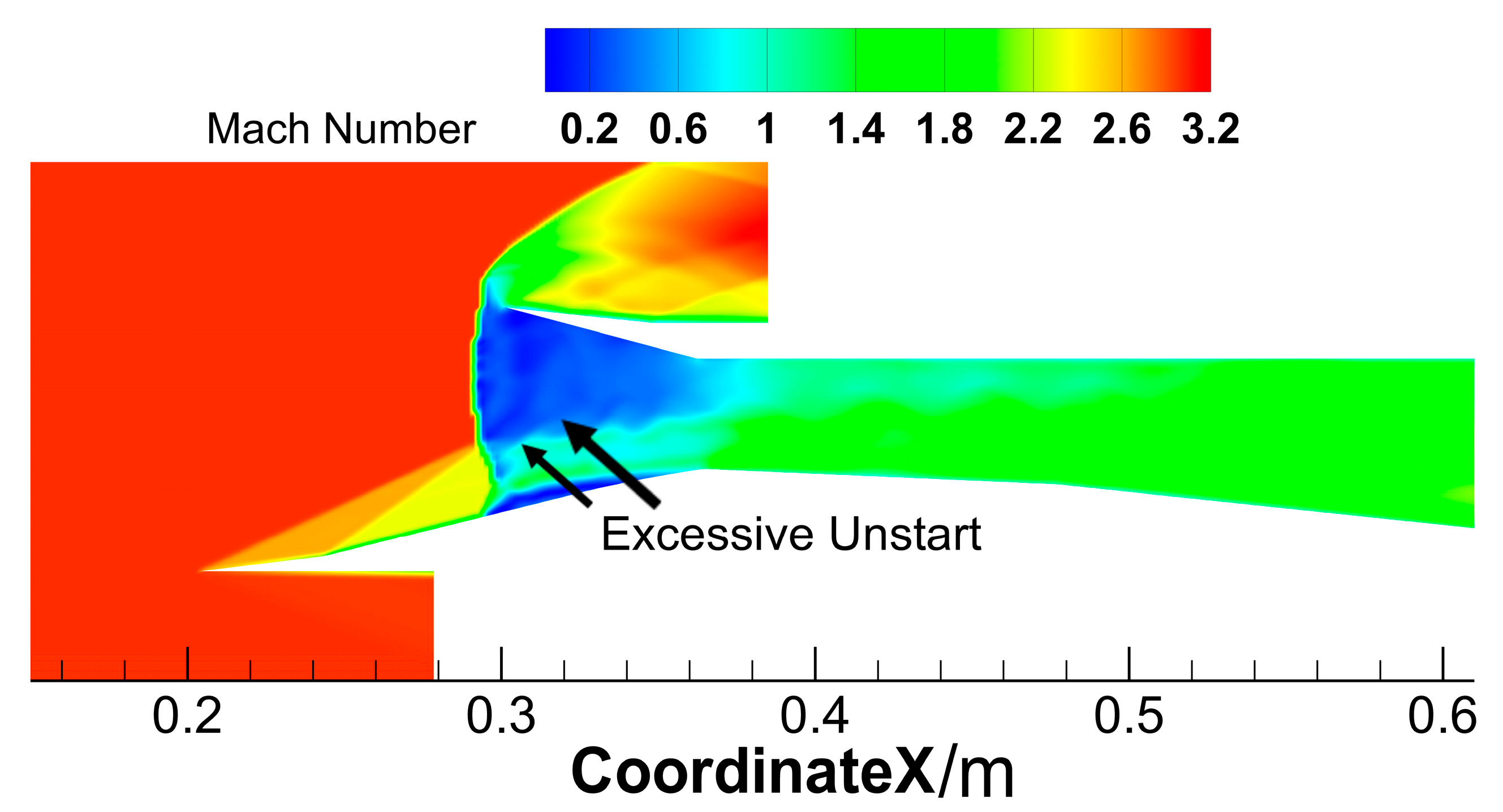
The inlet started to unstart abnormally when set to 16°, making 15° the maximum angle for running at Mach 3. The examination of Mach number patterns and pressure behavior at various deflection angles produced a better understanding of performance effects on the inlet. A comparison of Mach number values along the vertical axis at the inlet exit is presented, covering eight different upward deflection angles between 5° and 16°. The deflection angle of 5° resulted in the highest outlet Mach number, which started decreasing from 5° and continued to decrease until reaching 15°. A substantial unstart phenomenon occurred at 16°, as illustrated in the total pressure contour in Figure 14.

Table 2. Performance parameters at different cowl-lip upward deflection angles tested under Mach 3 flight conditions.

Parameter	5°	10°	14°	15°
Average Static Pressure (kPa) at Exit	59	63	74	76
Peak Mach No at Exit	2.51	2.3	2.1	1.99
Total Pressure Recovery at Exit	0.9	0.87	0.86	0.849
Mach number Gradient at Exit, ΔMa	6.87%	8.16%	8.76%	4.46%

compares the performance parameters for different cowl-lip deflection angles at Mach 3.

Table 3. Performance parameters for the baseline fixed geometry at different speeds.

Parameter	Mach 2.2	Mach 3
Average static pressure (kPa) at exit	38.4	36
Peak Mach No at exit	1.98	2.62
Total pressure recovery at the exit	0.964	0.85
Mach number gradient at exit, ΔMa	3.51%	13.28%

shows the performance parameters for the baseline fixed geometry inlet, which clarifies the performance degradation of the fixed geometry inlet when the speed is elevated. In addition, the parameters indicate that 15° exhibits the best performance regarding flow stability, compression efficiency, and flow deceleration; however, it does not have the best total pressure recovery value compared with other deflection angles. While investigating the performance, it was found that a 5° upward deflection offers the best total pressure recovery value. Flow stability might be prioritized over total pressure recovery to ensure stable engine operation in extreme conditions and avoid phenomena such as compressor stalls, flashbacks, and engine surges. This study periodized stability over the total pressure recovery to ensure safe operations in off-design conditions, which selects the 15° deflection. In addition, 5° is still a valid option for optimum operation that ensures the most efficient total pressure recovery.

The 15° upward deflection provided the best performance because it created results that accurately replicated the optimized Mach 2.2 operational parameters. Detailed contours describing the Mach number, static pressure, and total pressure are shown in Figure 15 during the initial optimized condition. The operational envelope was expanded to Mach 3 through variable-geometry configuration, but performance characteristics remained comparable, with a minor decrease in efficiency compared to the optimal Mach 2.2 performance. A minor drop in operational efficiency is expected due to the advanced aerodynamic problems that occur when operating at higher Mach numbers, as the performance parameters at Mach 3 with 15° upward deflection were not perfectly the same as those of Mach 2.2 with 4° downward deflection. The upcoming sections will examine the possibilities for enhancing Mach 3 performance through the exploration of active flow control technologies and the addition of more geometrical elements to boost the inlet’s operational capability across different flight conditions.

The effect of backpressure on inlet performance was considered, as this study conducted an inlet lip deflection investigation for Mach 3 operation while disregarding the effect of backpressure. A backpressure application at the pressure outlet allowed the examination of off-design performance for the inlet. A systematic pressure build-up at the back end was applied to study its influence on inlet performance. An initial analysis indicated that a stable flow was not maintained with a critical backpressure value 6 times bigger than the freestream pressure, as the inlet experienced unstart as a result of shock–boundary-layer interaction, as illustrated in the Mach contour shown in Figure 16.

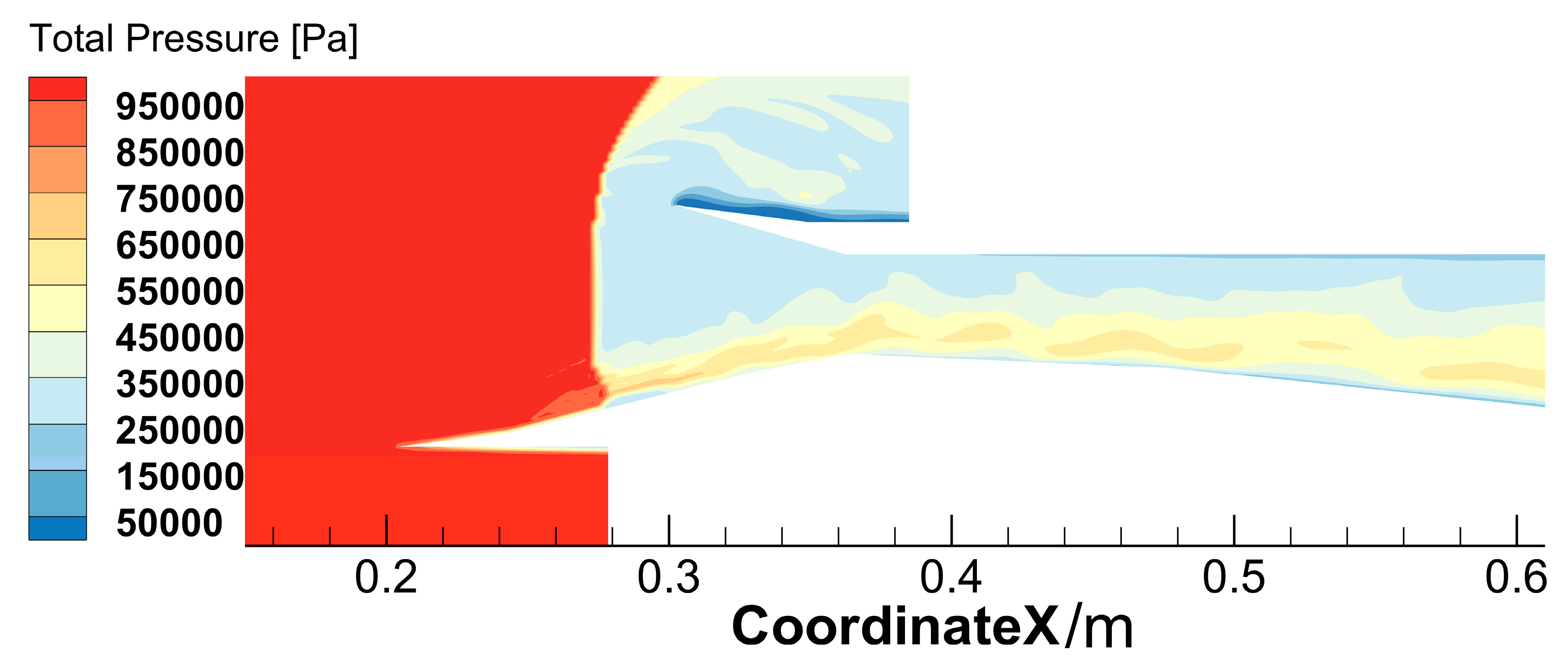
The analysis of the initial simulation results had already shown that the inlet operated near the unstart threshold, as in the Mach contour illustrated in Figure 15a. The observed behavior aligns with other studies. Research indicates that unstart signs demonstrate the inlet’s vulnerability to hostile pressure gradients, thus making further improvement strategies necessary. Additional simulation assessments investigated the inlet’s performance response when subjected to changing backpressure levels, which indicated a specific threshold for decline. The identified threshold allows this study to optimize future modifications that enhance inlet resistance to backpressure fluctuations in order to improve operational flexibility in off-design conditions, which will be discussed in the next section.

4.2. Effect of the Bleed Slot Implementation

The unstart phenomenon caused by backpressure required mitigation through a bleed control mechanism. The introduction of the bleed slot through a pressure outlet at the separation area, as can be seen in Figure 6, maintains a lower pressure value to regulate boundary layer expansion and shock interactions. The design change provides critical stabilization to the inlet flow, which enhances its operational capabilities across various conditions. A test was conducted on the inlet by applying strong backpressure that exceeded freestream pressure by 30 times to prove effectiveness under extreme off-design operational conditions. The simulation of the inlet performance became more challenging in operational conditions by increasing the flight altitude from 10 km to 15 km. At these settings, the free stream operated with a pressure of 12,111 Pa.

The higher altitude level added more complex aerodynamic conditions with reduced density levels and pressure, making it crucial to assess the modified inlet performance capabilities. Figure 17 illustrates the improvement in the total pressure recovery ratio after the implementation of the bleed slot and the application of backpressure, compared with the previous case without bleed. This shows a significant improvement in the total pressure recovery and a more stabilized curve.

The simulated Mach number, static pressure, and total pressure results with the bleed slot are illustrated in the contours shown in Figure 18. The addition of the bleed slot led to enhanced inlet operation because it created flow stabilization while blocking potential unstart conditions across various pressure conditions. The scientific results prove that boundary layer control technology effectively protects inlet stability throughout erratic operational conditions.

4.3. Effect of Bump Implementation on Inlet Performance

The analysis tested a compression enhancement method by adding a bump feature to the bottom wall near the lip. The literature has documented that bump elements succeed in reducing supersonic spillage while boosting the inlet performance when operating at Mach 2.2 with no upper lip deflection [19,20]. When the bump was attached to the inlet’s lower ramp, it had a significant effect on its performance during Mach 3 operation at 15° upward deflection. A bump introduced to the lower ramp stabilized flow and managed shockwaves but resulted in changes to the effectiveness of total pressure recovery. The section examines how the bump affects airstream dynamics and evaluates its performance against the inlet without the bump, introduced previously.

4.3.1. Flow Stability and Shockwave Alignment

The addition of the bump reduced the early unstart signs observed in the baseline design. The Mach contour for the 15° upward deflection with the bump illustrated in Figure 19 reveals smoother shock transitions and reduced spillage compared to the case without the bump, as shown in Figure 18a, where oblique shock reflections exhibited slightly less consistent reflection. The bump’s geometry altered the compression ramp’s curvature, aligning oblique shocks more effectively and minimizing flow separation near the throat. This stabilization is critical for preventing inlet unstart under extreme conditions, as the bump mitigates adverse shock–boundary-layer interactions.

4.3.2. Static Pressure Uniformity

The static pressure contour displayed in Figure 20 shows that the bump design maintains better static pressure distribution at the exit than the no-bump configuration. The compression efficiency achieved an improvement of 15%. In the static pressure contours that can be seen in Figure 20, compared to Figure 18b, a visual enhancement in compression efficiency is observed through more stable static pressure near the throat area while having fewer unstart signs.

4.3.3. Total Pressure Recovery Trade-Offs

Total pressure recovery suffered deterioration after the implementation of the bump, with an 8.5% drop after the implementation of the bump, as shown in Figure 21. The bump design reduces this outcome due to its geometrical structure, which led to fewer flow distortions when compared to the previous setup. Operational stability reaches higher levels despite the total pressure recovery loss. Figure 22 illustrates the total pressure contour with the bump, which is comparable to the previous case displayed in Figure 18c.

The 2 mm bump geometry was optimized for Mach 2.2 at 0° deflection in prior studies, following the investigation of more than one bump sizes to determine the best size for performance. This study only tested a 6 mm bump, which indicated enhancements in flow stabilization and compression efficiency while affecting the total pressure recovery to have 8.5% drop, so further studies should be conducted to investigate the optimum bump geometry for the operation at Mach 3 with upper lip 15° upward deflection to balance total pressure recovery losses with stability gains. In addition, the bump geometry should also be variable for optimum performance at different sp.

4.4. Results of Combined Methods

The findings of this study demonstrate that modifying the inlet geometry to enable variable lip deflection significantly enhances its operational range while preserving critical performance characteristics. The inlet proposed in this study delivers results that match the baseline for the Mach 2.2 condition with 4° downward deflection, in terms of exit Mach number and pressure profiles, at a 15° upward lip deflection setting for Mach 3 operation, as shown in Figure 23. Performance degradation at Mach 3 with 4° downward deflection resulted in severe issues, such as total pressure recovery problems and Mach number spikes reaching 2.63 at exit for the original geometry, while the modified design produced comparable results to the baseline at Mach 2.2 with 4° deflection. These problems become non-factors in the redesigned system, which enables reliable Mach 3 functionality. The redesigned inlet demonstrates nearly equivalent performance at Mach 3 and 15 km altitude to that achieved by the baseline at Mach 2.2 and 10 km altitude, thus proving its versatility under the Mach 3 configuration with 15° upward deflection. The developed technology brings useful applications to high-speed propulsion systems through its ability to operate efficiently at supersonic speeds with a unified adaptive inlet design that eliminates the need for fixed geometry. The applied bleed–boundary-layer control system strengthens the inlet’s reliability because it shows strong resistance to heavy backpressures. Variable-geometry inlets demonstrate their capability to serve the future aerospace platforms because they maintain performance benefits while expanding operational flexibility, according to the study outcomes. The integration of a 6 mm semi-conical bump on the lower cowl lip provided additional stabilization to the inlet at Mach 3 by reducing early unstart signs. At the same time, shock alignment behaved more efficiently, as seen in Figure 18, Figure 19, and Figure 21. The modification caused major improvements to static pressure stabilization at the inlet exit and core flow deceleration, while enhancing compression efficiency. The bump adjustment led to a total pressure recovery degradation of 8.5%. Future studies are needed to optimize bump geometry, which should investigate size, placement, and shape to minimize total pressure recovery losses and maintain stability across diverse operational conditions. Figure 23 illustrates the Mach number alignment between the original inlet designed for Mach 2.2 by S. Das and J. K. Prasad and the optimized inlet for Mach 3 introduced in this study, validating the redesigned geometry’s efficiency.

Table 4. Compact summary.

Case	Peak Ma at Exit	Total Pressure Recovery
4° Downward Ma 2.2 flight	1.9~2	96.4%
4° Downward Ma 3 flight	2.62	85%
5° Upward Mach 3 flight	2.51	90%
15° Upward Mach 3 flight	1.99	84.9%
15° Upward with bleed Mach 3 flight	1.99	86.8%
15° Upward with bleed + bump Mach 3 flight	2.1	79.4%

summarizes the evolution of the supersonic inlet the performance under critical working conditions. The baseline geometry (4° down deflection at Mach 2.2) achieves optimal stability, with a peak exit Mach number of 1.9–2.0 and 96.4% of the total pressure recovery. However, extending to Mach 3 caused a sharp performance loss, with a maximum Mach number of 2.62 and a total pressure recovery of 85%. Mach 3 was significantly enhanced by variable-geometry adjustments, where the Mach number decreased at the exit to 1.99 at a 15° upward deflection to restore flow stability as the baseline, and this gives a total pressure recovery penalty of 84.9%. The inclusion of a bleed slot also increases the total pressure recovery to 86.8% with remaining stable, and thus it is efficient in reducing unstart at high values of backpressure. However, the flow is stabilized with the incorporation of a 6 mm bump, which maximizes stabilization at the expense of high loss in the total pressure recovery, 79.4%.

5. Conclusions

This study addressed the operational limitations of a fixed-geometry supersonic inlet designed for Mach 2.2 by extending its performance to Mach 3 through variable-geometry modifications. By investigating upward cowl-lip deflection angles (5°~16°) and integrating a bleed system with a 6 mm semi-conical bump, this study demonstrated that a 15° upward deflection optimized shockwave alignment, compression efficiency, flow deceleration, and flow uniformity at the inlet exit at Mach 3, achieving an exit Mach number of 1.9, matching the baseline’s efficiency at Mach 2.2 while a 5° upward deflection showed the best values for total pressure recovery with a value of 0.9. The implementation of the bleed slot mitigated unstart risks under extreme backpressure for off-design conditions, while the bump enhanced flow stabilization despite an 8.5% drop in total pressure recovery, underscoring a stability–efficiency trade-off. These modifications enabled stable operation at Mach 3 and 15 km altitude, proving the inlet’s adaptability across a broader speed–altitude envelope.

The findings advance supersonic propulsion design by simplifying variable-geometry mechanisms and relying on localized cowl-lip adjustments rather than complex throat modifications and offering cost-effective solutions for wide speed range aerospace platforms. Additionally, the suboptimal bump geometry for Mach 3 necessitates further parametric studies.

This study demonstrated the following: (1) optimal operation at Mach 3 at a cowl deflection angle of 15° upward resulted in exit Mach 1.9 as in the baseline at Mach 2.2, while prioritizing flow uniformity; (2) the best total pressure recovery at Mach 3 was found at 5° upward deflection, with a value of 90%; (3) the elimination of the unstart while operating under extreme backpressure by implementing a bleed slot; and (4) a shock-stabilization procedure using a bump of 6 mm introduced a trade-off with the total pressure recovery. These adjustments together allowed the extension of the operational envelope to Mach 3 and 15 km altitude with efficiency comparable to that of the baseline.

Two-dimensional modeling can be computationally efficient for conducting the initial analysis of supersonic inlets. However, its inherent simplifications introduce serious limitations when modeling actual flow physics when compared to 3D modeling. Three-dimensional approaches can capture important phenomena, such as crossflow separation, vortex dynamics, and wall interactions, which introduce overly optimistic performance-scale predictions and an incomplete understanding of the limiting phenomenon. Although 2D modeling remains valuable during the initial concept phase, a supersonic inlet project making a transition to 3D modeling will achieve a more reliable design.

Future work should prioritize optimizing bump size, shape, and placement for Mach 3 with 15° deflection to maximize compression efficiency and ensure flow uniformity at the inlet exit. On the other hand, a 5° deflection minimized the total pressure losses. Cowl-lip deflection angle growth during acceleration should be investigated in future work. Developing adaptive bleed systems compatible with both Mach 2.2 and Mach 3 operations would enhance boundary layer control across speed regimes. Integrating experimental validation through wind tunnel testing is critical to bridging theoretical models with practical applications.