Modulation Recognition Algorithm for Long-Sequence, High-Order Modulated Signals Based on Mamba Architecture
Abstract
1. Introduction
- (1)
- Based on an in-depth analysis of the impact of long-sequence, high-order modulated signals on DL-AMR tasks, a hybrid architecture model named ConvMamba is proposed. This model cleverly combines the local feature extraction capability of a CNN with the long-sequence modeling capability of Mamba2 [24], constructing an efficient network model that can effectively capture long time dependencies.
- (2)
- Due to its soft-threshold denoising algorithm, the model can maintain more stable recognition performance in various complex environments, improving the robustness of the model; further, a feature fusion module is introduced into the model for sequence dimensionality reduction, achieving hierarchical feature representation and improving computational efficiency.
- (3)
- Experimental validation of the proposed model method was conducted on the Sig53 dataset. The results indicate that compared with traditional CNN-based models, ConvMamba achieves higher recognition accuracy while significantly reducing computational and storage requirements compared to Transformer-based models.
2. AMR Signal Model and DL-AMR Method Framework
2.1. AMR Signal Model
2.2. DL-AMR Basic Framework
3. ConvMamba Model Design
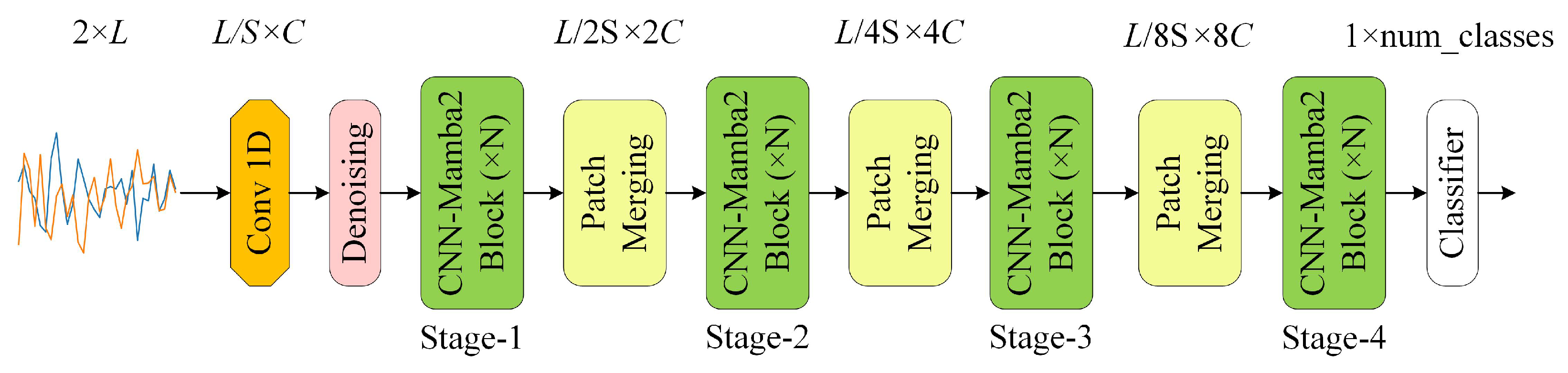
3.1. Overall Model Structure
3.2. Soft-Threshold Denoising
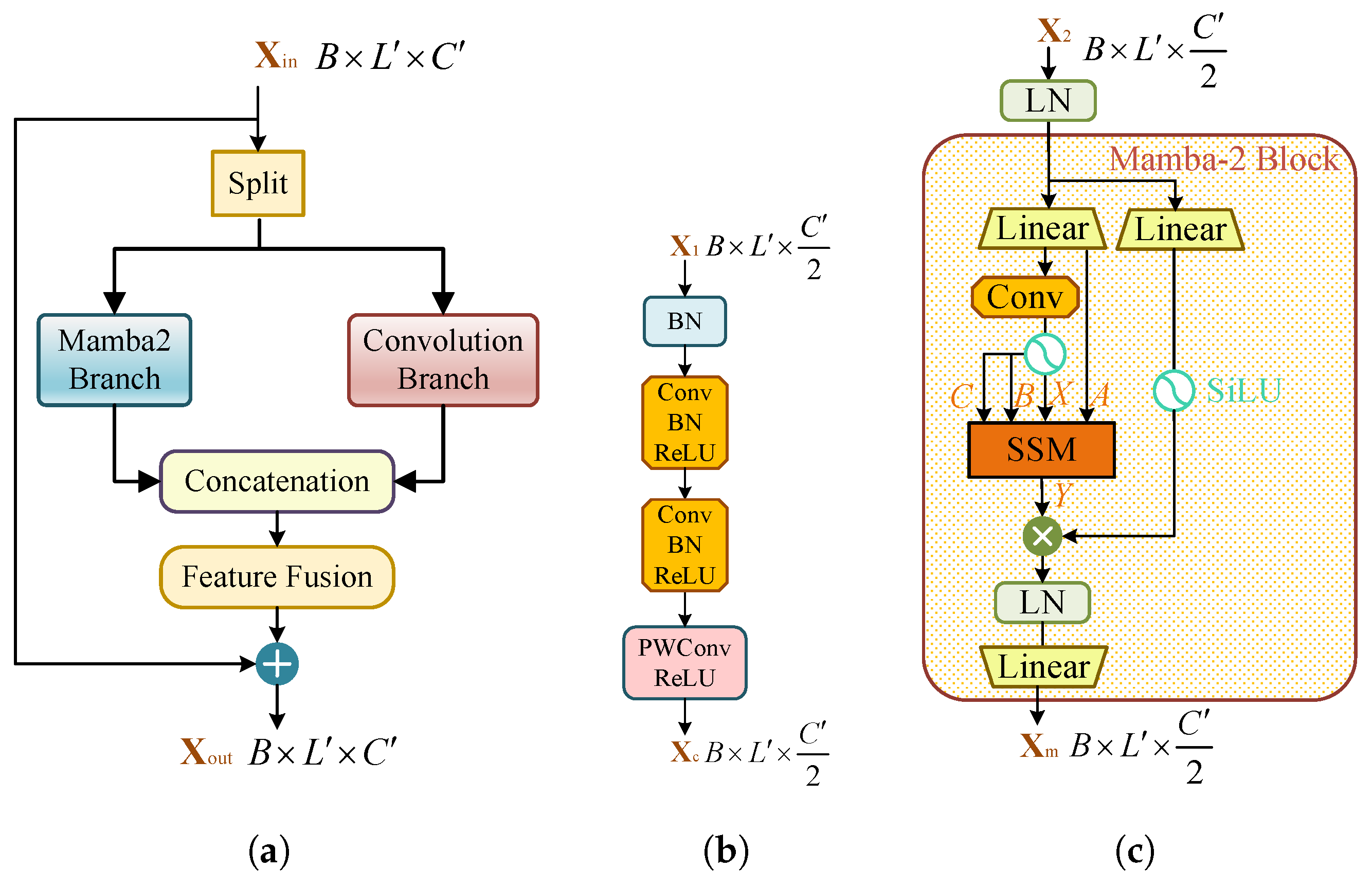
3.3. Feature Fusion Module
3.4. CNN–Mamba2 Module
4. Experiments and Results Analysis
4.1. Experimental Settings
- (1)
- Dataset
- (2)
- Experimental Environment and Parameter Settings
- (3)
- Benchmark Model Methods
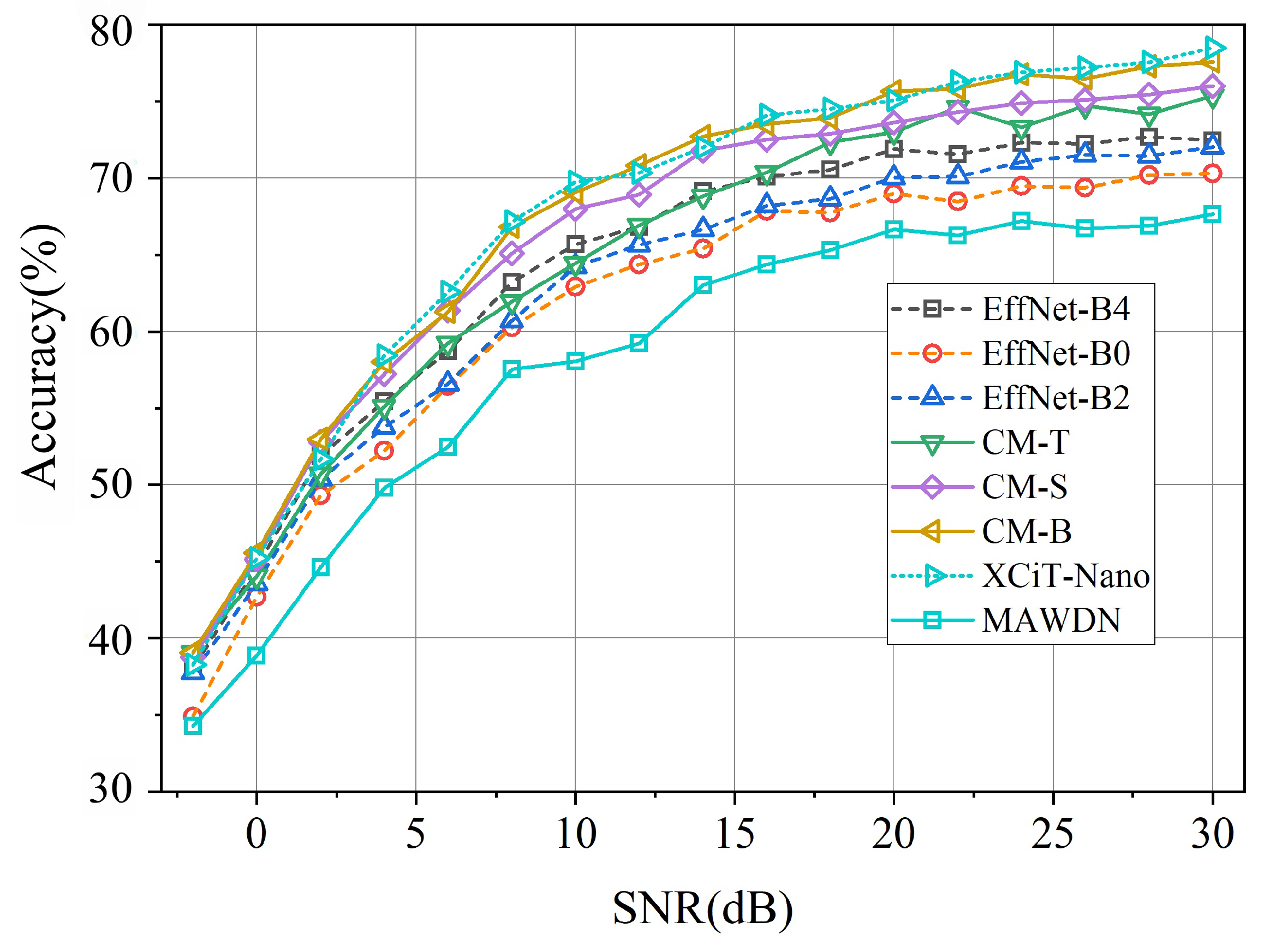
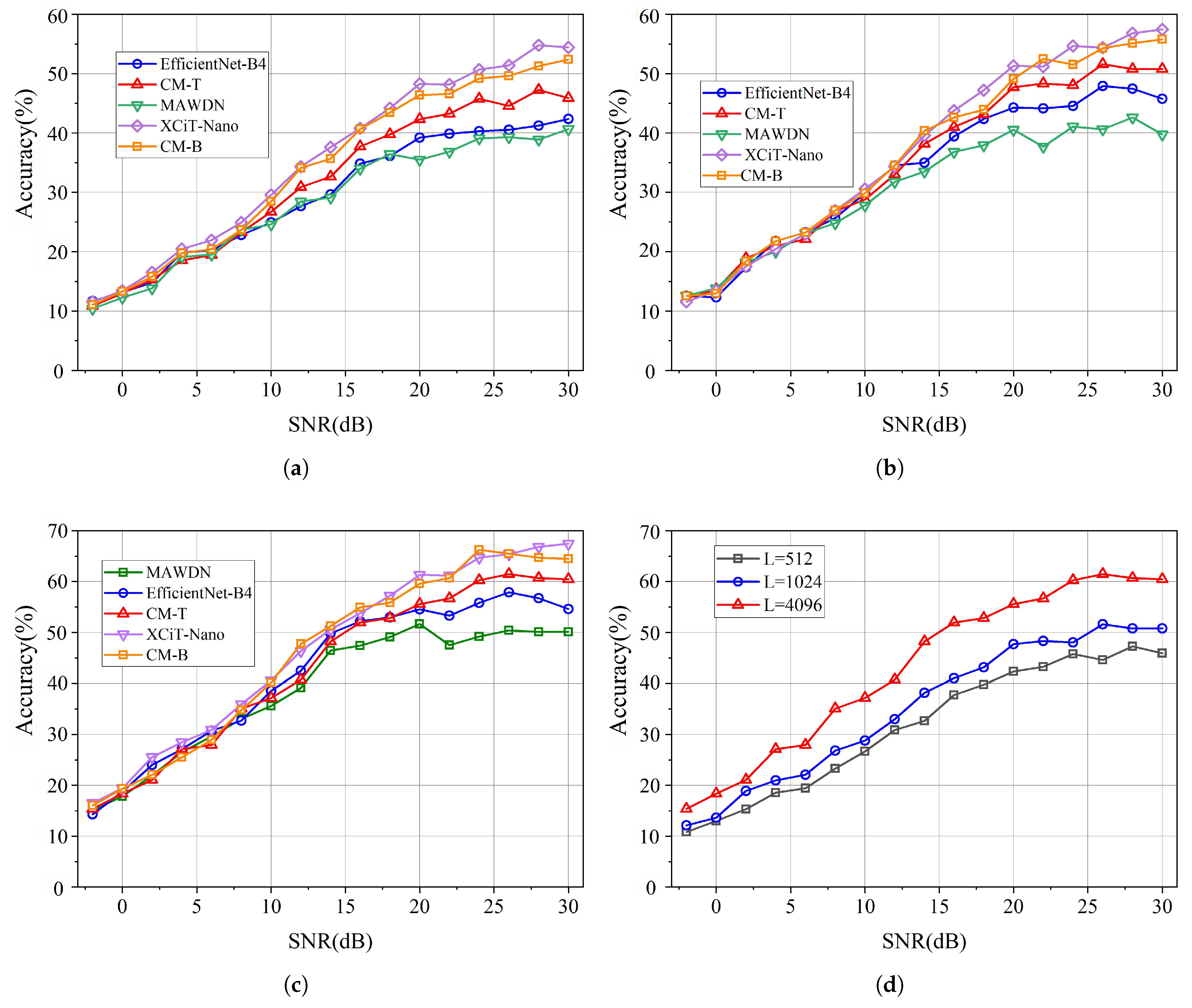
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huynh-The, T.; Pham, Q.V.; Nguyen, T.V.; Nguyen, T.T.; Ruby, R.; Zeng, M.; Kim, D.S. Automatic Modulation Classification: A Deep Architecture Survey. IEEE Access 2021, 9, 142950–142971. [Google Scholar] [CrossRef]
- Xie, W.; Hu, S.; Yu, C.; Zhu, P.; Peng, X.; Ouyang, J. Deep Learning in Digital Modulation Recognition Using High Order Cumulants. IEEE Access 2019, 7, 63760–63766. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.R.; Huang, Z.T. A Survey of Deep Transfer Learning in Automatic Modulation Classification. IEEE Trans. Cogn. Commun. Netw. 2025, 11, 1357–1381. [Google Scholar] [CrossRef]
- Peng, S.; Sun, S.; Yao, Y.D. A Survey of Modulation Classification Using Deep Learning: Signal Representation and Data Preprocessing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7020–7038. [Google Scholar] [CrossRef] [PubMed]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional Radio Modulation Recognition Networks. In Proceedings of the 17th International Conference on Engineering Applications of Neural Networks (EANN), Aberdeen, UK, 2–5 September 2016; pp. 213–226. [Google Scholar]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep Learning Models for Wireless Signal Classification with Distributed Low-Cost Spectrum Sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Dai, A.; Zhang, H.J.; Sun, H. Automatic Modulation Classification Using Stacked Sparse Auto-Encoders. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 248–252. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- West, N.E.; Shea, T.O. Deep Architectures for Modulation Recognition. In Proceedings of the 2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 6–9 March 2017; pp. 1–6. [Google Scholar]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A Spatiotemporal Multi-Channel Learning Framework for Automatic Modulation Recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Njoku, J.N.; Morocho-Cayamcela, M.E.; Lim, W. CGDNet: Efficient Hybrid Deep Learning Model for Robust Automatic Modulation Recognition. IEEE Netw. Lett. 2021, 3, 47–51. [Google Scholar] [CrossRef]
- Ma, J.T.; Qiu, T.S. Automatic Modulation Classification Using Cyclic Correntropy Spectrum in Impulsive Noise. IEEE Wirel. Commun. Lett. 2019, 8, 440–443. [Google Scholar] [CrossRef]
- Li, Y.B.; Shao, G.P.; Wang, B. Automatic Modulation Classification Based on Bispectrum and CNN. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 311–316. [Google Scholar]
- Teng, C.F.; Liao, C.C.; Chen, C.H.; Wu, A.Y.A. Polar Feature Based Deep Architectures for Automatic Modulation Classification Considering Channel Fading. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–28 November 2018; pp. 554–558. [Google Scholar]
- Kosuge, D.; Otsuka, H. Transmission Performance of OFDM-based 1024-QAM under Different Types of Multipath Fading Channels. In Proceedings of the 2021 IEEE VTS 17th Asia Pacific Wireless Communications Symposium (APWCS), Osaka, Japan, 30–31 August 2021. [Google Scholar]
- Khorov, E.; Levitsky, I.; Akyildiz, I.F. Current Status and Directions of IEEE 802.11be, the Future Wi-Fi 7. IEEE Access 2020, 8, 88664–88688. [Google Scholar] [CrossRef]
- Bauwelinck, J.; De Backer, E.; Melange, C.; Torfs, G.; Ossieur, P.; Qiu, X.-Z. A 1024-QAM Analog Front-End for Broadband Powerline Communication Up to 60 MHz. IEEE J. Solid-State Circuits 2009, 44, 1234–1245. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Xu, G.X.; Ma, C. A Novel Blind High-Order Modulation Classifier Using Accumulated Constellation Temporal Convolution for OSTBC-OFDM Systems. IEEE Trans. Circuits Syst. II 2022, 69, 3959–3963. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Cao, Y.; Li, G.; Li, X. MAMC—Optimal on Accuracy and Efficiency for Automatic Modulation Classification With Extended Signal Length. IEEE Commun. Lett. 2024, 28, 2864–2868. [Google Scholar] [CrossRef]
- He, J.; Xu, C.; Yin, C.; Zhang, Y. High-Order Modulation Recognition of Communication Signals Based on Feature Fusion. In Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 20–22 September 2024. [Google Scholar]
- Boegner, L.; Gulati, M.; Vanhoy, G.; Vallance, P.; Comar, B.; Kokalj-Filipovic, S.; Lennon, C.; Miller, R.D. Large Scale Radio Frequency Signal Classification. arXiv 2022, arXiv:2207.09918. [Google Scholar] [CrossRef]
- Cai, J.J.; Gan, F.M.; Cao, X.H.; Liu, W. Signal Modulation Classification Based on the Transformer Network. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1348–1357. [Google Scholar] [CrossRef]
- Ma, W.X.; Cai, Z.R.; Wang, C. A Transformer and Convolution-Based Learning Framework for Automatic Modulation Classification. IEEE Commun. Lett. 2024, 28, 1392–1396. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling With Selective State Spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Liu, M.; Guo, F.; Chen, Y.; Zhao, N. Blind Modulation Classification for OFDM in the Presence of Carrier Frequency Offsets. In Proceedings of the 2023 IEEE International Conference on Communications (ICC), Rome, Italy, 28 May–1 June 2023. [Google Scholar]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 4681–4690. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A. Transformers Are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality. arXiv 2024, arXiv:2405.21060. [Google Scholar] [CrossRef]
- Qin, X.; Jiang, W.; Gui, G.; Li, D.; Niyato, D.; Lu, J. Multilevel Adaptive Wavelet Decomposition Network Based Automatic Modulation Recognition: Exploiting Time-Frequency Multiscale Correlations. IEEE Trans. Cogn. Commun. Netw. 2025; early access. [Google Scholar]






| Parameter | Details |
|---|---|
| Generation | Python3 |
| Data format | I/Q, 2×4096 |
| Sample size | Training: ; Validation: |
| Modulation types | OOK, BPSK, 4PAM, 4ASK, QPSK, 8PAM, 8ASK, 8PSK, 16QAM, 16PAM, 16ASK, 16PSK, 32QAM, 32QAM_CROSS, 32PAM, 32ASK, 32PSK, 64QAM, 64PAM, 64ASK, 64PSK, 128QAM_CROSS, 256QAM, 512QAM_CROSS, 1024QAM, 2FSK, 2GFSK, 2MSK, 2GMSK, 4FSK, 4GFSK, 4MSK, 4GMSK, 8FSK, 8GFSK, 8MSK, 8GMSK, 16FSK, 16GFSK, 16MSK, 16GMSK, OFDM-64, OFDM-72, OFDM-128, OFDM-180, OFDM-256, OFDM-300, OFDM-512, OFDM-600, OFDM-900, OFDM-1024, OFDM-1200, OFDM-2048 |
| Noise | Additive White Gaussian Noise (AWGN) |
| Signal Impairments | Detailed Information | Probability |
|---|---|---|
| AWGN | SNR range: −2 dB to 30 dB | 100% |
| Random Pulse Shaping | Constellation diagrams: RRC filter, | 100% |
| GFSK/GMSK: | ||
| FSK/MSK: Low-pass filter with random passband | ||
| Phase Shift | Range: | 90% |
| Time Shift | Range: −32 to +32 I/Q samples | 90% |
| Frequency Shift | Range: −16% to 16% of the sampling rate | 70% |
| Rayleigh Fading | Constellation diagrams: RRC filter, | 50% |
| GFSK/GMSK: | ||
| FSK/MSK: Low-pass filter with random passband | ||
| I/Q Imbalance | Amplitude imbalance: −3 dB to +3 dB | 90% |
| Phase imbalance: to | ||
| DC offset: −0.1 to +0.1 dB | ||
| Random Resampling | Range: 0.75 to 1.5 | 50% |
| Layer Name | CM-T | CM-S | CM-B |
|---|---|---|---|
| Conv 1D | Number of channels → 64 | Number of channels → 128 | |
| Denoising | Soft - threshold denoising | ||
| Stage-1 | CNN–Mamba2 Block × 1 | CNN–Mamba2 Block × 2 | CNN–Mamba2 Block × 2 |
| Path-M | Number of channels → 128 | Number of channels → 256 | |
| Stage-2 | CNN–Mamba2 Block × 1 | CNN–Mamba2 Block × 2 | CNN–Mamba2 Block × 2 |
| Path-M | Number of channels → 256 | Number of channels → 512 | |
| Stage-3 | CNN–Mamba2 Block × 2 | CNN–Mamba2 Block × 4 | CNN–Mamba2 Block × 4 |
| Path-M | Number of channels → 512 | Number of channels → 768 | |
| Stage-4 | CNN–Mamba2 Block × 1 | CNN–Mamba2 Block × 2 | CNN–Mamba2 Block × 2 |
| Classifier | Global average pooling, linear layer, Softmax | ||
| Model | Parameters (M) | MACs (MMac) | Inference Time (s) | Accuracy (%) |
|---|---|---|---|---|
| EffNet-B0 | 3.93 | 537.04 | 0.023 | 61.3 |
| EffNet-B2 | 7.56 | 989.88 | 0.027 | 62.1 |
| EffNet-B4 | 17.21 | 2270 | 0.037 | 64.0 |
| CM-T | 2.04 | 841.6 | 0.025 | 64.9 |
| CM-S | 3.63 | 1460 | 0.043 | 66.1 |
| CM-B | 4.64 | 1980 | 0.086 | 67.1 |
| XCiT-Nano | 2.83 | 5130 | 0.186 | 67.3 |
| MAWDN | 0.60 | 345.61 | 0.047 | 58.3 |
| Modulation Type | CM-T | EffNet-B4 | Modulation Type | CM-T | EffNet-B4 |
|---|---|---|---|---|---|
| 64ASK | 0.362 | 0.335 | 1024QAM | 0.374 | 0.290 |
| 64PSK | 0.369 | 0.346 | OFDM-512 | 0.580 | 0.623 |
| 64PAM | 0.572 | 0.492 | OFDM-600 | 0.532 | 0.624 |
| 64QAM | 0.375 | 0.326 | OFDM-900 | 0.597 | 0.490 |
| 128QAM | 0.299 | 0.257 | OFDM-1024 | 0.551 | 0.506 |
| 256QAM | 0.212 | 0.194 | OFDM-1200 | 0.588 | 0.494 |
| 512QAM | 0.335 | 0.300 | OFDM-2048 | 0.648 | 0.587 |
| Modulation Type | Sequence Length | Modulation Type | Sequence Length | ||||
|---|---|---|---|---|---|---|---|
| 512 | 1024 | 4096 | 512 | 1024 | 4096 | ||
| 4PAM | 0.659 | 0.682 | 0.788 | 32PAM | 0.201 | 0.169 | 0.298 |
| 4ASK | 0.555 | 0.635 | 0.707 | 32ASK | 0.223 | 0.299 | 0.343 |
| QPSK | 0.595 | 0.607 | 0.686 | 32PSK | 0.147 | 0.184 | 0.204 |
| 8PAM | 0.424 | 0.467 | 0.599 | 64QAM | 0.141 | 0.261 | 0.291 |
| 8ASK | 0.414 | 0.356 | 0.506 | 64PAM | 0.391 | 0.411 | 0.418 |
| 8PSK | 0.352 | 0.402 | 0.460 | 64ASK | 0.285 | 0.227 | 0.281 |
| 16QAM | 0.300 | 0.410 | 0.485 | 64PSK | 0.192 | 0.110 | 0.286 |
| 16PAM | 0.287 | 0.309 | 0.447 | 128QAM_CROSS | 0.151 | 0.173 | 0.243 |
| 16ASK | 0.263 | 0.225 | 0.267 | 256QAM | 0.184 | 0.144 | 0.156 |
| 16PSK | 0.210 | 0.309 | 0.351 | 512QAM_CROSS | 0.229 | 0.265 | 0.375 |
| 32QAM | 0.230 | 0.382 | 0.489 | 1024QAM | 0.250 | 0.284 | 0.326 |
| 32QAM_CROSS | 0.342 | 0.409 | 0.465 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, E.; Li, R.; Ren, Y.; Lu, J.; Tang, L.; Huang, T. Modulation Recognition Algorithm for Long-Sequence, High-Order Modulated Signals Based on Mamba Architecture. Appl. Sci. 2025, 15, 9805. https://doi.org/10.3390/app15179805
Zhu E, Li R, Ren Y, Lu J, Tang L, Huang T. Modulation Recognition Algorithm for Long-Sequence, High-Order Modulated Signals Based on Mamba Architecture. Applied Sciences. 2025; 15(17):9805. https://doi.org/10.3390/app15179805
Chicago/Turabian StyleZhu, Enguo, Ran Li, Yi Ren, Jizhe Lu, Lu Tang, and Tiancong Huang. 2025. "Modulation Recognition Algorithm for Long-Sequence, High-Order Modulated Signals Based on Mamba Architecture" Applied Sciences 15, no. 17: 9805. https://doi.org/10.3390/app15179805
APA StyleZhu, E., Li, R., Ren, Y., Lu, J., Tang, L., & Huang, T. (2025). Modulation Recognition Algorithm for Long-Sequence, High-Order Modulated Signals Based on Mamba Architecture. Applied Sciences, 15(17), 9805. https://doi.org/10.3390/app15179805






