Equivalent Self-Noise Suppression of DAS System Integrated with Multi-Core Fiber Based on Phase Matching Scheme
Abstract
1. Introduction
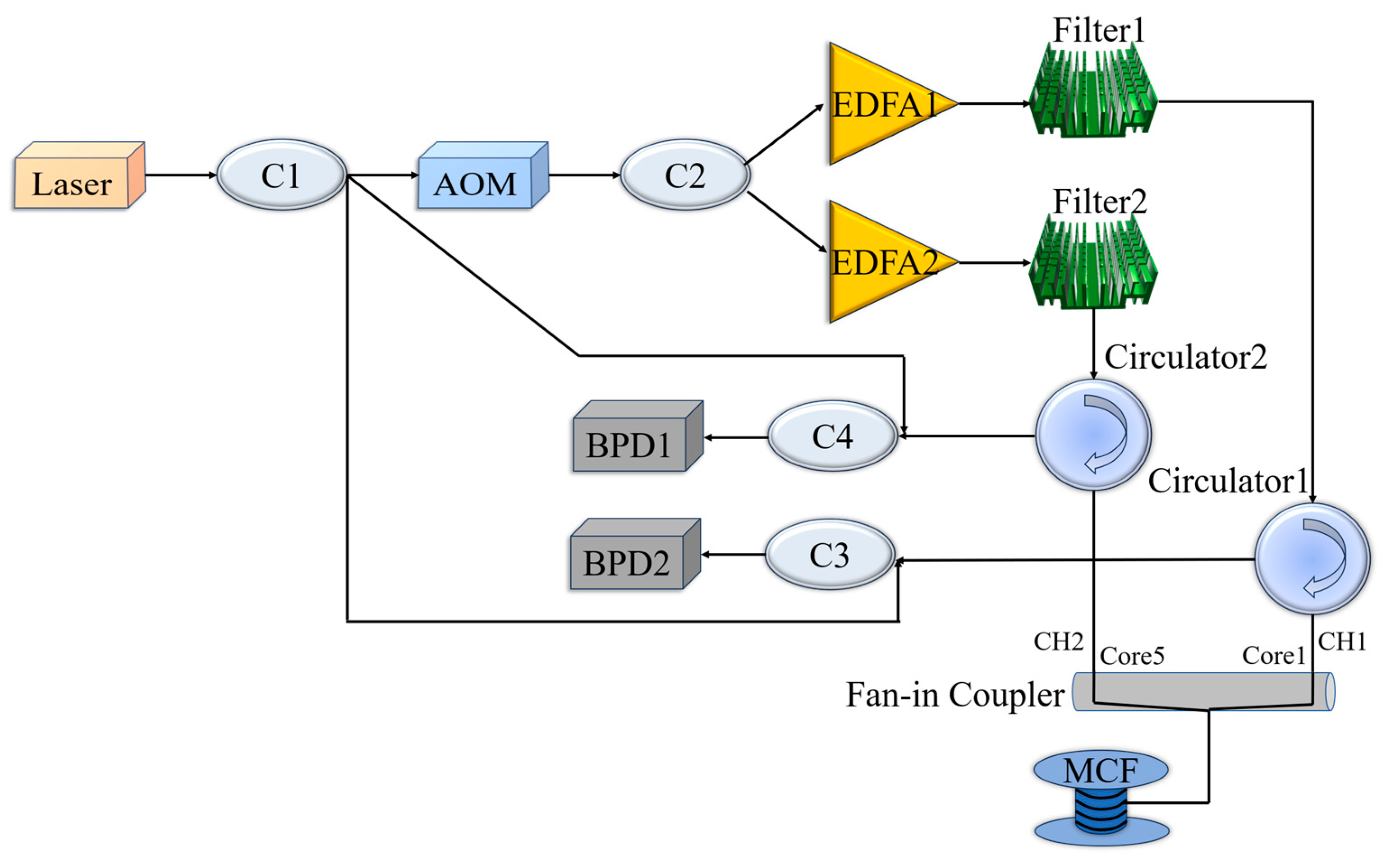
2. Methods
3. Results
3.1. Subsection SNR Gain Analysis with Signal Superposition of Seven Cores
3.2. SNR Gain Analysis After Noise Decorrelation
3.3. Suitability Analysis for Broadband Signals
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, W.; Cheng, G.; Xing, G.; Liu, B. Near-field target localization based on the distributed acoustic sensing optical fiber in shallow water. Opt. Fiber Technol. 2023, 75, 103198. [Google Scholar] [CrossRef]
- Wang, Z.N.; Zhang, L.; Wang, S.; Xue, N.; Peng, F.; Fan, M.; Sun, W.; Qian, X.; Rao, J.; Rao, Y. Coherent Φ-OTDR based on I/Q demodulation and homodyne detection. Opt. Exp. 2016, 24, 853–858. [Google Scholar] [CrossRef]
- Peng, Z.; Jian, J.; Wen, H.; Gribok, A.; Wang, M.; Liu, H.; Huang, S.; Mao, Z.-H.; Chen, K.P. Distributed fiber sensor and machine learning data analytics for pipeline protection against extrinsic intrusions and intrinsic corrosions. Opt. Exp. 2020, 28, 27277–27292. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Liu, F.; Wang, H.; Li, S.; Gan, W.; Jiang, R. Lateral positioning of vibration source for underground pipeline monitoring based on ultra-weak fiber Bragg grating sensing array. Measurement 2021, 172, 108892. [Google Scholar] [CrossRef]
- Du, Y.; Shang, Y.; Wang, C.; Yi, J.; Sun, M.; Yang, J.; Zhao, Y.; Ni, J. Intrusive and non-intrusive microflow measurement based on distributed optical fiber acoustic sensing. Measurement 2023, 210, 112513. [Google Scholar] [CrossRef]
- Li, T.; Fan, C.; Li, H.; He, T.; Qiao, W.; Shi, Z.; Yan, Z.; Liu, C.; Liu, D.; Sun, Q. Nonintrusive distributed flow rate sensing system based on flow-induced vibrations detection. IEEE Trans. Instrum. Meas. 2021, 70, 7001808. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Dawe, T.C.; Ajo-Franklin, J.B. Illuminating seafloor faults and sea dynamics with dark fiber distributed acoustic sensing. Science 2019, 366, 1103–1107. [Google Scholar] [CrossRef]
- Sladen, A.; Rivet, D.; Ampuero, J.P.; De Barros, L.; Hello, Y.; Calbris, G.; Lamare, P. Distributed sensing of earthquakes and sea-solid Earth interactions on seafloor telecom cables. Nat. Commun. 2019, 10, 5777. [Google Scholar] [CrossRef]
- Williams, E.F.; Fernández-Ruiz, M.R.; Magalhaes, R.; Vanthillo, R.; Zhan, Z.; González-Herráez, M.; Martins, H.F. Distributed sensing of microseisms and teleseisms with submarine dark fibers. Nat. Commun. 2019, 10, 5778. [Google Scholar] [CrossRef]
- Chen, J.F.; Li, H.; Xiao, X.; Fan, C.; Wen, P.; Yan, Z.; Sun, Q. Fully Continuous Fiber-Optic Hydrophone Streamer with Small Channel Spacing for Marine Seismic Acquisition. In Proceedings of the 27th International Conference on Optical Fiber Sensors, Alexandria, VA, USA, 29 August–2 September 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. W4.45. [Google Scholar]
- Currenti, G.; Allegra, M.; Cannavò, F.; Jousset, P.; Prestifilippo, M.; Napoli, R.; Sciotto, M.; Di Grazia, G.; Privitera, E.; Palazzo, S.; et al. Distributed dynamic strain sensing of very long period and long period events on telecom fiber-optic cables at Vulcano, Italy. Sci. Rep. 2023, 13, 4641. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Sun, G.; Bao, W.; You, Z.; Meng, F.; Dong, M. Structural deformation monitoring of flight vehicles based on optical fiber sensing technology: A review and future perspectives. Engineering 2022, 16, 39–55. [Google Scholar] [CrossRef]
- Li, D.; Yi, D.; Zhou, X.; Chen, X.; Geng, Y.; Li, X. Multisource threatening event recognition scheme targeting drone intrusion in the fiber optic DAS system. IEEE Sens. J. 2024, 24, 32185–32195. [Google Scholar] [CrossRef]
- Kutuzyan, A.; Sukiasyan, M.; Kirakosyan, A.; Avetisyan, V. Self-Formation of temporal dark solitons in a single-mode optical fiber. J. Contemp. Phys. (Armen. Acad. Sci.) 2025, 59, 238–243. [Google Scholar] [CrossRef]
- Nadav, A.; Moshe, T.; Avishay, E. Fiber-optic sensor array for distributed underwater ultrasound sensing. J. Lightw. Technol. 2024, 42, 945–954. [Google Scholar]
- Redding, B.; Murray, M.J.; Donko, A.; Beresna, M.; Masoudi, A.; Brambilla, G. Low-noise distributed acoustic sensing using enhanced backscattering fiber with ultralow-loss point reflectors. Opt. Exp. 2020, 28, 14638–14647. [Google Scholar] [CrossRef]
- Lavrov, V.S.; Plotnikov, M.Y.; Aksarin, S.M.; Efimov, M.E.; Shulepov, V.A.; Kulikov, A.V.; Kireenkov, A.U. Experimental investigation of the thin fiber-optic hydrophone array based on fiber Bragg gratings. Opt. Fiber Technol. 2017, 34, 47–51. [Google Scholar] [CrossRef]
- Yan, G.; Wang, D.; Long, J.; Jiang, L.; Gong, Y.; Ran, Z.; Rao, Y. High-performance towing cable hydrophone array with an improved ultra-sensitive fiber-optic distributed acoustic sensing system. Opt. Exp. 2023, 31, 25545–25556. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, H.; Xiao, X.; Fan, C.; Yan, B.; Zhang, S.; Liu, H.; Ai, K.; Yan, Z.; Sun, Q. Fully distributed hydroacoustic sensing based on ultra-highly sensitive and lightweight fiber-optic hydrophone cable. Opt. Lasers Eng. 2023, 169, 107734. [Google Scholar] [CrossRef]
- Lu, B.; Wu, B.; Gu, J.; Yang, J.; Gao, K.; Wang, Z.; Ye, L.; Ye, Q.; Qu, R.; Chen, X.; et al. Distributed optical fiber hydrophone based on Φ-OTDR and its field test. Opt. Exp. 2021, 29, 3147–3162. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Li, J.; Shen, X.; Zhao, Z.; Dang, H.; Zou, D.; Zhang, A.; Wang, P.; Zhao, Z.; et al. Fading suppression and noise reduction of a DAS system integrated with multi-core fiber. Opt. Exp. 2024, 32, 26793–26807. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Xiong, F.; Zhang, X.; Chen, X.; Ding, Z.; Zheng, Y.; Wang, F.; Chen, M. A space-division multiplexing method for fading noise suppression in the Φ-OTDR system. Sensors 2021, 21, 1694. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, M.; Wang, L.; Guo, N.; Tam, H.-Y.; Lu, C. Distributed vibration sensor based on space-division multiplexed reflectometer and interferometer in multicore fiber. J. Lightw. Technol. 2018, 36, 5764–5772. [Google Scholar] [CrossRef]
- Guan, Y.Z.; Wan, S.P.; Cheng, Y.N.; Wan, D.H.; Yu, J.S. Research on denoising algorithm of phase-sensitive optical time domain reflectometer based on moving variance average algorithm. Chin. J. Sci. Instrum. 2022, 43, 233–240. [Google Scholar]
- Li, Z.; Qin, Z.G.; Liu, Z.J. Phase-sensitive optical time domain reflectometry assisted by total variation techniques. Acta Opt. Sin. 2021, 41, 1706001. [Google Scholar] [CrossRef]
- Zabihi, M.; Chen, Y.; Zhou, T.; Liu, J.; Shan, Y.; Meng, Z.; Wang, F.; Zhang, Y.; Zhang, X.; Chen, M. Continuous fading suppression method for Φ-OTDR systems using optimum tracking over multiple probe frequencies. J. Lightw. Technol. 2019, 37, 3602–3610. [Google Scholar] [CrossRef]
- Xue, N.; Fu, Y.; Lu, C.; Xiong, J.; Yang, L.; Wang, Z. Characterization and compensation of phase offset in Φ-OTDR with heterodyne detection. J. Lightw. Technol. 2018, 36, 5481–5487. [Google Scholar] [CrossRef]
- Zhong, Z.; Zou, N.; Zhang, X.; Li, M. Noise suppression of phase signal in phase-optical time domain reflectometer. Chin. J. Lasers 2024, 51, 0506005. [Google Scholar]
- Pan, Z.Q.; Liang, K.Z.; Ye, Q.; Cai, H.; Qu, R.; Fang, Z. Phase-Sensitive OTDR System Based on Digital Coherent Detection. In Proceedings of the 2011 Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 13–16 November 2011; Volume 8311, p. 83110S-83110S-6. [Google Scholar]
- Gu, J.F.; Lu, B.; Yang, J.Q.; Wang, Z.Y.; Ye, L.; Ye, Q.; Qu, R.H.; Cai, H.W. Multi-core fiber distributed acoustic sensing. Acta Opt. 2021, 41, 0706003. [Google Scholar]
- Robert, J.U. Principle of Underwater Sound; Company of McGraw Hill Books: New York, NY, USA, 1990. [Google Scholar]
- Li, H. Highly-Sensitive and Broadband Optical Fiber Distributed Acoustic Sensing Technology and Its Applications. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar] [CrossRef]








| Device | Parameters | Value |
|---|---|---|
| Laser | Central wavelength/nm | 1550.12 |
| Line width/kHz | ≤1.5 | |
| Relative intensity noise/(dB/Hz) | ≤120 | |
| AOM | Frequency shift/MHz | 80 |
| Insertion loss/dB | <3 | |
| EDFA | Input optical power peak/dBm | 1 |
| Output optical power peak/mW | 1000 | |
| Noise coefficient/dB | 4.5 | |
| Filter | Operating wavelength/nm | 900–1700 |
| Spectral resolution/nm | 2–13 | |
| Average light transmittance/% | >90 | |
| BPD | Bandwidth/MHz | 100 |
| Responsivity/(A/W) @ 1550 nm | ≥0.95 | |
| Transimpedance gain/(KV/A) | ≥30 |
| Parameters | Value |
|---|---|
| Single core length/m | 2000 |
| PZT position/m | 1978–1980 |
| Fiber diameter/μm | 245 |
| Core diameter/μm | 8 |
| Core spacing/μm | 41.5 |
| Mold field diameter/μm | 9.5 |
| Attenuation/(dB/km) @ 1550 nm | ≤0.30 |
| PZT Sinusoidal Frequency/Hz | PZT Amplitude /V | Before Signal Superposition | After Signal Superposition | Gain | Mean Gain |
|---|---|---|---|---|---|
| 100 | 5 | 36.05 | 42.41 | 6.36 | 6.32 |
| 200 | 5 | 50.86 | 57.18 | 6.32 | |
| 500 | 5 | 47.24 | 53.52 | 6.28 | |
| 800 | 2 | 30.98 | 37.33 | 6.35 | |
| 1000 | 2 | 33.66 | 40.02 | 6.36 |
| PZT Sinusoidal Frequency /Hz | PZT Amplitude /V | Before Noise Decorrelating | After Noise Decorrelating | ||
|---|---|---|---|---|---|
| Gain | Average Gain | Gain | Average Gain | ||
| 100 | 5 | 6.36 | 6.32 | 8.26 | 8.26 |
| 200 | 5 | 6.32 | 8.33 | ||
| 500 | 5 | 6.28 | 8.21 | ||
| 800 | 2 | 6.35 | 8.21 | ||
| 1000 | 2 | 6.36 | 8.30 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gu, H.; Wang, P.; Liu, W.; Yao, G.; Pang, Y.; Wu, J.; Xu, D.; Wu, S.; Huang, J.; et al. Equivalent Self-Noise Suppression of DAS System Integrated with Multi-Core Fiber Based on Phase Matching Scheme. Appl. Sci. 2025, 15, 9806. https://doi.org/10.3390/app15179806
Wang J, Gu H, Wang P, Liu W, Yao G, Pang Y, Wu J, Xu D, Wu S, Huang J, et al. Equivalent Self-Noise Suppression of DAS System Integrated with Multi-Core Fiber Based on Phase Matching Scheme. Applied Sciences. 2025; 15(17):9806. https://doi.org/10.3390/app15179806
Chicago/Turabian StyleWang, Jiabei, Hongcan Gu, Peng Wang, Wen Liu, Gaofei Yao, Yandong Pang, Jing Wu, Dan Xu, Su Wu, Junbin Huang, and et al. 2025. "Equivalent Self-Noise Suppression of DAS System Integrated with Multi-Core Fiber Based on Phase Matching Scheme" Applied Sciences 15, no. 17: 9806. https://doi.org/10.3390/app15179806
APA StyleWang, J., Gu, H., Wang, P., Liu, W., Yao, G., Pang, Y., Wu, J., Xu, D., Wu, S., Huang, J., & Xu, C. (2025). Equivalent Self-Noise Suppression of DAS System Integrated with Multi-Core Fiber Based on Phase Matching Scheme. Applied Sciences, 15(17), 9806. https://doi.org/10.3390/app15179806






