Abstract
In urban underground construction, Earth Pressure Balance (EPB) tunneling faces complex geological uncertainties and dynamic operational risks. Traditional safety management approaches often struggle under such conditions. This paper proposes an integrated safety resilience assessment framework for EPB tunneling that combines an entropy-weighted TOPSIS method, the Analytic Network Process (ANP), and an extension cloud model to capture interdependencies and uncertainties. A hierarchical indicator system with four primary dimensions (stability, redundancy, efficiency, and fitness) is constructed. The entropy-TOPSIS algorithm provides objective initial weights and scenario ranking, while ANP models the feedback relationships among criteria. The extension cloud model quantifies fuzziness in expert judgments and converts qualitative assessments into probabilistic resilience ratings. The methodology is applied to a case study of the EPB shield tunnel section of Jinan Metro Line 6 (China). The section’s resilience is classified as a medium level, which agrees with expert evaluation. The results demonstrate that the proposed approach yields accurate and robust safety resilience evaluations, supporting data-driven decision-making. This framework offers a quantitative tool for resilience-based safety management of shield tunneling projects, providing guidance for shifting from traditional risk control toward a resilience-enhancement strategy.
1. Introduction
With the continuous acceleration of urbanization and increasing utilization of underground space, urban tunnel engineering has exhibited a development trend toward larger scales, deeper depths, and greater complexity [1]. The EPB shield method is widely used to address complex geology and control surface settlement [2]. Earth Pressure Balance (EPB) tunneling relies on the use of conditioned soil within the excavation chamber to balance the earth and water pressures at the tunnel face. By maintaining this equilibrium, ground settlement can be minimized and tunnel stability ensured. The method is particularly suitable for the soft and mixed ground conditions commonly encountered in urban areas. Compared with other tunneling techniques, EPB shields offer distinct advantages in adapting to variable strata, operating in constrained environments, and achieving strict control of surface deformation.
The structural configuration of an EPB shield (Figure 1) illustrates its main components, including the cutterhead, excavation chamber, screw conveyor, and segment erector. Its operation follows a cyclic process: excavation is performed by the cutterhead, chamber pressure is controlled through conditioned soil, muck is discharged by the screw conveyor, and lining segments are installed to provide ground support. This closed-loop mechanism ensures continuous advance while maintaining face stability and construction safety in complex environments.
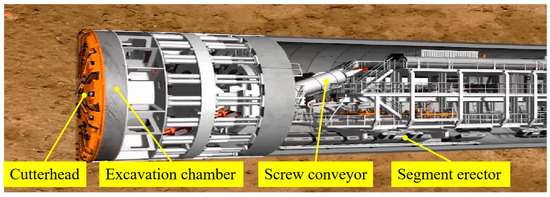
Figure 1.
A schematic diagram of the EPB shield.
The performance of EPB shields is significantly influenced by geological and hydrogeological conditions [3,4]. In homogeneous ground, torque and thrust distributions are relatively uniform, allowing smooth excavation. In contrast, heterogeneous strata containing sand, gravel, or abrupt interfaces induce uneven torque distribution and accelerate cutterhead wear. Soil conditioning with foam or polymer additives is typically employed to enhance plasticity, reduce friction, and improve muck flowability. Nevertheless, uncertainties in ground parameters such as cohesion, permeability, and abrasivity remain critical challenges. These uncertainties strongly affect penetration resistance, face support pressure, and torque demand, thereby introducing risks of instability and ground disturbance. Such risk events not only threaten construction progress and worker safety but may also trigger secondary hazards, causing severe disruptions to the stability of urban systems.
Under this context, the establishment of a systematic, dynamic, and intelligent safety risk management system for EPB construction is recognized as the critical pathway to ensure project safety and resilient operations. Whole-process perception, accurate assessment, and closed-loop control of multi-source risks are enabled through this framework. Particularly, the introduction of resilience management theory enables enhanced system robustness and recoverability [5,6]. Redundant fault-tolerant mechanisms and flexible response strategies are implemented at critical stages. According to Safety-II theory [7], system resilience is categorized into four capacities: risk identification, impact absorption, rapid recovery, and continuous evolution. Drawing on the resilience theory frameworks proposed by Leveson and Hollnagel [8,9], EPB construction safety resilience is defined in this study as the ability of construction systems to maintain operational stability (load-bearing capacity) and post-failure functional recoverability (restoration capacity) when exposed to multi-source coupled risk disturbances. This concept serves as a critical indicator for evaluating environmental adaptability and risk response efficiency in complex construction systems.
Current safety management approaches for EPB tunneling can generally be categorized into two types: qualitative analyses and quantitative modeling. Qualitative methods include the Analytic Hierarchy Process (AHP) [10], Fuzzy Comprehensive Evaluation (FCE) [10], Event Tree Analysis (ETA) [11], Failure Modes and Effects Analysis (FMEA) [12], Interval Fuzzy Evaluation (IFE) [13], and Hazard and Operability Analysis (HAZOP) [14]. For example, Zhao [15] combined AHP and fuzzy evaluation to assess the risk levels of shield tunneling in karst areas and proposed measures to mitigate construction risks. Lyu [16,17,18,19] investigated the influence of external environmental factors on metro system safety and developed a multi-criteria framework using fuzzy AHP to evaluate metro construction risks. Qin [20] proposed a hybrid decision model to address fuzzy uncertainty in risk assessment and applied it to dynamic risk evaluation in metro construction. Lyu [21] addressed the difficulty of constructing consistent judgment matrices in FAHP and applied the improved approach to risk assessment of shield tunneling in Jinan Metro. Hamidi [11] established a risk evaluation model based on event tree analysis and conducted a qualitative assessment of the risks associated with shield tunneling beneath the Han River. These methods demonstrate advantages in preliminary risk identification and system classification; however, they rely heavily on expert judgment, which may lead to biases in highly coupled systems. Moreover, their applicability is limited when dealing with multi-source dynamic data, nonlinear interactions, and complex engineering contexts.
In contrast, quantitative risk assessment methods are strengthened through mathematical modeling, which enhances the objectivity and systematic nature of the analysis and has therefore become a research focus. Bayesian Networks (BN) [22], with their causal reasoning mechanism, effectively capture the probabilistic dependencies among risk factors, supporting quantitative inference and state updating. For instance, Chung [23] developed a BN-based risk assessment model for shield tunneling that incorporated geological risk factors and tunnel boring machine (TBM) types, thereby addressing some of the limitations inherent in TBM construction methods. Dynamic Bayesian Networks (DBN) [24] further introduce temporal variables, improving the capacity to model the evolution of risks. For example, Xu [25] proposed a three-stage dynamic assessment model for shield tunneling safety risks based on an improved DBN, which overcomes the limitations of static methods in representing dynamic risk evolution and strengthens the expression of causal relationships. Similarly, Li [26] adopted a data-driven and knowledge-graph-based approach by developing a hybrid entity–relation extraction model (BBi-MA-DCGCN) to automatically identify multi-source heterogeneous risk factors and their couplings from tunneling accident texts. This method reduces dependence on expert judgment and addresses previous challenges in revealing complex semantic couplings and defining system boundaries.
However, such methods generally rely on high-quality prior knowledge and large volumes of observational data, and their predictive stability declines markedly when data are missing or incomplete. Machine learning techniques, such as Random Forest (RF) and Gaussian Process Regression (GPR) [27,28], demonstrate strong performance in handling high-dimensional and nonlinear data. For example, Huang [29] applied a backpropagation (BP) neural network to predict shield tunneling parameters in karst strata, which supported the selection of appropriate parameters to ensure safe and efficient construction. Although machine learning and other AI-based approaches, such as Long Short-Term Memory networks (LSTM) and Convolutional Neural Networks (CNN), have achieved notable progress in tunnel risk prediction and show advantages in nonlinear modeling, they also suffer from limited interpretability, strong dependence on large labeled datasets, and weak robustness when dealing with incomplete data. In particular, in complex systems such as shield tunneling, expert knowledge and fuzzy judgment remain indispensable sources of information.
Building on this basis, attention is gradually shifted toward the Analytic Network Process (ANP) method [30]. Structural modeling advantages and feedback mechanism representation capabilities are emphasized. The assumption of mutual independence among indicators in traditional Analytic Hierarchy Process (AHP) [31] is overcome by ANP. Multidimensional coupling relationships and causal feedback pathways among risk factors are systematically characterized. This approach is applicable to multi-criteria decision support for complex structural problems. Traditional ANP is dependent on expert qualitative scoring for weighting matrix establishment [32]. Uncertainties, fuzziness, and dynamic adjustment capabilities in indicator weights are inadequately expressed. Adaptation capability to complex construction scenarios is consequently constrained. To address these limitations, the extension cloud model has been integrated into the ANP framework. Digital characteristics (expectation, entropy, and hyper-entropy) are introduced for quantitative conversion of expert fuzzy judgments into probabilistic expressions [33,34]. Dynamic weight distribution correction is achieved through entropy optimization mechanisms. This enables the establishment of a bidirectional mapping weight adjustment model between qualitative expert judgments and quantitative dimensions. Consequently, the ANP combined with the extension cloud model achieves significantly improved capability in representing inherent uncertainties in indicator weights and capturing complex nonlinear feedback mechanisms within the risk network.
Existing studies are predominantly focused on safety risk identification and typical failure mode analysis in EPB shield tunneling [35]. A resilience assessment framework is constructed from a system evolution perspective. Predictive, preparatory, adaptive, resistant, and rapid recovery capacities of construction systems are further enhanced. This approach supports the shift from reactive risk management to proactive resilience building [36]. This study is focused on system safety resilience in EPB shield tunneling under complex environments. A resilience theory framework and structured decision modeling approaches are employed. An EPB shield tunneling resilience index system is established. An integrated evaluation method combining ANP and extension cloud model is proposed for safety resilience assessment. A typical EPB tunnel project in China is selected for empirical validation. The paper structure is organized as follows: Section 2 is dedicated to theoretical connotation and indicator system construction rationale of EPB shield tunneling safety resilience. Section 3, Section 4, Section 5 and Section 6 are allocated to methodology description, engineering application, results analysis and discussion, and research conclusions, respectively.
2. Safety Resilience in EPB Construction
Within the context of EPB tunneling, safety resilience describes how the system sustains performance, mitigates impacts, adapts its response, and regains normal operation under unexpected hazards or operational interferences. The system can be restored to the previous state by safety resilience. For example, safety resilience is demonstrated by the system’s capacity to absorb and mitigate the effects of a sudden risk or disruption. It also involves preventing subsequent risks or incidents and improving the system’s flexibility to deal with unpredictable occurrences. This is achieved through analyzing past accidents, learning from them, and using those lessons to optimize the system’s performance [37]. The safety resilience in EPB construction is shown by the concept curve in Figure 2. The stage from t0 to t1 marks the system’s initial safe state being affected by the emergence of risk or disturbance (Figure 2). The system faces risk impact and disturbance as its capacity to withstand such challenges surpasses a critical threshold at time t1. The system confronts continuously disturbances and risk shocks during stage t1~t2 and its capacity to mitigate the risks is progressively diminished which may result in accidents, damage to the system, and ultimately system breakdown (Figure 2). By introducing appropriate emergency actions in the t2~t4 stage, safety can be restored, while the period between t3 and t4 marks the recovery process (Figure 2). The system can be restored to the original security condition (X0) after the recovery t4~t5 stage. It can also establish a better security condition (X1) than the original condition (X0) to improve its safety and resilience. Inadequate management and learning ability may lead to the system with inability to restore at the original security condition (X2) (Figure 2).
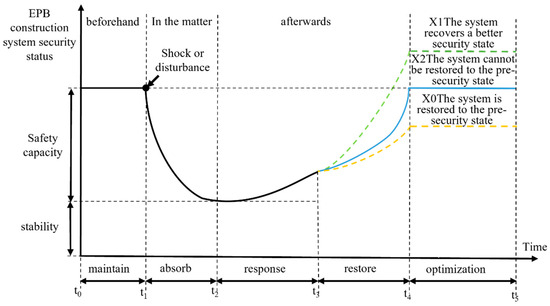
Figure 2.
The resilience concept curve of the safety system in EPB construction.
The safety system of the EPB construction is divided into five subsystems such as Personnel, equipment, environment, management and material (Figure 3). The process of the safety system’s resilience performance is concluded, and the resilience features regularity model is established based on the mutual interaction among five subsystems of the EPB construction. Stability, redundancy, efficiency and fitness are four characteristics to describe the resilience performance of the system. The stability is the innate characteristic of the system to resist external risk impacts and disruptions, ensuring that the system can uphold its safety condition to the greatest extent possible when confronted with risk occurrences and accidents. The redundancy degree functions as a backup mechanism, enabling the system to maintain normal operation even after suffering substantial losses or impairment of the initial equipment and machinery. System efficiency becomes the critical measure for assessing how quickly it can react when confronted with unfavorable events and the extent to which losses can be mitigated. Fitness represents the capacity of the system for absorbing accidents and overcoming deficiencies.
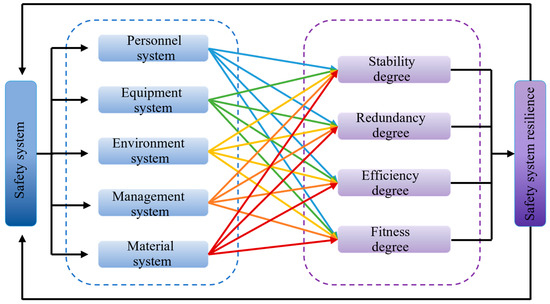
Figure 3.
Conceptual model of resilience of safety system in EPB construction.
In the initial phase, the system is maintained in a stable and secure condition. When risks or disruptions arise, the condition of the system is assessed through resilience attributes including stability, redundancy, efficiency, and fitness. As the system’s capacity to absorb risk diminishes, the five subsystems (personnel, equipment, environment, management, and material) collaborate to implement emergency actions. Through recovery, the system stands a chance of being brought back to its former safe condition or even achieving a safer state compared to what it was initially [38]. Alternatively, various factors could lead to the system facing damage and result it into an unsafe condition.
3. Methodology
A comprehensive evaluation framework has been proposed in this study to assess the resilience of the EPB shield tunneling construction system. This framework integrates the Entropy Weight TOPSIS Method, ANP Model, and Extension Cloud Model, aiming to evaluate the system from multiple dimensions and levels. The design of the methodology framework considers the interactions and uncertainties among the evaluation indices, and is implemented through the following steps.
Firstly, the Entropy Weight TOPSIS Method is employed to assign weights to the evaluation indices and perform the preliminary comprehensive assessment of different construction schemes. This method calculates the entropy of each index, objectively reflecting the relative importance of each index. In this stage, the weights of all evaluation indices are determined based on the data, avoiding the interference of expert subjectivity.
Secondly, based on the preliminary results from the Entropy Weight TOPSIS Method, the ANP Model is used to further analyze the interdependencies among the evaluation indices. The ANP Model reveals the complex feedback mechanisms and interrelations between the indices [39]. By constructing a network structure and hierarchical relationships, the weight distribution is optimized to improve the accuracy and reliability of the assessment results. In this stage, the ANP Model not only adjusts the weights of the indices but also ensures reasonable correlations through the calculation of dependency levels between the nodes.
Finally, considering the potential fuzziness and uncertainty in the evaluation process, the Extension Cloud Model is introduced. This model processes the fuzziness of expert judgment and evaluation data, further optimizing the assessment results. The Extension Cloud Model uses the three core characteristics of expectation, entropy, and hyper-entropy to convert qualitative data into quantitative results. This process eliminates errors caused by data uncertainty [40].
Figure 4 illustrates the overall process of the proposed methodology framework. Through the integration of the Entropy Weight TOPSIS Method, ANP Model, and Extension Cloud Model, this study enables a multi-dimensional and comprehensive resilience assessment of the EPB shield tunneling construction system, ensuring the scientific, objective, and efficient evaluation results.
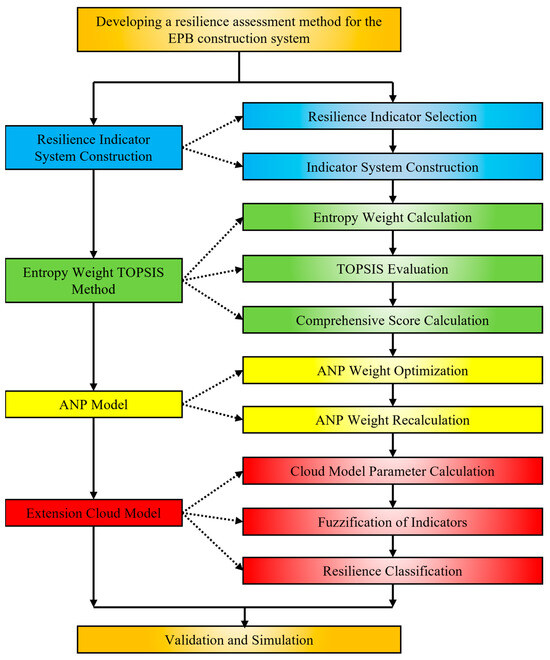
Figure 4.
Flow chart of the resilience assessment in EPB construction.
3.1. Resilience Indicator System Construction
The resilience assessment indicator system is established as the fundamental basis for conducting quantitative safety resilience analysis in EPB shield tunneling construction. Systematic identification and screening are conducted for key indicators characterizing EPB shield tunneling safety resilience. Bibliometric analysis methods are employed. Core collections from Web of Science (WOS) and China National Knowledge Infrastructure (CNKI) are selected as literature source databases. These databases are recognized for their comprehensive coverage of international and domestic high-quality journals. Engineering management, safety science, and underground space engineering disciplines are systematically included. Extensive representativeness and data authority are ensured through this selection process. Search keywords are defined as “safety resilience”, “tunnel resilience”, “underground engineering”, “earth pressure balance (EPB)”, “evaluation indicators”, “resilience index”, “metro construction”, and “resilience assessment”. The time span is set from 2000 to 2024. A total of 1200 relevant publications are obtained through this retrieval process. Manual screening is performed based on titles, abstracts, and full-text content. Duplicated publications, non-empirical studies, and research without resilience evaluation indicators are systematically excluded. A total of 86 high-quality studies are retained. Explicit construction and application of resilience indicator systems are verified in these selected publications.
Resilience evaluation indicators with high-occurrence frequency are extracted from the reviewed publications [41,42,43]. Term frequency statistics and co-occurrence analysis methods are systematically applied based on literature analysis results. Factor analysis methodology is implemented for clustering and classifying preliminary indicators. Redundant information is eliminated through this process. Indicators with low commonality contributions or deviated loading coefficients are systematically removed. A preliminary evaluation system containing 40 tertiary-level indicators is ultimately established. Structural validity of the indicator framework is enhanced accordingly.
Marginal indicators with extremely low entropy values and insufficient discriminatory power are eliminated based on entropy weights and TOPSIS ranking results [44,45,46]. An EPB shield tunneling safety resilience indicator system is ultimately established. This system comprises 1 objective layer, 4 primary resilience dimensions, 20 secondary indicators, and 35 tertiary indicators (Table 1).

Table 1.
Assessment index system for safety resilience in EPB construction.
3.2. Entropy Weight TOPSIS Method
3.2.1. Overview of the Entropy Weight TOPSIS Method
The Entropy Weight TOPSIS method integrates the entropy weight method and TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) method. It objectively assigns weights to evaluation indicators and performs a comprehensive assessment based on the distance to the ideal and negative ideal solutions, ultimately determining the priority of each alternative [47]. This method ensures strong objectivity and effectively reduces human bias [48,49].
The entropy weight method calculates the information entropy of each evaluation indicator, objectively reflecting the relative importance of the indicators. A higher entropy value indicates greater uncertainty of the indicator, thus leading to a lower weight. The formula for calculating the information entropy is as follows:
where represents the value of the -th alternative for the -th indicator, is the total number of alternatives, and is the entropy value of the -th indicator. A higher entropy value indicates greater uncertainty and thus lower weight.
The TOPSIS method calculates the distance between each alternative and both the ideal and negative ideal solutions. The formula for the distances to the ideal and negative ideal solutions is as follows:
where and represent the distance of the -th alternative from the ideal and negative ideal solutions, respectively, and and represent the ideal and negative ideal values for the -th indicator.
3.2.2. Implementation Steps of the Entropy Weight TOPSIS Method
In the implementation of the Entropy Weight TOPSIS method, the first step is to establish a complete evaluation indicator system and define the types of indicators (such as positive or negative indicators). Next, the information entropy of each indicator is calculated based on the evaluation data. The higher the entropy, the lower the weight assigned to the corresponding indicator. The reciprocal of the entropy value is used as the weight, as shown in the following formula:
where represents the weight of the -th indicator and is the entropy value of that indicator.
After determining the weights, the TOPSIS method is used to perform a comprehensive evaluation by calculating the distance between each alternative and both the ideal and negative ideal solutions. Then, the relative closeness (or similarity to the ideal solution) of each alternative is calculated using the following formula:
where represents the relative closeness of the -th alternative, and and are the distances from the ideal and negative ideal solutions, respectively. Finally, the alternatives are ranked according to their relative closeness, and the optimal alternative is selected.
3.2.3. Advantages and Limitations of the Entropy Weight TOPSIS Method
The Entropy Weight TOPSIS method offers significant advantages [50]. Firstly, it objectively reflects the importance of each indicator by using entropy values, which helps avoid the subjective bias that may occur when assigning weights based on expert judgment. Secondly, the method is simple to compute, making it suitable for large datasets and capable of handling complex evaluation problems involving multiple indicators. Lastly, the method is flexible and can be applied to a wide range of multi-criteria decision-making problems.
However, the method also has some limitations. It relies heavily on the quality of the data, and any large errors in the input data may affect the accuracy of the assessment results. Although the entropy method reduces subjective bias, the data collection and preprocessing stages still involve expert judgment, which may affect the reliability of the results. Additionally, the TOPSIS method assumes that the indicators are independent, but in practical applications, there are often correlations between the indicators, which may impact the accuracy of the results.
3.3. ANP Model
3.3.1. Overview of the ANP Model
The ANP model is a powerful tool for multi-criteria decision analysis, capable of handling complex interdependencies and feedback among evaluation criteria. Unlike the Analytic Hierarchy Process (AHP), ANP considers not only the independence of evaluation criteria but also their interrelationships. Therefore, ANP is particularly suitable for evaluating systems where complex feedback effects and dependencies exist. In practice, ANP constructs a network structure of criteria and quantifies the relationships among them, ultimately optimizing the weight distribution of the evaluation criteria.
The ANP model involves constructing a network structure, creating a judgment matrix, calculating weights, and optimizing the weights through feedback mechanisms [51,52]. Weight calculation is based on the dependencies between the criteria, which are derived from the judgment matrix and its eigenvalue decomposition.
3.3.2. Implementation Steps of the ANP Model
The implementation of the ANP model involves four main steps. The first step is to construct the ANP network structure. In this step, the hierarchy of the evaluation criteria is defined, and the dependencies between each criterion are clarified. The core of ANP is to identify which criteria are independent and which are dependent on others. This process is often supported by expert discussions, historical data analysis, and domain knowledge.
Next, a judgment matrix is constructed based on expert judgment or data analysis, evaluating the relative importance between evaluation criteria. Each element in the matrix, , represents the relative importance between the -th and -th criteria. The following formula normalizes the judgment matrix:
where is the normalized value of the matrix element, and is the original value of the matrix element.
Then, the weight of each criterion is calculated by performing eigenvalue decomposition of the judgment matrix. The eigenvector corresponding to the maximum eigenvalue represents the weight of each criterion. The weight is calculated using the following formula:
where is the maximum eigenvalue of the judgment matrix, is the matrix element, and and are the corresponding weights of the criteria.
Finally, the weights are optimized using the feedback mechanism in the ANP model. Through iterative calculations, the ANP model adjusts the weights and ensures that the final weight distribution reflects the interdependencies among the criteria, thus optimizing the overall evaluation results.
3.3.3. Advantages and Limitations of the ANP Model
The main advantage of the ANP model is its ability to handle the complex interdependencies among evaluation criteria and optimize weight distribution through feedback mechanisms. Compared with traditional AHP, ANP is more suitable for multi-criteria decision-making problems where there are complex interdependencies. ANP provides more accurate decision support by reflecting the dynamic relationships between criteria [53,54].
However, the ANP model has certain limitations. First, the implementation of ANP requires substantial expert judgment and data support, which may be influenced by subjective factors. Second, the computation process in ANP is relatively complex, especially when there are numerous criteria and complex interdependencies, leading to a significant increase in computation time and complexity. Additionally, the accuracy of the ANP model is highly dependent on the quality of the judgment matrix, and the results may be unreliable if expert judgments are inaccurate.
3.4. Extension Cloud Model
3.4.1. Overview of the Extension Cloud Model
The Extension Cloud Model is a mathematical model designed to handle uncertainty and fuzziness in the evaluation process. It combines elements of fuzziness and uncertainty and employs key characteristics such as the expected value, entropy, and hyper-entropy to quantify uncertainty and fuzziness in the data. The Extension Cloud Model is capable of transforming qualitative expert judgments into quantitative results, thereby improving the reliability and precision of the evaluation results.
In the Extension Cloud Model, the expected value () represents the central tendency of the data, entropy () reflects the uncertainty of the data, and hyper-entropy () describes the distribution characteristics of the data. By using these characteristics, the Extension Cloud Model can effectively process incomplete and fuzzy data, providing reliable and accurate evaluation results.
3.4.2. Implementation Steps of the Extension Cloud Model
The implementation of the Extension Cloud Model involves several steps, including data collection, calculation of cloud digital features, cloud generation, and reverse cloud generation. First, expert judgments or qualitative data are collected to determine the fuzziness and uncertainty of each evaluation indicator. Based on these data, the expected value, entropy, and hyper-entropy are calculated for each indicator. The formulas for these characteristics are as follows:
where is the expected value, is the entropy value, and is the hyper-entropy value. represents the probability distribution of the data, and is the value of each data point.
Next, the cloud generator generates cloud droplets based on the expected value, entropy, and hyper-entropy. These droplets transform the qualitative judgments into quantitative data, while the reverse cloud generator converts the cloud droplets into specific evaluation results, reducing the uncertainty and fuzziness of the data.
For further optimization, the variance and fluctuation of the generated cloud droplets can be calculated as follows:
where is the mean of the data, and represents the variance, indicating the dispersion of the data.
Based on the cloud model, the evaluation data are further optimized to eliminate fuzziness and uncertainty. The optimized data generated by the reverse cloud generator can more accurately reflect the actual situation, thereby improving the reliability and precision of the evaluation results.
3.4.3. Advantages and Limitations of the Extension Cloud Model
The main advantage of the Extension Cloud Model lies in its ability to handle fuzziness and uncertainty in the evaluation process, particularly when expert judgments or qualitative data are involved. By utilizing the characteristics of cloud droplets, such as the expected value, entropy, and hyper-entropy, the Extension Cloud Model effectively reduces the uncertainty in the data, enhancing the accuracy of the evaluation results. The model is highly adaptable and can be applied to a wide range of complex evaluation problems.
However, the Extension Cloud Model also has limitations. It heavily relies on expert input, and the accuracy of expert judgments directly affects the results of the model. Although the cloud model handles uncertainty, the results may still be influenced by inaccurate or incomplete data. Furthermore, the computational complexity of the Extension Cloud Model increases with the amount of data and the number of indicators, which may limit its application in large-scale evaluations.
3.5. Example of Calculation Flow
To ensure reproducibility, a complete calculation flow is demonstrated for a representative indicator, the rotational stability of the cutterhead (D2).
Step 1: Raw data collection and normalization.
Cutterhead torque was monitored during tunneling. For one excavation cycle, the measured torque values fluctuated between 1650 and 1800 , while the rated torque capacity was 1900 . The normalized value of stability was calculated as
where is the normalized score of indicator for alternative.
Step 2: Entropy weight calculation.
The entropy of indicator D2 across multiple observation samples was computed as
For D2, the entropy value was calculated as 0.312. The corresponding entropy weight was:
Step 3: ANP adjustment of indicator weight.
The initial weight from the entropy method was refined through the Analytic Network Process. Pairwise comparisons were performed between D2 and related equipment indicators (D3: load capacity, D30: drive stability). The eigenvector of the comparison matrix yielded an adjusted priority of 0.081. After normalization across the equipment cluster, the final ANP-modified weight of D2 was confirmed as 0.0761 (Table 2).

Table 2.
Weight of safety resilience assessment index for EPB construction.
Step 4: Extension cloud model transformation.
The normalized score of 0.947 was converted into membership degrees of high, medium, and low resilience using the extension cloud model:
where is the expected value, is the entropy value, and is the hyper-entropy value. For D2, the high-resilience cloud model was defined as (97.5, 2.5, 0.1). Substituting, the resulting membership degrees were: High resilience: 0.962, Medium resilience: 0.038, Low resilience: 0.000.
Step 5: Integration into system resilience.
The membership degrees of D2 were aggregated with other indicators of the equipment subsystem (C2). The weighted synthesis produced subsystem-level membership values, which were further aggregated upward into the primary indicator “stability degree (B1)” as described in Section 5.1.1.
This example demonstrates the full computational pathway from raw monitoring data, through entropy weighting and ANP adjustment, to cloud model classification and system-level aggregation. All other indicators follow the same process, ensuring methodological consistency and reproducibility.
3.6. Summary
This study proposes a multi-level and multi-dimensional resilience assessment method that integrates the Entropy Weight TOPSIS method, ANP model, and Extension Cloud Model. The Entropy Weight TOPSIS method is used to assign weights to evaluation indicators and perform the initial comprehensive assessment. The ANP model optimizes the interdependencies among the indicators, while the Extension Cloud Model effectively handles the fuzziness and uncertainty in the evaluation process. This approach takes into account the interactions and uncertainties among evaluation indicators, ensuring the scientific, objective, and accurate results of the assessment [55].
By incorporating these methods, this study provides a systematic and quantitative framework for assessing the resilience of the EPB shield tunneling construction system. In future research, the application of these methods to practical case studies will further validate their applicability and effectiveness in complex engineering scenarios. Moreover, this methodology offers a valuable theoretical basis and practical guidance for improving engineering decision-making reliability and enhancing the safety and resilience of shield tunneling construction.
4. Case Application
4.1. Case Background
The shield tunneling section between Ligeng Road Station and Fenghuang Road Station on Jinan Metro Line 6 is located within the core zone of a high-density built-up area. High-rise building clusters, critical municipal roads, and dense underground utility networks are traversed along the alignment. This corridor is classified as a typical high-risk shield tunneling scenario. The tunnel section spans approximately 1.8 km and is constructed using the EPB shield method. Cover depth ranges between 12 and 18 m [56,57]. Complex geological formations are encountered, including sequential traversals of soft plastic silty clay strata, highly permeable gravel–sand interbeds, and miscellaneous fill layers containing construction waste. Strong formation heterogeneity and abrupt stratum interfaces are prevalent. Significant excavation-induced disturbances are generated.
To provide a clearer understanding of the geological complexity, a representative geological section has been added (Figure 5). The section illustrates the stratigraphic sequence encountered along the tunnel alignment, including miscellaneous fill, silty clay with gravel, soft silty clay, and the underlying diorite bedrock. The contrasting mechanical and hydraulic characteristics of these strata highlight the challenges faced by the shield machine. In particular, the loose and heterogeneous fill material may induce ground loss, while the silty clay with gravel layers exhibit local high permeability, resulting in difficulties in face pressure control. The transition to competent diorite further complicates excavation, as abrupt changes in strength and abrasivity significantly influence cutterhead performance. To complement the figure, the main engineering properties of the encountered strata are summarized in Table 3.
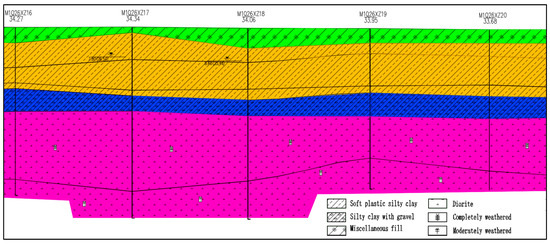
Figure 5.
Geological section of the shield tunnel alignment on Jinan Metro Line 6.

Table 3.
Representative geotechnical properties of soils along the Jinan Metro Line 6 shield tunnel alignment.
Resilience-related characteristics of typical operational conditions are repeatedly exhibited in the section during actual construction operations. For instance, frequent torque surges are observed at silty clay–gravel sand interfaces, with peak torque values exceeding 1800 . Poor stabilization control of chamber pressures is exhibited, showing high fluctuation frequency (±0.3 bar/min). In gravel-sand interbeds, cutter wear rates are significantly accelerated (maximum 0.8 mm/ring). Restricted grout diffusion and delayed surface settlements are identified in loose miscellaneous fill zones. Although no major safety incidents are triggered by these issues, insufficiencies in disturbance resistance capacity and recovery regulation mechanisms of shield systems are revealed under compound risk conditions.
Based on the comprehensive judgment of construction contractors and expert panels in engineering practices, the section is evaluated as medium resilience level (B) under conventional management modes. The evaluation is primarily based on two aspects. Stable operational capabilities and geological adaptability are possessed by shield equipment, allowing basic construction states to be maintained during initial risk emergence phases. However, significant deficiencies are observed in dynamic parameter adjustment responses, system component redundancy design, and cross-system emergency coordination [58]. Closed-loop mechanisms integrating “disturbance identification–rapid response–proactive recovery” are not effectively established.
4.2. Resilience Assessment for Jinan Metro Line 6
Within the ANP structural framework for assessing the safety resilience of Jinan Metro Line 6 EPB construction section, the complex interdependencies among the indicators listed in Table 1 are rigorously modeled (Figure 6). The weight distribution of safety resilience indicators is summarized in Table 2. The table presents the calculated weights of the primary, secondary, and tertiary indicators, which were obtained through the integrated methodology. Specifically, the ANP was used to capture the interdependencies among indicators, while the extension cloud model was employed to quantify uncertainties in expert judgments. The final weights were determined by combining ANP-derived network priorities with entropy-based optimization, ensuring both structural validity and objectivity. This weighting process provides the basis for subsequent resilience evaluation and classification. To establish a clear discriminative framework for resilience capabilities, we have defined a tripartite resilience classification system. As shown in Table 4, the safety resilience of EPB tunneling construction projects is categorized into three distinct grades: high resilience (Grade A), medium resilience (Grade B), and low resilience (Grade C).
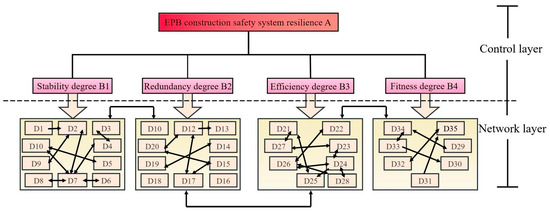
Figure 6.
ANP structure model for the resilience index system in EPB construction.

Table 4.
Resilience rating of safety system in EPB construction.
The resilience grades were mapped to the evaluation indicators through a cloud-based approach that integrates ANP with the extension cloud model. By embedding these weights into the cloud model framework, extension cloud models were formulated for each indicator (Table 5), where the transitional boundaries between resilience grades were mathematically defined through entropy and hyper-entropy-based optimization [59,60]. A computational framework base on Python Version 3.8 was developed to implement the extension cloud model generation algorithm, which synthesizes both the indicator data from Table 5 and the ANP weight structure to generate stochastic cloud charts. As exemplified in Figure 7. for indicators C1 and C2, the extension cloud distributions explicitly quantify the probabilistic affiliation of operational states to adjacent resilience tiers, with ANP-assigned weights influencing the cloud droplets’ distribution. This fuzzification process transforms traditional crisp classifications into fuzzy-probabilistic decision boundaries, where critical thresholds are recalibrated according to the relative importance of indicators within the safety hierarchy. The resultant framework ensures resilience assessments are simultaneously responsive to both operational uncertainties and systemic priority weightings.

Table 5.
Level limits of resilience assessment indices and development of a cloud model for level boundaries in the EPB safety system.
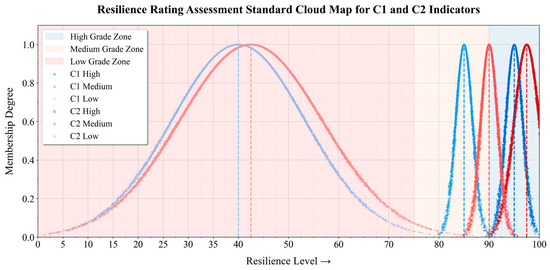
Figure 7.
Resilience rating assessment standard cloud map for C1 and C2 indicators.
4.3. Validation of Resilience Assessment Results
For illustration, the detailed calculation flow for indicator D2 has been provided in Section 3.5. This ensures that the methodology can be independently reproduced by researchers and practitioners.
Based on the computed cloud droplet parameters and their corresponding membership degrees derived from the extension cloud model for each EPB project’s safety system, Table 6 presents the tertiary evaluation indicators and their corresponding membership degrees for the safety resilience of the Jinan Metro Line 6 EPB construction projects. The hierarchical aggregation of resilience assessment was systematically executed, where the aggregation process involved computing the membership degree for each layer based on the cloud parameters (expectation, entropy, and hyper-entropy). For secondary indicators, the membership degrees were calculated by calculating the membership degrees based on the cloud affiliation metrics of their constituent tertiary indicators using extension cloud model parameters (Table 7). Analogously, the membership degrees of primary indicators were synthesized by integrating secondary indicator membership values based on extension cloud model parameters, ultimately propagating uncertainties upward to the primary layer (Table 8).

Table 6.
Resilience tertiary assessment indicators and membership degree of safety system in EPB construction.

Table 7.
The second-level assessment indicators of the resilience of the safety system in EPB construction and the calculation of the membership degree of the primary indicators.

Table 8.
The first-level assessment indicators of the resilience of the safety system in EPB construction and the calculation of the membership degree of the target layer.
This multi-stage computation framework ensures the probabilistic representation of resilience states across all system levels, with entropy and hyper-entropy driven cloud droplet distributions capturing epistemic uncertainties in expert-defined grade boundaries. The final membership distributions, validated through Monte Carlo simulations (10,000 iterations), demonstrated less than 5% deviation in maximum affiliation probabilities [61,62], confirming the robustness of the extension cloud model integrated with ANP methodology for tunneling risk governance. The shield tunneling section of Metro Line 6 is ultimately evaluated as medium resilience level based on the maximum membership principle, calculated using the membership degrees derived from the extension cloud model. The evaluation results are found to be highly consistent with practical assessments under conventional safety management systems, demonstrating the practical effectiveness and accuracy of the extension cloud model integrated with ANP methodology in real-world applications. The proposed methodology is thereby validated for scientific validity and practical effectiveness, particularly in enhancing the precision and reliability of shield tunneling safety resilience evaluation.
5. Analysis and Discussion
5.1. Analysis of Safety Resilience Evaluation Results
5.1.1. Resilience Evaluation Results of Primary Indicator Layer for EPB Shield Tunneling System
The integrated evaluation method combining extension cloud model and ANP is employed. The EPB shield tunneling system is characterized by dominant high-resilience structural features of stability–adaptability. As shown in Table 8, stability (B1) and fitness (B4) are assigned the highest weights, accounting for 0.3856 and 0.3181, respectively. Their high resilience membership degrees confirm that these two dimensions dominate the overall resilience performance of the system. These reflect the shield system’s disturbance resistance capacity against external perturbations and response regulation capability to complex geological environments, with the uncertainty and fuzziness being captured through the extension cloud model. These are identified as critical dimensions constituting the core of system resilience. High-resilience membership degrees of 0.793 and 0.824 are obtained for these two indicators. Strong performance assurance under normal operations and adaptation capabilities in geological variation scenarios are demonstrated by the system. The efficiency degree (B3) is assigned a weight of 0.1935, with a high resilience membership degree of 0.781. Time sensitivity and regulation capabilities are maintained in initial responses and loss control. Risk propagation is suppressed to certain extents. The redundancy degree (B2) is evaluated based on the membership degree derived from the extended cloud model, showing a high resilience membership degree of 0.538 and a medium resilience membership degree of 0.437. Significant deficiencies are exposed in critical component redundancy arrangements, personnel substitution, and fault path conversion. Closed-loop mechanisms for emergency switching and recovery paths are not fully established after sudden failures. Significant improvement potential is identified.
5.1.2. Analysis of Resilience Evaluation Results for Secondary Indicator Layer of EPB Shield Tunneling System
Heterogeneity in resilience characteristics is further revealed among different functional subsystems at the secondary indicator layer, with the extension cloud model providing a probabilistic representation of each subsystem’s performance. Table 6 illustrates the resilience performance of different subsystems. The equipment subsystem (C2) demonstrates high-level resilience across all four dimensions. Particularly, high-resilience membership degrees of 0.886 and 0.881 are achieved in stability and adaptability dimensions. Its core role as the main control unit and response capabilities in system operations are reflected. Operational continuity and structural stability of the shield machine are effectively maintained under complex geological conditions. The personnel subsystem (C1) demonstrates relatively good performance in redundancy (membership degree 0.613) and adaptability (membership degree 0.735). Elastic capabilities of field personnel in task allocation and emergency operations are reflected. Certain human resilience reserves are maintained. Disparate resilience performance is observed in environmental subsystem (C3) and material subsystem (C5). For C3, a high-resilience membership degree of merely 0.119 is recorded in the stability dimension. Perception and response mechanisms to external disturbances (e.g., precipitation, settlement) are exposed as insufficient. For C5, a membership degree of 0.297 is obtained under the redundancy dimension. Critical material supply chains and structural fault-tolerant capacities are identified for enhancement. Risk amplification effects from resource interruptions and functional degradation are demonstrated.
5.1.3. Analysis of Resilience Evaluation Results for Tertiary Indicator Layer of EPB Shield Tunneling System
The tertiary indicators serve as basic units for system resilience characterization. More detailed system performance composition and risk-sensitive points are revealed, results are listed in Table 5. By combining weight distribution and resilience membership degree results, 35 tertiary indicators are classified into four typical structural characteristics.
(1) High Weight–High Membership Type
These indicators are characterized by both high structural importance and excellent resilience performance, serving as “strong support elements” in system configuration. Examples include “Rotational stability of cutterhead (D2)” (weight 0.0761, membership degree 0.962), “Stability of main drive power output (D30)” (weight 0.1246, membership degree 0.912), and “Adaptability to complex geological conditions (D29)” (weight 0.0690, membership degree 0.785). Robustness and dynamic adaptation capabilities of shield equipment under disturbance and deformation scenarios are demonstrated. These are identified as critical stability nodes in the overall system resilience structure.
(2) High Weight–Low Membership Type
These indicators are recognized as system bottlenecks despite their prominent structural roles. Typical examples include “Rationality of dynamic tunneling parameter adjustment (D7)” (weight 0.0150, membership degree 0.000) and “Sealing integrity of screw conveyor (D9)” (weight 0.0290, membership degree 0.000). Agile adjustment capabilities are found lacking under high-frequency disturbances. Sealing guarantees are insufficient in high-pressure conveying scenarios. Weak recovery paths are observed, through which local risks are prone to escalate into systemic failures.
(3) Low Weight–High Membership Type
These indicators are defined as “reserve support elements” in the system. Significant redundancy regulation and protective capabilities are maintained despite relatively low importance. Examples include “Safety factor of synchronous grout (D20)” (weight 0.0096, membership degree 0.882) and “Coverage of chamber pressure instability contingency plans (D18)” (weight 0.0086, membership degree 0.932). Good buffering and absorption capacities are exhibited under sudden working conditions. These are recognized as critical reserve units for the “flexible regulation” mechanism of the system.
(4) Low Weight–Low Membership Type
These indicators are not prominent in either weight or resilience performance. While their overall impacts are limited, marginal robustness of the system’s redundancy system is enhanced through optimization. Examples include “Multi-stage design of tail seal brushes (D14)” (weight 0.0080) and “Grouting efficiency for ground settlement mitigation (D25)” (weight 0.0281). Phase-specific effectiveness is observed in certain dimensions, though overall contributions remain limited. Resource allocation efficiency is improved through function merging and cost optimization.
5.2. Resilience Enhancement Strategies and System Optimization Pathways
The resilience evaluation results indicate that the EPB shield tunneling system performs strongly in stability and fitness, which provide the core support for overall resilience [63]. In contrast, redundancy emerges as the weakest dimension, while several efficiency-related indicators also show notable deficiencies. The presence of high-weight but low-resilience indicators highlight potential system vulnerabilities that may undermine recovery under disturbance. Therefore, a comprehensive resilience enhancement pathway is required, one that combines structural reinforcement, functional redundancy, adaptive control, and organizational flexibility. This pathway should enable the system to transition from a “steady-state resistance” model toward a “dynamic adaptation–active recovery” mechanism [64].
At the system level, optimization should follow a hierarchical and integrated approach. First, redundancy construction must be prioritized, including improvements in equipment backup, personnel substitution, and material supply chain robustness. Second, adaptive control capacity should be strengthened by applying multi-source data fusion and AI-driven real-time regulation. Third, structural fault-tolerance and modularization should be incorporated to support rapid component replacement and functional reconfiguration. Finally, integration of digital twin simulations with field feedback data can serve as a decision-support tool, enabling proactive identification of vulnerabilities and continuous optimization of tunneling strategies.
5.2.1. Stability
The assessment results confirm that stability is one of the strongest resilience dimensions in the EPB shield tunneling system. Equipment-related indicators such as cutterhead rotational stability (D2) and main drive load capacity (D3) demonstrate high resilience levels, ensuring that the system maintains functionality under normal excavation disturbances. However, the environmental subsystem under stability exhibits significant weakness. Indicators such as variability of geological strata (D4), fluctuation of equipment operating temperature (D5), and ground settlement deformation (D6) show relatively low resilience scores, indicating that external environmental loads remain critical vulnerabilities.
To enhance stability, continuous multi-sensor monitoring of geological and operational conditions should be implemented. Real-time feedback from ground settlement sensors, chamber pressure monitors, and cutterhead torque detectors can provide early warnings of abnormal conditions. In addition, AI-driven adaptive control algorithms that dynamically adjust thrust, rotation speed, and chamber pressure can stabilize operations under variable strata. Reinforcement measures, such as pre-excavation grouting and enhanced drainage systems, are also recommended to control settlement and groundwater pressure. These improvements will strengthen the system’s inherent robustness and reduce susceptibility to external disturbances.
5.2.2. Redundancy
Redundancy is identified as the weakest dimension, with several second- and third-level indicators scoring poorly. For example, operator redundancy (D11) and backup capacities for critical equipment such as soil conditioners (D12) and drive motors (D13) show limited resilience. Similarly, contingency planning for chamber pressure instability (D18) and material-related safety margins (D19) reveal deficiencies. These results highlight that the system lacks sufficient backup capacity and substitution mechanisms to maintain functionality during unexpected failures.
Improving redundancy requires a multi-pronged approach. First, modular hot-standby designs should be adopted for critical equipment, such as duplicate drive motor units and backup conveyor systems. Second, predictive maintenance strategies based on digital twin simulations can forecast potential failures by analyzing real-time machine data, thus enabling proactive replacement before breakdown. Third, redundancy at the personnel level should be enhanced by cross-training operators, ensuring that multiple staff members can assume key responsibilities when needed. Finally, redundant supply of critical materials, such as grout and sealing components, must be guaranteed through diversified storage and procurement channels. These measures will build system slack, ensuring continuous operation even when primary components or staff are compromised.
5.2.3. Efficiency
The efficiency dimension achieved relatively strong results overall, but several critical bottlenecks were identified at the tertiary level. Indicators such as response time of soil conditioner injection (D22), erection speed of segments (D23), tunneling speed adaptation to burial depth (D24), and grouting efficiency (D25) demonstrate resilience gaps. These weaknesses imply that delays in auxiliary processes may reduce overall system responsiveness and increase disturbance recovery time.
Targeted measures can substantially improve efficiency. The automation of ring-building operations, including robotic segment erectors, can shorten installation cycles and reduce human error. In terms of ground treatment, optimizing the foaming ratio of soil conditioners and applying adaptive grouting pressure control will enhance ground settlement mitigation efficiency. Integrating machine-learning-based predictive control algorithms can also optimize excavation speed and resource allocation under varying geological conditions. Such enhancements will improve the rapidity of system responses and ensure effective resource utilization during disturbances.
5.2.4. Fitness
The fitness dimension is a core advantage of the EPB tunneling system, yet the evaluation reveals that several critical adaptive functions remain weak. Indicators such as hydraulic pressure resistance of the tail seal (D32) and flexibility of tunneling contingency plans (D33) show low resilience membership, suggesting insufficient adaptability to sudden hydraulic loads or unexpected environmental conditions. Furthermore, screw conveyor sealing integrity (D9) and cutterhead anti-caking capability (D31) highlight vulnerabilities in adapting to diverse and challenging strata.
Enhancing adaptability requires both mechanical and organizational strategies. For mechanical resilience, dual-layer sealing systems or inflatable gaskets can increase tail seal redundancy, while real-time monitoring of seal pressure and cutterhead conditions can provide early warnings of failure. For operational adaptability, expanding the range of contingency plans and rehearsing them regularly will enable faster and more flexible responses to evolving conditions. Digital twin technology can further support adaptability by providing real-time simulations of shield performance, allowing managers to test adaptive strategies virtually before implementing them in practice. These measures will significantly improve the system’s capacity to absorb shocks and evolve under changing conditions. Table 9 summarizes the weak sub-indicators identified in each resilience dimension and provides targeted improvement strategies.

Table 9.
Leak indicators and resilience enhancement strategies.
Figure 8 visualizes the critical weak tertiary indicators identified in the resilience assessment. Bubble size corresponds to indicator weight, while color differentiates the primary dimensions. This visualization highlights that indicators such as D32 (tail seal resistance) and D23 (segment erection speed) not only score low, but also exert significant influence on overall resilience, making them priority targets for improvement.
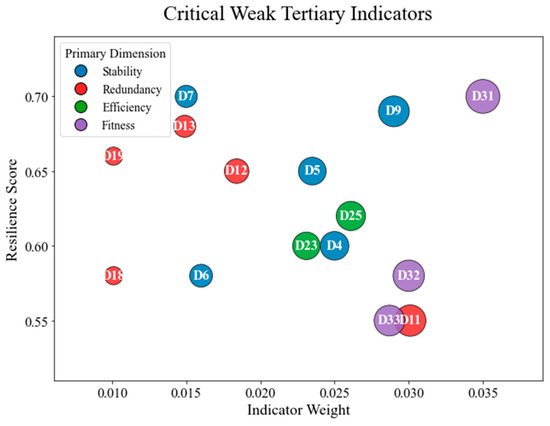
Figure 8.
Bubble chart of weak tertiary indicators.
In summary, resilience enhancement of EPB shield tunneling systems should be established on closed-loop logic of “assessment–feedback–optimization–reassessment”. Development of a resilience management platform for shield tunneling is recommended based on knowledge graph and digital twin technologies [39]. Construction parameters, environmental data, equipment status, and expert knowledge are integrated. Real-time resilience state identification, dynamic evolution simulation, and optimal intervention decision-making are promoted. A systemic enhancement pathway is achieved through hierarchical synergy of resilience units coupled with control and recovery mechanisms [65]. Transformation from traditional static risk response modes to dynamic resilience governance under multi-source disturbances is realized. Theoretical foundations and engineering guidance are provided for shield tunneling safety in complex geological and high-sensitivity zones [66].
6. Conclusions
EPB construction projects in China frequently experience accidents. The resilience of the safety system in EPB projects refers to the system’s capability to sustain operations, absorb disturbances, effectively respond, and restore functionality when encountering unexpected risks or challenges during tunneling activities. Strengthening safety resilience enhances adaptability and response efficiency while minimizing accident rates and shortening recovery periods. This research incorporates resilience theory into the safety management of EPB construction. It explores the fundamental aspects of resilience within safety systems and assesses system resilience using a series of resilience metrics. The proposed approach is applied to the EPB construction Jinan Metro Line 6 between Ligeng Road Station and Fenghuang Road Station.
To determine the resilience indicators, the entropy-weighted TOPSIS method was applied, while the extension cloud ANP model was developed by integrating cloud theory with the analytic network process to manage the uncertainty and complexity involved in assessing resilience at EPB construction projects. This paper introduces a new perspective for safety assessment in EPB construction projects, with resilience theory integrated into cloud and matter-element extension models. The traditional risk management approach is shifted to a resilience management approach, providing a theoretical foundation for future research in EPB construction engineering and serving as a reference for safety management in subway projects. Furthermore, safety management capabilities and emergency response are improved and optimized through three guarantee strategies.
The study is based on the risks and disturbances faced by tunneling engineers, without clear boundaries on specific accidents, disasters, or adverse events that may occur. Future studies can apply this framework to other cases to test resilience under disruptions. The resilience assessment index requires the integration of interdisciplinary knowledge and practical engineering characteristics. The resilience assessment indices are explained and evaluated qualitatively, stressing the need for quantifiable indicators to enhance the operability of the assessment process. The development of resilience indices involves integrating multiple disciplines knowledge with engineering practice. While these indices are usually described in qualitative terms, the introduction of measurable parameters is essential to strengthen the applicability of the assessment.
The proposed resilience assessment framework demonstrates strong potential for software implementation. By embedding the analytic network process and extension cloud model into a computational platform, data acquisition, weight calculation, and resilience evaluation can be automated. Such a platform will allow dynamic updates of resilience ratings as construction progresses and provide a transparent basis for decision-making. The modular design of the framework also facilitates integration with existing monitoring systems, enabling compatibility with industry-standard tunneling data formats.
In addition, future developments will focus on real-time application during shield tunneling projects. By linking the software with on-site monitoring devices, construction parameters such as face pressure, cutterhead torque, and soil conditioning rates can be continuously assessed. The system will then provide operators and managers with early warnings of potential instability and recommend corrective actions. This capability will transform the methodology from a theoretical assessment tool into a practical decision-support system, strengthening resilience-based safety management and supporting safer, more efficient tunneling operations.
Author Contributions
Conceptualization, J.B. and X.L.; methodology, J.B. and X.L.; software, J.B.; validation, X.L., X.H. and D.Z.; formal analysis, Y.Z.; investigation, X.H.; resources, X.L.; data curation, J.B.; writing—original draft preparation, J.B.; writing—review and editing, J.B. and X.L.; visualization, D.Z.; supervision, X.H.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China grant number (2024YFF0507903), the National Natural Science Foundation of China grant number (52508466) and the China Postdoctoral Science Foundation grant number (2025M773241). And The APC was funded by the National Key R&D Program of China grant number (2024YFF0507903).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, Y.; Zhou, J.; Zhang, B.; Wang, H.; Huang, M. Statistical Analysis of Major Tunnel Construction Accidents in China from 2010 to 2020. Tunn. Undergr. Space Technol. 2022, 124, 104460. [Google Scholar] [CrossRef]
- Terheijden, O.; van Gelder, P.; Broere, W. Impact of Occupational Risk Prevention Measures During Process Disturbances in Tbm Tunnelling. Tunn. Undergr. Space Technol. 2022, 127, 104576. [Google Scholar] [CrossRef]
- Cao, Y.; Nguyen, H.B.K.; Rahman, M.; Cheng, W.-C. Soil Behavior in the Earth Pressure Balance (Epb) Shield Tunnelling—A Dem Study. In GeoCongress on State of the Art and Practice in Geotechnical Engineering; Geo-Congress: Charlotte, NC, USA, 2022; pp. 690–698. [Google Scholar]
- Kwon, K.; Kang, M.; Hwang, B.; Choi, H. Study on Risk Priority for Tbm Tunnel Collapse Based on Bayes Theorem through Case Study. KSCE J. Civ. Environ. Eng. Res. 2023, 43, 785–791. [Google Scholar]
- Han, K.; Zhang, D.; Chen, X.; Su, D.; Ju, J.-W.W.; Lin, X.-T.; Cui, H. A Resilience Assessment Framework for Existing Underground Structures under Adjacent Construction Disturbance. Tunn. Undergr. Space Technol. 2023, 141, 105339. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, L.; Zhang, B.; Xiang, Y.; An, L.; Wang, W. Complex Equipment System Resilience: Composition, Measurement and Element Analysis. Reliab. Eng. Syst. Saf. 2022, 228, 108783. [Google Scholar] [CrossRef]
- Ham, D.-H. Safety-II and Resilience Engineering in a Nutshell: An Introductory Guide to Their Concepts and Methods. Saf. Health Work. 2021, 12, 10–19. [Google Scholar] [CrossRef]
- Hollnagel, E. From Safety to Safely: Principles and Practice of Systemic Management; Taylor & Francis: Oxfordshire, UK, 2024. [Google Scholar]
- Leveson, N. A Systems Approach to Risk Management through Leading Safety Indicators. Reliab. Eng. Syst. Saf. 2015, 136, 17–34. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Xu, Z.; Li, X.; Lin, P.; Lin, C. An Interval Risk Assessment Method and Management of Water Inflow and Inrush in Course of Karst Tunnel Excavation. Tunn. Undergr. Space Technol. 2019, 92, 103033. [Google Scholar] [CrossRef]
- Hamidi, J.K.; Shahriar, K.; Rezai, B.; Rostami, J.; Bejari, H. Risk Assessment Based Selection of Rock Tbm for Adverse Geological Conditions Using Fuzzy-Ahp. Bull. Eng. Geol. Environ. 2010, 69, 523–532. [Google Scholar] [CrossRef]
- Jia, X.; Wang, Y.-M.; Martínez, L. Enhancing Reliability of Failure Modes and Effects Analysis Dealing with Linguistic Distribution Assessments: A Consistency Based Approach. Eng. Appl. Artif. Intell. 2024, 133, 108333. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, J.; Wu, T. An Interval Intuitionistic Fuzzy Characterization Method Based on Heterogeneous Big Data and Its Application in Forest Land Quality Assessment. Int. J. Fuzzy Syst. 2025, 27, 558–581. [Google Scholar] [CrossRef]
- Nehal, N.; Mekkakia-Mehdi, M.; Lounis, Z.; Guetarni, I.H.M.; Lounis, Z. Hazop, Fmeca, Monitoring Algorithm, and Bayesian Network Integrated Approach for an Exhaustive Risk Assessment and Real-Time Safety Analysis: Case Study. Process. Saf. Prog. 2024, 43, 784–813. [Google Scholar] [CrossRef]
- Zhao, Y.; Fu, H.; Shi, Y.; Jiang, Y.; Tian, H. Risk Level Analysis of Large Diameter Shield Tunneling through Karst Area at River Bottom. J. China Foreign Highw. 2018, 39, 212–217. [Google Scholar]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.-N.; Zhou, W.-H. Flood Risk Assessment of Metro Systems in a Subsiding Environment Using the Interval Fahp-Fca Approach. Sustain. Cities Soc. 2019, 50, 101682. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Zhou, W.-H.; Shen, S.-L.; Zhou, A.-N. Inundation Risk Assessment of Metro System Using Ahp and Tfn-Ahp in Shenzhen. Sustain. Cities Soc. 2020, 56, 102103. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Sun, W.-J.; Shen, S.-L.; Arulrajah, A. Flood Risk Assessment in Metro Systems of Mega-Cities Using a Gis-Based Modeling Approach. Sci. Total Environ. 2018, 626, 1012–1025. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Data in Risk Assessment of Mega-City Infrastructures Related to Land Subsidence Using Improved Trapezoidal Fahp. Data Brief. 2020, 28, 105007. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Z.; Liu, X.; Li, M.; Kou, L. Dynamic Risk Assessment of Metro Station with Interval Type-2 Fuzzy Set and Topsis Method. J. Intell. Fuzzy Syst. 2015, 29, 93–106. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Sun, W.-J.; Shen, S.-L.; Zhou, A.-N. Risk Assessment Using a New Consulting Process in Fuzzy Ahp. J. Constr. Eng. Manag. 2020, 146, 04019112. [Google Scholar] [CrossRef]
- Gao, W.; Zeng, Z.; Ma, X.; Ke, Y.; Zhi, M. An Improved Hybrid Structure Learning Strategy for Bayesian Networks Based on Ensemble Learning. Intell. Data Anal. 2023, 27, 1103–1120. [Google Scholar] [CrossRef]
- Chung, H.; Lee, I.-M.; Jung, J.-H.; Park, J. Bayesian Networks-Based Shield Tbm Risk Management System: Methodology Development and Application. KSCE J. Civ. Eng. 2019, 23, 452–465. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, H.; Song, Z.; Dong, S.; Zhang, L.; Zhang, X. Dynamic Risk Assessment for Underground Gas Storage Facilities Based on Bayesian Network. J. Loss Prev. Process. Ind. 2023, 82, 104961. [Google Scholar] [CrossRef]
- Xu, N.; Guo, C.; Wang, L.; Zhou, X.; Xie, Y. A Three-Stage Dynamic Risk Model for Metro Shield Tunnel Construction. KSCE J. Civ. Eng. 2024, 28, 503–516. [Google Scholar] [CrossRef]
- Li, X.; Li, S.; Yuan, J.; Wan, Z.; Liu, X. A Data-Driven and Knowledge Graph-Based Research on Safety Risk-Coupled Evolution Analysis and Assessment in Shield Tunneling. Tunn. Undergr. Space Technol. 2025, 162, 106657. [Google Scholar] [CrossRef]
- Lalitha, R.; Sreelekha, P. A Methodology to Analyze and Estimate the Software Development Process Using Machine Learning Techniques. Int. J. Softw. Eng. Knowl. Eng. 2023, 33, 815–835. [Google Scholar] [CrossRef]
- Li, Y.-S.; Guo, C.-Y. Random Logistic Machine (Rlm): Transforming Statistical Models into Machine Learning Approach. Commun. Stat.-Theory Methods 2024, 53, 7517–7525. [Google Scholar] [CrossRef]
- Huang, J.S.Y.L.Y.; Zhang, C.; Jiang, C.; Su, B.Z. Prediction and Analysis of Shield Tunneling Parameters in Underwater Karst Stratum Based on Bp Neural Network. China Civ. Eng. J. 2020, 53, 75–80+98. [Google Scholar]
- Kaddoura, K.; Zayed, T. Defect- and Component-Based Assessment Model for Manholes. Tunn. Undergr. Space Technol. 2018, 82, 380–393. [Google Scholar] [CrossRef]
- Yue, L.; Niu, J.; Tian, Z.; Lin, Q.; Lu, Y. A Comprehensive Evaluation Framework for Building Energy Systems Considering Economic Efficiency, Independence, and Building-Grid Interaction Performance Indicators. Energy Build. 2024, 318, 114414. [Google Scholar] [CrossRef]
- Guo, Q.; Amin, S.; Hao, Q.; Haas, O. Resilience Assessment of Safety System at Subway Construction Sites Applying Analytic Network Process and Extension Cloud Models. Reliab. Eng. Syst. Saf. 2020, 201, 106956. [Google Scholar] [CrossRef]
- Yang, L.; Qin, H.; Zhang, J.; Su, H.; Li, G.; Bai, S. Cloud Model for Security State Recognition Based on Factor Space. IEEE Sens. J. 2021, 21, 25429–25436. [Google Scholar] [CrossRef]
- Zeng, X.; Zhuo, Y.; Liao, T.; Guo, J. Cloud-Gan: Cloud Generation Adversarial Networks for Anomaly Detection. Pattern Recognit. 2025, 157, 110866. [Google Scholar] [CrossRef]
- Chen, X.; Hu, Y.; Yao, K.; Sousa, R.L. Large-Deformation Finite-Element Modelling of Face Instability During Tunnelling in Clayey Soils: Incorporating Dynamic Excavation Process. Tunn. Undergr. Space Technol. 2024, 153, 106038. [Google Scholar] [CrossRef]
- Tian, R.; Zhang, Y.; Peng, L.; Wang, Y.; Wang, W.; Gu, Y. Measurement of Flood Resilience of Metro Station Based on Combination Weighting-Cloud Model. Int. J. Disaster Risk Reduct. 2024, 114, 104950. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Wan, R. Assessment of Water Disaster Resilience in Mountainous Urban Metro Stations by Combination Weighting Method and Extension Cloud Model. Water 2024, 16, 3266. [Google Scholar] [CrossRef]
- Xu, F.; Fang, D.; Chen, B.; Wang, H. Resilience Assessment of Subway System to Waterlogging Disaster. Sustain. Cities Soc. 2024, 113, 105710. [Google Scholar] [CrossRef]
- Liu, K.; Kou, Y.; Liu, Y.; Yang, X. Relationship Network of Safety Management Elements in the Construction Industry under the Perspective of Resilience. Eng. Constr. Arch. Manag. 2024. [Google Scholar] [CrossRef]
- Cheng, L.; Ren, H.; Guo, H.; Cao, D. Research on the Evaluation Method for Safety Cognitive Ability of Workers in High-Risk Construction Positions. Eng. Constr. Arch. Manag. 2024. [Google Scholar] [CrossRef]
- Han, K.; Zhai, Z.; Chen, X.; Zhang, C.; Ju, J.-W.W.; Bao, X.; Wang, S.; Hou, B. A Methodology for Evaluating the Safety Resilience of the Existing Tunnels Induced by Foundation Pit Excavation. Tunn. Undergr. Space Technol. 2025, 158, 106362. [Google Scholar] [CrossRef]
- Lin, X.-T.; Chen, X.; Su, D.; Han, K.; Zhu, M. An Analytical Model to Evaluate the Resilience of Shield Tunnel Linings Considering Multistage Disturbances and Recoveries. Tunn. Undergr. Space Technol. 2022, 127, 104581. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Q.-B. Modelling and Assessing Lifetime Resilience of Underground Infrastructure to Multiple Hazards: Toward a Unified Approach. Tunn. Undergr. Space Technol. 2025, 156, 106212. [Google Scholar] [CrossRef]
- Chen, C.; Xu, C.; Zhang, Z.; Zhi, Y.; Wang, Z.; Lyu, Z.; Zhang, Y. Highway Traffic Safety Evaluation Based on Topsis-Entropy Weight Method and Aerial Data. In Proceedings of the 12th International Conference on Traffic and Logistic Engineering (ICTLE), Macau, China, 23–25 August 2024; pp. 283–288. [Google Scholar]
- Peng, N.; Zhang, C.; Zhu, Y.; Zhang, Y.; Sun, B.; Wang, F.; Huang, J.; Wu, T. A Vulnerability Evaluation Method of Earthen Sites Based on Entropy Weight-Topsis and K-Means Clustering. Herit. Sci. 2024, 12, 161. [Google Scholar] [CrossRef]
- Tian, J.; Li, Z.; Zhuang, S.; Xi, J.; Li, M. Grading of Traffic Interruptions in Highways to Tibet Based on the Entropy Weight-Topsis Method and Fuzzy C-Means Clustering Algorithm. Appl. Sci. 2024, 14, 9094. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Kou, Y. Study on Construction Safety Management in Megaprojects from the Perspective of Resilient Governance. Saf. Sci. 2024, 173, 106442. [Google Scholar] [CrossRef]
- Feng, Z.; Shen, X.; Li, P.; Zhao, J.; Zhang, H.; Xu, Y.; Yuan, J. Performance Optimization and Scheme Evaluation of Liquid Cooling Battery Thermal Management Systems Based on the Entropy Weight Method. J. Energy Storage 2024, 80, 110329. [Google Scholar] [CrossRef]
- Xu, B.B.; Yang, W.G.; Yi, L.X.; Kong, D.K.; Liu, R.T. Topsis Model with Combination Weight for Demand Assessment of Flood Emergency Material Supplies. Aims Math. 2025, 10, 5373–5398. [Google Scholar] [CrossRef]
- Lin, S.-S.; Zhou, A.; Shen, S.-L. Safety Assessment of Excavation System Via Topsis-Based Mcdm Modelling in Fuzzy Environment. Appl. Soft Comput. 2023, 138, 110206. [Google Scholar] [CrossRef]
- Chen, Y.; Zhuang, T.; Liu, G. A Hybrid Approach to Supporting Physical-Change-Based Renewal Projects Selection Decisions in High-Density City: A Case Study of Chongqing. Eng. Constr. Arch. Manag. 2023, 30, 2879–2903. [Google Scholar] [CrossRef]
- Keniwe, M.S.S.; Ali, A.H.; Abdelaal, M.A.; Yassin, A.M.; Kineber, A.F.; Nosier, I.A.-R.; El Monayeri, O.D.; Elsayad, M. AIntroducing a Novel Decision Support System to Enhance Performance in Infrastructure Sanitation Projects within the Construction Industry. Eng. Constr. Arch. Manag. 2024, 32, 4581–4610. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; García, J.; Yepes, V. An Adaptive Anp & Electre Is-Based Mcdm Model Using Quantitative Variables. Mathematics 2022, 10, 2009. [Google Scholar] [CrossRef]
- Xu, J.; Li, L.; Ren, M. A Hybrid Anp Method for Evaluation of Government Data Sustainability. Sustainability 2022, 14, 884. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Song, L.; Ni, G.; Xu, N. Exploring the Metro Construction Accidents and Causations for Improving Safety Management Based on Data Mining and Network Theory. Eng. Constr. Arch. Manag. 2024, 31, 3508–3532. [Google Scholar] [CrossRef]
- Wang, Q.; Xue, H.; Yang, M.; Li, X.; Liu, C.; Zhao, S. Investigation of the Influence of Cutter Geometry on the Cutting Forces in Soft-Hard Composite Ground by Tunnel Boring Machine Cutters. Processes 2024, 12, 2243. [Google Scholar] [CrossRef]
- Yang, W.; Fang, Z.; Wang, M.; Wang, J.; Bai, J. Recognition of Formation Characteristics Based on Vibration Signals in Shield Tunneling. Tunn. Undergr. Space Technol. 2025, 155, 106199. [Google Scholar] [CrossRef]
- Xie, J.; Liu, B.; He, L.; Zhong, W.; Zhao, H.; Yang, X.; Mai, T.; Chen, Q. Quantitative Evaluation of the Adaptability of the Shield Machine Based on the Analytic Hierarchy Process (Ahp) and Fuzzy Analytic Hierarchy Process (Fahp). Adv. Civ. Eng. 2022, 2022, 3268150. [Google Scholar] [CrossRef]
- Kim, H.; Sanz-Alonso, D.; Yang, R. Optimization on Manifolds Via Graph Gaussian Processes\Ast. SIAM J. Math. Data Sci. 2024, 6, 1–25. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, J.; Su, L.; Pan, Y. Coherent Point Drift with Skewed Distribution for Accurate Point Cloud Registration. Comput. Graph. 2024, 122, 103974. [Google Scholar] [CrossRef]
- Cao, X.-Y.; Feng, D.-C.; Beer, M. A Kde-Based Non-Parametric Cloud Approach for Efficient Seismic Fragility Estimation of Structures under Non-Stationary Excitation. Mech. Syst. Signal Process. 2023, 205, 110873. [Google Scholar] [CrossRef]
- Khan, I.; Khan, D.M.; Noor-Ul-Amin, M.; Khalil, U.; Alshanbari, H.M.; Ahmad, Z. Hybrid Ewma Control Chart under Bayesian Approach Using Ranked Set Sampling Schemes with Applications to Hard-Bake Process. Appl. Sci. 2023, 13, 2837. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhuo, W.; Cui, J.; Luan, H.; Chen, Y.; Lin, D. Developing a Deep Reinforcement Learning Model for Safety Risk Prediction at Subway Construction Sites. Reliab. Eng. Syst. Saf. 2025, 257, 110885. [Google Scholar] [CrossRef]
- Huo, X.; Du, S.; Jiao, L. Critical Causal Path Analysis of Subway Construction Safety Accidents Based on Text Mining. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2025, 11, 04024075. [Google Scholar] [CrossRef]
- Yu, Y.; Shuai, B.; Huang, W. Resilience Evaluation of Train Control on-Board System Based on Multi-Dimensional Continuous-Time Bayesian Network. Reliab. Eng. Syst. Saf. 2024, 246, 110099. [Google Scholar] [CrossRef]
- Chen, H.; Yang, S.; Feng, Z.; Liu, Y.; Qin, Y. Safety Evaluation of Buildings Adjacent to Shield Construction in Karst Areas: An Improved Extension Cloud Approach. Eng. Appl. Artif. Intell. 2023, 124, 106386. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).