Parametric and Correlation Study of Effusion Cooling Applied to Gas Turbine Blades

Abstract

To pursue higher thermal efficiency in aero gas turbines, the contradiction between extreme high-temperature conditions and material temperature resistance limits has made advanced thermal management technologies crucial. Effusion cooling is a technique that utilizes a large number of small holes (around 0.1 mm in diameter) to cool more effectively. Through numerical simulation, the current research investigates the impact of different parameters on the effectiveness of effusion cooling, including porosities (φ), blowing ratios (Br), height of the porous structure (H), thermal conductivity (λ) of the porous structures, and the ratios of the mainstream temperature to the coolant temperature (R_t). The results show that with the increased porosity, the cooling effectiveness of the porous structure surface first increases and then decreases, while the averaged cooling effectiveness downstream of the mainstream gradually increases. The first two parameters have the greatest influence on the cooling effectiveness. And there is a positive relationship between the blowing ratios and cooling effectiveness, meaning that higher blowing ratios lead to greater cooling effectiveness. A larger height and a smaller thermal conductivity coefficient cause a non-uniform temperature distribution. Different temperature ratios have little influence on coolant coverage pattern. Finally, a correlation is built to predict the cooling effectiveness considering all the parameters which provides fundamental references for the application of effusion cooling.

1. Introduction

Increasing rotor inlet temperature (RIT) is an essential route to improving gas turbine efficiency [1]. However, the resulting thermal loads often approach or even exceed the allowable limits of blade materials [2,3]. Effective cooling strategies are therefore indispensable. Film cooling employs arrays of 1 mm diameter holes through which coolant is injected tangentially along the blade wall, forming a thin, adherent film that shields the metal surface from the hot mainstream and extends blade life. In contrast, effusion cooling utilizes a larger number of 0.1 mm diameter holes arranged more densely. Figure 1 illustrates this principle: the closely spaced micro-holes generate multiple interacting jets that adhere to the porous surface and establish a continuous protective layer. The enlarged coolant–solid interface enhances heat transfer and yields a more uniform temperature field across the surface [4].

As with film cooling, effusion-cooling performance is governed by numerous parameters, including blowing ratio [5,6,7,8,9,10], porosity [11,12,13,14], hole size [9,15,16,17], hole arrangement [9,15,18], and inclination angle [10,19,20]. Some scholars have performed a large number of investigations on this topic. Lin et al. [21] conducted combined experimental and numerical investigations of full-coverage inclined multi-hole film cooling. Their results indicate that hole arrangement and spacing are the dominant parameters controlling both the spatial distribution and the magnitude of local cooling effectiveness. Yang et al. [10] experimentally demonstrated that both hole arrangement and blowing ratio significantly affect cooling effectiveness and heat transfer. Specifically, increasing the blowing ratio enhances effectiveness but reduces the heat-transfer coefficient. Jun-Hee Kim and Kwang-Yong Kim [22] examined a novel convergent-inlet design for cylindrical film-cooling holes. By optimizing four geometric parameters—streamwise expansion angle, lateral expansion angle, injection angle, and the aspect ratio of the cylindrical section—they achieved a 46.5% improvement in effectiveness relative to conventional cylindrical holes.

Compared with film cooling, effusion cooling differs not only in hole diameter but also in the conjugate heat transfer that occurs within the porous structure [23,24,25,26,27,28]. Ji et al. [25] investigated conjugate heat transfer during effusion cooling of a swirl-stabilized combustor liner in a non-reacting three-nozzle gas turbine model. Their study showed that although main-flow impingement disrupts the cooling film, convection inside the cooling holes still removes substantial heat. Higher cooling-airflow rates improve performance despite the risk of film detachment. Arjun et al. [26] found that a conjugate heat-transfer model accounting for material thermal conduction provides more cooling protection than an adiabatic model and that the optimum cooling-hole angle is 30°. Chen et al. [28] numerically studied coupled heat transfer in impingement–effusion double-wall cooling under various cross-flow arrangements. Their results indicate that the integrated cooling performance of the conjugate system exceeds that of pure impingement cooling by 4.7% to 28.0% because it combines internal impingement with external film protection. Although effusion cooling is regarded as the most effective cooling method, its structural vulnerabilities remain a significant concern [29,30,31,32]. Huang et al. [33] experimentally and numerically examined transpiration cooling of an additively manufactured perforated plate with partition walls. They reported that partition walls have little effect on cooling effectiveness but significantly improve mechanical strength. Addressing the hole uniformity issue inherent in additively manufactured small holes, Huang and He [11] investigated the influence of hole heterogeneity on effusion cooling. They discovered that non-uniform porosity markedly alters both the surface coolant layer and the internal hole cooling performance.

Researchers have investigated combined cooling strategies that integrate effusion cooling with other techniques [24,34,35,36,37,38]. Oguntade [35] predicted the performance of individual effusion and impingement schemes and then compared them with their combined configuration, showing that the hybrid impingement–effusion approach yields synergistic heat-transfer enhancement unattainable by either method alone. Qu et al. [24] evaluated the cooling effectiveness of hybrid slot–effusion systems against isolated slot injection and effusion-only configurations, demonstrating that the combined design surpasses the limitations of each standalone technique. Cho and Rhee [36] experimentally measured heat and mass transfer on a perforated plate with impingement–effusion cooling. For plates with small cavity gaps, neighboring impingement jets interact negligibly, and the gap flow behaves like fully developed pipe flow, resulting in enhanced heat and mass transfer rates.

In the majority of current effusion-cooling studies, the influence of parameters on cooling efficiency has been studied, yet a numerical relationship between these parameters and cooling effectiveness is not established.

Through numerical simulation, this research investigates the effects of porosities (φ), blowing ratios (Br), porous structure heights (H), the thermal conductivity of the porous structure material (λ), and the ratio of the mainstream temperature to the coolant temperature (R_t) on the cooling effectiveness of effusion cooling. Based on the Levenberg–Marquardt algorithm and through successive fittings of individual variables, a correlation between these parameters and the averaged cooling effectiveness is derived.

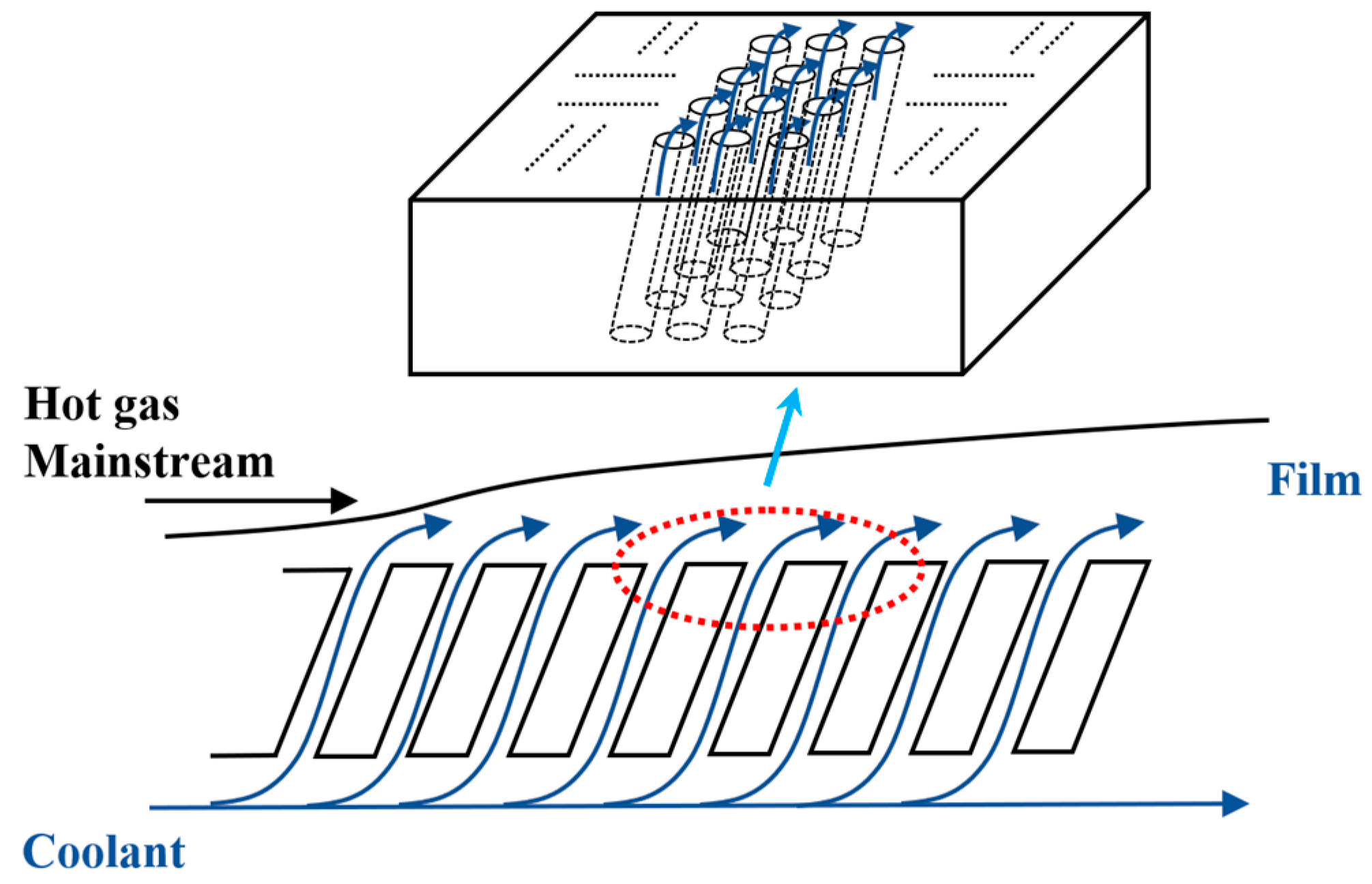
2. Numerical Setup

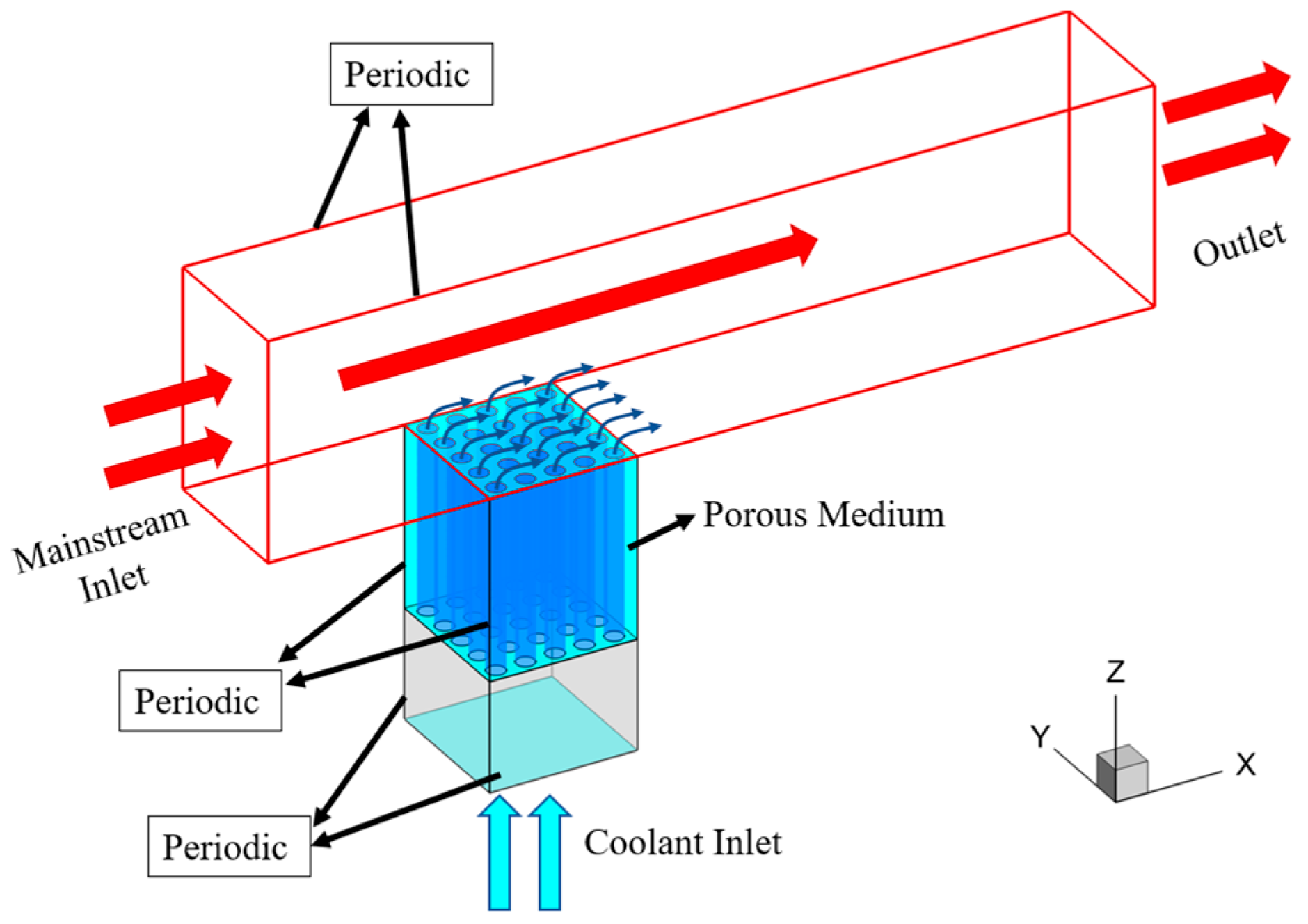
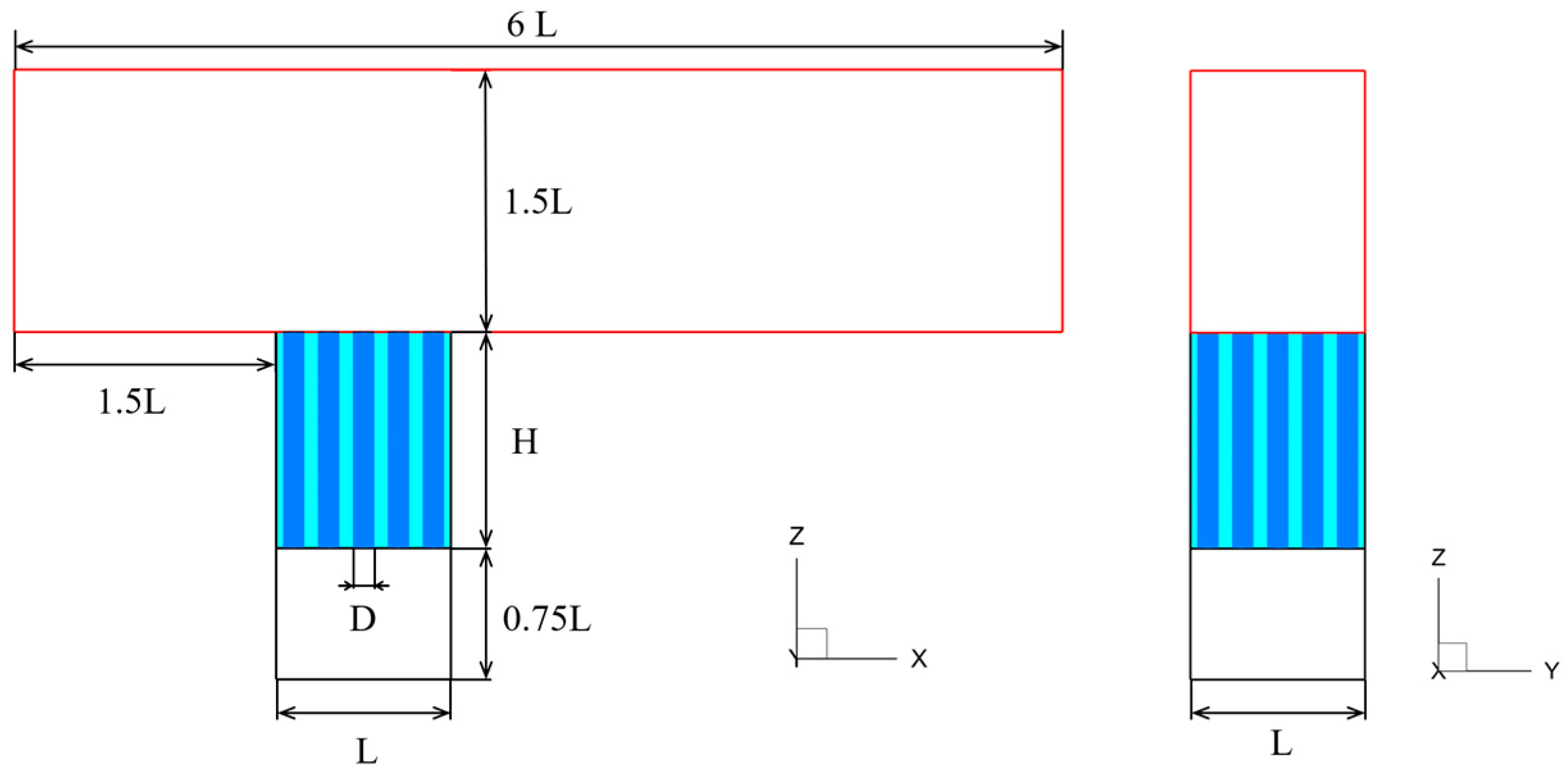
2.1. Geometric Model

The geometric model of this study is shown in Figure 2, divided into fluid and solid domains. High-temperature gas flows into the system through the mainstream inlet, and the coolant gas enters through the coolant inlet and passes through the porous structure to mix with the mainstream. Periodic conditions are set on the lateral sides perpendicular to the Y-axis.

The model dimensions are shown in Figure 3. The coolant channel is rectangular and measures L × L × 0.75 L with L = 1 mm. The mainstream channel is also a rectangular channel, with dimensions of 6 L × L × 1.5 L. The height of the porous structure is H which ranges from 6D to 14D, with hole diameter D. Five heights and five diameters are investigated. In this study, the porosity (φ) is defined as the hole volume (V_h) divided by the solid material volume in the perforated region (V_s, L × L × H), as shown in Equation (1). Each diameter corresponds to a unique porosity.

$$\phi ={\displaystyle \frac{V_{\mathrm{h}}}{V_{\mathrm{s}}}}$$

(1)

To control the variables, a reference model with 30% porosity, a hole diameter of 0.12 mm, and a porous structure height of 10D is employed. This model is used in all cases to explore the effects of blowing ratios, the thermal conductivity of the porous structure, and the ratios of the mainstream temperature to the coolant temperature on the cooling effectiveness. Keeping porosity at 30%, heights of 6D, 8D, 10D, 12D, and 14D are selected to study the influence of height. Conversely, with height fixed at 10D, porosities of 10%, 20%, 30%, 40%, and 50% are adopted to investigate the influence of porosity.

2.2. Boundary Conditions

Boundary conditions can be referred to in Figure 2. The fluid and solid domains are thermally coupled. The mainstream and the coolant inlet are both set as mass flow inlets, while the outlet is set as a pressure outlet. The fluid is set as an ideal gas with the thermophysical properties of air. Given the mainstream inlet mass flow rate of 0.15 g/s, the blowing ratio (Br) is defined as Equation (2):

$$\mathrm{Br}={\displaystyle \frac{{\rho }_{\mathrm{C}}{V}_{\mathrm{C}}}{{\rho }_{\mathrm{M}}{V}_{\mathrm{M}}}}$$

(2)

where ρ_C and V_C correspond to the coolant inlet density and velocity, and ρ_M and V_M correspond to the mainstream density and velocity. The coolant was held at a constant 300 K, and the effects of different ratios of temperature (R_t) varying from 1.3 to 5 on cooling effectiveness were explored by setting the mainstream temperatures at 400 K, 600 K, 900 K, 1200 K, and 1500 K.

Based on Equation (2) and to investigate the effect of different blowing ratios on the cooling effectiveness, five blowing ratios of 1%, 2%, 3%, 4%, and 5% were selected. The corresponding coolant mass flow rates at the inlet are 0.001, 0.002, 0.003, 0.004, and 0.005 g/s. The porous structure materials are set to titanium (Ti), steel, nickel (Ni), aluminum (Al), and copper (Cu), with corresponding thermal conductivities (λ) of 7.44 W/(m·K), 16.27 W/(m·K), 91.74 W/(m·K), 202.4 W/(m·K), and 387.6 W/(m·K) respectively, to investigate the effect of different material thermal conductivities on cooling effectiveness. The dimensionless parameter η represents cooling effectiveness, defined as Equation (3):

$$\eta ={\displaystyle \frac{T_{\mathrm{M}}–T_{\mathrm{W}}}{T_{\mathrm{M}}-T_{\mathrm{C}}}}$$

(3)

In this study, the dimensionless number θ is used to characterize the temperature distribution of the outer wall of the porous media; θ is defined as Equation (4):

$$\theta ={\displaystyle \frac{T_{\mathrm{W}}-T_{\mathrm{C}}}{T_{\mathrm{M}}-T_{\mathrm{C}}}}$$

(4)

where T_M is the temperature of the mainstream inlet, T_C is the temperature of the coolant inlet, and T_W is the surface temperature of the outer wall of the porous media.

And the averaged cooling effectiveness is defined as Equation (5):

$$\dot{\eta }={\displaystyle \frac{1}{A}}{\displaystyle \underset{A}{\iint }\eta (x,y)dxdy}$$

(5)

All cases and related parameters set in the current research are shown in

Table 1. All cases and related parameters set.

Case Name	φ	Br	H	Material, λ	Rt
A1	10%	0.3%	10D	Steel, 16.27 W/(m·K)	1.3
A2	20%
A3	30%
A4	40%
A5	50%
B1	30%	0.1%	10D	Steel, 16.27 W/(m·K)	1.3
B2		0.2%
B3		0.3%
B4		0.4%
B5		0.5%
C1	30%	0.3%	6D	Steel, 16.27 W/(m·K)	1.3
C2			8D
C3			10D
C4			12D
C5			14D
E1	30%	0.3%	10D	Titanium, 7.44 W/(m·K)	1.3
E2				Steel, 16.27 W/(m·K)
E3				Nickel, 91.74 W/(m·K)
E4				Aluminum, 202.4 W/(m·K)
E5				Copper, 387.6 W/(m·K)
F1	φ = 30%	0.3%	10D	Steel, 16.27 W/(m·K)	1.3
F2					2
F3					3
F4					4
F5					5

.

2.3. Numerical Method

This study employs Fluent Meshing to generate the computational grid illustrated in Figure 4. In the main region, the generated mesh is composed of unstructured polyhedrons, and the boundary layer mesh is a regular prism mesh. All cases presented in Table 1 follow the same methodology. To guarantee calculation accuracy, the mesh at the fluid–solid interface was refined and shared topology was employed to enforce node matching. The simulations were performed with Ansys Fluent 2022 R1.

Three-dimensional (3D) steady-state RANS simulations were conducted in this work. Based on the study reported in [12], the Shear Stress Transport (SST) k-ω turbulence model was employed and pressure–velocity coupling was handled by the SIMPLEC algorithm. The governing equations for density, momentum, turbulence parameters (k and ω), and energy were discretized with a second-order upwind scheme. Convergence was achieved when residuals fell below 10⁻⁶ for continuity/momentum/energy and 10⁻⁵ for turbulence quantities.

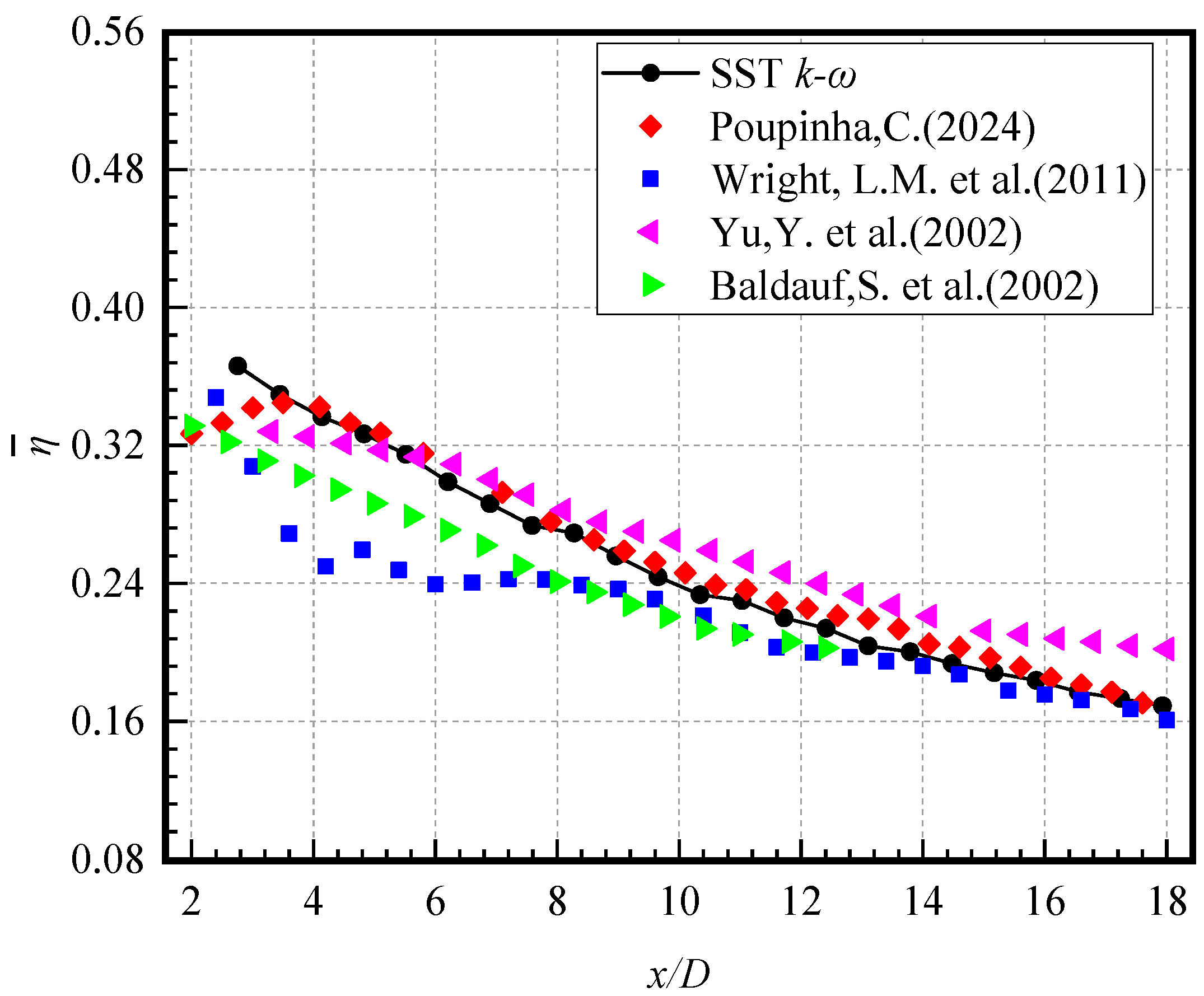
2.4. Turbulence Model Verification

Because film cooling and effusion cooling have certain similarities, this study employs the SST k-ω model, which has been validated against the film-cooling experiments reported in [39,40,41,42]. The cooling effectiveness of the cylindrical film cooling at Br = 0.5 was compared. Figure 5 reflects the simulation and experiment results of the lateral averaged cooling effectiveness ($\overline{\eta }$), which is defined as Equation (6):

$$\overline{\eta }={\displaystyle \frac{1}{\mathrm{L}}}{\displaystyle {\int }_0^{\mathrm{L}}\eta (x,y)}dy$$

(6)

As shown in Figure 5, the results calculated using the SST k-ω model exhibit a trend consistent with other experimental results, with the $\overline{\eta }$ gradually decreasing along the mainstream direction. Furthermore, the error between the simulation results obtained from the SST k-ω model and experimental results is less than 10%. Therefore, the SST k-ω model is appropriate for subsequent simulations in this study.

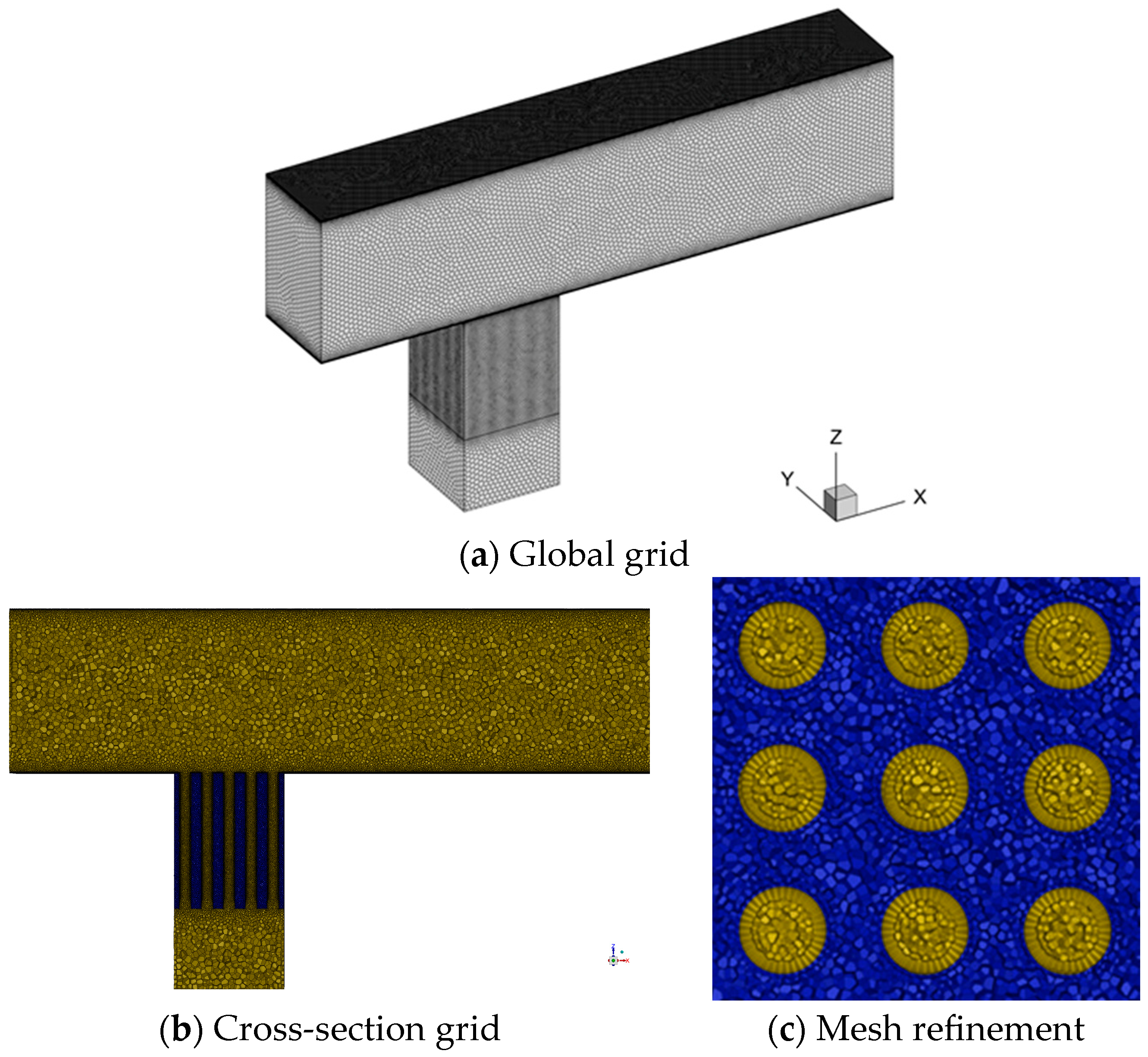
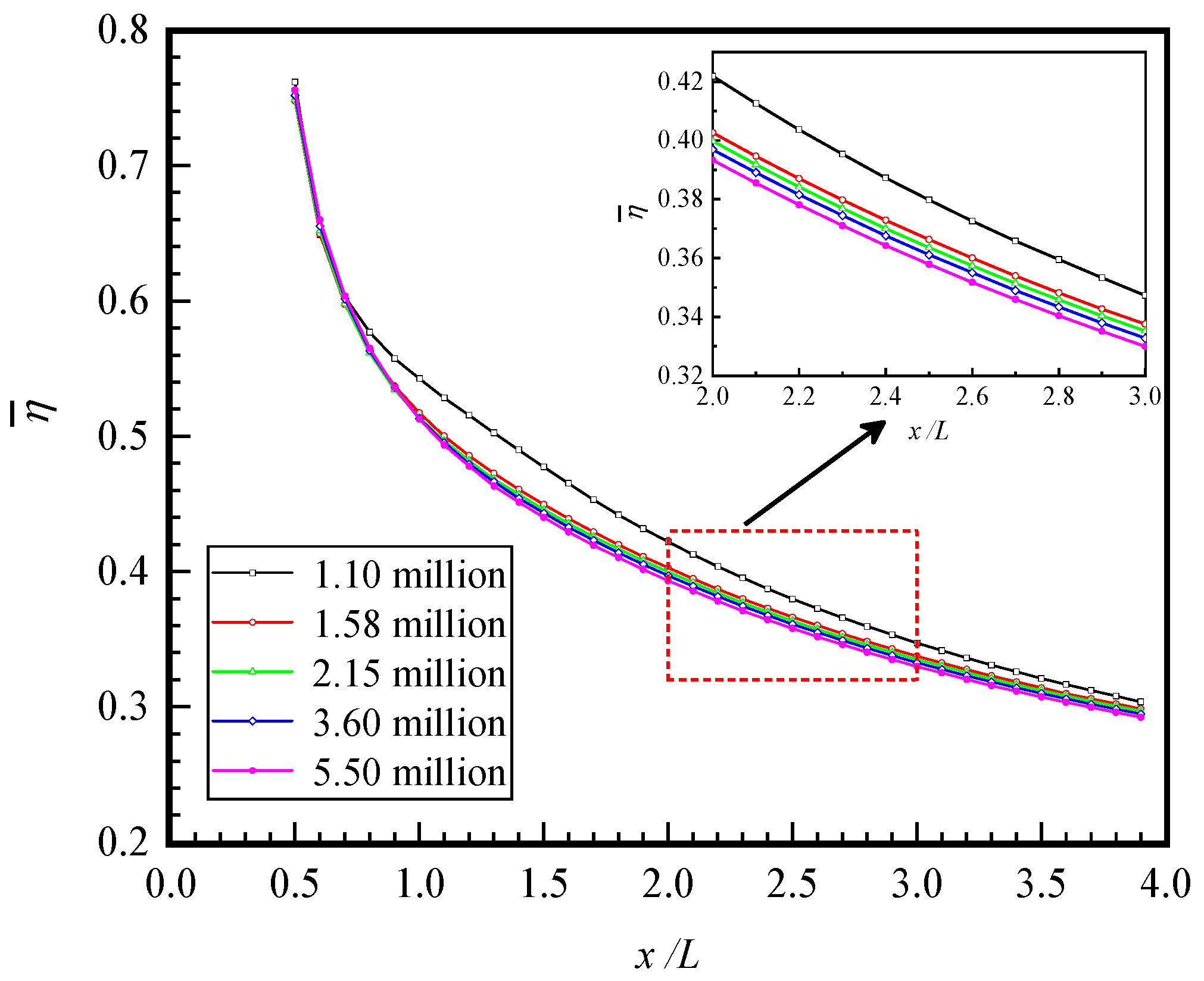
2.5. Grid Independence Verification

The grid independence verification was conducted with five different meshes: 1.10 million, 1.58 million, 2.15 million, 3.60 million, and 5.50 million elements. Simulations were performed under the boundary conditions of Case A3. The $\overline{\eta }$ downstream of the porous structure on the bottom surface of the mainstream channel is shown in Figure 6. The maximum difference in $\overline{\eta }$ for the 1.10 million grids and 1.58 million grids exceeds 6%. However, the difference in $\overline{\eta }$ for the 1.58 million grids and 2.15 million grids is less than 1%. And with further grid refinement, the difference in $\overline{\eta }$ between the 3.60 million grids and either the 2.15 grids or the 5.50 million grids remains below 1%. These results indicate that a grid comprising 3.60 million elements is sufficient for mesh-independent solutions and is therefore adopted for all subsequent simulations.

3. Results and Discussion

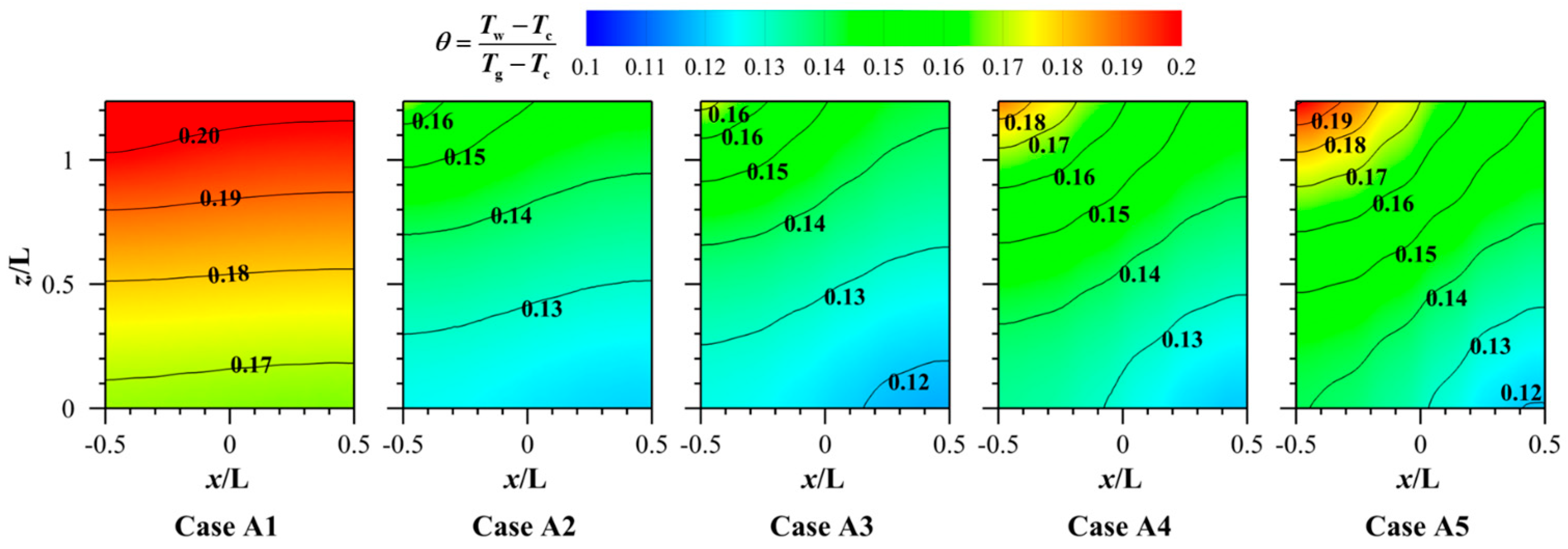
3.1. Effect of Different Porosities

Figure 7a presents the contours of η on the porous structures and the downstream regions for effusion cooling with different porosities, and Figure 7b illustrates the $\overline{\eta }$ downstream of the mainstream at different porosities. The porosities range from 10% to 50% corresponding to Cases A1 to A5 respectively. As shown in Figure 7a, the η of the porous structure exceeds that in the downstream region because the coolant, issuing directly from the porous channel, fully cools the structure. The η is higher in the upper downstream area than in the lower part, and a peak-shaped high-η region appears where the coolant is deflected by the mainstream. It can be observed that as the porosity increases from 10% (Case A1) to 30% (Case A3), the $\dot{\eta }$ of the porous structure surface gradually increases. However, when the porosity increases from 30% (Case A3) to 50% (Case A5), the $\dot{\eta }$ of the porous structure surface shows a decline. This indicates that the benefit of increasing porosity reaches saturation and structural integrity weakens. Figure 7b clearly shows the impact of porosity changes on η. As the porosity continuously increases, the $\overline{\eta }$ downstream of the mainstream also increases. This is because the continuous increase in porosity enlarges the coolant distribution range, resulting in stronger convective cooling effects. However, when the porosity increases from 30% (Case A3) to 50% (Case A5), the increase is relatively slight, indicating that the impact of porosity on η is approaching saturation, and further increasing the porosity cannot bring about significant improvements.

Figure 8 displays the velocity distribution in the middle cross-section at different porosities. In the downstream part of the mainstream, the near-wall layer exhibits significantly lower velocities compared to the mainstream, with a distinct low-velocity zone observed near the coolant channel exit. This results from the orthogonal momentum exchange between coolant injection and the mainstream. Simultaneously, this interaction impedes the downward heat transfer from the mainstream, forming an effective coolant coverage layer along the surface, and along the mainstream direction, a reduction in coolant coverage thickness is observed. As the porosity gradually increases, the velocity within the coolant channels decreases and the coolant coverage layer becomes slightly thinner, which is due to the fact that under a certain coolant mass flow rate, the increase in total flow area results in a reduction in velocity. The velocity of the coolant channels near the mainstream is lower because the high-speed airflow of the mainstream exerts a greater pressure, suppressing the outflow of the coolant. Additionally, with the increase in the porosity, the coolant coverage thickness decreases slightly, which is also caused by the reduction in the velocity of the coolant.

Figure 9 presents the θ distribution on the periodic interface of the porous structure at different porosities. Due to the structure symmetry and steady-state conditions, the temperature distribution at each interface of the porous structure is consistent. There is a significant temperature gradient in the solid porous structure. In Case A1, the lower porosity and smaller contact area limit heat transfer yet produce a relatively uniform temperature. With higher porosity (Case A3–Case A5), the temperature at the bottom near the downstream end is lower, but thermal hotspots persist near the leading edge of the mainstream, resulting in an uneven temperature distribution and a large gradient. This is because the coolant velocities in the channels remain low, and the mainstream pressure forms a certain blockage effect, weakening its heat dissipation performance, thus leading to local high temperatures. As porosity increases, the overall $\dot{\eta }$ of the porous surface improves, yet the reduced velocity in the coolant channels eventually lowers thermal performance. The local high-temperature zone shifts to the outer surface near the upper end of the mainstream and the temperature gradient grows. Nonetheless, the greater porosity allows the injected coolant to cover a wider region, thereby improving downstream η along the mainstream.

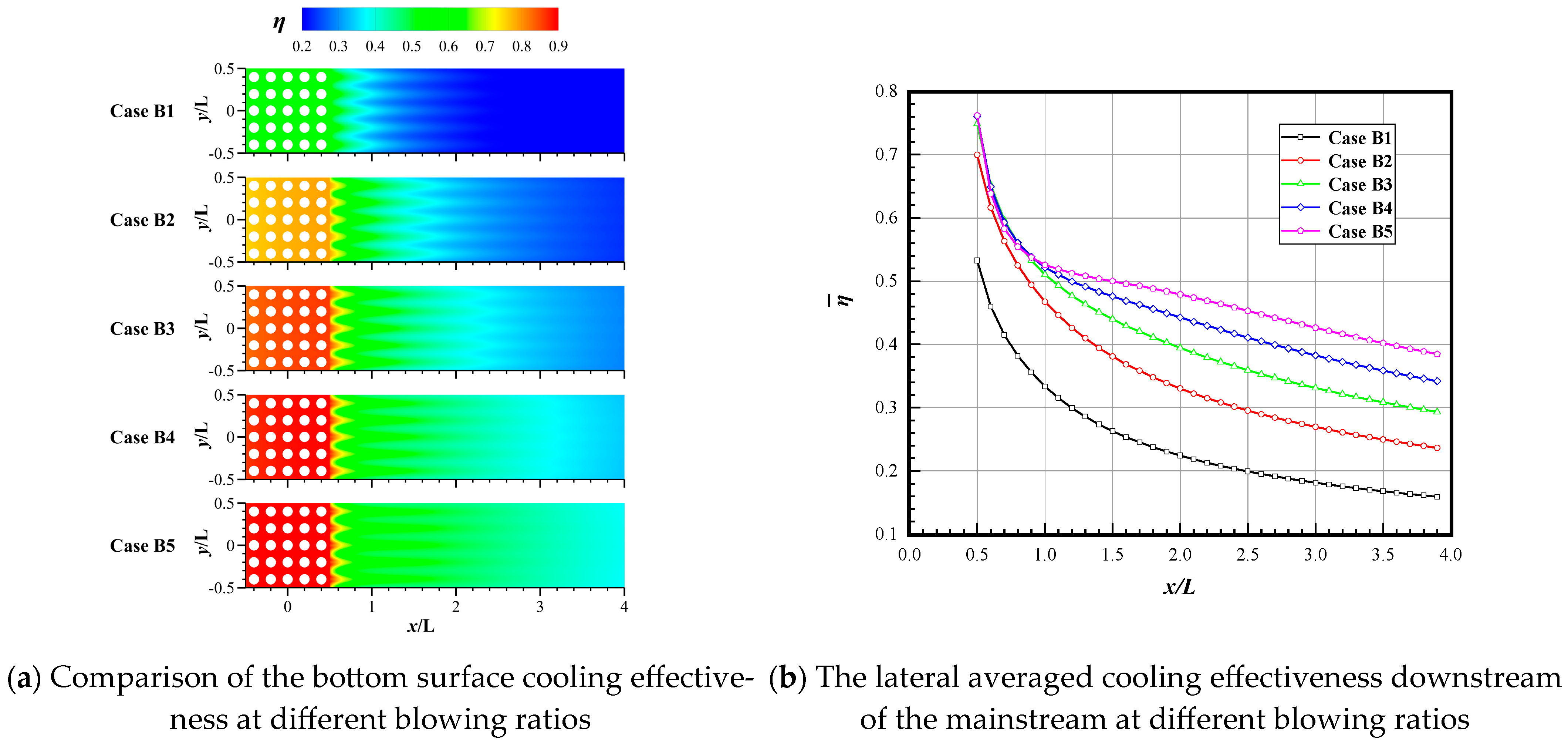
3.2. Effect of Different Blowing Ratios

Figure 10a reflects the contours of η on the bottom surface at different blowing ratios that range from 0.1% to 0.5%, corresponding to Cases B1 to B5, respectively. Similar to Figure 7, the porous structure area exhibits a higher and more uniform η than the downstream area. A peak-shaped high-effectiveness cooling zone also appears downstream of the leading edge. In Figure 10a, as the blowing ratio increases, the $\dot{\eta }$ of the porous structure continuously increases. At a blowing ratio of 0.5% (Case B5), the $\dot{\eta }$ of the porous structure surface reaches 0.9. The reason is that higher blowing ratios elevate the coolant mass flow rate, which can carry away more heat, resulting in stronger cooling capacity. Elevated blowing ratios contract the leading-edge peak cooling zone while homogenizing rear-region thermal coverage.

Figure 10b shows the $\overline{\eta }$ downstream of the mainstream at different blowing ratios that range from 0.1% to 0.5%, corresponding to Cases B1 to B5, respectively. The $\overline{\eta }$ along the mainstream downstream direction gradually increases with rising blowing ratio. As the blowing ratio rises from 0.2% (Case B2) to 0.5% (Case B5), the $\overline{\eta }$ remains relatively comparable between x/L = 0.5 and 1.0. Between x/L = 1.0 and 4.0, the $\overline{\eta }$ exhibits an increasing trend. This is because in this area, the effect of the mainstream on the coolant is weakened, and the coolant coverage is more uniform. Increasing the blowing ratio improves cooling performance. This reveals that the blowing ratio plays a positive role in enhancing the $\overline{\eta }$.

Figure 11 shows the velocity distribution in the middle cross-section at different blowing ratios. A distinct low-velocity zone appears downstream, created by the coolant jet, and forms an effective cooling layer that shields the wall from thermal erosion. Within the proximal zone adjacent to the coolant channel outlet in the downstream section, there is also a distinct low-velocity zone. Because Case B1 has the smallest blowing ratio, its low-velocity zone is noticeably smaller than those in Cases B2–B5, so the $\overline{\eta }$ of Case B1 is lower between x/L = 0.5 and 1.0. As the blowing ratio increases, channel velocity rises and the cooling layer thickens because the higher blowing ratio increases the coolant mass flow. In addition, the velocity in channels near the rear exceeds that in channels near the front because mainstream pressure at the front slows the coolant, whereas the rear remains less affected.

Figure 12 reflects the θ distribution on the periodic interface of the porous structure at different blowing ratios. As θ increases, the temperature also rises. It can be observed that as the blowing ratio increases, the temperature on the outer surface of the porous structure gradually decreases, and the temperature distribution becomes more uniform. From the top-left corner to the top-right corner, the temperature progressively rises. This is also due to the influence of the mainstream pressure, but this effect diminishes as the blowing ratio increases. With the increase in the blowing ratio from Case 1 to Case 5, the θ gradually decreases, indicating a progressive reduction in the temperature of the porous structure. This confirms enhanced thermal protection of the porous structure at higher blowing ratios. Higher blowing ratios thus yield greater cooling effectiveness.

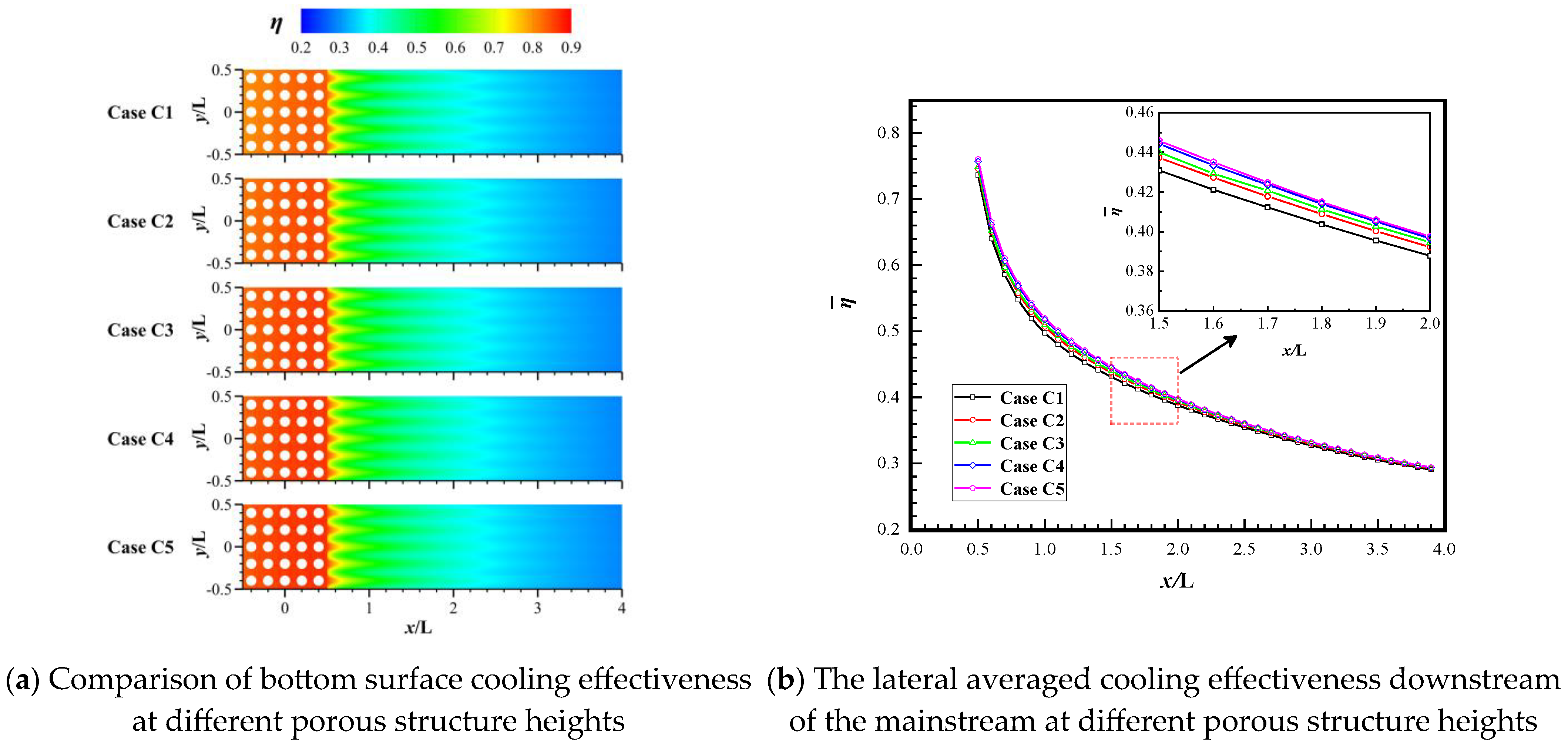
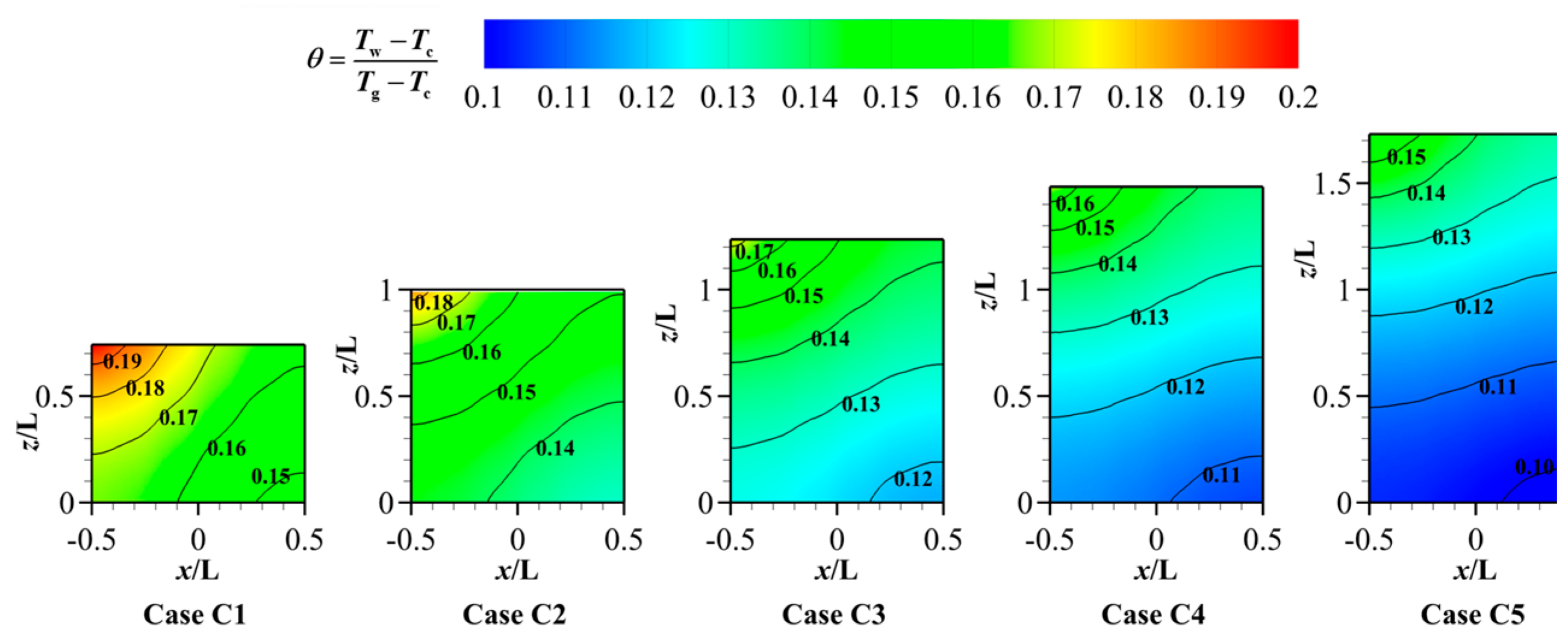
3.3. Effect of Different Porous Structure Heights (H)

Figure 13 reflects the contours of the bottom surface η and the $\overline{\eta }$ downstream of the mainstream at different porous structure heights that range from 6D to 14D, corresponding to Cases C1 to C5, respectively. Figure 13a shows that η within the porous region exceeds that in the downstream region, and a peak-shaped high-η zone appears near the front edge of the downstream area. The surface $\overline{\eta }$ of the porous structure improves slightly with increasing structure height, yet the gain remains marginal, because taller structures neither alter the flow pattern nor enhance heat transfer. Meanwhile, the η in the downstream region stays almost identical across Cases C1–C5. However, as shown in Figure 13b, with rising height of the porous structure, the $\overline{\eta }$ downstream of the mainstream gradually increases. There is a certain upward trend in the first half of the downstream mainstream, while in the second half of the downstream mainstream, the curves are very close to each other. Thus, structure height influences cooling effectiveness but does not govern it.

Figure 14 indicates the θ distribution of the periodic interface on the porous structure at different porous structure heights (H). Despite the height variations, the θ of the outer surface generally decreases diagonally from the upper-left to the lower-right corner. As H increases, the average temperature on the outer surface gradually decreases and no high-temperature zones appear. A larger low-temperature zone emerges near the coolant inlet on the right because greater height enlarges the coolant–solid contact area and strengthens heat transfer. Hence, increasing H enhances cooling performance.

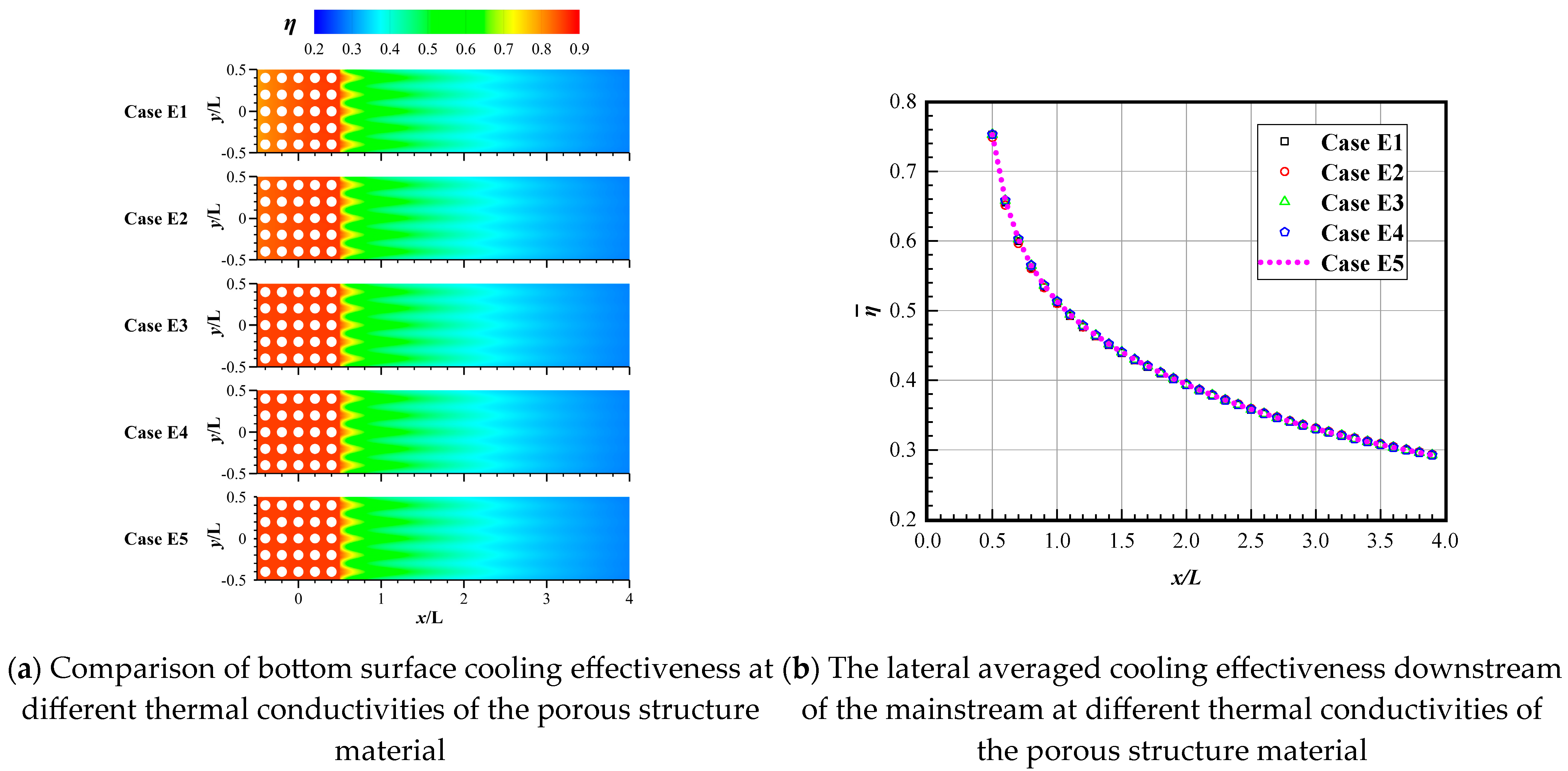
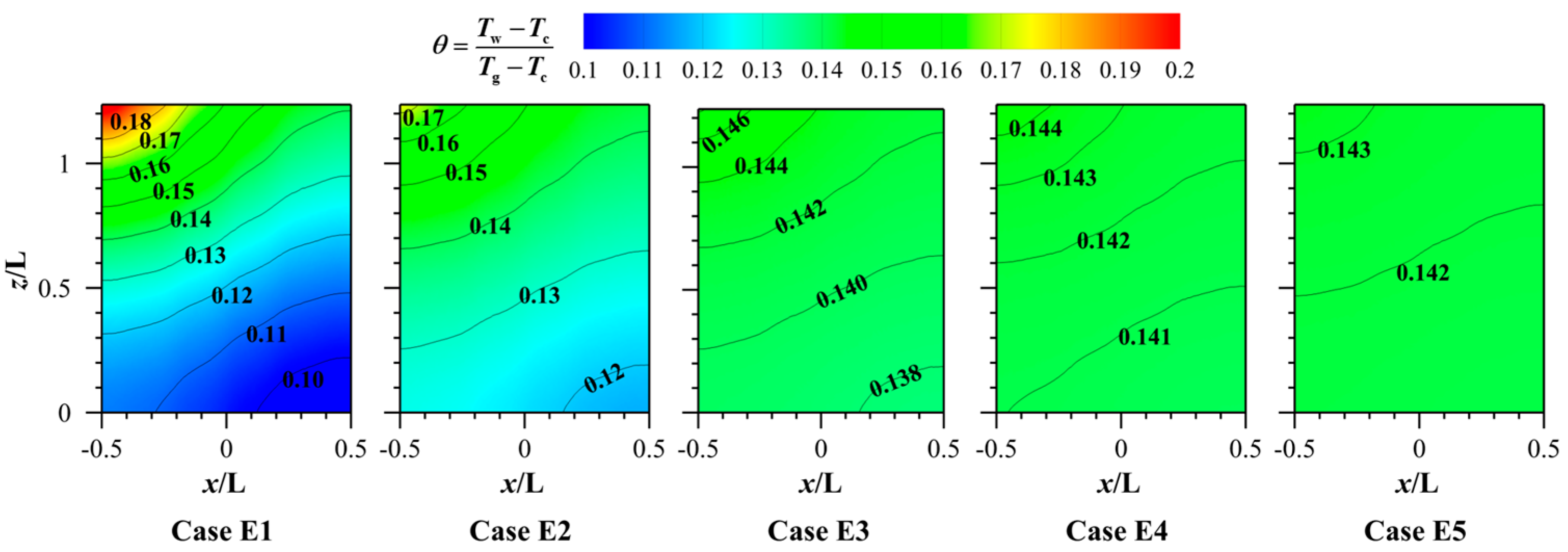
3.4. Effect of Different Thermal Conductivities (λ) of the Porous Structure Material

Figure 15 shows the contours of the bottom surface η and the $\overline{\eta }$ downstream of the mainstream at different thermal conductivities (λ) of the porous structure materials—titanium (7.44 W/(m·K)), steel (16.27 W/(m·K)), nickel (91.74 W/(m·K)), aluminum (202.4 W/(m·K)), and copper (387.6 W/(m·K))—corresponding to Cases E1 to E5, respectively. Figure 15a shows that the η within each porous region exceeds that in the downstream mainstream region, and peak-shaped high-effectiveness cooling zones form in all cases. For titanium materials (7.44 W/(m·K)), the porous structure region shows an uneven η, which decreases along the mainstream direction. With increasing λ, the η of the porous surface improves slightly and its distribution becomes more uniform because higher thermal conductivity enhances heat transfer, resulting in faster and more uniform cooling, consistent with the findings of [12]. Figure 15b presents the $\overline{\eta }$ downstream of the mainstream. It is shown that the $\overline{\eta }$ of the downstream region is essentially consistent in Cases E1 to E5. This indicates that changing the λ of materials cannot be a critical influence on the cooling performance.

Figure 16 reflects the θ distribution of the periodic interface of the porous structure at different thermal conductivities (λ) of materials. It can be observed that due to the low thermal conductivity of titanium (Case 1, 7.44 W/(m·K)), the θ distribution on the outer surface exhibits significant non-uniformity. Specifically, the θ near the coolant inlet is relatively low, corresponding to lower temperatures. Across all cases, the overall trend demonstrates a gradual decrease in θ from the upper-left to the lower-right corner. It is evident that with increasing λ, the temperature distribution becomes more uniform. As λ increases, the temperature field becomes progressively more uniform, heat transfer is enhanced, and the average outer-surface temperature falls. However, with the increase in λ, the difference in the average temperature of the outer surface becomes significantly reduced, reaching a threshold. Increasing the λ has a certain effect on improving the η of the porous surface, but it cannot markedly enhance the cooling performance downstream of the mainstream. Moreover, increasing the λ to a certain extent can reduce the temperature on the outer surface of the porous structure.

3.5. Effects of Different Temperature Ratios

Figure 17 reflects the contours of the bottom surface η and the $\overline{\eta }$ downstream of the mainstream at different ratios of the mainstream temperature to the coolant temperature. As shown in Figure 17a, the η of the porous structure surface decreases as the temperature ratio increases. This reveals that although η is a relative measure, differences in the mainstream inlet and coolant inlet temperatures also lead to variations in η. Figure 17b clearly demonstrates the $\overline{\eta }$ downstream of the mainstream at different ratios of the mainstream temperature to the coolant temperature. In conjunction with Figure 17a, it is obvious that the $\overline{\eta }$ downstream of the mainstream under various ratios of temperature is relatively close. However, the case with a lower temperature ratio has relatively lower η in the second half.

Figure 18 shows the vorticity contour of Case F1 based on the Q criterion. The boundary conditions of Cases A3, B3, C3, E3, and F1 are consistent. Since the model structures of each case are similar, the difference lies in the boundary conditions. Thus, the flow structures of all cases are similar. Therefore, the vorticity contour of Case F1 can reflect the overall flow situation. As can be seen from Figure 18, at the front end of the coolant outlet, a larger vortex structure can be observed, which is caused by the influence of the coolant jet, lifting the airflow in this area. Between each pair of holes in the coolant channel, a small vortex can be observed; this is because the mainstream and coolant are perpendicular to each other and interact, forming small recirculation zones between the holes. Downstream of the coolant outlet, numerous complex vortices can be clearly observed. These vortices are formed due to the interaction between the mainstream and the coolant jet, resulting in fragmented small-scale vortices that create an effective cooling protective layer near the wall surface. In the middle of the downstream region, a lifted vortex can be observed. This occurs because the coolant jet, after entering the mainstream flow, is pushed downward by the high-speed mainstream, causing the shear layers on both sides of the jet to roll up under the transverse pressure gradient. As a result, a pair of counter-rotating, streamwise-extending tubular vortices is formed.

4. Correlations

According to the simulation results obtained in this study, a correlation relationship between the $\overline{\eta }$ and the porosity (φ), the blowing ratio (Br), the height of the porous structure (H), the thermal conductivity of the porous structure material (λ), and the ratio of the mainstream temperature to the coolant temperature (Rt) was established to predict the $\dot{\eta }$ of the porous structure surface under different parameters.

Table 2. The averaged cooling effectiveness of the porous surface under various cases.

Case	φ	Br	H	Material, λ	Rt	$\dot{\mathit{\eta }}$
A1	10%	0.3%	10D	Steel, 16.27 W/(m·K)	1.3	0.7948708
A2	20%					0.8473646
A3	30%					0.8472585
A4	40%					0.8370339
A5	50%					0.8281744
B1	30%	0.1%	10D	Steel, 16.27 W/(m·K)	1.3	0.6036934
B2		0.2%				0.7765922
B3		0.3%				0.8472585
B4		0.4%				0.8831263
B5		0.5%				0.9037894
C1	30%	0.3%	6D	Steel, 16.27 W/(m·K)	1.3	0.8241882
C2			8D			0.8377439
C3			10D			0.8472585
C4			12D			0.8528423
C5			14D			0.8573566
E1	30%	0.3%	10D	Ti, 7.44 W/(m·K)	1.3	0.8363346
E2				Steel, 16.27 W/(m·K)		0.8472585
E3				Ni, 91.74 W/(m·K)		0.8557141
E4				Al, 202.4 W/(m·K)		0.8567652
E5				Cu, 387.6 W/(m·K)		0.8571849
F1	30%	0.3%	10D	Steel, 16.27 W/(m·K)	1.3	0.8472585
F2					2	0.82963384
F3					3	0.81644962
F4					4	0.80892233
F5					5	0.80399101

shows the averaged cooling effectiveness of the porous surface under various cases. Correlation fitting was performed using 1stOpt software (Version 15 Pro), which is independently developed by 7D-Soft High Technology Inc., Beijing, China. It is a set of mathematical optimization analysis and synthesis tool software packages with complete independent intellectual property rights. The built-in Levenberg–Marquardt (LM) algorithm in the software was used for fitting. The Levenberg–Marquardt (LM) algorithm is an efficient method for nonlinear least-squares optimization. It combines the stability of the gradient descent method with the fast convergence of the Gauss–Newton method by adaptively controlling the iteration step size through dynamic adjustment of the damping factor. When the parameters approach the optimal solution, the algorithm behaves more like the Gauss–Newton method to accelerate convergence; when the initial guess is poor, it reverts to the gradient descent method to ensure stability. Its core principle involves iteratively adjusting parameters to minimize the sum of squared errors between model predictions and actual data. This algorithm is widely used in curve fitting. Through successive fittings of individual variables using the Levenberg–Marquardt algorithm, the formulation presented in Equation (7) characterizing parameters φ, Br, H, λ, and R_t was established.

$$\begin{array}{l}\dot{\eta }=(0.959063{\phi }^{-0.119787}-{\displaystyle \frac{0.0325003}{\phi }})\cdot {\displaystyle \frac{Br}{0.962588Br+0.006765}}\cdot \\ (0.845718-0.0040695{\displaystyle \frac{H}{D}}+0.084524\ln {\displaystyle \frac{H}{D}})\cdot [0.7913308+{\displaystyle \frac{0.220928(\frac{\lambda }{16.27})}{0.05874886+(\frac{\lambda }{16.27})}}]\\ \cdot ({\displaystyle \frac{1}{6.752395747R_{\mathrm{t}}+4.145872303}}+0.9226068213)\end{array}$$

(7)

To verify the effectiveness of the formula, this study compared the results obtained from simulations with those calculated using Equation (7) by changing various parameters and model sizes.

Table 3. Formula validation.

Case	φ	Br	H	λ, W/(m·K)	Rt	$\dot{\mathit{\eta }}$	Formula (7)	Error
G1	0.25	0.015	16	16.27	3.33	0.69320353	0.690964779	0.323%
G2	0.25	0.04	16	297.73	4.67	0.8742778	0.864400342	1.13%
G3	0.25	0.035	9	297.73	2.67	0.8496429	0.844428195	0.614%
G4	0.3	0.015	10	297.73	1.67	0.70758362	0.70601803	0.221%
G5	0.45	0.03	16	16.27	5	0.8107224	0.797001194	1.69%

compares simulation results with the Equation (7) calculations. The errors are all below 2%, showing that Equation (7) accurately predicts the average cooling effectiveness of the porous structure.

5. Conclusions

This study investigates the impact of various parameters on the performance of effusion cooling, including porosity (φ), blowing ratio (Br), height of the porous structure (H), thermal conductivity (λ), and ratio of temperature (R_t). Additionally, a correlation for the averaged cooling effectiveness of porous structure surfaces is fitted. The key results are as follows:

• Porosity markedly affects cooling effectiveness. As porosity rises, the η of the porous structure surface first improves and then declines, whereas the averaged downstream η gradually increases. Higher porosity reduces the temperature on the outer surface of the porous structure yet produces a non-uniform temperature distribution.
• The blowing ratio and η are positively correlated. In general, as the blowing ratio increases, η also improves.
• Surprisingly, the height of the porous structure and the thermal conductivity of the material exert minimal influence on the cooling effectiveness of both the porous surface and the downstream region. This is because as the ventilation time increases, the temperature of the porous material will eventually reach equilibrium. The height of the porous structure and the material’s thermal conductivity mainly affect the heat conduction performance. In this coupling of convective heat transfer and thermal conduction, the effect of convective heat transfer is more intense, while the influence of thermal conduction is reduced. However, a larger height of the porous structure and a smaller thermal conductivity coefficient can lead to a non-uniform temperature distribution on the outer surface of the porous structure.
• Although the cooling effectiveness is a relative formula, different temperature ratios between the mainstream inlet and the coolant inlet make the cooling effectiveness change, and a similar coolant coverage pattern is formed.
• The formula fitted for the cooling effectiveness of the porous surface demonstrates high precision and all errors remain below 2%. The formula is capable of accurately predicting the cooling effectiveness of such surfaces. Future research can conduct correlation fitting between downstream cooling effectiveness and related parameters to predict their cooling effectiveness, providing references and options for design and optimization.