The Impact of the Cooling System on the Thermal Management of an Electric Bus Battery
Abstract
1. Introduction
2. Materials and Methods
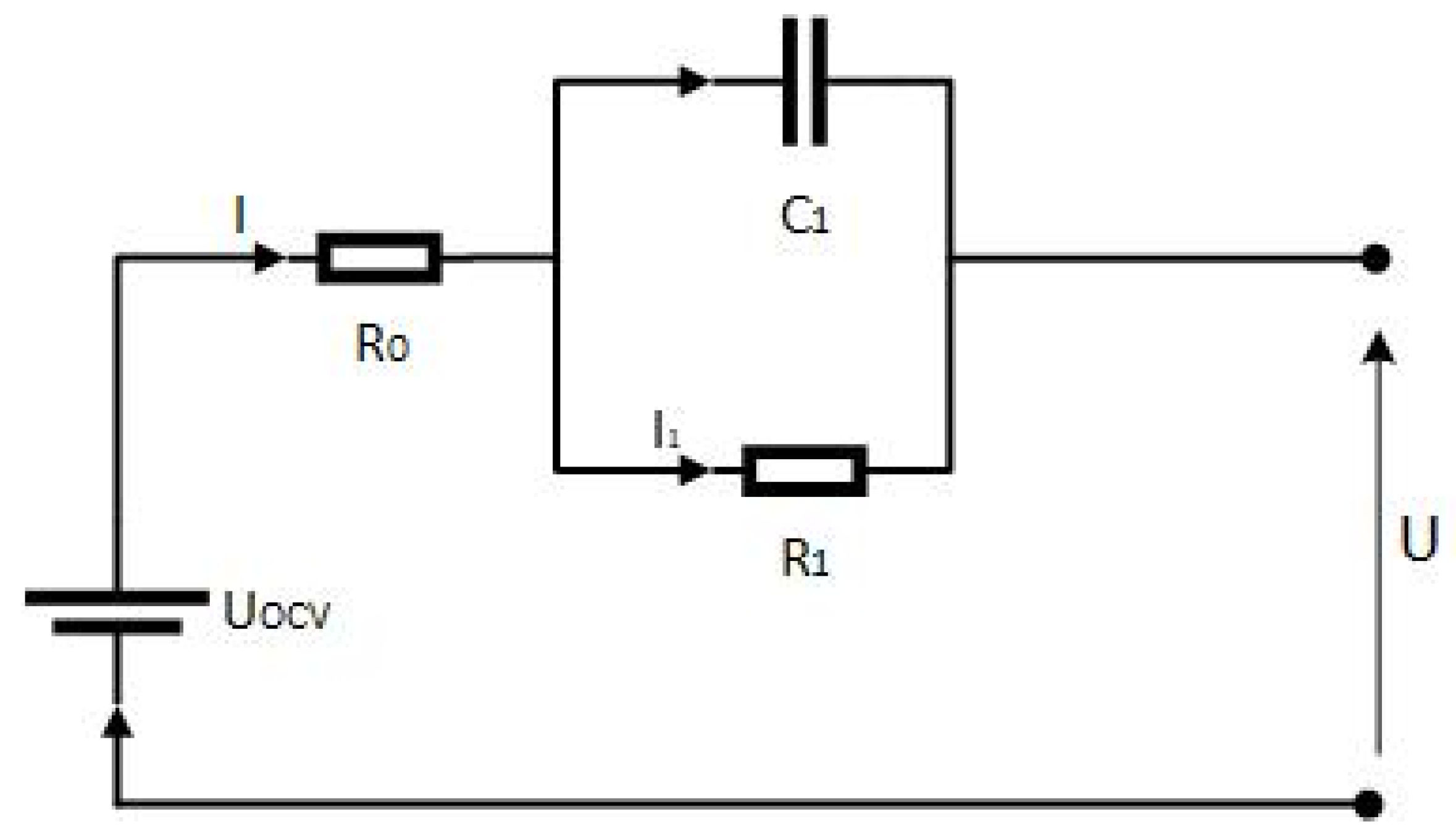
2.1. Cell Modeling
- U—total cell voltage [V];
- I—cell current [A];
- UOCV—open circuit voltage [V];
- U1—voltage drop on the RC pair [V];
- I1—resistor R1 current [A];
- R0, R1—resistance [Ω];
- C1—capacity [C].
- P—heat generated in the cell per unit of time [W].
- Q—heat [];
- t—time [];
- λ—thermal conductivity coefficient ;
- S—the surface area through which heat transfer occurs [];
- ∇T—local temperature gradient .
- q—local heat flux density ,
- ∇T—local temperature gradient .
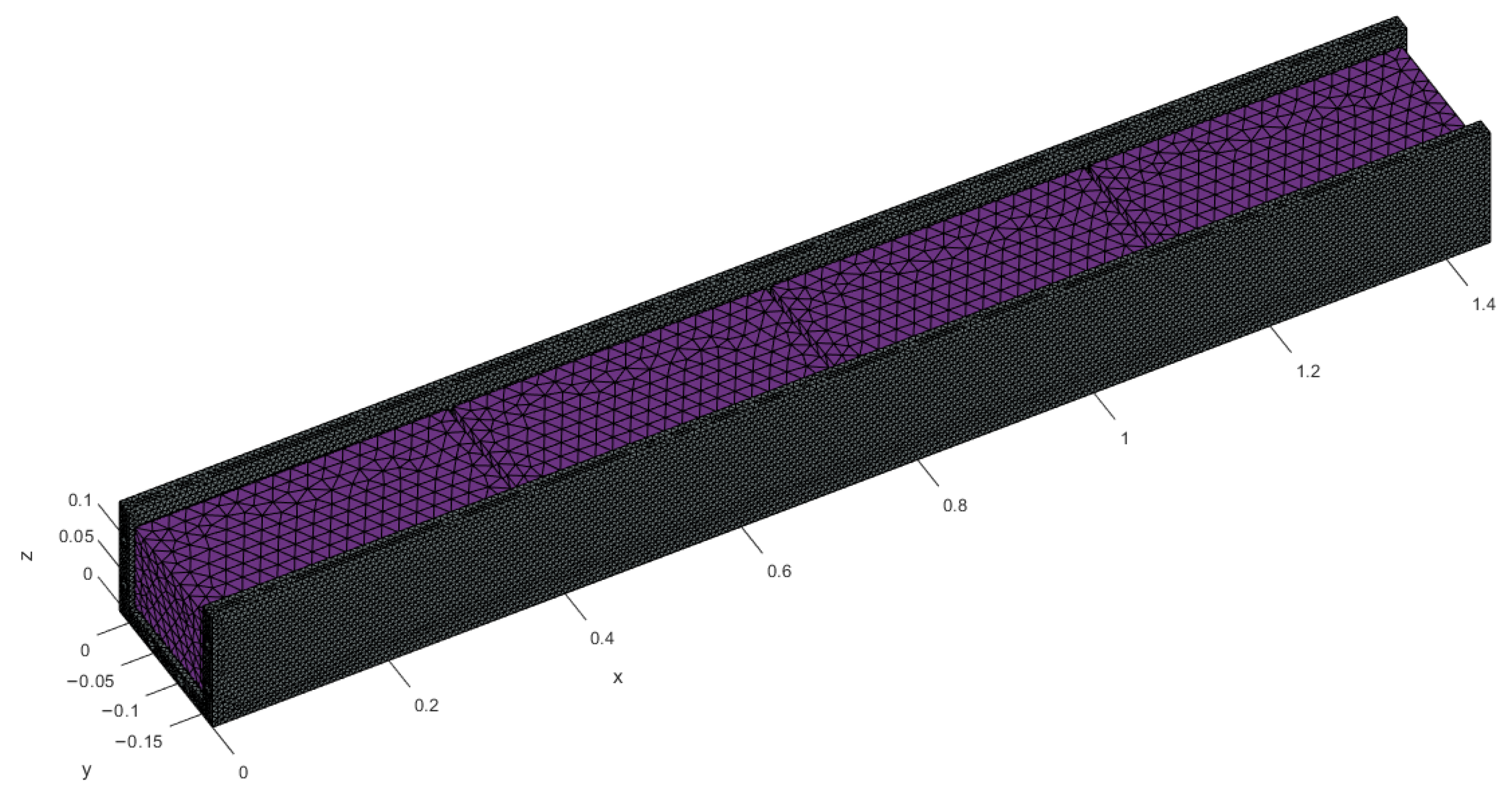
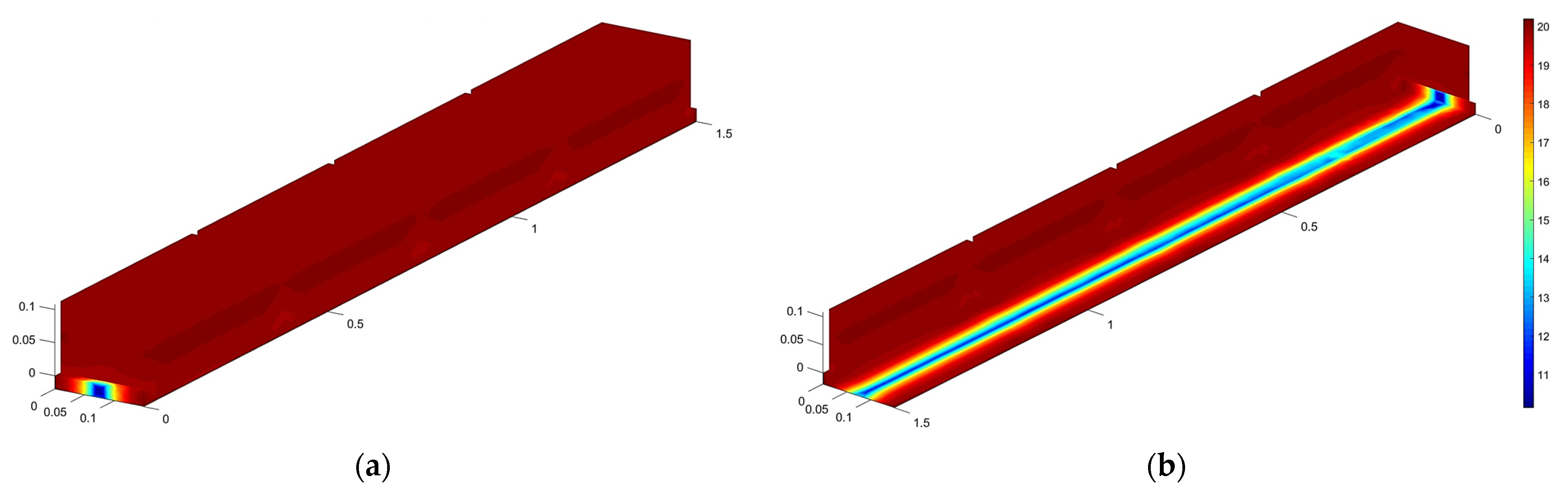
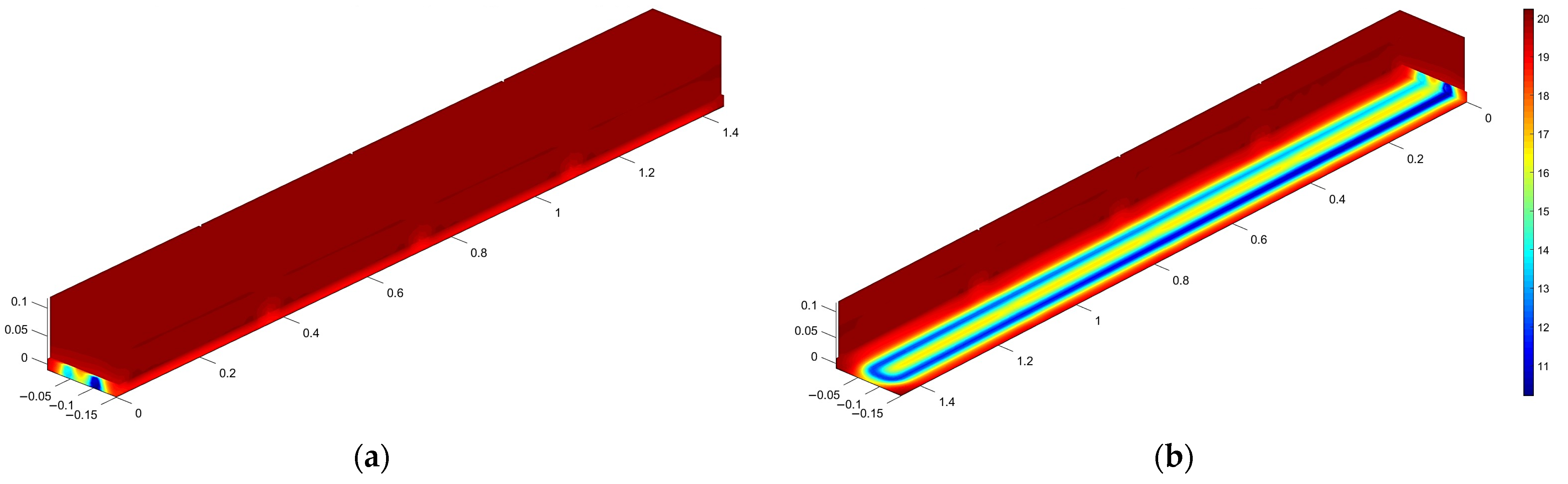
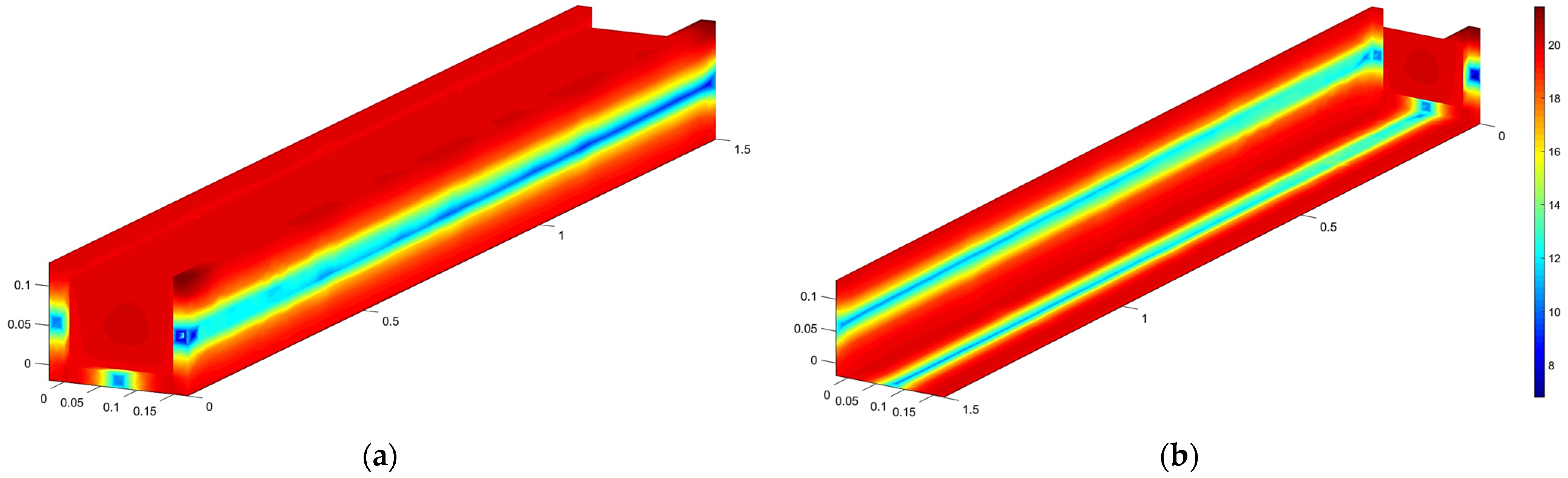
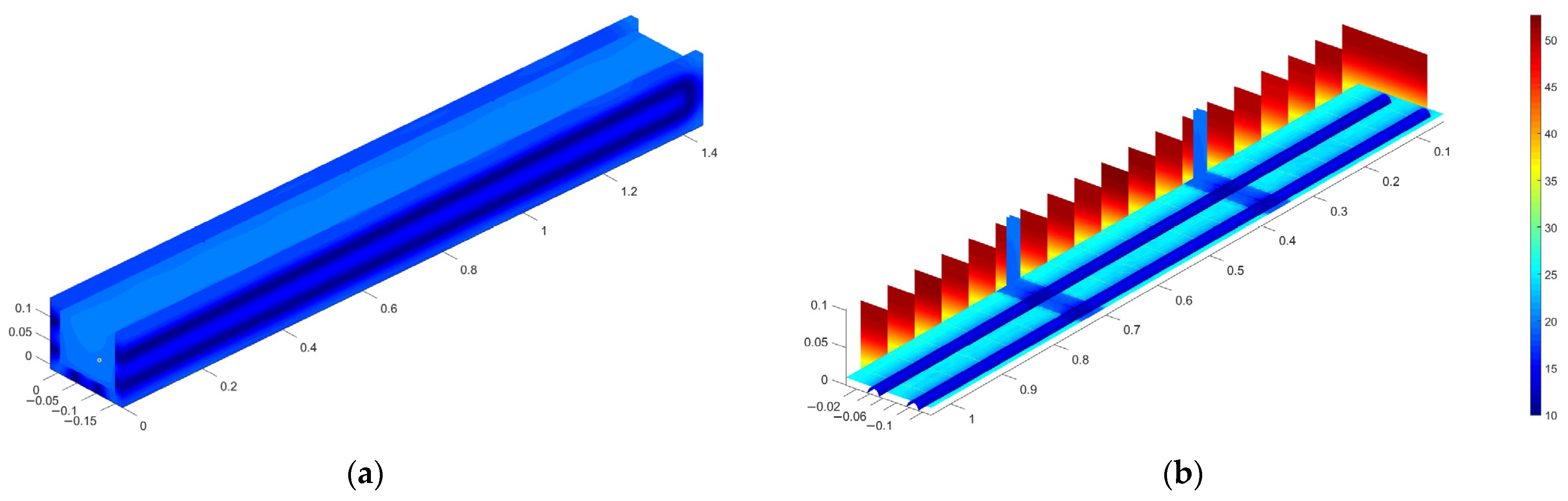
2.2. Cooling System Modeling
- A single cooling plate with a straight pipe underneath the battery.
- Three single cooling plates with straight pipes surrounding three sides.
- A single cooling plate with a U-shaped pipe underneath.
- Three single cooling plates with U-shaped pipes surrounding three sides.
- α—heat transfer coefficient ,
- ΔT—the difference between the temperature of the wall and the surrounding fluid [K].
- Nu—Nusselt number;
- λ—thermal conductivity coefficient ;
- d—diameter pipe [].
- For Reynolds number Re < 2000, the Nusselt number should be calculated from Michiejew’s equation for laminar flows:
- For Reynolds number 2000 < Re < 10,000, the Nusselt number should be calculated from Michiejew’s equation for transitional flows:
- For Reynolds number Re > 10,000, the Nusselt number should be calculated from Sieder and Tate’s equation for turbulent flows:
- Prf—Prandtl number for fluid;
- Prw—Prandtl number for wall;
- EL—correction depending on the ratio of the pipe length to its diameter;
- K0—correction factor based on the Reynolds number.
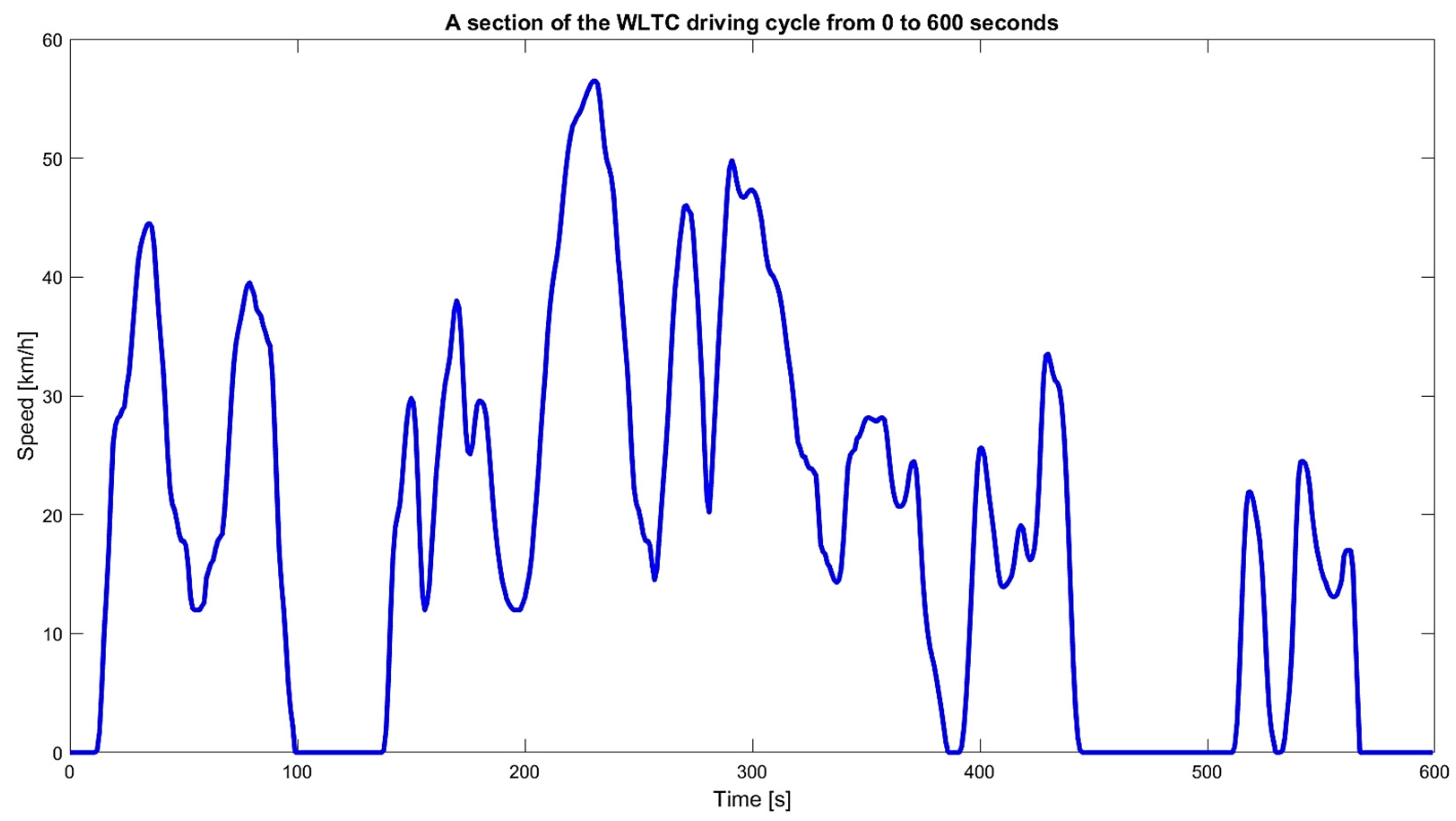
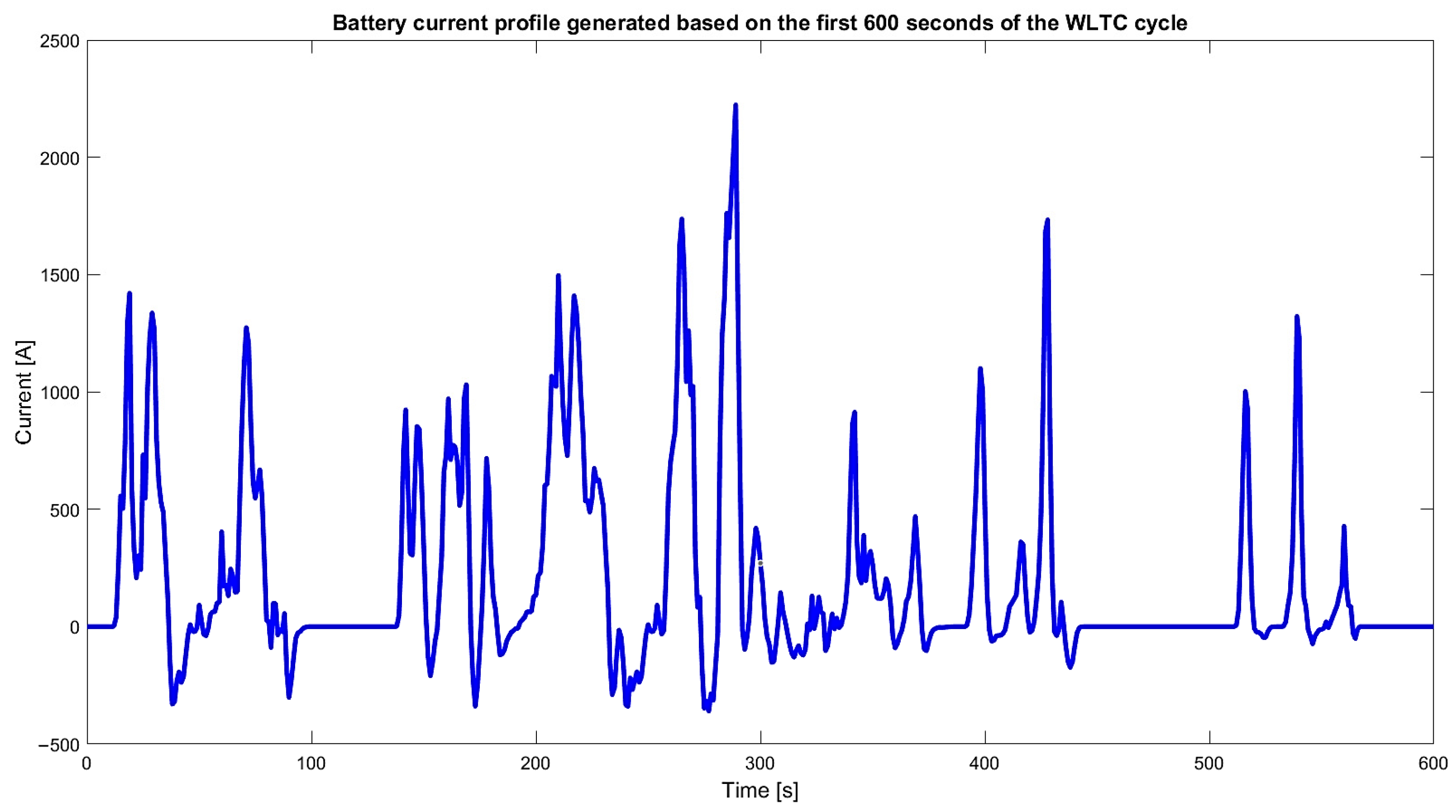
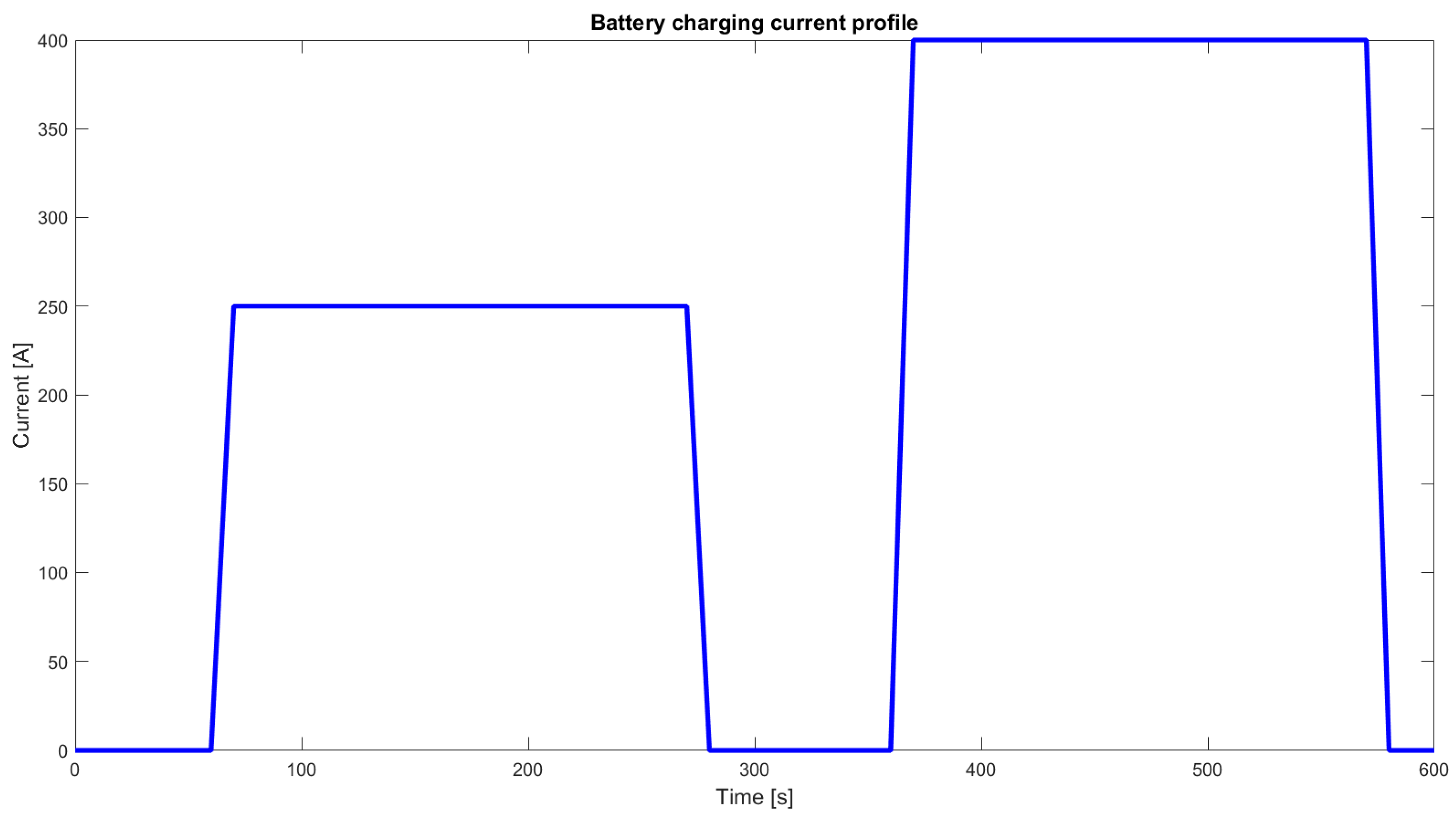
2.3. Current Profiles
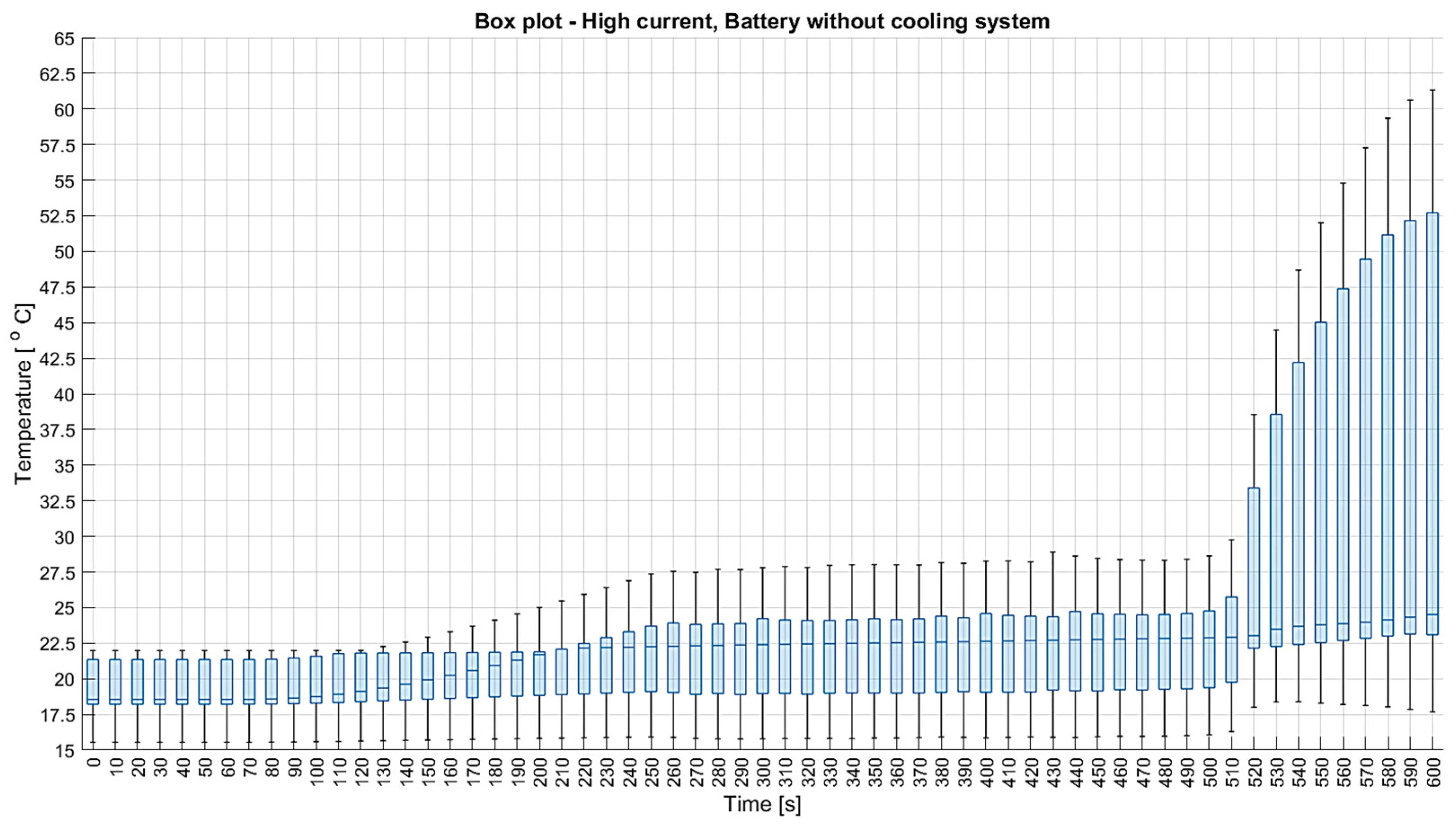
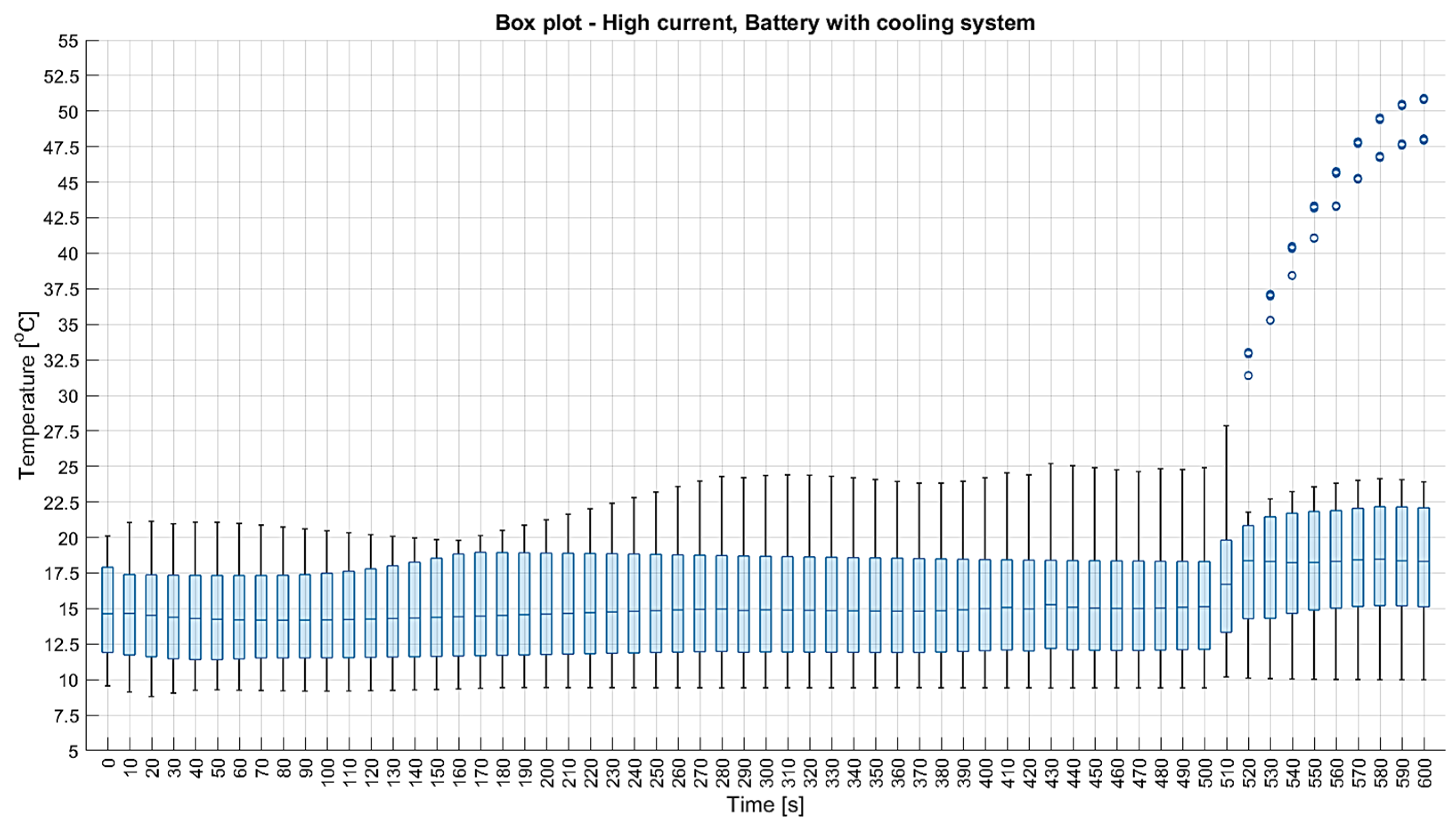
3. Results
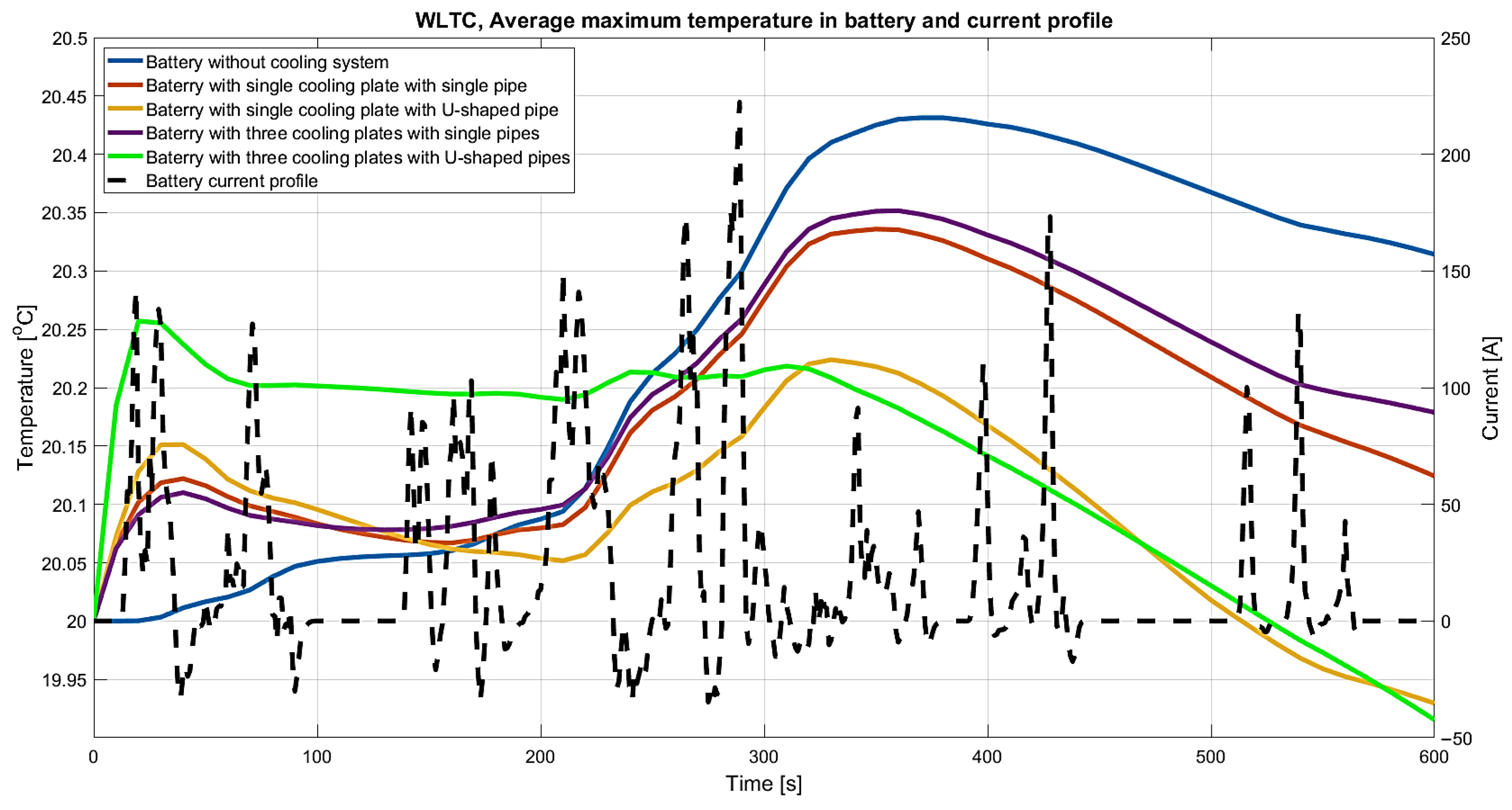
3.1. Current Profile Based on WLTC Cycle
- —mean value;
- —quantile of Student’s t-distribution;
- —standard deviation;
- —adopted significance level;
- —number of cells.
- —first quartile;
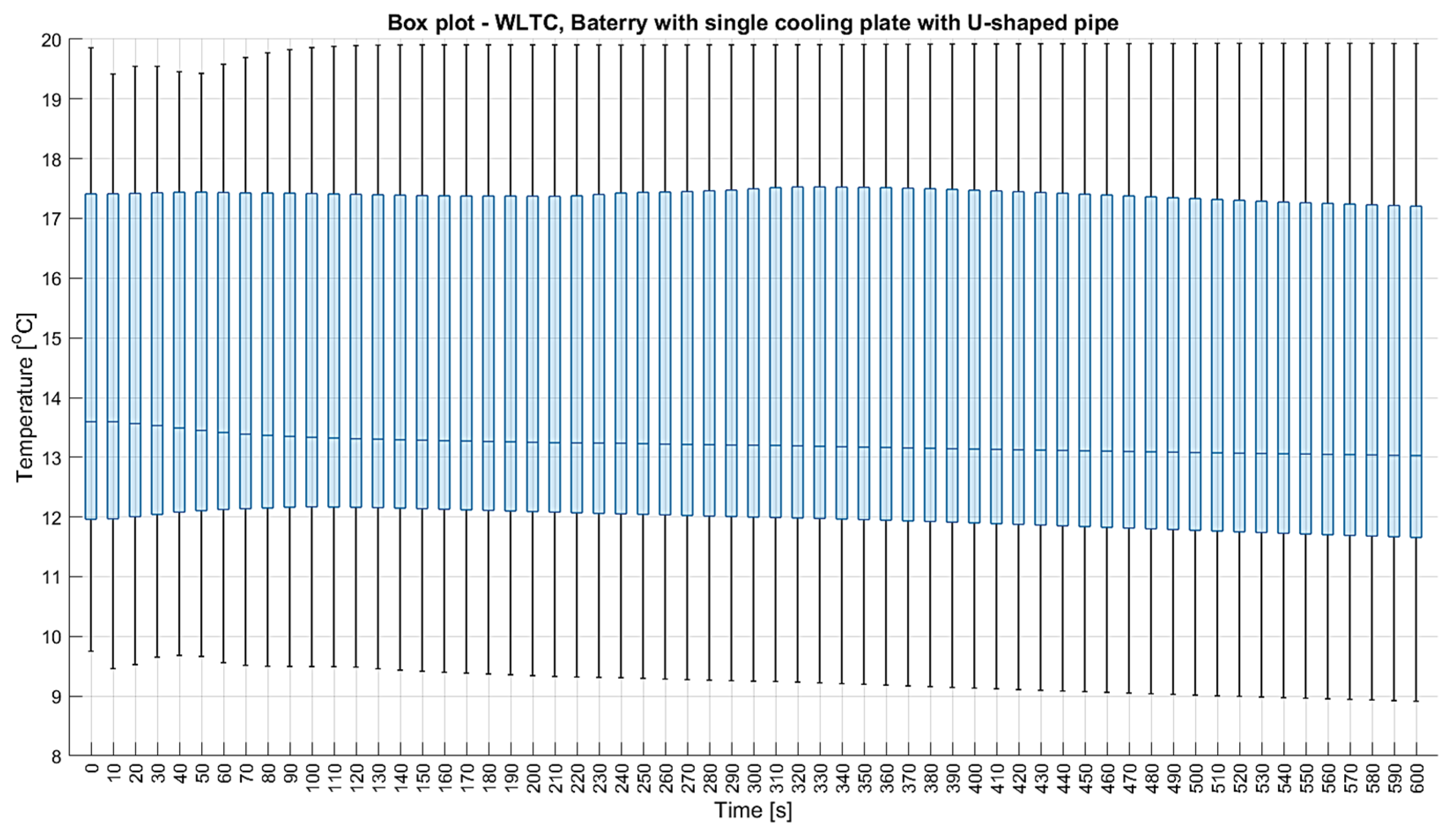
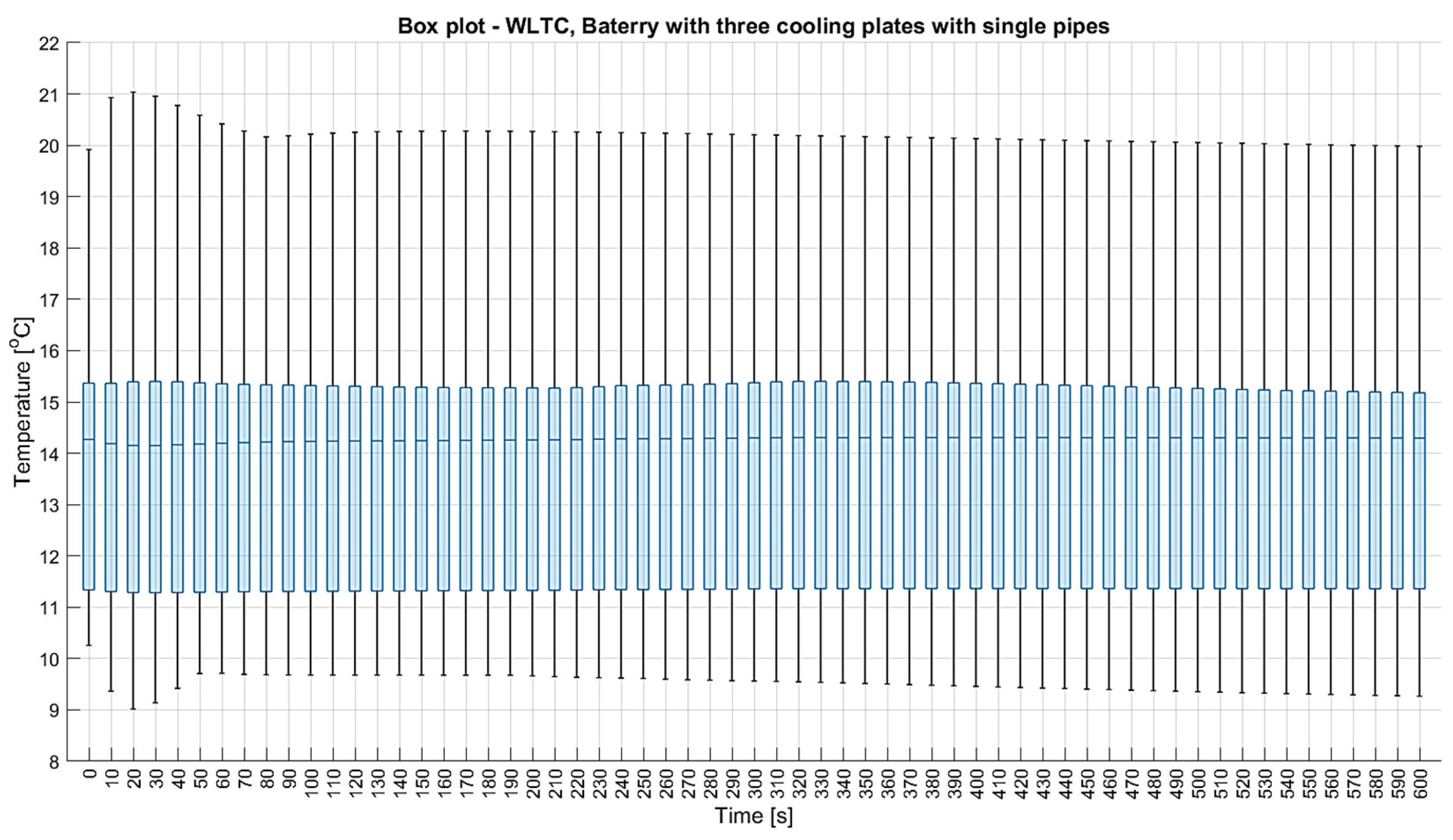
- —third quartile.
- Additionally, the center value is marked with a thick line within the rectangle itself.
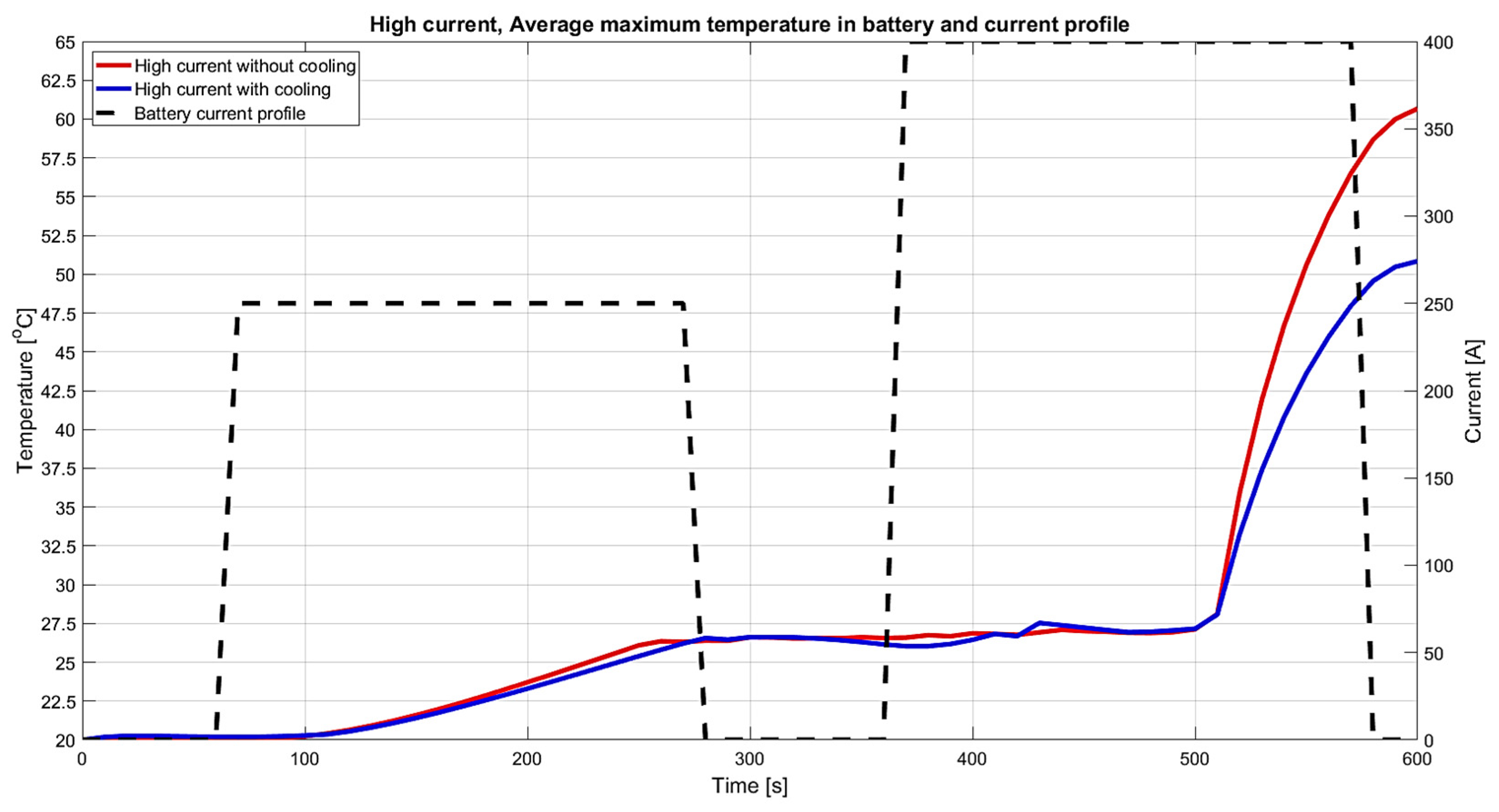
3.2. High-DC Current Profile
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S. A Review of Power Battery Thermal Energy Management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Waszczuk-Młyńska, A.; Radkowski, S. Circular Membrane with a Centrally-Located Opening—Analytical Model Using Parameterisation of the Non-Empty Torus. ZAMM Z. Angew. Math. Mech. 2019, 99, e201800167. [Google Scholar] [CrossRef]
- Chmielewski, A.; Mączak, J.; Szulim, P. Experimental Research of Electrochemical Energy Storage. In Automation 2017; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2017; Volume 550, pp. 227–235. ISBN 21945357 (ISSN). [Google Scholar]
- Chmielewski, A.; Mączak, J.; Szulim, P. Experimental Research and Simulation Model of Electrochemical Energy Stores. In Automation 2017; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2017; Volume 550, pp. 236–246. ISSN 21945357. [Google Scholar]
- Mei, N.; Xu, X.; Li, R. Heat Dissipation Analysis on the Liquid Cooling System Coupled with a Flat Heat Pipe of a Lithium-Ion Battery. ACS Omega 2020, 5, 17431–17441. [Google Scholar] [CrossRef]
- Chmielewski, A.; Mozaryn, J.; Bogdziński, K.; Piórkowski, P.; Mydłowski, T.; Gumiński, R.; Mączak, J. Selected Properties of the Hybrid Micro-Installation Model Based on Electrochemical Battery and PV Module. Int. J. Struct. Stab. Dyn. 2019, 19, 1941005. [Google Scholar] [CrossRef]
- Adeniran, A.; Park, S. Optimized Cooling and Thermal Analysis of Lithium-Ion Pouch Cell under Fast Charging Cycles for Electric Vehicles. J. Energy Storage 2023, 68, 107580. [Google Scholar] [CrossRef]
- Kalkan, O.; Celen, A.; Bakirci, K.; Dalkilic, A.S. Experimental Investigation of Thermal Performance of Novel Cold Plate Design Used in a Li-Ion Pouch-Type Battery. Appl. Therm. Eng. 2021, 191, 116885. [Google Scholar] [CrossRef]
- He, L.; Gu, Z.; Zhang, Y.; Jing, H.; Li, P. Review on Thermal Management of Lithium-Ion Batteries for Electric Vehicles: Advances, Challenges, and Outlook. Energy Fuels 2023, 37, 4835–4857. [Google Scholar] [CrossRef]
- Koundal, S.; Sharma, S.L.; Debbarma, A. Battery Thermal Management Systems for Electric Vehicles: An Overview of Cooling Techniques and Performance Optimization. J. Therm. Anal. Calorim. 2025, 150, 5855–5882. [Google Scholar] [CrossRef]
- Wahab, A.; Najmi, A.-U.-H.; Senobar, H.; Amjady, N.; Kemper, H.; Khayyam, H. Immersion Cooling Innovations and Critical Hurdles in Li-Ion Battery Cooling for Future Electric Vehicles. Renew. Sustain. Energy Rev. 2025, 211, 115268. [Google Scholar] [CrossRef]
- Mao, S.; An, Z.; Du, X.; Shi, T.; Zhang, D. Coupling Analysis on the Thermophysical Parameters and the Performance of Liquid Cooling-Based Thermal Management System for Lithium-Ion Batteries. Energies 2022, 15, 6865. [Google Scholar] [CrossRef]
- An, Z.; Gao, W.; Zhang, J.; Liu, H.; Gao, Z. Enhancing Heat Dissipation of Thermal Management System Utilizing Modular Dual Bionic Cold Plates for Prismatic Lithium Batteries. J. Energy Storage 2024, 87, 111541. [Google Scholar] [CrossRef]
- Li, R.; Gan, Y.; Luo, Q.; Yan, Y.; Li, Y. Research Progress on Efficient Thermal Management System for Electric Vehicle Batteries Based on Two-Phase Transformation. Appl. Therm. Eng. 2023, 234, 121270. [Google Scholar] [CrossRef]
- Choi, H.; Lee, H.; Han, U.; Jung, J.; Lee, H. Comparative Evaluation of Liquid Cooling-Based Battery Thermal Management Systems: Fin Cooling, PCM Cooling, and Intercell Cooling. Int. J. Energy Res. 2024, 2024, 5395508. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, Q.; Liu, Y.; Lai, B.; Ke, Z.; Wu, W. Investigations of Lithium-Ion Battery Thermal Management System with Hybrid PCM/Liquid Cooling Plate. Processes 2023, 11, 57. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. New Concept of Hybrid Cooling System for Fast Charging of Electric Vehicles. J. Energy Storage 2024, 97, 112994. [Google Scholar] [CrossRef]
- Zeng, X.; Men, Z.; Deng, F.; Chen, C. Optimization of the Heat Dissipation Performance of a Lithium-Ion Battery Thermal Management System with CPCM/Liquid Cooling. Materials 2022, 15, 3835. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Li, J.; Zhu, Z.; Lv, P. Numerical Investigation on Thermal Performance of Battery Module with LCP-AFC Cooling System Applied in Electric Vehicle. Energy Sci. Eng. 2022, 10, 4431–4446. [Google Scholar] [CrossRef]
- Panmuang, P.; Photong, C.; Soemphol, C. Experimental Investigation of Batteries Thermal Management System Using Water Cooling and Thermoelectric Cooling Techniques. Int. J. Power Electron. Drive Syst. 2024, 15, 201–212. [Google Scholar] [CrossRef]
- Roe, C.; Feng, X.; White, G.; Li, R.; Wang, H.; Rui, X.; Li, C.; Zhang, F.; Null, V.; Parkes, M.; et al. Immersion Cooling for Lithium-Ion Batteries—A Review. J. Power Sources 2022, 525, 231094. [Google Scholar] [CrossRef]
- Steingart, D.; Chang, W.; Bommier, C.; Mohr, R. Impact of Non-Arrhenius Temperature Behavior on the Fast-Charging Capabilities of LiCoO2−Graphite Lithium-Ion Batteries. J. Phys. Chem. C 2021, 125, 1731–1741. [Google Scholar] [CrossRef]
- Thakur, A.K.; Ahmed, M.S.; Kang, H.; Prabakaran, R.; Said, Z.; Rahman, S.; Sathyamurthy, R.; Kim, J.; Hwang, J.-Y. Critical Review on Internal and External Battery Thermal Management Systems for Fast Charging Applications. Adv. Energy Mater. 2023, 13, 2202944. [Google Scholar] [CrossRef]
- Lokhande, I.K.; Tiwari, N.; Sharma, A. A Review on Fast Charging/Discharging Effect in Lithium-Ion Batteries for Electric Vehicles. In Renewable Energy: Accelerating the Energy Transition; Energy Systems in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2024; Volume Part F2145, pp. 209–233. ISSN 21998582. [Google Scholar]
- Tai, L.D.; Garud, K.S.; Hwang, S.-G.; Lee, M.-Y. A Review on Advanced Battery Thermal Management Systems for Fast Charging in Electric Vehicles. Batteries 2024, 10, 372. [Google Scholar] [CrossRef]
- Waszczuk-Młyńska, A.; Radkowski, S. About a Certain Way of the Membrane Kinetic Energy Transformation into Electric Energy. Adv. Intell. Sys. Comput. 2015, 352, 303–312. [Google Scholar] [CrossRef]
- Commission Regulation (EU) 2017/1151 of 1 June 2017—WLTC Test and Cycle Modification—Sub Annex 1. Available online: https://eur-lex.europa.eu/legal-content/PL/TXT/?uri=CELEX:32017R1151/ (accessed on 4 July 2025).
- QuickerSim—CFD Analysis|Battery Simulation|Engineering Consulting. Available online: https://www.quickersim.com/ (accessed on 3 July 2025).
- Theory Guide|Quickersim. Available online: https://emobility.quickersim.com/theory-guide/ (accessed on 3 July 2025).
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics; PWN: Warszawa, Poland, 2013; Volume 2, ISBN 978-83-01-14107-3. (In Polish) [Google Scholar]
- Wiśniewski, S.; Wiśniewski, T.S. Wymiana Ciepła, 6th ed.; WNT: Warszawa, Poland, 2017; ISBN 978-83-01-19443-7. (In Polish) [Google Scholar]
- High Power (ChaoJi)|CHAdeMO. Available online: https://www.chademo.com/technology/high-power (accessed on 4 July 2025).
- Schervish, M.J. Theory of Statistics; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-1-4612-4250-5. [Google Scholar]
- Kornacki, J.; Mielniczuk, J. Statystyka Dla Studentów Kierunków Technicznych i Przyrodniczych, 3rd ed.; WNT: Warszawa, Poland, 2006; ISBN 83-204-3242-1. (In Polish) [Google Scholar]
- Piórkowski, P.; Chmielewski, A.; Bogdziński, K.; Możaryn, J.; Mydłowski, T. Research on Ultracapacitors in Hybrid Systems: Case Study. Energies 2018, 11, 2551. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Nominal voltage | 222 V |
| Capacity | 180 Ah |
| Energy | 40 kWh |
| Charging current | 180 A |
| Charging temperature | 0–55 °C |
| Discharge current | 180 A |
| Discharge temperature | −25 ÷ 55 °C |
| Parameter | Value |
|---|---|
| Minimal capacity | 100 Ah |
| Nominal voltage | 3.66 V |
| Resistivity | 2000 nΩm |
| Thermal conductivity in the x direction | |
| Thermal conductivity in the y direction | |
| Thermal conductivity in the z direction | |
| Specific heat capacity |
| Parameter | Value |
|---|---|
| Pipe diameter of a plate with a single pipe | 8 mm |
| Pipe diameter of a plate with U-shaped pipe | 8 mm |
| Thermal conductivity of the plate | |
| Resistivity of the fluid at 0 °C | 1070 nΩm |
| Thermal conductivity of the fluid at 0 °C | |
| Specific heat of the fluid at 0 °C | |
| Heat transfer coefficient | |
| Mass flow rate | |
| Fluid inlet temperature | 20 °C |
| Parameter | Battery Without Cooling System | Battery with Single Cooling Plate | Battery with Three Cooling Plates | ||||
|---|---|---|---|---|---|---|---|
| With Single Pipe | With U-Shaped Pipe | With Single Pipes | With U-Shaped Pipes | ||||
| Initial temperature of cells [°C] | 20 | 20 | 20 | 20 | 20 | ||
| Mean value and confidence interval for minimum temperatures [°C] | 20.093 (20.091; 20.095) | 19.31 (19.291; 19.329) | 19.123 (19.089; 19.156) | 19.237 (19.214; 19.259) | 18.684 (18.612; 18.756) | ||
| Mean value and confidence interval for maximal temperatures [°C] | 20.314 (20.313; 20.315) | 20.124 (20.121; 20.128) | 19.93 (19.920; 19.939) | 20.179 (20.176; 20.182) | 19.915 (19.912; 19.919) | ||
| Initial temperature of cooling fluid [°C] | - | 10 | 10 | 10 | 10 | ||
| Final temperature of cooling fluid [°C] | - | 11.28 | 13.31 | Bottom plate | 11.28 | Bottom plate | 10.50 |
| Left plate | 11.23 | Left plate | 10.44 | ||||
| Right plate | 11.23 | Right plate | 10.44 | ||||
| Parameter | Battery Without Cooling System | Battery with Three Cooling Plates and U-Shaped Pipes | Difference Between Temperatures [%] |
|---|---|---|---|
| Initial temperature of cells [°C] | 20 | 20 | - |
| Mean value and confidence interval for minimum temperatures [°C] | 32.178 (32.075; 32.280) | 28.077 (28.029; 28.126) | 12.74% |
| Mean value and confidence interval for maximal temperatures [°C] | 60.679 (60.332; 61.025) | 50.844 (50.771; 50.918) | 16.21% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miś, P.; Miś, K.; Waszczuk-Młyńska, A. The Impact of the Cooling System on the Thermal Management of an Electric Bus Battery. Appl. Sci. 2025, 15, 9776. https://doi.org/10.3390/app15179776
Miś P, Miś K, Waszczuk-Młyńska A. The Impact of the Cooling System on the Thermal Management of an Electric Bus Battery. Applied Sciences. 2025; 15(17):9776. https://doi.org/10.3390/app15179776
Chicago/Turabian StyleMiś, Piotr, Katarzyna Miś, and Aleksandra Waszczuk-Młyńska. 2025. "The Impact of the Cooling System on the Thermal Management of an Electric Bus Battery" Applied Sciences 15, no. 17: 9776. https://doi.org/10.3390/app15179776
APA StyleMiś, P., Miś, K., & Waszczuk-Młyńska, A. (2025). The Impact of the Cooling System on the Thermal Management of an Electric Bus Battery. Applied Sciences, 15(17), 9776. https://doi.org/10.3390/app15179776







