Recent Advances and a Hybrid Framework for Cooperative UAV Formation Control
Abstract
1. Introduction
- We present a comparative evaluation of recent formation-control algorithms for UAV swarms, including leader–follower, virtual structure, behavior-based, APF, and graph theory approaches.
- We propose a novel hybrid control framework that combines the leader–follower strategy with the collision-avoidance capabilities of APF.
- We analyze the proposed framework and conduct a stability analysis using Lyapunov-based methods.
- We demonstrate the effectiveness of the proposed framework through simulations, showing successful formation tracking and dynamic collision avoidance in multiple scenarios.
- We provide a quantitative comparison of three controllers, leader–follower, APF, and the proposed hybrid using standardized metrics.
2. Related Work
2.1. Formation-Control Schemes
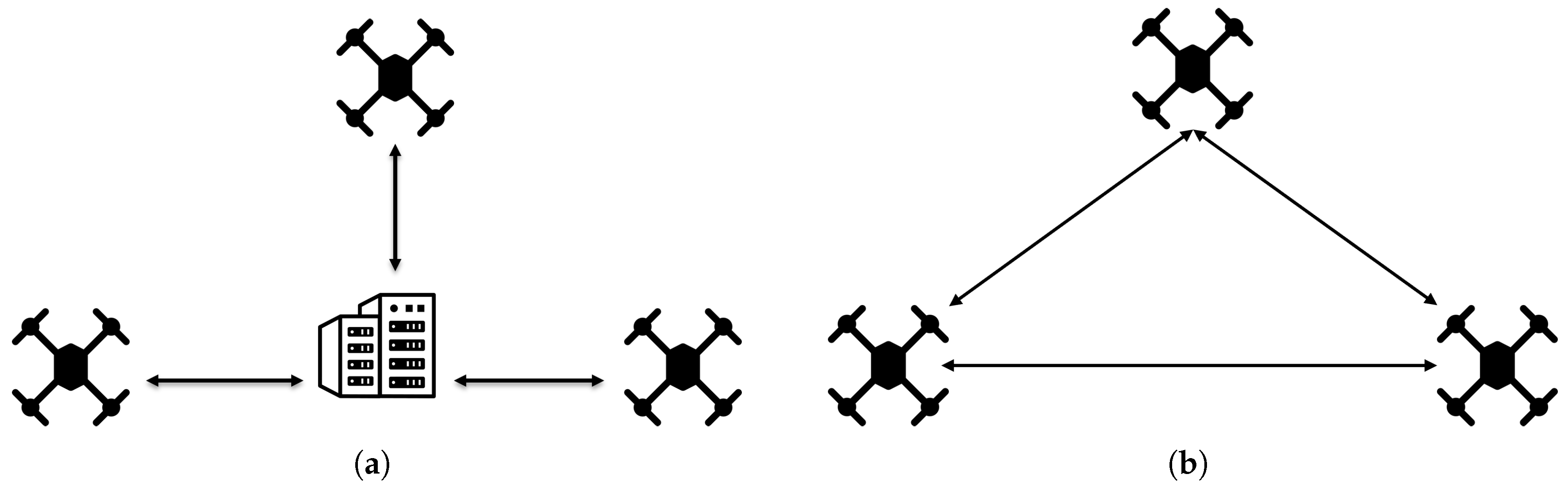
2.1.1. Centralized
2.1.2. Decentralized
2.2. Formation-Control Algorithms
2.2.1. Leader–Follower
2.2.2. Virtual Structure
2.2.3. Behavior-Based Formation Control
2.2.4. Artificial Potential Field
2.2.5. Graph Theory
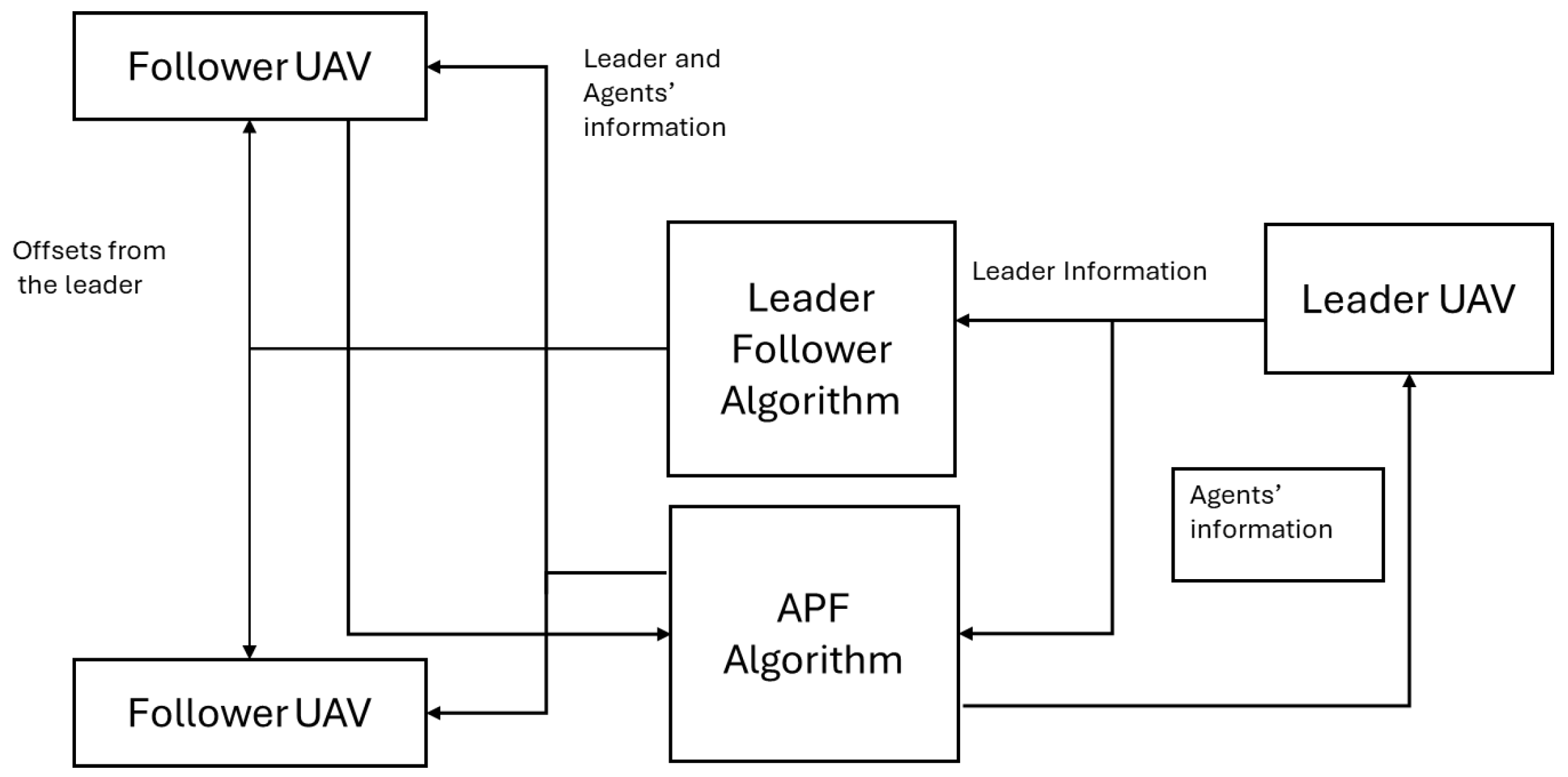
3. Proposed Hybrid Formation-Control Framework
3.1. Problem Formulation
3.2. Proposed Scheme Overview
3.3. Mathematical Modeling
3.4. Stability Analysis
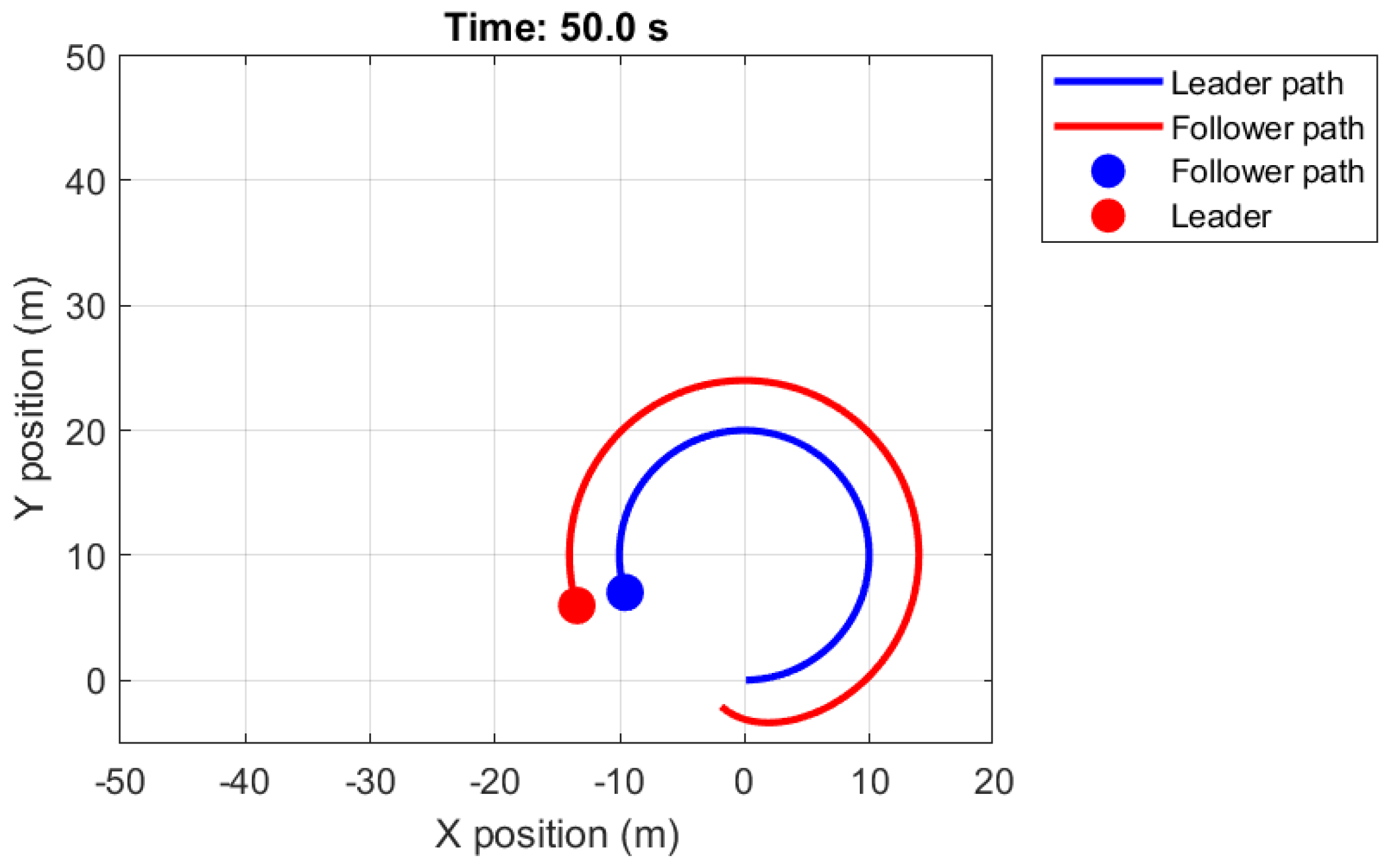
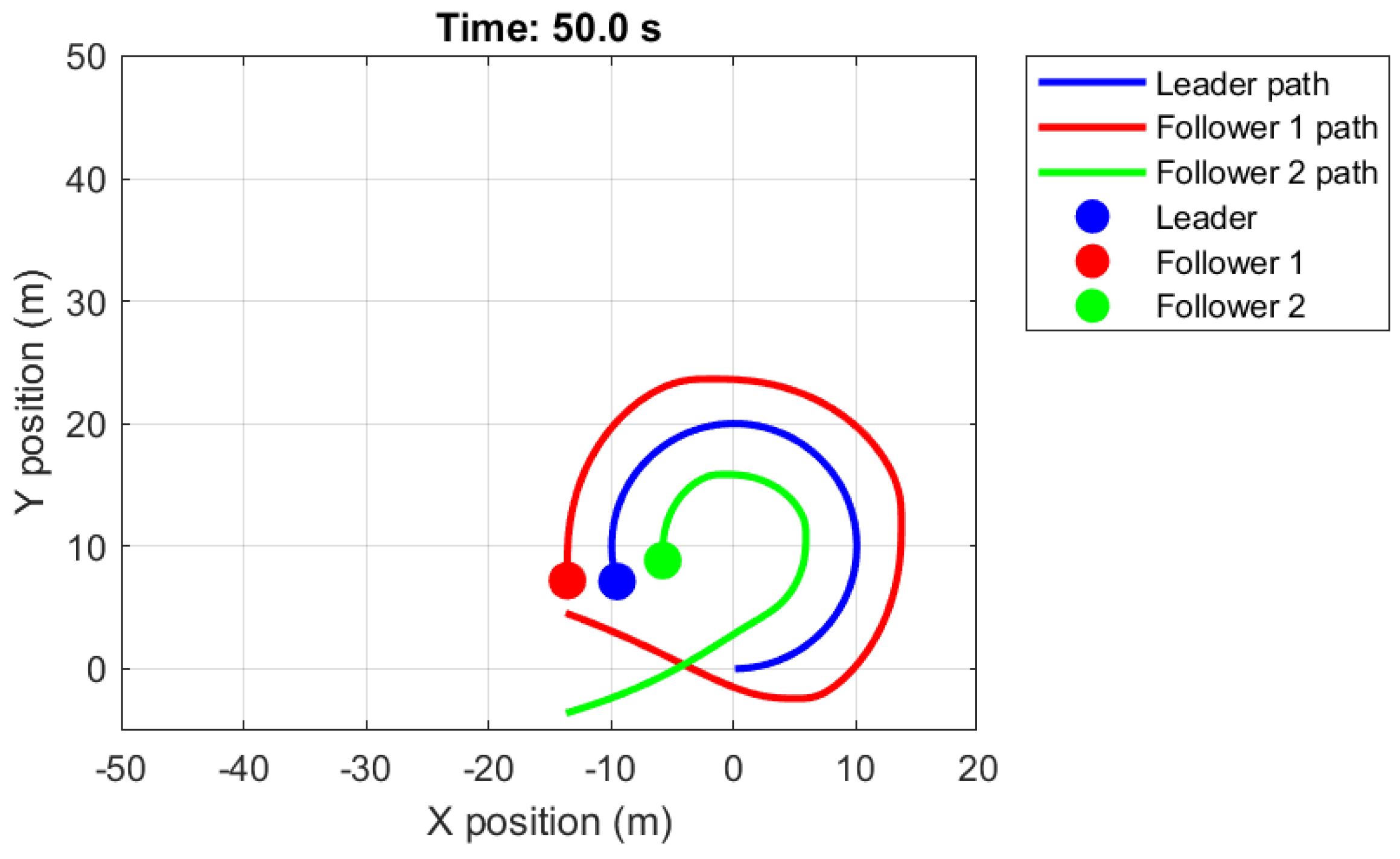
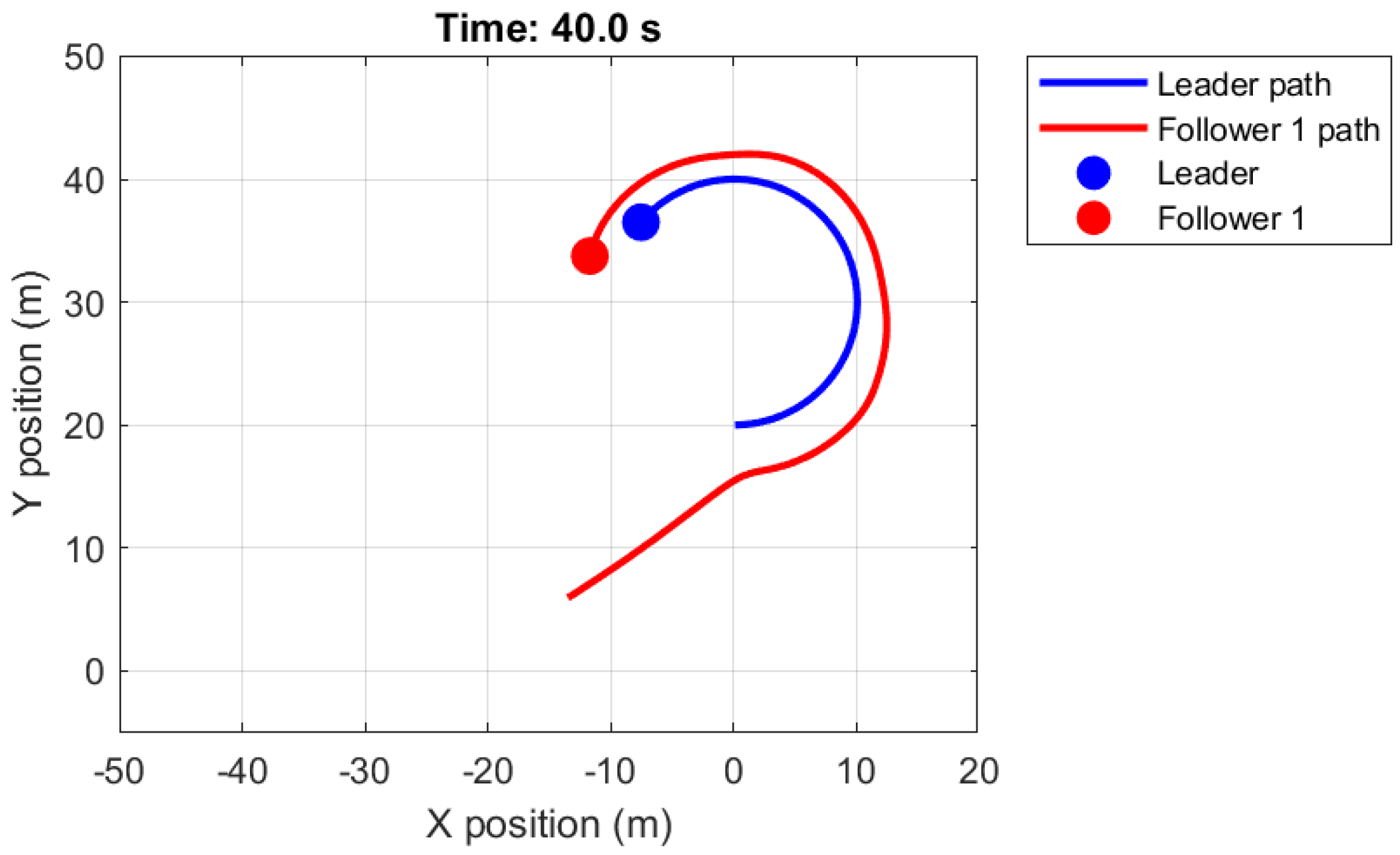
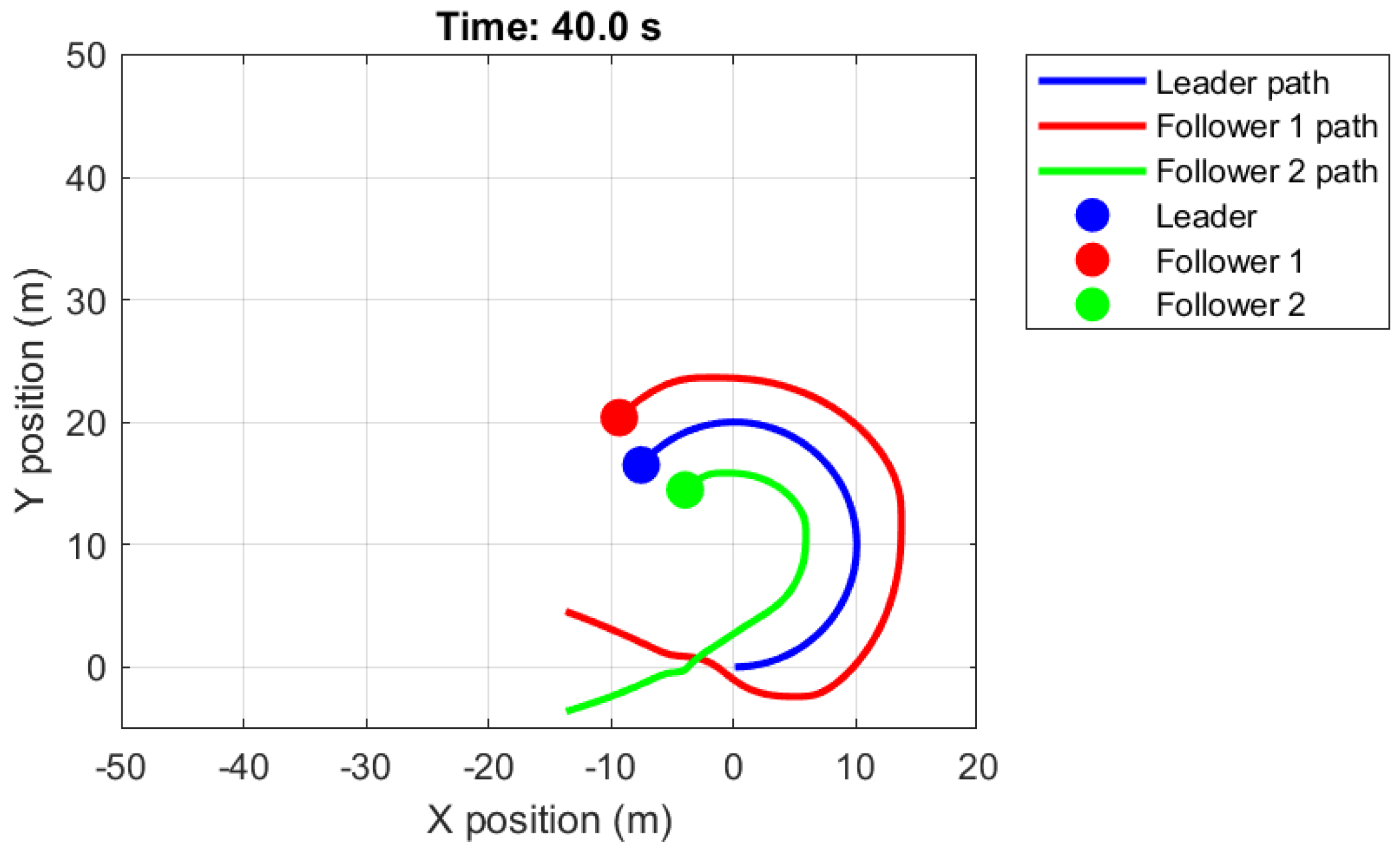
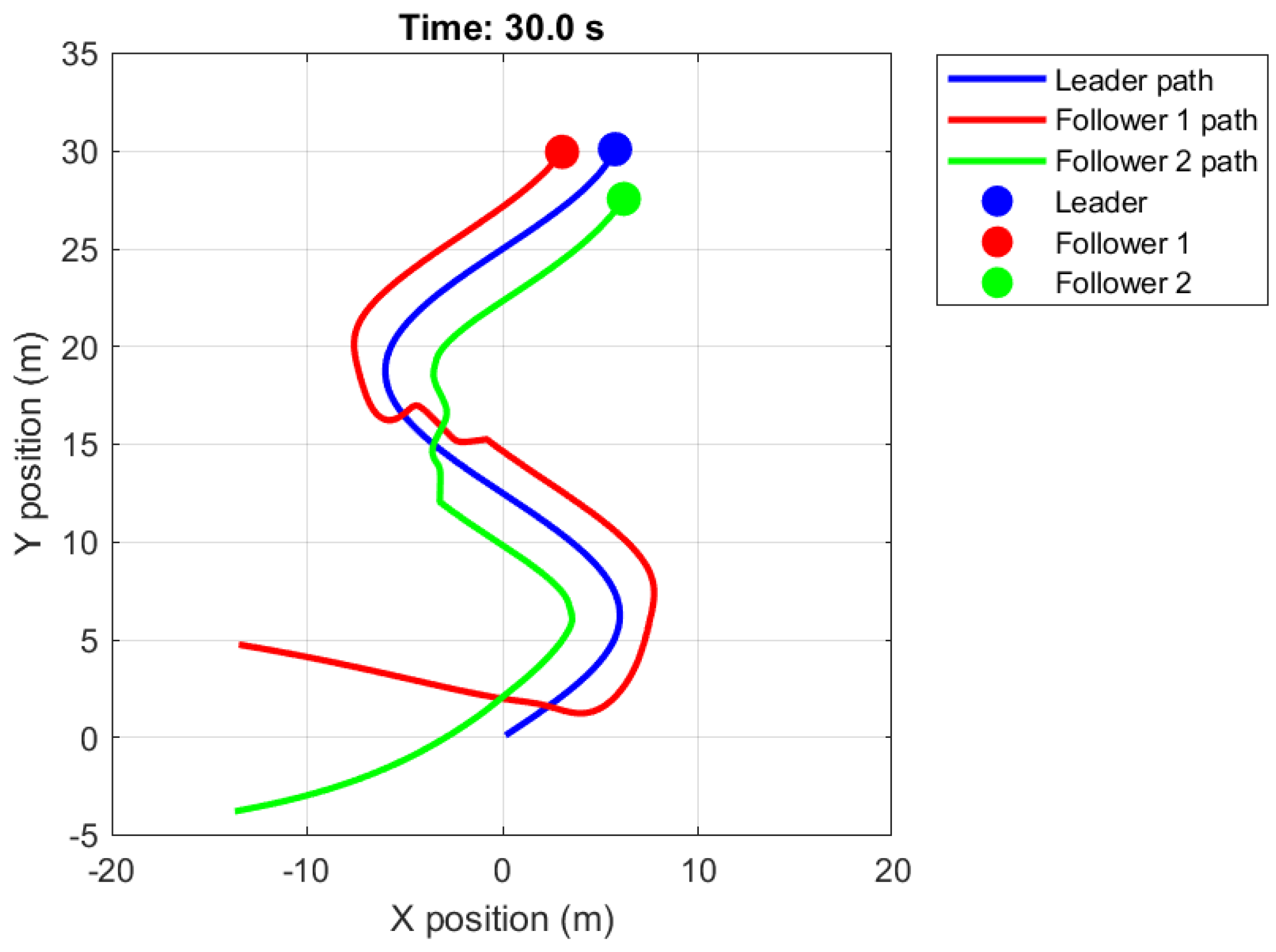
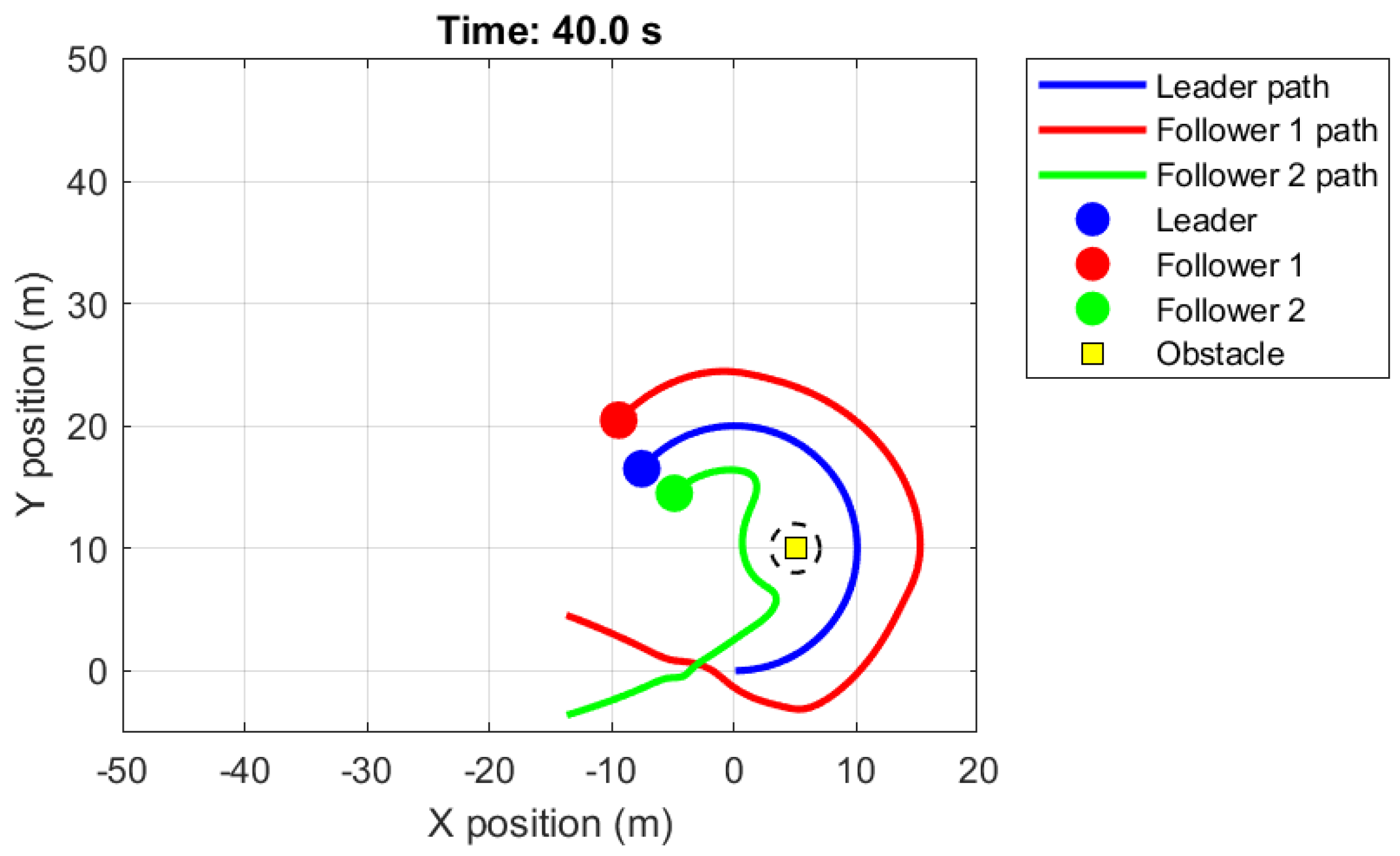
4. Illustrative Example
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hossain, N.U.I.; Lutfi, M.; Ahmed, I.; Akundi, A.; Cobb, D. Modeling and Analysis of Unmanned Aerial Vehicle System Leveraging Systems Modeling Language (SysML). Systems 2022, 10, 264. [Google Scholar] [CrossRef]
- Do, H.T. Formation Control Algorithms for Multiple-UAVs: A Comprehensive Survey. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 2021, 8, e3. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, H.; Chen, X.; Zhang, H.; Chen, B.; Han, Z. Blockchain-Based AR Offloading in UAV-Enabled MEC Networks: A Trade-off Between Energy Consumption and Rendering Latency. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Duong, D.V.A.; Akter, S.; Yoon, S. Task Offloading and Resource Allocation for Augmented Reality Applications in UAV-Based Networks Using a Dual Network Architecture. Electronics 2024, 13, 3590. [Google Scholar] [CrossRef]
- Qiu, X.; Liao, S.; Yang, D.; Li, Y.; Wang, S. Visual geo-localization and attitude estimation using satellite imagery and topographical elevation for unmanned aerial vehicles. Eng. Appl. Artif. Intell. 2025, 153, 110759. [Google Scholar] [CrossRef]
- Do, H.; Nguyen, H.; Nguyen, V.-C.; Nguyen, M.; Nguyen, M. Formation control of multiple unmanned vehicles based on graph theory: A Comprehensive Review. ICST Trans. Mob. Commun. Appl. 2022, 7, e3. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Peng, Z. Observer-based consensus tracking control for multiple quadrotor UAVs with unknown time-varying delays in leader–follower formations. Machines 2024, 12, 337. [Google Scholar]
- Hernández-González, O.; Targui, B.; Valencia-Palomo, G.; Guerrero-Sánchez, M.E. Robust cascade observer for a disturbance unmanned aerial vehicle carrying a load under multiple time-varying delays and uncertainties. Int. J. Syst. Sci. 2024, 55, 1056–1072. [Google Scholar] [CrossRef]
- Shi, Z.; Tu, J.; Zhang, Q.; Liu, L.; Wei, J. A Survey of Swarm Robotics System. In International Conference in Swarm Intelligence; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7331. [Google Scholar]
- Lau, H.K. Error Detection in Swarm Robotics: A Focus on Adaptivity to Dynamic Environments. Ph.D. Thesis, Department of Computer Science, University of York, York, UK, 2012. [Google Scholar]
- De La Cruz, C.; Carelli, R. Dynamic Modeling and Centralized Formation Control of Mobile Robots. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 3880–3885. [Google Scholar]
- Liu, Y.; Liu, J.; He, Z.; Li, Z.; Zhang, Q.; Ding, Z. A Survey of Multi-Agent Systems on Distributed Formation Control. Unmanned Syst. 2023, 12, 913–926. [Google Scholar] [CrossRef]
- Keshmiri, S.; Payandeh, S. Collaborative Agents—Research and Development; Guttmann, C., Dignum, F., Georgeff, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 85–98. [Google Scholar]
- Liao, D.; Zhang, Z.; Song, T.; Liu, M. An Efficient Centralized Multi-Agent Reinforcement Learner for Cooperative Tasks. IEEE Access 2023, 11, 139284–139294. [Google Scholar] [CrossRef]
- Baki, B.; Bouzid, M.; Ligęza, A.; Mouaddib, A.I. A centralized planning technique with temporal constraints and uncertainty for multi-agent systems. J. Exp. Theor. Artif. Intell. 2006, 18, 331–364. [Google Scholar] [CrossRef]
- Zheng, Z.; Tong, S.; Wang, E.; Zhu, Y.; Shao, J. Robust Consensus Tracking Control for Multi-Unmanned-Aerial-Vehicle (UAV) System Subjected to Measurement Noise and External Disturbance. Drones 2025, 9, 61. [Google Scholar] [CrossRef]
- Winfield, A.F. Distributed Sensing and Data Collection Via Broken Ad Hoc Wireless Connected Networks of Mobile Robots. In Distributed Autonomous Robotic Systems 4; Springer: Tokyo, Japan, 2000. [Google Scholar]
- Yang, M.; Guan, X.; Shi, M.; Li, B.; Wei, C.; Yiu, K.-F.C. Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm. Drones 2025, 9, 366. [Google Scholar] [CrossRef]
- Das, A.K.; Fierro, R.; Kumar, V.; Ostrowski, J.P.; Spletzer, J.; Taylor, C.J. A vision-based formation control framework. IEEE Trans. Robot. Autom. 2002, 18, 813–825. [Google Scholar] [CrossRef]
- Kowalczyk, W.; Kozlowski, K. Leader–Follower Control and Collision Avoidance for the Formation of Differentially-Driven Mobile Robots. In Proceedings of the 2018 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2018; pp. 132–137. [Google Scholar]
- Hirata-Acosta, J.; Pliego-Jiménez, J.; Cruz-Hernádez, C.; Martínez-Clark, R. Leader–Follower Formation Control of Wheeled Mobile Robots without Attitude Measurements. Appl. Sci. 2021, 11, 5639. [Google Scholar] [CrossRef]
- Guo, J.; Lin, Z.; Cao, M.; Yan, G. Adaptive leader–follower formation control for autonomous mobile robots. In Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6822–6827. [Google Scholar]
- Yu, H.; Shi, P.; Lim, C.-C.; Wang, D. Formation Control for Multi-Robot Systems with Collision Avoidance. Int. J. Control 2018, 92, 2223–2234. [Google Scholar] [CrossRef]
- Ghamry, K.A.; Zhang, Y. Formation control of multiple quadrotors based on leader–follower method. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 1037–1042. [Google Scholar]
- Chen, Y.; Deng, T. Leader–Follower UAV formation flight control based on feature modelling. Syst. Sci. Control Eng. 2023, 11, 2268153. [Google Scholar] [CrossRef]
- Kamel, M.A.; Yu, X.; Zhang, Y. Real-time optimal formation reconfiguration of multiple wheeled mobile robots based on particle swarm optimization. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 703–708. [Google Scholar]
- Yasin, J.N.; Haghbayan, M.H.; Yasin, M.M.; Plosila, J. Swarm formation morphing for congestion-aware collision avoidance. Heliyon 2021, 7, e07840. [Google Scholar] [CrossRef] [PubMed]
- Trejo, J.A.V.; Ponsart, J.C.; Adam-Medina, M.; Valencia-Palomo, G.; Theilliol, D. Distributed Observer-based Leader-following Consensus Control for LPV Multi-agent Systems: Application to multiple VTOL-UAVs Formation Control. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; pp. 1316–1323. [Google Scholar] [CrossRef]
- Yan, X.; Jiang, D.; Miao, R.; Li, Y. Formation Control and Obstacle Avoidance Algorithm of a Multi-USV System Based on Virtual Structure and APF. J. Mar. Sci. Eng. 2021, 9, 161. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Song, Y.; Yang, C.; Liang, C. Research on Multi-UAV Formation and Semi-Physical Simulation with Virtual Structure. IEEE Access 2023, 11, 126027–126039. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance. Intell. Serv. Robot. 2018, 11, 127–138. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L. Coordination control for multiple unmanned surface vehicles using hybrid behavior-based method. Ocean Eng. 2021, 232, 109147. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, X.; Zhu, Z.; Chen, C.; Yang, P. Behavior-Based Formation Control of Swarm Robots. Math. Probl. Eng. 2014, 2014, 205759. [Google Scholar] [CrossRef]
- Fu, X.; Pan, J.; Wang, H.; Gao, X. A Formation Maintenance and Reconstruction Method of UAV Swarm based on Distributed Control. Aerosp. Sci. Technol. 2020, 104, 105981. [Google Scholar] [CrossRef]
- Sheng, H. New multi-UAV formation keeping method based on improved APF. Chin. J. Aeronaut. 2023, 36, 249–270. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Z.; Zhu, Z.; Liang, Q.; Luo, J. Enhanced Multi-UAV Formation Control and Obstacle Avoidance Using IAAPF–SMC. Drones 2024, 8, 514. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Multi-UAV Formation Control Based on a Novel Back-Stepping Approach. IEEE Trans. Veh. Technol. 2020, 69, 2437–2448. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.; Kumar, V. Controlling formations of multiple mobile robots. In Proceeding of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 20 May 1998; pp. 2864–2869. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar]
| Control Scheme | Optimization | Scalability | Robustness |
|---|---|---|---|
| Centralized | sufficient | limited | limited |
| Decentralized | limited | sufficient | sufficient |
| Algorithm | Control Type | Strengths | Limitations |
|---|---|---|---|
| Leader–Follower [7,20,21,22,23,24,25,26,27,28] | Centralized | Simple design, easy implementation, and robust formation tracking | Dependence on leader, lack of feedback from followers to leader, and poor inherent obstacle avoidance |
| Virtual Structure [29,30] | Centralized | High stability and precise formation maintenance | Limited flexibility without replanning; poor inherent obstacle avoidance |
| Behavior-Based [31,32,33] | Decentralized | Handles multiple-goal missions effectively | Difficult to model mathematically and lower stability compared to other methods |
| Artificial Potential Fields (APFs) [34,35,36] | Decentralized | Smooth and continuous trajectories and effective obstacle avoidance | Less efficient in highly complex environments |
| Algorithm | Ref. | Application |
|---|---|---|
| Leader–Follower | [20] | Controlled robots while implementing collision avoidance |
| [21] | Controlled a group of differential-drive wheeled mobile robots | |
| [22] | Controlled a network of robots using two leaders’ scheme | |
| [23] | Controlled a team of mobile robots using leader–follower approach | |
| [24] | Combined Sliding Mode Control (SMC) with Linear Quadratic Regulator (LQR) for trajectory tracking of robots | |
| [25] | Optimized the attitude of multiple UAVs | |
| [26] | Achieved desired formation configuration efficiently in minimal time | |
| [27] | Optimized congestion management, obstacle avoidance, and formation restoration in swarms | |
| [28] | A distributed observer-based leader-following consensus control for LPV multi-agent of quadcopter UAVs to track a leader and maintain stable formations. | |
| [7] | Proposed an observer-based consensus-tracking-control algorithm for leader–follower quadrotor formations under unknown time-varying delays. | |
| Virtual Structure | [29] | Combined virtual structure with APF for precise and flexible formation maintenance |
| [30] | Virtual-structure formation controller where a virtual leader lets UAVs track assigned offsets with minimal inter-UAV communication | |
| Behavior Based | [31] | Utilized formation matrices using a behavior-based framework for flexible formations |
| [32] | Hybrid behavior-based (HB) method integrating multiple behaviors | |
| [33] | Extended behavior-based navigation from single robots to swarm-formation control | |
| [37] | Developed reactive behaviors for various formations and reference types | |
| APF | [34] | Swarm-formation control and obstacle avoidance using APF |
| [35] | Combined robust H∞ control with enhanced APF for UAV control | |
| [36] | Proposed an IAAPF with a sliding mode inner loop in a leader–follower setup scales attraction-repulsion and adds virtual inter-UAV forces to achieve robust, collision-free multi-UAV formations in cluttered scenes. | |
| Graph Theory | [38] | Cooperative guidance-control method for multiple UAVs |
| [39] | Formation control based on graph theory using local sensor information |
| Algorithm | Formation RMSE (m) | Safety Violations (%) | Average Execution Time (ms) | Max Execution Time (ms) |
|---|---|---|---|---|
| Leader–Follower | 2.0907 | 25.349 | 0.015068 | 2.0216 |
| APF | 2.9945 | 0 | 0.018085 | 2.6592 |
| Hybrid (proposed) | 2.3140 | 0 | 0.018253 | 3.3568 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhamees, S.N.; Alsaif, S.A.; Bin Salamah, Y. Recent Advances and a Hybrid Framework for Cooperative UAV Formation Control. Appl. Sci. 2025, 15, 9761. https://doi.org/10.3390/app15179761
Alkhamees SN, Alsaif SA, Bin Salamah Y. Recent Advances and a Hybrid Framework for Cooperative UAV Formation Control. Applied Sciences. 2025; 15(17):9761. https://doi.org/10.3390/app15179761
Chicago/Turabian StyleAlkhamees, Saleh N., Saif A. Alsaif, and Yasser Bin Salamah. 2025. "Recent Advances and a Hybrid Framework for Cooperative UAV Formation Control" Applied Sciences 15, no. 17: 9761. https://doi.org/10.3390/app15179761
APA StyleAlkhamees, S. N., Alsaif, S. A., & Bin Salamah, Y. (2025). Recent Advances and a Hybrid Framework for Cooperative UAV Formation Control. Applied Sciences, 15(17), 9761. https://doi.org/10.3390/app15179761






