Social Trusty Algorithm: A New Algorithm for Computing the Trust Score Between All Entities in Social Networks Based on Linear Algebra

Abstract

The growing importance of social networks has led to increased research into trust estimation and interpretation among network entities. It is important to predict the trust score between users in order to minimize the risks in user interactions. This article enables the identification of the most reliable and least reliable entities in a network by expressing trust scores numerically. In this paper, the social network is modeled as a graph, and trust scores are calculated by taking the powers of the ratio matrix between entities and summing them. Taking the power of the proportion matrix based on the number of entities in the network requires a lot of arithmetic load. After taking the powers of the eigenvalues of the ratio matrix, these are multiplied by the eigenvector matrix to obtain the power of the ratio matrix. In this way, the arithmetic cost required for calculating trust between entities is reduced. This paper calculates the trust score between entities using linear algebra techniques to reduce the arithmetic load. Trust detection algorithms use shortest paths and similar methods to eliminate paths that are deemed unimportant, which makes the result questionable because of the loss of data. The novelty of this method is that it calculates the trust score without the need for explicit path numbering and without any data loss.

1. Introduction

Trust, a complex social phenomenon, is one of the basic components of social interactions. If users readily accept information from a source, this indicates trust in that source [1]. Trust plays a central role in data exchange, which carries unknown risks, for example, from whom information can be accepted, from whom it cannot, or with whom information can be shared [2]. Therefore, modeling or expressing trust is important in many areas, especially in social network analysis. Trust is the relationship established between a trusting person (or truster) and a trusted person (or trustee), taking into account the direction of the relationship. Trust is subjective, asymmetric, non-transitive, propagative, context-dependent, composable, dynamic, self-reinforcing, and fragile [3].

Trust in social networks has been studied not only as a structural or probabilistic phenomenon but also as a socio-technical construct. Foundational works in the trust literature conceptualize trust as a multidimensional relationship shaped by ability, integrity, and benevolence [4], by users’ perceptions in technology-mediated interactions [5], and by institutional and interpersonal dimensions in online environments [6]. Incorporating these perspectives shows that our algorithmic approach only addresses one layer of trust: its structural–probabilistic dimension. However, it remains complementary to socio-technical foundations that emphasize cognitive, affective, and contextual factors.

The main objectives are to identify trustworthy entities to share information in social networks, to keep untrustworthy entities away from the network, and to prevent information from being misused [7]. Trust in social networks arises as a result of social interaction and resource sharing between entities. Entities can decide whether to trust the data they receive and spread it to other entities with a trust measure. The concept of distrust between entities negatively affects the interactions of entities. If social networks can offer sufficient and stable trust, they can provide entities with a well-established platform of collaboration and network expansion, effectively attract entities, and promote the consensus of the social network [8,9]. If trust relationships are found, clustering and group decision-making can also be performed in light of these data [10,11].

To reveal the trust score (degree of trust) of an entity’s relationship with another entity is the purpose of trust inference in the social network. Generally, this score is derived from the trusted interactions of mutual friends of entities. In addition, common interests, etc., are also used.

Traditional trust detection methods are insufficient for inferring common trust, as they consider each entity as an independent entity. However, in reality, entities are not independent entities but communities connected by social relations such as relationships of trust and distrust [12]. Many studies [13,14,15] ignore some connections or nodes in the network, leading to incomplete trust assessments. This study addresses these shortcomings by proposing a trust inference approach that utilizes the full graph structure without omitting any relationships and calculates trust levels efficiently using linear algebra-based methods instead of traditional path enumeration techniques.

In the context of a simple undirected graph G, let A denote the adjacency matrix of G. When a process similar to the Markov process is applied to matrix A, the resulting matrix can be treated as a probability transition matrix. The kth power of this matrix represents the trust between node pairs at k distance in G. When the first, second, …, kth powers of the matrix are taken and summed, the trust score between node pairs at max k distance in G is found. Finding the trust scores in this way incurs a high time cost of ${(\mathrm{k}-1)\mathrm{n}}^3$. In order to eliminate these time costs and obtain secure results without thinning or losing data, the trust calculation between entities has been performed using a low-cost linear algebra method. This is the main source of inspiration and motivation for this study.

While trust in social networks is a multifaceted phenomenon encompassing semantic, contextual, and temporal dimensions, this study focuses specifically on its structural–probabilistic layer. The present algorithm treats trust as a property emerging from the topology of interactions expressed through graph-based and algebraic computations. The proposed method provides a scalable basis for measuring structural trust scores.

2. Related Work

Graph algorithms such as shortest path, maximum flow, and node traversal are frequently used while finding the trust path [13]. TidalTrust is one of the most typical algorithms for finding the trust ratio between two users in a social network [14]. The TidalTrust algorithm determines a threshold based on the trust values obtained from the shortest paths between two users and eliminates the paths that it deems unimportant. Although the elimination of most trust paths has accelerated the operation of the algorithm, the accuracy of the trust score found is debatable. Taherian et al. developed the RN-Trust algorithm, which models trust as if it were a resistive network, in determining the trust scores of entities who are not directly connected to the social network [15]. This algorithm finds trust values with circuit likeness analysis, and while doing this, all paths are taken into account. Mao and his colleagues [13] use the trust-spreading strategy and weighted subject similarity to find trust paths between two users. While choosing the strong ones among the found trust paths, the decision is based on “small world” theory, and a depth restriction is applied.

The issue of trust in social networks is a widely studied topic, especially in recommendation systems, and it is based on the principle that users generally listen to the recommendations of their trusted friends. An entity gives relatively better and more reliable advice to entities that are closely related to it, compared to entities that have no social relationship with it [16]. Liu and his colleagues constructed a trust-sensitive recommendation system that combined explicit and implicit trust relationships [17]. Chen and his colleagues have redeveloped traditional trust spreading strategies such as TrustRank and Appleseed as a system that is sensitive to different issues to provide accurate recommendations in different categories according to users’ preferences [18]. To find trusted recommendations, Liu et al. applied a spread of trust model to the network, determined the trust relationship between pairs of unknown experts, and obtained subjective and objective weights [19]. In [20], a trust-based system using heterogeneous graphs of user–user, user–item, and item–item is presented. TTDNN (trust- and tag-aware deep neural network) is a recommendation system that calculates user similarity using users’ social links and tags [21]. In addition, a recommendation system that uses trust scores to provide location recommendations to users has been developed, and thus, more accurate and personalized recommendations have been provided to users [22]. As another example of a recommendation system, KTPGN (knowledge-enhanced trust propagation graph neural network) overcomes the limitations of traditional group recommendation methods by using social trust propagation in recommending groups to users [23].

In group decision-making (GDM) processes, trust also comes into play when evaluating the opinions of entities/experts in choosing the most appropriate alternative [24,25,26,27]. Xing et al. model how trust relationships among experts change over time and how these relationships can be fostered through interaction in order to increase consensus in group decision-making processes [24].

It has been seen that studies that find the trust score produce solutions with approaches such as probability, cloud modeling, machine learning, and fuzzy analysis [8]. Most of the trust inference algorithms in the social network use the trust values at the edges and the topological information of the network to find the trust scores. These algorithms, which are graph-based, make a restricted traversal and path selection. Finally, the trust scores are found using aggregation strategies. In addition to these, semantic information such as social distance between users is also used when finding the trust score [13]. Jethava and Rao have studied the prediction of trust using characteristics such as trait similarity of adjacent users, similarity of preferences made by nonadjacent users, and social proximity [28]. Acharjee and Panicker also showed that trust depends on the size of the network and the interactions between users [29].

While proposed method focuses on structural–probabilistic trust inference, other approaches in the literature address complementary aspects of trust. For example, overlapping community detection methods based on symmetric nonnegative matrix factorization provide insights into how community structures affect trust propagation [30], while emotion-driven frameworks employing BERT [31] capture the semantic and affective layers of trust in social media content.

Unlike all these studies, our proposed algorithm determines the trust score without any restriction and regardless of the path. In this paper, a relational probability-based calculation is performed for trust analysis in social networks. These calculations are grounded in a transition probability matrix, which naturally reveals the structural differences and trust dynamics among entities within a social network.

3. Concepts and Definitions

In this study, we briefly recall the fundamental concepts of graph theory [32] and linear algebra that underpin our approach.

Definition 1.

Graph: A graph $G=\left(V,E\right)$ consists of a set of vertices $V$ and edges $E$. Graphs are widely used to represent complex systems such as social networks, communication platforms, and biological systems [33,34].

Definition 2.

Graph types: Depending on the application, graphs may be directed or undirected and weighted or unweighted. Directed graphs assign orientation to edges, while weighted graphs associate a numerical value (e.g., cost, distance, probability) with each edge [32].

Definition 3.

Eigenvalues and eigenvectors: For a square matrix $A$, an eigenvalue $\lambda$ and corresponding eigenvector $x$ satisfy the relation $Ax=\lambda x$. Eigenvalues and eigenvectors are widely used in linear algebra to capture structural properties of matrices and play a central role in spectral decompositions applied to graphs [35].

4. Proposed Method: Social Trusty Algorithm

The establishment of a relationship with an element of the network is dependent upon the reliability of that element being clearly expressed numerically and concrete evidence being presented. Such evidence would facilitate the determination of a relationship based on reliability and would also enable careful action to be taken. The present study investigates the relationship between entities in a social network by determining numerical trust values. The entities that an entity in the network trusts the most and trusts the least are identified. Furthermore, the method also identifies the most trusted and least trusted entities in the network.

When interactions are used to obtain the trust score between two entities on social networks, a score matrix (P) similar to a Markov probability matrix is first obtained using the adjacency matrix. This matrix provides the trust score between all pairs of entities at a distance of 1 step. By taking the powers of the matrix, the trust ratios at distances of 1, 2, …, k steps are found. If all of these are found and summed, an upper bound for the trust scores is obtained. This process is quite computationally expensive. Therefore, the eigenvalues and eigenvectors of the P matrix are found, and trust scores for individual pairs are determined by applying orthogonal operations to them. The powers of the eigenvalues are taken in order and summed. Then, the resulting expression is multiplied by the eigenvector. The approach applied in this study is summarized in Figure 1.

In this study, the process begins with the construction of a model of the social network. During the construction of the model, which is a ratio-based graph model, graph theory is used. A social network is modeled as a weighted or unweighted and undirected graph. The next step is to find the adjacency matrix of the graph.

In Figure 2, a simple social network is modeled and shown as a graph.

Table 1. Adjacency matrix of the example graph.

Actor/Actor	${\mathbf{V}}_1$	${\mathbf{V}}_2$	${\mathbf{V}}_3$	${\mathbf{V}}_4$	${\mathbf{V}}_5$
${\mathrm{V}}_1$	0	2	3	0	0
${\mathrm{V}}_2$	2	0	4	5	4
${\mathrm{V}}_3$	3	4	0	3	0
${\mathrm{V}}_4$	0	5	3	0	6
${\mathrm{V}}_5$	0	4	0	6	0

shows the adjacency matrix formed by the nodes and edges of this weighted graph.

Then, by applying the trust score model to the graph, a trust scores matrix (probability transition matrix), which is the representation of inter-entity relations, in which the sum of each row is 1 (probability sum), is formed (

Table 2. Transition score matrix.

Actor/Actor	${\mathbf{V}}_1$	${\mathbf{V}}_2$	${\mathbf{V}}_3$	${\mathbf{V}}_4$	${\mathbf{V}}_5$
${\mathrm{V}}_1$	0	0.4	0.6	0	0
${\mathrm{V}}_2$	0.13	0	0.27	0.33	0.27
${\mathrm{V}}_3$	0.3	0.4	0	0.3	0
${\mathrm{V}}_4$	0	0.36	0.21	0	0.43
${\mathrm{V}}_5$	0	0.4	0	0.6	0

). As a result, the reliability problem in social networks can be considered as a Markov process [36,37].

Social networks are modeled as graphs where the adjacency matrix represents the structure of a weighted or unweighted graph. Therefore, Definition 4 gives us the trust score for adjacent nodes. In this way, a social network graph model can be used to obtain the trust score matrix for a step. This means that a social network can be modeled as a trust score matrix process in order to obtain the trust score between two adjacent nodes.

Definition 4.

Trust degree (Td) expresses the degree of trust (trust score) between entities defined in the range (0 ≤ Td ≤ 1). If ${Td}_{XY}$= 0, it is said that X and Y do not trust each other at all. If ${Td}_{XY}$= 1, it is said that X and Y are very closely related and they trust each other very absolutely. Equation (1) gives the formula for finding trust scores for adjacent nodes.

$${Td}_{XY}={\displaystyle \frac{w(x,y)}{\sum _{v_j\in N\left(X\right)}w(x,v_j)}}$$

(1)

To calculate the trust score of entities in social networks, paths are found between two related nodes, and the degree of trust is obtained by using these paths. If the aim is to find the degree of trust of only two entities to each other, it is shown by the method developed in this study that calculating all paths is a costly process, and there is no need for this. For this purpose, after obtaining the transition scores matrix of a social network, the degree of trust is calculated according to the distance between entities. In this context, in the proposed method, after obtaining the transition score matrix for the trust process of the social network, when the strength of this matrix is taken according to distance and summed, each element of the resulting matrix gives the trust level of the entities in the relevant indices.

Before the proposed method is explained in detail, it is necessary to give information about linear algebra.

Assume that P is the proportion matrix. P$\mathrm{x}=\lambda \mathrm{x}$ equality is provided, where P is a square matrix and x is a column vector, and for this equality, the value of λ is called the eigenvalue and the column vector corresponding to this eigenvalue is the eigenvector x. Matrix P has n eigenvalues and n eigenvectors if it is an $\mathrm{n}\times \mathrm{n}$ matrix. Eigenvalues and eigenvector pairs can be given as $\left({\lambda }_1,{\mathrm{v}}_1\right),\left({\lambda }_2,{\mathrm{v}}_2\right),\left({\lambda }_3,{\mathrm{v}}_3\right),\dots ,\left({\lambda }_{\mathrm{n}},{\mathrm{v}}_{\mathrm{n}}\right)$. In this case, the following Equation (2) can be written.

$$\mathrm{P}{\mathrm{v}}_{\mathrm{i}}={\lambda }_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}$$

(2)

Computing ${\mathrm{P}}^{\mathrm{k}}$ by direct multiplication requires O($\mathrm{k}.{\mathrm{n}}^3$). It is an arithmetically costly operation, and the eigenvalues and eigenvectors of the matrix can be used to reduce the multiplication and addition operations here.

The power k of matrix $\mathrm{P}$ can be calculated as in (3). Figure 3 illustrates the matrix product vector and scaler product vector.

$${\mathrm{P}}^{\mathrm{k}}{\mathrm{v}}_{\mathrm{i}}={\mathrm{P}}^{\mathrm{k}-1}\mathrm{P}{\mathrm{v}}_{\mathrm{i}}={\mathrm{P}}^{\mathrm{k}-1}\left({\lambda }_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}\right)={\mathrm{P}}^{\mathrm{k}-2}{\lambda }_{\mathrm{i}}^2{\mathrm{v}}_{\mathrm{i}}={\mathrm{P}}^{\mathrm{k}-3}{\lambda }_{\mathrm{i}}^3{\mathrm{v}}_{\mathrm{i}}=\dots ={\lambda }_{\mathrm{i}}^{\mathrm{k}}{\mathrm{v}}_{\mathrm{i}}$$

(3)

In this step, when the powers of the scalar numbers are taken, the kth power of the $\mathrm{P}$ matrix is calculated with $\mathrm{n}\times \mathrm{n}$ scalar products. At this aim, ${\mathrm{P}}^{\mathrm{k}}={\lambda }^{\mathrm{k}}\left({\mathrm{v}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{T}}\right){\left({\mathrm{v}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{T}}\right)}^{-1}={\lambda }^{\mathrm{k}}\mathrm{D}$ where $\mathrm{D}=\left({\mathrm{v}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{T}}\right){\left({\mathrm{v}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{T}}\right)}^{-1}$ should be computed.

Figure 3. Matrix, eigenvalues, and eigenvector relations.

Figure 3. Matrix, eigenvalues, and eigenvector relations.

In order to model a system as a trust process, the transition scores between the states of that system are calculated and the transition scores matrix is obtained. The matrix given in Table 2 is used as the transition score matrix for the trust process. The transition score matrix P is calculated as follows.

$$\mathrm{P}=\begin{array}{cc}\mathrm{i}& \begin{array}{c}\mathrm{j}\\ \left[\begin{array}{cc}\begin{array}{cc}{\mathrm{p}}_{\mathrm{1,1}}& ⋮\\ ⋮& {\mathrm{t}}_{\mathrm{i},\mathrm{j}}\end{array}& \begin{array}{c}{\mathrm{p}}_{1,\mathrm{n}}\\ ⋮\end{array}\\ \begin{array}{cc}⋮& \dots \\ {\mathrm{p}}_{\mathrm{n},1}& \dots \end{array}& \begin{array}{c}⋮\\ {\mathrm{p}}_{\mathrm{n},\mathrm{n}}\end{array}\end{array}\right]\end{array}\end{array}$$

(4)

The ${\mathrm{t}}_{\mathrm{i},\mathrm{j}}$ value of the $\mathrm{P}$ matrix represents the scores of going from state i to state j in one step. The transition score matrix (Table 2) obtained from the social network can be used in this way, and in this case, the value ${\mathrm{t}}_{\mathrm{i},\mathrm{j}}$ will show the trust of entity i in entity j. In a trust process, whose transition scores matrix is given as P, the scores of transitioning from one state to another after k steps will be the value transition scores represented by the relevant indices after taking the k power of the P matrix (5).

$${\mathrm{P}}^{\mathrm{k}}=\mathrm{Q}=\begin{array}{cc}\mathrm{i}& \begin{array}{c}\mathrm{j}\\ \left[\begin{array}{cc}\begin{array}{cc}{\mathrm{q}}_{\mathrm{1,1}}& ⋮\\ ⋮& {\mathrm{r}}_{\mathrm{i},\mathrm{j}}\end{array}& \begin{array}{c}{\mathrm{q}}_{1,\mathrm{n}}\\ ⋮\end{array}\\ \begin{array}{cc}⋮& \dots \\ {\mathrm{q}}_{\mathrm{n},1}& \dots \end{array}& \begin{array}{c}⋮\\ {\mathrm{q}}_{\mathrm{n},\mathrm{n}}\end{array}\end{array}\right]\end{array}\end{array}$$

(5)

The value of r in the matrix gives the scores of starting from state i and being in state j at the end of k steps. If there is a probability of staying in the same state for this matrix, then it is taken into account. When the values given in Table 2 are evaluated as one-step trust degrees, it will be seen that the diagonal values are zero. This means that it will not stand on itself and cause repetition. When Table 2 is represented as a matrix, let this matrix be represented as ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}$. The ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}$ matrix shows the degree of trust of entities who are directly connected to each other in the relevant social network. When the ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}$ matrix is squared, the degree of trust of entities with a distance of 2 to each other is calculated. If the ${\mathrm{k}}^{\mathrm{t}\mathrm{h}}$ power of this matrix is taken, the degree of trust between entities at a distance of k is obtained. As a result, the degree of trust of entities in each other is calculated (Figure 4). Figure 4 depicts the matrix power relation with eigenvalues and eigenvectors relations. This method gets rid of finding all paths by using breadth first search or other technique like breadth first search. For this purpose, the powers of the ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}$ matrix will need to be taken, and this is a costly operation (more multiplication operations). In the present model, eigenvalues and eigenvectors have been used to calculate the powers of the transition score matrix. The eigenvalue and eigenvector pairs of the ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}$ matrix are $\left({\eta }_1,{\mathrm{y}}_1\right),\left({\eta }_2{,\mathrm{y}}_2\right),\left({\eta }_3{,\mathrm{y}}_3\right),\dots ,\left({\eta }_{\mathrm{n}}{,\mathrm{y}}_{\mathrm{n}}\right)$ and are shown in (6).

$$\begin{gathered} {\mathrm{T}\mathrm{d}}_{\mathrm{p}}{\mathrm{y}}_1={\eta }_1{\mathrm{y}}_1 \\ {\mathrm{T}\mathrm{d}}_{\mathrm{p}}{\mathrm{y}}_2={\eta }_2{\mathrm{y}}_2 \\ \dots \\ {\mathrm{T}\mathrm{d}}_{\mathrm{p}}{\mathrm{y}}_{\mathrm{n}}={\eta }_{\mathrm{n}}{\mathrm{y}}_{\mathrm{n}} \end{gathered}$$

(6)

The degree of trust of entities with a distance of 2 to each other is shown in (7).

$${\mathrm{T}\mathrm{d}}_{\mathrm{p}}^2{\mathrm{y}}_{\mathrm{i}}={\eta }_{\mathrm{i}}^2{\mathrm{y}}_{\mathrm{i}}$$

(7)

In cases where entities are at a distance of 3 from each other, their degree of trust is calculated with the following Equation (8).

$${\mathrm{T}\mathrm{d}}_{\mathrm{p}}^3{\mathrm{y}}_{\mathrm{i}}={\eta }_{\mathrm{i}}^3{\mathrm{y}}_{\mathrm{i}}$$

(8)

When the distances of entities from each other are k, the relation in (9) finds the degree of trust.

$${\mathrm{T}\mathrm{d}}_{\mathrm{p}}^{\mathrm{k}}{\mathrm{y}}_{\mathrm{i}}={\eta }_{\mathrm{i}}^{\mathrm{k}}{\mathrm{y}}_{\mathrm{i}}$$

(9)

After all, to calculate the degrees of trust of entities in each other, it is necessary to sum the degrees of trust on all roads with distances of 1, 2, …, k. As a result, the maximum values of the degree of trust of entities to each other can be calculated with the following relation (10), and in this case, there will be no need to find all the paths between entities ($\mathrm{T}\mathrm{d}$ is the trust matrix). This operation requires the trust scores of all entities to a specific entity.

$$\mathrm{T}\mathrm{d}\le \sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{T}\mathrm{d}}_{\mathrm{p}}^{\mathrm{i}}{\mathrm{y}}_{\mathrm{r}}=\sum _{\mathrm{i}=1}^{\mathrm{k}}{\eta }_{\mathrm{r}}^{\mathrm{i}}{\mathrm{y}}_{\mathrm{r}}$$

(10)

Any power of the $\mathrm{T}\mathrm{d}$ matrix is multiplied by a column vector; however, to compute the trust score, the power of $\mathrm{T}\mathrm{d}$ matrix is required. To obtain the trust score of any length, the corresponding power of $\mathrm{T}\mathrm{d}$ should be computed. There are two ways to compute these values:

1st way: Any power of $\mathrm{T}\mathrm{d}$ should be computed by using matrix multiplication. This step requires many arithmetic operations.

2nd way: ${\mathrm{T}\mathrm{d}}_{\mathrm{p}}^{\mathrm{k}}\left({\mathrm{y}}_{\mathrm{r}}{\mathrm{y}}_{\mathrm{r}}^{\mathrm{T}}\right){\left({\mathrm{y}}_{\mathrm{r}}{\mathrm{y}}_{\mathrm{r}}^{\mathrm{T}}\right)}^{-1}={\mathrm{T}\mathrm{d}}_{\mathrm{p}}^{\mathrm{k}}$.

The working steps of the developed method are given as pseudocode in Algorithm 1:

Algorithm 1 Social Trusty Algorithm

1. Start 2. G = (V, E) //Convert social network to graph 3. ${\mathrm{P}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\mathrm{G}}_{\mathrm{i}\mathrm{j}}}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{G}}_{\mathrm{i}\mathrm{k}}}}1\le \mathrm{i},\mathrm{j}\le \mathrm{n}$ //Find transition scores matrix 4. $\mathrm{P}\mathrm{x}=\lambda \mathrm{x}$ // Find P’s eigenvalues and eigenvectors 5. ${\mathrm{S}}_{\mathrm{i}}=\sum _{\mathrm{k}=1}^{\mathrm{n}}{\lambda }_{\mathrm{i}}^{\mathrm{t}}\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{n}$ 6. $\mathrm{T}\mathrm{d}=\mathrm{S}.\mathrm{E}\mathrm{v}\mathrm{e}\mathrm{c}$// $\mathrm{E}\mathrm{v}\mathrm{e}\mathrm{c}$ eigenvector matrix 7. $\mathrm{rowMax}\left[\mathrm{i}\right]=\max \left({\mathrm{T}\mathrm{d}}_{\mathrm{i}}\right),\mathrm{rowMin}\left[\mathrm{i}\right]=\min \left({\mathrm{T}\mathrm{d}}_{\mathrm{i}}\right) \mathrm{i}=\mathrm{1,2},\dots ,\mathrm{n}$ 8. $\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{S}\mathrm{u}\mathrm{m}\left(\mathrm{j}\right)=\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{T}\mathrm{d}(\mathrm{i},\mathrm{j})$ 9. $\mathrm{m}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{T}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{y}=\max \left({\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{S}\mathrm{u}\mathrm{m}}_{\mathrm{j}}\right),\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{T}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{y}=\min \left({\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{S}\mathrm{u}\mathrm{m}}_{\mathrm{j}}\right)$ 10. End

In step 7, trust between entity pairs is expressed by finding the max and min values on a row-by-row basis. The resulting Td matrix is summed on a column-by-column basis, and as seen in step 9, the most trusted and least trusted entities across the entire network are identified using the max and min values.

The steps of the method based on linear algebra can be briefly explained as follows:

Step 1: The adjacency matrix of the given social network is taken as input. The transition probability matrix is obtained.

Step 2: All powers of the transition probability matrix from 1 to the (n − 1) are calculated.

Step 3: All the resulting matrices are summed and the (i, j) element of the total matrix will give the trust of node i to node j. Since calculating the powers of the matrix is costly, the eigenvalues and eigenvectors of the matrix whose power will be calculated are calculated. After the powers of the eigenvalues are calculated, the product of the matrix whose main diagonal consists of these values and the eigenvectors matrix will give the power of the corresponding matrix.

Step 4: The resulting matrix gives the trust scores for all pair nodes.

5. Simulation Results

When all processes in the Social Trust Algorithm are applied to the graph in Figure 2, the matrix in

Table 3. Trust scores of the graph given in Figure 2 (Td matrix).

Actor/Actor	${\mathbf{V}}_1$	${\mathbf{V}}_2$	${\mathbf{V}}_3$	${\mathbf{V}}_4$	${\mathbf{V}}_5$
${\mathrm{V}}_1$	2.236068	3.716654	2.179268	3.306984	3.164772
${\mathrm{V}}_2$	0.239529	0.007645	0.048473	0.338074	0.135764
${\mathrm{V}}_3$	0.662383	0.628117	0.756419	0.010245	0.784918
${\mathrm{V}}_4$	0.28105	0.168186	0.313189	0.118871	0.230325
${\mathrm{V}}_5$	0.231522	0.229073	0.280051	0.185444	0.179303

is obtained. As shown in this matrix, trust scores are clearly distinguishable. To illustrate this, consider node ${\mathrm{V}}_1$, which shows maximum trust in ${\mathrm{V}}_2$ with a score of 3.716654. Conversely, node ${\mathrm{V}}_1$ has the lowest level of trust in ${\mathrm{V}}_3$, with a score of 2.179268.

The results for each entity of the example graph in Figure 2 are shown in Figure 5.

It can be seen in Figure 5 that ${\mathrm{V}}_1$’s most trusted entity in the network is ${\mathrm{V}}_2$, and its least trusted entity is ${\mathrm{V}}_3$. Similarly, it can be seen that ${\mathrm{V}}_2$’s most trusted entity in the network is ${\mathrm{V}}_4$, and her least trusted entity is ${\mathrm{V}}_3$ and vice versa.

When the algorithm is applied to the social network, a Td matrix is obtained. The trust score of each entity can be obtained by adding up the columns of the Td matrix. In addition, an inference can be made about the overall network. The entity with the lowest trust score is designated as the most distrusted, while the entity with the highest score is regarded as the most trusted.

Table 4. Algorithm results with datasets based on real networks.

Dataset	Number of Nodes (n)	Number of Edges (m)	Node Meaning	Edge Meaning	Most Trusted Node Label	Most Distrusted Node Label
Kangaroos 1	17	91	Kangaroo	Interaction	3	12
Zachary Karate Club 1	34	78	Member	Tie	8	31, 32
Windsurfers 1	43	336	Person	Contact	33	20
Dolphins 1	62	159	Dolphin	Association	TR77	DN21
Train bombing 1	64	243	Terrorist	Contact	48	64
Les Misérables 1	77	254	Character	Co-occurence	Bossuet	Thenardier
Political books 1	105	441	Book	Co-purchase	4	14
David Copperfield 1	112	425	Word	Adjacency	time	world, year
American football 1	115	613	Team	Game	9	12
PDZBase 1	212	244	Protein	Interaction	87	211
Residence hall 1	217	2672	Person	Friendship	146	14
Similarities (DBpedia) 1	430	565	Concept	Similarity	330	228
R1000.5 2	1000	238,267			821	845
R1000.1 2	1000	14,378			465	989
flat1000_50_0 2	1000	245,000			290	902
DSJC1000.9 2	1000	449,449			403	665
Euroroads 1	1174	1417	City	Road	46	1152

¹ Taken from the Konect project implemented by Kunegis [28]. This study is a project that compiles real-world networks used in network analysis. ² Graphs taken from DIMACS benchmark [29].

illustrates the results obtained when the Social Trusty Algorithm is run on real networks. The datasets we used are Windsurfers, Zachary Karate Club, Dolphins, Les Misérables, etc., which are frequently used in social network analysis. For example, Lesmis is a weighted graph in which the characters in Victor Hugo’s novel. Les Misérables are represented as nodes, and the relationships of these characters with those in the same chapter of the book are represented as edges. The graph consists of 77 nodes and 254 edges. While the most trusted entity of the network is Bossuet, the most distrusted is Bahorel.

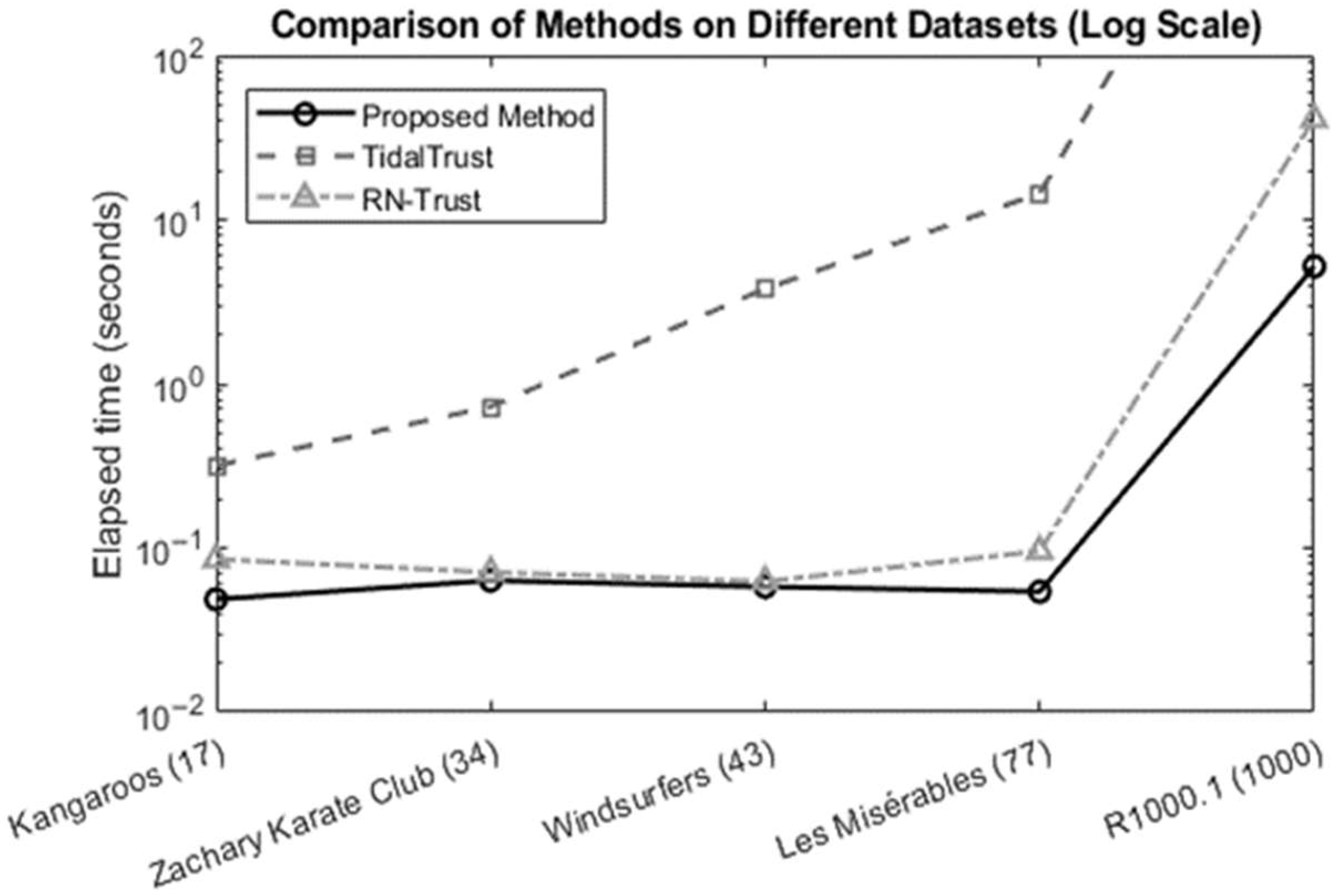
The graph in Figure 6 shows the runtimes of the algorithms while finding the trust scores on various datasets. The datasets used are 17-node Kangaroos, 34-node Zachary Karate Club [38], 43-node Windsurfers [38], 77-node Les Misérables [38], and 1000-node R1000.1 [39]. In this study, a comparison was made between the proposed method and the RN-Trust [15] and TidalTrust [14] algorithms. A comparative analysis was conducted on the three distinct methods in terms of their execution times on various datasets. The results indicated that the proposed method exhibited superior performance in all instances. It is evident that as the number of nodes in the dataset increases, the superiority of the proposed algorithm becomes more pronounced. This discrepancy is particularly pronounced in the “Les Misérables” dataset.

6. Conclusions

This paper emphasizes the importance of trust in social networks and can find the trust score and label users in the network as trustworthy or untrustworthy. Most solutions to the problem of finding a trust score work within a limited search range, such as the shortest path. Trust degradation and path dependency emerge as common issues in trust propagation. Considering these issues, a Markov process-like method has been developed to find the trust score without applying any constraints or without explicit path enumeration.

As the proposed algorithm is an approach method, soundness and completeness are not sought. Since the initial scores of other algorithms differ from ours, the resulting numerical trust scores are also different, making them unsuitable for direct comparison. Therefore, a comparative analysis was conducted with other algorithms in terms of runtime and data loss. The experimental results demonstrate that our algorithm achieves lower runtime complexity compared to RN-Trust and TidalTrust, particularly in larger networks. Moreover, by preserving all transition probabilities, it avoids the structural information loss inherent in pruning-based approaches. While eigendecomposition provides a computationally efficient way to compute matrix powers, it does not yield formal guarantees of soundness or completeness. As such, the Social Trusty Algorithm should be regarded as a computational shortcut that emphasizes efficiency and structural preservation, rather than a fully rigorous model.

Although the present method is able to conceptualize trust as a structural and probabilistic construct, it does not encompass the semantic, contextual, or temporal dynamics of trust that have been emphasized in the broader information systems literature. Despite these limitations, this study provides a valuable methodological contribution. The Social Trusty Algorithm can support a range of applications, from identifying malicious actors in social networks to enhancing recommender systems, improving information security, and informing governance in digital platforms. Once trust scores are obtained, users can establish relationships with trustworthy users, share information, and interact with them, while taking necessary precautions against untrustworthy users.

In this paper, a method for inferring trust in social networks has been designed and its applicability demonstrated. In the future, the dynamic structure of social networks will be taken into account to obtain dynamic trust inference. This method will be expanded to provide a multidimensional trust assessment by integrating online social networks and additional social factors.