A Numerical Investigation on the Influence of Geometric Curvature on Delamination Growth in Curved Stiffened Composite Panels

Abstract

Composite materials have gained prominence in aerospace engineering due to their high strength-to-weight and stiffness-to-weight ratios. However, their susceptibility to interlaminar damage, particularly delamination, remains a significant concern, especially under compressive loads. This study presents a detailed numerical investigation into the buckling behavior and delamination propagation in flat and curved composite panels with centrally located circular delaminations. Four configurations were analyzed, differing by geometry (flat vs. curved) and delamination interface. The critical buckling load was first estimated through linear eigenvalue analysis, while post-buckling behavior and damage progression were studied using a nonlinear static analysis enhanced by the Smart-time XB (SMXB) tool. Numerical results, including out-of-plane displacements and delamination length evolution, were validated against experimental data from the literature. The findings confirm the accuracy of the adopted FEM approach and highlight the beneficial role of curvature in increasing buckling resistance and improving damage tolerance, offering valuable insights for the design of aerospace composite structures.

1. Introduction

Composite material structures have played a pivotal role in the aerospace sector, owing to their excellent mechanical properties [1,2], notably their high strength-to-weight and stiffness-to-weight ratios [3,4]. These characteristics have significantly contributed to improving the structural and performance efficiency of aircraft [5,6,7]. However, alongside these numerous advantages, composite materials have also exhibited certain critical limitations that may compromise their structural integrity [8,9].

The literature highlights several typical damage mechanisms in composite materials. Mishani et al. [10] emphasized the critical role of interlaminar delamination, noting that Mode II (shear) fracture toughness is significantly higher than Mode I (opening). This underscores the importance of quality control [11,12] and proper laminate design to ensure performance and safety. Manufacturing defects and anomalies, due to the inherent variability of composites, can alter both static and dynamic properties. A thorough understanding of failure and damage mechanisms is, therefore, essential to enhance durability and reliability. In this context, research on delamination growth and the interaction between curvature and laminate defects has gained increasing attention. Nasr-Isfahani et al. [13] showed that, despite advancements, composite structures remain vulnerable, particularly to matrix-dominated failure modes, especially in components with long continuous fibers under compression. Recent studies [14,15,16,17] further stress the need for detailed experimental testing and numerical analyses to assess and mitigate risks associated with composite use in aerospace applications.

Moreover, the impact behavior of composite aerospace structures is influenced by several additional factors [18,19]. Panel thickness and curvature can significantly affect energy absorption and damage distribution, with thicker or curved panels generally enhancing stiffness but also modifying stress propagation and damage patterns. Stiffener configuration has been shown to strongly influence residual strength and post-buckling response after impact, as demonstrated in previous studies [20] where different layouts were found to either delay instability or promote stress localization. Low-velocity impacts are particularly critical, often inducing barely visible impact damage (BVID) such as delamination, matrix cracking, or fiber breakage, which can compromise performance without immediately evident external signs. These considerations highlight the importance of impact-tolerant design, aiming to ensure that, even in the presence of localized damage, the structural integrity and functionality of composite aerospace components are maintained throughout their service life.

An important area of research in the field of composite materials concerns the buckling and post-buckling behavior of laminated panels, with particular focus on the influence of curvature and the presence of structural defects. Numerous studies have investigated how curvilinear geometry affects both local instability and the progression of pre-existing delaminations. In particular, Reeder et al. conducted an analysis of buckling and delamination growth in composite panels subjected to axial compression, highlighting how loading conditions and initial imperfections have compromised structural integrity [21].

Other researchers, such as Han et al., have examined the post-buckling behavior of laminated composite panels under combined loading conditions, emphasizing the mechanical complexity and engineering relevance of these phenomena in composite materials [22]. Within comparative studies between flat and curved structures, significant differences in buckling response have been identified. For instance, Wu et al. carried out investigations on variable-angle composite panels, demonstrating that the nonlinearly elastic behavior exhibited by curvilinear structures has resulted in increased buckling resistance compared to flat panels [23]. This variability in structural response has been further confirmed by the work of Diaconu and Weaver, who explored buckling in asymmetric laminates, underlining the impact of geometry and asymmetry on the buckling threshold [24]. Moreover, the experimental results obtained by Reeder have provided a solid foundation for validating the numerical simulations conducted in the present study, which considers the behavior of composite panels containing delaminations in both flat and curved configurations. The comparison between experimental findings and analytical models has proven essential for verifying the reliability of the analytical and design methodologies used for composite structures, as confirmed by recent contributions in the literature [21].

In the study of composite structures, the analysis of delamination growth has emerged as a critical topic, as this type of damage has been shown to severely compromise the strength and durability of components. The use of finite element models (FEM) has enabled accurate evaluations of how and when delamination initiates and propagates under structural loading conditions. Among the most widely adopted numerical techniques, the Virtual Crack Closure Technique (VCCT) has become a standard method for simulating delamination propagation in composite materials due to its ability to efficiently and accurately estimate the energy release rate associated with crack growth [25]. The VCCT is based on the principle that the energy required to open a crack is directly related to the work needed to close it. This approach has allowed for the effective assessment of energy release rates and delamination mechanisms, and it has often been preferred over Cohesive Zone Models (CZMs), which may require complex definitions of constitutive laws. Recent research has proposed advanced numerical approaches for delamination growth prediction, including Cohesive Zone Models (CZMs) with additional mechanisms such as fiber bridging effects. For example, Duan et al. [26] developed a mechanism-based CZM for Mode I loading validated against experimental results, confirming the relevance of refined numerical strategies in this field. While CZMs have provided detailed insights into fracture mechanisms, the VCCT has generally offered faster computation and more accurate results [27,28]. Nevertheless, the VCCT has not been without its limitations. One of the main challenges involves its sensitivity to mesh discretization, meaning that variations in mesh quality can significantly affect simulation accuracy [29]. To address these limitations, a tool called SMart time XB (SMXB) has been developed, which builds upon VCCT principles while offering enhanced capabilities and improved numerical robustness. SMXB has been designed to mitigate mesh dependency and optimize delamination simulations, making it a more powerful tool than conventional VCCT approaches [20,30,31,32,33]. The integration of FEM approaches with techniques such as the VCCT and advanced tools like SMXB has represented a significant advancement in the understanding and prediction of delamination behavior in composite structures, thereby contributing to more reliable and effective design [34,35].

The aim of this study has been to investigate the influence of panel curvature on the buckling load and the evolution of delamination length in composite structures. Particular attention has been given to assessing the effectiveness of the SMart time XB (SMXB) tool for the numerical simulation of delamination propagation under compressive loading. The adopted modeling strategies have been described in detail, and a comparative analysis has been carried out between the results obtained from the numerical simulations of both flat and curved panels and the experimental data available in the literature [21]. The investigated structure consists of two composite panels: a flat panel and a curved panel with a curvature radius of 760 mm. Both configurations have been characterized by the presence of a centrally located artificial delamination, introduced to simulate initial debonding conditions. To evaluate the influence of the delamination position through the laminate thickness, two different interlaminar interfaces have been considered: Interface 1, between the fourth and fifth plies, and Interface 2, between the fifth and sixth plies. This approach has enabled the analysis of how the delamination location affects both the buckling behavior and damage progression. The numerical results, expressed in terms of delamination length versus applied load (kN) and out-of-plane displacements, have been validated through direct comparison with experimental data presented in [21]. The outcomes have confirmed the reliability of the SMXB tool and the proposed finite element modeling approach in capturing the critical aspects of delamination evolution and structural instability in both flat and curved composite panels.

2. Theoretical Background

The SMXB tool (SMart-time Xie-Biggers) is an advanced numerical methodology developed for analyzing delamination growth in composite materials. It is based on the integration of the Virtual Crack Closure Technique (VCCT) with an enhanced approach known as the Fail Release (FR) method [30,31]. Designed to overcome the limitations of traditional delamination modeling techniques, SMXB proves particularly effective in the analysis of composite panels used in aerospace engineering applications [32,33].

In the present study, SMXB has been employed to explore the interaction between local and global buckling phenomena and the propagation of interlaminar delamination in a typical aeronautical composite panel.

Delamination growth has been simulated using a hybrid numerical strategy that combines the Virtual Crack Closure Technique (VCCT) with the Fail Release (FR) approach. The VCCT is employed to evaluate the energy release rate at each node along the delamination front for all three fracture modes: Mode I (opening), Mode II (sliding), and Mode III (tearing). The energy release rate ${\mathrm{G}}_{\mathrm{j}}$ for each mode j is computed according to Equation (1), which relates the crack tip force and the corresponding opening displacement to the energy released per unit area:

$$G_j={\displaystyle \frac{F_j∆u_j}{2∆A}} with j=I,II,II$$

(1)

where ${\mathrm{F}}_{\mathrm{j}}$ represents the force at the delamination tip for fracture mode j, $∆{\mathrm{u}}_{\mathrm{j}}$ denotes the opening displacement for fracture mode j, and $∆\mathrm{A}$ is the crack surface generated by the delamination opening. The propagation of delamination under mixed-mode loading was modeled using the Power–Law criterion, which combines the energy release rates of the three fracture modes (I, II, and III) into a single failure condition. The criterion is expressed as follows:

$${\left({\displaystyle \frac{G_I}{G_{Ic}}}\right)}^{\propto }+{\left({\displaystyle \frac{G_{II}}{G_{IIc}}}\right)}^{\beta }+{\left({\displaystyle \frac{G_{III}}{G_{IIIc}}}\right)}^{\gamma }\ge 1$$

(2)

where ${\mathrm{G}}_{\mathrm{I}},{\mathrm{G}}_{\mathrm{I}\mathrm{I}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{G}}_{\mathrm{I}\mathrm{I}\mathrm{I}}$ are the Mode I, II, and III energy release rates, respectively, and ${\mathrm{G}}_{\mathrm{I}\mathrm{c}}, {\mathrm{G}}_{\mathrm{I}\mathrm{I}\mathrm{c}}\mathrm{and} {\mathrm{G}}_{\mathrm{I}\mathrm{I}\mathrm{I}\mathrm{c}}$ are the corresponding critical values. The exponents, α, β, and γ govern the interaction between fracture modes and allow the criterion to represent a wide range of material behaviors.

In this study, the exponents were all set equal to 1 (α = β = γ = 1), corresponding to a linear interaction between modes. This choice is supported by previous works showing that linear formulations can be appropriate under specific conditions. Murri [36] emphasizes the suitability of Power–Law formulations for describing delamination growth in unidirectional composites, demonstrating that, under certain loading scenarios, a linear expression accurately represents the relationship between delamination growth rate and energy release rate. Similarly, Alfano and Crisfield [37] discuss interface models indicating that a linear interaction assumption simplifies the analysis without significantly compromising accuracy for composite materials. Zhao et al. [38] further confirm that Power–Law approaches are widely adopted and effective for modeling mixed-mode delamination.

The Power–Law criterion was selected over alternative criteria, such as the quadratic form or the Benzeggagh–Kenane (BK) criterion, because of its generality and ability to capture both linear and nonlinear mixed-mode interactions by adjusting the exponents. This flexibility makes it suitable for investigating a range of behaviors without imposing restrictive assumptions on the interaction between fracture modes.

What distinguishes SMXB from other tools is its SMART approach, composed of two core modules—SMART-TIME and SMART-CORNER—which effectively remove mesh and load step dependencies from the analysis. The SMART-TIME module dynamically adjusts the load step size to ensure consistency between the numerically estimated delaminated area and the area calculated based on mesh discretization. If a discrepancy is detected between the two (as shown in Equations (3) and (4)), the load step is automatically reduced until convergence is achieved. This ensures that delamination grows realistically, regardless of element size.

$$A_{num}=\sum _{i=1}^N{A}_i^{EL}$$

(3)

$$A_{es}=\sum _{i=1}^N{A}_i^{es}=\sum _{i=1}^N({\displaystyle \frac{F_{iI}∆u_{iI}}{2G_{Ic}}}+{\displaystyle \frac{F_{iII}∆u_{iII}}{2G_{IIc}}}+{\displaystyle \frac{F_{iIII}∆u_{iIII}}{2G_{IIIc}}})$$

(4)

The “SMART-TIME” approach requires solving the problem iteratively. For each load step, the solution is computed starting from the configuration frozen at the previous step, using a load increment as the initial guess. The energy release rates (GI, GII, and GIII) are then calculated, along with the two quantities AES and ANUM. The equivalence between these two areas is checked, and, if necessary, the load step size is adjusted according to the sign of the imbalance detected (e.g., if AES > ANUM, the load step is reduced). The solution phase is then restarted from the last converged state, and this process is repeated until convergence is achieved, with a tolerance defined for satisfying the criterion.

The SMART-CORNER module addresses numerical instabilities at the corner nodes of the delamination front, where abrupt geometric transitions can lead to spurious peaks in energy release rate calculations. To overcome this, the growth criterion is enforced over the segments connecting adjacent nodes rather than at individual nodes.

Additionally, SMXB enhances the XB algorithm to better capture the actual geometry of the evolving delamination front. A local coordinate system is established at each node of the front using eight vectors, two of which (normal and tangent) distinguish connected from unconnected nodes. The normal and tangent vectors at the crack front are computed, forming a basis for defining the local coordinate system used in VCCT evaluations. The virtually closed area, required by the VCCT, is then calculated as a polygon with n vertices derived from this local framework.

The main advantage of the SMXB tool lies in its independence from the mesh, which addresses a key limitation of the traditional VCCT. This is achieved through an iterative approach that controls the equivalence between AES and ANUM at each load step. While this may result in a higher computational cost compared to direct methods such as the standard VCCT, it provides much more accurate and mesh-independent results. Of course, the degree of mesh independence also depends on the chosen solver: using ANSYS 18 with a very coarse mesh can lead to a loss of information on buckling, which may compromise the results. Another limitation of the method is that it is not fully standardized for all types of structures. It has been validated primarily for composite panels with single debonding and circular delamination. For these structures, the approach has been further extended to account for fiber bridging effects and fatigue behavior.

The entire SMXB framework has been implemented in ANSYS Parametric Design Language (APDL), making it highly customizable and fully parametric.

The SMXB tool has been extensively validated in previous works against experimental and numerical benchmarks [27,28,29,30,31]. Its proven accuracy and robustness ensure reliable predictions of nonlinear and damage-sensitive behaviors, such as delamination growth under post-buckling.

Several analytical and theoretical models have been proposed to address post-buckling and damage mechanisms in composite structures [39]. These advanced formulations, although accurate, demonstrate the inherent complexity of capturing geometric nonlinearity and delamination growth analytically. Consequently, numerical methods such as FEM remain the most practical and robust approach for investigating such highly nonlinear phenomena.

3. Numerical Application

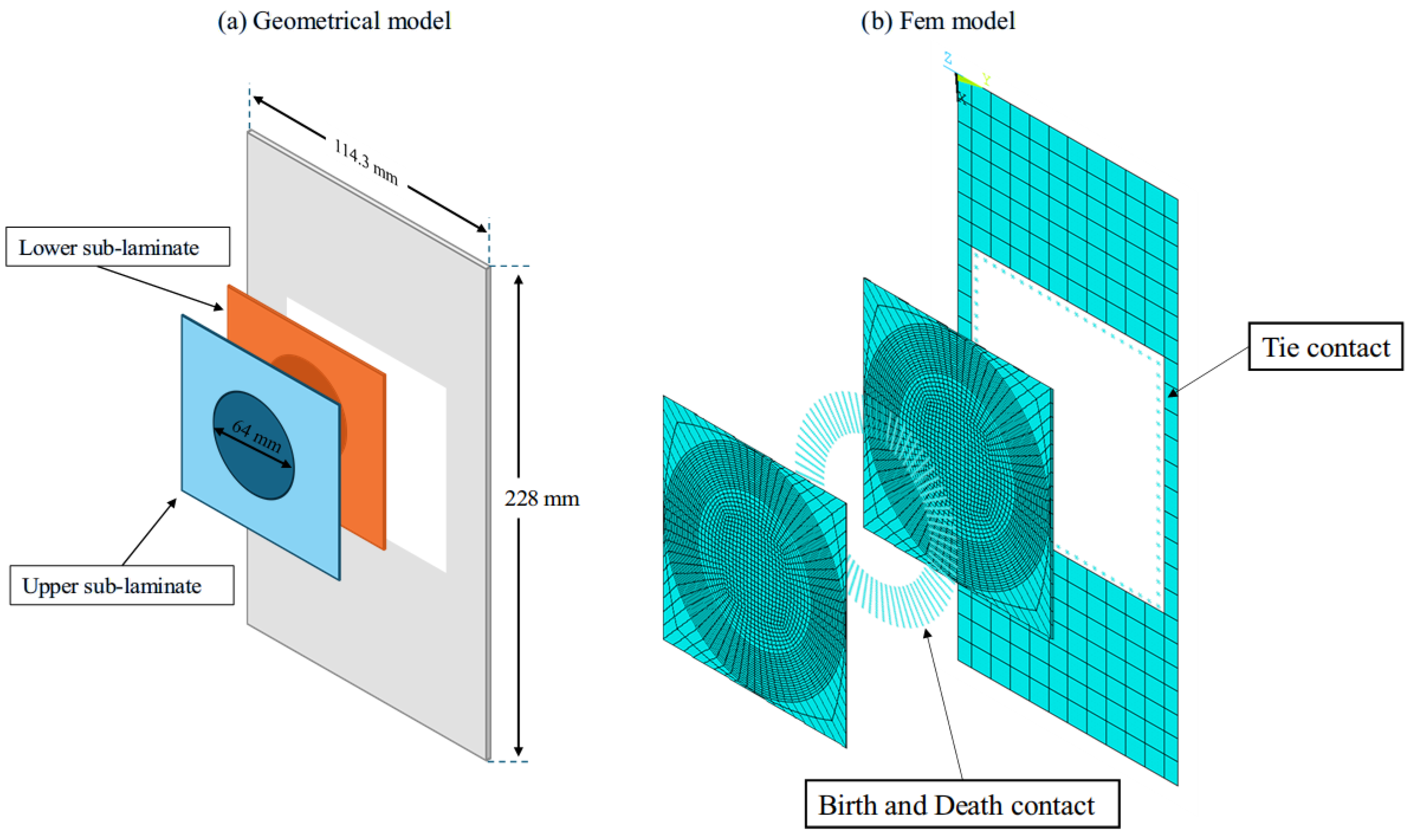
To investigate the influence of curvature on circular delamination propagation in composite panels, both flat and cylindrical configurations replicate the experimental conditions described in [21]. The specimens consisted of flat and curved composite panels with an overall size of 114 mm × 229 mm in the unsupported region, representative of the test setup in [21]. One level of curvature has been considered, a slightly curved panel with a radius of 760 mm, in addition to a flat configuration. The models include a centrally located pre-existing circular delamination with a diameter of 64 mm. The numerical simulations were carried out using ANSYS 18 through the APDL scripting language. The skin was modelled with shell elements (Shell 188), while the sublaminates were represented using solid elements (Solid 186). A schematic view of the geometric configuration and the finite element mesh is provided in Figure 1. The load was applied along the cylinder axis for the curved panels, while for the flat panels, it was applied along the longitudinal axis. The composite models were made of graphite/epoxy material with the AS4/3501-6 system (see

Table 1. Graphite/epoxy material with the AS4/3501-6 system.

Property	Value	Description
${\mathit{E}}_{\mathbf{11}}$	127,557 MPa	Young’s modulus in the fibers’ direction.
${\mathit{E}}_{\mathbf{22}}={\mathit{E}}_{\mathbf{33}}$	11,375 MPa	Young’s modulus in the transverse directions.
${\mathit{G}}_{\mathbf{12}}$	5998 MPa	Shear modulus in the 1–2 and 1–3 planes.
${\mathit{\nu }}_{\mathbf{12}}$	0.3	Poisson’s ratio in the 1–2 plane.
${\mathit{G}}_{\mathit{I}\mathit{c}}$	175 J/m2	Mode I critical energy release rate.
${\mathit{G}}_{\mathit{I}\mathit{I}\mathit{c}}={\mathit{G}}_{\mathit{I}\mathit{I}\mathit{I}\mathit{c}}$	532 J/m2	Mode II and Mode III critical strain energy release rate.
${\mathit{t}}_{\mathit{h}}$	0.135 mm	Ply thickness.

). The laminate stacking sequence used ${\left[{\left(\pm \mathrm{45,90,0}\right)}_2,\pm 60,\pm 15\right]}_s$ represents the skin structure of a reusable launch vehicle. Each model contains a circular delamination located at one of two possible interfaces: Interface 1, between the fourth and fifth plies, corresponding to the interface between the 0° and +45° fiber orientations, and Interface 2, between the fifth and sixth plies, located between the +45° and −45° fiber orientations. A total of four configurations were analyzed, as shown in

Table 2. Identification codes of the configurations analyzed.

ID Configuration	Type	Interface
FI1	Flat	Interface 1 (0°/45°)
FI2	Flat	Interface 2 (45°/−45°)
CI1	Curved	Interface 1 (0°/45°)
CI2	Curved	Interface 2 (45°/−45°)

. The first, a flat panel with delamination at Interface 1 (0°/45°), is referred to as FI1. The second, also flat but with delamination at Interface 2 (45°/−45°), is referred to as FI2. The third configuration, a curved panel with Interface 1 (0°/45°), is labelled CI1, while the fourth, a curved panel with Interface 2 (45°/−45°), is labelled CI2.

To optimize computational efficiency, the FEM model was developed using a global–local modeling approach. In this framework, a coarse mesh was employed to represent the overall panel (global model), while a refined mesh was used in the delaminated region and the anticipated propagation zone (local model). The global and local domains were coupled using contact elements with multipoint constraint (MPC) formulations.

The area containing the circular delamination was modelled as two distinct sublaminates—an upper and a lower one—connected via contact elements with birth and death capabilities. These elements were strategically placed along the perimeter of the delamination, where damage propagation is expected to initiate, as illustrated in Figure 2. The interfacial behavior between the sublaminates was modeled using contact elements CONTA175 and TARGE170 arranged in a contact–target pairing. These elements allow for the transition from bonded to debonded states as damage propagates. The simulation was managed through the SMXB tool, which combines the Virtual Crack Closure Technique (VCCT) and a Fail Release strategy to control the evolution of the delamination front. At each load increment, the strain energy release rates $G_j$ for Modes I, II, and III were computed according to Equation (1). Delamination propagation was governed by the linear Power–Law criterion (Equation (2)), which evaluates the interaction between fracture modes. When the criterion was met, the Fail Release approach deactivated the corresponding contact elements (CONTA175) via an element birth-and-death procedure, simulating the progressive growth of the delamination front. The nodes at the boundaries of the local model were coupled with the corresponding nodes of the global model using contact elements with multipoint constraint (MPC) formulations. The structural model adopts a hybrid discretization approach to balance computational efficiency and accuracy in capturing interlaminar phenomena. The fracture process zone and its vicinity, where through-thickness kinematics and interlaminar stresses are critical, are modeled using layered three-dimensional solid elements (SOLID186 elements—20-node hexahedral elements with three degrees of freedom per node). Conversely, the far-field regions, characterized by negligible through-thickness gradients and no interlaminar damage, are represented with layered shell elements. This modeling strategy significantly reduces the number of degrees of freedom while preserving accuracy in the region of interest. To ensure a consistent transition between the two domains, the shell–solid interface was modeled to avoid spurious stiffness. Displacement and rotation continuity between the shell mid-surface and the adjacent solid face was enforced through multipoint constraint (MPC) equations, preventing node duplication or redundant constraints. The shell mid-surface was aligned with the mid-thickness of the adjoining solid laminate to avoid artificial bending effects due to offset errors. Additionally, the stacking sequence and equivalent ply properties were matched across the interface so that the in-plane and bending stiffness of the shell region accurately reflected the stiffness of the corresponding solid region. The global model, used to capture the overall structural response, was discretized with a coarser mesh characterized by an average element size of approximately 9 mm. Conversely, the local model, focused on the critical region near the delamination, was discretized with a much finer mesh, with an average element size of about 2 mm. In total, the FEM discretization consisted of 10,924 elements.

The critical load for sublaminate buckling was estimated through a linear buckling analysis, based on the first eigenvalue. To capture the post-buckling behavior and predict delamination propagation, a static nonlinear analysis was performed using the SMXB tool. This nonlinear analysis included a small initial geometric imperfection to trigger sublaminate buckling. The imperfection had a magnitude of 0.1 mm—corresponding to approximately 5% of the total panel thickness—and its shape matched the panel’s first buckling mode. In the analysis of structural stability, particularly for buckling and post-buckling behavior, the definition of an appropriate initial imperfection amplitude is critical. A commonly adopted value in the literature is 0.1 mm, corresponding to approximately 5% of the total panel thickness. This choice is consistent with previous studies, which have shown that small imperfections, expressed as a fraction of the structural thickness, have a limited effect on overall buckling and post-buckling response [40,41]. These findings highlight the importance of selecting a realistic yet moderate imperfection amplitude to ensure reliable and representative numerical predictions. In both the linear and nonlinear analyses, appropriate boundary conditions were applied: all translational and rotational degrees of freedom were fully constrained on one edge of the panel, while an axial compressive displacement was applied on the opposite edge. Lateral anti-buckling guides were also included to prevent global panel instability (see Figure 2).

4. Validation of FEM Results Through Literature Data

To validate the finite element model (FEM) adopted in this study, a comparison was carried out between numerical results and data available in the literature [21]. It is important to note that the numerical results in [18], used here as a validation benchmark, were experimentally confirmed in the original study. Therefore, the present comparison indirectly includes experimental verification. Four different numerical configurations were analyzed, consisting of composite panels featuring a pre-existing delamination. Specifically, two flat panels were modelled, each presenting delamination at a different interface: one at Interface 1 and the other at Interface 2. In addition, two curved panels with a radius of curvature of 760 mm were analyzed, mirroring the geometry and delamination location of the flat counterparts.

The critical buckling load under axial compression was investigated for all configurations through a linear eigenvalue buckling analysis. Boundary conditions were applied such that one edge of the panel was fully clamped, preventing both translational and rotational degrees of freedom. The opposite edge was subjected to axial compressive load, while the remaining two edges were constrained by anti-buckling guides to avoid lateral displacements and ensure controlled buckling behavior.

Subsequently, nonlinear static analyses were performed using the SMXB methodology. This approach allowed for the assessment of both the out-of-plane displacement evolution at the center of the delaminated sublaminate and the corresponding energy release rate (ERR). The computed ERR was used to evaluate the onset and propagation of delamination under compressive loading, enabling a comprehensive understanding of the post-buckling behavior.

The results obtained through FEM were compared with benchmark cases reported in the literature, demonstrating good agreement in terms of both critical buckling loads and damage evolution trends. This validation supports the accuracy and reliability of the adopted numerical strategy for simulating delaminated composite structures under compressive loads.

Figure 3 reports the critical buckling loads obtained for the four analyzed configurations, along with a comparison against both numerical and experimental results available in the literature. The numerical results obtained in this study are in excellent agreement with the reference numerical data, confirming the consistency and accuracy of the adopted FEM approach. However, a noticeable discrepancy emerges when comparing the numerical results with the corresponding experimental values reported in the same reference study. It is worth noting that the original authors also highlighted this divergence, suggesting potential experimental uncertainties or limitations in reproducing ideal boundary conditions and initial imperfections in the physical specimens. This mismatch may be attributed to several factors, including the following:

• Geometric and material imperfections in the experimental samples, which are not captured in the idealized numerical model;
• Inaccurate or non-uniform boundary conditions during testing, leading to the early onset of local instabilities;
• Sensitivity of buckling behavior in delaminated composite structures to small deviations in geometry or loading alignment;
• Potential measurement uncertainties or limitations in identifying the exact load corresponding to the onset of buckling.

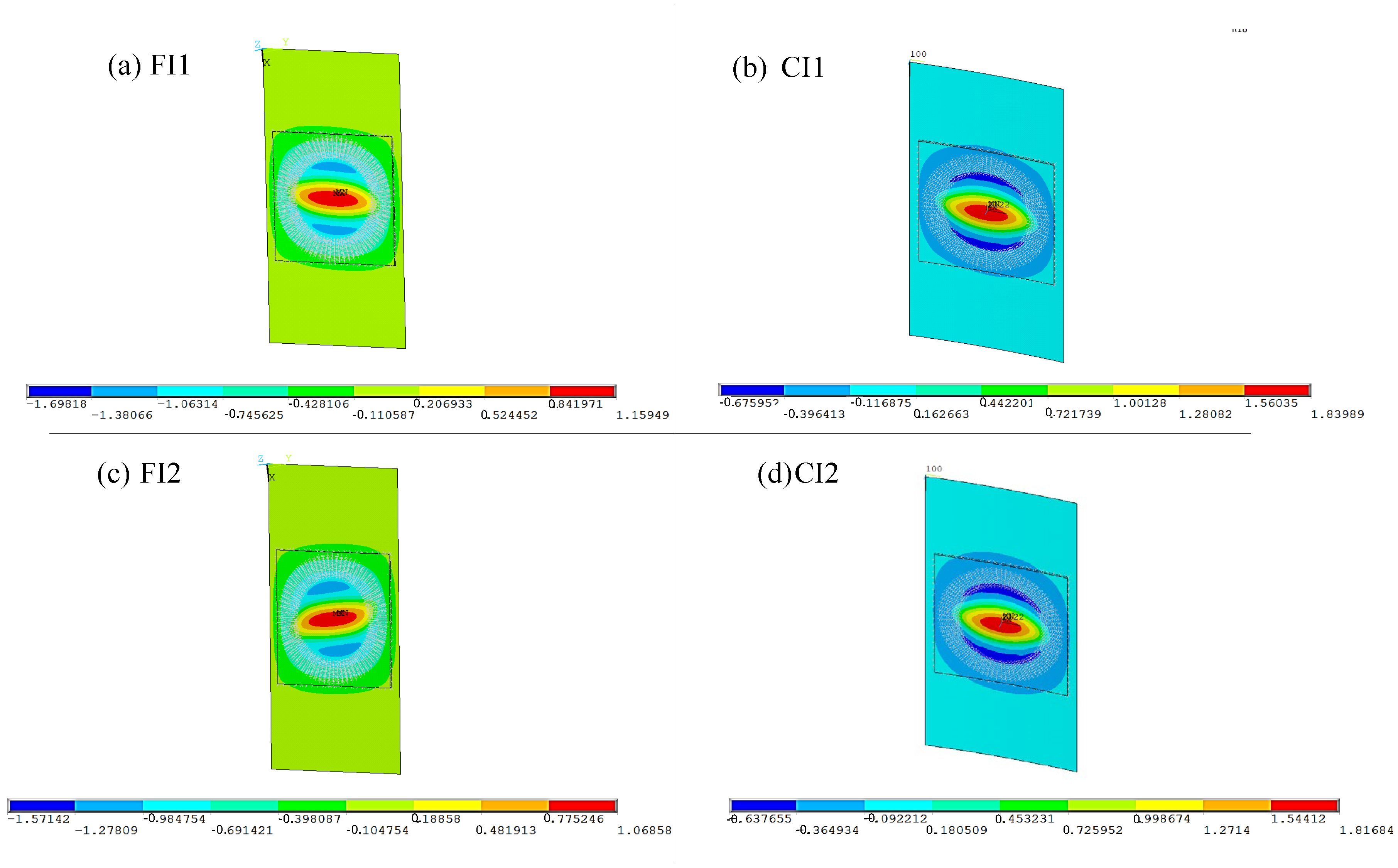
Figure 4 shows the qualitative shape of the first buckling mode obtained through linearized eigenvalue buckling analysis for configurations FI1 (Flat Interface 1) and CI1 (Curved Interface 1). As expected, the presence of the delamination significantly influences the global deformation pattern, promoting localized out-of-plane displacements in the region surrounding the defect. In both configurations, the buckling mode exhibits a clear tendency for local instability within the delaminated sublaminate, confirming the role of the damage in reducing the structural stiffness and altering the global stability behavior. In particular, the curved panel (CI1) shows a more asymmetric deformation field, likely due to the combined effect of curvature-induced stiffness and the location of the delamination.

It is important to note that the deformation shapes presented are qualitative and normalized for visualization purposes. Nonetheless, they provide useful insights into the interaction between panel curvature, the interface location of the delamination, and the resulting buckling behavior, which are further explored through nonlinear static analyses in the following sections.

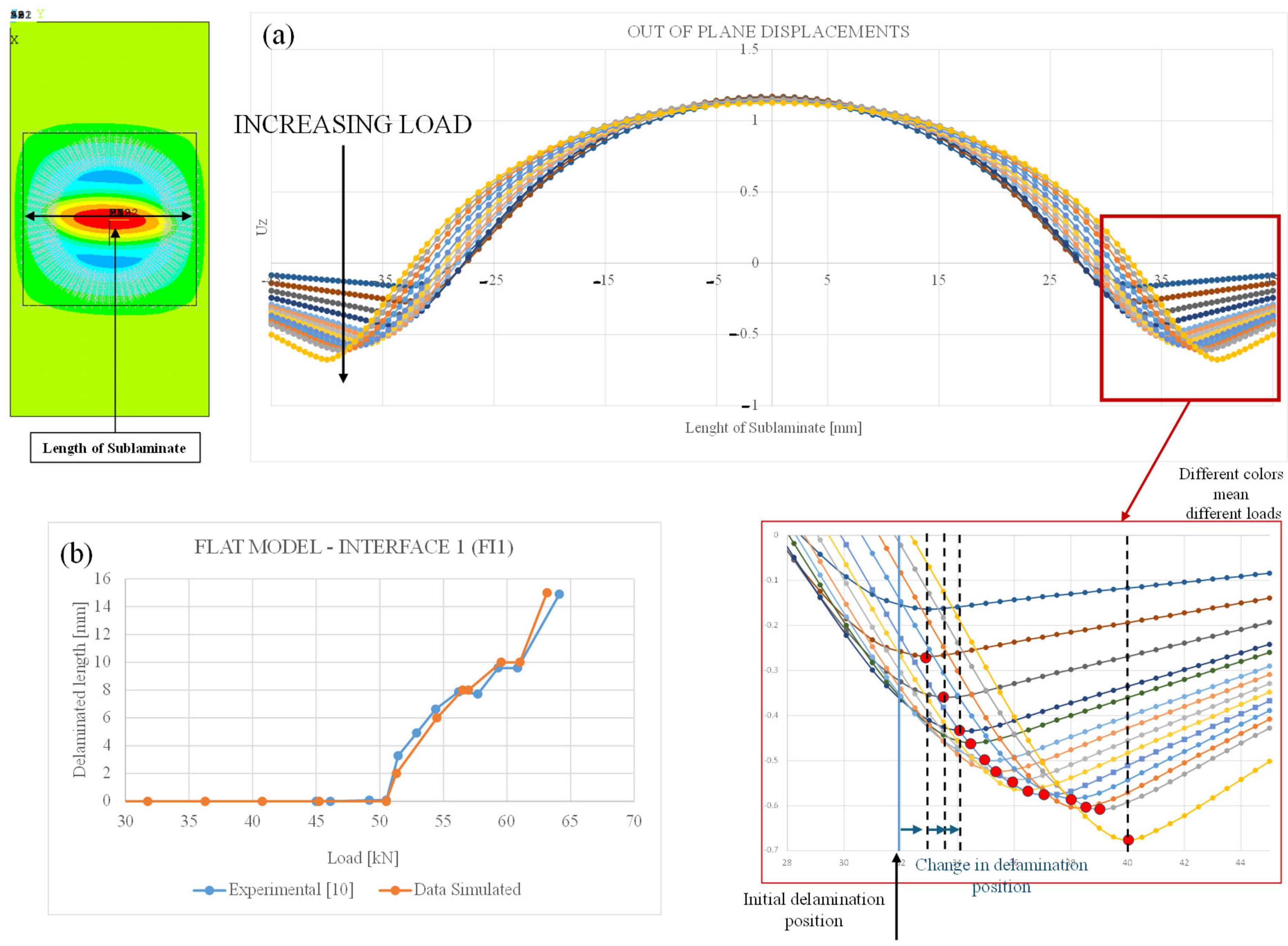
In Figure 5, the evolution of the delamination length with increasing structural reaction load is analyzed specifically for configuration FI1 (Flat Interface 1). This analysis was carried out using two complementary approaches. The first method is based on tracking the out-of-plane displacements at the mid-length of the sublaminate, the region where the panel exhibits maximum deformation. As shown in Figure 5, the displacement profile broadens as the applied load increases, with a noticeable shift in the inflection point of the curve. This shift indicates the progression of the delamination front. This method was adopted in alignment with the reference literature, which used the same criterion to estimate delamination propagation.

The second approach, shown in Figure 5, involves evaluating the energy release rate (ERR) through the SMXB methodology. Based on the ERR, the evolution of the delamination length was computed and compared with the experimental data reported in the literature. The results demonstrate a high level of agreement, confirming the reliability of the numerical model. Notably, the experimental results used for comparison were themselves derived using the displacement-based method described above.

Although Figure 5 refers exclusively to the FI1 configuration, similar trends and consistency between numerical and experimental results were observed for the other configurations (CI1, FI2, and CI2). These results were not included here for brevity, as they exhibit qualitatively analogous behavior and validate the same conclusions drawn for the FI1 case.

Figure 6 presents the delamination length as a function of the applied load for all four analyzed configurations. A remarkable agreement is observed between the numerical predictions and the experimental data, particularly for configurations FI1, FI2, and CI1. In these three cases, both the onset load for delamination growth and the overall evolution of the delamination front with increasing structural reaction load show near-identical trends between simulation and experiment.

Specifically, the initiation of growth of the pre-existing delamination occurs at the same load level in both numerical and experimental results, confirming the model’s accuracy in capturing the critical conditions that trigger delamination propagation. Furthermore, the evolution of delamination length with increasing load follows an almost identical slope, indicating that the FEM model reliably reproduces the damage growth mechanism under compressive loading.

For configuration CI2, however, a slight discrepancy is observed: the numerically predicted onset of delamination propagation occurs at 55 kN, whereas the experimental data indicate an onset at approximately 57 kN. This minor difference—less than 4%—could be attributed to several factors, including sensitivity to initial imperfections, slight geometric asymmetries in the curved geometry, or local variations in material properties that are difficult to replicate precisely in the numerical model.

5. Influence of Curvature on Delamination Propagation

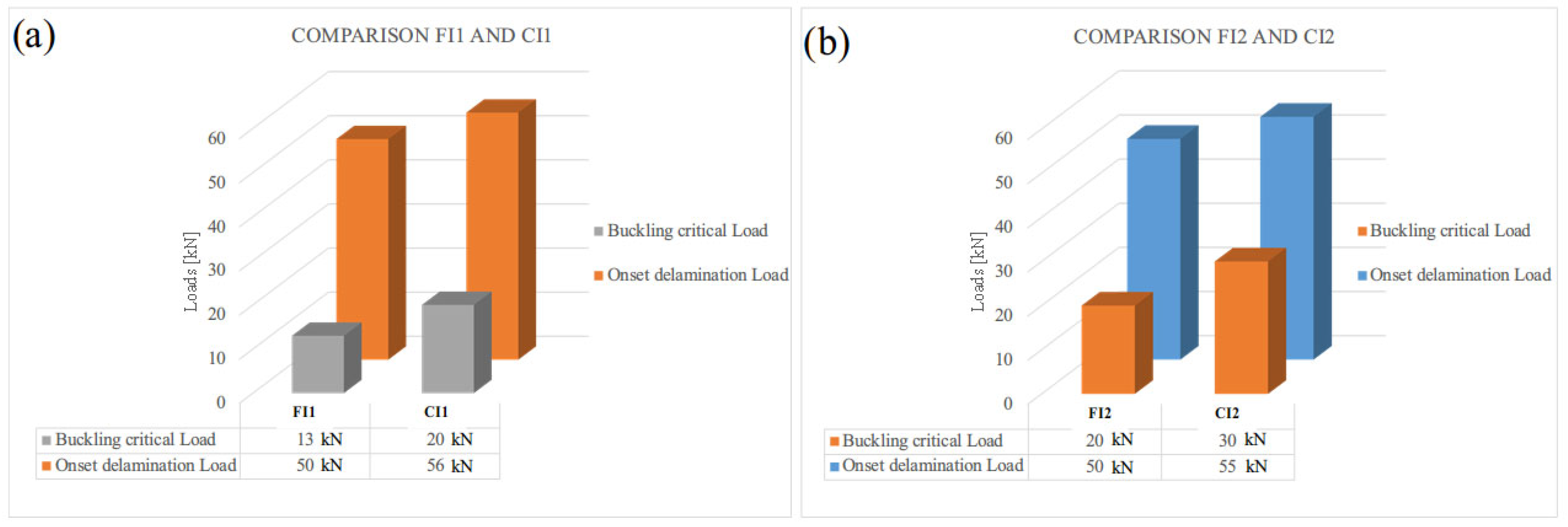
To investigate the influence of panel curvature on the onset and propagation of delamination, a comparative analysis was conducted between configurations FI1 and CI1, which are identical in all aspects—geometry, layup, and damage location—except for the curvature: CI1 features a cylindrical curvature with a radius of 760 mm, while FI1 is flat.

Figure 7a compares the critical buckling loads of the two configurations. It is evident that the curved panel (CI1) buckles at a significantly higher load than the flat panel (FI1), with critical loads of 20 kN and 13 kN, respectively. This result is consistent with the well-established notion that geometric curvature increases the bending stiffness of the structure, thereby enhancing its resistance to global instability. The comparison also extends to the initiation load of delamination propagation. In this case as well, configuration CI1 demonstrates improved performance, with damage onset occurring at a higher load than in FI1. This suggests that curvature not only delays buckling, but also contributes to increased damage tolerance by postponing the activation of delamination growth mechanisms.

Figure 7b reinforces this trend through the comparison of configurations FI2 and CI2, which, again, differ only by the presence of curvature. In these cases, the panels feature a deeper delamination located at a different interface. The flat panel (FI2) exhibits a critical buckling load of 20 kN, while the curved counterpart (CI2) shows a significantly higher critical load of 30 kN. Similarly, the delamination onset occurs at 50 kN for FI2 and at 55 kN for CI2.

These results clearly indicate that curvature plays a beneficial role in improving both the buckling resistance and the damage tolerance of composite structures. The increase in structural stiffness due to curvature delays the onset of instability and reduces the susceptibility to delamination growth under compressive loading. This observation is particularly relevant for the design of curved aerospace and automotive components, where both weight reduction and damage resistance are critical design requirements.

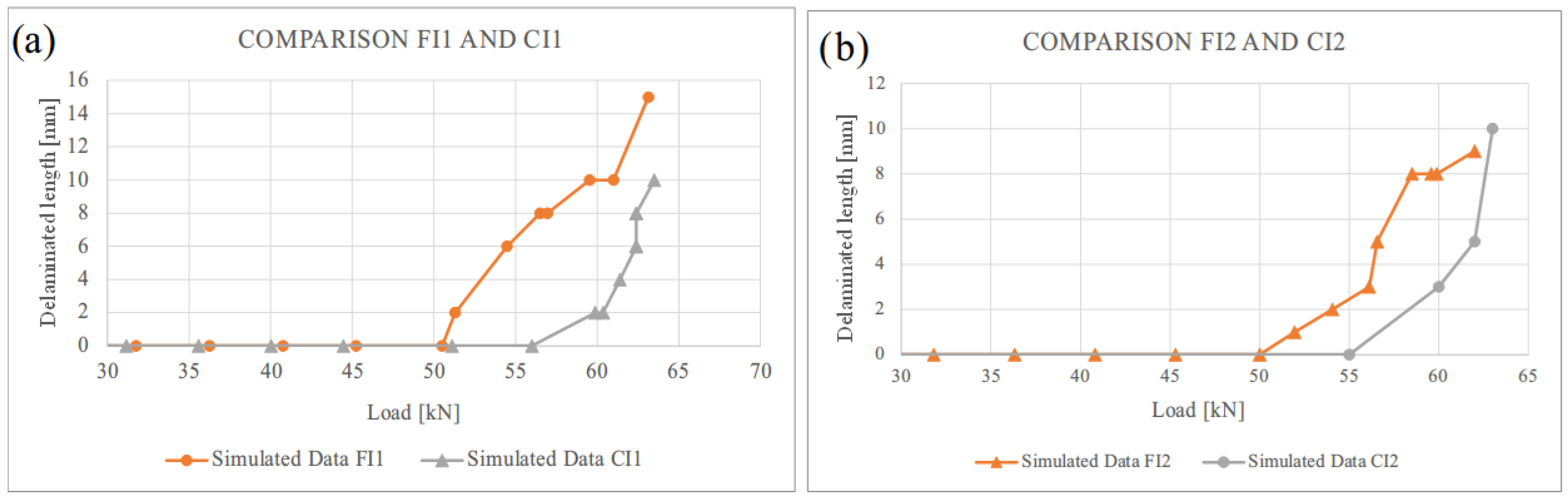
Figure 8 illustrates the evolution of delamination length as a function of the applied load for configurations FI1 and CI1. While previous figures highlighted the beneficial effect of curvature in delaying both buckling and damage initiation, here, a different trend emerges once delamination propagation begins. As expected, the curved configuration (CI1) delays the onset of delamination compared to the flat configuration (FI1). However, once propagation initiates, the growth rate in CI1 is steeper and more abrupt than in the flat case. This behavior suggests that, while curvature increases the threshold load required to trigger damage propagation, it may also lead to a more unstable progression once that threshold is exceeded.

Despite this more rapid evolution, the curved panel still maintains an advantage in terms of total damage at a given load. At an applied load of 63 kN, configuration FI1 exhibits a delamination length of 16 mm, whereas CI1 reaches only 10 mm. This corresponds to a 37.5% reduction in delamination length for the curved configuration, further reinforcing its improved damage tolerance under compressive loading.

To further illustrate the effect of curvature on post-buckling behavior and delamination response, Figure 9 shows the three-dimensional deformed shapes of configurations FI1 and CI1 at a representative load level beyond the buckling threshold. These visualizations highlight the differences in deformation patterns between flat and curved panels. In the flat configuration FI1, the deformation is more symmetric and spreads widely around the delaminated region. Conversely, in CI1, the presence of curvature induces a more localized and asymmetric out-of-plane displacement field. This is likely due to the curvature-induced increase in bending stiffness, which modifies the distribution of deformation and delays the growth of delamination. These differences further support the conclusion that curvature improves both buckling resistance and damage tolerance.

A similar trend is observed when comparing configurations FI2 and CI2, which differ only in curvature but share a deeper delamination located at Interface 2 (between the +45° and −45° plies). In this case, the flat configuration FI2 exhibits a more asymmetric deformation shape, particularly in the post-buckling regime. This is likely due to the coupling effects associated with the 45°/−45° interface, which introduces additional shear-driven deformation modes and amplifies the geometric asymmetry. The curved configuration CI2, instead, shows a more stable and localized deformation, again confirming the stiffening and stabilizing effect of curvature in laminated composite structures.

6. Conclusions

This study presented a comprehensive numerical investigation into the influence of panel curvature on delamination growth and buckling behavior in composite structures. Through the use of the SMXB tool, four configurations were analyzed to evaluate the combined effects of curvature and delamination interface depth under axial compression.

From a mechanical perspective, the results highlight several key trends and their underlying causes:

• Curvature significantly increases buckling resistance because the initial out-of-plane stiffness is higher, reducing the susceptibility to local instabilities. This effect is consistent with classical shell theory, which predicts a stabilizing influence of geometric curvature on global buckling [23,24].
• The delayed onset of delamination propagation in curved panels can be attributed to the redistribution of interlaminar stresses induced by curvature, which reduces the energy release rates at the crack front during the pre-buckling phase.
• The accelerated growth rate post initiation in curved panels suggests that, once local buckling occurs, the curvature-induced membrane forces amplify mixed-mode fracture conditions, promoting rapid damage evolution. Nevertheless, for equivalent load levels, the total delaminated area remains lower compared to flat panels, indicating a net improvement in damage tolerance.
• Comparison with experimental data from the literature confirms the accuracy of these trends, reinforcing the reliability of the SMXB approach in capturing post-buckling and progressive damage phenomena.
• The SMXB method offers mesh-independent and robust predictions, which is particularly advantageous when studying post-buckling regimes where conventional VCCT-based approaches may lose accuracy due to mesh sensitivity.

These outcomes emphasize the importance of considering curvature effects in the design of composite panels, especially for aerospace applications where stability and damage resistance are critical. The validated numerical framework can serve as a predictive tool to support the design and optimization of curved composite structures with known or anticipated interlaminar defects.