Comparative Study of Force and Deformation Characteristics of Closed Cavity Thin-Walled Components in Prefabricated Metro Station
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of Prefabricated Metro Station
2.2. Three-Dimensional Modeling
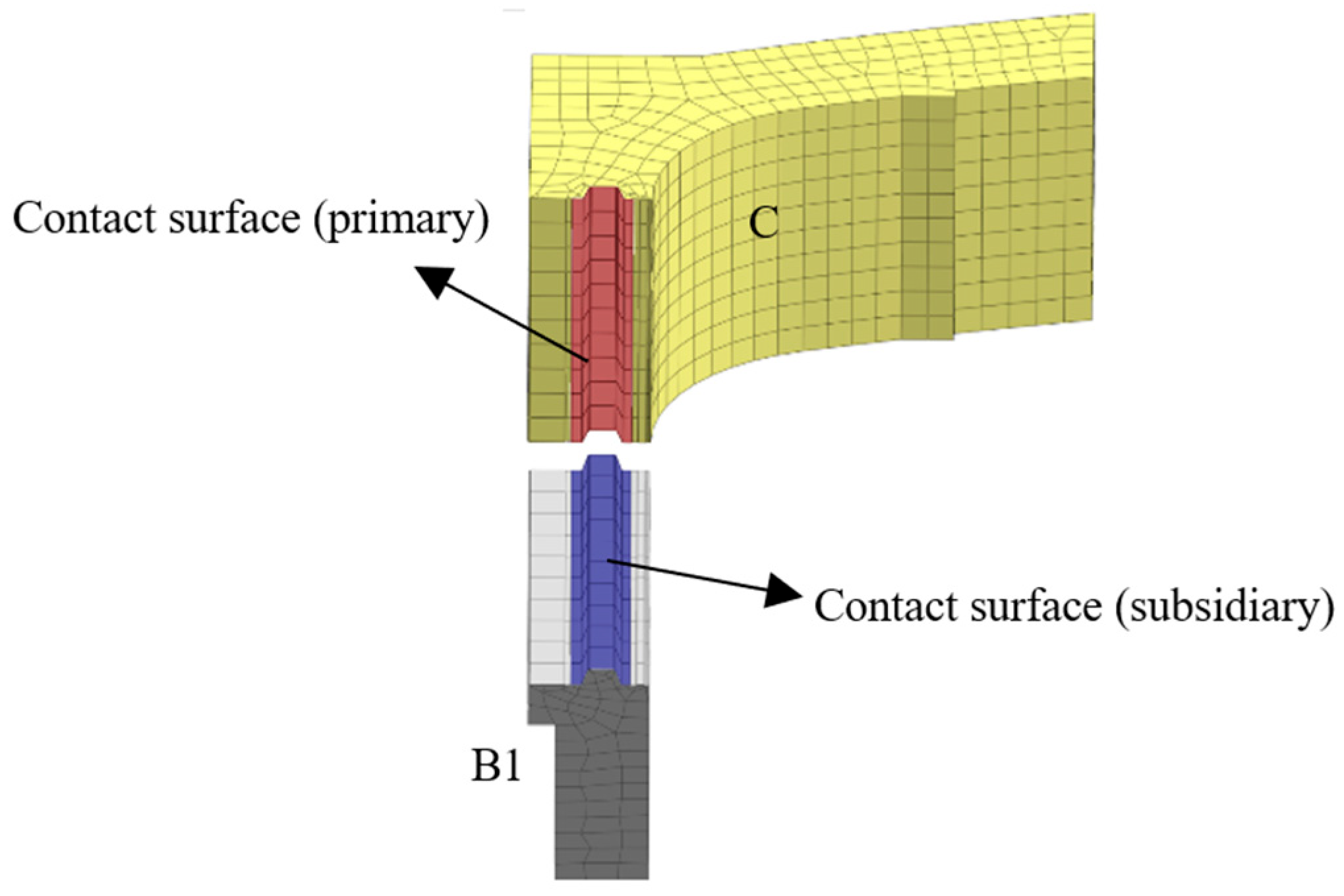
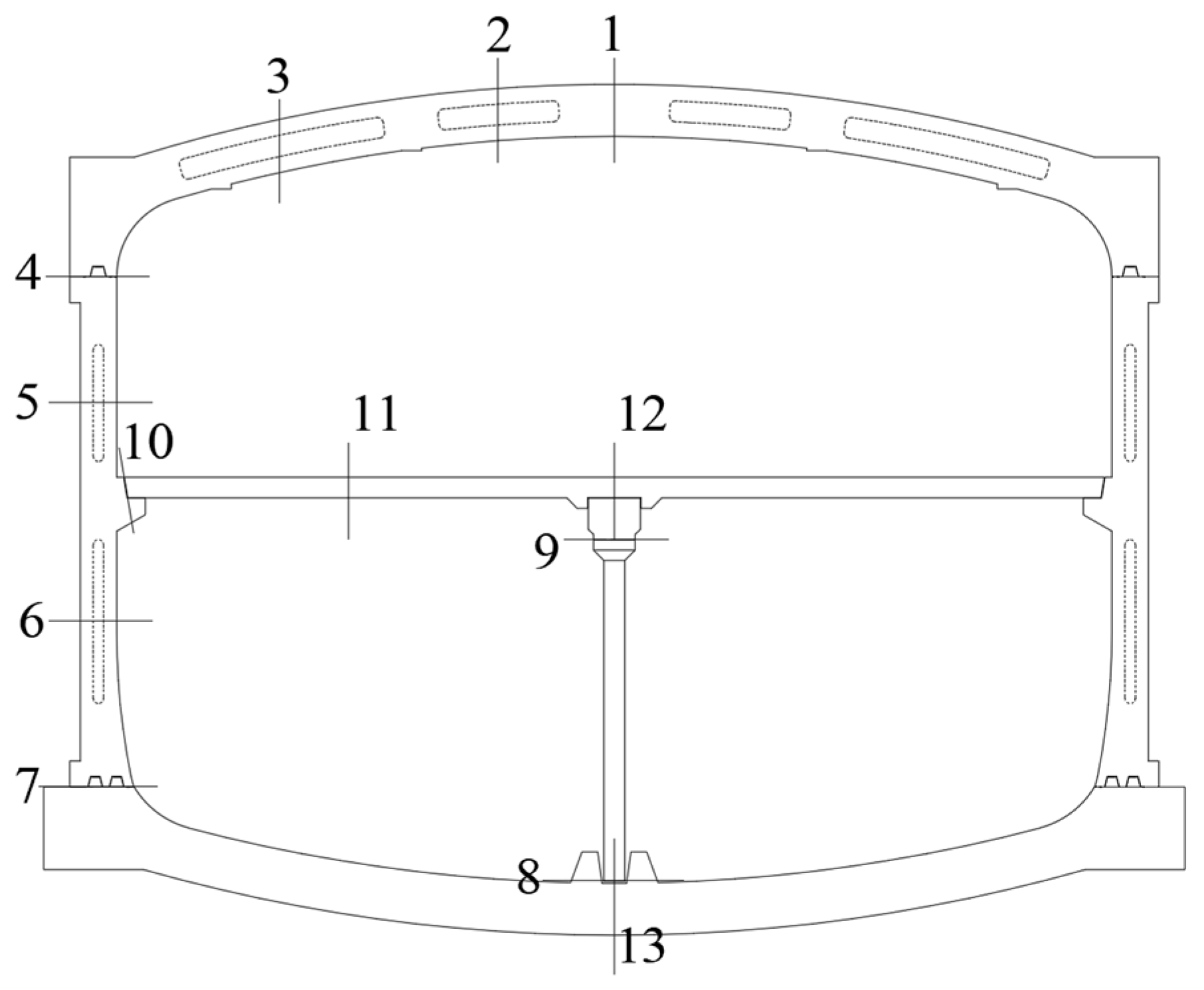
2.2.1. Key Elements of Solid Structure and Cavity Structure Modeling
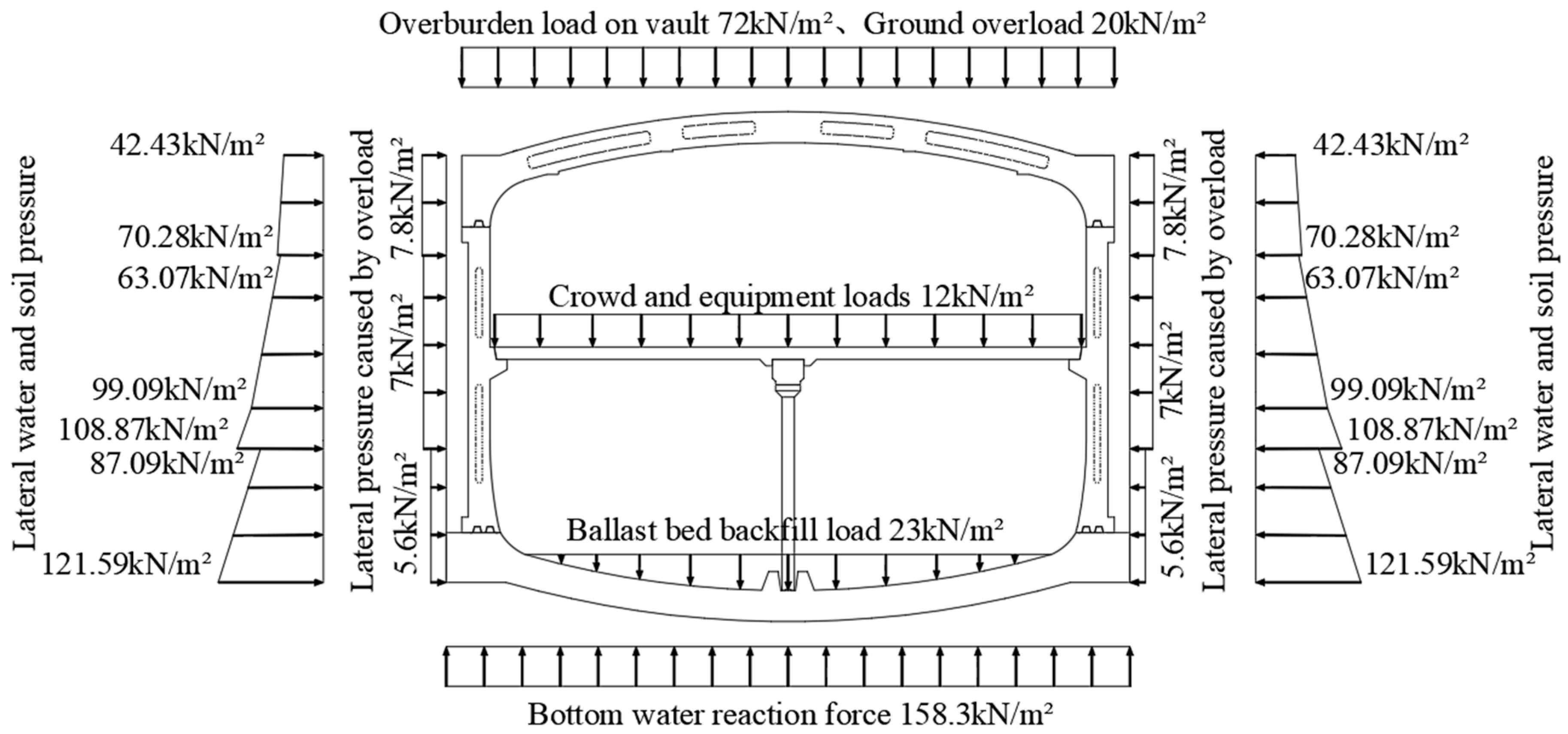
2.2.2. The Finite Element Modeling
2.3. On-Site Monitoring Plan
3. Results
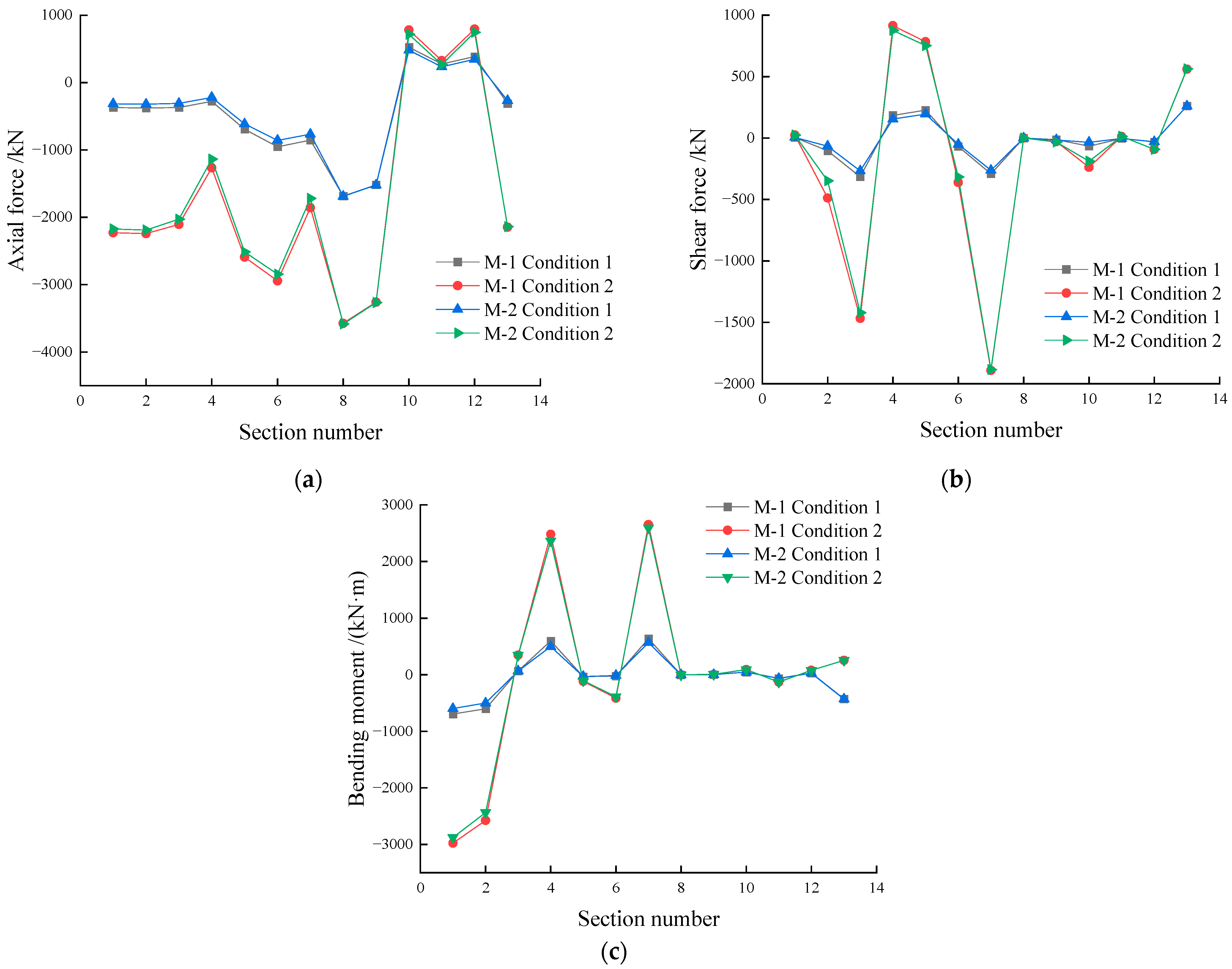
3.1. Comparative Analysis of Structural Internal Forces
3.2. Comparative Analysis of Structural Deformation
3.3. Comparative Analysis of Structural Stresses
3.4. Validation of On-Site Monitoring
4. Discussion
4.1. Analysis of Mechanism of Structural Internal Force Changes
4.2. Exploration of Structural Deformation Performance and Safety
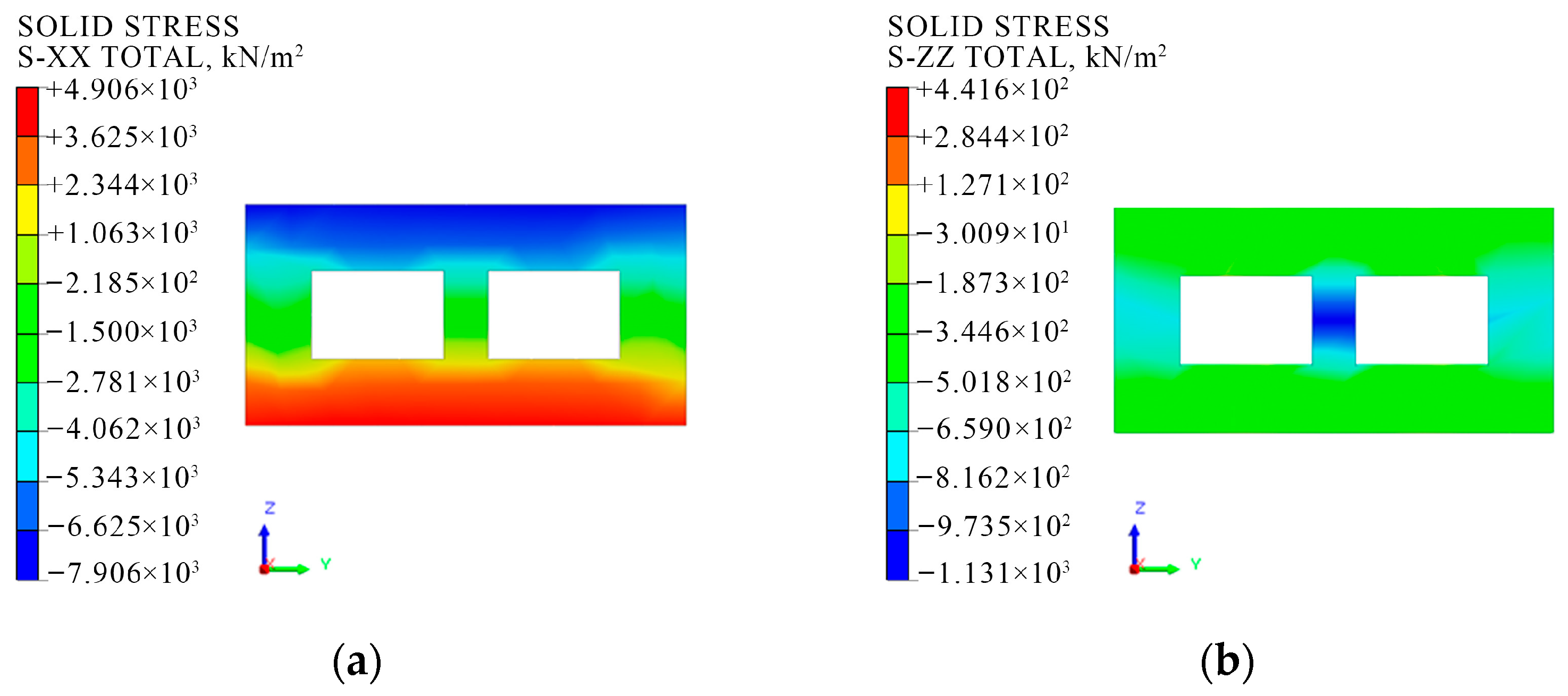
4.3. Structural Stress Distribution and Optimization Design Recommendations
4.4. Research Limitations and Application Value
5. Conclusions
- When closed cavities are set within the structure, the internal forces in most cross-sections decrease, particularly at the mortise–tenon joint, where the axial force decreases by approximately 10.2%. Furthermore, as the applied load increases, the reduction rate of internal forces in the cavity structure also decreases. The maximum reduction rate for the axial force decreases from 10.19% to 3.4%, the maximum reduction rate for the shear force decreases from 15.12% to 3.12%, and the maximum reduction rate for the bending moment decreases from 14.14% to 3.37%.
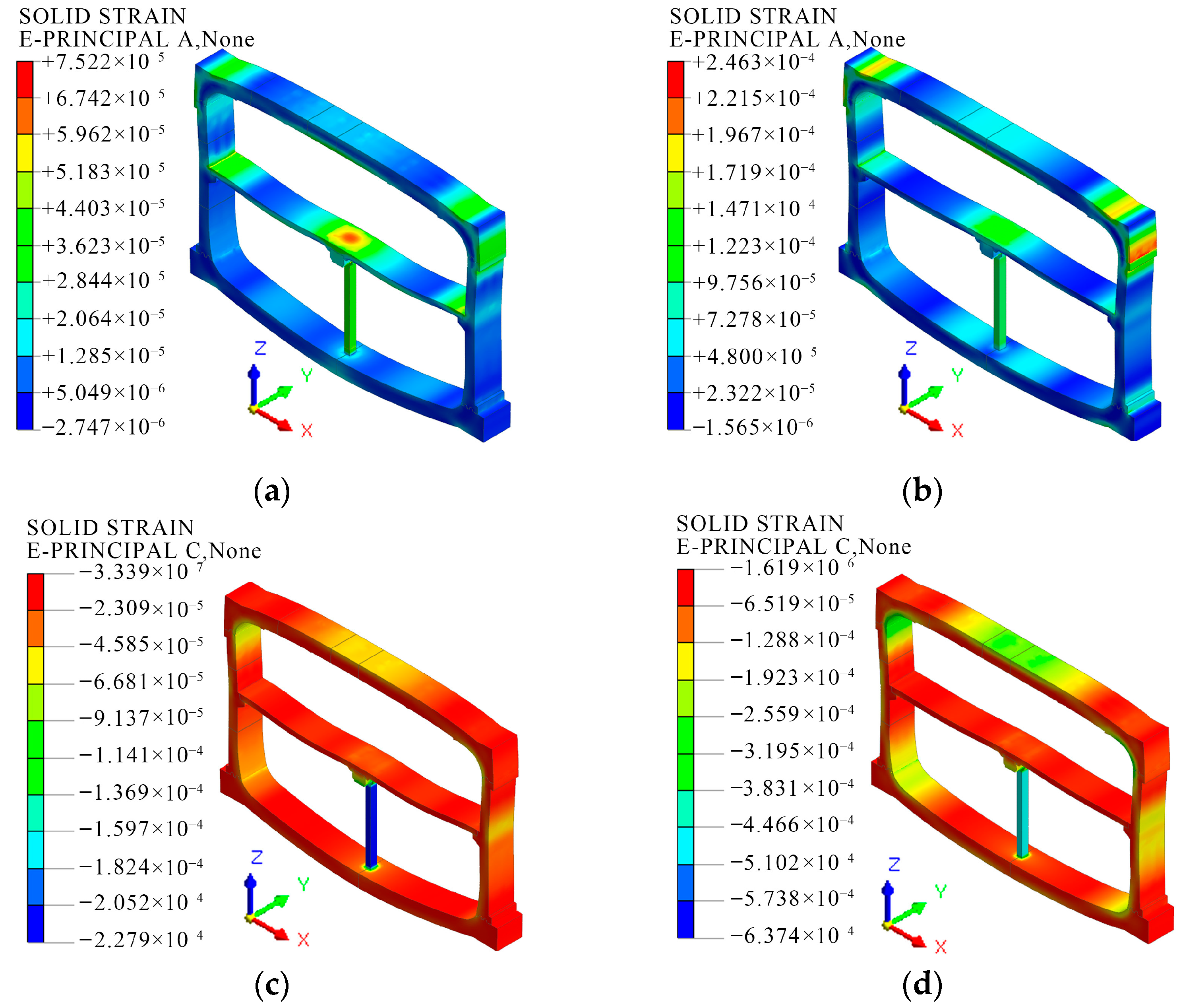
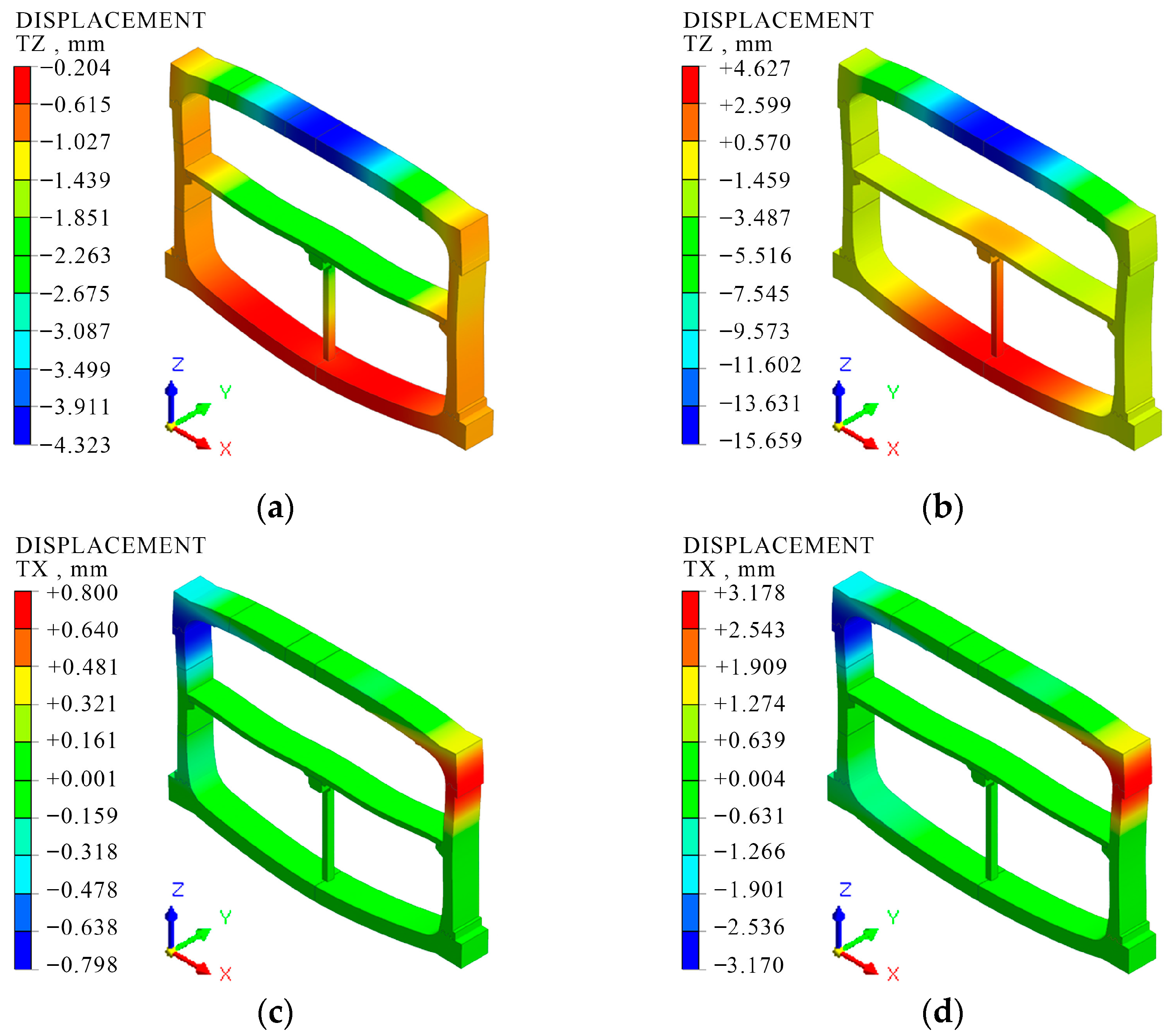
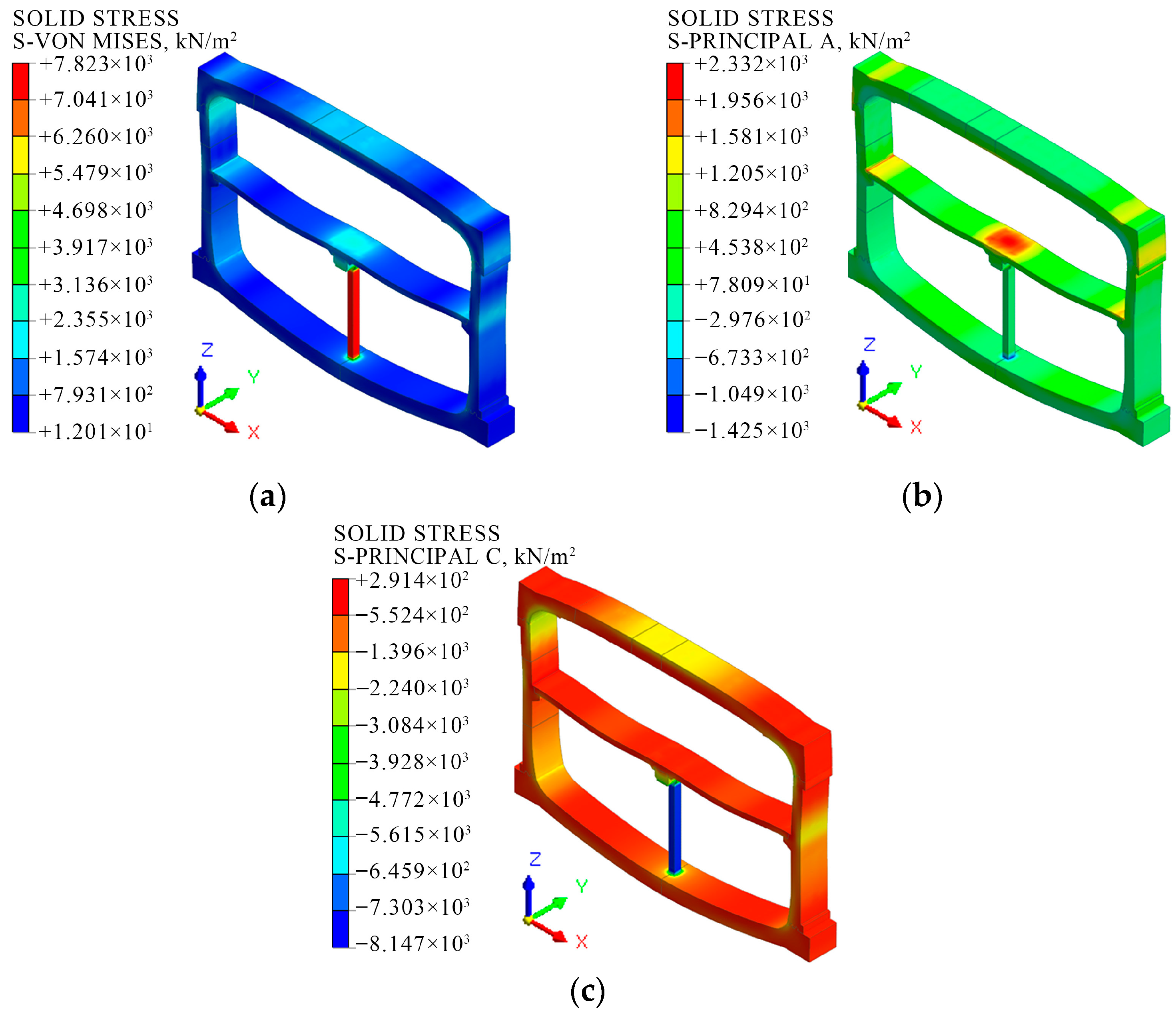
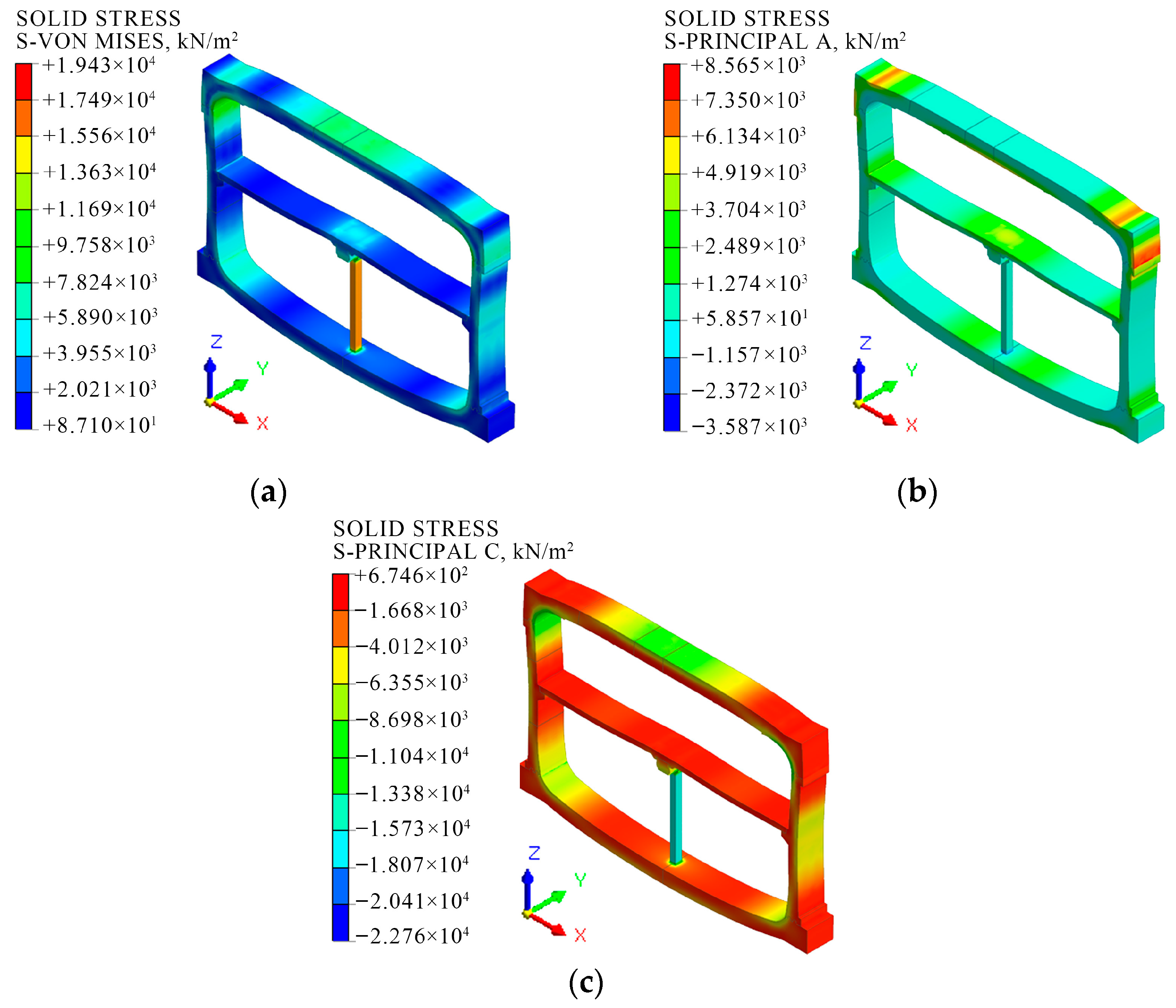
- After adding the closed cavities, the principal strain, displacement, and stress of the structure slightly increase. As the applied load increases, the incremental vertical displacement deformation decreases from 0.48 mm to 0.05 mm, and the incremental horizontal displacement deformation decreases from 0.12 mm to 0.07 mm, which is beneficial for the overall stability of the structure. When subjected only to self-weight, the column functions as the primary load-bearing component at the midspan, with a significant stress concentration and a peak stress magnitude of 7.8 MPa. As the load increases, the location of maximum tensile and compressive deformation shifts from the column to the upper mortise–tenon joint, with the peak stress increasing to 19.43 MPa.
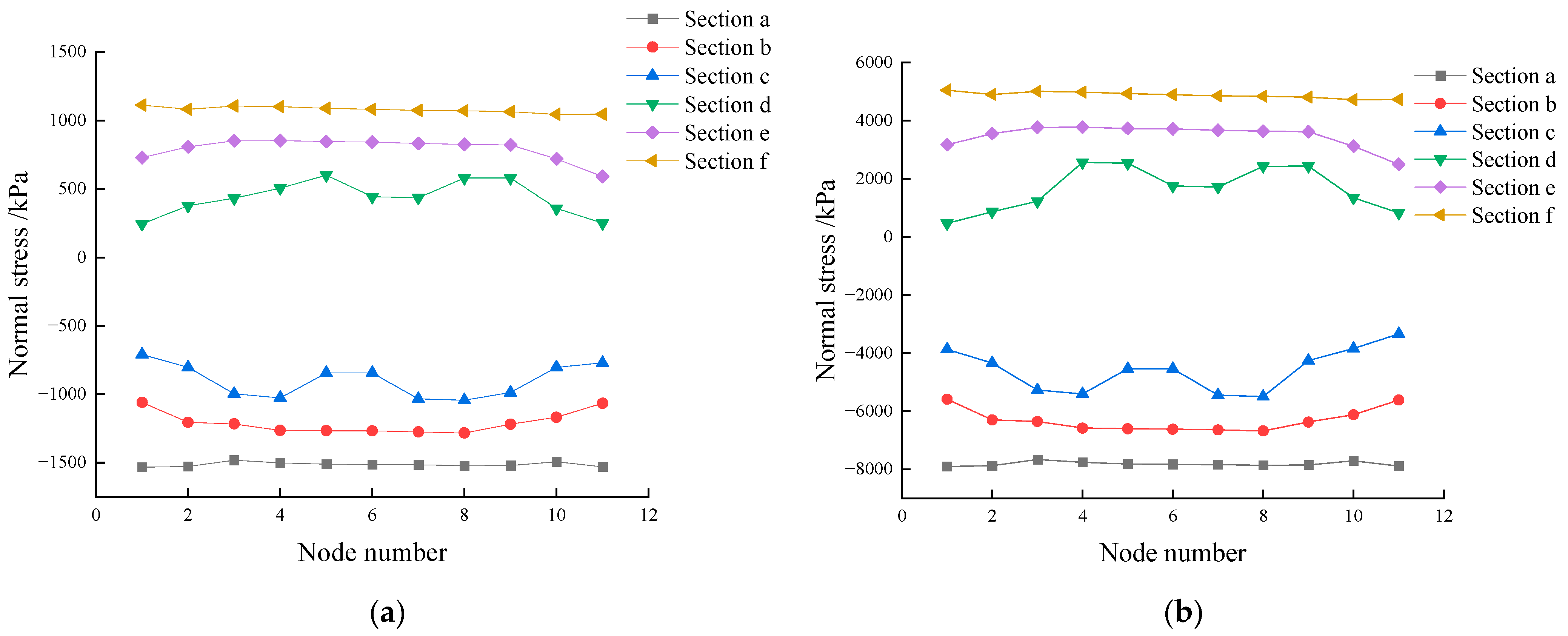
- For closed cavity sections, a substantial shear lag effect is observed. The shear force is transmitted through the rib plate, resulting in the maximum shear stress in the middle rib. Since the shear force decreases as it is transmitted laterally toward both sides of the flange, the maximum normal stress occurs near the middle rib, while the minimum normal stress is found at the side ribs, resulting in an uneven distribution. Under self-weight conditions alone, the stress in the middle rib is found to be 2.47 times greater than that observed in the side ribs. As the load increases, the stress difference between the middle rib and the side ribs increases to 5.51 times, with the shear lag effect becoming more pronounced.
- The maximum stress observed at the mortise–tenon joint reaches 19.43 MPa. As this is an unfavorable location for load bearing, novel connection technologies and joint types can be developed to prevent collapse and ensure overall stability. The internal space of the closed cavity can be filled with self-healing lightweight materials, which can serve both insulating and structural strengthening purposes. These cavities can also be embedded with sensors for real-time intelligent monitoring. Alternatively, the space can be used as a pipeline channel to improve space utilization and promote the development of prefabricated metro stations in the direction of more lightweight, intelligent, and sustainable designs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baghchesaraei, O.R.; Lavasani, H.; Baghchesaraei, A. Behavior of Prefabricated Structures in Developed and Developing Countries. In Bulletin de la Société Royale des Sciences de Liège; Société Royale des Sciences de Liège: Liège, Belgium, 2016. [Google Scholar]
- Zhu, M.; Rao, W.; Hong, C.Y.; Chen, X.S.; Dai, J.; Wu, C.G.; Li, M.T. Displacement measurement of underground prefabricated metro stations by computer vision technology. Measurement 2024, 231, 114500. [Google Scholar] [CrossRef]
- Qiu, T.; Chen, X.S.; Su, D.; Zhang, J.Q.; Xu, Z.Y. Multi-hazard vulnerability for single-walled full-assembled underground stations. Structures 2023, 48, 602–615. [Google Scholar] [CrossRef]
- Huang, M.Q.; Chen, X.L.; Ninic, J.; Bai, Y.; Zhang, Q.B. A framework for integrating embodied carbon assessment and construction feasibility in prefabricated stations. Tunn. Undergr. Space Technol. 2023, 132, 104920. [Google Scholar] [CrossRef]
- Yang, X.R.; Lin, F. Research and application of prefabrication and assembly construction technology for metro station structures. In Proceedings of the ITA-AITES World Tunnel Congress (WTC)/49th General Assembly of the International-Tunnelling-and-Underground-Space-Association (ITA-AITES), Athens, Greece, 12–18 May 2023; pp. 1101–1109. [Google Scholar]
- Lin, F.; Yang, X.R. Mechanical properties analysis of joints for prefabricated metro station structure based on Whole-process in-situ monitoring. Tunn. Undergr. Space Technol. 2023, 138, 105202. [Google Scholar] [CrossRef]
- Xiuren, Y.; Meiqun, H.; Zhiyong, P.; Fang, L. Calculation of dynamic assembly and tensioning loads at multiple points of prefabricated structure. Tunn. Undergr. Space Technol. 2022, 126, 104564. [Google Scholar] [CrossRef]
- Li, Q.L.; Li, Y.Z.; Tan, Z.S.; Li, L.F.; Cao, Y.X. Research on the Mechanism of Load Transfer Structures in the Construction Process of “Internal Support-Large Block” Prefabricated Subway Stations. Sustainability 2024, 16, 10594. [Google Scholar] [CrossRef]
- Yang, X.R.; Lin, F. Research on prefabricated metro station structure and key assembly technologies. Tunn. Undergr. Space Technol. 2024, 153, 106029. [Google Scholar] [CrossRef]
- Yang, X.R.; Shi, Z.H.; Lin, F. Research on Shear Capacity and Checking Method of MT•G-Joint for Application in Prefabricated Underground Structures. Adv. Mater. Sci. Eng. 2019, 2019, 4065301. [Google Scholar] [CrossRef]
- Tao, L.J.; Ding, P.; Yang, X.R.; Lin, P.; Shi, C.; Bao, Y.; Wei, P.C.; Zhao, J. Comparative study of the seismic performance of prefabricated and cast-in-place subway station structures by shaking table test. Tunn. Undergr. Space Technol. 2020, 105, 103583. [Google Scholar] [CrossRef]
- Qiu, T.; Sun, X.H.; Chen, X.S.; Su, D.; Zhang, J.Q.; Xu, Z.Y.; Song, R.; Wang, X.Y. Experimental study and resilience modeling for prefabricated hollow diaphragm walls of full-assembled underground stations under urban multi-disturbance conditions. Tunn. Undergr. Space Technol. 2023, 135, 105044. [Google Scholar] [CrossRef]
- Liu, Z.H.; Ma, X.F.; Wang, J.J.; Lu, L.H.; Zhang, H.H.; Han, H.; Zhou, D.Y.; Wang, W.D. Evaluation of seismic performance of novel prefabricated metro station roof-to-wall connection nodes. J. Build. Eng. 2025, 105, 112508. [Google Scholar] [CrossRef]
- Liu, T.J.; Lu, J.D.; Wang, D.; Liu, H.Y. Experimental Investigation of the Mechanical Behaviour of Wall-Beam-Strut Joints for Prefabricated Underground Construction. Int. J. Concr. Struct. Mater. 2021, 15, 2. [Google Scholar] [CrossRef]
- Wu, J.Y.; Ma, S.; Wang, R.; Ou, F.Q.; Liang, Y.; Zhao, W.G.; Xie, K.Z.; Wang, S.P. A novel technique for constructing prefabricated subway stations under open excavation with inner support. Proc. Inst. Civ. Eng.-Eng. Sustain. 2023, 177, 299–308. [Google Scholar] [CrossRef]
- Cao, K.; Wan, Y.C.; Zhou, X.H. Application and research progress of prefabricated assembly technology in underground engineering. Chin. J. Undergr. Space Eng. 2023, 19, 2055–2071. [Google Scholar]
- Wu, C.G.; Li, M.T.; Peng, Z.Y. Cross-section structure selection of prefabricated station in Shenzhen metro line 16. Tunn. Constr. 2022, 42, 320–327. [Google Scholar]
- Yang, X.R.; Lin, F.; Huang, M.Q. Experimental Analysis of Bending Stiffness Characteristics of Grouted Double Mortise-Tenon Joint for Prefabricated Metro Station Structure. Adv. Civ. Eng. 2021, 2021, 9958436. [Google Scholar] [CrossRef]
- Yang, X.R.; Lin, F.; Huang, M.Q. Experimental Research on Bending Bearing Capability of Grouted Double Mortise-Tenon Joint for Prefabricated Metro Station Structure. Adv. Civ. Eng. 2021, 2021, 6635409. [Google Scholar] [CrossRef]
- Yang, X.R.; Shi, Z.H.; Lin, F. Influence of Geometrical Parameters on Performance of Grouted Mortise and Tenon Joints for Application in Prefabricated Underground Structures. Adv. Civ. Eng. 2019, 2019, 3747982. [Google Scholar] [CrossRef]
- Xiang, B.Q.; Cui, L.Z.; Ding, W.T.; Tang, W.D.; Yue, T.S.; Qin, W. Study on the Influence of Geometric Parameters and Shape Optimization of Single Tenon Joint in Assembled Subway Station. Adv. Civ. Eng. 2023, 2023, 278404. [Google Scholar] [CrossRef]
- Qiu, T.; Chen, X.S.; Su, D.; Zhang, J.Q.; Song, R.; Wang, J.; Meng, D. Full-scale experimental study and mechanical model for beam-wall joints of prefabricated enclosure structure. Eng. Struct. 2023, 294, 116807. [Google Scholar] [CrossRef]
- Qiu, T.; Zhang, J.Q.; Chen, X.S.; Xu, Z.Y.; Su, D.; Song, R.; Cui, T. Experimental investigation and mechanical model for assembled joints of prefabricated two-wall-in-one diaphragm walls. Eng. Struct. 2023, 275, 115285. [Google Scholar] [CrossRef]
- Yang, X.R.; Lin, F.; Huang, M.Q. Analysis of the Law of Joint Deformation for Grouted Mortise-Tenon Joint. Adv. Civ. Eng. 2022, 2022, 2909993. [Google Scholar] [CrossRef]
- Ding, P.; Tao, L.J.; Yang, X.R.; Zhao, J.; Shi, C. Three-dimensional dynamic response analysis of a single-ring structure in a prefabricated subway station. Sustain. Cities Soc. 2019, 45, 271–286. [Google Scholar] [CrossRef]
- Tao, L.J.; Shi, C.; Ding, P.; Yang, X.R.; Bao, Y.; Wang, Z.G. Shaking table test of the effect of an enclosure structure on the seismic performance of a prefabricated subway station. Tunn. Undergr. Space Technol. 2022, 125, 104533. [Google Scholar] [CrossRef]
- Liu, H.T.; Xu, C.S.; Du, X.L. Seismic response analysis of assembled monolithic subway station in the transverse direction. Eng. Struct. 2020, 219, 110970. [Google Scholar] [CrossRef]
- Chen, J.N.; Xu, C.S.; El Naggar, H.M.; Du, X.L. Study on seismic performance and index limits quantification for prefabricated subway station structures. Soil Dyn. Earthq. Eng. 2022, 162, 107460. [Google Scholar] [CrossRef]
- Tao, L.J.; Li, Z.Y.; Yang, X.R.; Ding, P.; Shan, X.Y. Research of the mechanical behaviors of subway station structure assembled with prefabricated elements based on ABAQUS. Mod. Tunn. Technol. 2018, 55, 115–123. [Google Scholar] [CrossRef]
- Khakimov, A.; Kutumova, G.; Mirzaeva, Z. Current trends in the development of automation surveying support in the construction of subways. In Proceedings of the 2nd International Scientific Conference on Essays of Mining Science and Practice, Dnipro, Ukraine, 22–24 April 2020. [Google Scholar]
- Ding, X.L.; Zhang, Z.G.; Wang, X.X.; Wang, R.; Huang, R.J.; Zhao, W.G.; Gao, S.; Xie, K.Z.; Wang, S.P. Three-dimensional analysis of a prefabricated subway station during construction. Proc. Inst. Civ. Eng.-Civ. Eng. 2023, 177, 89–102. [Google Scholar] [CrossRef]
- Hong, C.Y.; Rao, W.; Qiu, T.; Chen, X.S.; Dai, J.; Wu, C.G.; Li, M.T.; Chen, W.B. Monitoring and assessment of mechanical response of large-scale prefabricated structures in underground subway stations during construction process. Measurement 2024, 235, 115015. [Google Scholar] [CrossRef]
- Qiu, T.; Chen, X.S.; Song, R.; Su, D.; Zhang, R.X.; Zhang, J.Q.; Xu, Z.Y.; Cui, T.; Wang, X.Y. Experimental investigation and modeling for assembled precast hollow components in full-assembled underground station application. Tunn. Undergr. Space Technol. 2024, 144, 105543. [Google Scholar] [CrossRef]
- Yang, X.R.; Lin, F. Prefabrication technology for underground metro station structure. Tunn. Undergr. Space Technol. 2021, 108, 103717. [Google Scholar] [CrossRef]
- Ding, P.; Tao, L.J.; Yang, X.R.; Zhao, J.; Liu, C.X.; Li, S.C. Optimum design of closed cavity structure for prefabricated metro station. J. Beijing Univ. Technol. 2019, 45, 946–955. [Google Scholar]
- Tao, L.J.; Shi, C.; Ding, P.; Li, S.C.; Wu, S. Study on the influence of thin-walled closed cavity on the mechanical properties of the prefabricated subway station. Chin. J. Undergr. Space Eng. 2021, 17, 776–785. [Google Scholar]
- Han, Y.Z.; Zhang, L.; Nie, X.F.; Zhang, L.W.; Pan, H. Study on the Stress Transfer Principle of Closed Cavity Thin-Walled Components in Assembled Underground Structures. In Proceedings of the 22nd COTA International Conference of Transportation Professionals (CICTP)—Intelligence, Connectivity, and Mobility, Changsha, China, 8–11 July 2022; pp. 2363–2373. [Google Scholar]
- Yang, X.R. Theory and Application of Prefabricated Open-Cut Metro Station Structure. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Han, Y.Z.; Zhang, L.; Nie, X.F.; Pan, H.; Zhang, L.W. Study on Shear Lag Effect of Closed Cavity Thin-Walled Components in Assembled Underground Structures. In Proceedings of the 22nd COTA International Conference of Transportation Professionals (CICTP)—Intelligence, Connectivity, and Mobility, Changsha, China, 8–11 July 2022; pp. 2315–2320. [Google Scholar]
- Han, Y.Z.; Zhang, L.; Nie, X.F.; Pan, H.; He, J.Z. Study on Shear Sharing Principle of Closed Cavity Thin-Walled Components in Assembled Underground Structures. In Proceedings of the 22nd COTA International Conference of Transportation Professionals (CICTP)—Intelligence, Connectivity, and Mobility, Changsha, China, 8–11 July 2022; pp. 2321–2328. [Google Scholar]
- Huang, M.Q. Key technology for design of closed-cavity thin-walled precast components of underground structures. Tunn. Constr. 2022, 42, 471–477. [Google Scholar]
- GB 50666-2011; Code for Construction of Concrete Structures. China Architecture & Building Press: Beijing, China, 2011.
- Zan, Z.H.; Wang, R. Research on mechanical properties of assembled subway stations based on new connection joints. Chin. J. Undergr. Space Eng. 2024, 20, 518–526. [Google Scholar] [CrossRef]
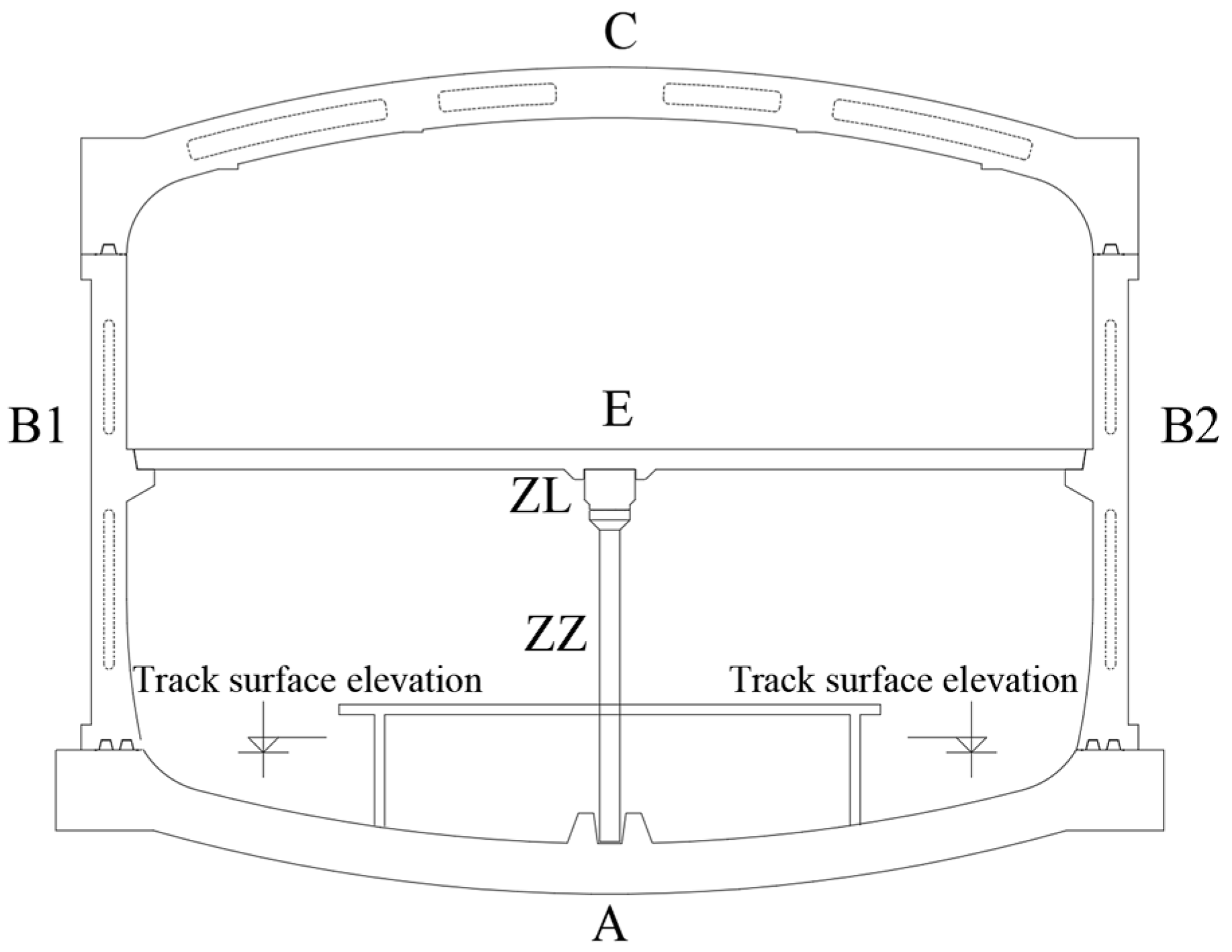
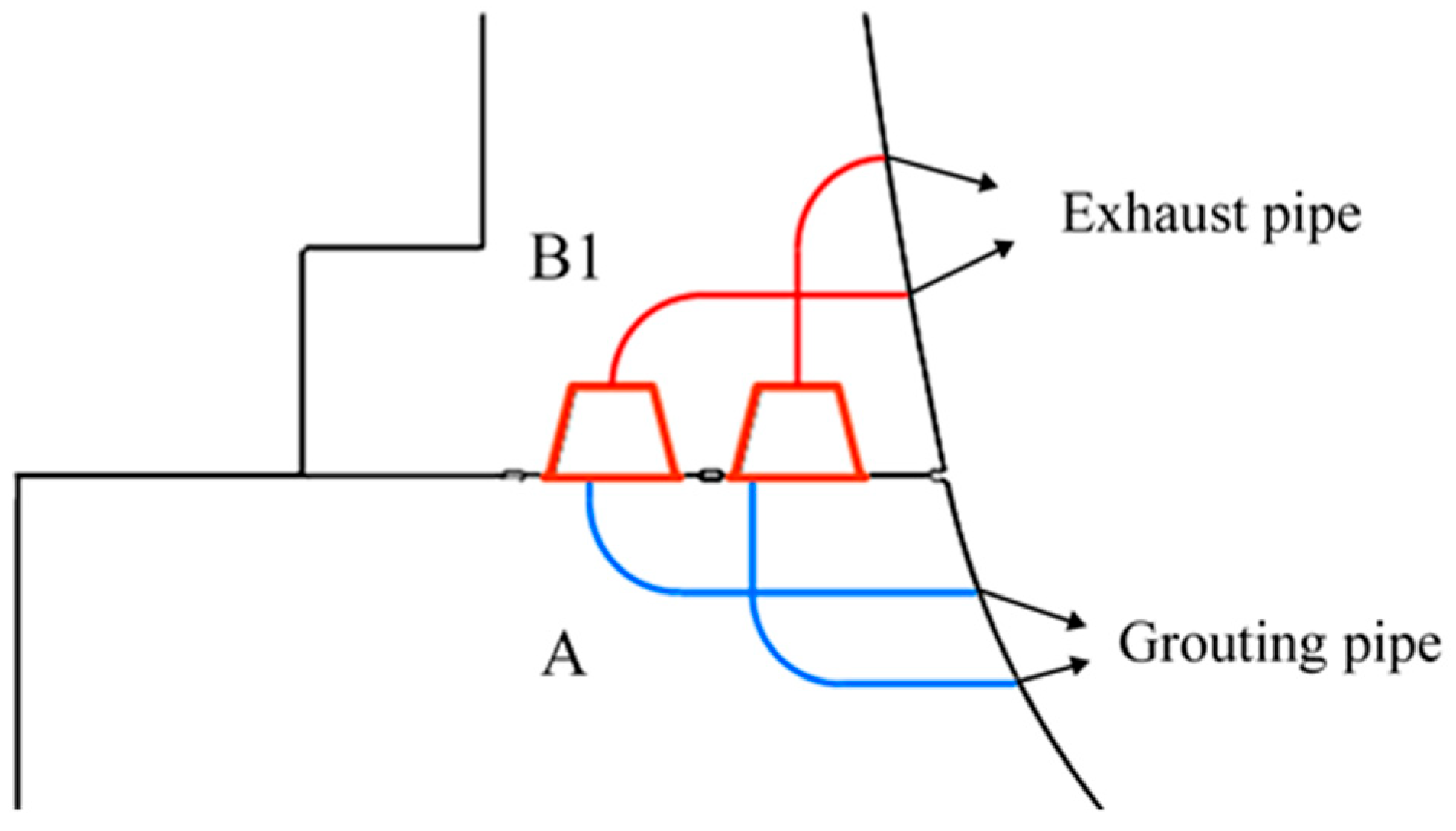
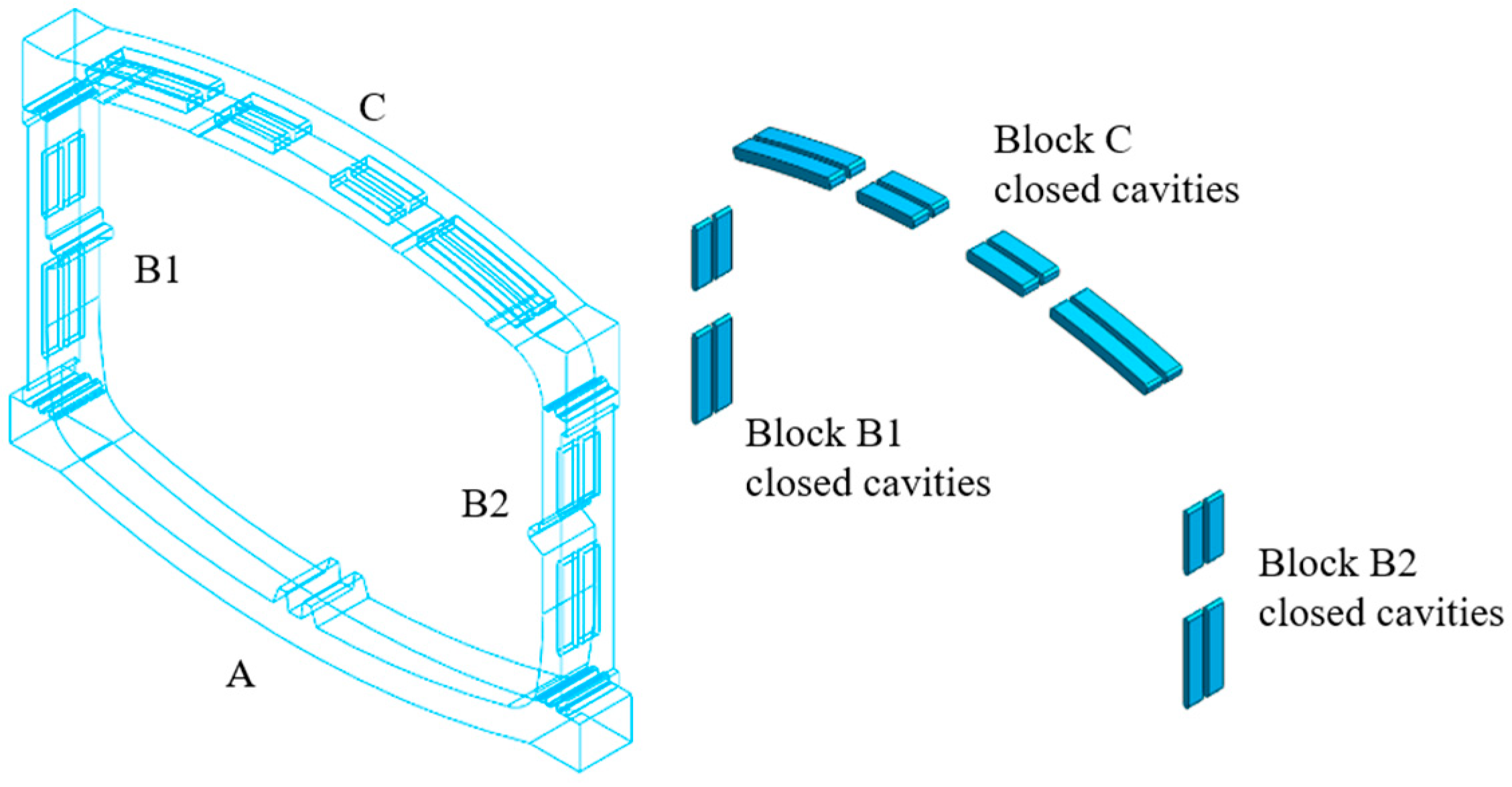
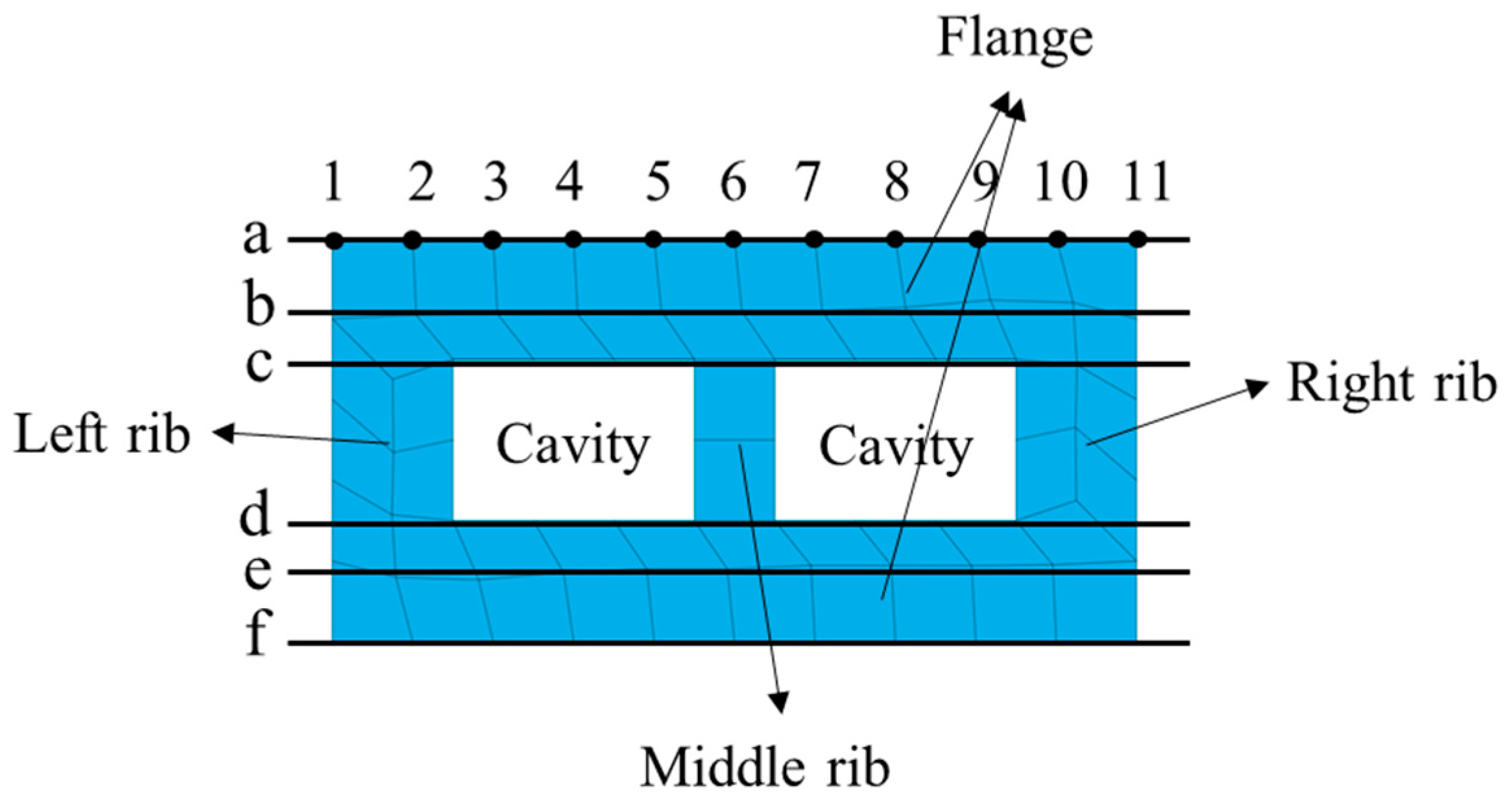
| Physical Parameter | Single-Ring Solid Structure (C+B1+B2) | Total | ||
|---|---|---|---|---|
| C | B1 | B2 | ||
| Volume/m3 | 48.76 | 17.62 | 17.62 | 84 |
| Mass/t | 121.89 | 44.06 | 44.06 | 210.01 |
| Prefabricated Components | Strength Grade | Capacity/(kN/m3) | Poisson’s Ratio | Modulus of Elasticity/MPa |
|---|---|---|---|---|
| E, ZL | C35 | 25 | 0.2 | 3.15 × 104 |
| A, B, C | C45 | 25 | 0.2 | 3.35 × 104 |
| ZZ | C50 | 25 | 0.2 | 3.45 × 104 |
| Model | Structural Type | Layout of Closed Cavities | Width of Single Closed Cavity/mm | Cavity Rate/% | Number of Units | Grouted Mortise–Tenon Joints | Contact Pairs | Type of Load | |
|---|---|---|---|---|---|---|---|---|---|
| Condition 1 | Condition 2 | ||||||||
| M-1 | Solid structure | None | 0 | 0 | 200,564 | Yes | Yes | Dead weight | Use phase load |
| M-2 | Cavity structure | 2 rows | 600 | 9.71 | 246,021 | Yes | Yes | Dead weight | Use phase load |
| Name of Soil Layer | Thickness/m | Volumetric Weight/(kN/m3) | Lateral Pressure Coefficient | Vertical Bed Coefficient/ (MPa/m) | Horizontal Bed Coefficient/ (MPa/m) |
|---|---|---|---|---|---|
| Plain fill | 1.99 | 20 | 0.65 | 10 | 10 |
| Silty clay | 3.2 | 20 | 0.47 | 18 | 16 |
| Medium sand | 3.4 | 21 | 0.39 | 15 | 15 |
| Coarse sand | 4.9 | 21 | 0.35 | 50 | 45 |
| Strongly weathered muddy siltstone | 1.3 | 21.5 | 0.35 | 160 | 135 |
| Moderately weathered muddy siltstone | 12.66 | 22 | 0.28 | 220 | 200 |
| Cross-Section | Vault Structure | Side Wall | Floor | Medium Plate | Grouted Mortise–Tenon Joints | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 5 | 6 | 13 | 10 | 12 | 4 | 7 | ||
| Axial force/kN | M-1 | −2229.6 | −2241.8 | −2104.8 | −2590.9 | −2943.6 | −2146.6 | 780.06 | 794.1 | −1266 | −1859.7 |
| M-2 | −2173.6 | −2189.5 | −2028.8 | −2514.3 | −2843.4 | −2139.8 | 716.5 | 746.65 | −1136.3 | −1720 | |
| Reduction rate/% | 2.5 | 2.3 | 3.6 | 2.9 | 3.4 | 0.3 | 8.1 | 5.9 | 10.2 | 7.5 | |
| Shear force/kN | M-1 | 23.494 | −487.7 | −1468.1 | 783.9 | −361.72 | 560.45 | −238.87 | −92.145 | 914.11 | −1891.1 |
| M-2 | 24.367 | −348.12 | −1422.3 | 751.81 | −316.65 | 562.13 | −188.25 | −92.861 | 875.7 | −1784.6 | |
| Reduction rate/% | −3.7 | 28.6 | 3.1 | 4.1 | 12.5 | −0.3 | 21.2 | −0.8 | 4.2 | 5.6 | |
| Bending moment/(kN·m) | M-1 | −2976.2 | −2573.8 | 348.78 | −113.11 | −409.48 | 257.93 | 93.673 | 80.716 | 2480.1 | 2652.8 |
| M-2 | −2876 | −2434.6 | 346.43 | −103.24 | −385.53 | 257.62 | 92.385 | 80.077 | 2363 | 2594.3 | |
| Reduction rate/% | 3.3 | 5.4 | 0.7 | 8.7 | 5.8 | 0.1 | 1.4 | 0.8 | 4.7 | 2.2 | |
| Internal Forces | Condition 1 | Condition 2 | ||||
|---|---|---|---|---|---|---|
| M-1 | M-2 | Reduction Rate % | M-1 | M-2 | Reduction Rate % | |
| Axial force/kN | 954.97 | 857.66 | 10.19 | 2943.6 | 2843.4 | 3.40 |
| Shear force/kN | 315.5 | 267.3 | 15.12 | 1468.1 | 1422.3 | 3.12 |
| Bending moment/(kN·m) | 693.74 | 595.67 | 14.14 | 2976.2 | 2876 | 3.37 |
| Principal Strain and Location | Condition 1 | Condition 2 | ||
|---|---|---|---|---|
| M-1 | M-2 | M-1 | M-2 | |
| Maximum principal strain/10−5 | 7.41 | 7.52 | 22.36 | 24.63 |
| Location | ZZ-ZL junction | Outside of B-C joints | ||
| Minimum principal strain/10−5 | −22.74 | −22.79 | −61.73 | −63.74 |
| Location | Lower end of ZZ | Inside of B-C joints | ||
| Displacement and Location | Condition 1 | Condition 2 | ||
|---|---|---|---|---|
| M-1 | M-2 | M-1 | M-2 | |
| Maximum vertical displacement/mm | −3.84 | −4.32 | −15.61 | −15.66 |
| Location | The vault structure (C) | |||
| Maximum horizontal displacement/mm | 0.68 | 0.80 | 3.11 | 3.18 |
| Location | B-C Joints | |||
| Stress and Location | Condition 1 | Condition 2 | ||
|---|---|---|---|---|
| M-1 | M-2 | M-1 | M-2 | |
| Maximum MISES stress/MPa | 7.8 | 7.8 | 18.48 | 19.43 |
| Location | column (ZZ) | Inside of B-C joints | ||
| Maximum principal stress/MPa | 2.35 | 2.33 | 7.69 | 8.56 |
| Location | Medium plate (E) | Outside of B-C joints | ||
| Minimum principal stress/MPa | −8.12 | −8.15 | −22.37 | −22.76 |
| Location | column (ZZ) | Inside of B-C joints | ||
| Data Categories | Vertical Displacement of Vault/mm | Horizontal Displacement at the Top of the Side Wall/mm |
|---|---|---|
| Simulated values | 4.3 | 0.8 |
| Monitoring values 1 | 3.4 | 0.4 |
| Monitoring values 2 | 2.7 | 0.4 |
| Monitoring values 3 | 3.6 | 0.6 |
| Monitoring values 4 | 4.6 | 0.6 |
| Monitoring values 5 | 4.4 | 0.5 |
| Monitoring values 6 | 5.2 | 0.8 |
| Monitoring values 7 | 3.8 | 0.7 |
| Monitoring values 8 | 4.5 | 1.1 |
| Monitoring values 9 | 3.6 | 0.9 |
| Monitoring values 10 | 3.5 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, D.; Kong, D. Comparative Study of Force and Deformation Characteristics of Closed Cavity Thin-Walled Components in Prefabricated Metro Station. Appl. Sci. 2025, 15, 9674. https://doi.org/10.3390/app15179674
Cao D, Kong D. Comparative Study of Force and Deformation Characteristics of Closed Cavity Thin-Walled Components in Prefabricated Metro Station. Applied Sciences. 2025; 15(17):9674. https://doi.org/10.3390/app15179674
Chicago/Turabian StyleCao, Dechun, and Desen Kong. 2025. "Comparative Study of Force and Deformation Characteristics of Closed Cavity Thin-Walled Components in Prefabricated Metro Station" Applied Sciences 15, no. 17: 9674. https://doi.org/10.3390/app15179674
APA StyleCao, D., & Kong, D. (2025). Comparative Study of Force and Deformation Characteristics of Closed Cavity Thin-Walled Components in Prefabricated Metro Station. Applied Sciences, 15(17), 9674. https://doi.org/10.3390/app15179674





