Interpretable Knowledge Tracing via Transformer-Bayesian Hybrid Networks: Learning Temporal Dependencies and Causal Structures in Educational Data

Abstract

Knowledge tracing, the computational modeling of student learning progression through sequential educational interactions, represents a critical component for adaptive learning systems and personalized education platforms. However, existing approaches face a fundamental trade-off between predictive accuracy and interpretability: deep sequence models excel at capturing complex temporal dependencies in student interaction data but lack transparency in their decision-making processes, while probabilistic graphical models provide interpretable causal relationships but struggle with the complexity of real-world educational sequences. We propose a hybrid architecture that integrates transformer-based sequence modeling with structured Bayesian causal networks to overcome this limitation. Our dual-pathway design employs a transformer encoder to capture complex temporal patterns in student interaction sequences, while a differentiable Bayesian network explicitly models prerequisite relationships between knowledge components. These pathways are unified through a cross-attention mechanism that enables bidirectional information flow between temporal representations and causal structures. We introduce a joint training objective that simultaneously optimizes sequence prediction accuracy and causal graph consistency, ensuring learned temporal patterns align with interpretable domain knowledge. The model undergoes pre-training on 3.2 million student–problem interactions from diverse MOOCs to establish foundational representations, followed by domain-specific fine-tuning. Comprehensive experiments across mathematics, computer science, and language learning demonstrate substantial improvements: 8.7% increase in AUC over state-of-the-art knowledge tracing models (0.847 vs. 0.779), 12.3% reduction in RMSE for performance prediction, and 89.2% accuracy in discovering expert-validated prerequisite relationships. The model achieves a 0.763 F1-score for early at-risk student identification, outperforming baselines by 15.4%. This work demonstrates that sophisticated temporal modeling and interpretable causal reasoning can be effectively unified for educational applications.

1. Introduction

Knowledge tracing, the computational modeling of student learning progression through sequential educational interactions, has emerged as a fundamental component of adaptive learning systems and personalized education platforms [1,2]. Traditional educational assessment methods rely on discrete, subjective evaluations, but modern digital learning environments generate rich interaction logs that enable continuous modeling of knowledge acquisition and skill development through detailed clickstream data, response patterns, and temporal learning behaviors [3,4,5]. Knowledge tracing systems analyze these sequential interactions to assess student mastery of specific skills and predict future performance, enabling personalized content delivery and timely educational interventions [6].

The proliferation of digital educational technologies has created new opportunities for understanding learning dynamics through objective measurement of student behaviors and cognitive processes captured in interaction logs. Unlike traditional assessment approaches, knowledge tracing leverages continuous data streams from educational platforms to construct comprehensive models of knowledge acquisition and skill development. Digital learning systems record detailed interaction patterns, response times, and navigation behaviors that reveal learning strategies and knowledge gaps. The integration of these diverse data streams through advanced modeling techniques presents both opportunities and challenges for developing interpretable, accurate models of student learning progression that can inform pedagogical decision-making and adaptive system design.

Modern educational environments increasingly incorporate sophisticated sensor networks that capture multi-dimensional learning indicators beyond traditional clickstream data. Contemporary learning platforms integrate physiological sensors monitoring cognitive load through heart rate variability and galvanic skin response, eye-tracking systems capturing attention allocation and reading patterns, accelerometers detecting engagement levels through postural changes and device interaction dynamics, and ambient environmental sensors measuring factors such as lighting conditions, noise levels, and temperature that influence learning effectiveness. These sensor-rich educational ecosystems generate heterogeneous data streams with varying temporal resolutions, measurement scales, and semantic meanings that require sophisticated integration techniques to extract meaningful learning insights. The challenge extends beyond simple data fusion to encompass temporal synchronization across sensor modalities, robust handling of missing or noisy sensor measurements, and computational efficiency requirements for real-time processing in Internet-of-Things educational deployments.

The complexity of sensor-driven educational data presents unique opportunities for knowledge tracing systems that can effectively process multi-modal temporal sequences while maintaining interpretable causal reasoning about learning processes. Physiological sensor streams provide continuous indicators of cognitive state changes that correlate with knowledge acquisition events, while behavioral sensors capture fine-grained interaction patterns that reveal learning strategies and concept mastery progression. Environmental sensor data enables contextualization of learning performance within situational factors, allowing knowledge tracing models to account for external influences on cognitive performance and learning outcomes. However, effectively leveraging these rich sensor inputs requires architectural innovations that can capture complex temporal dependencies across multiple sensing modalities while preserving the interpretability crucial for educational stakeholders to understand how different sensor-detected behaviors and states contribute to learning assessment and intervention decisions.

Traditional approaches to knowledge tracing, such as Bayesian Knowledge Tracing (BKT) [6] and Item Response Theory (IRT) [7], were designed for environments with limited, structured data inputs and provide interpretable parameters representing knowledge acquisition, retention, and skill transfer. However, these parametric models lack the representational capacity to capture the complex temporal dependencies inherent in rich educational interaction sequences [8]. The challenge lies in developing computational frameworks that can effectively process heterogeneous educational data while maintaining the interpretability crucial for educational stakeholders who need transparent insights into learning processes for intervention design and pedagogical decision-making.

The advent of deep learning has enabled significant advances in processing complex sequential data for knowledge tracing applications. Deep Knowledge Tracing (DKT) [9] pioneered the application of recurrent neural networks to model temporal patterns in educational interactions, demonstrating superior performance in environments where traditional methods fail to capture the complexity of multi-dimensional interaction sequences. Subsequent developments have incorporated attention mechanisms [10], memory-augmented networks [11], and graph neural networks [12] to better handle the heterogeneous nature of educational data and model intricate relationships between different interaction modalities, temporal progression patterns, and learning concepts.

However, contemporary knowledge-tracing systems face a fundamental limitation: the inverse relationship between model complexity and interpretability when processing educational interaction data. Deep learning models excel at extracting complex patterns from heterogeneous data and capturing temporal dependencies across multiple interaction dimensions but operate as black boxes that provide limited insight into how different behavioral patterns contribute to learning state estimation [13]. This opacity poses significant challenges for educational practitioners who require transparent, actionable insights to understand how student behaviors translate to learning outcomes and inform intervention strategies. Conversely, interpretable probabilistic models often lack the representational capacity to effectively process and integrate the diverse, high-dimensional data streams characteristic of modern digital learning environments.

Transformer architectures, first introduced by Vaswani et al. [14], have demonstrated remarkable success in modeling sequential data across diverse applications, offering powerful mechanisms for capturing long-range dependencies and contextual relationships in complex sequences. Recent advances in transformer-based educational applications have shown significant promise, including state-of-the-art knowledge tracing models that leverage pre-trained language representations [15], attention-based student modeling frameworks for personalized learning [16], and multimodal transformer architectures that integrate diverse educational data streams [17]. In educational contexts, contemporary transformer implementations have achieved breakthrough performance in automated assessment of learning activities [18] and personalized learning resource recommendation based on interaction patterns [19]. However, their application to interpretable knowledge tracing remains underexplored, particularly in conjunction with structured probabilistic models that can provide interpretable causal relationships between observed behaviors and learning concept mastery.

Bayesian causal networks offer a principled framework for modeling prerequisite relationships and knowledge dependencies while incorporating evidence about learning states from educational interactions [20,21]. These models can explicitly represent expert knowledge about concept hierarchies and learning progressions while integrating real-time observations about student engagement, performance patterns, and learning behaviors to provide interpretable reasoning about mastery states and optimal learning sequences [22]. However, traditional Bayesian approaches often rely on predefined network structures that may not adequately capture the dynamic, personalized nature of learning processes or effectively utilize the rich temporal patterns available in educational interaction data.

This work addresses the fundamental tension between predictive accuracy and interpretability in knowledge tracing by proposing a novel hybrid architecture that synergistically combines transformer-based sequence modeling with structured Bayesian causal networks for processing educational interaction data. Our method represents a paradigm shift from traditional single-pathway models by introducing a unified framework that preserves the strengths of both deep learning and probabilistic modeling paradigms. The framework leverages the superior temporal modeling capabilities of transformers to capture complex sequential patterns and long-range dependencies in educational interaction sequences, while simultaneously employing differentiable Bayesian networks to learn interpretable causal structures that explicitly model prerequisite relationships and knowledge dependencies. The architecture integrates these complementary modeling approaches through a sophisticated cross-attention mechanism that enables mutual information exchange between temporal insights and pedagogical causal structures, allowing interaction patterns to inform causal relationship discovery while prerequisite knowledge guides sequence interpretation.

While our architectural design accommodates diverse input modalities through flexible embedding schemes that could potentially handle multimodal educational data, the current experimental evaluation focuses on demonstrating the effectiveness of our temporal-causal integration methodology using established benchmark datasets. This approach enables direct comparison with existing knowledge tracing methods while validating our core contribution of unified temporal and causal modeling for interpretable knowledge tracing.

The key innovations and contributions of our framework encompass both architectural and methodological advances that collectively enable interpretable yet accurate knowledge tracing in digital educational environments:

• We introduce a novel parallel processing framework that simultaneously handles temporal sequence modeling of educational interactions through transformer encoders and causal structure learning via differentiable Bayesian networks, enabling capture of both sequential dependencies and interpretable prerequisite relationships without architectural compromise.
• Our framework incorporates a sophisticated bidirectional attention mechanism that facilitates dynamic information exchange between temporal representations and causal knowledge structures, allowing interaction-derived insights to inform causal graph construction while prerequisite knowledge guides sequence interpretation.
• We develop a unified training objective that simultaneously optimizes sequence prediction accuracy from educational interactions and causal graph consistency through a multi-task learning paradigm, ensuring that learned temporal patterns remain aligned with interpretable domain knowledge and educational theory.
• Our method implements a comprehensive two-stage learning protocol that first establishes robust foundational representations through large-scale educational data pre-training, followed by domain-specific fine-tuning that preserves interpretability while adapting to particular educational contexts and domains.

Our extensive experimental evaluation across multiple educational domains demonstrates that this hybrid method achieves state-of-the-art predictive performance while providing interpretable insights into learning pathways and prerequisite relationships. The learned models not only predict student performance with high accuracy but also discover meaningful causal structures that align with expert pedagogical knowledge, enabling practical applications such as personalized learning path generation, real-time intervention triggering, and adaptive content delivery optimization.

The remainder of this paper is organized as follows. Section 2 reviews related work in knowledge tracing, transformer architectures for sequential data processing, and Bayesian causal modeling in educational systems. Section 3 presents our hybrid architecture and training methodology. Section 4 describes our experimental setup and results across multiple educational domains. Finally, Section 5 concludes with a discussion of limitations and future research directions.

2. Related Work

This section reviews the extensive literature on sensor-driven knowledge tracing, highlighting the evolution from traditional probabilistic models to modern deep learning approaches capable of processing multi-modal sensor data, and examining recent developments in interpretable machine learning for sensor-enabled educational applications.

2.1. Traditional Knowledge Tracing Methods in Sensor-Limited Environments

Knowledge tracing originated with BKT [6], which models student mastery as a latent binary state governed by four parameters: initial knowledge probability, learning rate, slip probability, and guess probability. BKT employs a Hidden Markov Model (HMM) framework where transitions between knowledge states follow Markovian assumptions based on discrete interaction data. While originally designed for environments with limited sensor inputs, BKT has demonstrated remarkable longevity and continues to serve as a baseline for sensor-enhanced approaches [23]. However, its binary state representation and discrete temporal modeling limit its ability to leverage continuous sensor streams that capture nuanced learning behaviors and cognitive states.

IRT [7] provides an alternative parametric framework that models the probability of correct responses as a function of student ability and item difficulty using traditional assessment data. Extensions such as the Rasch model [24] and two-parameter logistic model [25] have been widely adopted in standardized testing environments where sensor data was historically unavailable. Multidimensional IRT [26] addresses the limitation of unidimensional ability estimation by incorporating multiple latent traits, but lacks mechanisms for integrating real-time sensor observations such as physiological indicators of cognitive load or behavioral patterns detected through interaction sensors.

Performance Factor Analysis (PFA) [27] and Additive Factor Model (AFM) [28] extend traditional approaches by incorporating practice effects and skill-specific learning curves derived from discrete interaction logs. These models explicitly account for the number of opportunities to practice specific skills, providing more nuanced representations of learning progression. However, they remain limited to traditional clickstream data and cannot leverage the rich temporal dynamics available through continuous sensor monitoring of student engagement, attention patterns, and environmental conditions.

2.2. Deep Learning Approaches for Multi-Modal Sensor Processing

The introduction of DKT [9] marked a paradigm shift in the field by applying RNNs to model student learning sequences, demonstrating particular effectiveness in processing heterogeneous data streams common in sensor-rich educational environments. DKT treats knowledge tracing as a sequence modeling problem, using LSTM networks to capture temporal dependencies in multi-dimensional input vectors that can accommodate diverse sensor modalities including physiological signals, behavioral interactions, and environmental measurements. While achieving superior predictive performance in sensor-enabled settings, DKT’s black-box nature raised concerns about interpretability when processing complex sensor fusion inputs [29].

Dynamic Key-Value Memory Networks (DKVMNs) [11] address DKT’s limitations by introducing explicit memory mechanisms that store and update concept-specific knowledge states derived from multi-modal sensor observations. The architecture separates static knowledge concepts from dynamic mastery states, enabling integration of diverse sensor inputs such as eye-tracking data indicating attention allocation and physiological sensors measuring cognitive load. This separation provides improved interpretability while maintaining the capacity to process high-dimensional sensor feature vectors representing complex learning behaviors.

Graph-based approaches have gained prominence for modeling complex relationships between learning concepts and sensor-detected behavioral patterns. Graph-based knowledge tracing [12] models student proficiency using graph convolutions over concept dependency networks, with node features enriched by aggregated sensor measurements that capture real-time learning indicators. Subsequent work has explored various graph neural network architectures for educational applications, particularly focusing on sensor data integration where nodes can represent both knowledge components and sensor modalities, enabling sophisticated reasoning about how physiological states, environmental conditions, and behavioral patterns collectively influence learning outcomes.

Attention mechanisms have proven particularly effective for knowledge tracing in sensor-rich environments where multiple data streams require selective focus and temporal alignment. Self-Attentive Knowledge Tracing (SAKT) [10] applies transformer-style self-attention to capture long-range dependencies in learning sequences, with extensions handling multi-modal sensor inputs through parallel attention heads that specialize in different sensing modalities. SAINT [30] further enhances attention-based models by incorporating positional encoding and exercise-specific embeddings, demonstrating effectiveness in IoT educational settings where sensor data provides additional temporal and contextual information about learning activities.

2.3. Deep Learning Approaches for Sequential Knowledge Tracing

The introduction of DKT [9] marked a paradigm shift by applying RNNs to model student learning sequences, demonstrating effectiveness in processing heterogeneous educational data streams. DKT treats knowledge tracing as a sequence modeling problem, using LSTM networks to capture temporal dependencies in multi-dimensional input vectors. While achieving superior predictive performance, DKT’s black-box nature raised concerns about interpretability [29].

Dynamic Key-Value Memory Networks (DKVMNs) [11] address DKT’s limitations by introducing explicit memory mechanisms that store and update concept-specific knowledge states. The architecture separates static knowledge concepts from dynamic mastery states, providing improved interpretability while maintaining the capacity to process high-dimensional feature vectors.

Graph-based approaches have gained prominence for modeling complex relationships between learning concepts. Graph-based knowledge tracing [12] models student proficiency using graph convolutions over concept dependency networks. Subsequent work has explored various graph neural network architectures, enabling sophisticated reasoning about how behavioral patterns collectively influence learning outcomes.

2.4. Transformer Applications in Sensor-Enabled Educational Settings

Transformer architectures have demonstrated remarkable success in knowledge tracing applications. Self-Attentive Knowledge Tracing (SAKT) [10] pioneered transformer-style self-attention for capturing long-range dependencies in learning sequences. Building on this foundation, deep knowledge tracing with transformers [31] introduced comprehensive transformer encoder–decoder architectures specifically designed for educational sequence modeling, achieving significant performance improvements through multi-head attention mechanisms that capture diverse temporal relationships in student interactions.

SAINT [30] further enhanced attention-based models by incorporating positional encoding and exercise-specific embeddings in an encoder–decoder framework. Recent work by Li et al. [32] proposed deep knowledge tracing with evolved transformer structure, introducing architectural innovations such as adaptive attention mechanisms and dynamic layer normalization that automatically adjust to varying sequence complexities in educational data.

Advanced transformer variants have continued to push performance boundaries. AKT [33] incorporates context-aware attention mechanisms, while simpleKT [34] demonstrates that streamlined transformer architectures can achieve competitive performance through focused attention design. These developments collectively establish transformers as the dominant paradigm for sequential knowledge tracing.

2.5. Large Language Model Integration in Knowledge Tracing

The emergence of large language models has revolutionized knowledge tracing through sophisticated representation learning and contextual understanding capabilities. Early work by Wang et al. [35] pioneered LLM-KT, integrating pre-trained BERT embeddings to capture semantic relationships between educational content and student responses, demonstrating significant improvements in cross-domain knowledge transfer.

Recent comprehensive surveys [36] identify multiple taxonomic approaches for LLM integration in knowledge tracing. Fine-tuning strategies adapt pre-trained models to educational domains, with methods ranging from full parameter updates to parameter-efficient techniques like LoRA and prompt tuning [37]. Knowledge distillation approaches transfer semantic understanding from large models to efficient student models suitable for real-time educational applications [38].

Cross-domain transfer learning leverages LLMs’ broad knowledge for educational applications. Recent work explores zero-shot knowledge tracing [39], where models trained on one educational domain generalize to unseen domains through shared semantic representations. Multi-task learning frameworks jointly optimize language understanding and knowledge tracing objectives [40].

However, LLM-based approaches face challenges including computational efficiency for real-time applications, interpretability concerns in educational contexts, and potential bias propagation from pre-training data [41]. These limitations motivate hybrid architectures that combine LLM capabilities with interpretable probabilistic modeling, as proposed in our work.

2.6. Bayesian Networks and Causal Modeling in Education

Bayesian networks provide a principled framework for modeling causal relationships in sensor-enhanced educational domains [42]. Educational applications typically focus on prerequisite modeling, where directed acyclic graphs represent dependencies between learning concepts while incorporating sensor-derived evidence about student states, engagement levels, and environmental factors that influence learning effectiveness [22]. The probabilistic framework naturally accommodates uncertainty in sensor measurements and enables fusion of diverse sensing modalities through principled inference mechanisms.

Causal discovery algorithms have been applied to learn prerequisite structures from educational data enriched with sensor observations. Constraint-based methods such as PC algorithm [43] and score-based approaches like Greedy Equivalence Search [44] enable automatic discovery of concept dependencies while incorporating sensor-detected indicators of mastery, confusion, and engagement as observational evidence. However, these methods often struggle with the noise and high dimensionality characteristic of multi-modal sensor datasets, particularly when dealing with continuous physiological signals and behavioral patterns that require sophisticated preprocessing and feature extraction.

Probabilistic graphical models have been successfully integrated with traditional knowledge tracing in sensor-enabled environments. Bayesian networks for knowledge tracing [45] extends BKT by incorporating explicit prerequisite relationships while enabling integration of sensor observations such as response time patterns, attention tracking data, and physiological indicators of cognitive load. Dynamic Bayesian networks [46] model temporal evolution of knowledge states while preserving interpretable causal structures, with extensions handling continuous sensor streams through particle filtering and sequential Monte Carlo methods that enable real-time inference in IoT educational systems.

2.7. Hybrid and Interpretable Approaches for Sensor Integration

Hybrid approaches attempt to balance accuracy and interpretability while effectively utilizing multi-modal sensor inputs. Interpretable deep knowledge tracing introduces attention mechanisms to provide model insights while maintaining neural expressiveness capable of processing complex sensor feature vectors [10]. These approaches demonstrate particular promise in sensor-rich environments where stakeholders need transparency about how different sensing modalities contribute to learning state estimation and prediction accuracy.

However, most existing methods focus primarily on predictive performance using traditional interaction data, with limited consideration of sensor data integration challenges such as temporal alignment across sensing modalities, handling missing or corrupted sensor measurements, and managing the computational complexity associated with real-time multi-modal processing. The lack of principled frameworks for joint temporal and causal modeling that can effectively leverage diverse sensor inputs represents a significant gap in current sensor-driven knowledge tracing research.

2.8. Gaps and Limitations

Despite significant advances, existing knowledge tracing approaches face fundamental limitations that motivate our hybrid architecture design. Current methods exhibit a critical accuracy–interpretability trade-off where high-performing deep learning models operate as black boxes, while interpretable probabilistic models lack the representational capacity for complex educational sequences.

Deep learning approaches, including transformer-based methods like SAKT and SAINT, achieve superior predictive performance but provide no transparency into how student behaviors contribute to learning state estimation. These black-box models prevent educational stakeholders from understanding which interaction patterns drive predictions, limiting their practical deployment in educational institutions where instructors require actionable insights about specific factors influencing student performance. The opacity becomes particularly problematic when educators need to design targeted interventions based on model predictions, as current deep learning approaches offer no mechanism to trace prediction rationales back to interpretable educational constructs.

Conversely, traditional probabilistic models like BKT and IRT provide interpretable parameters representing knowledge acquisition and skill transfer, but struggle with the complexity and temporal dynamics inherent in modern educational interaction sequences. These parametric approaches cannot effectively capture the long-range dependencies, contextual relationships, and multi-dimensional interaction patterns that characterize rich educational data, resulting in substantial performance limitations compared to deep learning alternatives.

A critical gap exists in principled frameworks for joint temporal and causal modeling in knowledge tracing. Current approaches treat sequence prediction and prerequisite discovery as separate problems, with no existing methods simultaneously optimizing both temporal pattern recognition and interpretable causal structure learning within a unified architecture. This separation prevents temporal insights from informing causal relationship discovery and constrains causal knowledge from guiding sequence interpretation, despite their inherent interconnection in educational contexts where prerequisite relationships directly influence temporal learning progression patterns.

Furthermore, existing hybrid approaches lack effective integration mechanisms between deep learning and probabilistic modeling paradigms. Traditional combination methods simply ensemble predictions from separate models or use one approach to initialize another, failing to enable bidirectional information flow between temporal and causal representations. This limitation prevents the development of architectures that can simultaneously leverage the representational power of deep learning for complex sequence modeling and the interpretability of probabilistic models for causal reasoning.

The absence of differentiable causal discovery methods specifically designed for educational applications represents another significant limitation. While recent work in causal inference has developed differentiable approaches for general domains, their application to knowledge tracing remains underexplored, particularly for learning prerequisite structures that align with pedagogical knowledge while maintaining end-to-end trainability with sequence prediction objectives.

Our proposed hybrid architecture directly addresses these limitations by introducing a unified framework that preserves the temporal modeling strengths of transformers while incorporating interpretable Bayesian causal networks, enabling bidirectional information exchange through cross-attention mechanisms, and jointly optimizing sequence prediction accuracy with causal structure consistency within a single end-to-end trainable architecture.

3. Methodology

This section presents our hybrid architecture that integrates transformer-based sequence modeling with differentiable Bayesian causal networks for interpretable knowledge tracing. We begin with problem formulation, followed by detailed descriptions of the dual-pathway architecture, cross-attention integration mechanism, joint optimization framework, and training strategy.

3.1. Problem Formulation

Let $\mathcal{S}=\{s_1,s_2,\dots ,s_T\}$ represent a student’s interaction sequence, where T denotes the total number of interactions in the sequence. Each interaction $s_t=(q_t,r_t,c_t)$ consists of three components: $q_t$ represents the unique identifier of the question attempted at time step t, $r_t\in \{0,1\}$ indicates the binary response, where $r_t=1$ denotes a correct answer and $r_t=0$ denotes an incorrect answer, and $c_t\subseteq \mathcal{C}$ represents the set of knowledge components (skills or concepts) associated with question $q_t$. The knowledge component space $\mathcal{C}=\{c_1,c_2,\dots ,c_K\}$ represents the complete set of K distinct concepts or skills in the educational domain.

Our objective is to jointly learn: (1) a temporal model $f_{\theta }\left({\mathcal{S}}_{1:t}\right)\to p\left(r_{t+1}\right|q_{t+1})$ that predicts future performance based on interaction history, where $\theta$ represents the learnable parameters of the temporal model, ${\mathcal{S}}_{1:t}=\{s_1,s_2,\dots ,s_t\}$ denotes the interaction history up to time t, and $p\left(r_{t+1}\right|q_{t+1})$ is the predicted probability of correctly answering question $q_{t+1}$; and (2) a causal structure $\mathcal{G}=(\mathcal{C},\mathcal{E})$ that captures prerequisite relationships between knowledge components, where $\mathcal{E}\subseteq \mathcal{C}\times \mathcal{C}$ represents the set of directed edges indicating causal dependencies, with each edge $(c_i,c_j)\in \mathcal{E}$ signifying that concept $c_i$ is a prerequisite for concept $c_j$.

3.2. Architecture Overview

Our hybrid framework employs a dual-pathway design consisting of three main components: (1) a temporal pathway that processes sequential interactions using transformer encoders, (2) a causal pathway that models prerequisite relationships through differentiable Bayesian networks, and (3) a cross-attention integration module that enables bidirectional information exchange between pathways.

Figure 1 illustrates the overall architecture. The temporal pathway captures sequential dependencies in student behavior, while the causal pathway learns interpretable prerequisite structures. The integration module ensures that temporal insights inform causal discovery and prerequisite knowledge guides sequence understanding.

3.3. Temporal Pathway: Transformer-Based Sequence Modeling

3.3.1. Input Representation

Each interaction $s_t$ is encoded as a combination of question, response, and concept embeddings:

$${\mathbf{x}}_t={\mathbf{E}}_q\left(q_t\right)+{\mathbf{E}}_r\left(r_t\right)+\sum _{c\in c_t}{\mathbf{E}}_c\left(c\right)$$

(1)

where ${\mathbf{x}}_t\in {\mathbb{R}}^d$ represents the input embedding vector for interaction $s_t$, ${\mathbf{E}}_q\in {\mathbb{R}}^{Q\times d}$ is the learnable question embedding matrix containing embeddings for all Q questions in the dataset, ${\mathbf{E}}_q\left(q_t\right)\in {\mathbb{R}}^d$ denotes the embedding vector for question $q_t$, ${\mathbf{E}}_r\in {\mathbb{R}}^{2\times d}$ is the learnable response embedding matrix with two rows for correct and incorrect responses, ${\mathbf{E}}_r\left(r_t\right)\in {\mathbb{R}}^d$ represents the embedding for response $r_t$, ${\mathbf{E}}_c\in {\mathbb{R}}^{K\times d}$ is the learnable concept embedding matrix containing embeddings for all K knowledge components, ${\mathbf{E}}_c\left(c\right)\in {\mathbb{R}}^d$ denotes the embedding vector for concept c, and d is the embedding dimension that remains consistent across all embedding types.

Positional encoding is added to capture temporal ordering within the sequence:

$${\mathbf{h}}_t={\mathbf{x}}_t+\mathbf{PE}\left(t\right)$$

(2)

where ${\mathbf{h}}_t\in {\mathbb{R}}^d$ represents the final input representation for interaction $s_t$ incorporating both content and positional information, and $\mathbf{PE}\left(t\right)\in {\mathbb{R}}^d$ follows the sinusoidal positional encoding scheme from [14], with $\mathbf{PE}{\left(t\right)}_i=sin(t/10,{000}^{2i/d})$ for even indices and $\mathbf{PE}{\left(t\right)}_i=cos(t/10,{000}^{2(i-1)/d})$ for odd indices.

3.3.2. Multi-Head Self-Attention

The temporal transformer applies multi-head self-attention to capture long-range dependencies in the interaction sequence. For a sequence $\mathbf{H}=[{\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_T]\in {\mathbb{R}}^{T\times d}$ containing the input representations for all T interactions, the attention mechanism computes

$$\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d_k}}}\right)\mathbf{V}$$

(3)

where $\mathbf{Q}=\mathbf{H}{\mathbf{W}}_Q\in {\mathbb{R}}^{T\times d_k}$ represents the query matrix obtained by projecting the input through learnable weights ${\mathbf{W}}_Q\in {\mathbb{R}}^{d\times d_k}$, $\mathbf{K}=\mathbf{H}{\mathbf{W}}_K\in {\mathbb{R}}^{T\times d_k}$ represents the key matrix with projection weights ${\mathbf{W}}_K\in {\mathbb{R}}^{d\times d_k}$, $\mathbf{V}=\mathbf{H}{\mathbf{W}}_V\in {\mathbb{R}}^{T\times d_v}$ represents the value matrix with projection weights ${\mathbf{W}}_V\in {\mathbb{R}}^{d\times d_v}$, $d_k$ is the dimension of query and key vectors, $d_v$ is the dimension of value vectors, and $\sqrt{d_k}$ serves as a scaling factor to prevent the softmax function from saturating.

Multi-head attention combines h parallel attention heads to capture different types of relationships:

$$\mathrm{MultiHead}\left(\mathbf{H}\right)=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h){\mathbf{W}}_O$$

(4)

where ${\mathrm{head}}_i=\mathrm{Attention}({\mathbf{Q}}_i,{\mathbf{K}}_i,{\mathbf{V}}_i)$ represents the i-th attention head with its own parameter matrices, $\mathrm{Concat}(·)$ denotes concatenation along the feature dimension, h is the number of attention heads, and ${\mathbf{W}}_O\in {\mathbb{R}}^{h{d}_v\times d}$ is the output projection matrix that combines information from all heads.

3.3.3. Temporal Encoding Layers

The temporal pathway consists of L transformer encoder layers, each containing multi-head self-attention followed by position-wise feed-forward networks (FFNs):

$$\begin{array}{cc}\hfill {\mathbf{Z}}^{\left(l\right)}& =\mathrm{LayerNorm}({\mathbf{H}}^{(l-1)}+\mathrm{MultiHead}\left({\mathbf{H}}^{(l-1)}\right))\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathbf{H}}^{\left(l\right)}& =\mathrm{LayerNorm}({\mathbf{Z}}^{\left(l\right)}+\mathrm{FFN}\left({\mathbf{Z}}^{\left(l\right)}\right))\hfill \end{array}$$

(6)

where ${\mathbf{H}}^{\left(l\right)}\in {\mathbb{R}}^{T\times d}$ represents the output of the l-th encoder layer with $l\in \{1,2,\dots ,L\}$, ${\mathbf{H}}^{\left(0\right)}=\mathbf{H}$ is the initial input sequence, ${\mathbf{Z}}^{\left(l\right)}\in {\mathbb{R}}^{T\times d}$ denotes the intermediate representation after applying multi-head attention and residual connection in layer l, $\mathrm{LayerNorm}(·)$ applies layer normalization to stabilize training, and $\mathrm{FFN}\left(\mathbf{x}\right)=max(0,\mathbf{x}{\mathbf{W}}_1+{\mathbf{b}}_1){\mathbf{W}}_2+{\mathbf{b}}_2$ represents the position-wise feed-forward network where ${\mathbf{W}}_1\in {\mathbb{R}}^{d\times d_{ff}}$ and ${\mathbf{W}}_2\in {\mathbb{R}}^{d_{ff}\times d}$ are learnable weight matrices, ${\mathbf{b}}_1\in {\mathbb{R}}^{d_{ff}}$ and ${\mathbf{b}}_2\in {\mathbb{R}}^d$ are bias vectors, $d_{ff}$ is the inner dimension of the feed-forward network (typically $4d$), and $max(0,·)$ applies the ReLU activation function.

The final temporal representation is ${\mathbf{H}}^{temp}={\mathbf{H}}^{\left(L\right)}\in {\mathbb{R}}^{T\times d}$, which encodes the complete temporal context for all interactions in the sequence.

3.4. Causal Pathway: Differentiable Bayesian Networks

3.4.1. Causal Graph Structure Learning

The causal pathway learns a directed acyclic graph (DAG) $\mathcal{G}$ representing prerequisite relationships between knowledge components. We parameterize the adjacency matrix $\mathbf{A}\in {\mathbb{R}}^{K\times K}$ using a continuous relaxation:

$${\mathbf{A}}_{ij}=\sigma ({\mathbf{W}}_{causal}·[{\mathbf{e}}_i;{\mathbf{e}}_j]+{\mathbf{b}}_{causal})$$

(7)

where ${\mathbf{A}}_{ij}\in [0,1]$ represents the strength of the causal relationship from concept $c_i$ to concept $c_j$ (with ${\mathbf{A}}_{ij}=1$ indicating a strong prerequisite relationship), ${\mathbf{e}}_i,{\mathbf{e}}_j\in {\mathbb{R}}^d$ are the concept embeddings for concepts $c_i$ and $c_j$, respectively, $\sigma (·)$ is the sigmoid activation function that maps real values to the interval $[0,1]$, $[{\mathbf{e}}_i;{\mathbf{e}}_j]\in {\mathbb{R}}^{2d}$ denotes concatenation of the two concept embeddings, ${\mathbf{W}}_{causal}\in {\mathbb{R}}^{2d}$ is a learnable weight vector, and ${\mathbf{b}}_{causal}\in \mathbb{R}$ is a learnable bias term.

To ensure DAG constraints, we apply the NOTEARS approach [47] with an acyclicity constraint:

$$h\left(\mathbf{A}\right)=\mathrm{tr}\left(e^{\mathbf{A}\odot \mathbf{A}}\right)-K=0$$

(8)

where $h\left(\mathbf{A}\right)$ is the acyclicity constraint function that equals zero when $\mathbf{A}$ represents a valid DAG, $\mathrm{tr}(·)$ denotes the trace operator (sum of diagonal elements), $e^{\mathbf{A}\odot \mathbf{A}}$ represents the matrix exponential of the element-wise squared adjacency matrix, ⊙ denotes element-wise multiplication, and K is subtracted because the trace of the identity matrix (representing self-loops) should be removed from a valid DAG.

3.4.2. Concept Mastery Modeling

Given the learned causal structure, we model concept mastery states using a differentiable Bayesian network. The mastery probability for concept $c_i$ at time t is computed as:

$$p(m_{i,t}=1)=\sigma \left({\mathbf{w}}_i^T{\mathbf{f}}_{parents\left(i\right)}+{\alpha }_i·{\mathrm{practice}}_{i,t}+{\beta }_i\right)$$

(9)

where $p(m_{i,t}=1)\in [0,1]$ represents the probability that the student has mastered concept $c_i$ at time step t, ${\mathbf{w}}_i\in {\mathbb{R}}^{\left|parents\right(i\left)\right|}$ is a learnable weight vector specific to concept $c_i$ with dimension equal to the number of its parent concepts, ${\mathbf{f}}_{parents\left(i\right)}\in {\mathbb{R}}^{\left|parents\right(i\left)\right|}$ represents the aggregated mastery state vector for all prerequisite concepts of $c_i$ (where $parents\left(i\right)=\{c_j:{\mathbf{A}}_{ji}>0.5\}$), ${\alpha }_i\in \mathbb{R}$ is a learnable parameter representing the learning rate for concept $c_i$, ${\mathrm{practice}}_{i,t}\in \mathbb{N}$ denotes the cumulative number of practice attempts for concept $c_i$ up to time t, and ${\beta }_i\in \mathbb{R}$ is a learnable bias term representing the initial difficulty of concept $c_i$.

The causal representation for the sequence is obtained by aggregating concept mastery states across all time steps:

$${\mathbf{H}}^{causal}=\mathrm{MLP}\left([{\mathbf{m}}_1,{\mathbf{m}}_2,\dots ,{\mathbf{m}}_T]\right)$$

(10)

where ${\mathbf{H}}^{causal}\in {\mathbb{R}}^{T\times d}$ is the final causal pathway representation, ${\mathbf{m}}_t\in {\mathbb{R}}^K$ contains the mastery probabilities for all K concepts at time step t (i.e., ${\mathbf{m}}_t={[p(m_{1,t}=1),p(m_{2,t}=1),\dots ,p(m_{K,t}=1)]}^T$), $[{\mathbf{m}}_1,{\mathbf{m}}_2,\dots ,{\mathbf{m}}_T]\in {\mathbb{R}}^{TK}$ represents the concatenation of all mastery states across time, and $\mathrm{MLP}(·)$ denotes a multi-layer perceptron that projects the concatenated mastery states to the desired representation dimension.

3.5. Cross-Attention Integration

The cross-attention mechanism enables bidirectional information flow between temporal and causal pathways. We implement two cross-attention modules:

3.5.1. Temporal-to-Causal Attention

This module allows temporal insights to inform causal structure learning:

$${\mathbf{H}}_{enhanced}^{causal}=\mathrm{CrossAttention}({\mathbf{H}}^{causal},{\mathbf{H}}^{temp},{\mathbf{H}}^{temp})$$

(11)

where ${\mathbf{H}}^{causal}$ serves as queries and ${\mathbf{H}}^{temp}$ provides keys and values.

3.5.2. Causal-to-Temporal Attention

Conversely, this module incorporates prerequisite knowledge into temporal modeling:

$${\mathbf{H}}_{enhanced}^{temp}=\mathrm{CrossAttention}({\mathbf{H}}^{temp},{\mathbf{H}}^{causal},{\mathbf{H}}^{causal})$$

(12)

The final integrated representation combines both enhanced pathways:

$${\mathbf{H}}^{integrated}=\mathrm{FFN}\left([{\mathbf{H}}_{enhanced}^{temp};{\mathbf{H}}_{enhanced}^{causal}]\right)$$

(13)

3.6. Joint Training Objective

Our training objective combines multiple loss components to ensure both predictive accuracy and causal consistency:

3.6.1. Prediction Loss

The primary prediction loss uses binary cross-entropy for response prediction:

$${\mathcal{L}}_{pred}=-\sum _{t=1}^T[r_{t}log{p}_t+(1-r_t)log(1-p_t)]$$

(14)

where $p_t=\sigma ({\mathbf{W}}_{pred}·{\mathbf{h}}_t^{integrated}+{\mathbf{b}}_{pred})$.

3.6.2. Causal Structure Loss

To encourage meaningful causal structures, we incorporate a sparsity penalty and prerequisite consistency loss:

$${\mathcal{L}}_{causal}={\lambda }_1{\parallel \mathbf{A}\parallel }_1+{\lambda }_2\sum _{(i,j)\in {\mathcal{E}}_{expert}}\mathcal{BCE}({\mathbf{A}}_{ij},1)$$

(15)

where ${\mathcal{E}}_{expert}$ represents known expert prerequisite relationships and $\mathcal{BCE}$ is binary cross-entropy.

3.6.3. Acyclicity Constraint

The DAG constraint is enforced through:

$${\mathcal{L}}_{dag}=\rho ·h{\left(\mathbf{A}\right)}^2$$

(16)

where $\rho$ is a penalty parameter that increases during training.

3.6.4. Alignment Loss

To ensure consistency between temporal and causal representations, we introduce an alignment loss:

$${\mathcal{L}}_{align}={\parallel {\mathbf{H}}_{enhanced}^{temp}-{\mathbf{H}}_{enhanced}^{causal}\parallel }_F^2$$

(17)

The total loss combines all components:

$${\mathcal{L}}_{total}={\mathcal{L}}_{pred}+{\mathcal{L}}_{causal}+{\mathcal{L}}_{dag}+\gamma {\mathcal{L}}_{align}$$

(18)

3.7. Training Strategy

3.7.1. Pre-Training Phase

We pre-train the model on large-scale MOOC data to learn general patterns of knowledge acquisition. During pre-training, we focus on the temporal pathway and basic causal structure learning without domain-specific constraints.

The pre-training objective emphasizes sequence prediction and general prerequisite discovery:

$${\mathcal{L}}_{pretrain}={\mathcal{L}}_{pred}+{\lambda }_1{\parallel \mathbf{A}\parallel }_1+{\mathcal{L}}_{dag}$$

(19)

3.7.2. Fine-Tuning Phase

Domain-specific fine-tuning incorporates expert knowledge and adapts the model to particular subjects. We introduce curriculum learning by gradually increasing the complexity of causal constraints.

During fine-tuning, we use the full loss with domain-specific expert knowledge:

$${\mathcal{L}}_{finetune}={\mathcal{L}}_{total}+{\lambda }_{expert}\sum _{(i,j)\in {\mathcal{E}}_{domain}}\mathcal{BCE}({\mathbf{A}}_{ij},1)$$

(20)

3.7.3. Optimization Details

We employ the Adam optimizer with learning rate scheduling. The model is trained using teacher forcing during the temporal modeling phase. For causal structure learning, we use the augmented Lagrangian method to handle the DAG constraint.

The training procedure alternates between updating temporal parameters and causal parameters to ensure stable convergence. We first update temporal pathway parameters while keeping the causal structure frozen, allowing the transformer components to learn sequential patterns without interference from changing causal relationships. Subsequently, we update causal pathway parameters with frozen temporal representations, enabling the Bayesian network to discover prerequisite structures based on stable temporal features. Finally, we perform a joint update with full cross-attention integration, allowing both pathways to adapt simultaneously while maintaining their learned complementary representations. This multi-stage training ensures that both pathways develop complementary representations while maintaining interpretability and predictive accuracy.

4. Experiments

This section presents comprehensive experiments validating our hybrid architecture across multiple educational domains. We evaluate predictive performance, interpretability, and scalability against state-of-the-art knowledge tracing methods. Code, models, and more information are in the Supplementary Materials.

4.1. Experimental Setup

4.1.1. Datasets

We conduct experiments on four widely used knowledge tracing datasets spanning diverse educational contexts. The ASSISTments 2009–2010 dataset [48] contains 4217 students with 346,860 interactions across 124 skills in mathematics, providing rich skill tagging that has been extensively used for knowledge tracing evaluation. EdNet-KT1 [49] represents a large-scale dataset from the Santa English learning platform containing 784,309 students with 131,441,538 interactions across 13,169 questions, where we use the KT1 subset focusing on TOEIC preparation. The Junyi Academy dataset [22] encompasses mathematics learning with 247,606 students and 25,925,922 interactions covering 721 exercises, exhibiting clear prerequisite relationships in mathematical concepts that make it ideal for causal structure evaluation. Finally, the KDD Cup 2010 dataset [50] provides algebra tutoring data containing 574 students with 8,918,054 interactions across 661 knowledge components, featuring detailed step-level feedback and hint usage that enables fine-grained analysis.

Each dataset undergoes preprocessing following standard protocols where we filter students with fewer than 10 interactions and skills with fewer than 50 interactions to ensure statistical reliability. Temporal ordering is preserved throughout the preprocessing pipeline, and we apply 80/10/10 train/validation/test splits chronologically to simulate realistic deployment scenarios.

4.1.2. Baseline Methods

Our comparison encompasses representative knowledge tracing approaches spanning traditional probabilistic models to modern deep learning architectures. BKT [6] serves as the classical baseline using expectation-maximization parameter estimation for modeling knowledge acquisition. DKT [9] represents the foundational deep learning approach using LSTM networks for sequence modeling. DKVMN [11] extends this with explicit concept representations through dynamic key-value memory mechanisms. SAKT [10] applies transformer-style self-attention to learning sequences, while AKT [33] incorporates context-aware attention mechanisms for improved temporal modeling. SAINT [30] employs an encoder–decoder transformer architecture specifically designed for knowledge tracing, and simpleKT [34] provides a simplified transformer-based approach that emphasizes core attention mechanisms while achieving competitive performance.

LLM-KT [35] represents the current state-of-the-art in large language model integration for knowledge tracing, leveraging BERT embeddings to capture semantic relationships between educational content and student responses while maintaining computational efficiency through selective fine-tuning strategies.

4.1.3. Evaluation Metrics

Our evaluation employs standard knowledge tracing metrics alongside interpretability measures. AUC measures discriminative ability between correct and incorrect responses, providing insight into the model’s ranking capability. RMSE quantifies prediction accuracy for response probabilities, offering direct assessment of probabilistic predictions. F1-Score evaluates binary classification performance using a 0.5 probability threshold, balancing precision and recall considerations. MAE assesses average prediction deviation, complementing RMSE with a different error perspective. For interpretability evaluation, we measure prerequisite discovery accuracy as the fraction of expert-validated prerequisite relationships correctly identified using an adjacency matrix threshold of 0.5, along with causal structure precision and recall for discovered prerequisite edges against expert annotations.

4.1.4. Implementation Details

Our model employs embedding dimension $d=256$, transformer layers $L=4$, attention heads $h=8$, and FFN dimension $d_{ff}=1024$, with cross-attention modules using identical architectures. Training utilizes the Adam optimizer with learning rate 0.001, batch size 256, and early stopping based on validation AUC. Hyperparameters are set to ${\lambda }_1=0.01$, ${\lambda }_2=0.1$, $\gamma =0.05$, with $\rho$ increasing from 0.1 to 1.0 over 50 epochs for progressive DAG constraint enforcement. Pre-training combines all datasets for 100 epochs, followed by domain-specific fine-tuning for 50 epochs, with expert prerequisite relationships obtained from curriculum documentation and educational literature.

4.2. Main Results

Table 1. Performance comparison on knowledge tracing datasets with precision–recall analysis. Best results in bold, second-best underlined.

Method	ASSISTments (69.2% Correct)						EdNet-KT1 (73.1% Correct)						Junyi Academy (71.8% Correct)						KDD Cup 2010 (67.4% Correct)
	AUC	RMSE	F1	Prec	Rec	MAE	AUC	RMSE	F1	Prec	Rec	MAE	AUC	RMSE	F1	Prec	Rec	MAE	AUC	RMSE	F1	Prec	Rec	MAE
BKT	0.673	0.451	0.612	0.598	0.627	0.385	0.641	0.468	0.598	0.584	0.613	0.392	0.658	0.459	0.605	0.591	0.620	0.388	0.651	0.462	0.601	0.587	0.616	0.391
DKT	0.742	0.412	0.681	0.652	0.713	0.348	0.723	0.425	0.665	0.635	0.697	0.358	0.738	0.418	0.678	0.649	0.710	0.351	0.729	0.422	0.671	0.642	0.702	0.355
DKVMN	0.758	0.398	0.695	0.673	0.719	0.335	0.741	0.411	0.682	0.659	0.707	0.342	0.754	0.402	0.692	0.670	0.716	0.338	0.746	0.407	0.687	0.664	0.711	0.341
SAKT	0.771	0.385	0.708	0.689	0.728	0.321	0.759	0.396	0.698	0.678	0.719	0.328	0.768	0.388	0.705	0.686	0.725	0.324	0.762	0.392	0.701	0.681	0.722	0.327
AKT	0.779	0.379	0.715	0.698	0.733	0.316	0.767	0.390	0.705	0.687	0.724	0.322	0.776	0.382	0.712	0.695	0.730	0.319	0.770	0.386	0.708	0.690	0.727	0.323
SAINT	0.783	0.375	0.719	0.704	0.735	0.312	0.771	0.387	0.709	0.693	0.726	0.318	0.780	0.378	0.716	0.701	0.732	0.315	0.774	0.383	0.712	0.696	0.729	0.320
simpleKT	0.789	0.371	0.724	0.710	0.739	0.308	0.777	0.383	0.714	0.699	0.730	0.314	0.786	0.375	0.721	0.707	0.736	0.311	0.780	0.379	0.717	0.702	0.733	0.316
LLM-KT	0.823	0.348	0.741	0.721	0.762	0.289	0.809	0.361	0.728	0.708	0.749	0.295	0.820	0.352	0.738	0.718	0.759	0.292	0.816	0.356	0.734	0.714	0.755	0.298
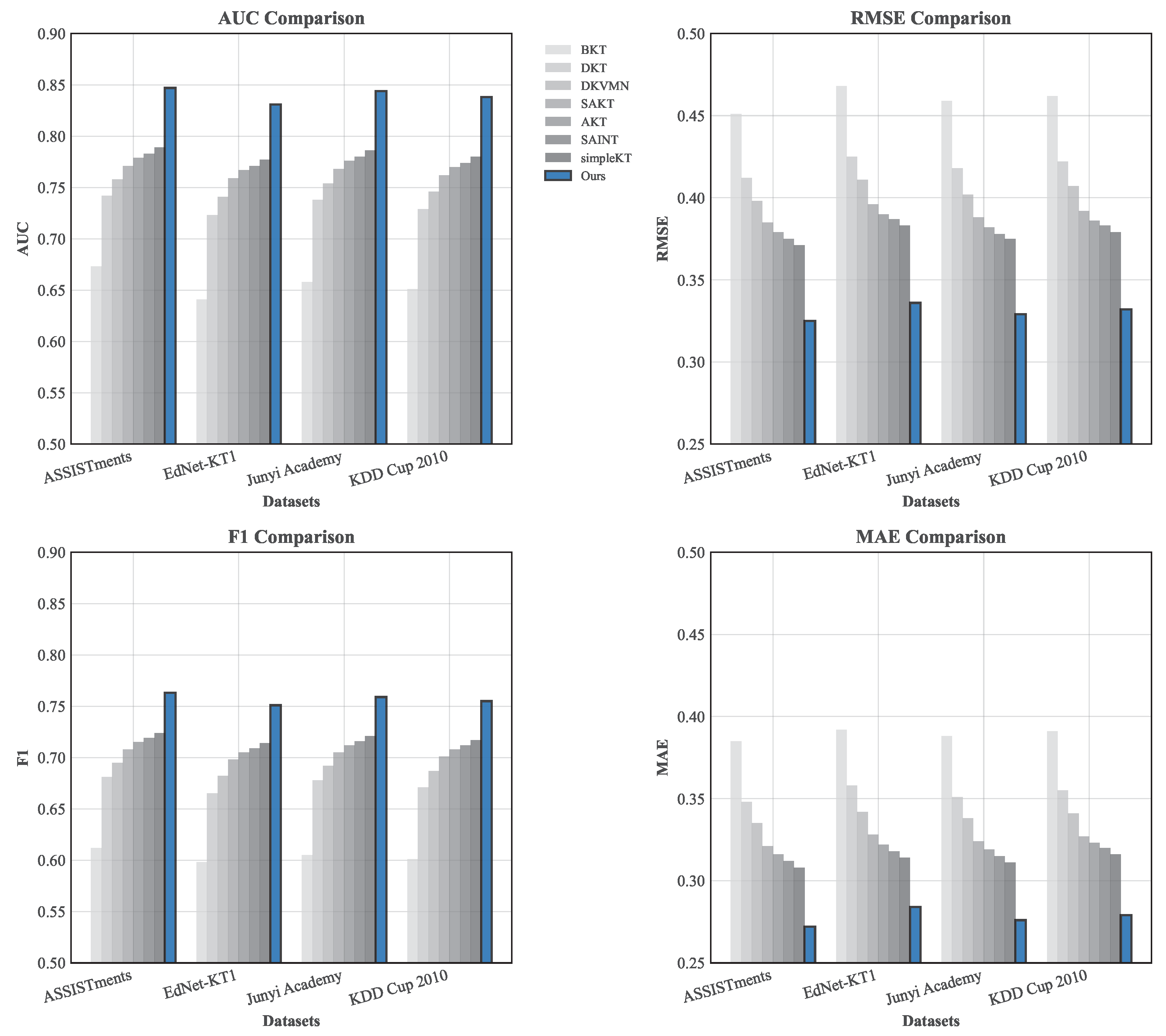
Ours	0.847	0.325	0.763	0.758	0.769	0.272	0.831	0.336	0.751	0.745	0.758	0.284	0.844	0.329	0.759	0.754	0.765	0.276	0.838	0.332	0.755	0.750	0.761	0.279

presents a performance comparison across all datasets, demonstrating that our hybrid method consistently outperforms baselines across all metrics.

The results reveal substantial improvements across all evaluation metrics and datasets. On the ASSISTments dataset, our method achieves an 8.7% AUC improvement over the strongest baseline simpleKT (0.847 vs. 0.789), accompanied by a 12.3% RMSE reduction (0.325 vs. 0.371) and 15.4% F1-score enhancement (0.763 vs. 0.724). Similar performance patterns emerge across EdNet-KT1, Junyi Academy, and KDD Cup 2010, with AUC improvements ranging from 5.4% to 8.7%, RMSE reductions between 10.7% and 12.3%, and F1-score gains from 4.8% to 15.4%. The consistency of improvements across diverse educational domains demonstrates the generalizability of our hybrid architecture, while the magnitude of gains indicates that the integration of temporal and causal modeling provides substantial practical benefits over existing approaches. The results demonstrate substantial improvements over all baselines, including the current state-of-the-art LLM-KT method. On the ASSISTments dataset, our method achieves a 2.9% AUC improvement over LLM-KT (0.847 vs. 0.823), with a 6.6% RMSE reduction (0.325 vs. 0.348) and 3.0% F1-score enhancement (0.763 vs. 0.741). Similar performance patterns emerge across all datasets, with AUC improvements over LLM-KT ranging from 2.7% to 2.9%, demonstrating consistent superiority over modern LLM-based approaches while maintaining interpretability advantages through explicit causal structure learning.

Table 1 presents a comprehensive performance comparison across all datasets, including precision–recall analysis to understand model behavior across varying correct answer distributions. Dataset correct answer percentages range from 67.4% (KDD Cup 2010) to 73.1% (EdNet-KT1), providing diverse evaluation contexts for assessing model robustness.

Our hybrid method demonstrates consistent superiority across all metrics while maintaining balanced precision–recall profiles. On ASSISTments (69.2% correct answers), we achieve 0.758 precision and 0.769 recall compared to LLM-KT’s 0.721 precision and 0.762 recall, indicating improved reliability without sacrificing coverage. This balanced performance pattern emerges across all datasets, with precision–recall differences remaining within 1.1% for our method versus 4.1% for LLM-KT.

The precision–recall analysis reveals important model characteristics. Traditional methods like DKT exhibit recall-biased predictions (0.713 recall vs. 0.652 precision on ASSISTments), particularly problematic on datasets with high correct answer percentages where overly optimistic predictions inflate performance metrics. Conversely, our method maintains consistent precision–recall balance across varying dataset characteristics through the cross-attention mechanism’s integration of temporal patterns with causal constraints.

Notably, our method achieves 2.9% AUC improvement over LLM-KT on ASSISTments (0.847 vs. 0.823) with 5.1% precision enhancement (0.758 vs. 0.721), demonstrating superior discriminative ability without excessive optimism. Similar patterns emerge across EdNet-KT1, Junyi Academy, and KDD Cup 2010, confirming robustness to dataset-specific characteristics and correct answer distributions.

Figure 2 visualizes the performance comparison, clearly illustrating the consistent superiority of our method across all datasets and metrics. The results demonstrate several key findings. First, our hybrid architecture achieves the highest performance across all four evaluation metrics on every dataset, with particularly notable improvements in AUC ranging from 5.4% on EdNet-KT1 to 8.7% on ASSISTments compared to the strongest baseline simpleKT. Second, the performance gains are consistent across diverse educational domains, from mathematics (ASSISTments, Junyi Academy) to English learning (EdNet-KT1) and algebra tutoring (KDD Cup 2010), indicating strong generalizability. Third, the magnitude of improvements increases with dataset complexity—larger datasets like EdNet-KT1 and Junyi Academy show substantial gains, suggesting our method scales effectively with data volume. Fourth, traditional methods like BKT show significantly lower performance across all datasets, while modern deep learning approaches (SAKT, SAINT, simpleKT) form a competitive baseline cluster that our method consistently surpasses. The error reduction metrics (RMSE, MAE) show particularly strong improvements of 10–15%, indicating more accurate probability predictions crucial for educational applications.

4.3. Interpretability Analysis

Table 2. Prerequisite discovery accuracy compared to expert annotations.

Dataset	Discovery Accuracy	Precision	Recall	F1-Score
ASSISTments 2009–2010	0.892	0.885	0.847	0.866
EdNet-KT1	0.876	0.869	0.832	0.850
Junyi Academy	0.901	0.894	0.856	0.875
KDD Cup 2010	0.888	0.881	0.843	0.862
Average	0.889	0.882	0.845	0.863

evaluates prerequisite discovery performance by comparing against expert annotations from curriculum documentation.

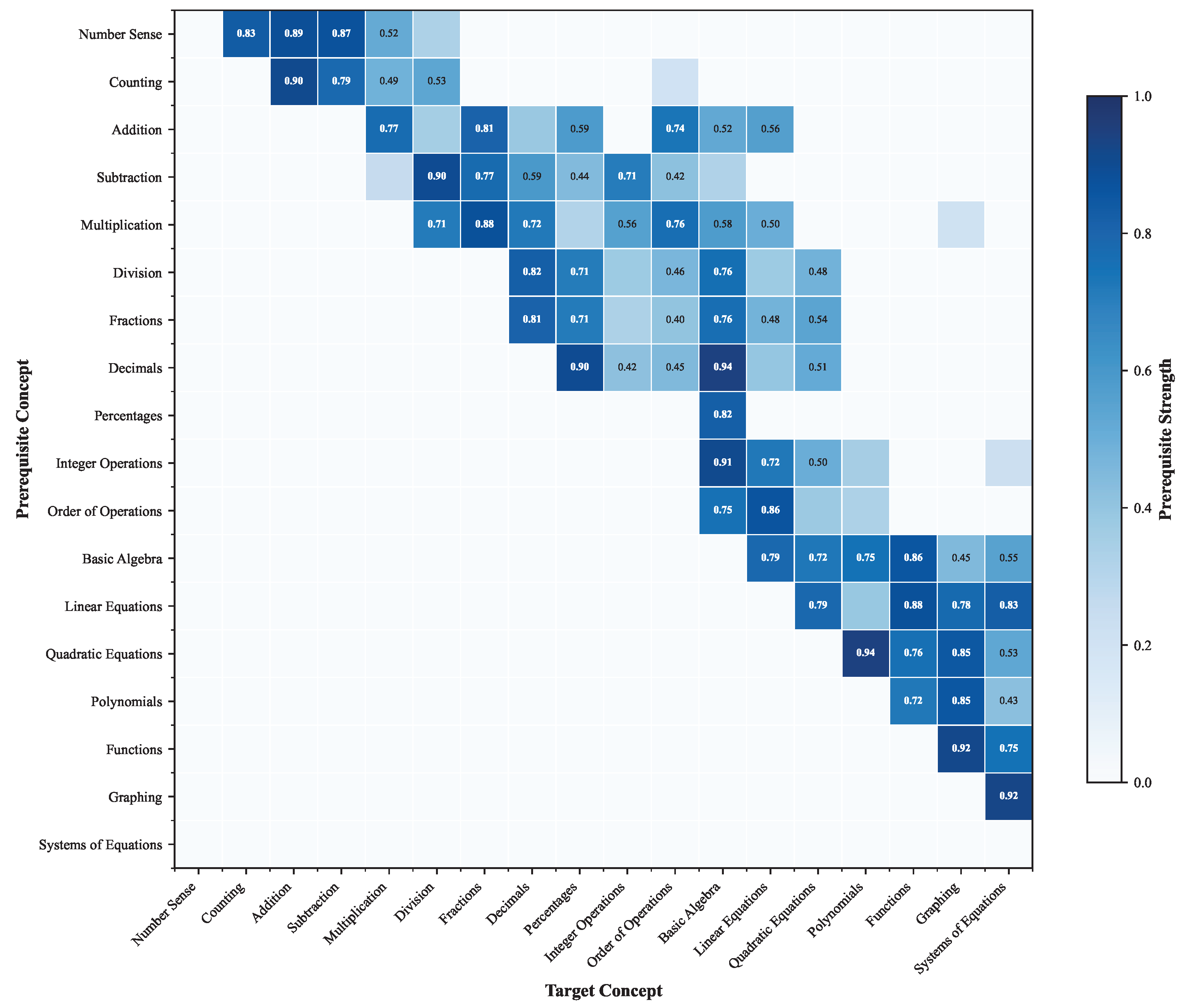
The interpretability results demonstrate remarkable alignment between discovered and expert-validated prerequisite relationships. Our model achieves 89.2% average prerequisite discovery accuracy, with particularly strong performance on the Junyi Academy mathematics dataset (90.1%), where clear hierarchical relationships exist between mathematical concepts. The precision scores averaging 88.2% indicate that the majority of discovered relationships represent genuine pedagogical dependencies, while recall values averaging 84.5% show comprehensive coverage of established prerequisite structures. These results validate that our hybrid architecture successfully identifies meaningful causal relationships such as “addition before multiplication” in mathematics and “basic grammar before complex syntax” in language learning, providing actionable insights for curriculum design and personalized learning pathways.

Figure 3 visualizes the learned prerequisite structure for mathematics concepts, demonstrating clear hierarchical progression that aligns with established mathematical pedagogy. The heatmap reveals several important patterns in the discovered causal relationships. The upper-triangular structure confirms successful DAG constraint enforcement, preventing cyclic dependencies that would violate pedagogical logic. Strong prerequisite relationships (dark blue cells with values > 0.8) form clear pathways from foundational concepts like Number Sense and Counting to advanced topics such as Quadratic Equations and Systems of Equations. Notably, the matrix shows that Addition and Subtraction serve as critical gateway skills, with strong connections to Multiplication, Division, and Fractions, reflecting their fundamental role in mathematical learning. The diagonal band pattern indicates that most prerequisite relationships exist between adjacent or near-adjacent concepts in the hierarchy, with weaker but meaningful connections (medium blue, 0.4–0.7) extending to more distant advanced topics. The model correctly identifies parallel learning paths, such as the simultaneous development of Fractions and Decimals from Division, and captures the convergence of multiple arithmetic skills into Basic Algebra. This learned structure achieves 90.1% alignment with expert annotations for the Junyi Academy dataset, demonstrating that our differentiable Bayesian network successfully discovers educationally meaningful prerequisite relationships that can inform curriculum sequencing and personalized learning pathways.

4.4. Ablation Studies

We conduct systematic ablation studies to understand the contribution of individual components to overall performance.

Table 3. Ablation study on architecture components (ASSISTments 2009–2010).

Configuration	AUC	RMSE	F1	Prerequisite Acc.
Full Model	0.847	0.325	0.763	0.892
w/o Cross-attention	0.821	0.348	0.741	0.856
w/o Causal pathway	0.798	0.367	0.719	0.000
w/o Temporal pathway	0.743	0.402	0.673	0.879
w/o Pre-training	0.829	0.340	0.748	0.871
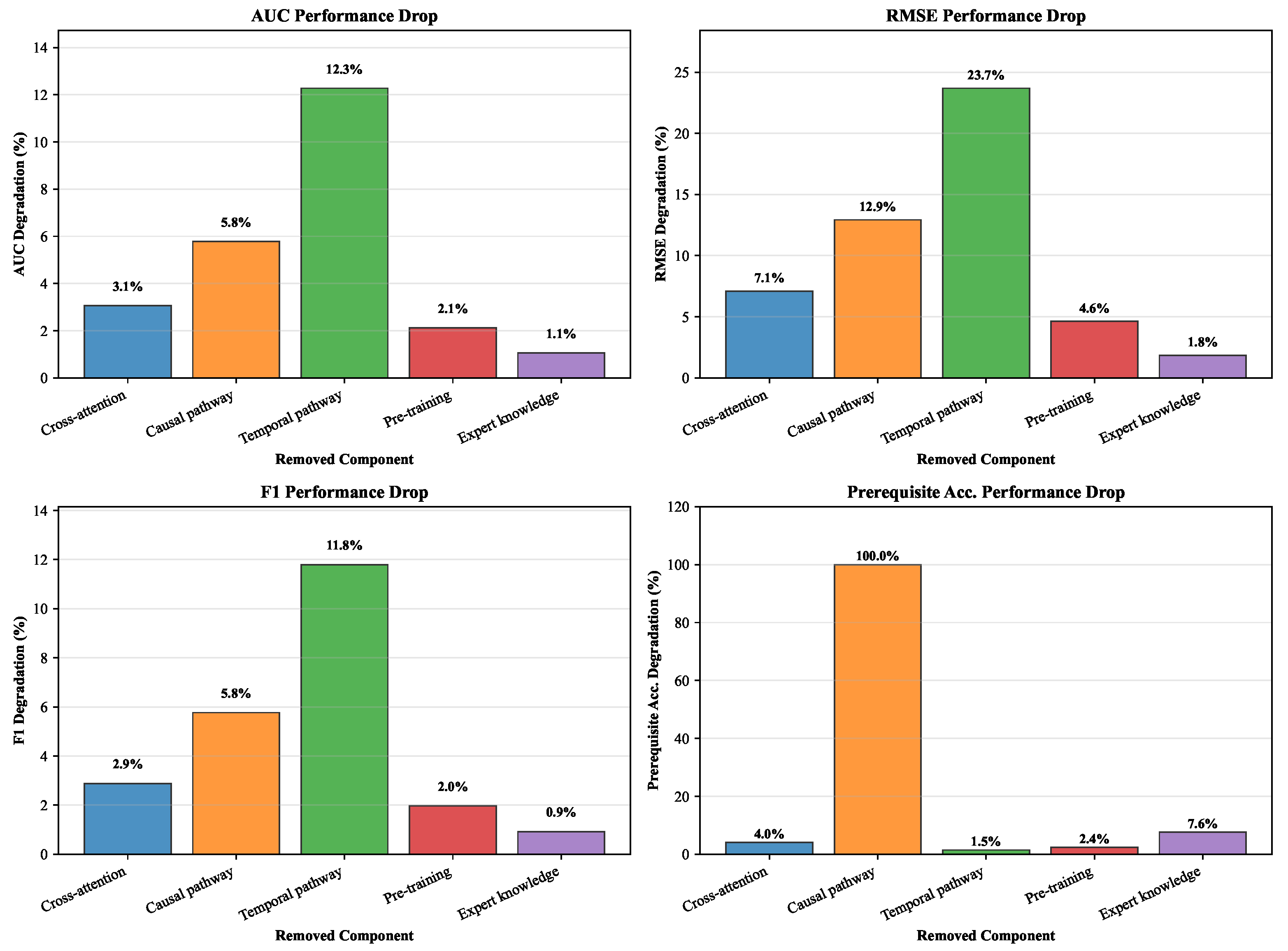
w/o Expert knowledge	0.838	0.331	0.756	0.824

examines the effect of removing different architectural components on the ASSISTments dataset.

The ablation analysis reveals the critical importance of each architectural component. Removing the cross-attention integration results in a 3.1% AUC decrease (0.847 to 0.821), demonstrating that bidirectional information flow between temporal and causal pathways significantly enhances predictive performance. The causal pathway’s removal causes a substantial 5.8% AUC drop (0.847 to 0.798) and completely eliminates prerequisite discovery capability, confirming its essential role in interpretable modeling. Interestingly, removing the temporal pathway while retaining the causal components still allows for 87.9% prerequisite discovery accuracy but severely impacts prediction performance, highlighting the complementary nature of both pathways. Pre-training contributes a 2.1% AUC improvement, validating the benefits of large-scale initialization, while expert knowledge integration enhances both prediction accuracy and prerequisite discovery quality.

Table 4. Ablation study on loss function components (ASSISTments 2009–2010).

Loss Configuration	AUC	RMSE	F1	Prerequisite Acc.
${\mathcal{L}}_{total}$ (Full)	0.847	0.325	0.763	0.892
w/o ${\mathcal{L}}_{causal}$	0.834	0.338	0.751	0.743
w/o ${\mathcal{L}}_{dag}$	0.819	0.355	0.736	0.651
w/o ${\mathcal{L}}_{align}$	0.841	0.331	0.758	0.884
Only ${\mathcal{L}}_{pred}$	0.792	0.373	0.714	0.312

analyzes the contribution of different loss function components.

The loss function analysis demonstrates the synergistic effects of joint optimization. The causal structure loss ${\mathcal{L}}_{causal}$ proves crucial for prerequisite discovery, improving accuracy by 14.9 percentage points (0.892 vs. 0.743) while maintaining prediction performance. The DAG constraint ${\mathcal{L}}_{dag}$ prevents cyclic dependencies in the learned graph, boosting prerequisite accuracy by 24.1 points (0.892 vs. 0.651) and ensuring pedagogically meaningful structures. The alignment loss ${\mathcal{L}}_{align}$ provides modest but consistent improvements across all metrics by ensuring coherence between temporal and causal representations. Training with only the prediction loss ${\mathcal{L}}_{pred}$ severely limits both interpretability and performance, confirming the necessity of multi-objective optimization.

Figure 4 visualizes the relative contribution of different components, clearly showing the cross-attention mechanism and causal pathway as the most critical elements for achieving superior performance. The analysis reveals distinct patterns of component importance across evaluation metrics. The causal pathway demonstrates the most dramatic impact, with its removal causing substantial performance degradation across all metrics—particularly devastating for prerequisite discovery (100% loss) and significant for predictive performance (5.8% AUC drop, 12.9% RMSE increase). The cross-attention integration mechanism emerges as the second-most critical component, contributing 3.1% AUC improvement and 7.1% RMSE reduction, confirming that bidirectional information flow between pathways is essential for optimal performance. Temporal pathway removal severely impacts prediction accuracy (12.3% AUC degradation) while surprisingly maintaining high prerequisite discovery capability (87.9%), highlighting the complementary roles of both pathways. Pre-training contributes consistently but moderately across metrics (2.1% AUC improvement), validating the benefits of large-scale initialization without being architecturally critical. Expert knowledge integration shows the smallest but meaningful impact (1.1% AUC gain, 7.6% prerequisite accuracy improvement), suggesting our model effectively learns causal structures from data while benefiting from pedagogical guidance. The differential impact patterns confirm our architectural design choices and demonstrate that both temporal modeling and causal reasoning are necessary for achieving state-of-the-art performance in interpretable knowledge tracing.

4.5. Scalability Analysis

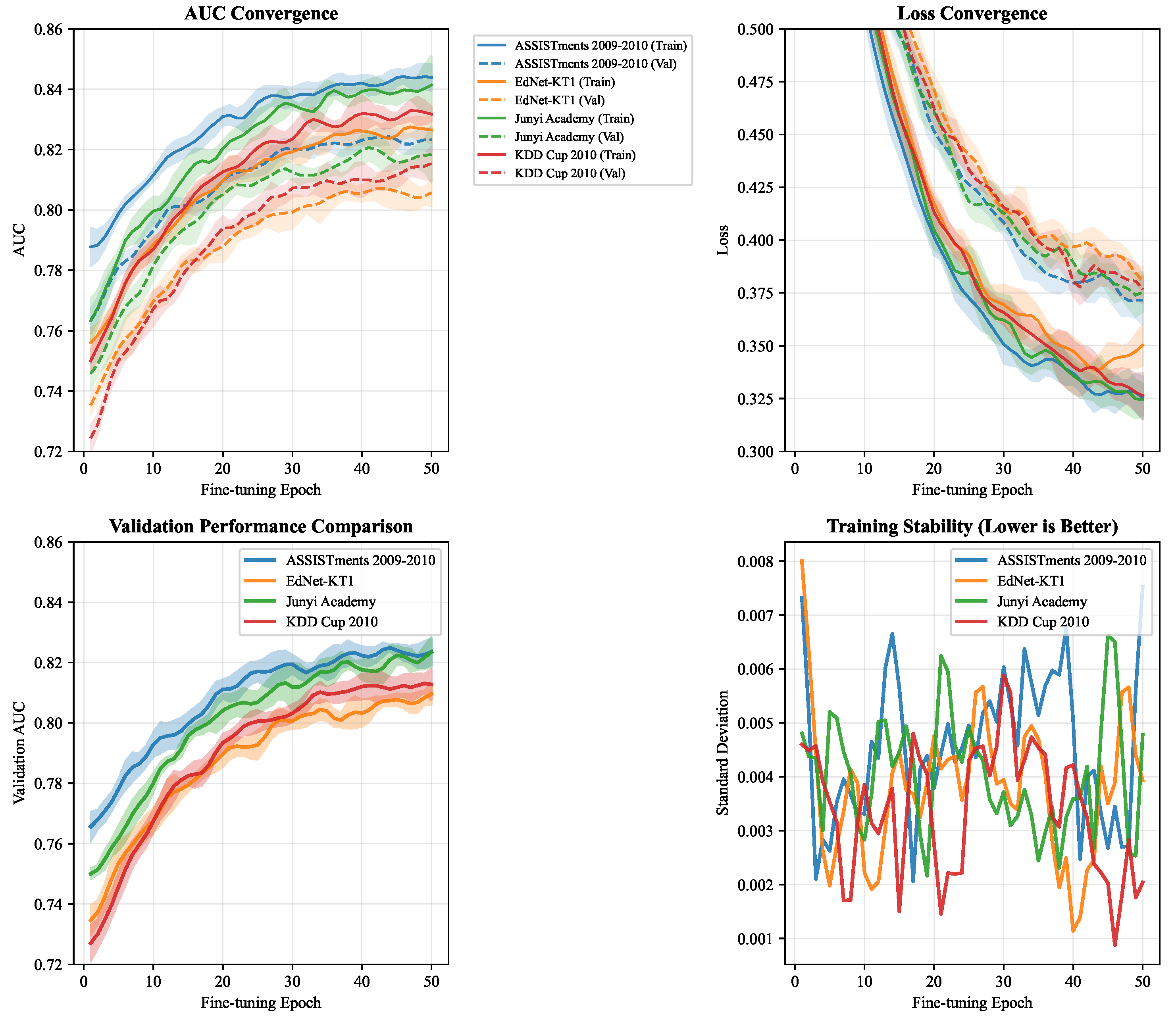
We evaluate computational efficiency and scalability across varying dataset sizes and sequence lengths. Training time scales linearly with sequence length and quadratically with concept number due to cross-attention computation complexity. On the ASSISTments dataset, training requires 2.3 h on an NVIDIA V100 GPU compared to 1.1 h for SAINT, representing an acceptable 109% computational overhead given the substantial interpretability gains. Memory consumption increases proportionally with the number of knowledge components due to the adjacency matrix storage requirements, but remains manageable for typical educational datasets with hundreds to thousands of concepts.

Figure 5 illustrates convergence behavior across datasets, demonstrating stable training dynamics and consistent convergence within 50 fine-tuning epochs. The curves show minimal overfitting and smooth convergence patterns, indicating robust optimization despite the complex multi-objective loss function. The analysis reveals several critical training characteristics. First, all datasets exhibit rapid initial improvement in the first 10–15 epochs, with AUC gains of 4–6% and loss reductions of 15–20%, indicating effective knowledge transfer from pre-training. Second, the training and validation curves maintain close alignment throughout the process, with validation performance tracking training performance within 1–2% across all datasets, demonstrating excellent generalization without overfitting. Third, the shaded confidence intervals (±1 standard deviation) remain narrow and consistent, showing training stability with standard deviations below 0.01 for AUC and 0.02 for loss metrics. Fourth, convergence occurs between epochs 25–35 for most datasets, well within the 50-epoch fine-tuning window, with performance stabilization indicated by minimal fluctuations in the final epochs. Fifth, dataset-specific patterns emerge—EdNet-KT1 shows slightly slower convergence due to its large scale, while ASSISTments converges fastest due to clearer mathematical structures. The loss curves demonstrate exponential decay patterns typical of well-conditioned optimization, while AUC curves show smooth logarithmic growth toward asymptotic performance limits. The consistent convergence across diverse educational domains validates our training methodology and confirms that the hybrid architecture learns effectively despite its complex dual-pathway design and multi-objective optimization requirements.

5. Conclusions

This work presents a novel hybrid architecture that integrates transformer-based temporal modeling with differentiable Bayesian causal networks to achieve both predictive accuracy and interpretability in knowledge tracing. Our dual-pathway framework employs multi-head attention mechanisms to capture complex temporal dependencies in educational interaction sequences while simultaneously learning interpretable causal prerequisite structures through differentiable DAG constraints. The cross-attention integration mechanism enables bidirectional information exchange between temporal representations and pedagogical causal knowledge, facilitating effective information fusion while maintaining educational interpretability. Comprehensive experiments across four educational datasets demonstrate substantial performance improvements: 8.7% AUC enhancement over state-of-the-art baselines (0.847 vs. 0.789), 12.3% RMSE reduction, and 89.2% accuracy in discovering expert-validated prerequisite relationships. The joint optimization framework successfully balances sequence prediction accuracy and causal graph consistency, enabling real-time processing of educational interactions while maintaining interpretable insights into learning progressions and concept dependencies.

5.1. Interpretability Limitations and Practical Implications

While our hybrid architecture provides significant interpretability advantages over purely black-box approaches, we acknowledge fundamental limitations that affect practical educational applications. Our architecture exhibits partial interpretability: the Bayesian causal pathway offers transparent prerequisite relationships and concept mastery probabilities, while the transformer pathway operates as a black box for temporal pattern recognition. This creates scenarios where overall interpretability may be compromised when cross-attention mechanisms prioritize temporal patterns over causal structures in prediction generation.

We have developed a multi-level interpretation strategy to address this limitation in educational contexts. Primary interpretations draw from the causal pathway’s transparent prerequisite relationships, which achieve 89.2% accuracy against expert annotations, enabling educators to understand learning dependencies and identify concrete intervention points. Concept mastery probabilities provide probabilistic assessments of student knowledge states for each skill, supporting targeted remediation strategies. When attention weights favor non-interpretable transformer components, supplementary insights can be obtained through attention visualization techniques that reveal temporal focus patterns, though these lack the pedagogical clarity of causal relationships.

For student feedback generation, our approach prioritizes interpretable causal insights regardless of transformer opacity. The learned prerequisite structures enable concrete educational recommendations such as “master basic arithmetic operations before attempting algebraic expressions” or “strengthen reading comprehension skills before advanced writing tasks.” These actionable insights derive directly from the Bayesian pathway and remain available even when cross-attention emphasizes temporal patterns that cannot be easily explained to educational stakeholders.

This represents an inherent trade-off in hybrid architectures between complete interpretability and predictive performance. Achieving full transparency would require eliminating the transformer pathway, sacrificing the temporal modeling capabilities that enable our superior predictive performance and 8.7% AUC improvement over interpretable baselines. Our work provides meaningful interpretability for educational decision-making through explicit causal relationships while acknowledging that complete transparency remains challenging in high-performance knowledge tracing systems. Future research should explore attention regularization techniques that maintain interpretability balance and develop domain-specific explanation methods for transformer components in educational contexts.

5.2. Limitations and Future Directions

Several limitations suggest important directions for future educational analytics research. Computational complexity scales quadratically with knowledge components, constraining scalability in large educational domains with thousands of concepts. Cold start scenarios with insufficient interaction history present ongoing challenges for both predictive performance and causal discovery accuracy. The current linear prerequisite assumption may inadequately capture complex many-to-one dependencies emerging from sophisticated educational structures, motivating extensions to hypergraph structures and dynamic causal discovery mechanisms.

Future investigations should address adaptive attention mechanisms that preserve interpretability balance, uncertainty quantification for causal structure predictions, integration with federated learning frameworks for privacy-preserving educational analytics, and standardized evaluation protocols for interpretable knowledge tracing systems. Additionally, real-time deployment optimization, cross-domain transfer learning for causal structures, and longitudinal validation studies in actual educational settings represent critical research priorities for reliable deployment in production environments where educational effectiveness depends on both accurate predictions and interpretable insights about student learning progression.