Predictive Modeling for Carbon Footprint Optimization of Prestressed Road Flyovers
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study: Description of the Lightweight Prestressed Slab Bridge
2.2. Inputs and Carbon Inventory
2.3. Sampling and Optimization Strategy
2.4. Surrogate Models
2.4.1. Radial Basis Functions
2.4.2. Kriging Metamodel
2.4.3. Artificial Neural Networks
2.4.4. Gaussian Process Regression
2.5. Model Evaluation Metrics
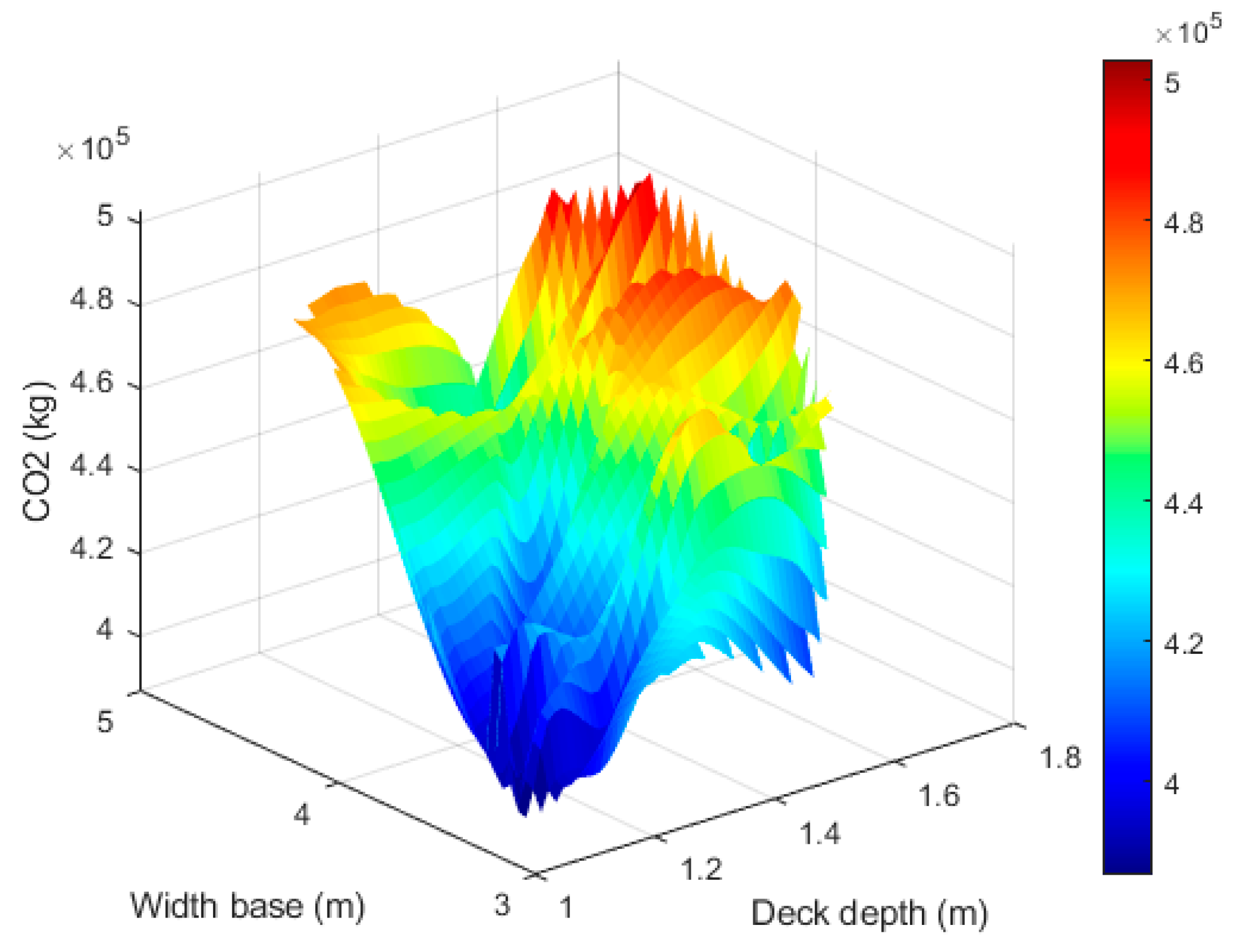
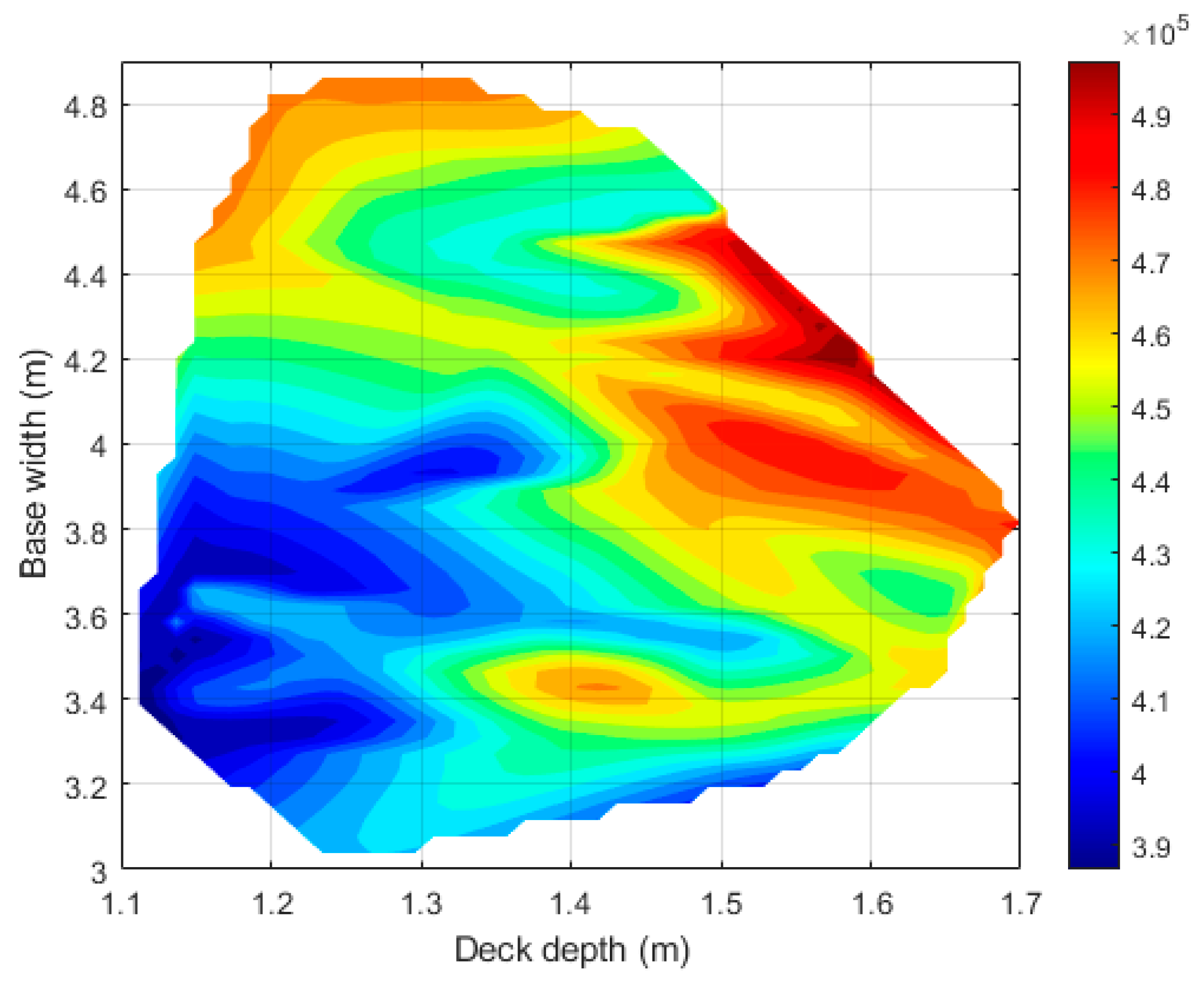
3. Results
4. Discussion
4.1. Comparison with Previous Studies
4.2. Surrogate Model Performance
4.3. Practical Design Recommendations
4.4. Limitations and Future Work
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alhorr, Y.; Eliskandarani, E.; Elsarrag, E. Approaches to reducing carbon dioxide emissions in the built environment: Low carbon cities. Int. J. Sustain. Built Environ. 2014, 3, 167–178. [Google Scholar] [CrossRef]
- World Green Building Council (WGBC). How We Are #Building the Transition to Support the Sustainable Development Goals. 2023. Available online: https://worldgbc.org/wp-content/uploads/2023/09/Buildings-SDG-graphic-1.pdf (accessed on 23 July 2025).
- Gursel, A.P.; Masanet, E.; Horvath, A.; Stadel, A. Life-cycle inventory analysis of concrete production: A critical review. Cem. Concr. Compos. 2014, 51, 38–48. [Google Scholar] [CrossRef]
- Opoku, D.G.J.; Agyekum, K.; Ayarkwa, J. Drivers of environmental sustainability of construction projects: A thematic analysis of verbatim comments from built environment consultants. Int. J. Constr. Manag. 2022, 22, 1033–1041. [Google Scholar] [CrossRef]
- Halder, A.; Batra, S. Application of predictive analytics in built environment research: A comprehensive bibliometric study to explore knowledge domains and future research agenda. Arch. Comput. Methods Eng. 2023, 30, 4299–4324. [Google Scholar] [CrossRef]
- Salah, M.; Alabdullatief, A. Architecture of tomorrow: The construction industry in the era of artificial intelligence. Autom. Constr. 2025, 178, 106429. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Boquera, L.; Chàfer, M.; Vérez, D. Embodied energy and embodied carbon of structural building materials: Worldwide progress and barriers through literature map analysis. Energy Build. 2021, 231, 110612. [Google Scholar] [CrossRef]
- Hasan, S.M.; Mashud, A.H.M.; Miah, S.; Daryanto, Y.; Lim, M.K.; Tseng, M.L. A green inventory model considering environmental emissions under carbon tax, cap-and-offset, and cap-and-trade regulations. J. Ind. Prod. Eng. 2023, 40, 538–553. [Google Scholar] [CrossRef]
- Konstandakopoulou, F.; Tsimirika, M.; Pnevmatikos, N.; Hatzigeorgiou, G.D. Optimization of reinforced concrete retaining walls designed according to European provisions. Infrastructures 2020, 5, 46. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Yang, J.; Chen, S.; Liu, H.; Zhao, J. Lightweight design method of orthotropic steel bridge deck with U-ribs based on multi-objective optimization. Ain Shams Eng. J. 2024, 15, 102414. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Roy, D.; Chakrabortty, R.K.; Tseng, M.L.; Pervin, M. An optimum balance among the reduction in ordering cost, product deterioration and carbon emissions: A sustainable green warehouse. Environ. Sci. Pollut. Res. 2022, 29, 78029–78051. [Google Scholar] [CrossRef] [PubMed]
- Ni, W.; Shu, J. Trade-off between service time and carbon emissions for safety stock placement in multi-echelon supply chains. Int. J. Prod. Res. 2015, 53, 6701–6718. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Moradi, S.; Burton, H.V. Performance-Based Design Optimization of Structures: State-of-the-Art Review. J. Struct. Eng. 2024, 150, 03124001. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Martí, P. Robust design optimization using Kriging models: Application to the robust design optimization of truss structures. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2014, 30, 97–105. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. Embodied energy optimization of prestressed concrete road flyovers by a two-phase Kriging surrogate model. Materials 2023, 16, 6767. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. Surrogate-assisted cost optimization for post-tensioned concrete slab bridges. Infrastructures 2025, 10, 43. [Google Scholar] [CrossRef]
- YiFei, L.; MaoSen, C.; Hoa, T.N.; Khatir, S.; Minh, H.L.; SangTo, T.; Cuong-Le, T.; Wahab, M.A. Metamodel-assisted hybrid optimization strategy for model updating using vibration response data. Adv. Eng. Softw. 2023, 185, 103515. [Google Scholar] [CrossRef]
- Sánchez-Zabala, V.F.; Gómez-Acebo, T. Building energy performance metamodels for district energy management optimization platforms. Energy Convers. Manag. X 2024, 21, 100512. [Google Scholar] [CrossRef]
- Neto, T.F.C.; Cascudo, O. Prediction of natural carbonation depths in concretes with ensemble metamodel based on artificial neural networks from time series analysis with 20 years of exposure. J. Build. Eng. 2025, 111, 113352. [Google Scholar] [CrossRef]
- Martí-Vargas, J.R.; Ferri, F.J.; Yepes, V. Prediction of the transfer length of prestressing strands with neural networks. Comput. Concr. 2013, 12, 187–209. [Google Scholar] [CrossRef]
- Nayak, S.C.; Dehuri, S.; Cho, S.B. An evolutionary functional link artificial neural network for assessment of compressive strength of concrete structures. Ain Shams Eng. J. 2024, 15, 102462. [Google Scholar] [CrossRef]
- Zheng, S.; Li, Z.; Wang, H. A Genetic Fuzzy Radial Basis Function Neural Network for Structural Health Monitoring of Composite Laminated Beams. Expert Syst. Appl. 2011, 38, 11837–11842. [Google Scholar] [CrossRef]
- Machavaram, R.; Shankar, K. Structural Damage Identification Using Improved RBF Neural Networks in Frequency Domain. Adv. Struct. Eng. 2012, 15, 1689–1703. [Google Scholar] [CrossRef]
- Saida, T.; Rashid, M.; Nishio, M. System Fragility Analysis of Highway Bridge Using Multi-Output Gaussian Process Regression Surrogate Model. Adv. Struct. Eng. 2024, 27, 2803–2822. [Google Scholar] [CrossRef]
- da Silva, S.; Figueiredo, E.; Moldovan, I. Damage Detection Approach for Bridges under Temperature Effects Using Gaussian Process Regression Trained with Hybrid Data. J. Bridge Eng. 2022, 27, 04022107. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 emission optimization of precast-prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Automation Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Alcalá, J.; Pérez-López, E. Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges. Eng. Struct. 2015, 92, 112–122. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V. Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- Suwondo, R.; Keintjem, M.; Suangga, M.; Cunningham, L. Assessing embodied carbon and financial implications in concrete T-girder bridge design for cost-effective sustainability. Innov. Infrastruct. Solut. 2024, 9, 136. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. An optimization-LCA of a prestressed concrete precast bridge. Sustainability 2018, 10, 685. [Google Scholar] [CrossRef]
- Kim, B.-S.; Lee, Y.-B.; Choi, D.-H. Comparison study on the accuracy of metamodeling technique for non-convex functions. J. Mech. Sci. Technol. 2009, 23, 1175–1181. [Google Scholar] [CrossRef]
- Li, Y.F.; Ng, S.H.; Xie, M. A systematic comparison of metamodeling techniques for simulation optimization in decision support systems. Appl. Soft Comput. 2010, 10, 1257–1273. [Google Scholar] [CrossRef]
- Ryberg, A. Metamodel-Based Design Optimization—A Multidisciplinary Approach for Automotive Structures. 2013. Available online: https://liu.diva-portal.org/smash/get/diva2:601789/FULLTEXT01.pdf (accessed on 19 June 2025).
- Jin, R.; Chen, W.; Simpson, T. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Elwy, I.; Hagishima, A. The artificial intelligence reformation of sustainable building design approach: A systematic review on building design optimization methods using surrogate models. Energy Build. 2024, 323, 114769. [Google Scholar] [CrossRef]
- Catalonia Institute of Construction Technology. BEDEC PR/PCT ITEC Materials Database. Barcelona, Spain. Available online: http://www.itec.cat (accessed on 29 January 2025).
- Lophaven, N.S.; Nielsen, H.B.; Søndergaard, J. MATLAB Kriging Toolbox DACE (Design and Analysis of Computer Experiments) Version 2.0. 2002. Available online: http://www2.imm.dtu.dk/pubdb/p.php?1460 (accessed on 22 May 2025).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial basis functions. Acta Numer. 2000, 9, 1–38. [Google Scholar] [CrossRef]
- Cressie, N. The origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L.; PDP Research Group. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1: Foundations; MIT Press: Cambridge, UK, 1986. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox User’s Guide; The MathWorks: Natick, MA, USA, 2017; p. 512. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Satria Palar, P.; Rizki Zuhal, L.; Shimoyama, K. Gaussian process surrogate model with composite kernel learning for engineering design. AIAA J. 2020, 58, 1864–1880. [Google Scholar] [CrossRef]
- Kianifar, M.R.; Campean, F. Performance evaluation of metamodelling methods for engineering problems: Towards a practitioner guide. Struct. Multidiscip. Optim. 2020, 61, 159–186. [Google Scholar] [CrossRef]
- Dirección General de Carreteras. Obras de Paso de Nueva Construcción: Conceptos Generales; Ministerio de Fomento, Centro de Publicaciones: Madrid, Spain, 2000. [Google Scholar]
- SETRA. Ponts-Dalles. Guide de Conception; Ministère de l’Équipement, du Logement des Transports et de la Mer: Paris, France, 1989. [Google Scholar]
- Manterola, J. Puentes: Apuntes para su Diseño, Cálculo y Construcción; Colegio de Ingenieros de Caminos, Canales y Puertos: Madrid, Spain, 2006. [Google Scholar]
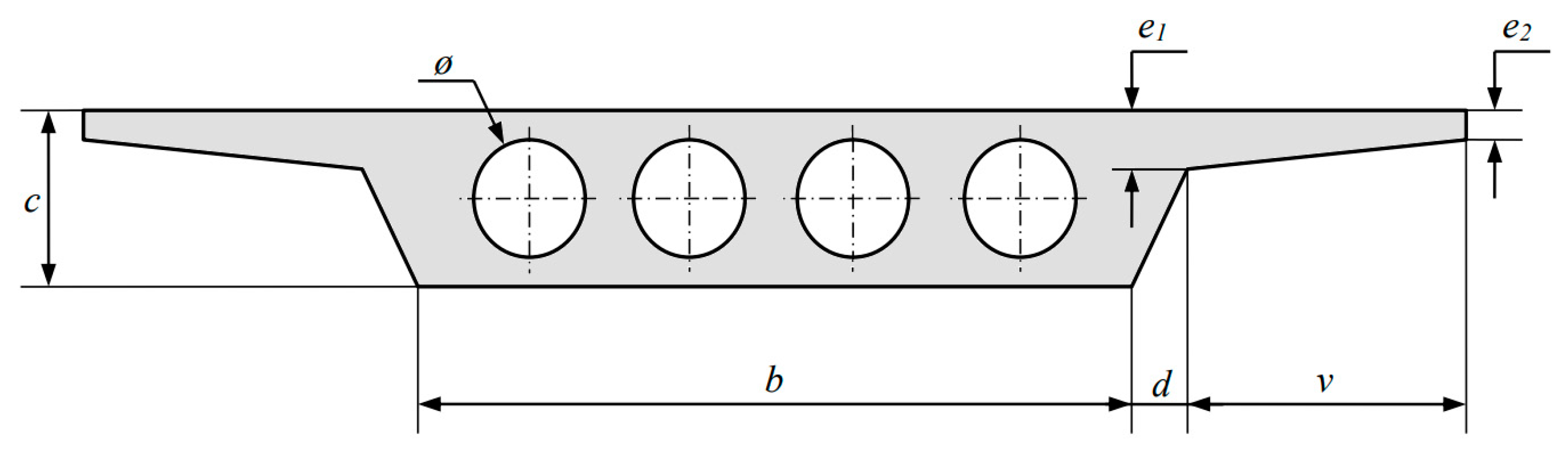
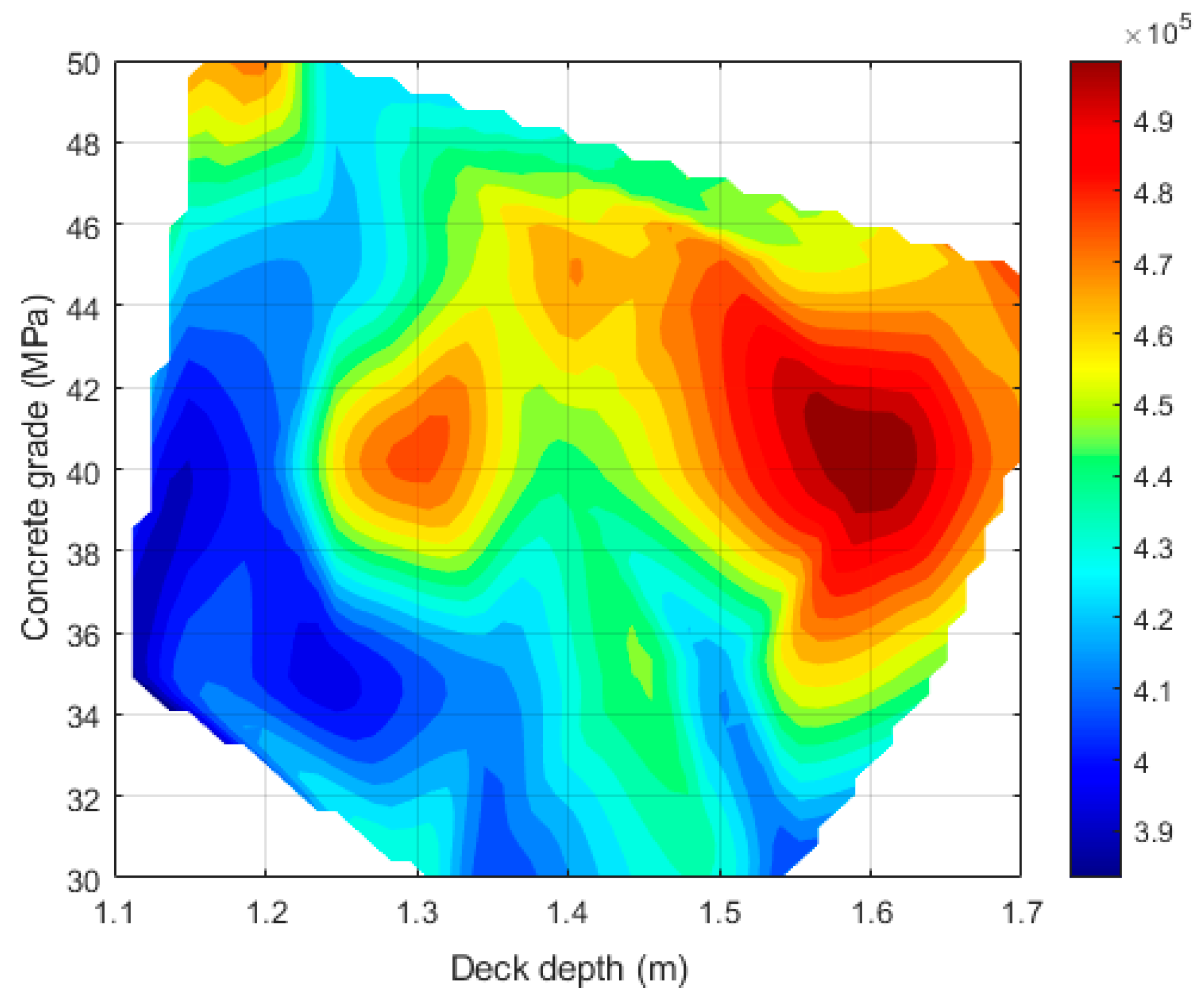
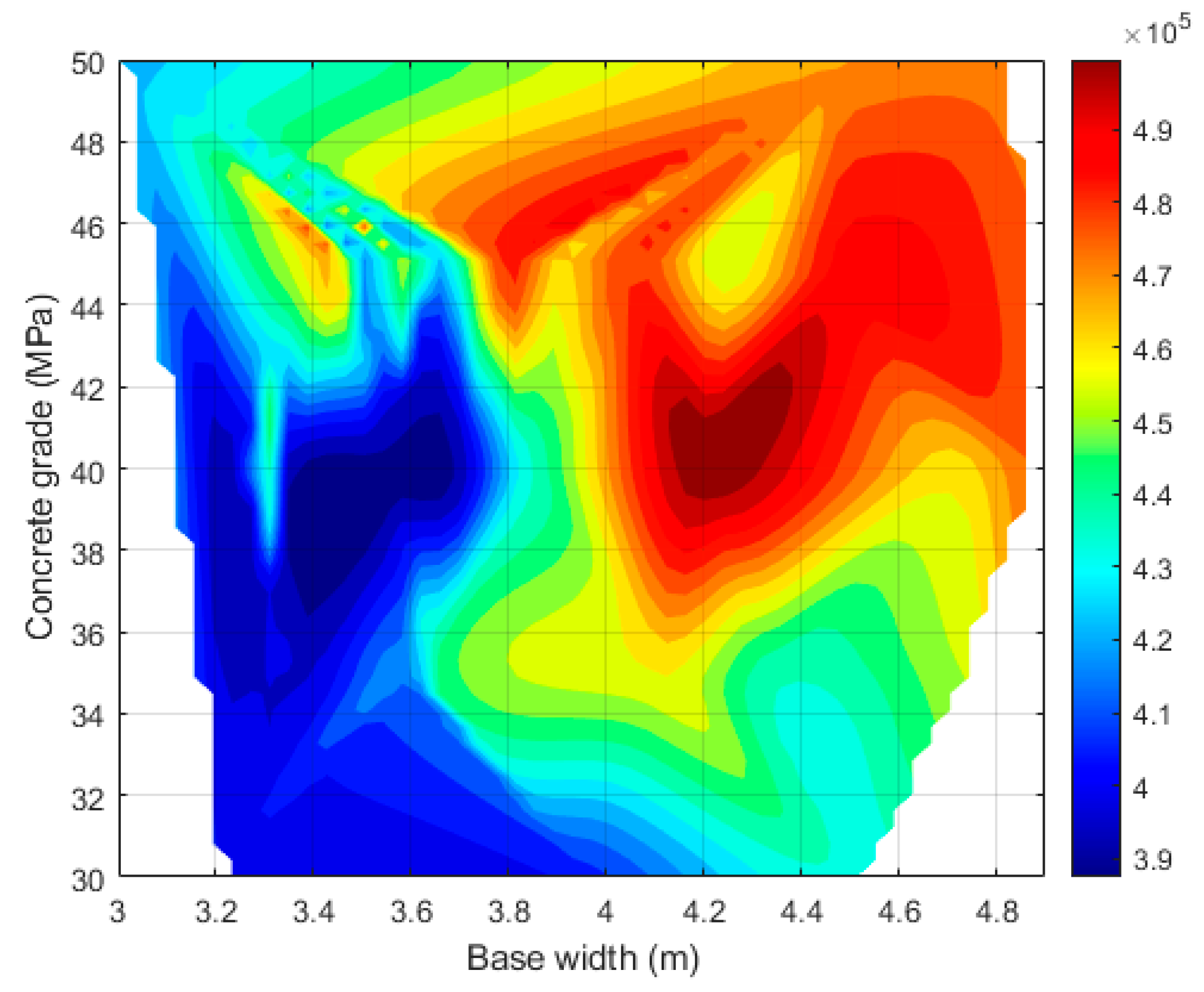
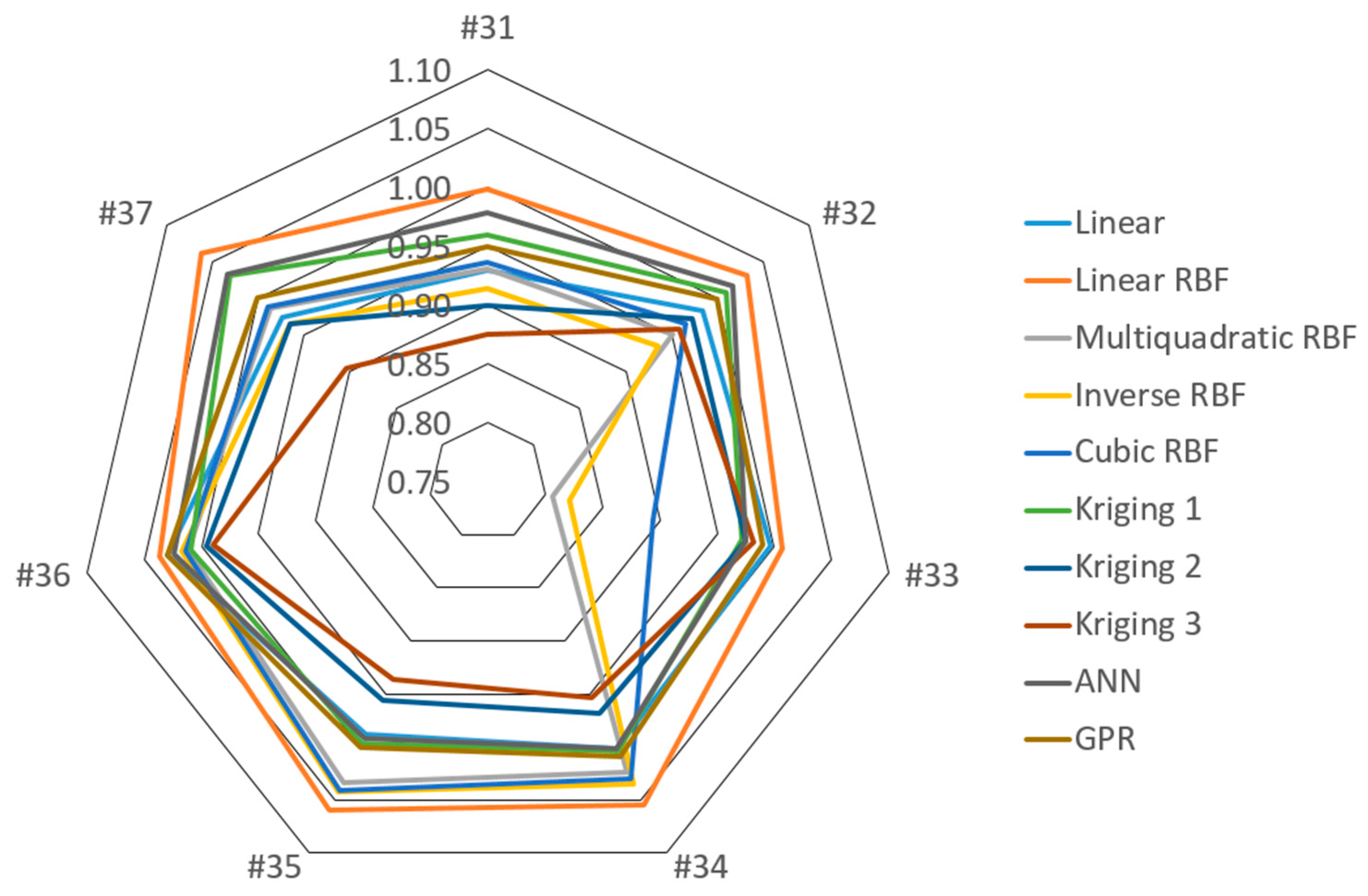
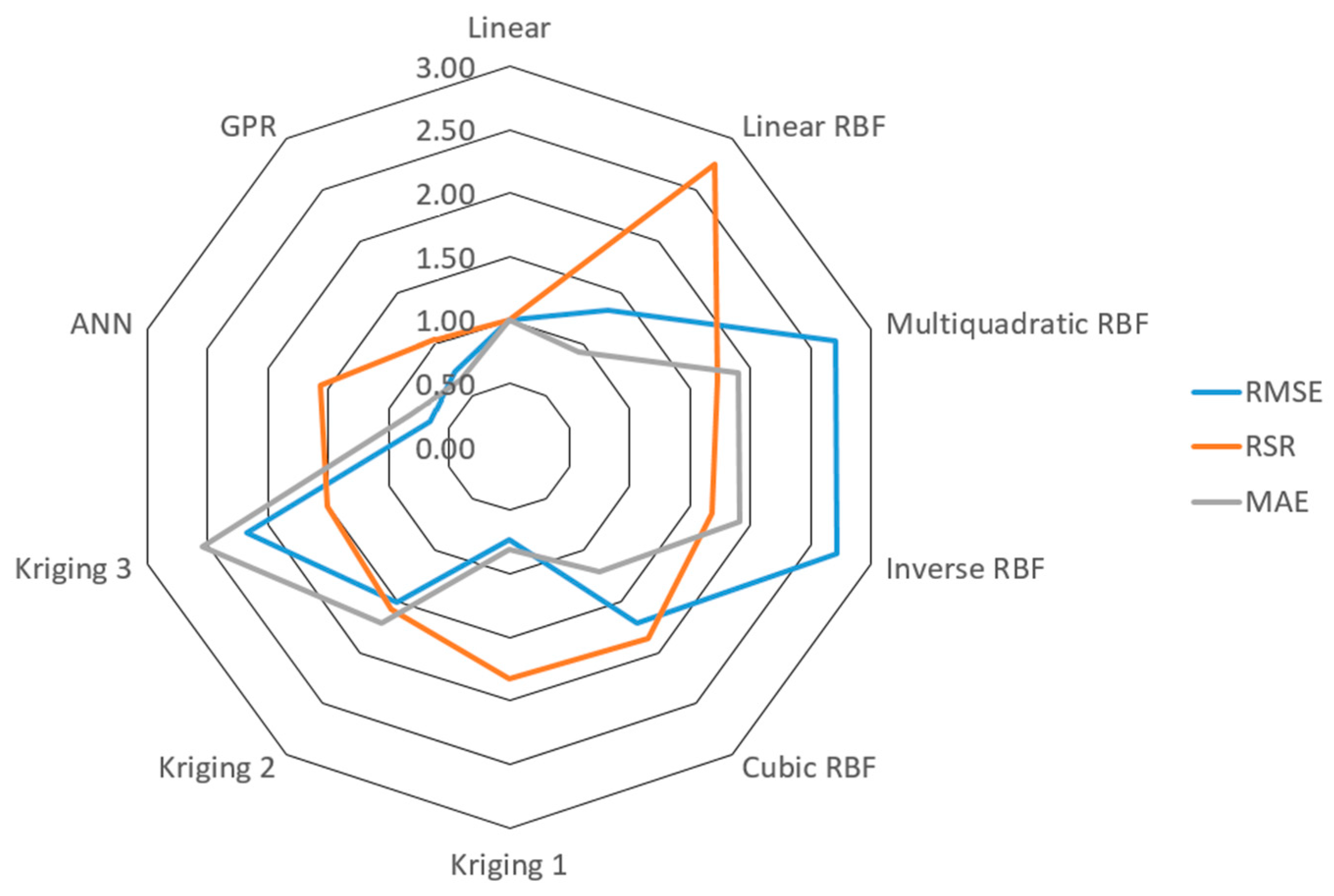
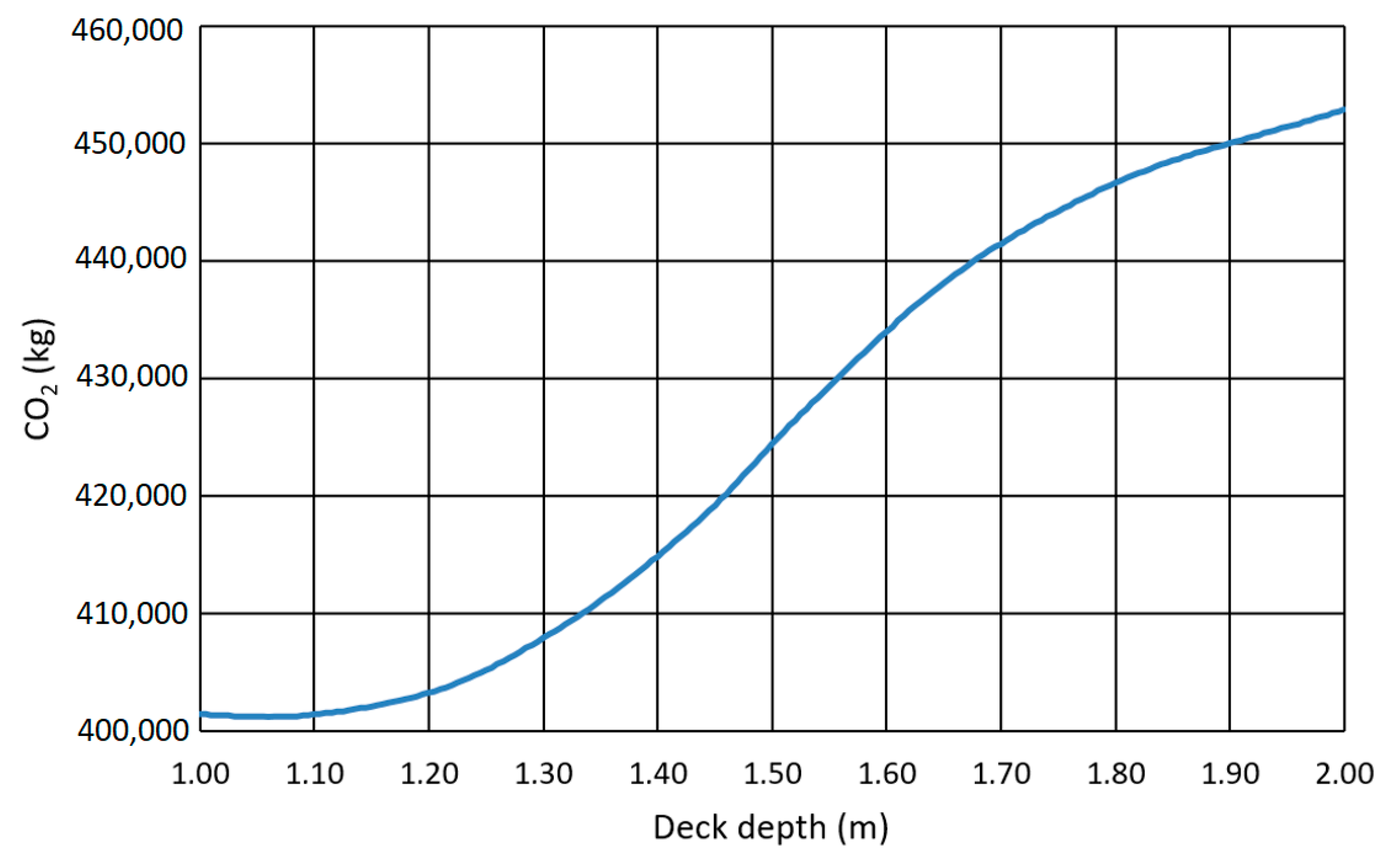

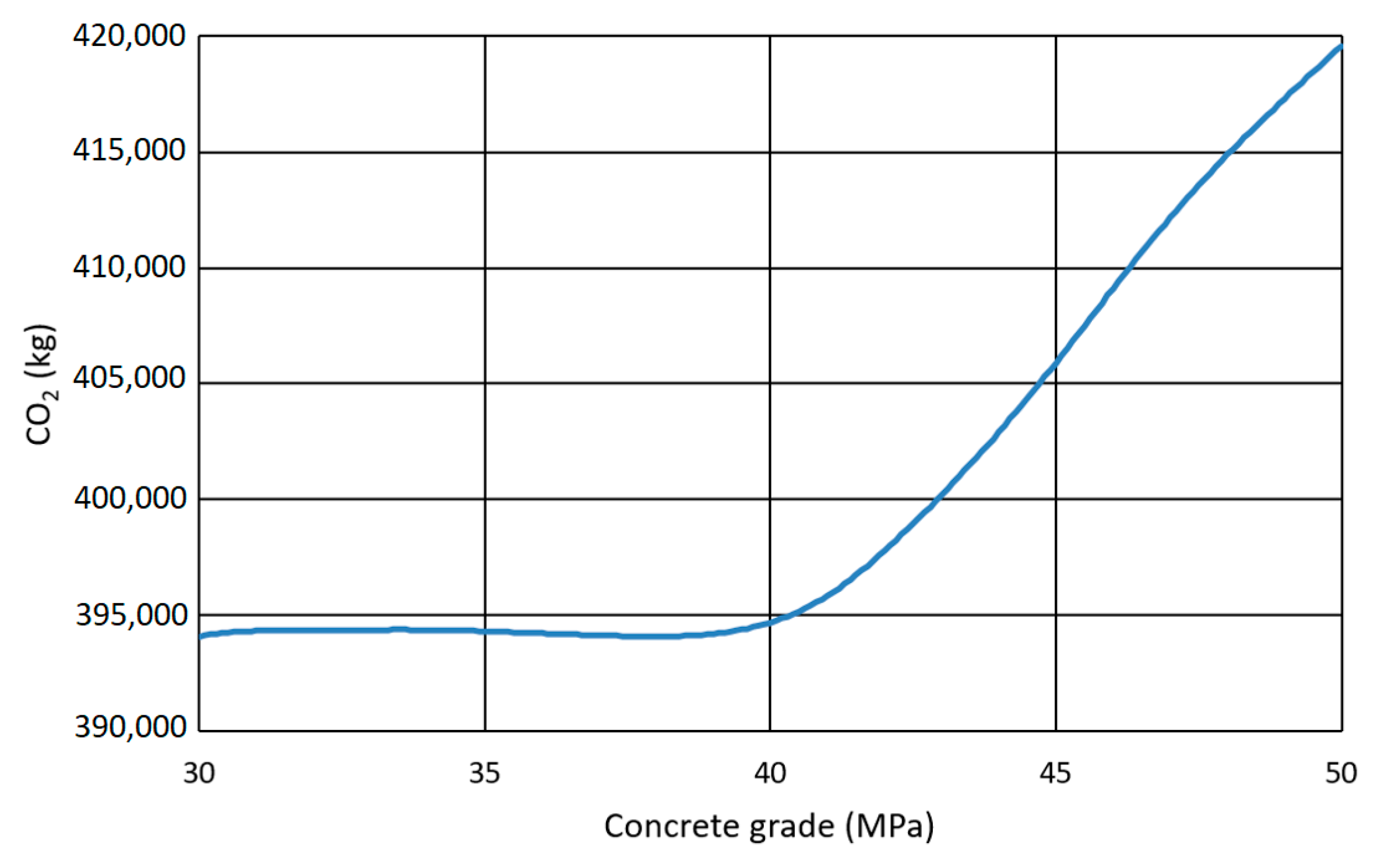
| Deck Unit | Unit | CO2 (kg) |
|---|---|---|
| C-30 concrete | m3 | 227.01 |
| C-35 concrete | m3 | 263.96 |
| C-40 concrete | m3 | 298.57 |
| C-45 concrete | m3 | 330.25 |
| C-50 concrete | m3 | 358.97 |
| Steel reinforcement | kg | 3.03 |
| Steel prestressed | kg | 5.64 |
| Formwork | m2 | 2.24 |
| Voids | m3 | 604.42 |
| Deck | Deck Depth (m) | Base Width (m) | Concrete Grade (MPa) | CO2 (kg) |
|---|---|---|---|---|
| 1 | 1.45 | 4.35 | 35 | 439,416 |
| 2 | 1.55 | 4.10 | 35 | 460,393 |
| 3 | 1.45 | 4.75 | 35 | 455,722 |
| 4 | 1.70 | 3.80 | 45 | 484,897 |
| 5 | 1.20 | 3.85 | 40 | 407,988 |
| 6 | 1.55 | 3.60 | 45 | 456,668 |
| 7 | 1.20 | 4.85 | 50 | 472,401 |
| 8 | 1.15 | 4.50 | 50 | 471,362 |
| 9 | 1.35 | 3.95 | 30 | 406,654 |
| 10 | 1.30 | 4.45 | 30 | 436,703 |
| 11 | 1.35 | 4.25 | 45 | 455,374 |
| 12 | 1.50 | 4.55 | 30 | 434,674 |
| 13 | 1.60 | 4.20 | 40 | 503,797 |
| 14 | 1.25 | 4.70 | 40 | 462,915 |
| 15 | 1.50 | 4.05 | 45 | 482,659 |
| 16 | 1.30 | 4.90 | 40 | 477,491 |
| 17 | 1.65 | 3.65 | 35 | 444,714 |
| 18 | 1.65 | 3.45 | 45 | 464,051 |
| 19 | 1.25 | 3.50 | 45 | 420,514 |
| 20 | 1.40 | 3.30 | 40 | 443,840 |
| 21 | 1.45 | 3.90 | 45 | 464,536 |
| 22 | 1.35 | 3.60 | 35 | 416,584 |
| 23 | 1.50 | 3.35 | 45 | 455,442 |
| 24 | 1.50 | 4.50 | 45 | 490,669 |
| 25 | 1.55 | 3.20 | 30 | 403,972 |
| 26 | 1.25 | 3.00 | 50 | 423,112 |
| 27 | 1.40 | 3.45 | 45 | 470,008 |
| 28 | 1.50 | 3.55 | 35 | 418,839 |
| 29 | 1.70 | 3.85 | 40 | 468,898 |
| 30 | 1.15 | 3.70 | 40 | 394,616 |
| 31 | 1.15 | 3.40 | 35 | 411,077 |
| 32 | 1.25 | 3.35 | 35 | 398,614 |
| 33 | 1.15 | 3.65 | 45 | 422,934 |
| 34 | 1.15 | 3.35 | 40 | 395,465 |
| 35 | 1.15 | 3.25 | 40 | 397,154 |
| 36 | 1.15 | 3.55 | 40 | 391,370 |
| 37 | 1.10 | 3.40 | 35 | 386,515 |
| Objective Function | Slab Height (m) | Span/Deck Depth | Concrete (m3/m2) | Passive Steel (kg/m2) | Active Steel (kg/m2) |
|---|---|---|---|---|---|
| Reference | 1.35 | 25.19 | 0.72 | 73.45 | 16.64 |
| Cost | 1.30 | 26.15 | 0.61 | 73.53 | 14.76 |
| CO2 | 1.10 | 30.91 | 0.56 | 77.00 | 16.48 |
| Energy | 1.15 | 29.57 | 0.61 | 69.41 | 16.65 |
| Local Optima | Relative Error (%) | |||
|---|---|---|---|---|
| #36 | #37 | #36 | #37 | |
| Observed | 391,370 | 386,515 | 0.00 | 0.00 |
| Linear | 402,802 | 376,571 | 2.92 | −2.57 |
| Linear RBF | 405,515 | 410,217 | 3.61 | 6.13 |
| Multiquadratic RBF | 395,904 | 381,208 | 1.16 | −1.37 |
| Inverse multiquadratic RBF | 397,924 | 373,258 | 1.67 | −3.43 |
| Cubic RBF | 396,853 | 382,225 | 1.40 | −1.11 |
| Kriging 1 | 394,808 | 398,496 | 0.88 | 3.10 |
| Kriging 2 | 389,612 | 373,195 | −0.45 | −3.45 |
| Kriging 3 | 387,247 | 349,638 | −1.05 | −9.54 |
| ANN average | 400,619 | 399,219 | 2.36 | 3.29 |
| GPR average | 403,150 | 386,880 | 3.01 | 0.09 |
| Predictive Models | RMSE | RSR | MAE | Rank (RMSE-RSR-MAE) |
|---|---|---|---|---|
| Linear | 12,652 | 0.87 | 9012 | 4-1-4 |
| Linear RBF | 16,793 | 2.38 | 14,193 | 5-10-5 |
| Multiquadratic RBF | 34,182 | 1.50 | 23,144 | 9-7-9 |
| Inverse multiquadratic RBF | 34,439 | 1.45 | 26,686 | 10-6-10 |
| Cubic RBF | 21,773 | 1.62 | 17,433 | 7-9-7 |
| Kriging 1 | 9235 | 1.59 | 7236 | 2-8-2 |
| Kriging 2 | 19,189 | 1.37 | 15,428 | 6-5-6 |
| Kriging 3 | 27,612 | 1.31 | 22,926 | 8-3-8 |
| ANN average | 8372 | 1.36 | 7356 | 1-4-3 |
| GPR average | 9246 | 0.90 | 5873 | 3-2-1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yepes-Bellver, L.; Alcalá, J.; Yepes, V. Predictive Modeling for Carbon Footprint Optimization of Prestressed Road Flyovers. Appl. Sci. 2025, 15, 9591. https://doi.org/10.3390/app15179591
Yepes-Bellver L, Alcalá J, Yepes V. Predictive Modeling for Carbon Footprint Optimization of Prestressed Road Flyovers. Applied Sciences. 2025; 15(17):9591. https://doi.org/10.3390/app15179591
Chicago/Turabian StyleYepes-Bellver, Lorena, Julián Alcalá, and Víctor Yepes. 2025. "Predictive Modeling for Carbon Footprint Optimization of Prestressed Road Flyovers" Applied Sciences 15, no. 17: 9591. https://doi.org/10.3390/app15179591
APA StyleYepes-Bellver, L., Alcalá, J., & Yepes, V. (2025). Predictive Modeling for Carbon Footprint Optimization of Prestressed Road Flyovers. Applied Sciences, 15(17), 9591. https://doi.org/10.3390/app15179591








