Electromagnetic Wave Absorption Properties of Cation-Substituted Ba_0.5Sr_0.5Zn_2−xMe_xFe₁₆O₂₇ (Me = Fe, Ni, Co, Cu, Mn) W-Type Hexagonal Ferrites

Abstract

W-type hexaferrites with compositions Ba_0.5Sr_0.5Zn_2-xMe_xFe₁₆O₂₇ (Me = Fe, Ni, Co, Cu, Mn; x = 1) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0–2.0) were synthesized via solid-state reaction and optimized using a two-step calcination process to obtain single-phase or nearly single-phase structures. Their electromagnetic (EM) wave absorption properties were investigated by fabricating composites with 10 wt% epoxy and measuring the complex permittivity and permeability across two frequency bands: 0.1–18 GHz and 26.5–40 GHz. Reflection loss (RL) was calculated and visualized as two-dimensional (2D) maps with respect to frequency and sample thickness. In the 0.1–18 GHz range, only the Co-substituted sample exhibited strong ferromagnetic resonance (FMR) and broadband absorption, achieving a minimum RL of −41.5 dB at 4.84 GHz and a −10 dB bandwidth of 11.8 GHz. In contrast, the other Ba_0.5Sr_0.5Zn_2-xMe_xFe₁₆O₂₇ samples (Me = Fe, Mn, Ni, Cu) showed no significant absorption in this range due to the absence of FMR. However, all these samples clearly exhibited FMR characteristics and distinct absorption peaks in the 26.5–40 GHz range, particularly the Mn-substituted series, which demonstrated RL values below −10 dB over the 32.0–40 GHz range with absorber thicknesses below 1 mm. The FMR frequency varied depending on the substitution type and amount. In the Mn-substituted series, the FMR frequency was lowest at x = 1.0 and increased as x deviated from this composition. This study confirms the potential of Co-free W-type hexaferrites as efficient, cost-effective, and broadband EM wave absorbers in the 26.5–40 GHz range.

1. Introduction

The increasing demand for effective electromagnetic (EM) wave absorbers in fields such as telecommunications, defense, and aerospace has led to extensive research into materials that exhibit strong absorption across wide frequency ranges, particularly in the GHz regime. To achieve efficient EM wave absorption, materials must exhibit either dielectric loss, magnetic loss, or a combination of both [1,2,3]. Among various candidates, magnetic ceramics such as hexaferrites are of particular interest due to their intrinsic magnetic loss behavior associated with ferromagnetic resonance (FMR), a phenomenon that enables strong absorption at specific resonance frequencies [4,5,6].

W-type hexaferrites, with the general formula AMe₂Fe₁₆O₂₇ (A = Ba or Sr; Me = divalent metal ions such as Zn, Co, or Ni), are considered one of the most promising classes of magnetic ceramics for GHz to tens of GHz applications. Their high saturation magnetization (M_S), elevated Curie temperature, and well-defined FMR behavior make them ideal for EM wave absorber applications [7,8,9,10,11,12]. Importantly, the FMR frequency (f_FMR) in W-type hexaferrites can be tailored through the substitution of cations, which directly affects their magnetic anisotropy. This tunability enables precise control over the frequency band in which absorption occurs, offering a path toward designing materials for specific operational ranges. W-type hexaferrites exhibit either c-axis or c-plane magnetic anisotropy, which can be described by the following two equations [3,13,14].

$$f_{\mathrm{F}\mathrm{M}\mathrm{R}}={\displaystyle \frac{\gamma {\mu }_0}{2\pi }}{H}_a$$

(1)

$$f_{\mathrm{F}\mathrm{M}\mathrm{R}}={\displaystyle \frac{\gamma {\mu }_0}{2\pi }}{\left(H_{\theta }{H}_{\phi }\right)}^{1/2}$$

(2)

In these expressions, f_FMR denotes the FMR frequency, H_a represents the anisotropy field associated with c-axis magnetic anisotropy, and H_θ and H_φ correspond to the anisotropy fields related to c-plane anisotropy. Moreover, γ is the gyromagnetic ratio, and μ₀ is the permeability of free space. The f_FMR can be effectively tuned through cation substitution.

Traditionally, Co-containing W-type hexaferrites have been widely studied due to their strong magnetic anisotropy and low FMR frequencies suitable for sub-18 GHz applications. However, cobalt is a relatively expensive and strategically sensitive raw material, motivating the exploration of Co-free alternatives. Replacing Co with other transition metal ions such as Mn, Ni, Cu, or Fe presents an opportunity to develop cost-effective hexaferrite-based absorbers while still maintaining desirable magnetic properties. Moreover, these substitutions can extend the f_FMR into higher GHz ranges, making them attractive for applications in the millimeter-wave regime. In recent years, studies have reported the substitution of Mn, Cu, and Cr into Zn or Fe sites in W-type hexaferrites [15,16,17]; however, there appear to be very few reports that explicitly correlate such substitutions with shifts in f_FMR and their resulting EM wave absorption characteristics above 18 GHz.

In this study, we investigate the EM wave absorption behavior of Ba_0.5Sr_0.5Zn_2−xMe_xFe₁₆O₂₇ (Me = Fe, Ni, Co, Cu, Mn; x = 1), a series of cation-substituted W-type hexaferrites synthesized via solid-state reaction. Additionally, for Me = Mn, the substitution level (x) was varied from 0.0 to 2.0 to further explore the tunability of f_FMR and its effect on EM wave absorption. All powders were composited with 10 wt% epoxy and processed into toroidal and rectangular geometries for high-frequency characterization in the ranges of 0.1–18 GHz and 26.5–40 GHz, respectively. For ferrite-based EM wave absorbers, powder–polymer composites are generally preferred over sintered ceramic bodies due to the superior formability offered by polymer matrices. In the present samples, magnetic loss is considered the dominant EM absorption mechanism, as both the W-type hexaferrite and the epoxy resin exhibit high electrical resistivity, thereby minimizing the contribution of dielectric loss to the overall absorption. Reflection loss (RL) maps were generated to identify frequency–thickness regions of strong absorption and to evaluate the influence of composition on broadband absorption behavior. This work demonstrates that Co-free W-type hexaferrites can achieve significant EM wave absorption in the high-frequency range (26.5–40 GHz), with the potential to tune the absorption band via careful cation substitution. The successful synthesis of Co-free W-type hexaferrites with tunable FMR behavior and efficient absorption in the millimeter-wave band highlights the potential of these materials for next-generation EM wave absorbing applications. This study offers valuable insights into the design of high-frequency EM absorbers using cation substitution in W-type hexaferrites and opens pathways toward cobalt-free, cost-effective solutions for advanced electromagnetic interference (EMI) shielding technologies.

2. Materials and Methods

W-type hexaferrites with the chemical compositions Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0) were synthesized via the conventional solid-state reaction method. The precursor powders—Fe₂O₃ (99.9%, Kojundo Chemical, Seoul, Republic of Korea) BaCO₃ (99+%, Kojundo Chemical), SrCO₃ (99.9%, Kojundo Chemical), ZnO (99.9%, Kojundo Chemical), Mn₂O₃ (99.9%, Kojundo Chemical), NiO (99.97%, Kojundo Chemical), and CuO (99.9%, Kojundo Chemical)—were weighed according to the desired cation ratios. The weighed mixtures were placed in polypropylene bottles with deionized water and ZrO₂ balls, dried in an oven at 120 °C, and then subjected to a first calcination in an air atmosphere furnace at 900 °C for 6 h. The calcined powders were ground to pass through a #80 mesh sieve and then underwent a second calcination at 1300 °C for 6 h, followed by furnace cooling. A heating rate of 5 °C/min was applied for both calcinations. The resulting powders were further ground to pass through a #200 mesh sieve. To prepare samples for vector network analyzer (VNA) measurements, each powder was mixed with an epoxy binder (YD-014, Kukdo Chemical, Seoul, Republic of Korea) at a ratio of 90 wt% powder to 10 wt% epoxy. Approximately 0.3 g of the mixture was molded into a toroidal shape (inner diameter: 3.03 mm, outer diameter: 7.00 mm). Additionally, 0.15 g of the same mixture was molded into a rectangular shape (3.5 mm × 7.4 mm). The molded samples were heat-treated in a drying oven at 180 °C for 20 min, followed by post-processing to meet the dimensional requirements for VNA measurements.

The crystalline structure of the ferrite powders was analyzed by X-ray diffraction (XRD, D8 Advance, Bruker, Karlsruhe, Germany) using Cu Kα radiation (λ = 0.154056 nm). The microstructure of the calcined powders was observed using field-emission scanning electron microscopy (FE-SEM, JSM-7610F, JEOL, Tokyo, Japan). M–H curves were measured on second-calcined powder samples using a vibrating-sample magnetometer (VSM, EZ9, MicroSense, Lowell, MA, USA) at room temperature with a sweeping H field within ±25 kOe. For the measurements, the powder samples were mixed with paraffin in a 1:1 ratio and solidified. The complex permittivity (ε = ε′ − jε″) and complex permeability (μ = μ′ − jμ″) of the ferrite–epoxy composites were measured over two frequency ranges. In the 0.1–18 GHz range, toroidal samples (inner diameter: 3.03 mm, outer diameter: 7.00 mm) were tested using a vector network analyzer (VNA, E50356A, Keysight, Santa Rosa, CA, USA) with an airline kit (85052BR03) and N1500A software. For the 26.5–40 GHz range, rectangular samples (3.5 mm × 7.4 mm) were measured using a VNA (E8364A, Agilent Technologies, Santa Rosa, CA, USA) connected to a waveguide calibration kit (R11644A, Keysight), with measurements performed using 85071E software.

3. Results and Discussion

Figure 1a,b shows the X-ray diffraction (XRD) patterns of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0) powders after the second calcination at 1300 °C. Phase identification of the W-type hexaferrite was performed by matching the diffraction peaks with reference data from the ICDD database (PDF card No. 01-084-0927), and the corresponding standard peaks are displayed at the bottom of each figure. The diffraction planes (hkl indices) of the W-type phase are also labeled accordingly. In Figure 1a, single-phase W-type structures were observed for Me = Fe and Mn. In contrast, minor secondary phases of spinel-type Fe₃O₄ were detected in samples with Me = Co and Ni, while the sample with Me = Cu exhibited the most prominent spinel secondary peaks. The peak located near 2θ ~35.5° corresponds to the (311) plane, the main diffraction peak of the spinel phase, and may suggest partial substitution of Zn into the Fe₃O₄ lattice. Given the relatively high calcination temperature of 1300 °C—higher than typical values—it is possible that some trivalent cations, such as Fe³⁺, were partially reduced. This may explain why divalent Mn and Fe resulted in more stable formation of the W-phase compared to Ni, Co, and Cu. In Figure 1b, a similar trend was observed in the Mn-substituted series. While the composition with x = 0 (i.e., Ba_0.5Sr_0.5Zn₂Fe₁₆O₂₇) exhibited minor spinel peaks, the samples with x > 0 showed complete suppression of these peaks, indicating successful synthesis of a single-phase W-type hexaferrite. Given that spinel phases, owing to their cubic symmetry and high multiplicity factors, tend to produce relatively intense XRD peaks even when present in small amounts, the results indicate that all the synthesized samples are predominantly composed of the W-type hexaferrite phase, with only minimal, if any, contributions from secondary spinel phases.

The lattice parameters and unit cell volumes of the W-type hexaferrites were calculated from the d_hkl values derived from the 2θ peak positions corresponding to the (1 1 0), (1 0 10), (1 1 6), and (1 0 11) planes, as summarized in

Table 1. Lattice parameters (a and c), unit cell volume (Vol.), saturation magnetization (M_S), and coercivity (H_C) values of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ samples.

Composition	Me or x	a (Å)	c (Å)	Vol. (Å3)	MS (emu/g)	HC (Oe)
Ba0.5Sr0.5ZnMeFe16O27	Fe	5.901	32.88	991.4	78.5	237
	Ni	5.899	32.85	990.1	77.4	144
	Co	5.907	32.88	993.7	81.7	23.9
	Mn	5.893	32.85	987.9	74.0	166
	Cu	5.901	32.85	990.5	74.1	104
Ba0.5Sr0.5Zn2−xMnxFe16O27	0.0	5.913	32.92	996.9	70.7	101
	0.5	5.902	32.87	991.5	73.8	162
	1.0	5.893	32.85	987.9	74.0	166
	1.5	5.894	32.85	988.0	66.9	259
	2.0	5.895	32.86	989.1	63.2	242

[5]. The unit cell volume of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (x = 0), in which no substitution occurs at the Zn site, is larger than those of the Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu) samples with x = 1.0, further supporting the trend that Zn²⁺ has a larger ionic radius than the substituted Me²⁺ ions. Among them, the sample with Mn substitution shows the smallest unit cell volume. In the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0) series, a significant decrease in unit cell volume is observed with increasing x up to x = 1.5. However, beyond this point, the cell volume remains nearly constant (x = 1.0 and x = 1.5) and even shows a slight increase at x = 2.0, suggesting a limit in lattice contraction or possible structural relaxation at higher Mn substitution levels.

Figure 2a–i present the microstructures of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ powders (Me = Fe, Ni, Co, Mn, Cu; Figure 2a–e) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ powders (x = 0.0, 0.5, 1.0, 1.5, 2.0; Figure 2f–i) after the second calcination at 1300 °C in air followed by mechanical grinding. The image corresponding to x = 1.0 in the Mn-substituted series is omitted, as it is identical to that of the Me = Cu sample shown in Figure 2c. In all samples, high-temperature calcination promoted the growth of plate-like hexaferrite grains to sizes ranging from several to tens of micrometers. Due to subsequent hand grinding, the grains appear irregularly fractured. Among the Me-substituted samples, the Me = Cu composition exhibited the most pronounced grain growth, resulting in visibly larger particles even after grinding. This observation is consistent with the relatively intense (0012) peak observed in the XRD pattern of the Me = Cu sample in Figure 1a, likely due to the preferential alignment of large plate-like grains parallel to the sample holder surface during XRD sample preparation, leading to preferred orientation along the (00l) planes [18,19,20]. In the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ series, the x = 0 composition (i.e., no Mn substitution) exhibited the largest grain size, while no significant systematic variation in microstructure was observed with increasing Mn content. Within the grain size range of several to several tens of micrometers, such variations in particle size are not expected to have a meaningful impact on the high-frequency dielectric and magnetic properties or on the EM wave absorption performance of hexaferrites.

Figure 3a,b present the M–H curves of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0) samples. In each figure, the region near the origin is enlarged and displayed as an inset in the upper left corner. The M_S values measured at H = 25 kOe and the coercivity (H_C) values are summarized in Table 1. Among the various substituted elements, the Me = Co sample exhibits the fastest magnetization, the highest M_S of 81.7 emu/g, and the lowest H_C of 23.9 Oe. It is well known that the main factors influencing H_C are the magnetocrystalline anisotropy constant (K₁) and grain size; for the Me = Co sample, the low H_C is primarily attributed to its lower K₁ compared with the other samples. For the Me = Cu sample, the relatively fast initial magnetization and low H_C are likely due to the significantly enlarged grains, as shown in Figure 2e. The Cu- and Mn-substituted samples exhibit lower M_S values compared with the other samples. The variation in M_S is considered to originate from the Bohr magneton (μ_B) values of the substituting ions and their preferential occupation sites within the ferrimagnetic W-type crystalline structure; however, a detailed analysis of this effect is beyond the scope of the present study. For the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ series (Figure 3b), it is noteworthy that M_S increases with Mn substitution up to x = 1.0 and subsequently decreases, while H_C generally increases with increasing x.

Figure 4a–d present the high-frequency complex permittivity and permeability spectra of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Co, Mn, Cu)–epoxy (10 wt%) composites. In the ε′ and ε″ spectra shown in Figure 4a,b, the most notable feature is that the Cu-substituted sample exhibits the highest permittivity values. Above 10 GHz, noise signals are commonly observed across all samples. As previously reported [11], EM wave absorption in hexaferrites is predominantly governed by magnetic loss mechanisms. Therefore, such permittivity-related noise or relative differences in dielectric behavior are expected to have minimal influence on the overall absorption performance. In the μ′ and μ″ spectra in Figure 4c,d, the most significant variation is observed for the Co-substituted sample. In hexaferrites, the real part of permeability (μ′) is influenced primarily by domain wall motion (f < 1 GHz) and FMR phenomena (f > 1 GHz). The Ba_0.5Sr_0.5ZnCoFe₁₆O₂₇ sample, which exhibits the lowest magnetic anisotropy among the compositions, shows substantially higher permeability values in the entire frequency range (0.1 ≤ f ≤ 18 GHz) owing to both active domain wall motion and the presence of FMR. The f_FMR for this sample is identified at 4.3 GHz, as indicated by the peak in the μ″ spectrum in Figure 4d. For the other four samples (Me = Fe, Mn, Ni, Cu), no clear FMR signature is observed within the measured frequency range, suggesting that their FMR frequencies lie beyond 18 GHz due to higher magnetic anisotropy. At frequencies below 1 GHz, these samples display μ′ > 1 and μ″ > 0 due to domain wall motion. However, as the frequency increases beyond 1 GHz, the contribution from domain wall motion diminishes, resulting in μ′ approaching 1 and μ″ approaching 0. As expressed in Equations (1) and (2), magnetic anisotropy and f_FMR are directly proportional. According to Snoek’s limit law [13], as expressed following equation, the static permeability (μ_s) decreases as the f_FMR increases.

$$({\mu }_s-1)\text{·}{f}_{\mathit{FMR}}={\displaystyle \frac{2}{3}\gamma ·4\pi M_s}$$

(3)

Here, γ is a constant called gyromagnetic ratio, and M_s is the saturation magnetization value. At f = 0.1 GHz, the μ′ values of the four samples with relatively high magnetic anisotropy (Me = Fe, Mn, Ni, Cu) range from 2.0 to 2.5, whereas the μ′ value of the Me = Co sample reaches approximately 4.6, exhibiting a significant difference. The relatively high permeability observed in Ba_0.5Sr_0.5ZnCoFe₁₆O₂₇ over the 0.1–18 GHz range is consistent with this principle.

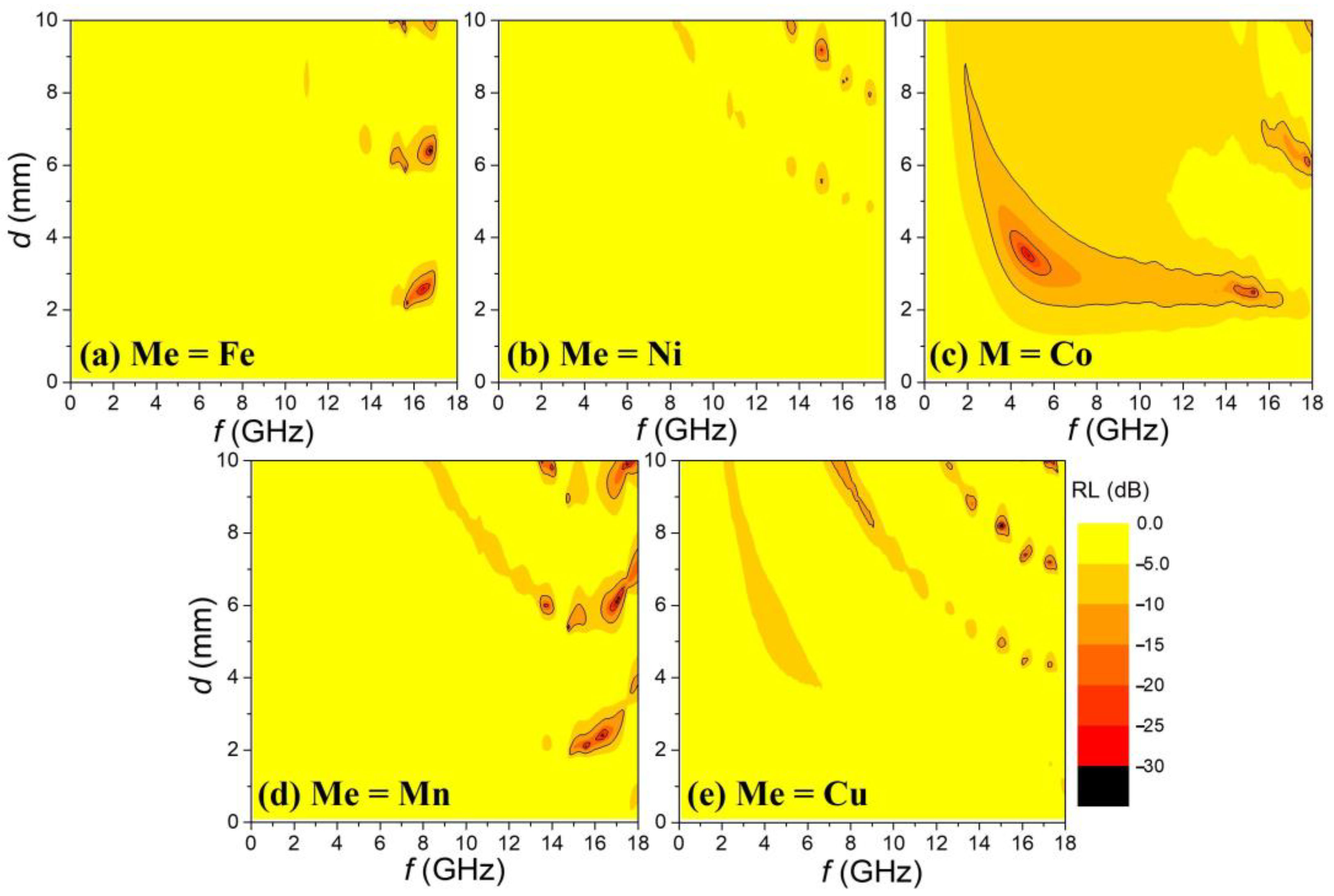
Figure 5a–e shows two-dimensional maps of reflection loss (RL) values as functions of frequency and sample thickness (0 ≤ d ≤ 10 mm), calculated from the ε′, ε″, μ′, and μ″ spectra in Figure 4 using the transmission line theory [21] equations described below.

$$\mathrm{R}\mathrm{L}\left(\mathrm{d}\mathrm{B}\right)=20\mathrm{l}\mathrm{o}\mathrm{g}\left|{\displaystyle \frac{\frac{Z_{in}}{Z_o}-1}{\frac{Z_{in}}{Z_o}+1}}\right|,$$

(4)

$${\displaystyle \frac{Z_{in}}{Z_o}}=\sqrt{{\displaystyle \frac{{\mu }_r}{{\epsilon }_r}}}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[j\right({\displaystyle \frac{2\pi fd}{c}}\left)\sqrt{{\mu }_r{\epsilon }_r}\right],$$

(5)

Here, $Z_{in}$ is the normalized input impedance of the absorber, $Z_0=\sqrt{{\mu }_0{\epsilon }_0}$ is the characteristic impedance of free space, c is the speed of light, f is the frequency of the incident EM wave, and d is the thickness of the absorber.

In the RL maps, regions with more negative RL values are represented by progressively darker shading in 5 dB intervals. Additionally, the areas enclosed by solid lines indicate regions where RL < −10 dB, with solid contours drawn at every 10 dB decrement within this range. Only the sample with Me = Co, which exhibits high μ′ and μ″ spectra over the measured frequency range (0.1 ≤ f ≤ 18 GHz), shows a broad EM wave absorption pattern. In contrast, the other samples do not exhibit significant absorption patterns due to the absence of FMR, which is the primary magnetic loss mechanism for EM wave absorption.

Accordingly, for the Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Mn, and Cu) powder–epoxy (10 wt%) samples, it was anticipated that FMR would occur at higher frequency ranges. Therefore, ε′, ε″, μ′, and μ″ spectra were measured in the frequency range of 26.5 ≤ f ≤ 40 GHz and are presented in Figure 6a–d. As expected, distinct FMR signals varying with substitution composition were observed in the μ′ and μ″ spectra of Figure 6c,d. The f_FMR was identified from the peak frequency in the μ″ spectra. Among the samples, Me = Mn exhibited the lowest f_FMR at 32.8 GHz, while Me = Cu showed the highest at 36.8 GHz, with the other two samples falling in between. In addition, the μ′ and μ″ spectra of the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0) powder–epoxy (10 wt%) samples were measured and are shown in Figure 6e–h. The f_FMR values also varied with the amount of Mn substitution: the lowest f_FMR was observed at x = 1.0, and a gradual increase in f_FMR was seen as the x value either decreased or increased from this point. The f_FMR values for each sample are summarized in

Table 2. EM wave absorption properties of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Mn, Cu) powder–epoxy (10 wt%) and Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0)–epoxy (10 wt%) composites: ferromagnetic resonance frequency (f_FMR), frequency at minimum reflection loss (f_RLmin), minimum reflection loss (RL_min), thickness at minimum reflection loss (d_RLmin), frequency range and bandwidth for RL < −10 dB (f-range, Δf), and thickness (d_WB) at which the maximum bandwidth (Δf) is observed.

Composition	Me or x	fFMR (GHz)	fRLmin (GHz)	RLmin (dB)	dRLmin (mm)	f-Range (GHz)	Δf (GHz)	dWB (mm)
Ba0.5Sr0.5ZnMeFe16O27	Fe	33.3	29.54	−40.52	3.81	32.6~40.0(+)	>7.39	0.59
	Ni	34.4	35.01	−40.59	0.49	34.4~40.0(+)	>5.53	0.55
	Co	4.30	4.84	−41.49	3.49	4.74~16.54	11.80	2.30
	Mn	32.8	31.31	−51.17	2.05	32.0~40.0(+)	>7.97	0.65
	Cu	36.8	31.36	−44.74	5.99	36.16~40.0(+)	>3.84	0.44
Ba0.5Sr0.5Zn2−xMnx Fe16O27	0.0	34.7	33.85	−50.39	1.65	34.1~40.0(+)	>5.89	0.53
	0.5	33.4	32.02	−49.01	1.91	32.7~40.0(+)	>7.33	0.59
	1.0	32.8	31.31	−51.17	2.05	32.0~40.0(+)	>7.97	0.65
	1.5	33.8	32.17	−55.58	2.09	32.9~40.0(+)	>7.07	0.65
	2.0	35.5	34.13	−43.92	1.92	34.7~40.0(+)	>5.25	0.61

.

The variation in f_FMR can be explained by changes in magnetic anisotropy resulting from cation substitution, as indicated by Equations (1) and (2). In the case of the Me = Co sample, it is known that the substitution of Zn by Co effectively reduces the magnetic anisotropy, leading to a transition from c-axis anisotropy to planar anisotropy in the substitution level range of x = 0.75–1.0 [11,22]. Consequently, the f_FMR decreases from 35 GHz in Ba_0.5Sr_0.5Zn₂Fe₁₆O₂₇ to 4.3 GHz in Ba_0.5Sr_0.5ZnCoFe₁₆O₂₇ when Co is substituted at the x = 1.0 level. In contrast, the samples with Me = Ni, Cu, Mn, and Fe appear to retain c-axis anisotropy even at the x = 1.0 substitution level, with f_FMR values remaining within the 32–35 GHz range. As shown in Figure 3b and Table 1, in the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ series, the M_S increases with Mn content up to x = 1.0 and decreases thereafter. This trend suggests that variations in M_S play a dominant role in determining the anisotropy field (H_a = 2K₁/M_S), where changes in H_a are primarily governed by M_S. Consequently, through Equations (1) and (2), the observed changes in f_FMR are correlated with variations in M_S. The fact that the x = 1.0 sample exhibits the lowest f_FMR is therefore closely related to its highest M_S value within the series.

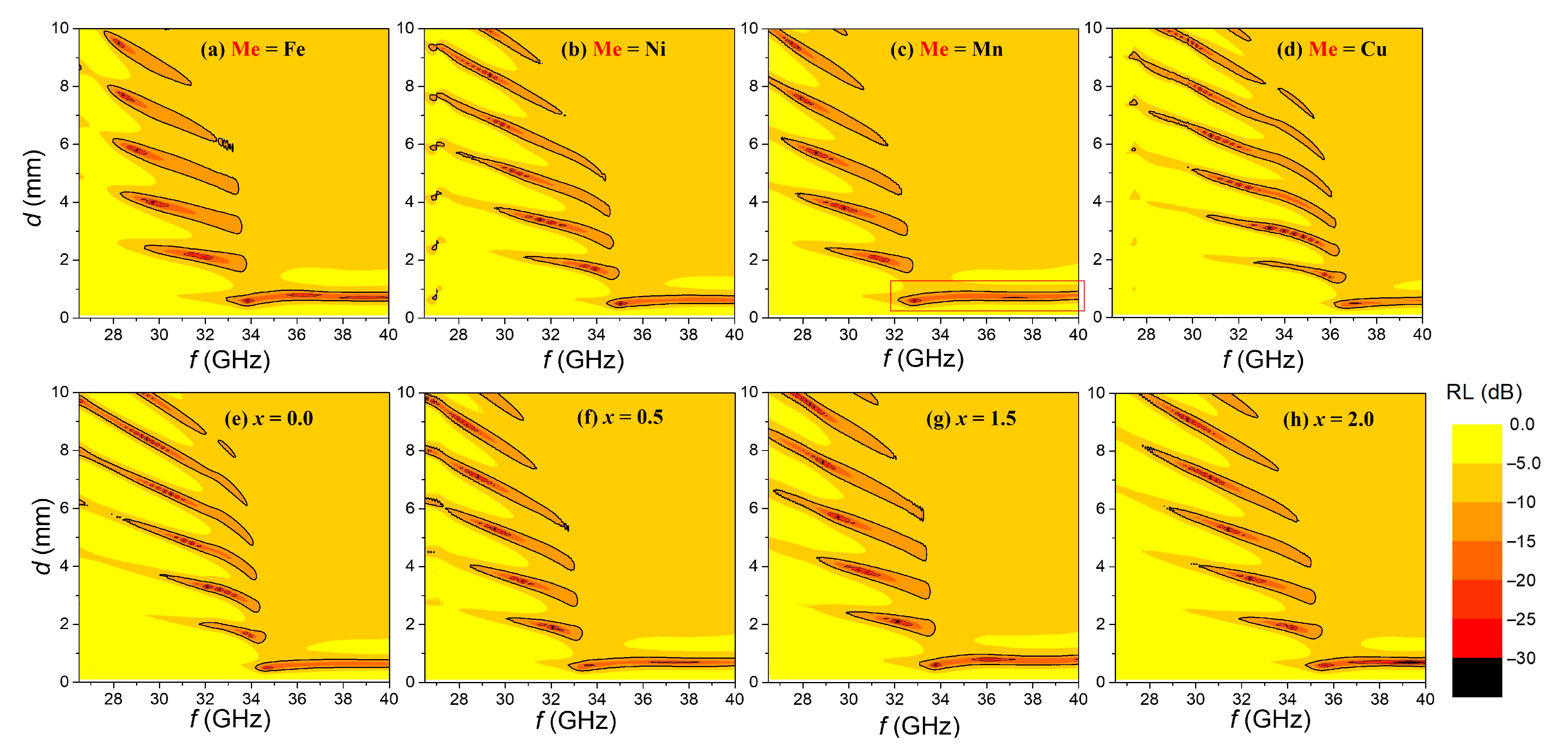
Figure 7a–h present the RL maps derived from the ε′, ε″, μ′, and μ″ spectra shown in Figure 6, calculated using Equations (4) and (5). Figure 7a–d correspond to Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Mn, and Cu)–epoxy composites, while Figure 7e–h depict the RL maps for Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ samples with varying Mn substitution levels (x). In all samples, the EM wave absorption bands satisfying RL < −10 dB—indicated by solid contour lines—appear periodically as a function of thickness. A primary absorption band elongated horizontally is observed at the lowest thickness, and with increasing thickness, additional absorption bands reappear repeatedly at thicknesses that satisfy impedance matching conditions. Of particular interest is the primary absorption band at the lowest-thickness region (d < 1 mm), where the minimum reflection loss (RL_min), the corresponding frequency, and the bandwidth (Δf) satisfying RL < −10 dB are clearly seen.

Among the Me = Fe, Ni, Mn, and Cu samples, the Mn-substituted sample exhibits the primary absorption band extending to the lowest frequencies. In Figure 7c, the primary absorption band region is highlighted with a red box. Since frequencies above 40 GHz are beyond the measurement range, the exact cutoff frequency of the absorption band is unknown; however, changes in the primary absorption band frequency range closely correspond to the samples’ f_FMR values. It is evident that the absorption frequency band shifts lower as f_FMR decreases. For the Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ series (x = 0.0, 0.5, 1.0, 1.5, 2.0), the sample with x = 1.0 shows the lowest f_FMR, and when comparing its RL map (Figure 7c) with those of samples with x = 0.0, 0.5, 1.5, and 2.0 (Figure 7e–h), the primary absorption band shifts progressively toward higher frequencies in correspondence with increasing f_FMR values. Because the EM wave absorption mechanism of W-type hexaferrites is governed by FMR [11], the precise shift of the primary absorption band directly follows the variation in the f_FMR. As noted earlier, changes in the f_FMR arise from cation substitution, which alters intrinsic material parameters such as the M_S and the K₁.

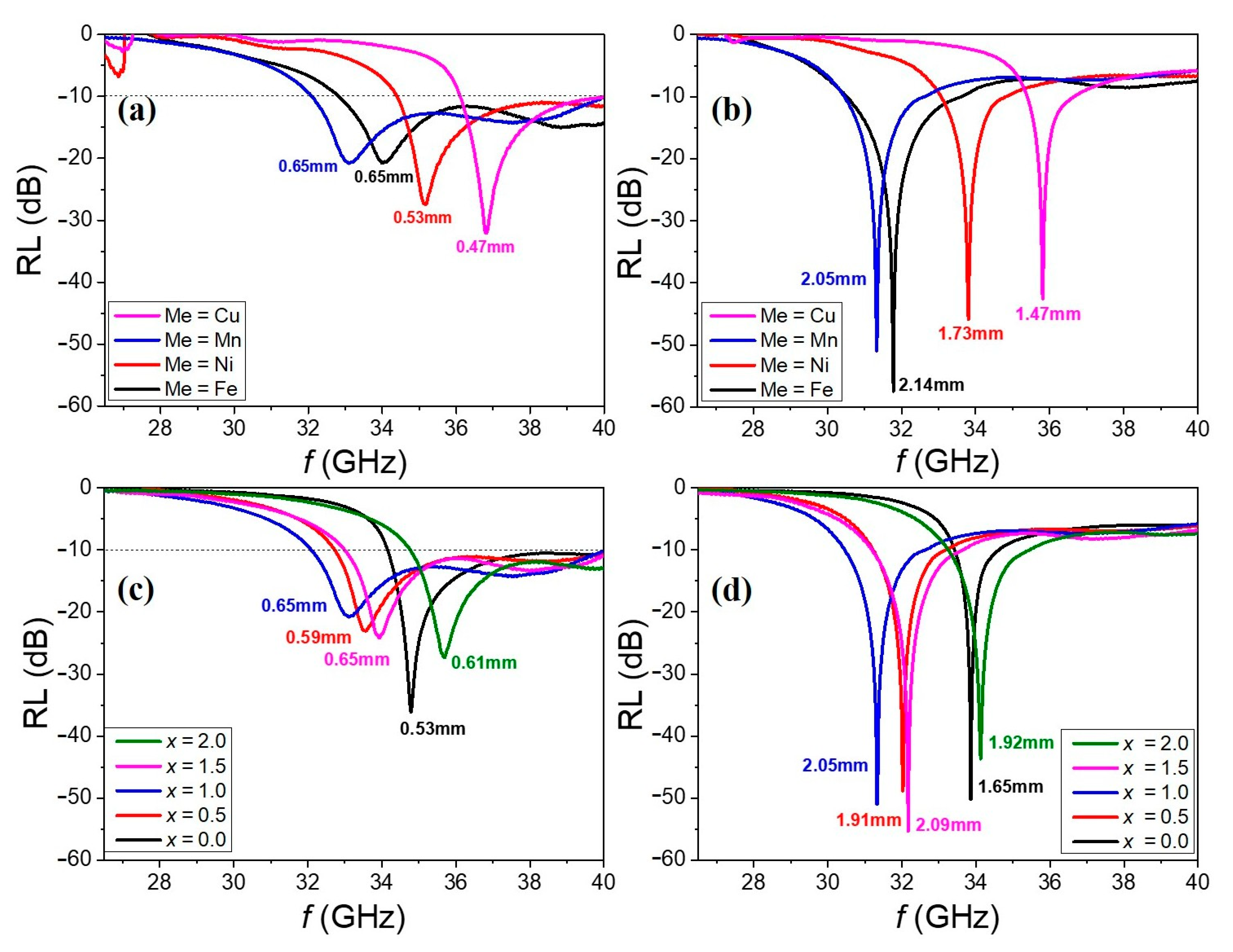
Figure 8a,b present the RL spectra of Ba_0.5Sr_0.5ZnMeFe₁₆O₂₇ (Me = Fe, Ni, Mn, Cu)–epoxy (10 wt%) composites, while Figure 8c,d show the RL spectra of Ba_0.5Sr_0.5Zn_2−xMn_xFe₁₆O₂₇ (x = 0.0, 0.5, 1.0, 1.5, 2.0)–epoxy (10 wt%) composites at selected thicknesses. Figure 8a,c correspond to the RL spectra measured at the thicknesses where the absorption bandwidth (Δf) is maximized for each composition within the measured frequency range. Figure 8b,d show the RL spectra at the thicknesses where the minimum reflection loss (RL_min) is observed. The values of RL_min, the corresponding frequency (f_RLmin), and the absorber thickness at RL_min (d_RLmin), as well as the maximum Δf values along with their respective thicknesses and frequency ranges, are summarized in Table 2. Although the absorption bands vary slightly with changes in the cation substitution levels and corresponding f_FMR shifts, all samples exhibit excellent absorption performance within the 32–40 GHz range at thicknesses around 0.4 to 0.6 mm. If the measurement frequency range had extended beyond 40 GHz, it is expected that the bandwidth Δf for all samples would have exceeded 10 GHz.

4. Conclusions

Single-phase or nearly single-phase W-type hexaferrites with the composition Ba_0.5Sr_0.5Zn_2−xMe_xFe₁₆O₂₇ (M = Fe, Ni, Co, Cu, Mn) were successfully synthesized via a two-step solid-state calcination process. Their EM wave absorption properties were evaluated in the frequency ranges of 0.1–18 GHz and 26.5–40 GHz using epoxy composites. Among all the samples, only the Co-substituted ferrite exhibited a strong absorption pattern in the 0.1–18 GHz range, as confirmed by the RL map. This behavior arises because the substitution of Co for Zn significantly reduced the magnetocrystalline anisotropy of Ba_0.5Sr_0.5Zn₂Fe₁₆O₂₇, shifting its FMR frequency from ~35 GHz down to 4.3 GHz. Consequently, the Co-substituted sample demonstrated excellent absorption, with a minimum reflection loss of −41.5 dB at 4.84 GHz with a thickness of 3.49 mm and broadband absorption (RL < −10 dB) in the range of 4.74–16.54 GHz at a thickness of 2.30 mm.

In contrast, Mn-, Ni-, Fe-, and Cu-substituted samples exhibited significant absorption in the higher frequency range (26.5–40 GHz). In particular, the Mn-substituted ferrites showed broadband absorption (RL < −10 dB) across 32–40 GHz at thicknesses below 1 mm. By varying the Mn content (x = 0–2.0), the FMR frequency could be tuned, with x = 1.0 producing the lowest f_FMR value. These results indicate that the type and amount of substituent ions strongly influence the intrinsic properties of the materials—such as K₁ and M_S—leading to shifts in the f_FMR and corresponding changes in the EM absorption bands. Notably, even without the use of Co, the absorption characteristics of W-type hexaferrites can be tailored in the 26.5–40 GHz band at reduced sample thicknesses, making them highly promising candidates for future EM absorbers, particularly in 5G frequency applications.