A Short-Term Load Forecasting Method for Typical High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks
Abstract
1. Introduction
- (1)
- Feature refinement via nonlinear correlation analysis: Maximal Information Coefficient (MIC) analysis is applied to identify input features that exhibit strong nonlinear associations with the target load, enabling the removal of redundant variables and the construction of a compact, information-rich input space.
- (2)
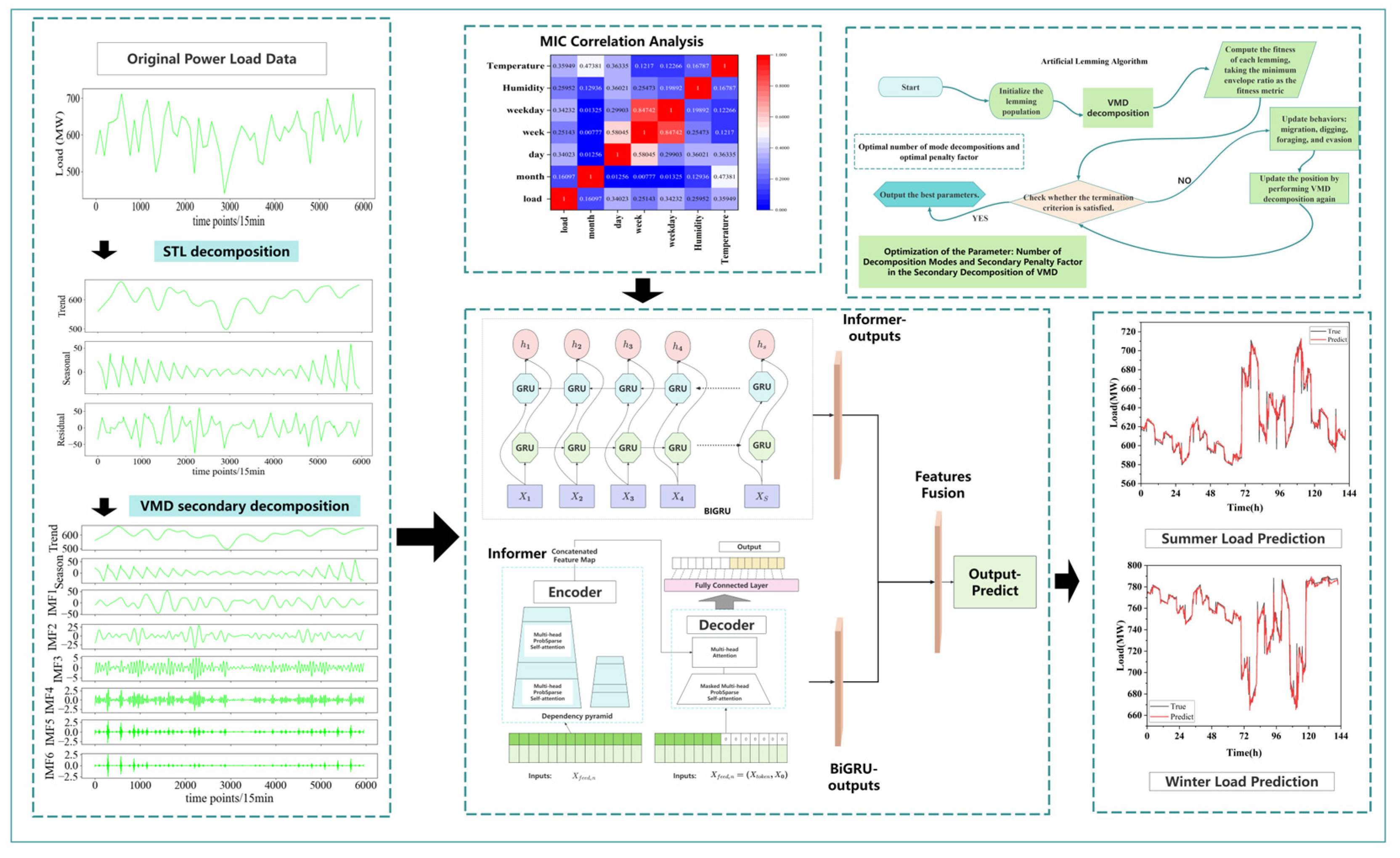
- Hierarchical multimodal decomposition: A two-stage decomposition scheme is employed to reduce signal complexity. The raw load series is first processed using seasonal-trend decomposition via Loess (STL) to extract trend and periodic components, while the residual is further decomposed using variational mode decomposition (VMD) to capture multi-scale fluctuations. This hierarchical design enables mode-specific learning and enhances interpretability.
- (3)
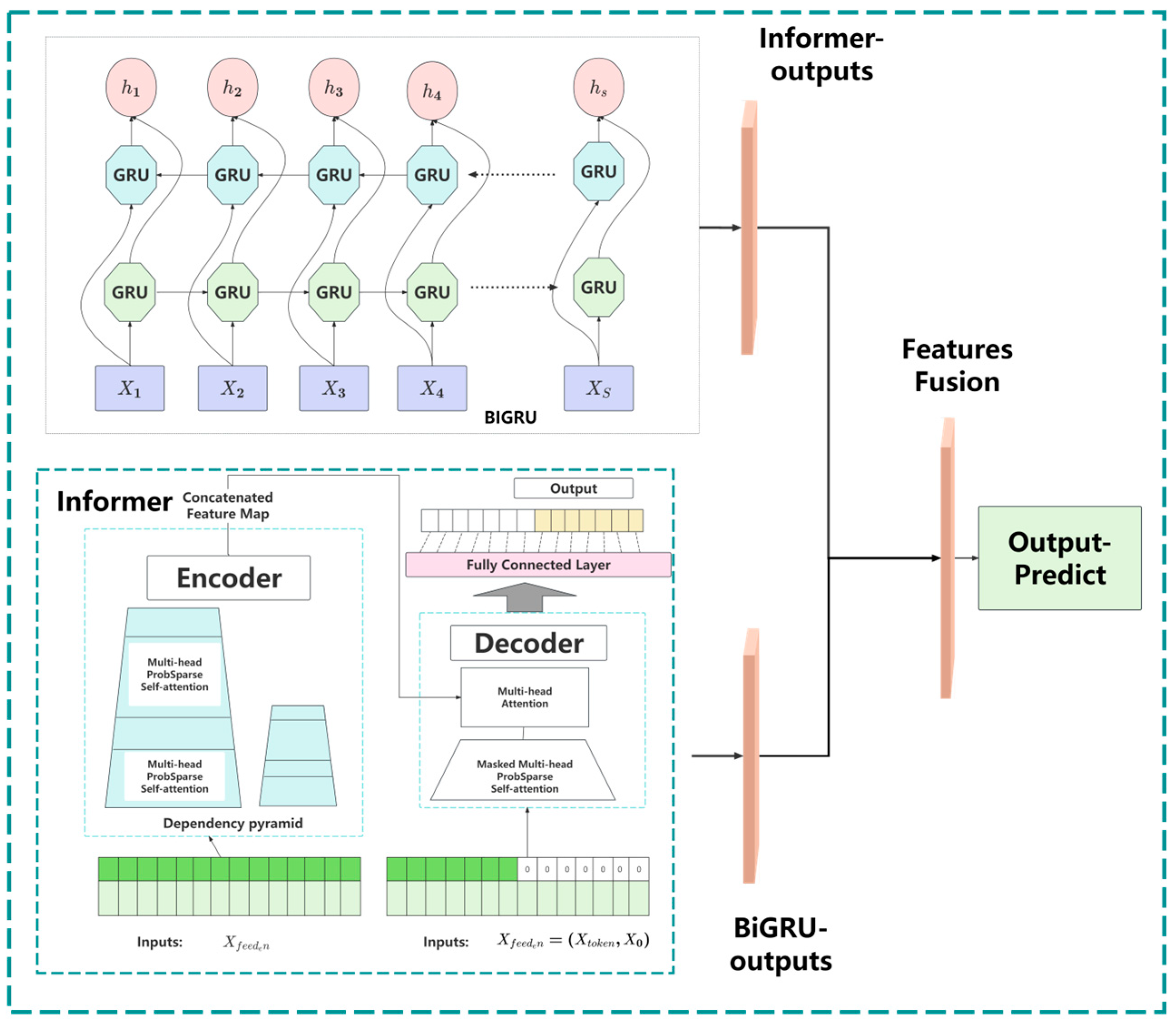
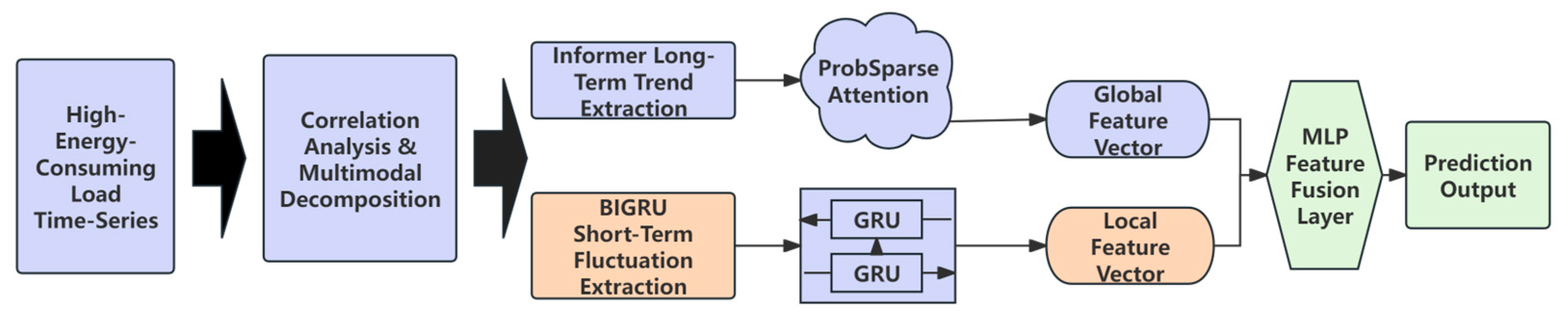
- Parallel hybrid forecasting architecture: A dual-branch network is constructed by combining a bidirectional gated recurrent unit (BiGRU) with an Informer model. BiGRU captures short-term dynamics and local variations, while the Informer leverages sparse attention to model long-range dependencies. Their complementary strengths enable the model to extract both fine-grained and global temporal features, improving prediction accuracy and robustness.
2. Correlation Analysis and Hierarchical Modeling of High Energy-Consuming Loads
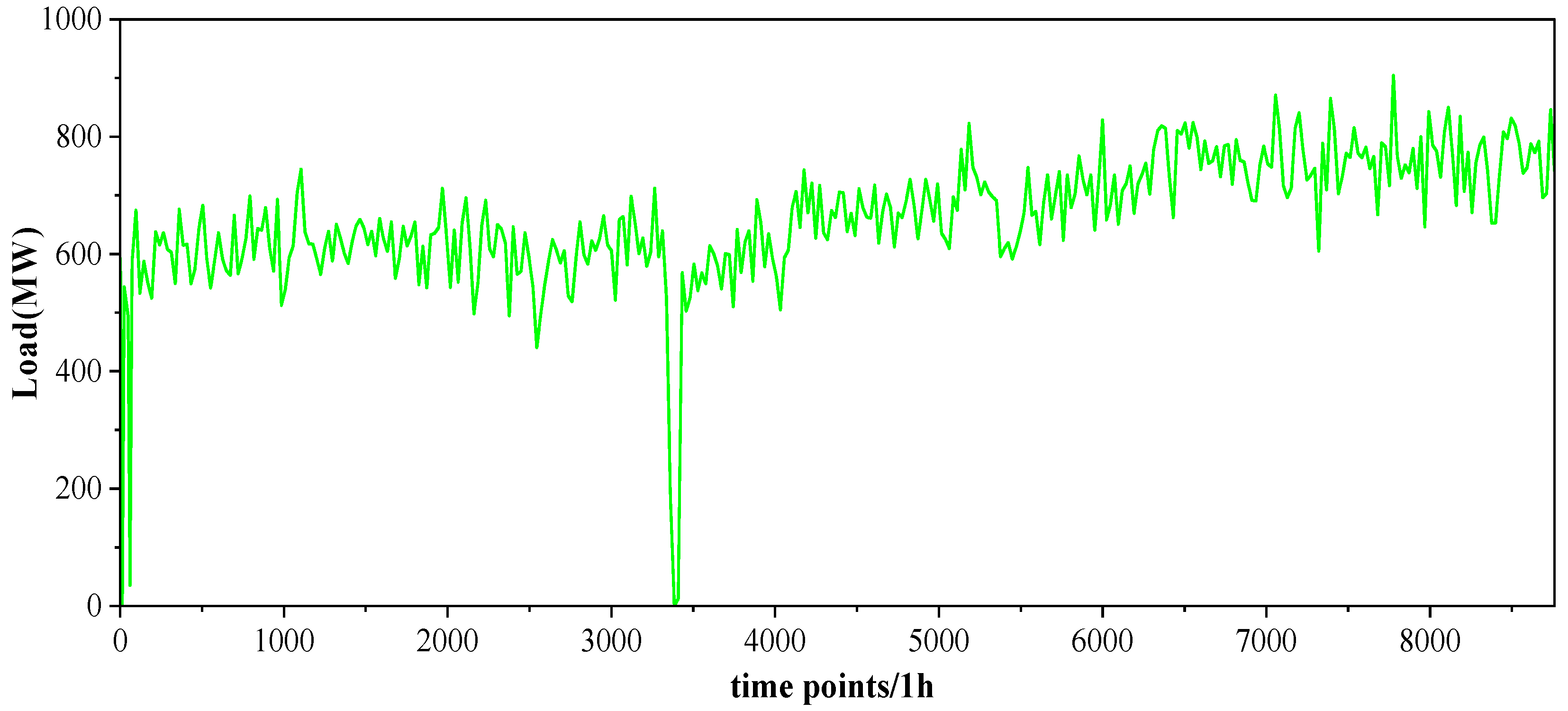
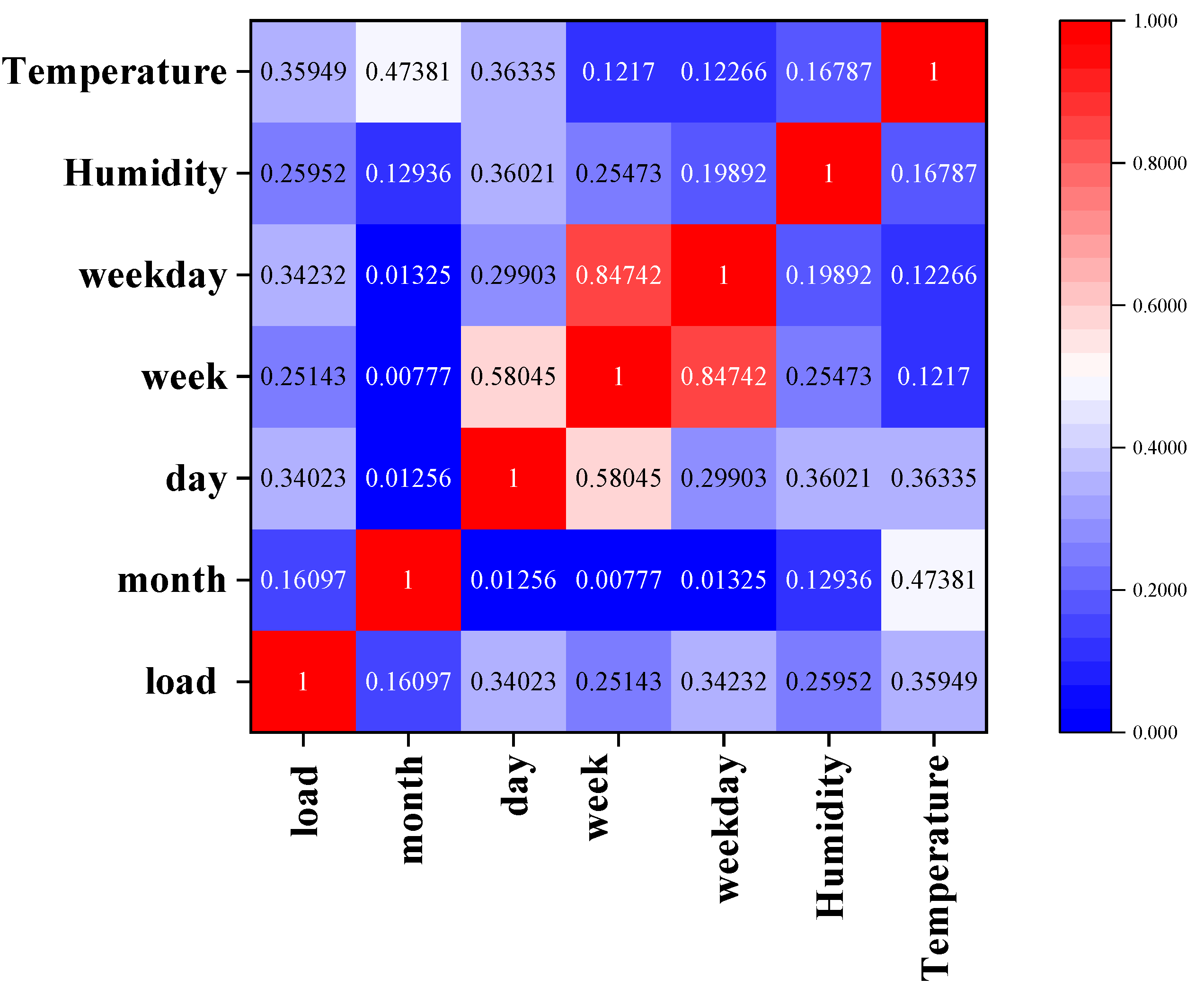
2.1. Correlation Analysis of Typical High Energy-Consuming Loads
2.2. Hierarchical Modeling of Typical High Energy-Consuming Loads
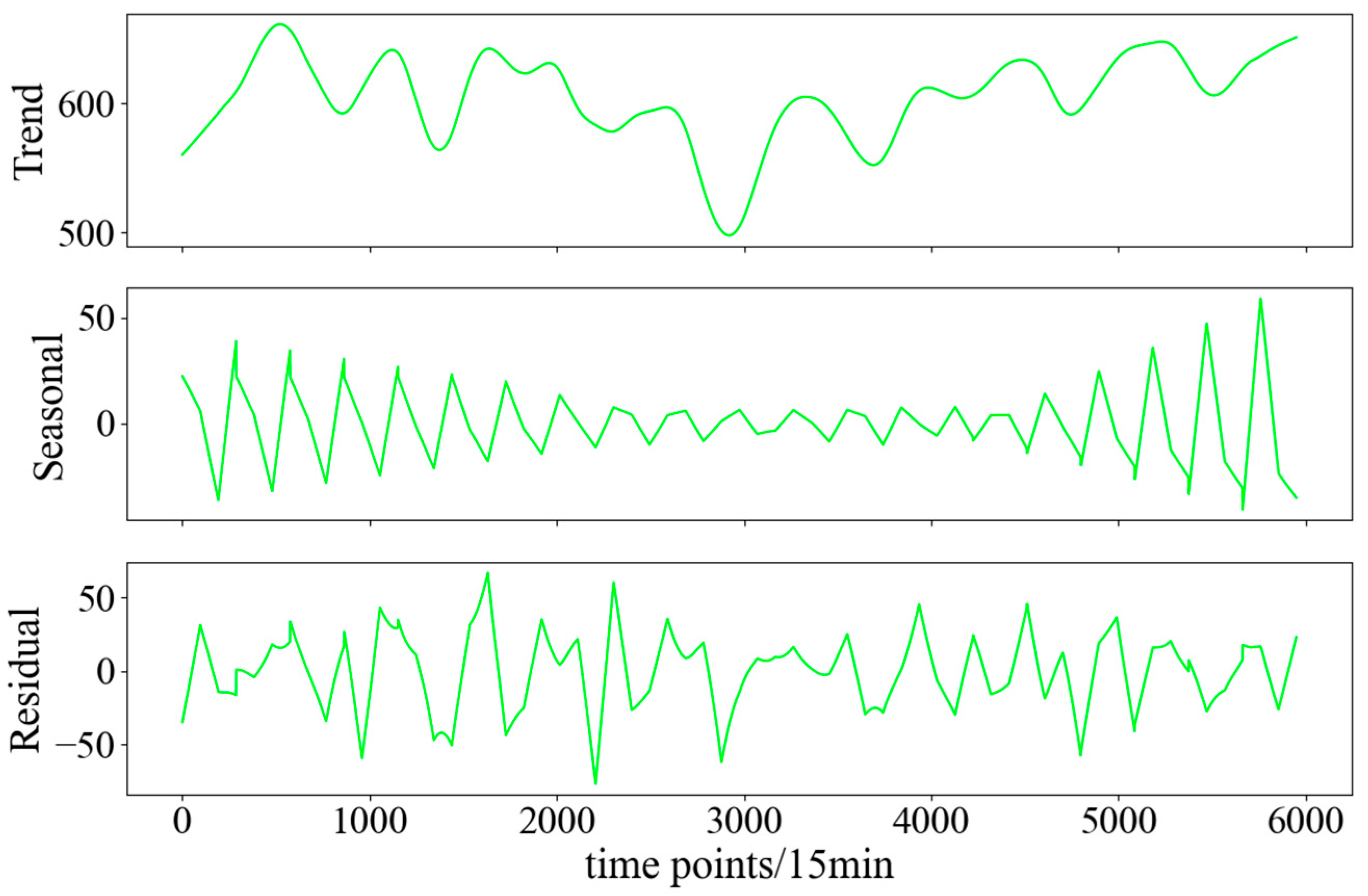
2.2.1. STL Decomposition of High Energy-Consuming Loads
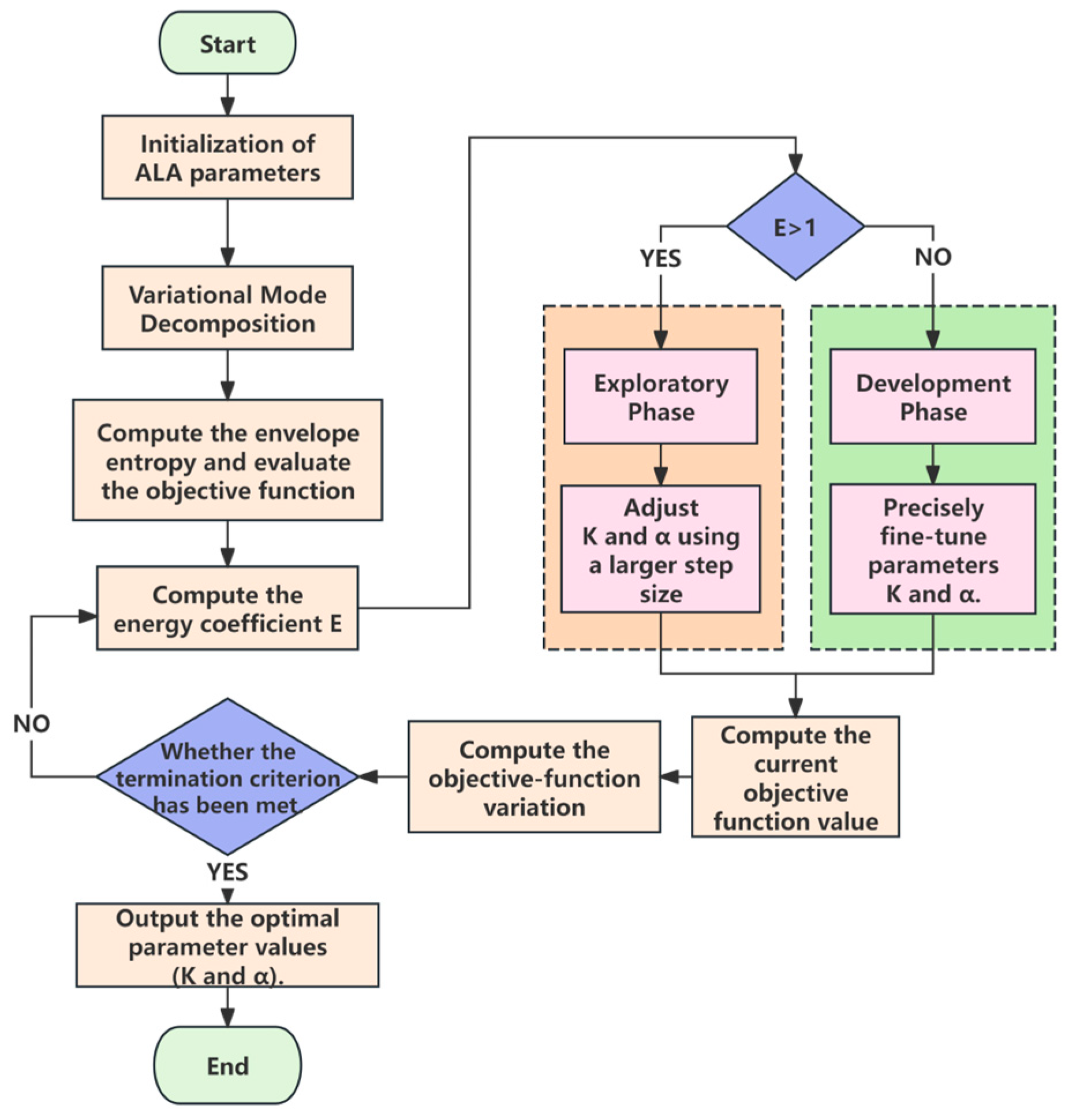
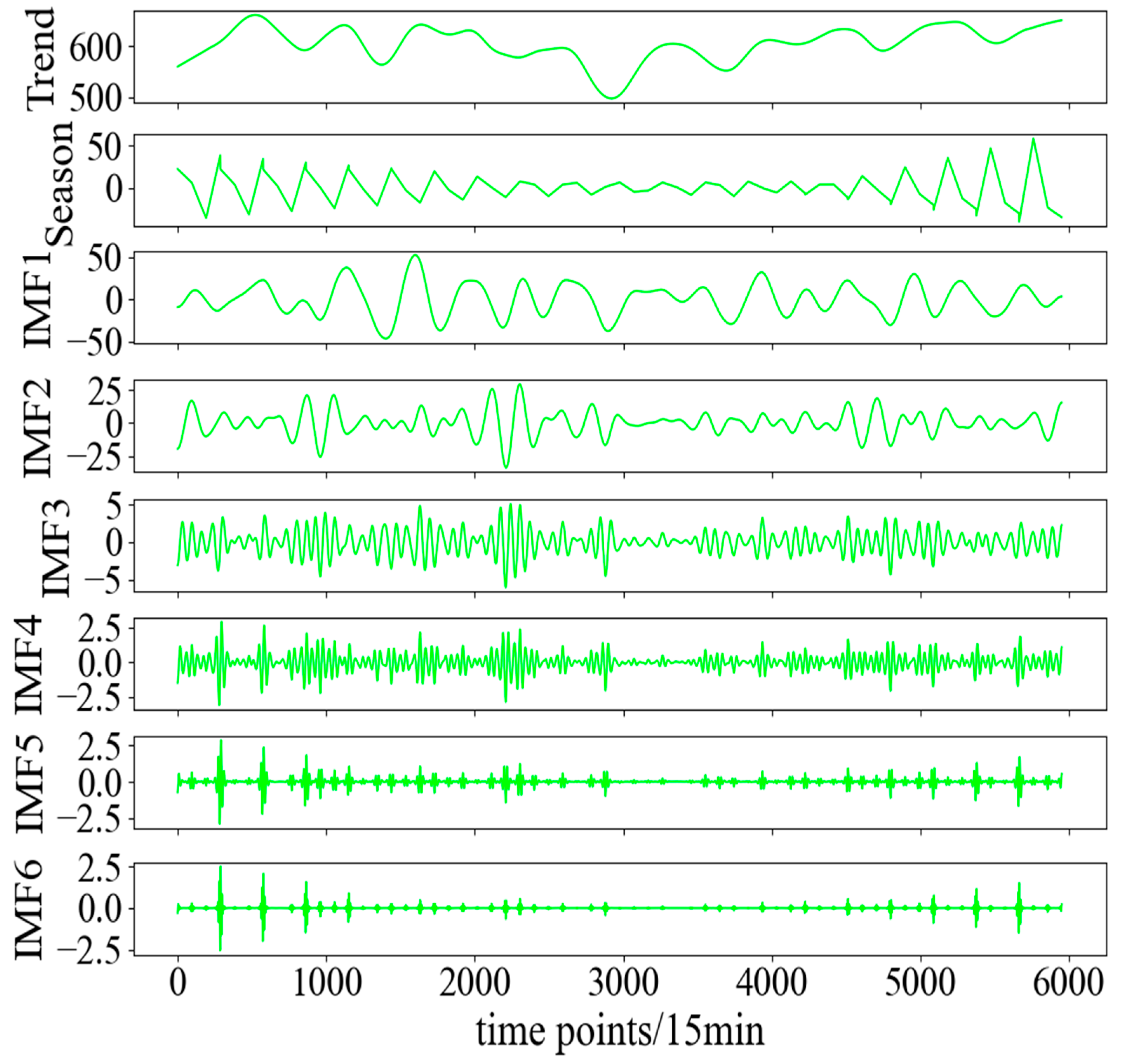
2.2.2. VMD Decomposition Based on the Artificial Lemming Algorithm (ALA)
3. Parallel Forecasting of High Energy-Consuming Loads Based on Informer and BiGRU
4. Construction of a Load Forecasting Framework for Typical Loads in High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks
5. Numerical Example and Simulation Analysis
5.1. Data Preprocessing and Feature Input of High Energy-Consuming Loads
5.2. Prediction Experiments and Evaluation Metrics for High Energy-Consuming Loads
5.3. Forecasting Results of High Energy-Consuming Loads
5.3.1. Ablation Experiments and Analysis
5.3.2. Analysis of the Impact of Different Modal Decomposition Methods on Prediction Performance
5.3.3. STL, MIC, and ALA Methods’ Effectiveness Ablation Experiments
6. Conclusions
- (1)
- During VMD decomposition, the minimum average envelope entropy is adopted as the objective function, and an adaptive learning algorithm is employed to automatically optimise both the number of modes and the penalty factor, thereby ensuring a rational and stable separation of frequency-domain components in the high energy-consuming load series. A maximum information coefficient correlation analysis is then applied to identify features that are strongly related to load fluctuations, thus refining the input feature set for high energy-consuming load forecasting.
- (2)
- In the ablation experiments, starting from the baseline BiGRU module and sequentially introducing the VMD, Informer and STL components, RMSE, MAE and MAPE consistently decreased, while R2 steadily increased across both the summer and winter datasets, unequivocally demonstrating the indispensability of each module within the overall framework.
- (3)
- In the comparative experiments, the proposed STL + VMD hierarchical modelling strategy—unlike combinations based on other decomposition methods (such as STL, EMD, CEEMD or stand-alone VMD) and various deep-learning predictors—first explicitly extracts the seasonal and trend components, then applies multi-modal frequency decomposition to the residual, thereby capturing the fine-grained nonlinear characteristics of the load series more thoroughly. The parallel BiGRU–Informer ensemble simultaneously learns short-term dynamic patterns and long-range dependencies. Experiments show that, on both the summer and winter test sets, this framework reduces RMSE by an average of 30.94%, lowers MAE by 19.26%, decreases MAPE by 19.02%, and raises R2 by 0.68% relative to the stand-alone VMD + parallel-prediction architecture, thereby confirming the synergistic benefits of hierarchical modelling and parallel forecasting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Z.; Wu, Z.; Wei, L.; Yang, L.; Yuan, B.; Zhou, M. Understanding the synergy of energy storage and renewables in decarbonization via random forest-based explainable AI. Appl. Energy 2025, 390, 125891. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Y.; Wang, B.; Liu, C.; Zhao, Y. Review of Market Implementation and Scheduling Models Considering the Flexibility Extraction of Differentiated Industrial Energy-Intensive Loads. Trans. China Electrotech. Soc. 2025, 40, 2043–2062, 2161. [Google Scholar]
- Chen, L.; Wang, C.; Wu, Z. Reinforcement Learning-Based Time of Use Pricing Design Toward Distributed Energy Integration in Low Carbon Power System. IEEE Trans. Netw. Sci. Eng. 2025, 12, 997–1010. [Google Scholar] [CrossRef]
- Zhou, X.; Qi, L.; Pan, N.; Hou, M.; Yang, J. Optimization method for load aggregation scheduling in industrial parks considering multiple interests and adjustable load classification. Energy 2025, 326, 135887. [Google Scholar] [CrossRef]
- Ma, S.; Wang, Q.; Nie, T.; Chen, Z.; Teng, Y. Collaborative optimization model of industrial high-energy consumption park under green and low-carbon transformation. Electron. Lett. 2024, 60, 13187. [Google Scholar] [CrossRef]
- Han, F.; Wang, X.; Qiao, J.; Shi, M.; Pu, T. Review on Artificial Intelligence Based Load Forecasting Research for the New-type Power System. Proc. Chin. Soc. Electr. Eng. 2023, 43, 8569–8591. [Google Scholar]
- Yang, T.; Zhao, L.; Wang, C. Review on Application of Artificial Intelligence in Power System and Integrated Energy System. Autom. Electr. Power Syst. 2019, 43, 2–14. [Google Scholar]
- Gao, S.; Li, F. Short-term wind speed forecasting based on CEEMD-SE-PSR-BP method. Acta Energiae Solaris Sin. 2025, 46, 415–422. [Google Scholar]
- Guo, W.; Liu, J.; Ma, J.; Lan, Z. Short-Term Power Load Forecasting Using Adaptive Mode Decomposition and Improved Least Squares Support Vector Machine. Energies 2025, 18, 2491. [Google Scholar] [CrossRef]
- Ye, J.; Cao, J.; Yang, L.; Luo, F. Ultra Short-term Load Forecasting of User Level Integrated Energy System Based on Variational Mode Decomposition and Multi-model Fusion. Power Syst. Technol. 2022, 46, 2610–2618. [Google Scholar]
- Huang, H.; Zhang, A.a. Load Forecasting of Integrated Energy System Based on Combination of Decomposition Algorithms and Meta-learning. Autom. Electr. Power Syst. 2024, 48, 151–160. [Google Scholar]
- Liu, W.; Hua, F.; Cui, Y.P.; Xu, Y.C.; Liu, H. An Optimized Power Load Forecasting Algorithm Based on VMD-SMA-LSTM. Energy Sci. Eng. 2025, 13, 3243–3253. [Google Scholar] [CrossRef]
- Xiao, W.; Mo, L.; Xu, Z.; Liu, C.; Zhang, Y. A hybrid electric load forecasting model based on decomposition considering fisher information. Appl. Energy 2024, 364, 123149. [Google Scholar] [CrossRef]
- Wang, H.; Yan, J.; Zhang, J.; Liu, S.; Liu, Y.; Han, S.; Qu, T. Short-term integrated forecasting method for wind power, solar power, and system load based on variable attention mechanism and multi-task learning. Energy 2024, 304, 132188. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yang, C.; Bozkurt, A. An advanced framework for net electricity consumption prediction: Incorporating novel machine learning models and optimization algorithms. Energy 2024, 296, 131259. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, J.; Xia, Y. Combined electricity load-forecasting system based on weighted fuzzy time series and deep neural networks. Eng. Appl. Artif. Intell. 2024, 132, 108375. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Z.; Wei, L.; Yang, L.; Zhang, Y.; Yuan, B.; Zhou, M. Evaluating the externality value of distributed photovoltaics: Industry-specific investment decisions under diverse pricing schemes. Renew. Energy 2025, 247, 122986. [Google Scholar] [CrossRef]
- You, W.; Guo, D.; Wu, Y.; Li, W. Multiple Load Forecasting of Integrated Energy System Based on Sequential-Parallel Hybrid Ensemble Learning. Energies 2023, 16, 3268. [Google Scholar] [CrossRef]
- Gong, J.; Qu, Z.; Zhu, Z.; Xu, H. Parallel TimesNet-BiLSTM model for ultra-short-term photovoltaic power forecasting using STL decomposition and auto-tuning. Energy 2025, 320, 135286. [Google Scholar] [CrossRef]
- Gu, L.; Wang, J.; Liu, J. A combined system based on data preprocessing and optimization algorithm for electricity load forecasting. Comput. Ind. Eng. 2024, 191, 110114. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, H.; Abu Khurma, R.; Castillo, P.A. Artificial lemming algorithm: A novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar] [CrossRef]

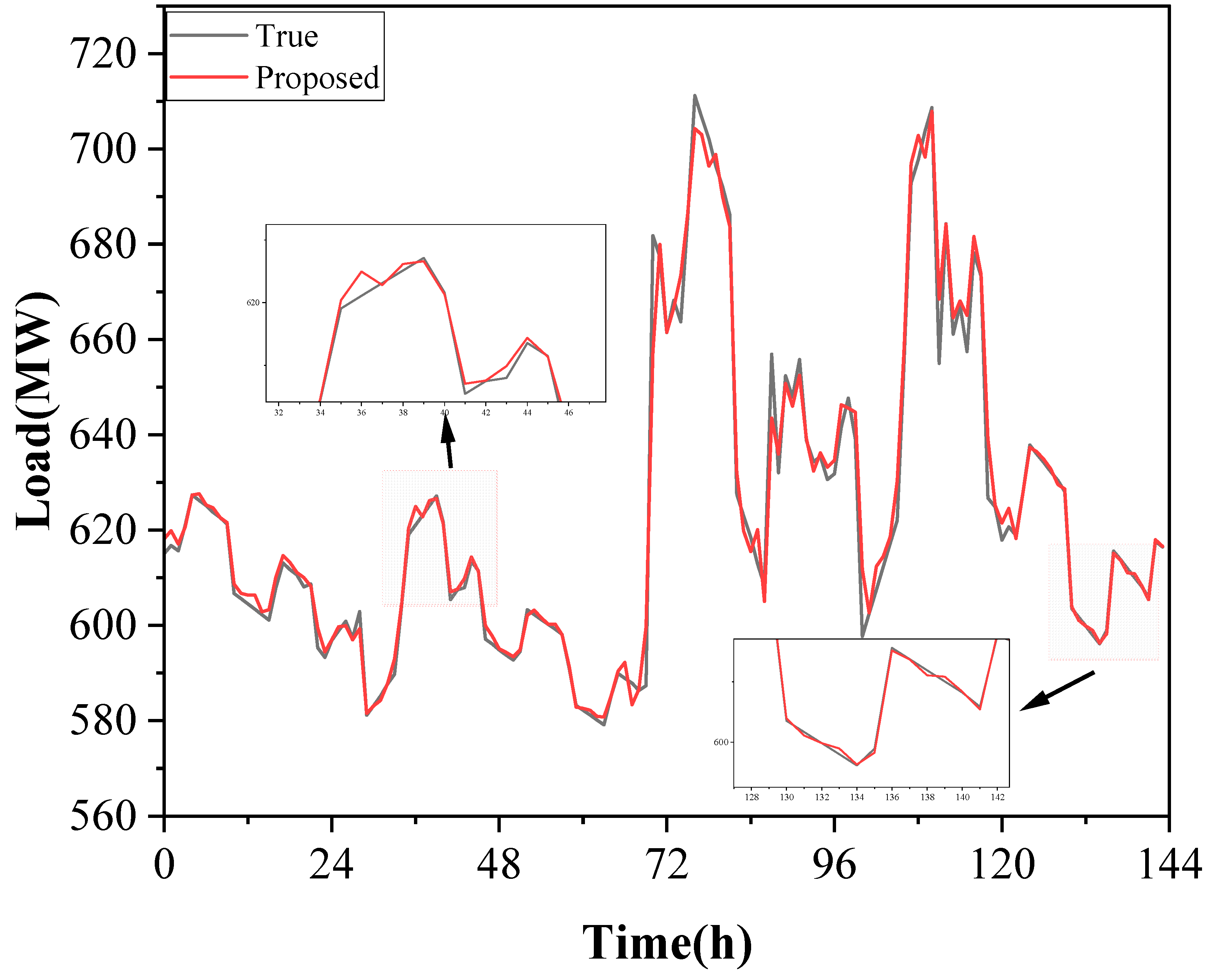
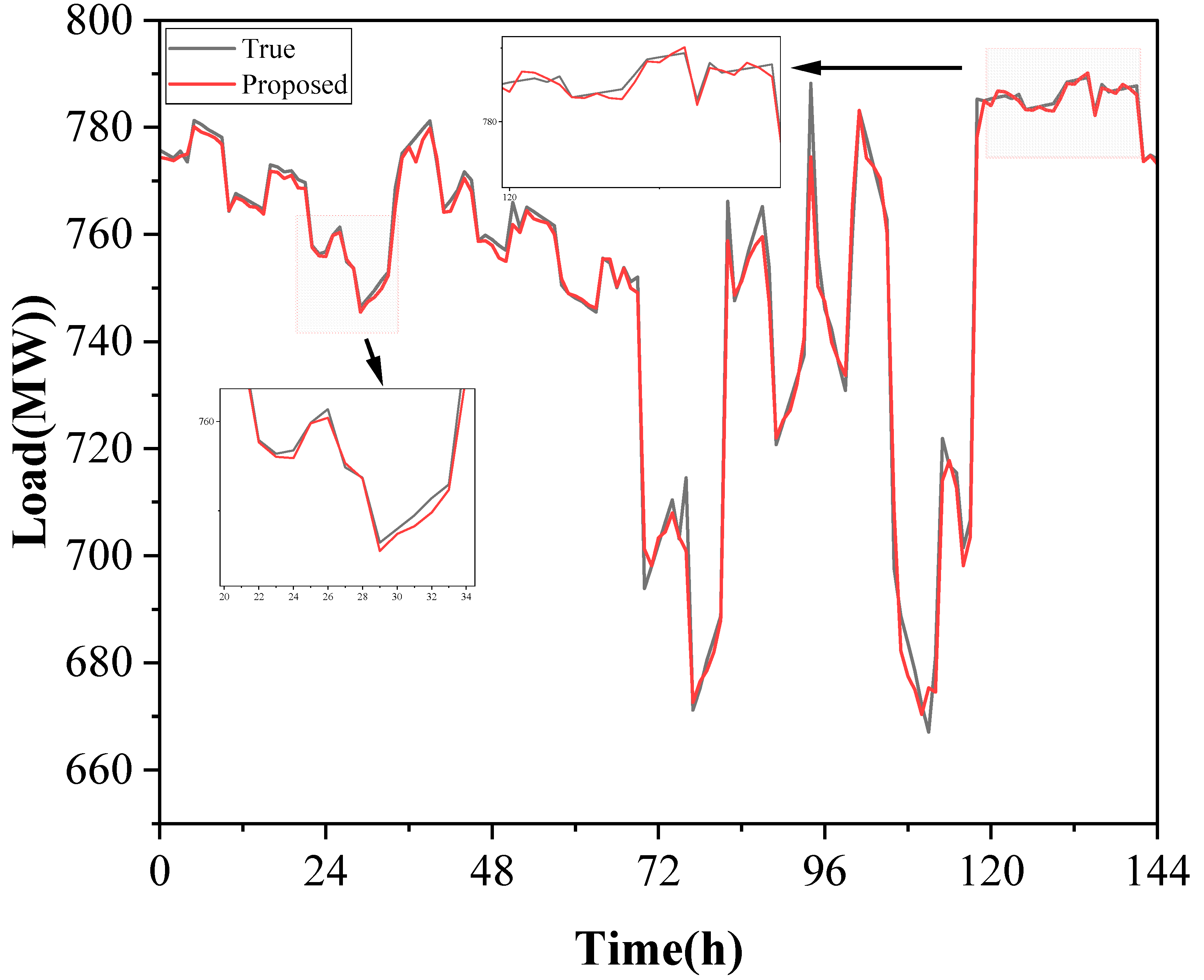
| Forecasting Model | RMSE (MW) | MAE (MW) | MAPE (%) | R2 |
|---|---|---|---|---|
| Proposed | 13.4910 | 2.4764 | 0.3934 | 0.9873 |
| VMD + Informer + BIGRU | 19.8362 | 2.8849 | 0.4569 | 0.9813 |
| VMD + BIGRU | 24.9529 | 3.6625 | 0.5821 | 0.9764 |
| BIGRU | 32.6001 | 4.5581 | 0.7582 | 0.9638 |
| Forecasting Model | RMSE (MW) | MAE (MW) | MAPE (%) | R2 |
|---|---|---|---|---|
| Proposed | 10.0276 | 2.1844 | 0.2931 | 0.9896 |
| VMD + Informer + BIGRU | 14.2988 | 2.8880 | 0.3863 | 0.9822 |
| VMD + BIGRU | 19.8578 | 3.2298 | 0.4078 | 0.9795 |
| BIGRU | 30.7696 | 4.7782 | 0.6209 | 0.9621 |
| Decomposition Method | Forecasting Model | Evaluation Metrics | |||
|---|---|---|---|---|---|
| RMSE (MW) | MAE (MW) | MAPE (%) | R2 | ||
| Proposed | Proposed | 13.4910 | 2.4764 | 0.3934 | 0.9873 |
| GRU | 26.6500 | 3.5556 | 0.5630 | 0.9748 | |
| BIGRU | 19.7821 | 2.7768 | 0.4378 | 0.9803 | |
| Informer | 38.9499 | 3.7252 | 0.5879 | 0.9632 | |
| VMD | Proposed | 19.8362 | 2.8849 | 0.4569 | 0.9813 |
| GRU | 26.6500 | 3.9556 | 0.6630 | 0.9748 | |
| BIGRU | 24.9529 | 3.6625 | 0.5821 | 0.9764 | |
| Informer | 41.3376 | 4.5571 | 0.7263 | 0.9610 | |
| STL | Proposed | 49.2103 | 4.8283 | 0.7673 | 0.9536 |
| GRU | 95.2175 | 7.9350 | 1.1803 | 0.9101 | |
| BIGRU | 61.8220 | 6.2445 | 1.0014 | 0.9417 | |
| Informer | 116.7262 | 9.3450 | 1.3593 | 0.8898 | |
| CEEMD | Proposed | 32.6542 | 4.4334 | 0.7067 | 0.9692 |
| GRU | 62.3968 | 5.0029 | 0.8792 | 0.9412 | |
| BIGRU | 44.2110 | 4.7052 | 0.7612 | 0.9583 | |
| Informer | 87.0930 | 7.3448 | 1.2826 | 0.9178 | |
| EMD | Proposed | 57.2780 | 5.0476 | 0.8588 | 0.9460 |
| GRU | 88.9855 | 6.9149 | 0.8126 | 0.9160 | |
| BIGRU | 85.0418 | 6.3420 | 0.6826 | 0.9197 | |
| Informer | 102.5272 | 7.1956 | 0.9764 | 0.9032 | |
| Decomposition Method | Forecasting Model | Evaluation Metrics | |||
|---|---|---|---|---|---|
| RMSE (MW) | MAE (MW) | MAPE (%) | R2 | ||
| Proposed | Proposed | 10.0276 | 2.1844 | 0.2931 | 0.9896 |
| GRU | 22.0870 | 3.6171 | 0.4840 | 0.9773 | |
| BIGRU | 16.8595 | 2.7426 | 0.3691 | 0.9826 | |
| Informer | 33.9730 | 3.7129 | 0.5015 | 0.9650 | |
| VMD | Proposed | 14.2988 | 2.8880 | 0.3863 | 0.9822 |
| GRU | 26.1351 | 3.6466 | 0.4305 | 0.9731 | |
| BIGRU | 19.8578 | 3.2298 | 0.4078 | 0.9795 | |
| Informer | 35.2796 | 4.3651 | 0.5878 | 0.9637 | |
| STL | Proposed | 48.4631 | 4.9510 | 0.6663 | 0.9502 |
| GRU | 72.2094 | 6.8342 | 0.8223 | 0.9258 | |
| BIGRU | 57.0786 | 5.4687 | 0.7031 | 0.9413 | |
| Informer | 100.6742 | 7.1747 | 0.9624 | 0.8965 | |
| CEEMD | Proposed | 34.8901 | 3.9259 | 0.5307 | 0.9641 |
| GRU | 56.1002 | 5.4158 | 0.6958 | 0.9423 | |
| BIGRU | 48.3011 | 4.8123 | 0.6462 | 0.9503 | |
| Informer | 70.2164 | 6.6317 | 0.8509 | 0.9278 | |
| EMD | Proposed | 54.0975 | 4.8922 | 0.6553 | 0.9444 |
| GRU | 74.8017 | 6.2771 | 0.8704 | 0.9231 | |
| BIGRU | 69.3855 | 6.0497 | 0.8166 | 0.9287 | |
| Informer | 79.3710 | 7.7964 | 0.9501 | 0.9084 | |
| Forecasting Model | RMSE (MW) | MAE (MW) | MAPE (%) | R2 |
|---|---|---|---|---|
| Proposed | 13.4910 | 2.4764 | 0.3934 | 0.9873 |
| Without STL | 19.8362 | 2.8849 | 0.4569 | 0.9813 |
| Without STL + ALA | 21.6321 | 3.8641 | 0.5232 | 0.9732 |
| Without STL + ALA + MIC | 22.2368 | 4.1635 | 0.6421 | 0.9692 |
| Forecasting Model | RMSE (MW) | MAE (MW) | MAPE (%) | R2 |
|---|---|---|---|---|
| Proposed | 10.0276 | 2.1844 | 0.2931 | 0.9896 |
| VMD + Informer + BIGRU | 14.2988 | 2.8880 | 0.3863 | 0.9822 |
| VMD + BIGRU | 19.8578 | 3.2298 | 0.4078 | 0.9795 |
| BIGRU | 30.7696 | 4.7782 | 0.6209 | 0.9621 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shi, Y.; Zhang, N.; Chen, Y. A Short-Term Load Forecasting Method for Typical High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks. Appl. Sci. 2025, 15, 9578. https://doi.org/10.3390/app15179578
Li J, Shi Y, Zhang N, Chen Y. A Short-Term Load Forecasting Method for Typical High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks. Applied Sciences. 2025; 15(17):9578. https://doi.org/10.3390/app15179578
Chicago/Turabian StyleLi, Jingyu, Yu Shi, Na Zhang, and Yuanyu Chen. 2025. "A Short-Term Load Forecasting Method for Typical High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks" Applied Sciences 15, no. 17: 9578. https://doi.org/10.3390/app15179578
APA StyleLi, J., Shi, Y., Zhang, N., & Chen, Y. (2025). A Short-Term Load Forecasting Method for Typical High Energy-Consuming Industrial Parks Based on Multimodal Decomposition and Hybrid Neural Networks. Applied Sciences, 15(17), 9578. https://doi.org/10.3390/app15179578





