Inversion Analysis of Stress Fields Based on the LSTM–Attention Neural Network
Abstract
1. Introduction
2. Inversion of the Non-Linear Geostress Field
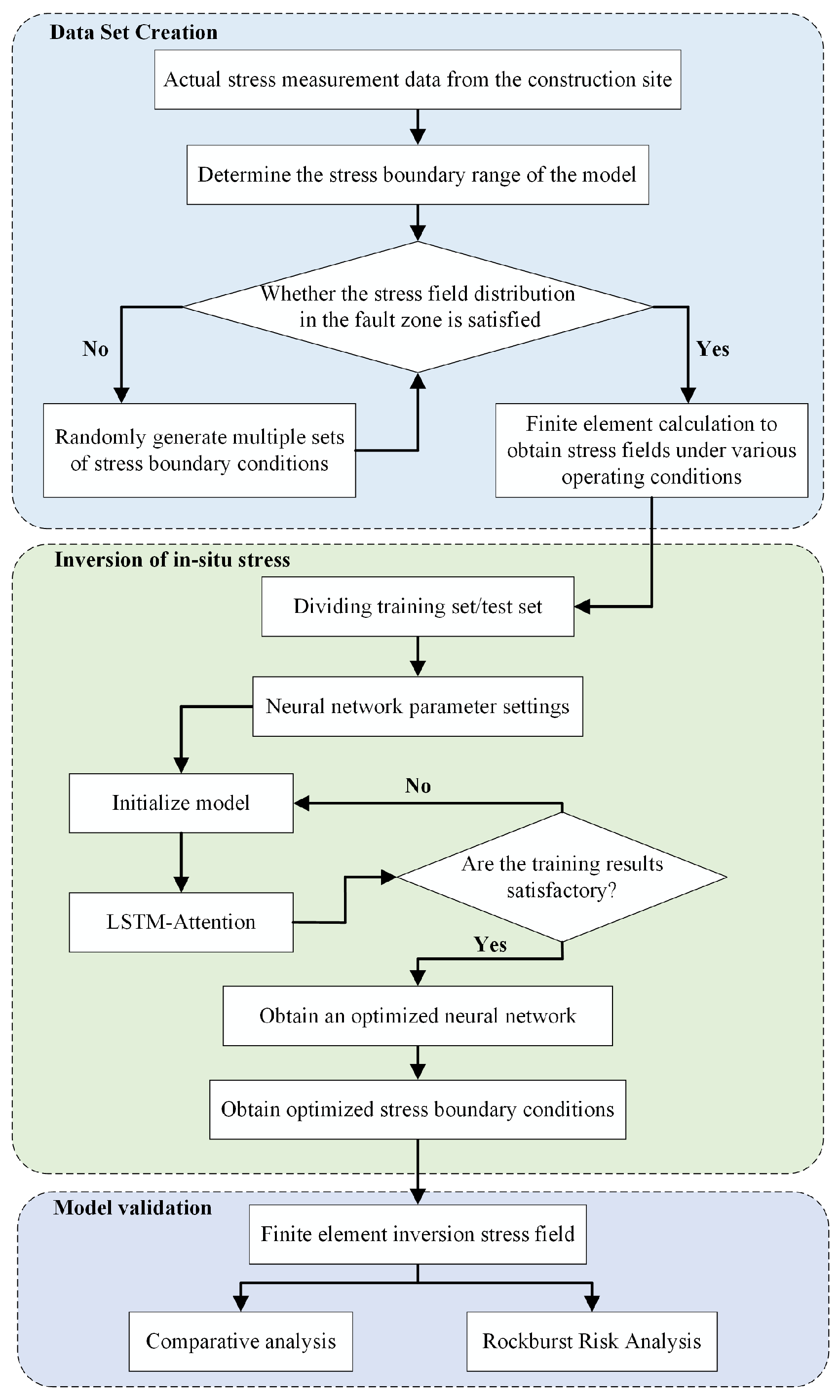
2.1. Basic Procedure of Inversion
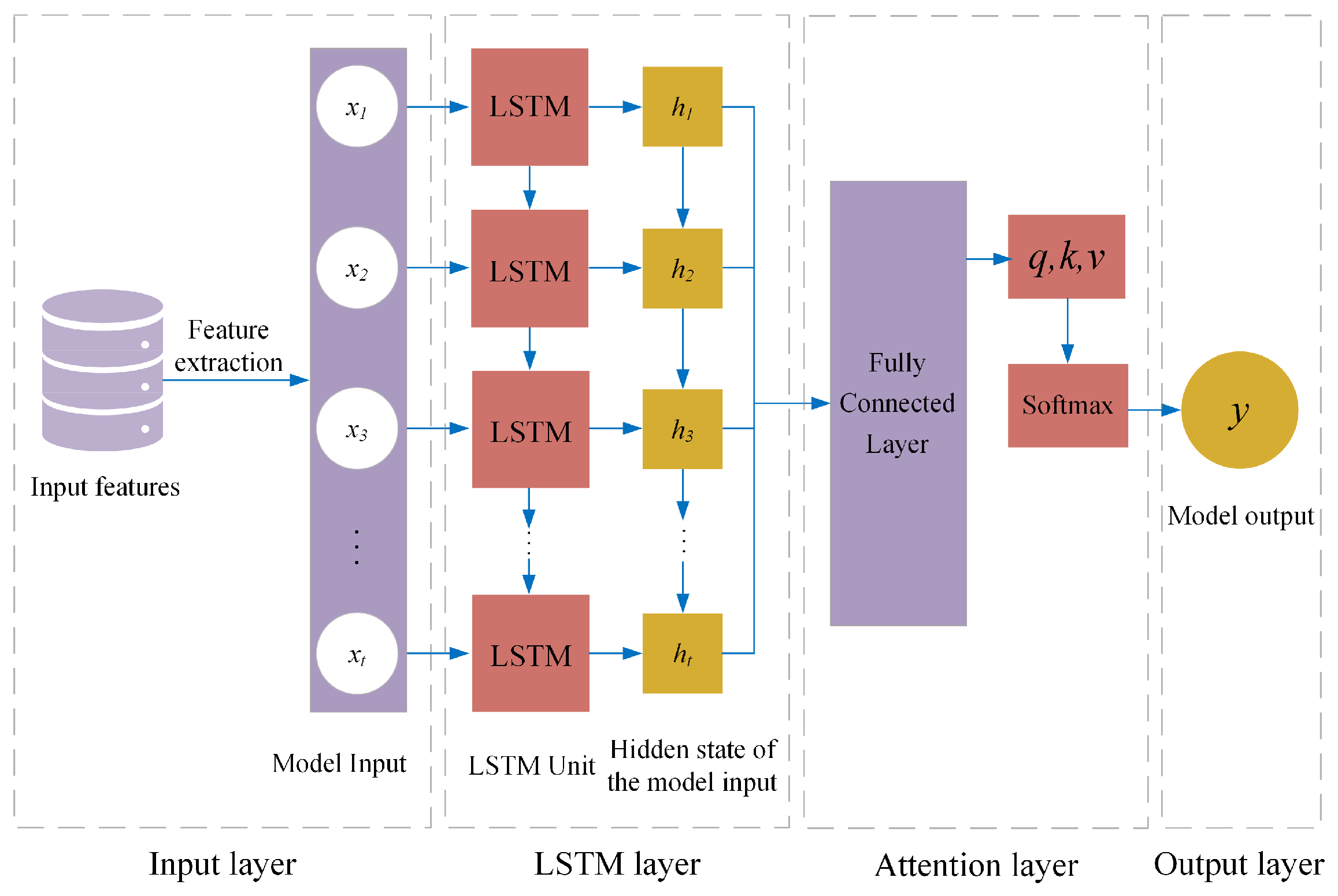
2.2. LSTM–Attention Neural Network Algorithm
3. Calculation of Geostress Around a Hydropower Station
3.1. Overview of Engineering Geology
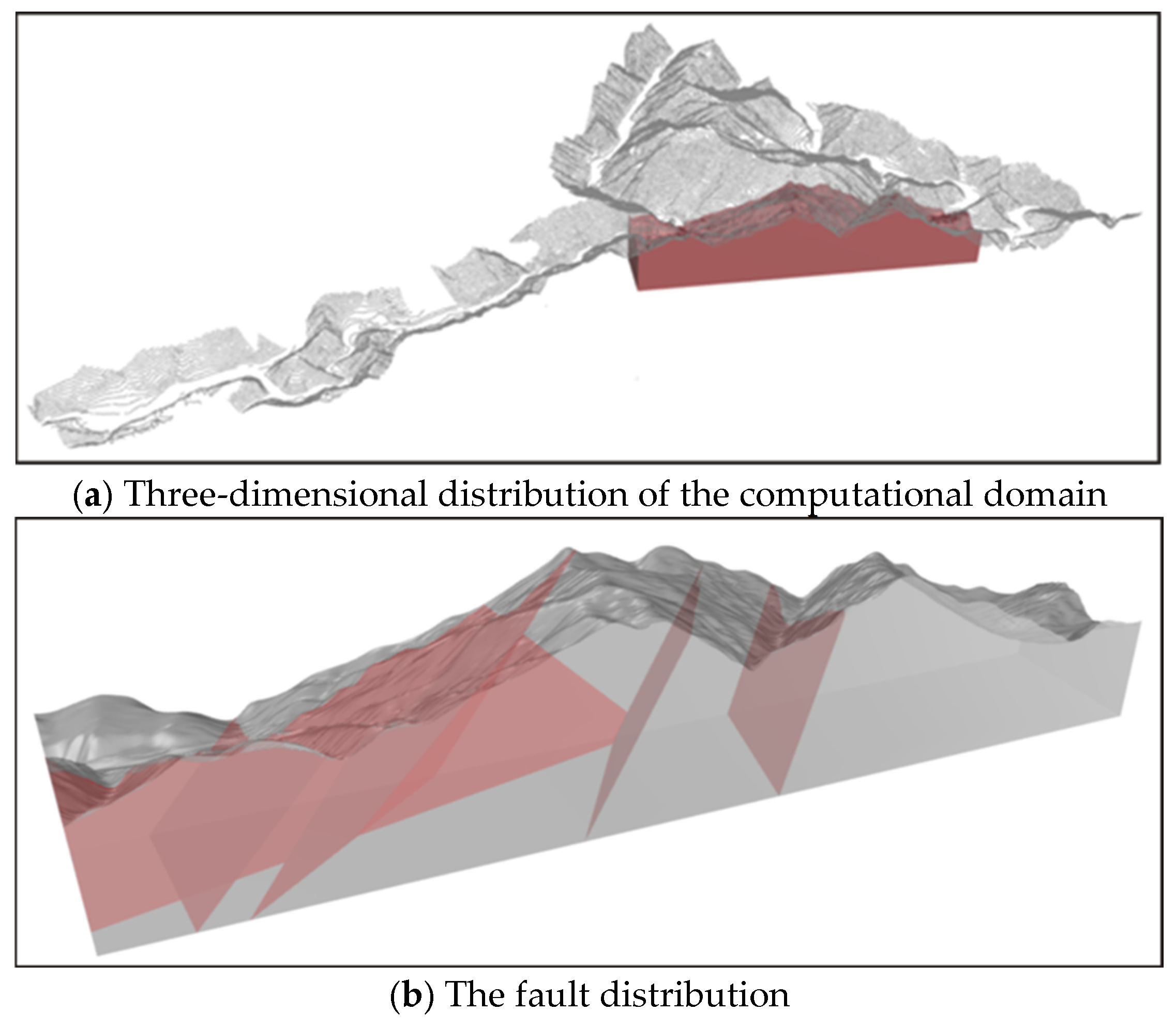
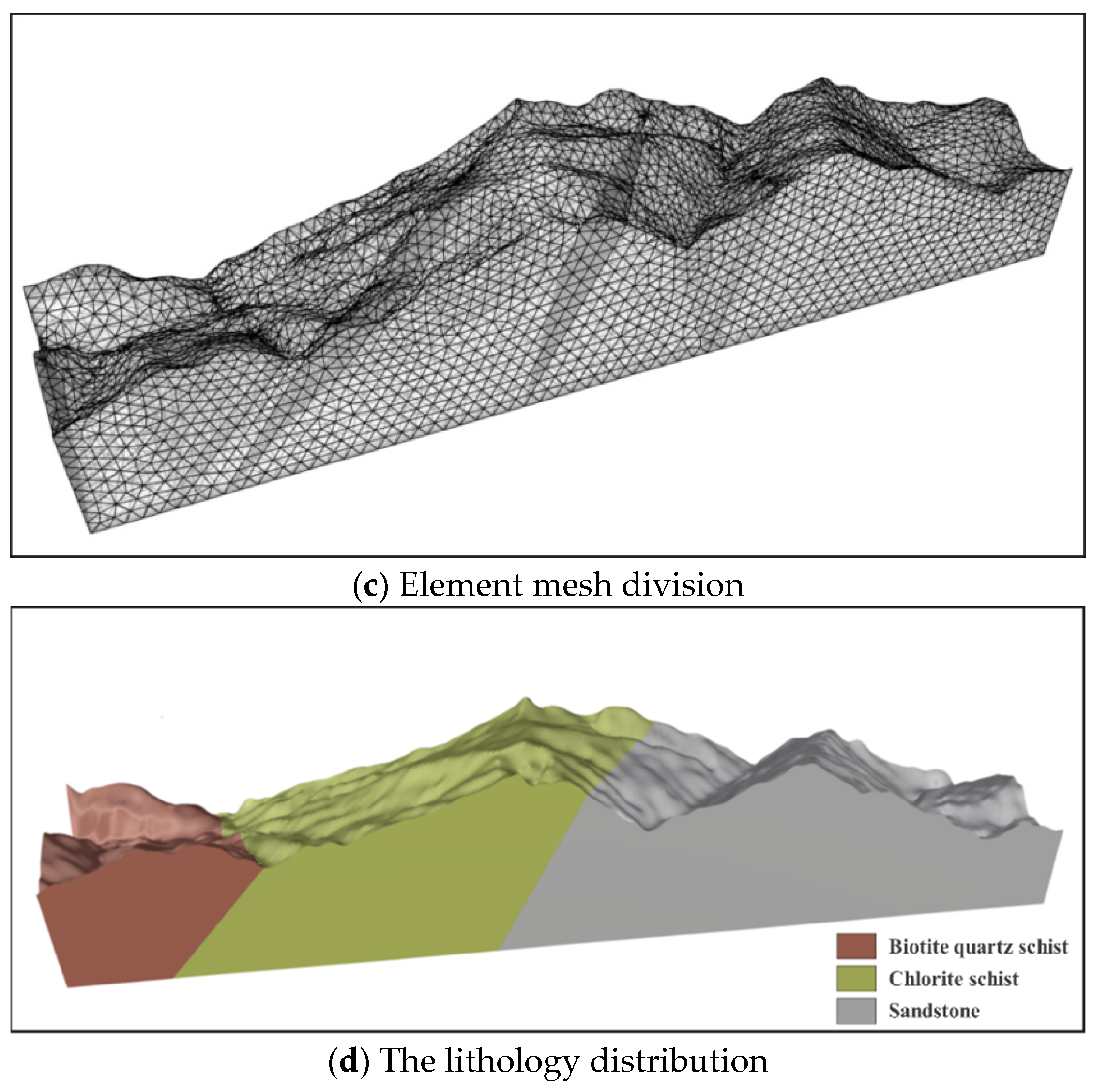
3.2. Computational Model
3.3. Geostress Measurement Results
4. Inversion of the Geostress Field
4.1. Inversion Process of the Geostress Field
4.1.1. Boundary Conditions of the Model
4.1.2. Data Preprocessing
4.1.3. Training of the LSTM–Attention Neural Network
4.1.4. Calculation and Optimization of the Measured Stress Field
4.2. Geostress Inversion Results
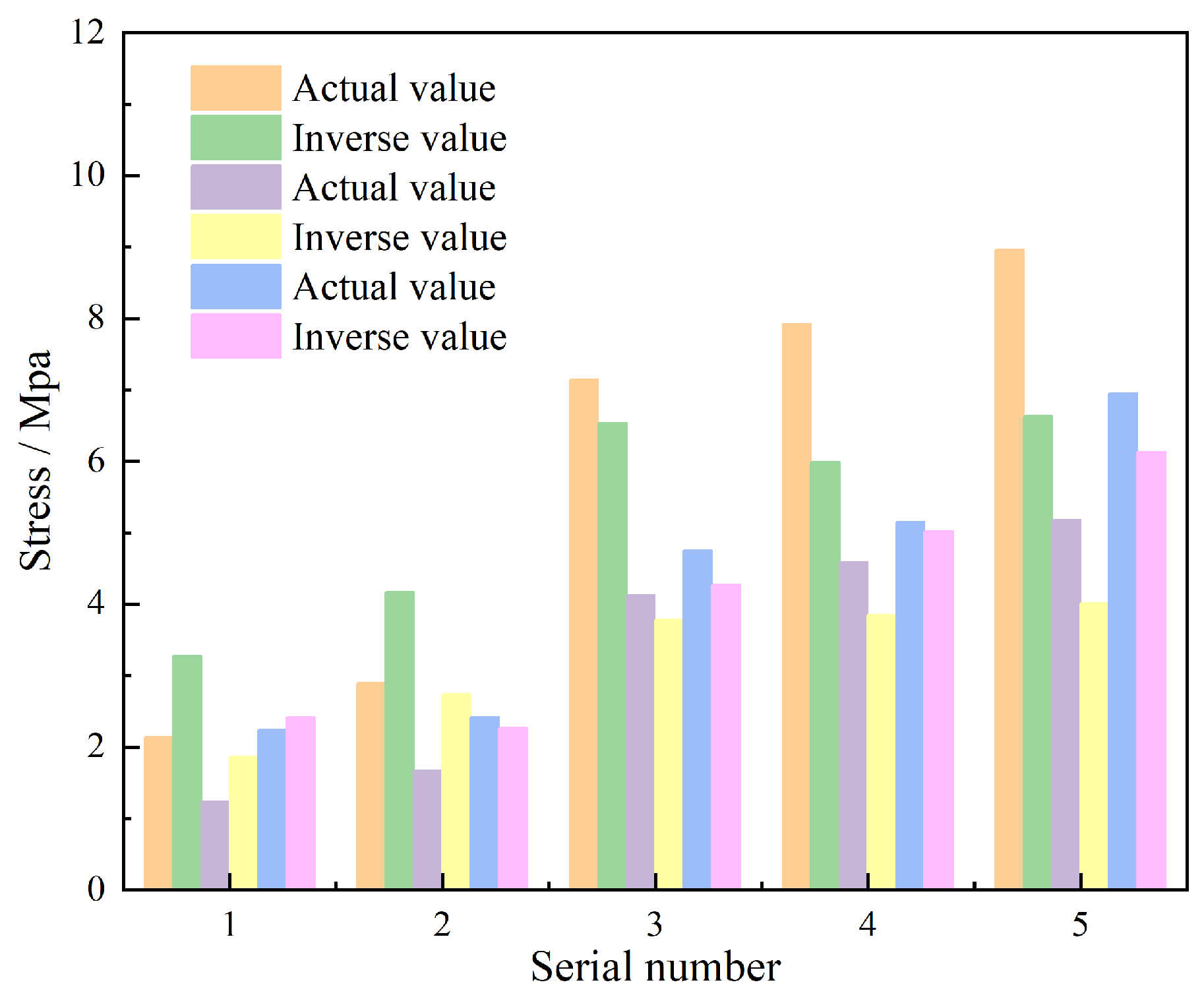
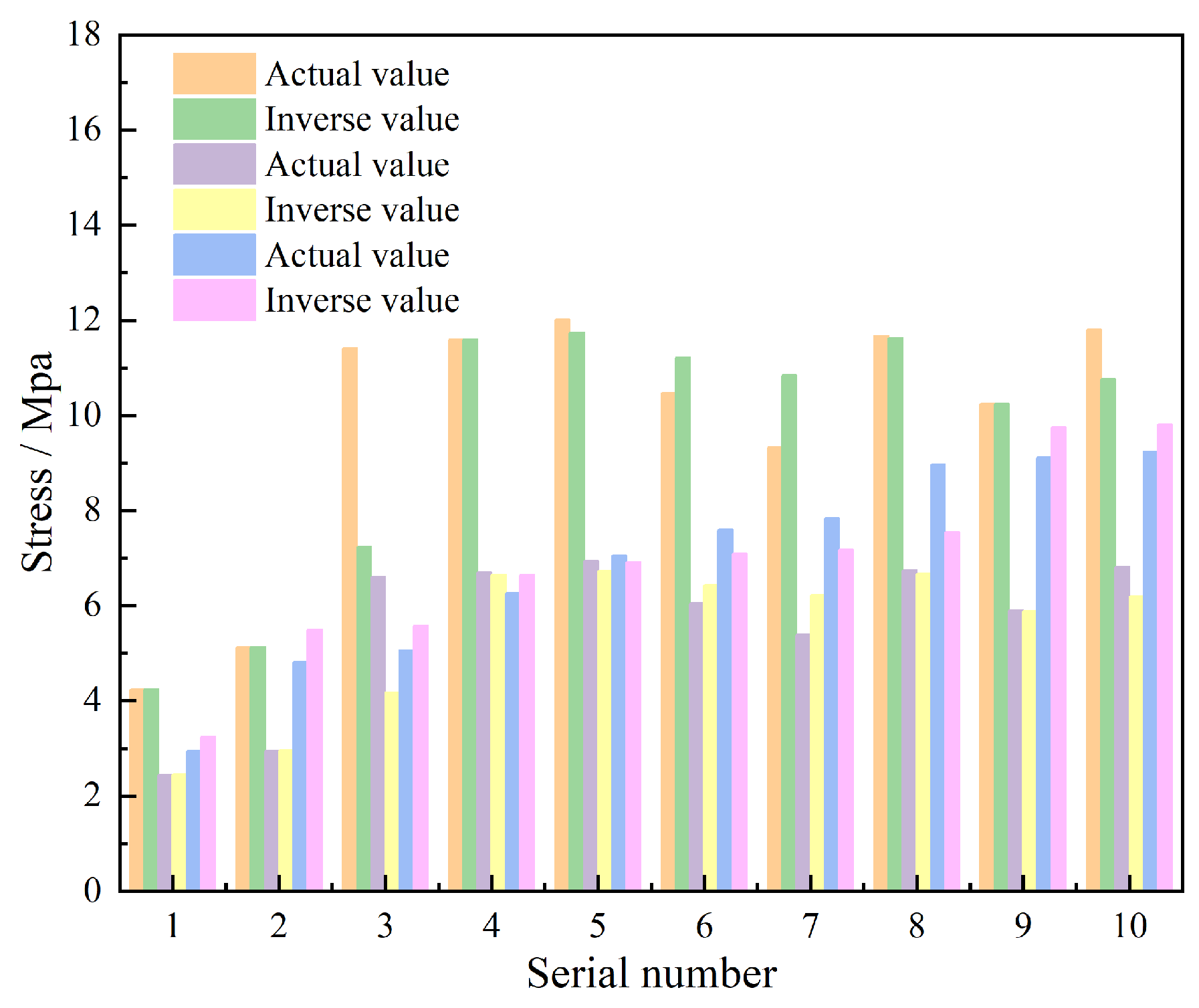
4.2.1. Comparison of Inversion and Measured Values of Geostress
4.2.2. Model Robustness Analysis
4.2.3. Comparison and Analysis of Other Models
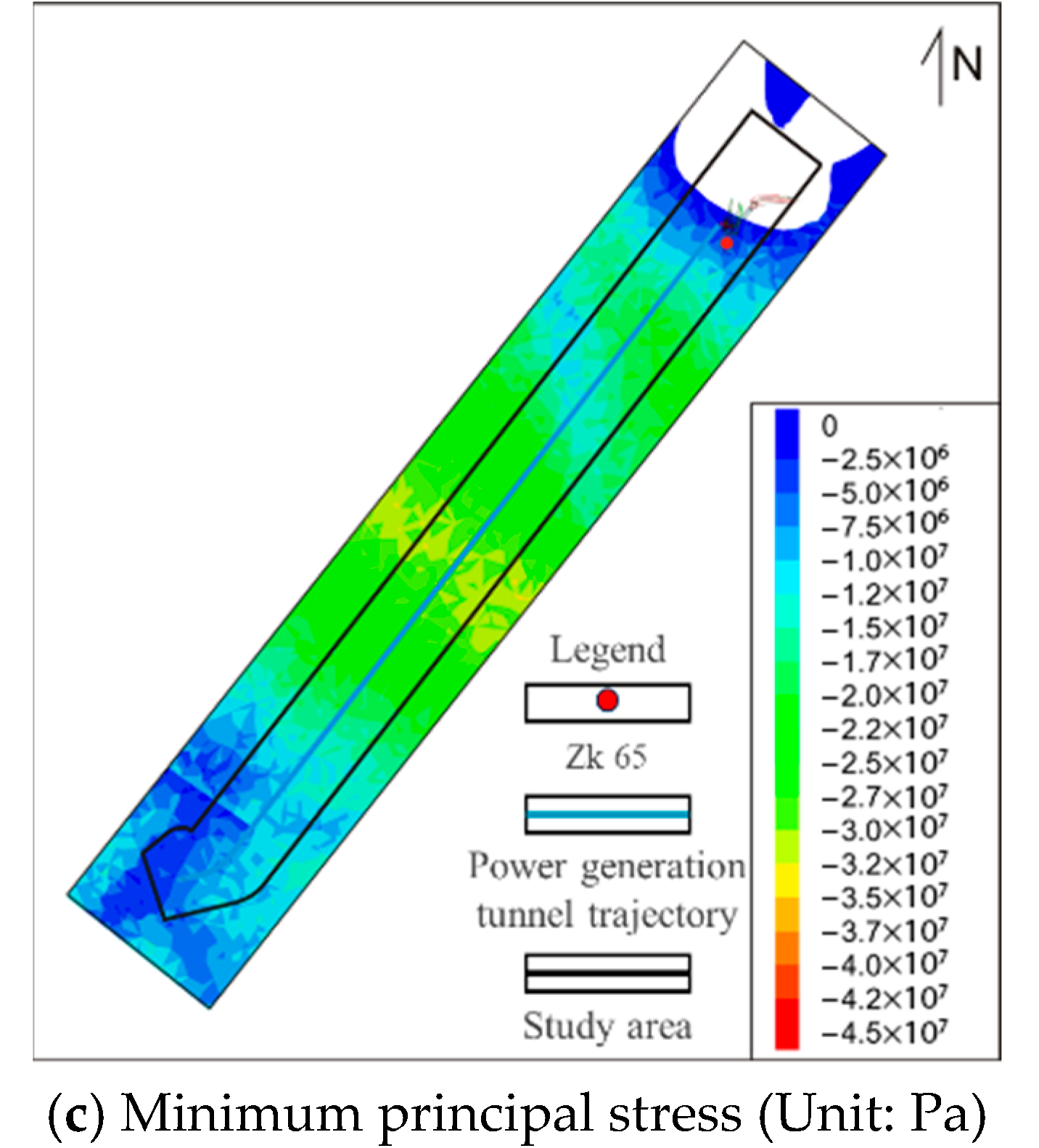
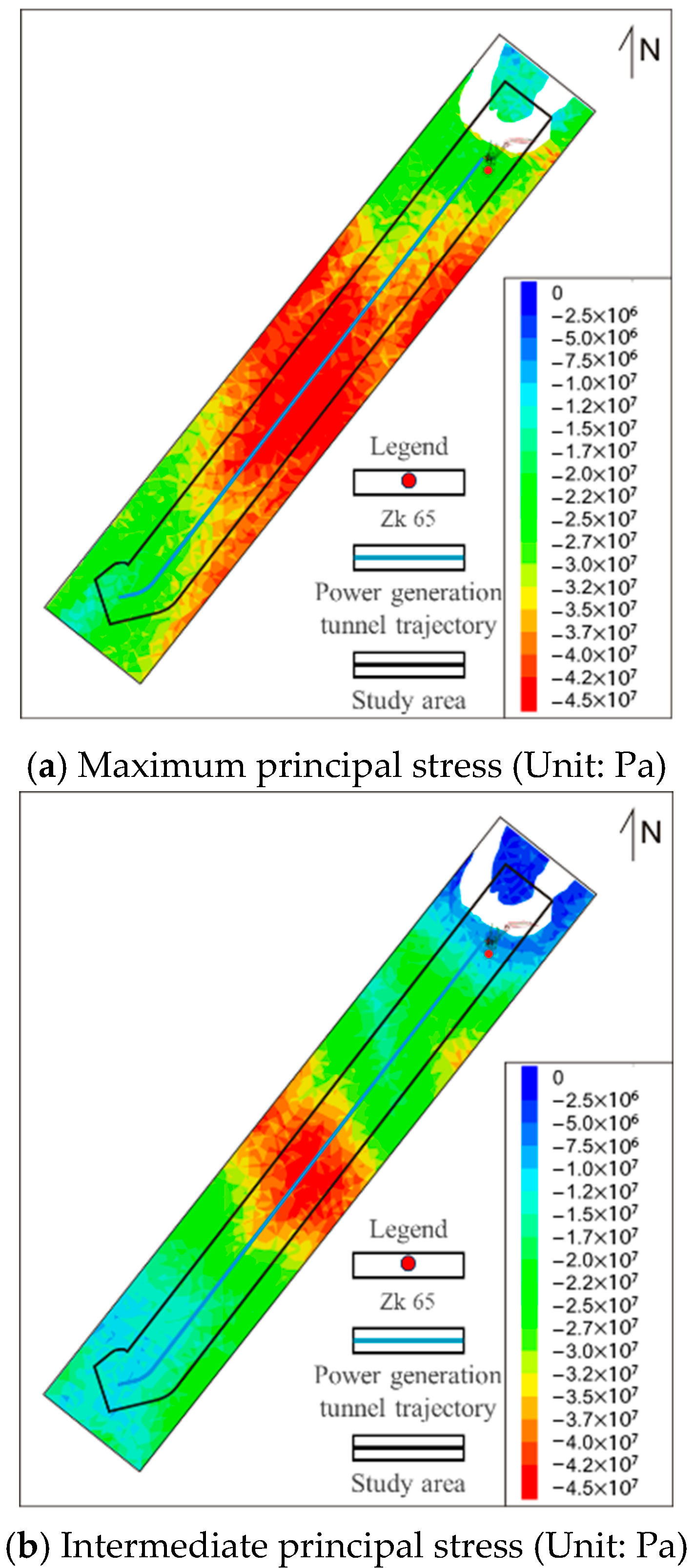
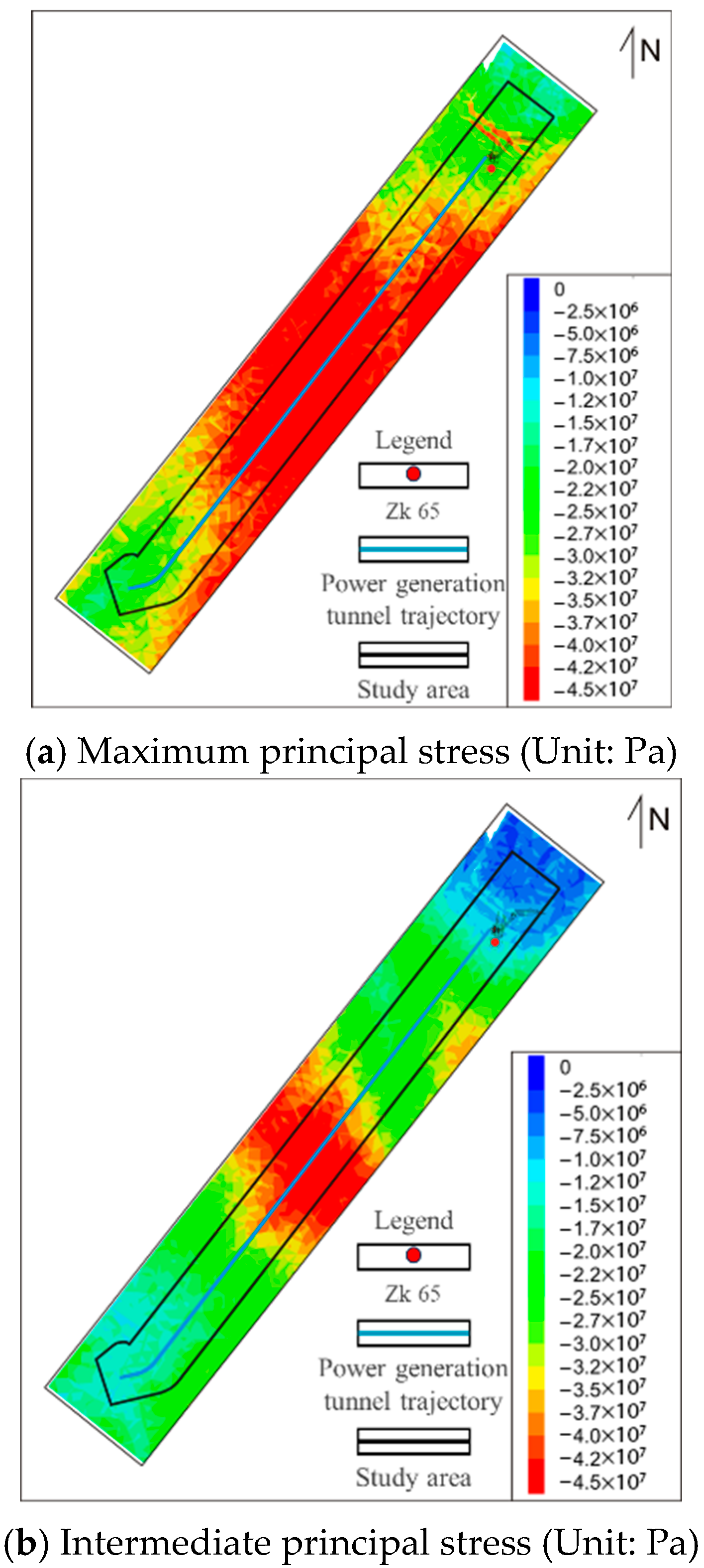
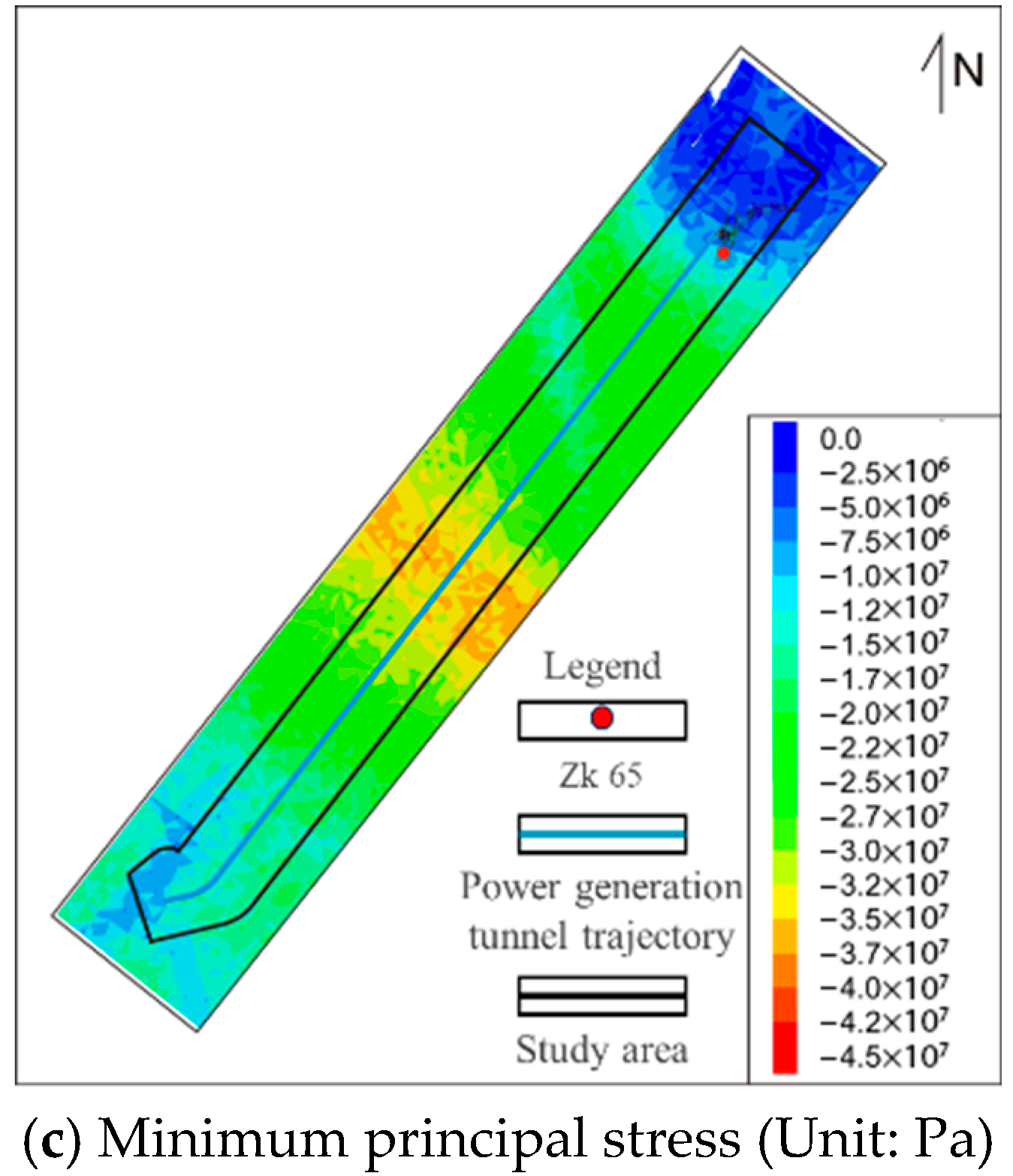
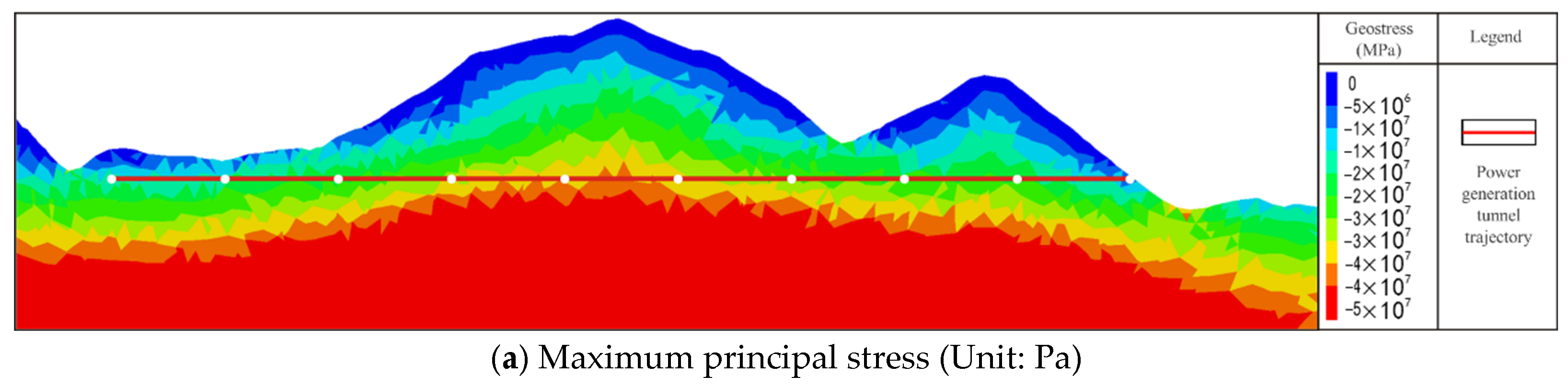
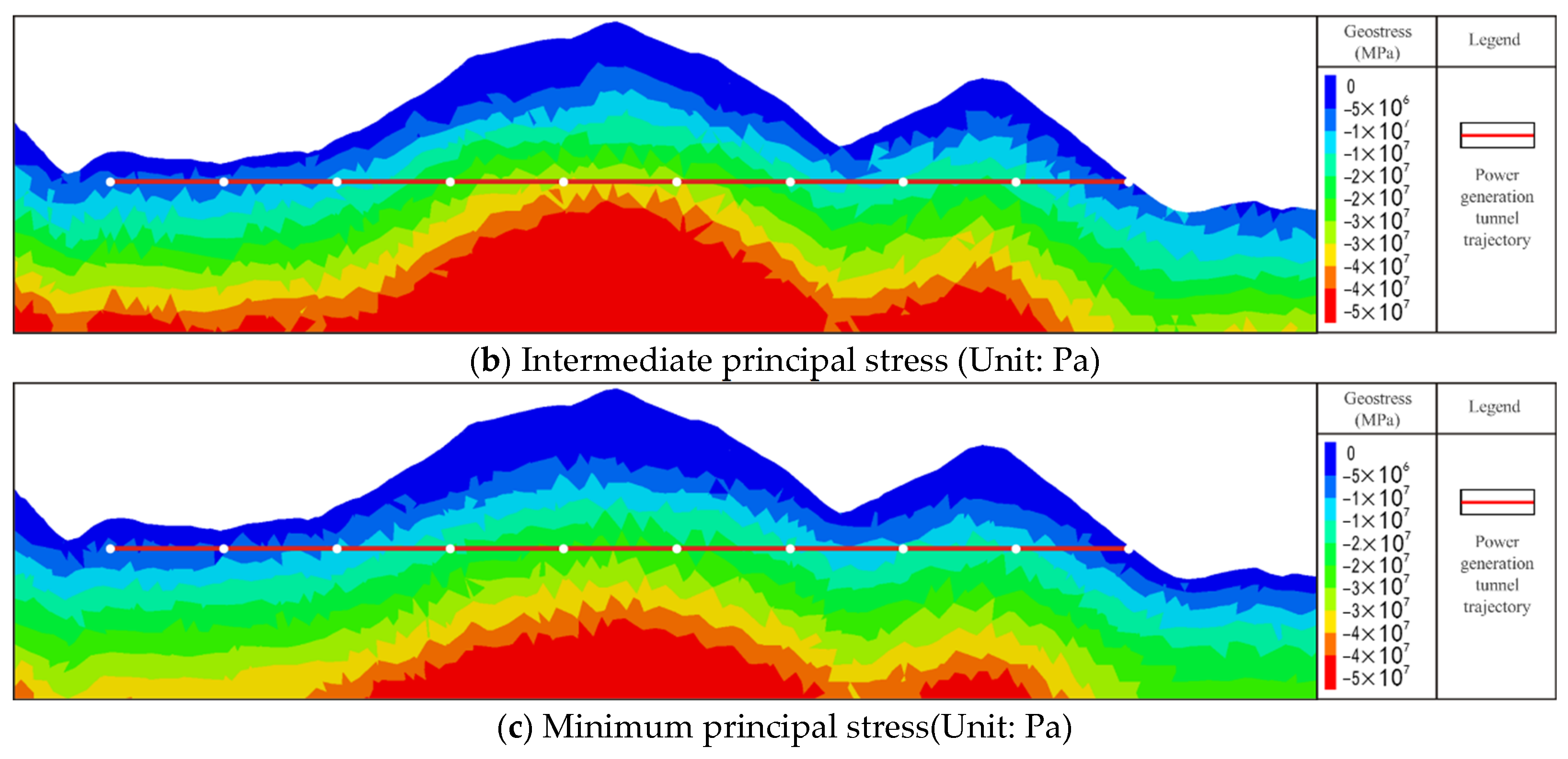
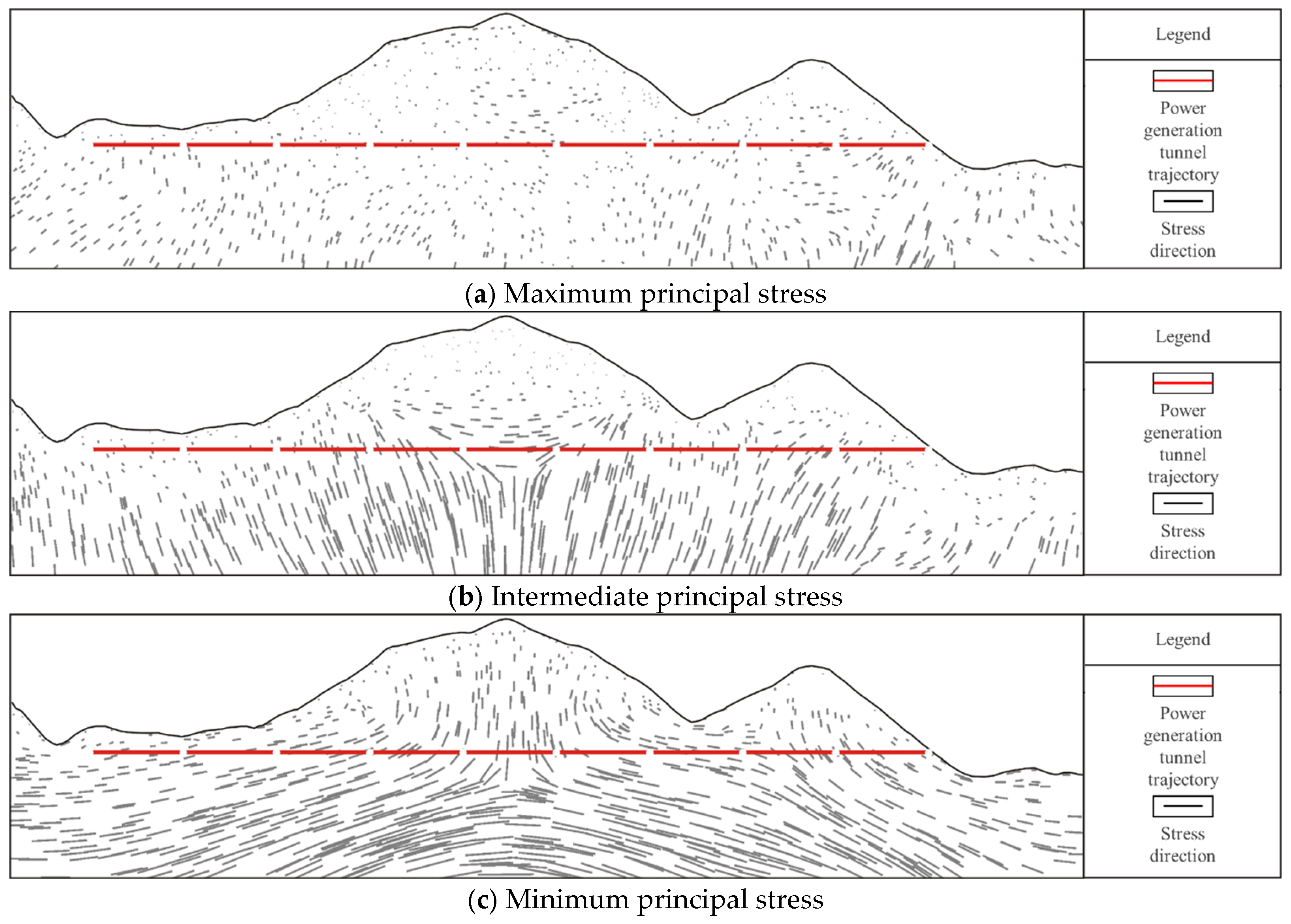
4.2.4. Distribution of the Regional Stress Field
4.3. Rockburst Risk Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Z.Q.; Wang, C.Y.; Wang, Y.T.; Wang, C. Borehole cross-sectional shape analysis under in situ stress. Int. J. Geomech. 2020, 20, 04020045. [Google Scholar] [CrossRef]
- Lakirouhani, A.; Detournay, E.; Bunger, A.P. A reassessment of in situ stress determination by hydraulic fracturing. Geophys. J. Int. 2016, 205, 1859–1873. [Google Scholar] [CrossRef]
- Huang, J.S.; Griffiths, D.V.; Wong, S.-W. In situ stress determination from inversion of hydraulic fracturing data. Int. J. Rock Mech. Min. Sci. 2011, 48, 476–481. [Google Scholar] [CrossRef]
- Zhang, L.M.; Zhang, D.; Cong, Y.; Wang, Z.Q.; Wang, X.S. Constructing a three-dimensional creep model for rocks and soils based on memory-dependent derivatives: A theoretical and experimental study. Comput. Geotech. 2023, 159, 105366. [Google Scholar] [CrossRef]
- Li, F.; Zhou, J.X.; Wang, J.A. Nonlinear in-situ stress construction method for deep multi-field coupling effects. J. China Coal Soc. 2021, 46 (Suppl. S1), 116–129. [Google Scholar]
- Liu, X.G.; Huang, C.C.; Zhu, W.C.; Oh, J.; Zhang, C.G.; Si, G.Y. In situ stress inversion using nonlinear stress boundaries achieved by the bubbling method. J. Rock Mech. Geotech. Eng. 2024, 17, 1510–1527. [Google Scholar] [CrossRef]
- Jayasinghe, L.B.; Shang, J.L.; Zhao, Z.Y.; Goh, A.T.C. Numerical investigation into the blasting-induced damage characteristics of rocks considering the role of in-situ stresses and discontinuity persistence. Comput. Geotech. 2019, 116, 103207. [Google Scholar] [CrossRef]
- Hu, Z.H.; Wu, B.B.; Xu, N.W.; Wang, K. Effects of discontinuities on stress redistribution and rock failure: A case of underground caverns. Tunn. Undergr. Space Technol. 2022, 127, 104583. [Google Scholar] [CrossRef]
- Wang, B.L.; Ma, Q.C. Boundary element analysis methods for ground stress field of rock masses. Comput. Geotech. 1986, 2, 261–274. [Google Scholar] [CrossRef]
- Zhang, L.M.; Cong, Y.; Meng, F.Z.; Wang, Z.Q.; Zhang, P.; Gao, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2021, 16, 569–580. [Google Scholar] [CrossRef]
- Liu, J.S.; Ding, W.L.; Yang, H.M.; Wang, R.Y.; Yin, S.; Li, A.; Fu, F.Q. 3D geomechanical modeling and numerical simulation of in-situ stress fields in shale reservoirs: A case study of the lower Cambrian Niutitang formation in the Cen’gong block, South China. Tectonophysics 2017, 712, 663–683. [Google Scholar] [CrossRef]
- Zhao, H.J.; Ma, F.S.; Xu, J.M.; Guo, J. In situ stress field inversion and its application in mining-induced rock mass movement. Int. J. Rock Mech. Min. Sci. 2012, 53, 120–128. [Google Scholar] [CrossRef]
- Liang, J.; Zhu, Q.J.; Sui, L.K.; Duan, L.; Wang, D.C. Research on elaborate construction of complex 3D geological model and in-situ Stress inversion. Geotech. Geol. Eng. 2024, 42, 1373–1388. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Chen, Z.Q.; Wang, B.; Jiang, C.W.; Li, T.S.; Meng, W. Study on the applicability of various in-situ stress inversion methods and their application on sinistral strike-slip faults. Rock Mech. Rock Eng. 2023, 56, 3093–3113. [Google Scholar] [CrossRef]
- Song, W.H.; Jiao, H.C.; Xu, X.T.; He, P. An optimized modeling for in-situ stresses based on Rhino accurate modeling and large-scale transverse isotropic theory. Sci. Rep. 2023, 13, 691. [Google Scholar] [CrossRef] [PubMed]
- Oral, E.; Ampuero, J.P.; Ruiz, J.; Asimaki, D. A Method to Generate Initial Fault Stresses for Physics-Based Ground-Motion Prediction Consistent with Regional Seismicity. Bull. Seismol. Soc. Am. 2022, 112, 2812–2827. [Google Scholar] [CrossRef]
- Sun, L.N.; Liu, S.C.; Zhang, L.M.; He, K.Q.; Yan, X.Z. Prediction of the displacement in a foundation pit based on neural network model fusion error and variational modal decomposition methods. Measurement 2025, 240, 115534. [Google Scholar] [CrossRef]
- Zhang, K.H.; Zhou, Y.S.; Liu, Y.M.; Wang, P. Mechanism for seismic supershear dynamic rupture based on in-situ stress: A case study of the Palu earthquake in 2018. Geomat. Nat. Hazards Risk 2022, 13, 1987–2005. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Michael, A.J. Damped regional-scale stress inversions: Methodology and examples for southern California and the Coalinga aftershock sequence. J. Geophys. Res. 2006, 111, B11310. [Google Scholar] [CrossRef]
- Vavrycuk, V. Iterative joint inversion for stress and fault orientations from focal mechanisms. Geophys. J. Int. 2014, 199, 69–77. [Google Scholar] [CrossRef]
- Schliwa, N.; Gabriel, A.A.; Premus, J.; Gallovic, F. The Linked Complexity of Coseismic and Postseismic Faulting Revealed by Seismo-Geodetic Dynamic Inversion of the 2004 Parkfield Earthquake. J. Geophys. Res.-Solid Earth 2024, 129, e2024JB029410. [Google Scholar] [CrossRef]
- Zhang, B.J.; Tan, Z.S.; Zhao, J.P.; Wang, F.X.; Lin, K. Research on stress field inversion and large deformation level determination of super deep buried soft rock tunnel. Sci. Rep. 2024, 14, 12739. [Google Scholar] [CrossRef] [PubMed]
- Thakur, P.; Srivastava, D.C.; Gupta, P.K. The genetic algorithm: A robust method for stress inversion. J. Struct. Geol. 2017, 94, 227–239. [Google Scholar] [CrossRef]
- Zhang, C.; Shen, B.; Liu, G.W. 3D in-situ stress inversion technology for a long-deep tunnel on Haoji Railway. J. Railw. Eng. Soc. 2022, 39, 30–34. [Google Scholar]
- Li, G.; Hu, Y.; Li, Q.B.; Yin, T.; Miao, J.X.; Yao, M.D. Inversion method of in-situ stress and rock damage characteristics in dam site using neural network and numerical simulation-a case study. IEEE Access 2020, 8, 46701–46712. [Google Scholar] [CrossRef]
- Fu, H.L.; Li, J.; Li, G.L.; Chen, J.J.; An, P.T. Determination of in situ stress by inversion in a superlong tunnel site based on the variation law of stress-a case study. KSCE J. Civ. Eng. 2023, 27, 2637–2653. [Google Scholar] [CrossRef]
- Song, Z.B.; Jiang, Q.; Chen, P.F.; Xia, Y.; Xiang, T.B. Nonlinear Intelligent Inversion Method and Practice for In-situ Stress in Stratified Rock Masses with Deep Valley. Rock Mech. Rock Eng. 2024, 58, 1933–1955. [Google Scholar] [CrossRef]
- Zhou, J.X.; Wang, J.A.; Li, F. Inversion method of in-situ stress field in discontinuous zones of deep coal seams. J. Tsinghua Univ. (Sci. Technol.) 2024, 64, 2166–2176. [Google Scholar]
- Li, L.; Zhang, R.X.; Sun, J.D.; He, Q.; Kong, L.Z.; Liu, X. Monitoring and prediction of dust concentration in an open-pit mine using a deep-learning algorithm. J. Environ. Health Sci. Eng. 2021, 19, 401–414. [Google Scholar] [CrossRef]
- Zhang, L.M.; Chao, W.W.; Liu, Z.Y.; Cong, Y.; Wang, Z.Q. Crack propagation characteristics during progressive failure of circular tunnels and the early warning thereof based on multi-sensor data fusion. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 172. [Google Scholar] [CrossRef]
- Mubarak, H.; Stegen, S.; Bai, F.F.; Abdellatif, A.; Sanjari, M.J. Enhancing interpretability in power management: A time-encoded household energy forecasting using hybrid deep learning model. Energy Convers. Manag. 2024, 315, 118795. [Google Scholar] [CrossRef]
- Shi, P.; Chen, Z.H. Inversion analysis and application of initial in-situ stress field based on finite element analysis and multiple linear regression. Mech. Res. 2022, 11, 69–78. [Google Scholar]
- Dai, J.H.; Gong, F.Q.; Xu, L. Rockburst criterion and evaluation method for potential rockburst pit depth considering excavation damage effect. J. Rock Mech. Geotech. Eng. 2024, 16, 1649–1666. [Google Scholar] [CrossRef]
- Farhadian, H. A new empirical chart for rockburst analysis in tunnelling: Tunnel rockburst classification (TRC). Int. J. Min. Sci. Technol. 2021, 31, 603–610. [Google Scholar] [CrossRef]
- Zhang, L.M.; Wang, X.S.; Cong, Y.; Wang, Z.Q.; Liu, J. Transfer mechanism and criteria for static–dynamic failure of granite under true triaxial unloading test. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 104. [Google Scholar] [CrossRef]
- Gong, F.Q.; Dai, J.H.; Xu, L. A strength-stress coupling criterion for rockburst: Inspirations from 1114 rockburst cases in 197 underground rock projects. Tunn. Undergr. Space Technol. 2023, 142, 105396. [Google Scholar] [CrossRef]
- Ministry of Construction of the People’s Republic of China. National Standard of the People’s Republic of China: Standard for Engineering Classification of Rock Masses; China Planning Press: Beijing, China, 1995.



| Serial Number of Fault Groups | Occurrence | Included Angle with the Chamber Axis |
|---|---|---|
| 1 | 110~25° NW∠35~66° | Large |
| 2 | 310~330° SW∠35~48° | Large |
| 3 | 335~340° SW∠55~70° | Large |
| 4 | 15~30° NW∠55~60° | 22~57° |
| 5 | 325~350° SW∠55~70° | 52~77° |
| 6 | 320° SW (NE)∠75° | 82° |
| Lithology | Elastic Modulus /GPa | Poisson’s Ratio | Density /(kg/m3) |
|---|---|---|---|
| Biotite quartz schist | 41.33 | 0.23 | 2730 |
| Chlorite schist | 48.29 | 0.22 | 2800 |
| Sandstone | 64.08 | 0.22 | 2650 |
| Fault Parameters | Normal Stiffness /GPa | Shear Stiffness /GPa | Cohesion /MPa | Internal Friction Angle /° |
| 20 | 15 | 0.22 | 15 |
| Borehole | Serial Number | Depth /m | Stress Value /MPa | Direction of SH /° | ||
|---|---|---|---|---|---|---|
| SH | Sh | Sv | ||||
| ZK59 | 1 | 36.00–36.80 | 12.11 | 7.25 | 6.04 | N3° W |
| 2 | 56.00–56.80 | 9.95 | 5.25 | 6.57 | ||
| 3 | 62.00–62.80 | 9.81 | 5.31 | 6.72 | N10° E | |
| 4 | 70.00–70.80 | 10.69 | 6.69 | 6.93 | ||
| 5 | 79.30–80.10 | 14.28 | 7.78 | 7.18 | ||
| ZK60 | 1 | 24.00–24.80 | 2.47 | 2.24 | 6.91 | |
| 2 | 43.00–43.80 | 3.34 | 2.42 | 7.41 | ||
| 3 | 56.00–56.80 | 8.25 | 4.75 | 7.75 | ||
| 4 | 66.00–66.80 | 9.15 | 5.15 | 8.02 | N8° E | |
| 5 | 76.30–77.10 | 10.35 | 6.95 | 8.29 | ||
| ZK65 | 1 | 112.40–113.20 | 4.90 | 3.10 | 2.94 | N17° W |
| 2 | 184.30–185.10 | 5.91 | 3.01 | 4.82 | ||
| 3 | 193.20–194.00 | 13.19 | 7.79 | 5.06 | ||
| 4 | 239.40–240.20 | 13.39 | 7.85 | 6.26 | ||
| 5 | 269.30–270.10 | 13.88 | 7.84 | 7.05 | ||
| 6 | 290.30–291.10 | 12.09 | 6.44 | 7.60 | ||
| 7 | 299.80–300.60 | 10.78 | 5.64 | 7.84 | ||
| 8 | 335.50–336.30 | 13.48 | 6.99 | 8.96 | ||
| 9 | 348.10–348.90 | 11.82 | 5.91 | 9.11 | ||
| 10 | 353.10–353.90 | 13.62 | 7.06 | 9.24 | ||
| Number | Boundary Direction | Gravitational Acceleration m/s2 | |
|---|---|---|---|
| x/MPa | y/MPa | ||
| 1 | 8 | 8 | 8 |
| 2 | 8 | 8 | 10 |
| 3 | 8 | 8 | 12 |
| 4 | 10 | 10 | 8 |
| 5 | 10 | 10 | 9.8 |
| 6 | 10 | 10 | 10 |
| 7 | 10 | 10 | 12 |
| 8 | 12 | 12 | 8 |
| 9 | 12 | 12 | 10 |
| 10 | 12 | 12 | 12 |
| Borehole | Serial Number | Results | Stress Components /MPa | ||
|---|---|---|---|---|---|
| σxx | σyy | σzz | |||
| ZK60 | 1 | Measured value | 2.14 | 1.24 | 2.24 |
| Inversion value | 3.27 | 1.86 | 2.42 | ||
| Absolute error | 0.57 | 0.31 | 0.09 | ||
| 2 | Measured value | 2.89 | 1.67 | 2.42 | |
| Inversion value | 4.17 | 2.74 | 2.27 | ||
| Absolute error | 0.64 | 0.54 | 0.08 | ||
| 3 | Measured value | 7.14 | 4.13 | 4.75 | |
| Inversion value | 6.54 | 3.78 | 4.27 | ||
| Absolute error | 0.30 | 0.17 | 0.24 | ||
| 4 | Measured value | 7.92 | 4.58 | 5.15 | |
| Inversion value | 5.99 | 3.85 | 5.02 | ||
| Absolute error | 0.97 | 0.36 | 0.07 | ||
| 5 | Measured value | 8.96 | 5.18 | 6.95 | |
| Inversion value | 6.63 | 4.01 | 6.13 | ||
| Absolute error | 1.16 | 0.59 | 0.41 | ||
| ZK59 | 1 | Measured value | 10.49 | 6.06 | 7.25 |
| Inversion value | 10.14 | 6.87 | 7.58 | ||
| Absolute error | 0.18 | 0.40 | 0.16 | ||
| 2 | Measured value | 8.62 | 4.98 | 5.25 | |
| Inversion value | 7.59 | 4.20 | 5.14 | ||
| Absolute error | 0.52 | 0.39 | 0.05 | ||
| 3 | Measured value | 8.50 | 4.91 | 5.31 | |
| Inversion value | 8.77 | 5.96 | 6.10 | ||
| Absolute error | 0.13 | 0.52 | 0.40 | ||
| 4 | Measured value | 9.26 | 5.35 | 6.69 | |
| Inversion value | 10.03 | 5.03 | 6.62 | ||
| Absolute error | 0.38 | 0.16 | 0.03 | ||
| 5 | Measured value | 12.37 | 7.14 | 7.78 | |
| Inversion value | 12.62 | 7.21 | 7.61 | ||
| Absolute error | 0.13 | 0.04 | 0.09 | ||
| ZK65 | 1 | Measured value | 4.24 | 2.45 | 2.94 |
| Inversion value | 4.25 | 2.46 | 3.25 | ||
| Absolute error | 0.01 | 0.00 | 0.16 | ||
| 2 | Measured value | 5.12 | 2.96 | 4.82 | |
| Inversion value | 5.13 | 2.97 | 5.50 | ||
| Absolute error | 0.00 | 0.00 | 0.34 | ||
| 3 | Measured value | 11.42 | 6.60 | 5.06 | |
| Inversion value | 7.23 | 4.18 | 5.58 | ||
| Absolute error | 2.10 | 1.21 | 0.26 | ||
| 4 | Measured value | 11.60 | 6.70 | 6.26 | |
| Inversion value | 11.60 | 6.65 | 6.65 | ||
| Absolute error | 0.00 | 0.02 | 0.20 | ||
| 5 | Measured value | 12.02 | 6.94 | 7.05 | |
| Inversion value | 11.74 | 6.73 | 6.92 | ||
| Absolute error | 0.14 | 0.10 | 0.07 | ||
| 6 | Measured value | 10.47 | 6.05 | 7.60 | |
| Inversion value | 11.22 | 6.44 | 7.10 | ||
| Absolute error | 0.38 | 0.19 | 0.25 | ||
| 7 | Measured value | 9.34 | 5.39 | 7.84 | |
| Inversion value | 10.85 | 6.22 | 7.18 | ||
| Absolute error | 0.75 | 0.41 | 0.33 | ||
| 8 | Measured value | 11.67 | 6.74 | 8.96 | |
| Inversion value | 11.62 | 6.67 | 7.55 | ||
| Absolute error | 0.02 | 0.04 | 0.70 | ||
| 9 | Measured value | 10.24 | 5.91 | 9.11 | |
| Inversion value | 10.24 | 5.89 | 9.76 | ||
| Absolute error | 0.00 | 0.01 | 0.33 | ||
| 10 | Measured value | 11.80 | 6.81 | 9.24 | |
| Inversion value | 10.76 | 6.19 | 9.81 | ||
| Absolute error | 0.52 | 0.31 | 0.28 | ||
| Principal Stress | Evaluation of Indicators | |||
|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | R2 | |
| Maximum principal stress | 1.4684 | 0.7840 | 8.3548 | 0.8804 |
| Intermediate principal stress | 0.8446 | 0.4630 | 8.5710 | 0.8824 |
| Minimum principal stress | 0.6648 | 0.5820 | 8.3568 | 0.9190 |
| Outliers | Evaluation of Indicators | |||
|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | R2 | |
| 0% | 0.6648 | 0.5820 | 8.3568 | 0.9190 |
| 1% | 0.7462 | 0.6943 | 9.1240 | 0.9014 |
| 2% | 0.9532 | 0.8674 | 10.3784 | 0.8939 |
| 3% | 1.8640 | 0.9842 | 11.7649 | 0.8694 |
| Model | Evaluation of Indicators | |||
|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | R2 | |
| SVR | 2.2037 | 1.1760 | 12.5322 | 0.3251 |
| MLR | 1.2661 | 0.6920 | 12.8219 | 0.3314 |
| GA-BP | 0.5932 | 0.4400 | 6.2747 | 0.6620 |
| LSTM–Attention | 0.6648 | 0.5820 | 8.3568 | 0.9190 |
| Depth /m | SH /MPa | Sh /MPa | Sv /MPa | Angle/° | σmax /MPa | σθmax /MPa | Rc /MPa | ||
|---|---|---|---|---|---|---|---|---|---|
| 274.3 m | 14.28 | 7.78 | 7.18 | 39 | 10.4 | 23.9 | 73 | 0.33 | 7.05 |
| Rock Burst Level | Recommended Engineering Mitigation Measures |
|---|---|
| No rockbursts | None |
| Weak rockbursts | Short excavation lengths reduce disturbance to the surrounding rock; stress-relief holes should be made when necessary. |
| Medium rockbursts | The system is equipped with high-prestressed anchor bolts, and flexible protective nets are added in key areas to prevent rock fragments from being ejected. |
| Strong rockbursts | Before excavation, advance anchor bolts are installed, or pre-decompression blasting is carried out to form a stress buffer zone. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, L.; Sun, J. Inversion Analysis of Stress Fields Based on the LSTM–Attention Neural Network. Appl. Sci. 2025, 15, 9567. https://doi.org/10.3390/app15179567
Wang J, Zhang L, Sun J. Inversion Analysis of Stress Fields Based on the LSTM–Attention Neural Network. Applied Sciences. 2025; 15(17):9567. https://doi.org/10.3390/app15179567
Chicago/Turabian StyleWang, Jianxin, Liming Zhang, and Junyu Sun. 2025. "Inversion Analysis of Stress Fields Based on the LSTM–Attention Neural Network" Applied Sciences 15, no. 17: 9567. https://doi.org/10.3390/app15179567
APA StyleWang, J., Zhang, L., & Sun, J. (2025). Inversion Analysis of Stress Fields Based on the LSTM–Attention Neural Network. Applied Sciences, 15(17), 9567. https://doi.org/10.3390/app15179567





