Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft
Abstract
1. Introduction
1.1. The Tiltrotor Concept and Challenges
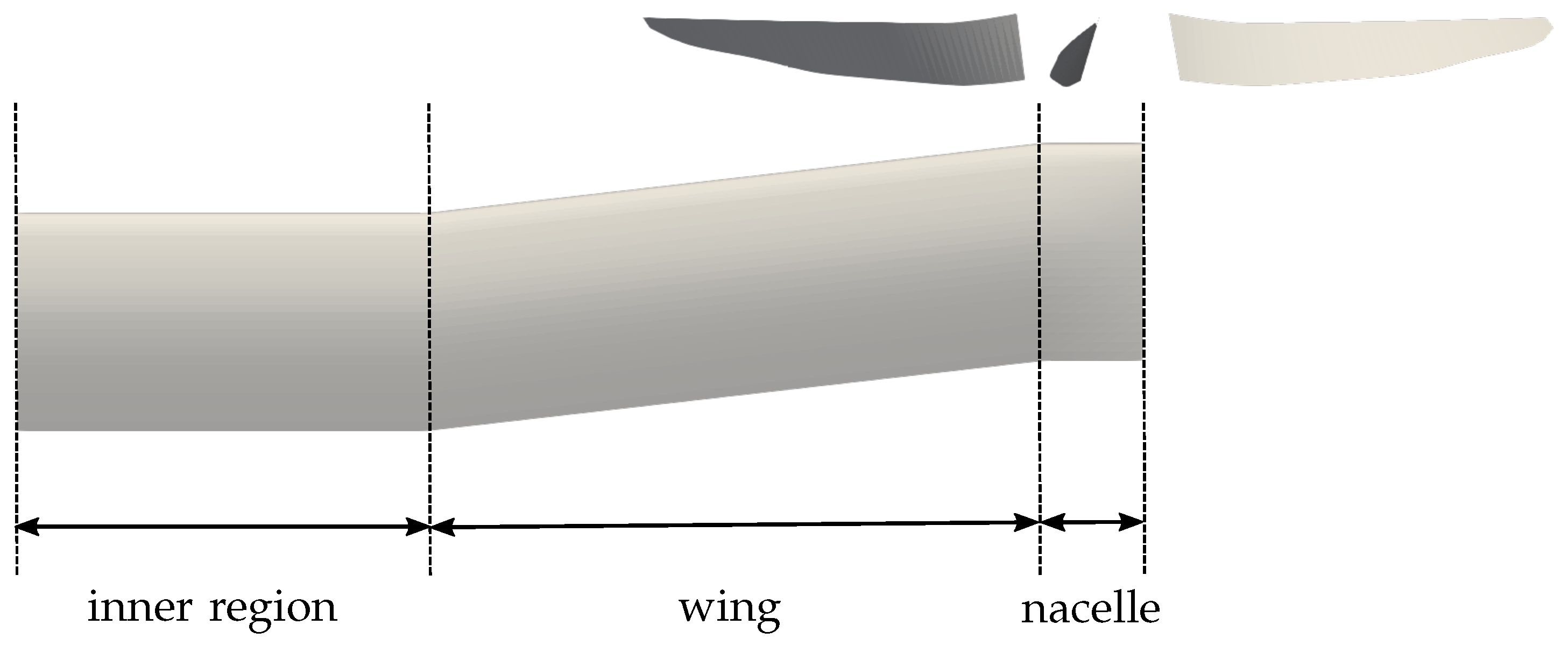
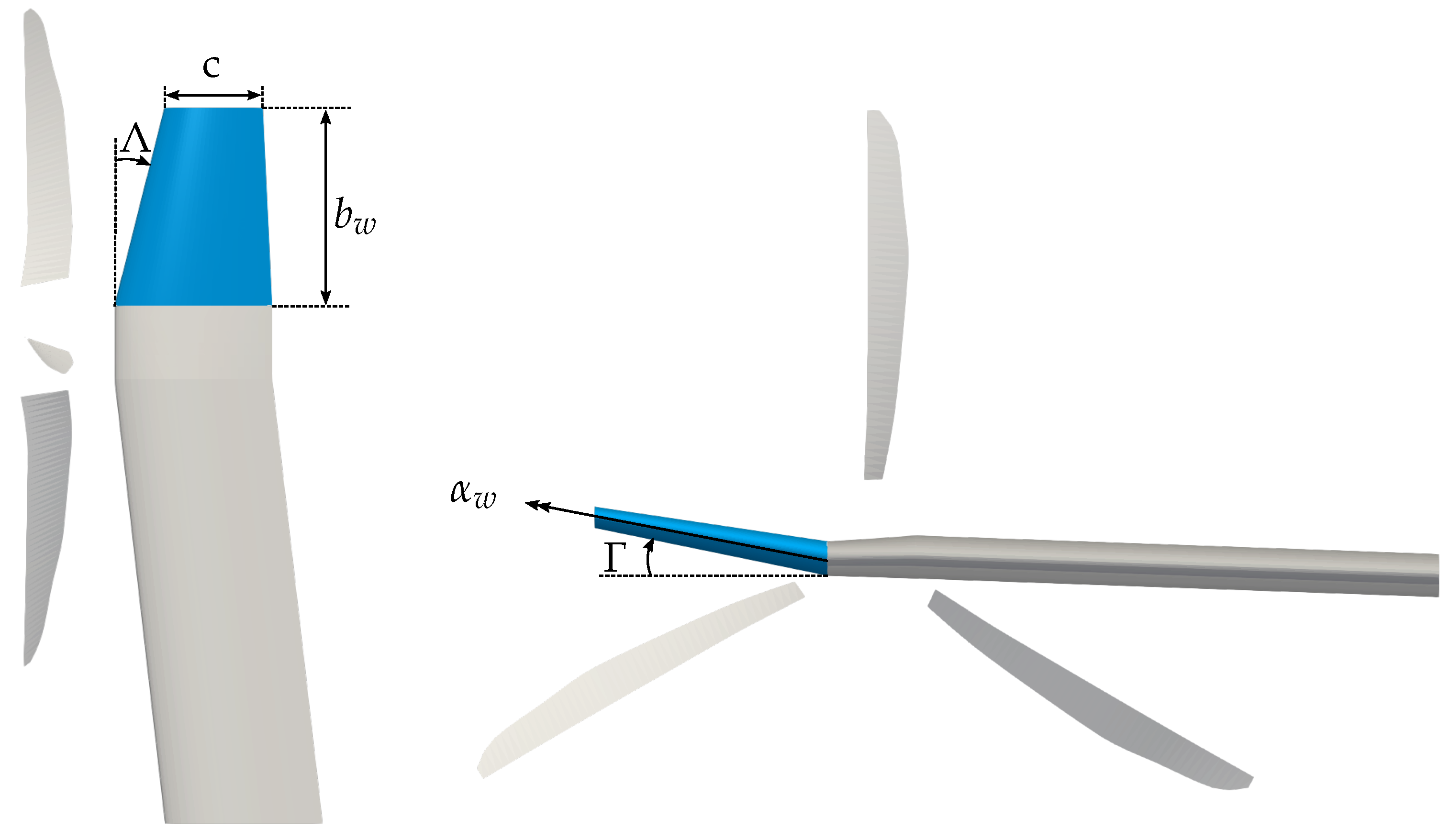
1.2. The Wing Extension Concept
1.3. Present Work
2. Numerical Model
2.1. Mid-Fidelity Numerical Model
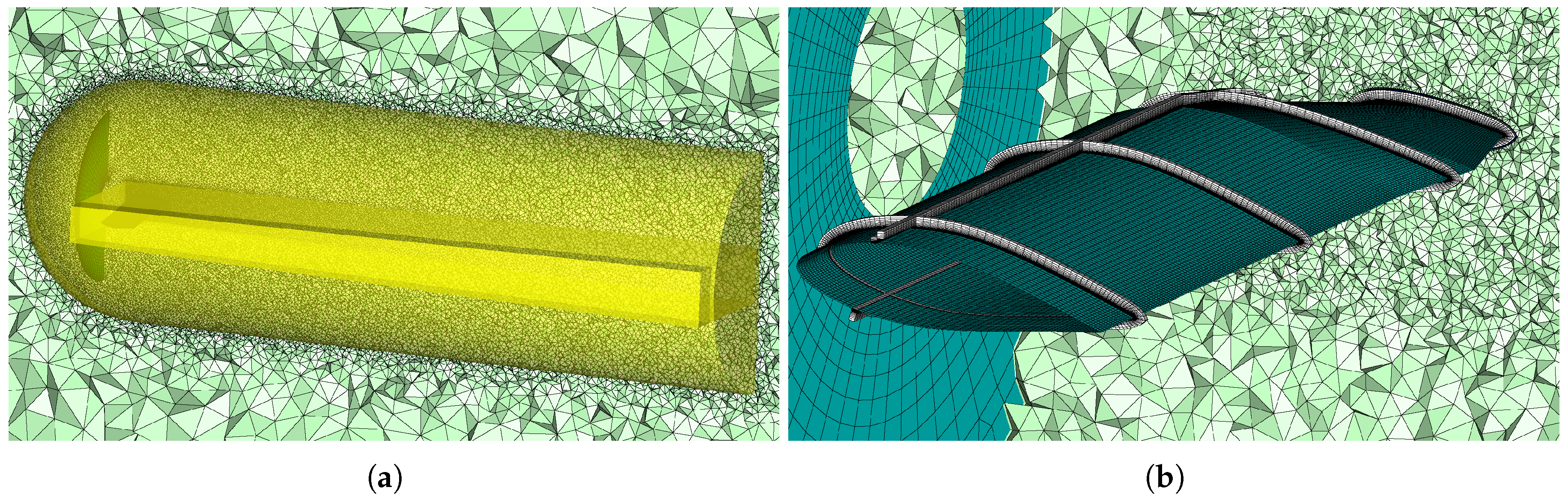
2.2. High-Fidelity Numerical Model
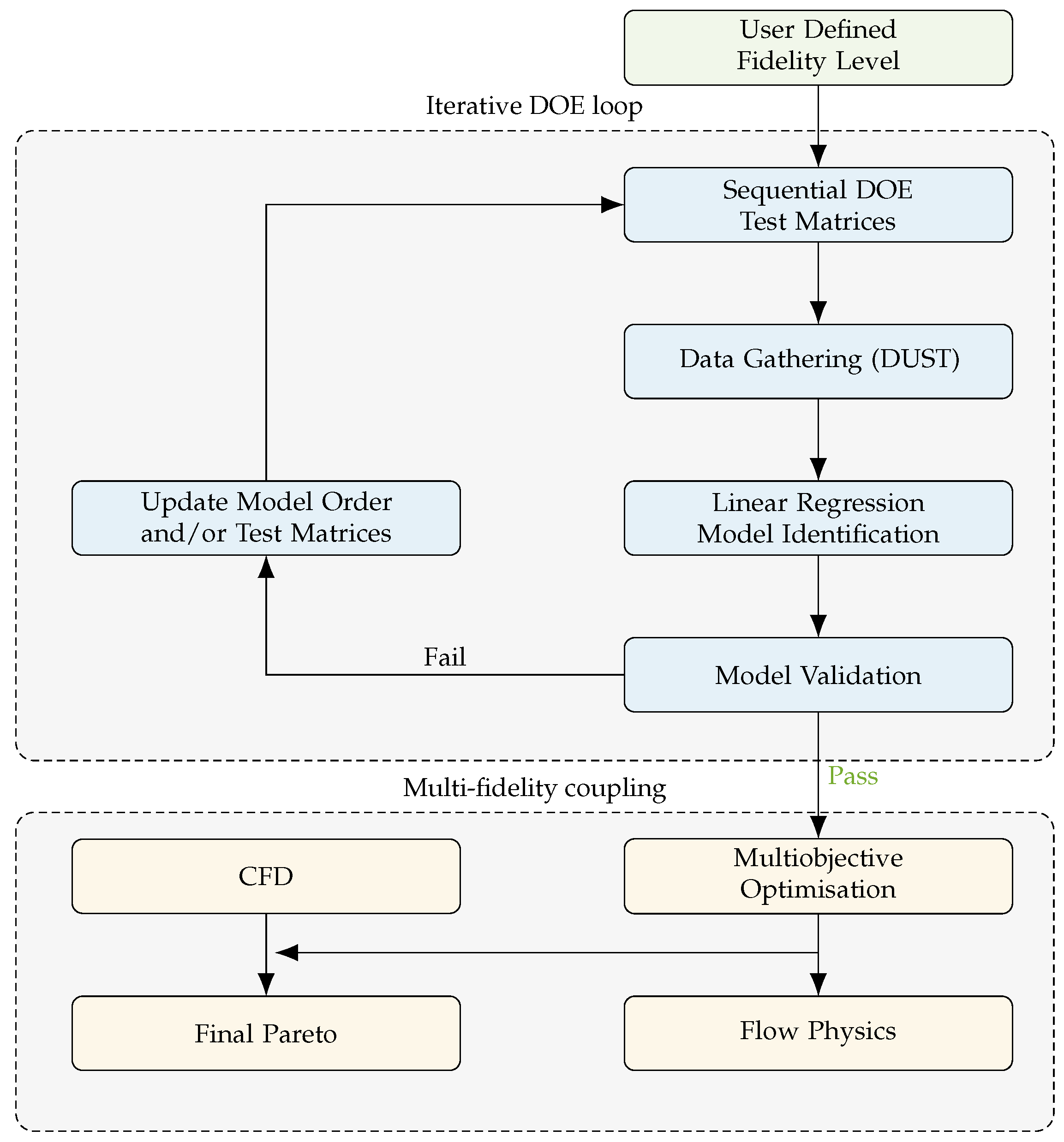
3. Design Methodology
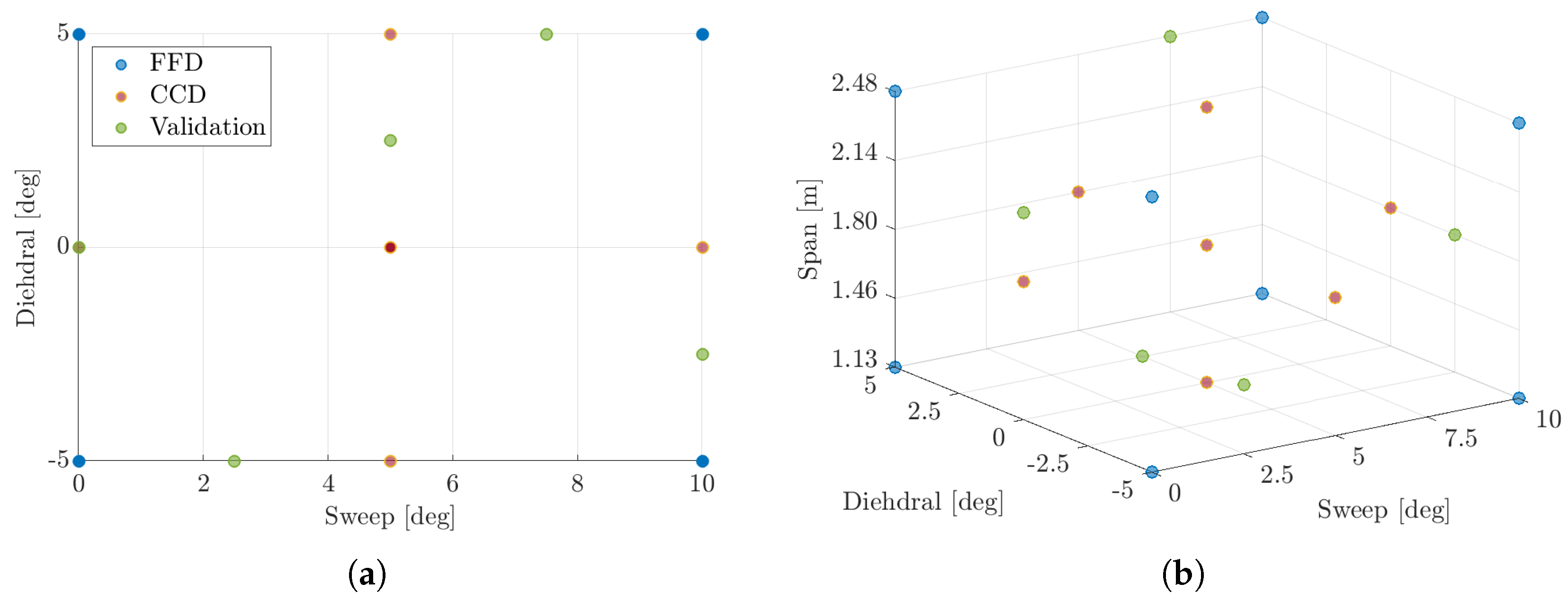
3.1. Iterative DOE Loop
3.2. Multi-Fidelity Coupled Design
4. Results
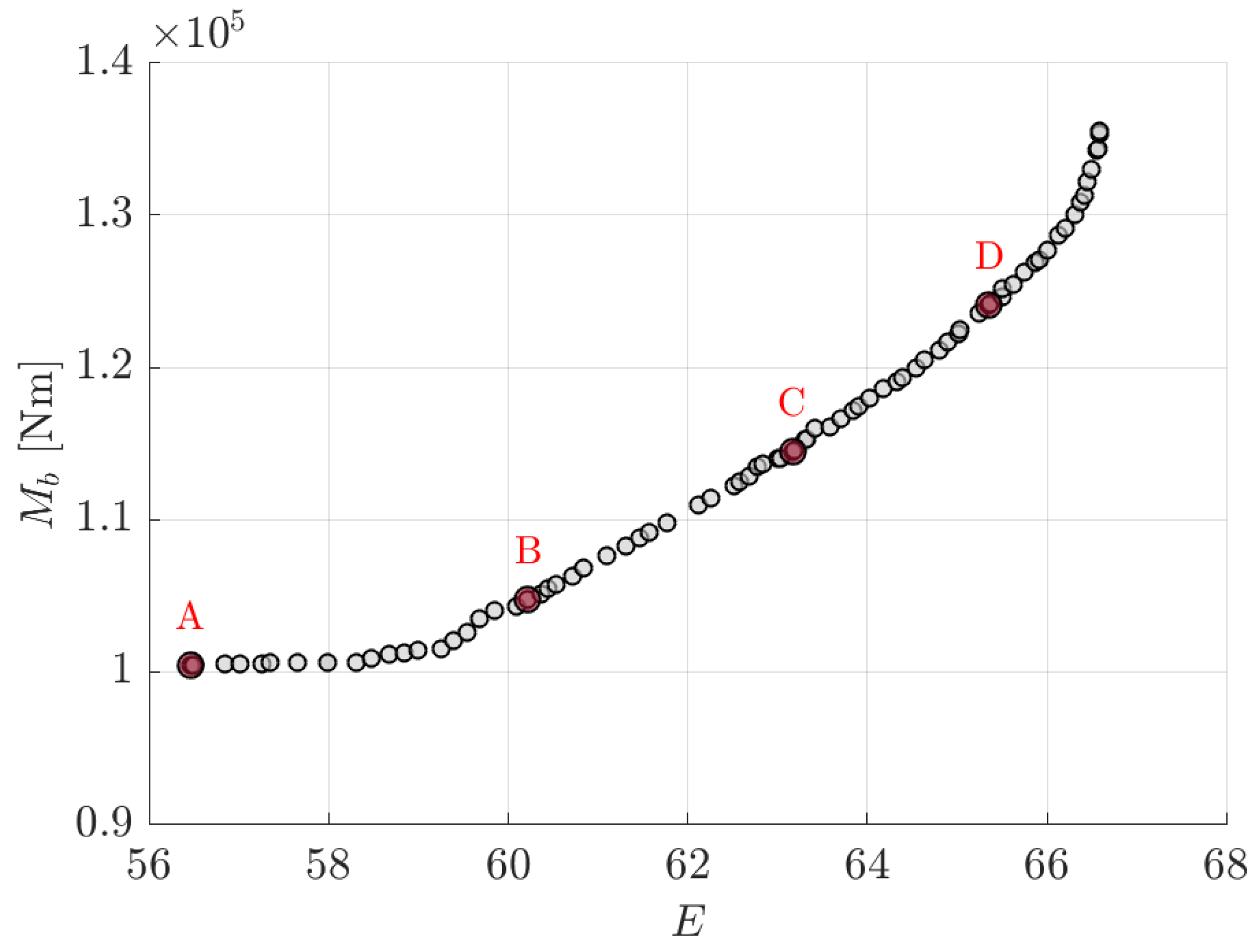
4.1. Pareto-Optimal Front: Optimization
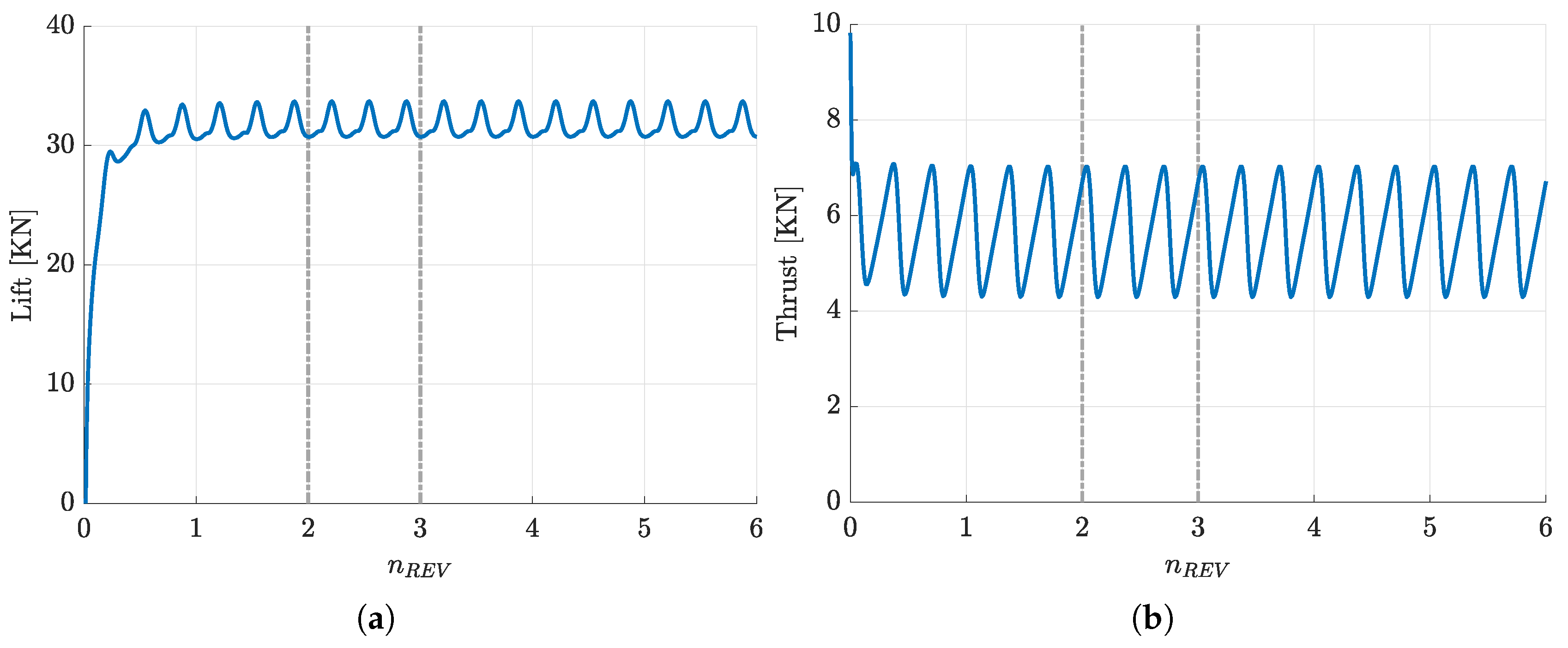
4.2. Rotor Loads
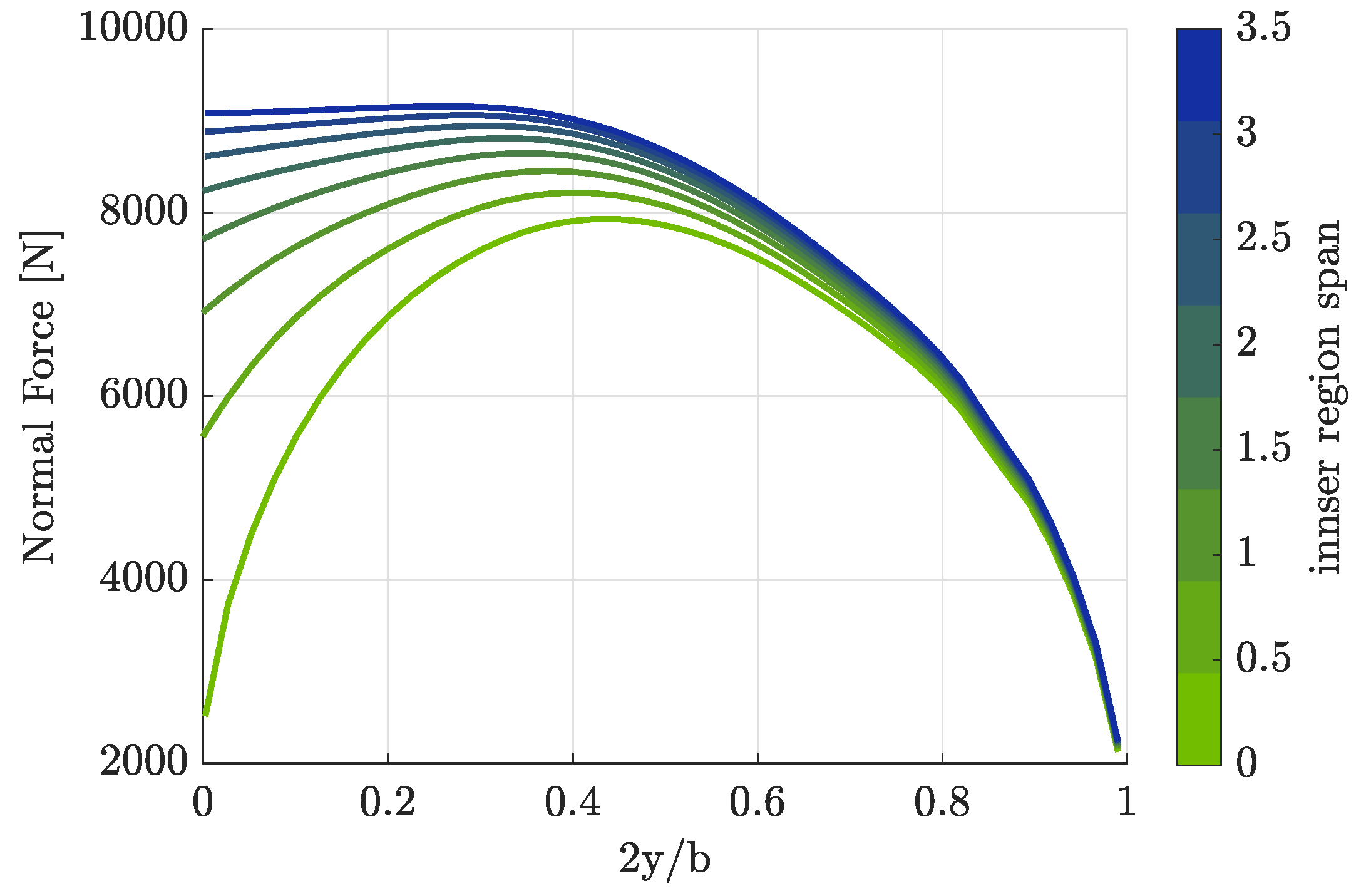
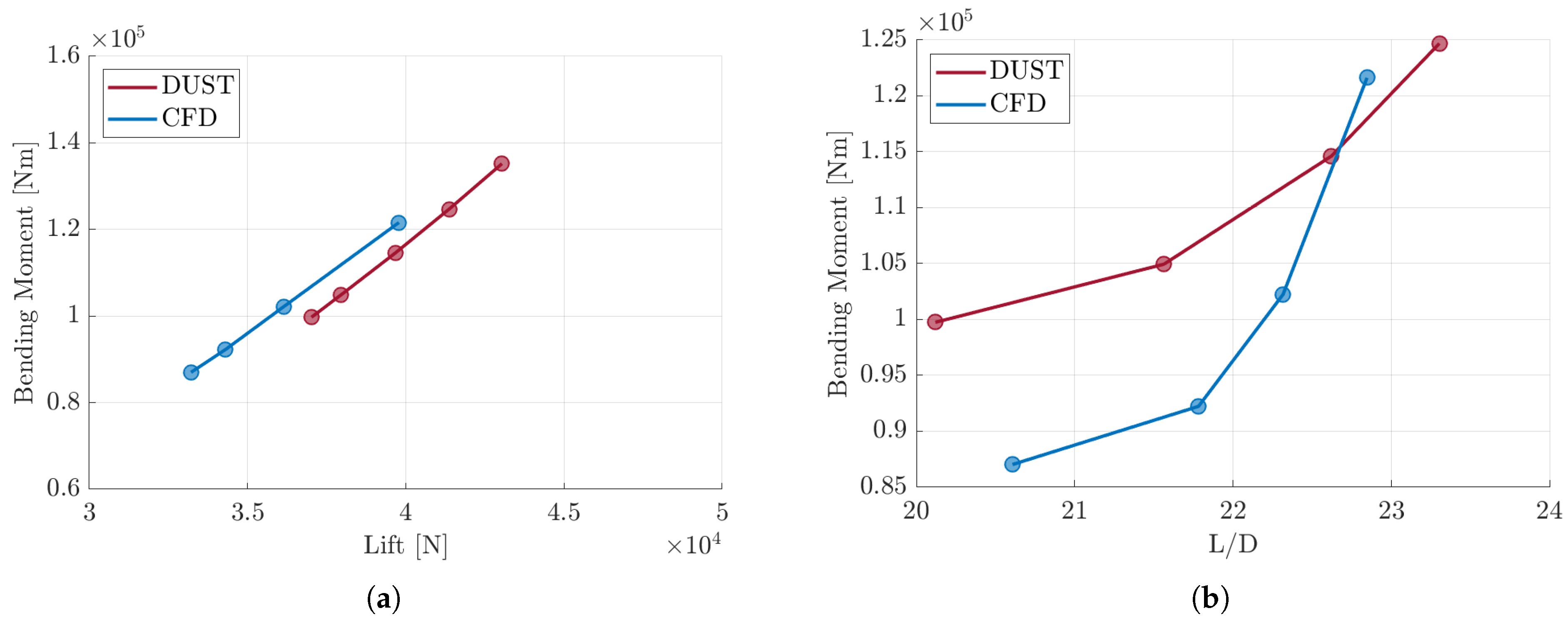
4.3. Wing Loads
4.4. CFD Comparison
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VPM | Vortex Particle Method |
| CFD | Computational Fluid Dynamics |
| PO | Pareto Optimal front |
| DOE | Design of Experiment |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| OFAT | One Factor At a Time |
| FFD | Full Factorial Design |
| CCD | Central Composite Design |
References
- Maisel, M.D. The History of the XV-15 Tilt Rotor Research Aircraft: From Concept to Flight; NASA: Washington, DC, USA, 2000; p. 17. [Google Scholar]
- Johnson, W. Analytical Model for Tilting Proprotor Aircraft Dynamics, Including Blade Torsion and Coupled Bending Modes, and Conversion Mode Operation. Technical Report. 1974. Available online: https://ntrs.nasa.gov/citations/19740023385 (accessed on 24 August 2025).
- Johnson, W. Dynamics of Tilting Proprotor Aircraft in Cruise Flight. Technical Report. 1974. Available online: https://ntrs.nasa.gov/citations/19740019387 (accessed on 24 August 2025).
- Kvaternik, R.G. Studies in Tilt-Rotor VTOL Aircraft Aeroelasticity. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 1973. [Google Scholar]
- Weiberg, J.A.; Maisel, M.D. Wind-Tunnel Tests of the XV-15 Tilt Rotor Aircraft. Technical Report. 1980. Available online: https://ntrs.nasa.gov/api/citations/19800015802/downloads/19800015802.pdf (accessed on 24 August 2025).
- Magee, J.; Wernicke, K. XV-15 flight test results compared with design goals. In Proceedings of the Aircraft Systems and Technology Meeting, New York, NY, USA, 20–22 August 1979; p. 1839. [Google Scholar]
- McVeigh, M.; Rosenstein, H.; McHugh, F. Aerodynamic design of the XV-15 advanced composite tilt rotor blade. In Proceedings of the American Helicopter Society, Annual Forum, 39th, St. Louis, MO, USA, 9–11 May 1983; Volume 9. [Google Scholar]
- Gazdag, D. Potential Use of Tiltrotor Aircraft in Canadian Aviation; Ames Research Center, National Aeronautics and Space Administration: Washington, DC, USA, 1990; Volume 102245. [Google Scholar]
- McVeigh, M. The V-22 Tilt-rotor large-scale rotor performance/wing download test and comparison with theory. Vertica 1986, 10, 281–297. [Google Scholar]
- Felker, F.F. Wing Download Results from a Test of a 0.658-Scale V-22 Rotor and Wing. J. Am. Helicopter Soc. 1992, 37, 58–63. [Google Scholar] [CrossRef]
- Felker, F.F.; Signor, D.B.; Young, L.A.; Betzina, M.D. Performance and Loads Data from a Hover Test of a 0.658-Scale V-22 Rotor and Wing. Technical Report. 1987. Available online: https://ntrs.nasa.gov/citations/19870015863 (accessed on 24 August 2025).
- Felker, F.F.; Shinoda, P.R.; Heffernan, R.M.; Sheehy, H.F. Wing Force and Surface Pressure Data from a Hover Test of a 0.658-Scale V-22 Rotor and Wing. Technical Report. 1990. Available online: https://ntrs.nasa.gov/api/citations/19920013621/downloads/19920013621.pdf (accessed on 24 August 2025).
- Droandi, G.; Gibertini, G.; Grassi, D.; Campanardi, G.; Liprino, C. Proprotor–wing aerodynamic interaction in the first stages of conversion from helicopter to aeroplane mode. Aerosp. Sci. Technol. 2016, 58, 116–133. [Google Scholar] [CrossRef]
- Droandi, G.; Zanotti, A.; Gibertini, G.; Grassi, D.; Campanardi, G. Experimental investigation of the rotor-wing aerodynamic interaction in a tiltwing aircraft in hover. Aeronaut. J. 2015, 119, 591–612. [Google Scholar] [CrossRef]
- Potsdam, M.A.; Strawn, R.C. CFD simulations of tiltrotor configurations in hover. J. Am. Helicopter Soc. 2005, 50, 82–94. [Google Scholar] [CrossRef]
- Lim, J.W. Fundamental investigation of proprotor and wing interactions in tiltrotor aircraft. In Proceedings of the 75th Annual Vertical Flight Society Forum and Technology Display, Philadelphia, PA, USA, 13–16 May 2019; pp. 13–16. [Google Scholar]
- Tran, S.A.; Lim, J.W. Investigation of the interactional aerodynamics of the XV-15 tiltrotor aircraft. In Proceedings of the 76th Annual Vertical Flight Society Forum and Technology Display, Virtual, 5–8 October 2020; pp. 6–8. [Google Scholar]
- Lim, J.; Tran, S. Interactional structural loads of the xv-15 rotor in airplane mode. In Proceedings of the 45th European Rotorcraft Forum, Warsaw, Poland, 17–20 September 2019; pp. 17–20. [Google Scholar]
- Tran, S.; Lim, J.; Nunez, G.; Wissink, A.; Bowen-Davies, G. CFD Calculations of the XV-15 tiltrotor during transition. In Proceedings of the American Helicopter Society 75th Annual Forum, Philadelphia, PA, USA, 13–16 May 2019; pp. 13–16. [Google Scholar]
- Gennaretti, M.; Bernardini, G. Novel boundary integral formulation for blade-vortex interaction aerodynamics of helicopter rotors. AIAA J. 2007, 45, 1169–1176. [Google Scholar] [CrossRef]
- Gennaretti, M.; Colella, M.M.; Bernardini, G. Prediction of tiltrotor vibratory loads with inclusion of wing-proprotor aerodynamic interaction. J. Aircr. 2010, 47, 71–79. [Google Scholar] [CrossRef]
- Wentrup, M.; Yin, J.; Kunze, P.; Streit, T.; Wendisch, J.H.; Schwarz, T.; Pinacho, J.P.; Kicker, K.; Fukari, R. An overview of DLR compound rotorcraft aerodynamics and aeroacoustics activities within the CleanSky2 NACOR Project. In Proceedings of the AHS Forum 2018, San Francisco, CA, USA, 16–18 January 2018. [Google Scholar]
- Opoku, D.G.; Triantos, D.G.; Nitzsche, F.; Voutsinas, S.G. Rotorcraft aerodynamic and aeroacoustic modelling using vortex particle methods. In Proceedings of the 23rd International Congress of Aeronautical Sciences (ICAS 2002), Toronto, ON, Canada, 8–13 September 2002; pp. 8–13. [Google Scholar]
- Tan, J.F.; Zhou, T.Y.; Sun, Y.M.; Barakos, G.N. Numerical investigation of the aerodynamic interaction between a tiltrotor and a tandem rotor during shipboard operations. Aerosp. Sci. Technol. 2019, 87, 62–72. [Google Scholar] [CrossRef]
- Zanotti, A.; Savino, A.; Palazzi, M.; Tugnoli, M.; Muscarello, V. Assessment of a Mid-Fidelity Numerical Approach for the Investigation of Tiltrotor Aerodynamics. Appl. Sci. 2021, 11, 3385. [Google Scholar] [CrossRef]
- Droandi, G.; Syal, M.; Bower, G. Tiltwing multi-rotor aerodynamic modeling in hover, transition and cruise flight conditions. In Proceedings of the AHS International 74th Annual Forum & Technology Display, Phoenix, AZ, USA, 14–17 May 2018; AHS International: Fairfax, VA, USA, 2018; Volume 1, pp. 46–62. [Google Scholar]
- Montagnani, D.; Tugnoli, M.; Zanotti, A.; Syal, M.; Droandi, G. Analysis of the interactional aerodynamics of the vahana evtol using a medium fidelity open source tool. In Proceedings of the VFS Aeromechanics for Advanced Vertical Flight Technical Meeting, San Jose, CA, USA, 21–23 January 2020; Vertical Flight Society: Fairfax, VA, USA, 2020; pp. 436–451. [Google Scholar]
- Piccinini, R.; Tugnoli, M.; Zanotti, A. Numerical Investigation of the Rotor-Rotor Aerodynamic Interaction for eVTOL Aircraft Configurations. Energies 2020, 13, 5995. [Google Scholar] [CrossRef]
- Zhang, J.; Smith, E. Influence of aeroelastically tailored wing extensions and winglets on whirl flutter stability. In Proceedings of the 2nd Asian/Australian Rotorcraft Forum, ARF 2013, Tianjin, China, 8–11 September 2013; American Helicopter Society International: Fairfax, VA, USA, 2013; pp. 188–200. [Google Scholar]
- Karem, A. Tilt Outboard Wing for Tilt Rotor Aircraft. US Patent 7,802,754, 2010. [Google Scholar]
- Acree, C.W. Aerodynamic limits on Large Civil Tiltrotor sizing and efficiency. In Proceedings of the Decennial AHS Aeromechanics Specialists’ Conference, San Francisco, CA, USA, 22–24 January 2014; p. ARC-E-DAA-TN12696. [Google Scholar]
- Simmons, B.M.; Buning, P.G.; Murphy, P.C. Full-envelope aero-propulsive model identification for lift+ cruise aircraft using computational experiments. In Proceedings of the AIAA Aviation 2021 Forum, Virtual, 2–6 August 2021; p. 3170. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Tugnoli, M.; Montagnani, D.; Syal, M.; Droandi, G.; Zanotti, A. Mid-fidelity approach to aerodynamic simulations of unconventional VTOL aircraft configurations. Aerosp. Sci. Technol. 2021, 115, 106804. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An open-source suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Winckelmans, G.S. Topics in Vortex Methods for the Computation of Three-and Two-Dimensional Incompressible Unsteady Flows. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1989. [Google Scholar]
- Cottet, G.; Mas-Gallic, S. A particle method to solve the Navier-Stokes system. Numer. Math. 1990, 57, 805–827. [Google Scholar] [CrossRef]
- Morino, L.; Kuot, C.C. Subsonic potential aerodynamics for complex configurations: A general theory. AIAA J. 1974, 12, 191–197. [Google Scholar] [CrossRef]
- Acree, C.W., Jr. An Improved CAMRAD Model for Aeroelastic Stability Analysis of the XV-15 with Advanced Technology Blades; TM 4448; NASA: Washington, DC, USA, 1993. [Google Scholar]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Proceedings of the Low Reynolds Number Aerodynamics, Notre Dame, IN, USA, 5–7 June 1989; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Viterna, L.A.; Janetzke, D.C. Theoretical and Experimental Power from Large Horizontal-Axis Wind Turbines; Technical Report; Washington Procurement Operations Office: Washington, DC, USA, 1982. [Google Scholar]
- Johnson, W. CAMRAD II, Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics, Volume I: Theory; Johnson Aeronautics: Palo Alto, CA, USA, 1992. [Google Scholar]
- Palazzi, M. Mid-Fidelity Approach to Tiltrotor Aerodynamics. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2020. [Google Scholar]
- Muscarello, V.; Quaranta, G. Structural Coupling and Whirl-Flutter Stability with Pilot-in-the-Loop. J. Am. Helicopter Soc. 2021, 66, 1–16. [Google Scholar] [CrossRef]
- Maisel, M. NASA/Army XV-15 Tilt-Rotor Research Aircraft Familiarization Document; TM X-62,407; NASA: Washington, DC, USA, 1975. [Google Scholar]
- Lindsay, K.; Krasny, R. A particle method and adaptive treecode for vortex sheet motion in three-dimensional flow. J. Comput. Phys. 2001, 172, 879–907. [Google Scholar] [CrossRef]
- Saetta, L.; Tognaccini, R. Implementation and validation of a new actuatordisk model in SU2. In Proceedings of the SU2 Conference, Princeton, NJ, USA, 10–12 June 2020. [Google Scholar]
- Murphy, P.C.; Hatke, D.; Aubuchon, V.V.; Weinstein, R.; Busan, R.C. Preliminary Steps in Developing Rapid Aero Modeling Technology. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0764. [Google Scholar]
- Murphy, P.C.; Buning, P.G.; Simmons, B.M. Rapid Aero Modeling for Urban Air Mobility Aircraft in Computational Experiments. In Proceedings of the AIAA SciTech 2021 Forum, Online, 19–21 January 2021; p. 1002. [Google Scholar]
- Murphy, P.C.; Simmons, B.M.; Hatke, D.B.; Busan, R.C. Rapid Aero Modeling for Urban Air Mobility Aircraft in Wind-Tunnel Tests. In Proceedings of the AIAA SciTech 2021 Forum, Online, 19–21 January 2021; p. 1644. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Alexopoulos, E.C. Introduction to multivariate regression analysis. Hippokratia 2010, 14, 23. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–34. [Google Scholar]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]




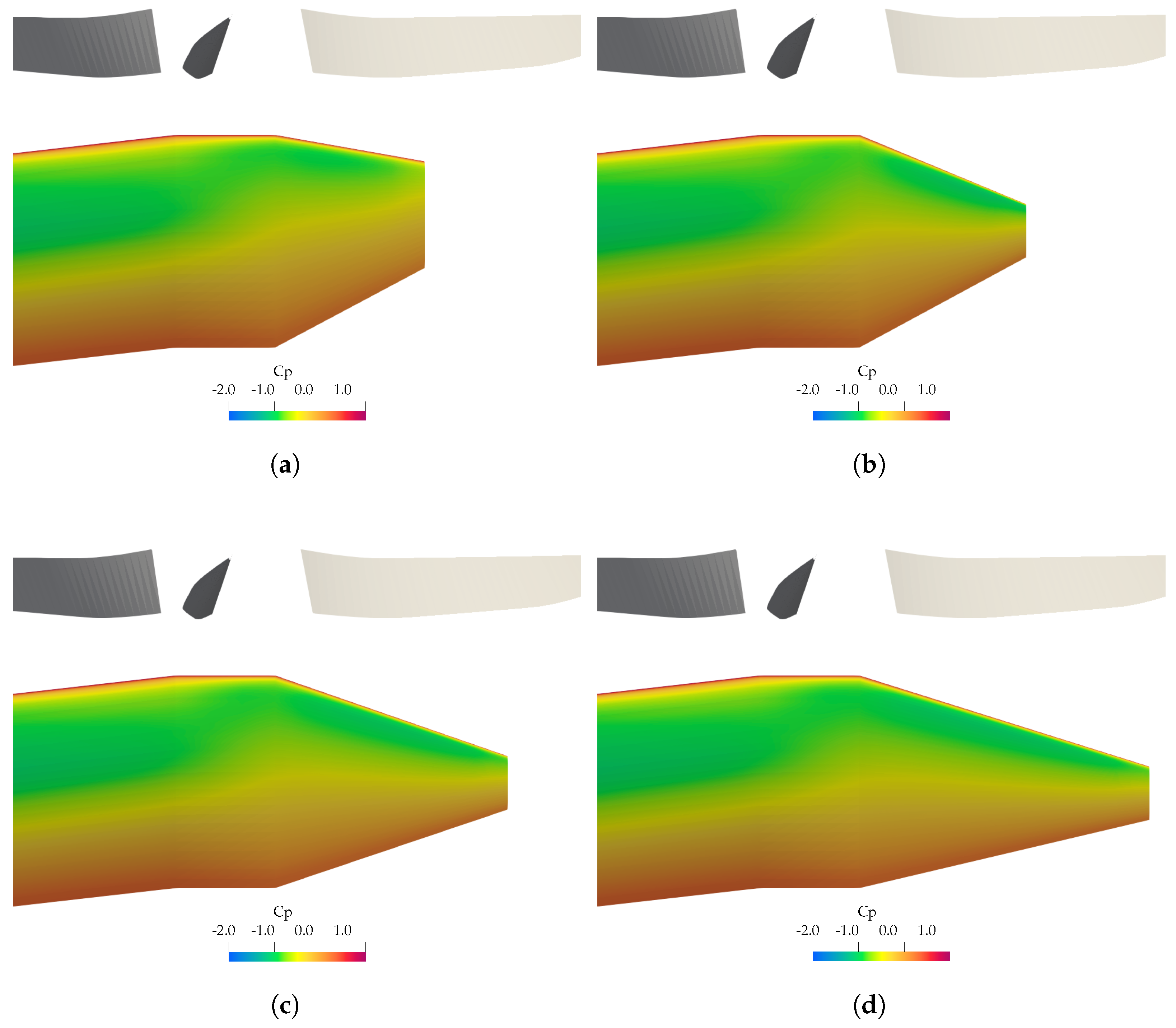
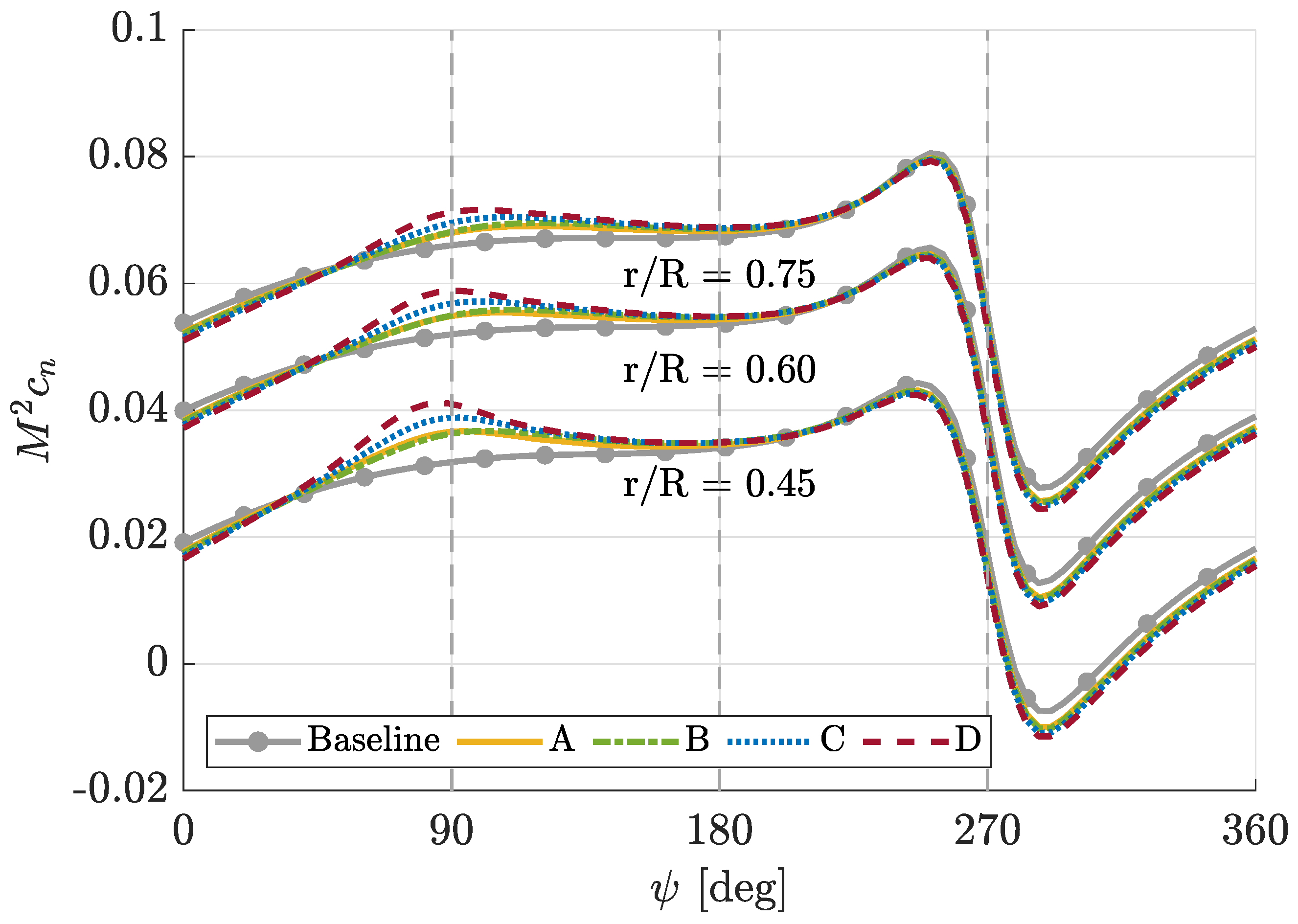

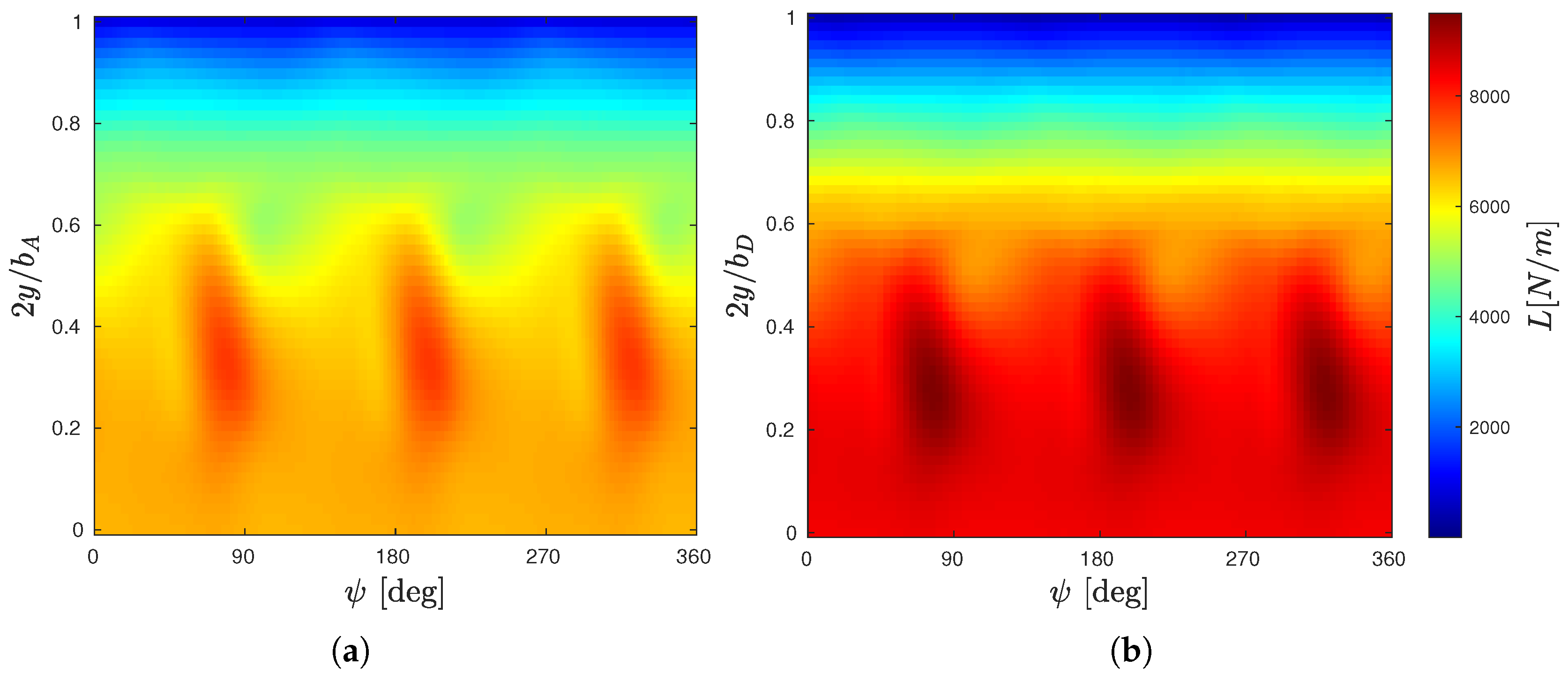
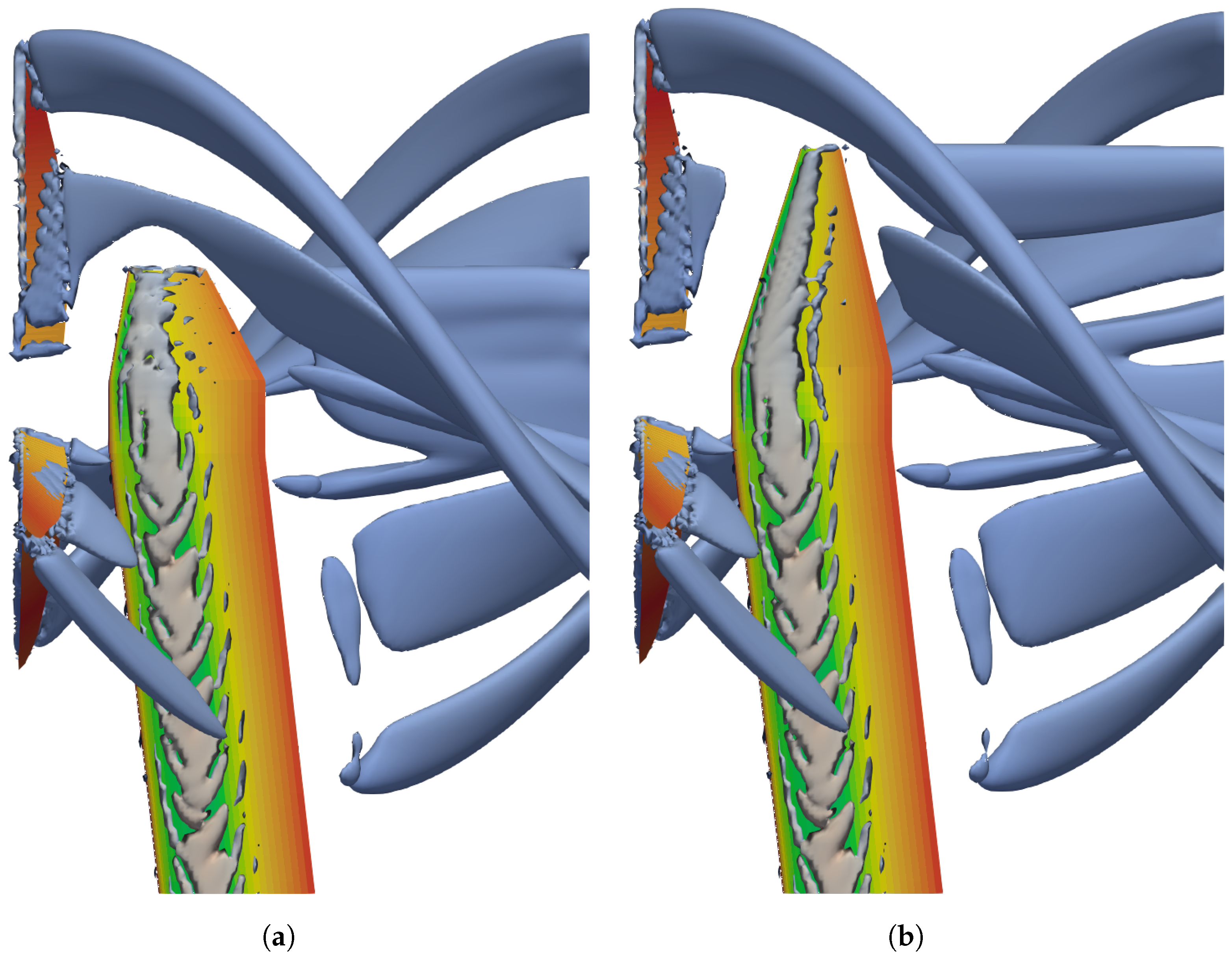
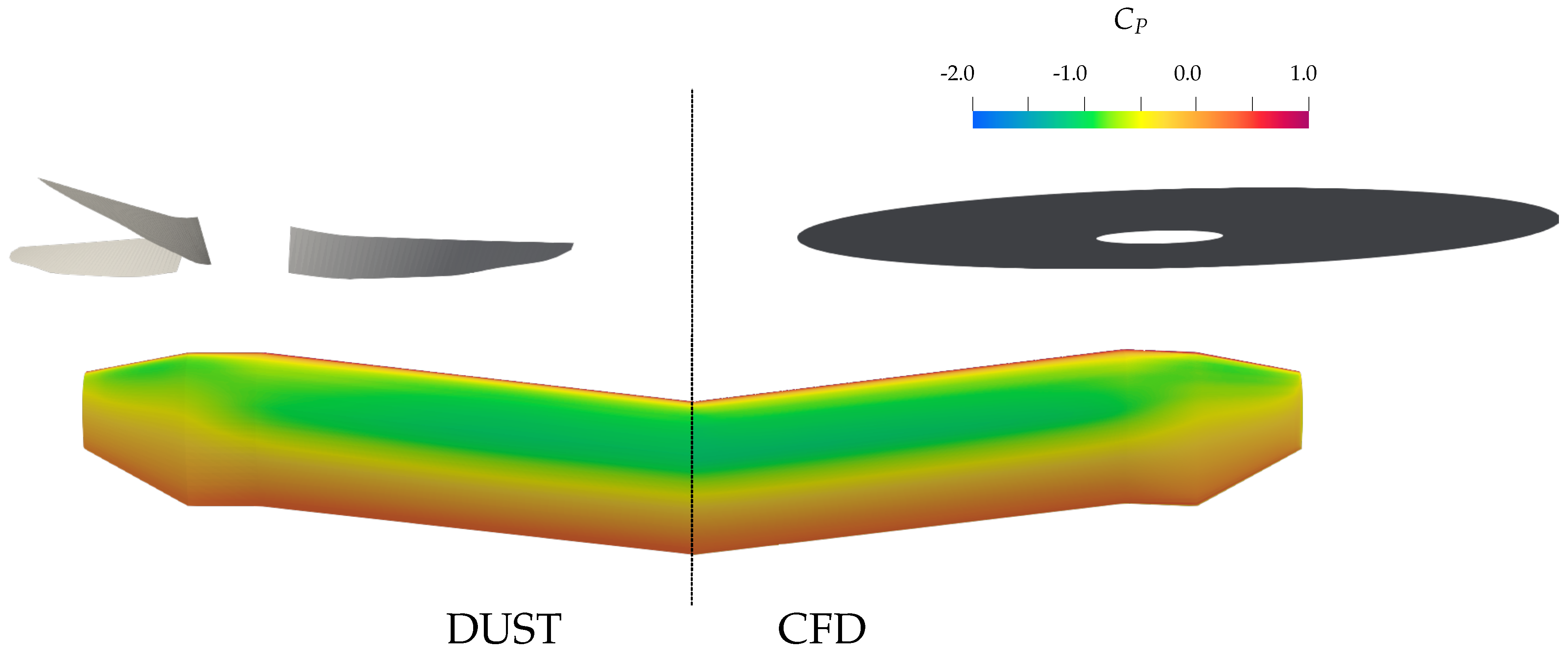
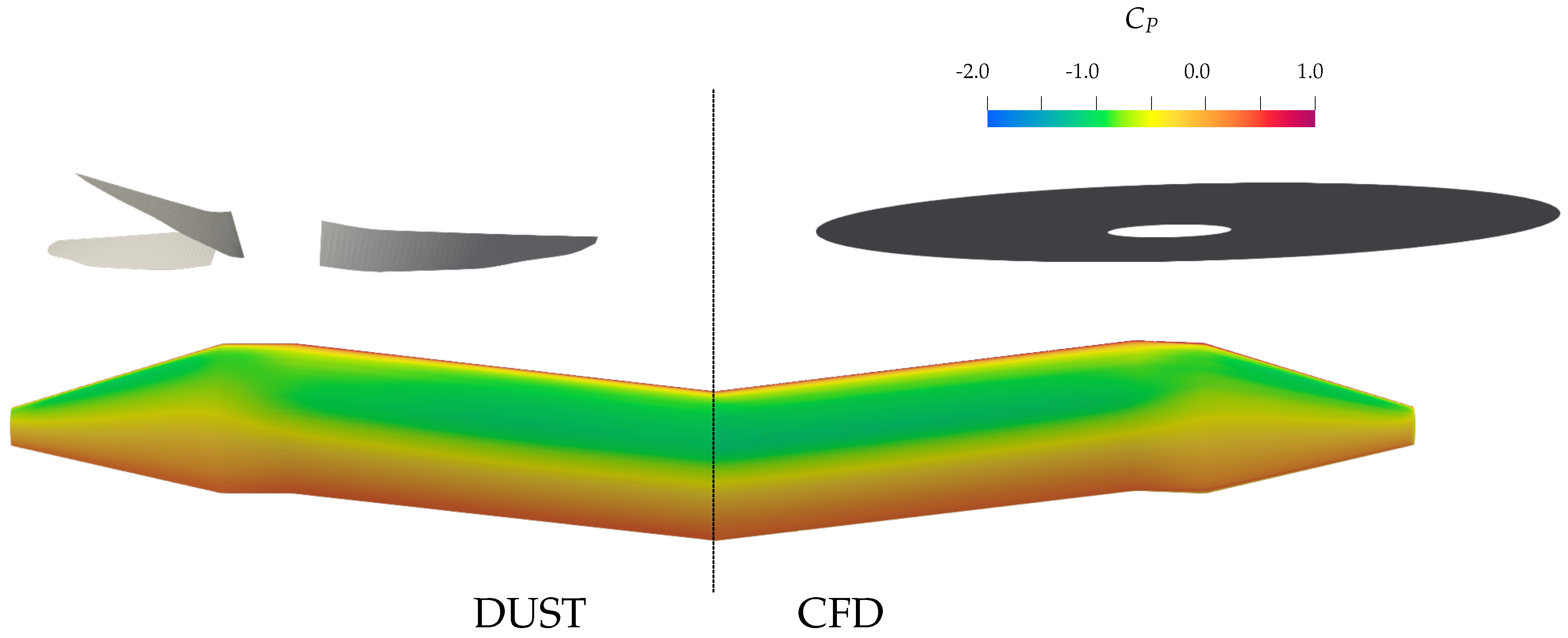
| Rotor Data | ||
|---|---|---|
| Number of blades | 3 | |
| Solidity | 0.103 | |
| Radius | 3.81 | |
| Precone | 1.5 | deg |
| Helicopter speed (HP) | 601 | RPM |
| Airplane speed (AP) | 480.8 | RPM |
| Design Variables | Minimum | Maximum |
|---|---|---|
| Sweep () | 0° | 10° |
| Dihed () | −5° | 5° |
| Span () | 1.125 m | 2.275 m |
| Incidence () | 0° | 3° |
| Chord (c) | 0.4 m | 1.2 m |
| E | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 2 | 3 | 4 | |
| FFD | 1.4% | 3.0% | 1.5% | 0.7% | 13% | 10% |
| FFD+CCD | 0.3% | 2.0% | 10% | 0.1% | 1.2% | 12% |
| Design Variables | A | B | C | D |
|---|---|---|---|---|
| Sweep () | 0° | 10° | 9.96° | 10° |
| Dihed () | −5° | −4.55° | −0.42° | 3.37° |
| Span () | 1.125 m | 1.253 m | 1.75 m | 2.18 m |
| Incidence () | 0° | 1.83° | 0.09° | 0.27° |
| Chord (c) | 0.8 m | 0.4 m | 0.4 m | 0.4 m |
| DUST | SU2 | |||||||
|---|---|---|---|---|---|---|---|---|
| L [N] | D [N] | [N m−1] | E | L [N] | D [N] | [N m−1] | E | |
| A | 37,017 | 659 | 99,721 | 56.2 | 33,211 | 1612 | 86,997 | 20.6 |
| B | 37,958 | 630 | 104,919 | 60.2 | 34,290 | 1574 | 92,204 | 21.8 |
| C | 39,673 | 628 | 114,595 | 63.1 | 36,152 | 1620 | 102,221 | 22.3 |
| D | 41,365 | 636 | 124,675 | 65.1 | 39,783 | 1741 | 121,605 | 22.8 |
| E | 43,036 | 649 | 135,196 | 66.3 | 39,682 | 1776 | 123,493 | 22.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savino, A. Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft. Appl. Sci. 2025, 15, 9491. https://doi.org/10.3390/app15179491
Savino A. Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft. Applied Sciences. 2025; 15(17):9491. https://doi.org/10.3390/app15179491
Chicago/Turabian StyleSavino, Alberto. 2025. "Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft" Applied Sciences 15, no. 17: 9491. https://doi.org/10.3390/app15179491
APA StyleSavino, A. (2025). Multi-Fidelity Aerodynamic Optimization of the Wing Extension of a Tiltrotor Aircraft. Applied Sciences, 15(17), 9491. https://doi.org/10.3390/app15179491






