Distance-Based Compression Method for Large Language Models
Abstract
1. Introduction
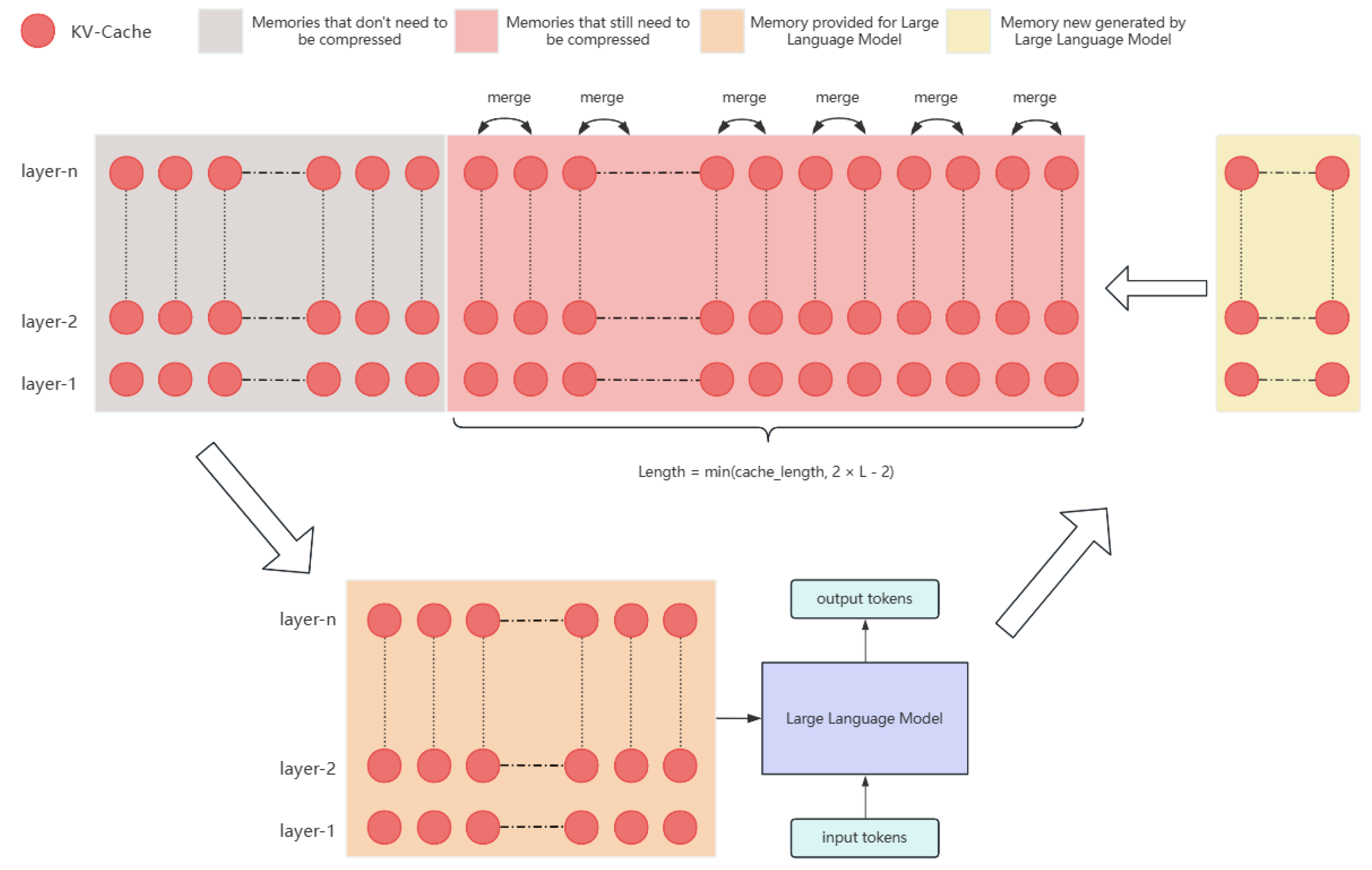
- It employs a trainable model such as MLP, which we called the merge model, to merge two token-specific cache units with the same compression ratio into a new cache unit.
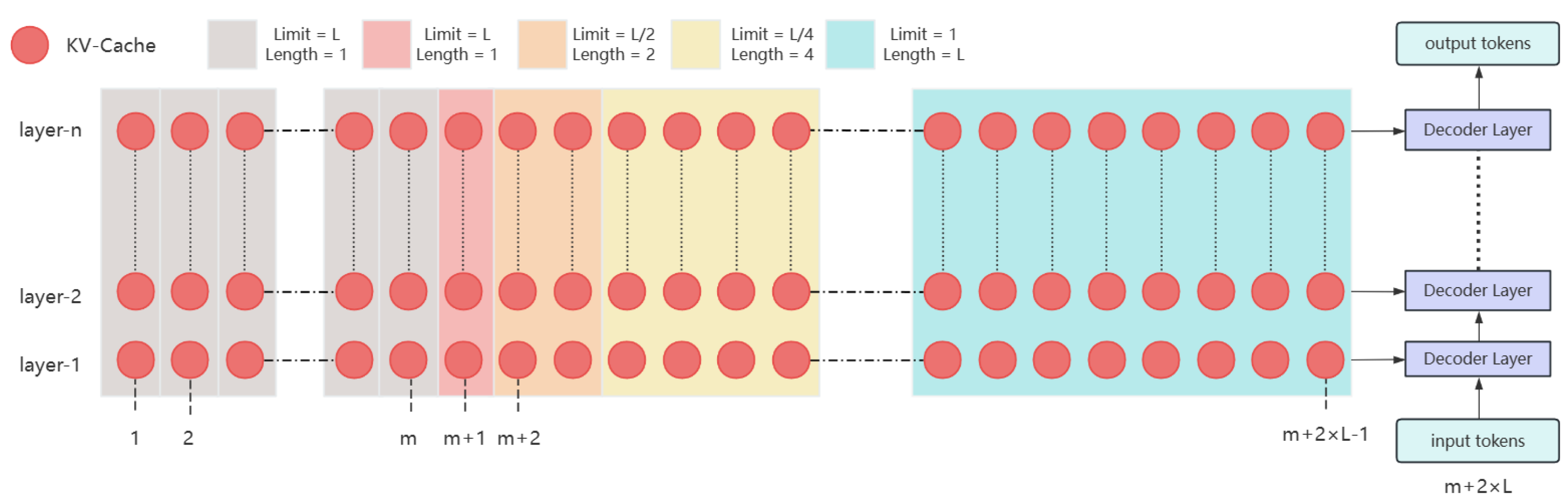
- We aim to implement a distance-based compression method for past memory during inference, where the compression ratio progressively increases with the distance from the next token, halting once the compression ratio reaches a predefined threshold.
- The compression strategy in our method is deterministic, with the specific positions of compression being predetermined, thus eliminating the need for additional computation during inference.
2. Related Work
2.1. Long-Context Processing
2.2. Long-Context Pre-Training
3. Method
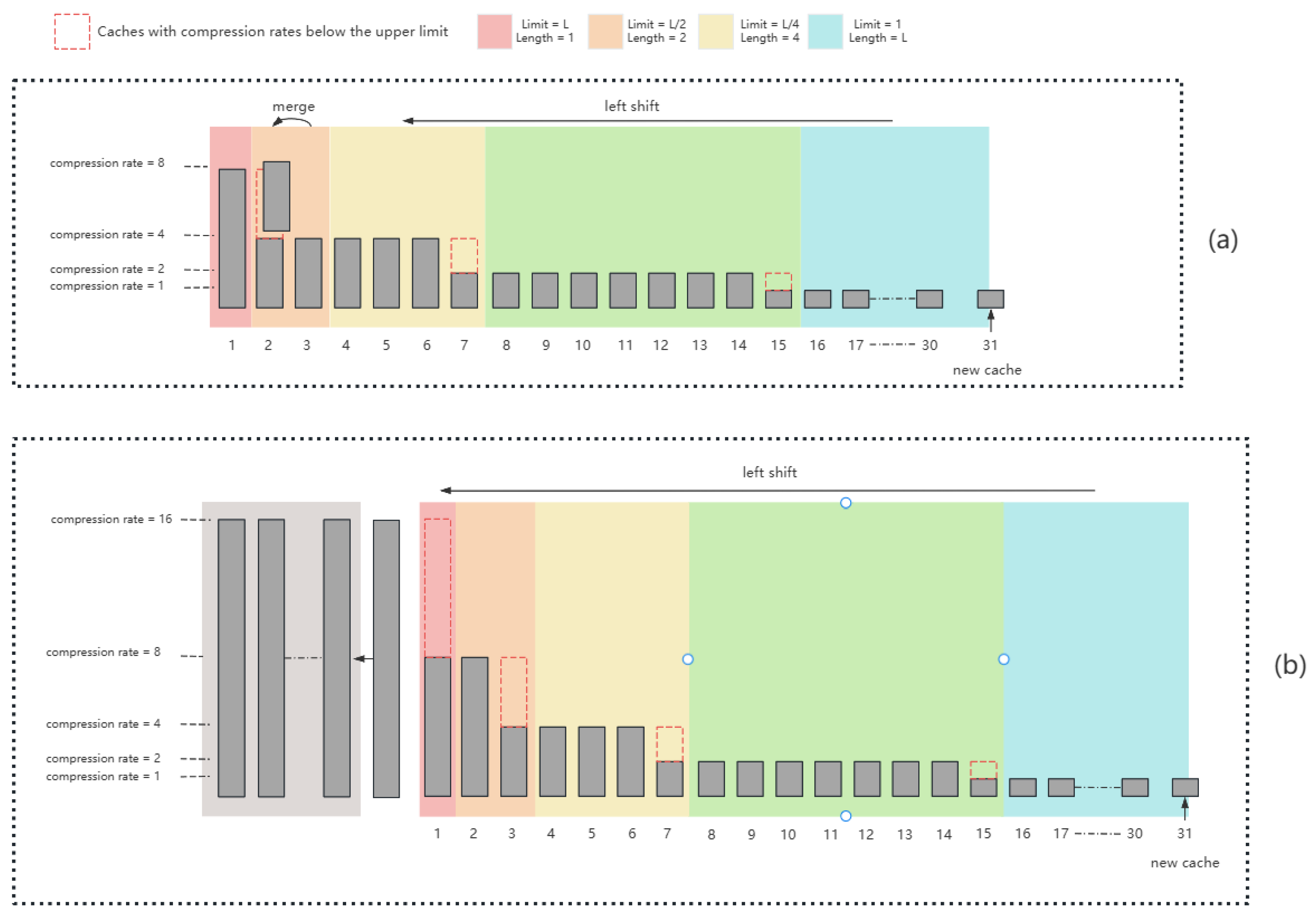
3.1. Merge Planning
- If , enqueue the new ;
- Otherwise, apply for the earliest unsatisfied ;
- If all positions meet their limits, the tail of is moved to , and the process restarts from .
- First, invoke , ensuring merges at more distant key positions are performed before handling p;
- At position p, perform a merge and record it via ;
- Invoke again to ensure that, after processing p, all further positions still satisfy the compression schedule.
| Algorithm 1 Merge scheduling for first segment |
|
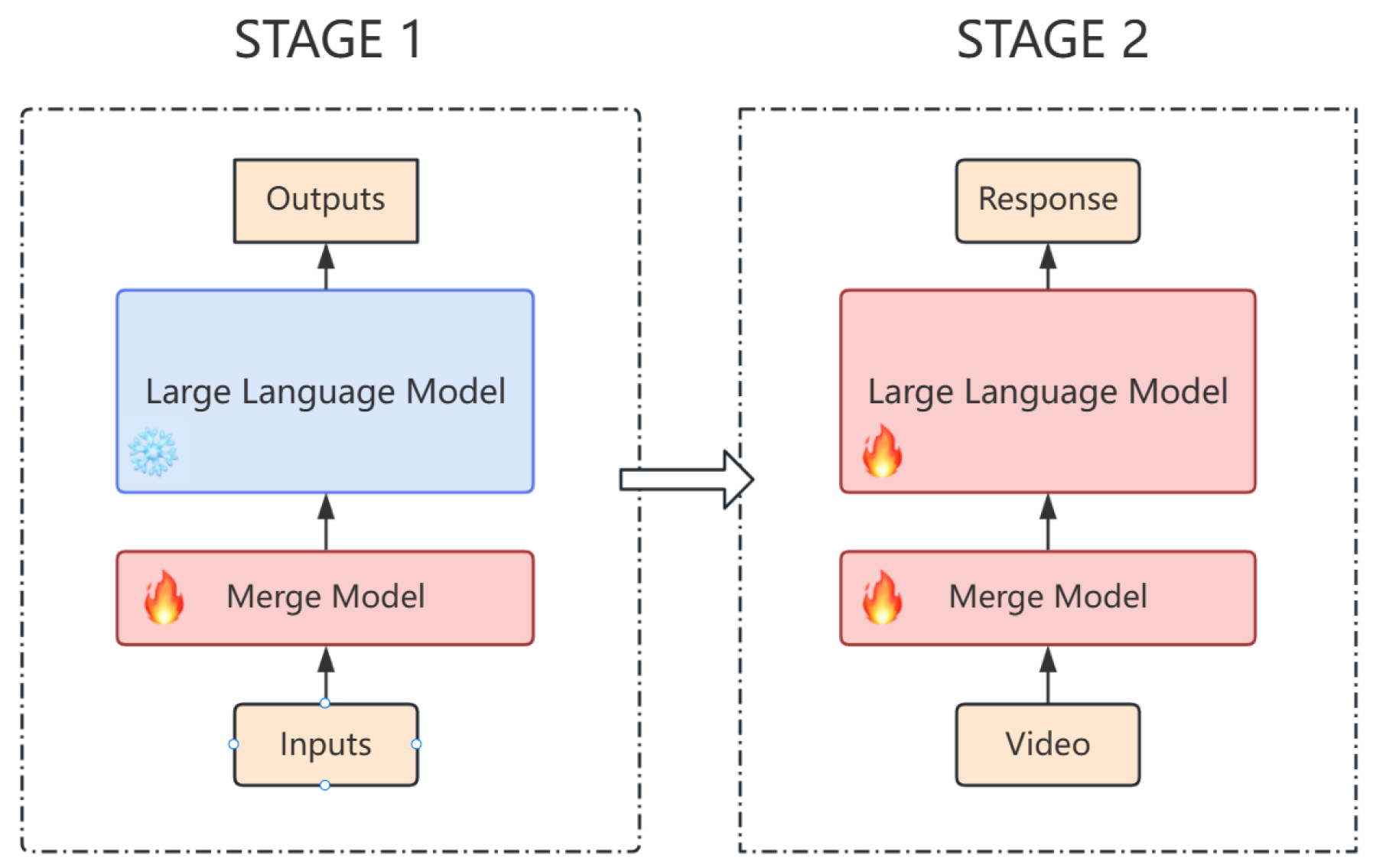
3.2. Merge Model
4. Experiment
4.1. Datasets
4.2. Hyperparameter Selection
4.2.1. MLP Layer Depths
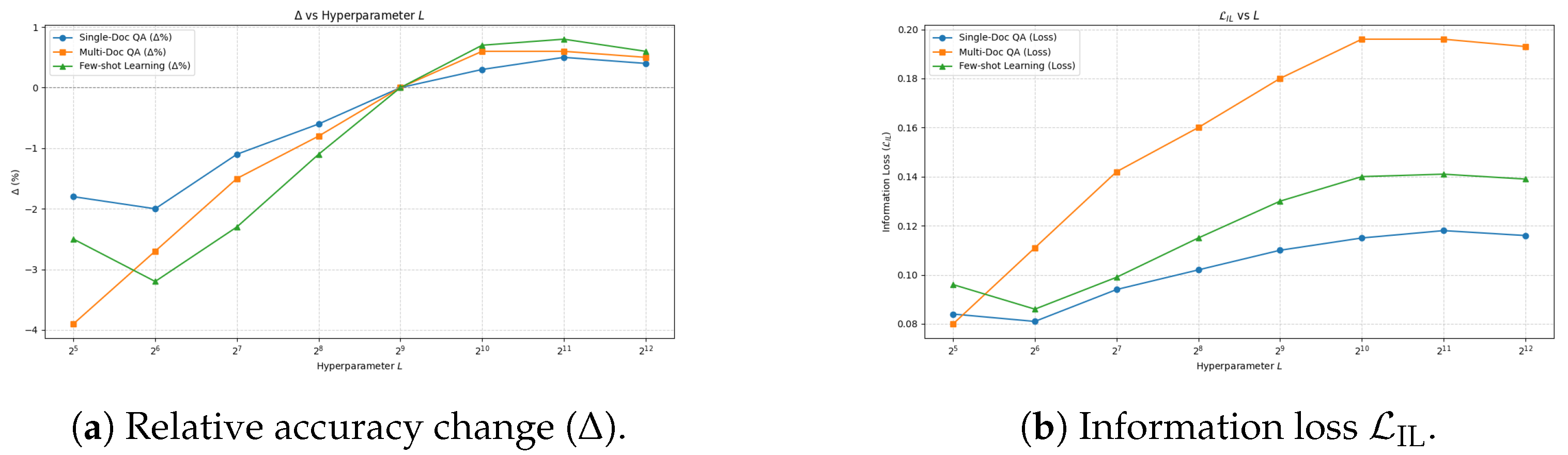
4.2.2. Group Length
4.3. Quality, Stability, and Efficiency of Hierarchical Cache Compression
4.4. Prediction Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [CrossRef] [PubMed]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Xia, F.; Chi, E.; Le, Q.V.; Zhou, D. Chain-of-thought prompting elicits reasoning in large language models. Adv. Neural Inf. Process. Syst. 2022, 35, 24824–24837. [Google Scholar]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar] [CrossRef]
- Zaheer, M.; Guruganesh, G.; Dubey, K.A.; Ainslie, J.; Alberti, C.; Ontanon, S.; Pham, P.; Ravula, A.; Wang, Q.; Yang, L.; et al. Big bird: Transformers for longer sequences. Adv. Neural Inf. Process. Syst. 2020, 33, 17283–17297. [Google Scholar]
- Dai, Z. Transformer-xl: Attentive language models beyond a fixed-length context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Rae, J.W.; Potapenko, A.; Jayakumar, S.M.; Lillicrap, T.P. Compressive transformers for long-range sequence modelling. arXiv 2019, arXiv:1911.05507. [Google Scholar] [CrossRef]
- Munkhdalai, T.; Faruqui, M.; Gopal, S. Leave no context behind: Efficient infinite context transformers with infini-attention. arXiv 2024, arXiv:2404.07143. [Google Scholar] [CrossRef]
- Xiao, C.; Zhang, P.; Han, X.; Xiao, G.; Lin, Y.; Zhang, Z.; Liu, Z.; Han, S.; Sun, M. Infllm: Unveiling the intrinsic capacity of llms for understanding extremely long sequences with training-free memory. arXiv 2024, arXiv:2402.04617. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 2020, 21, 1–67. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Rajpurkar, P. Squad: 100,000+ questions for machine comprehension of text. arXiv 2016, arXiv:1606.05250. [Google Scholar]
- Zhang, Y. Dialogpt: Large-Scale generative pre-training for conversational response generation. arXiv 2019, arXiv:1911.00536. [Google Scholar]
- Tay, Y.; Dehghani, M.; Abnar, S.; Shen, Y.; Bahri, D.; Pham, P.; Rao, J.; Yang, L.; Ruder, S.; Metzler, D. Long range arena: A benchmark for efficient transformers. arXiv 2020, arXiv:2011.04006. [Google Scholar] [CrossRef]
- Bai, Y.; Tu, S.; Zhang, J.; Peng, H.; Wang, X.; Lv, X.; Cao, S.; Xu, J.; Hou, L.; Dong, Y.; et al. Longbench v2: Towards deeper understanding and reasoning on realistic long-context multitasks. arXiv 2024, arXiv:2412.15204. [Google Scholar]
- Li, T.; Zhang, G.; Do, Q.D.; Yue, X.; Chen, W. Long-context llms struggle with long in-context learning. arXiv 2024, arXiv:2404.02060. [Google Scholar]
- Zhang, X.; Chen, Y.; Hu, S.; Xu, Z.; Chen, J.; Hao, M.K.; Han, X.; Thai, Z.L.; Wang, S.; Liu, Z.; et al. ∞ Bench: Extending Long Context Evaluation Beyond 100K Tokens. arXiv 2024, arXiv:2402.13718. [Google Scholar]
- Wu, Y.; Rabe, M.N.; Hutchins, D.; Szegedy, C. Memorizing transformers. arXiv 2022, arXiv:2203.08913. [Google Scholar] [CrossRef]
- Chandar, S.; Ahn, S.; Larochelle, H.; Vincent, P.; Tesauro, G.; Bengio, Y. Hierarchical memory networks. arXiv 2016, arXiv:1605.07427. [Google Scholar] [PubMed]
- Wu, Y.; Zhao, Y.; Hu, B.; Minervini, P.; Stenetorp, P.; Riedel, S. An efficient memory-augmented transformer for knowledge-intensive nlp tasks. arXiv 2022, arXiv:2210.16773. [Google Scholar]
- Su, J.; Ahmed, M.; Lu, Y.; Pan, S.; Bo, W.; Liu, Y. Roformer: Enhanced transformer with rotary position embedding. Neurocomputing 2024, 568, 127063. [Google Scholar] [CrossRef]
- Xiong, W.; Liu, J.; Molybog, I.; Zhang, H.; Bhargava, P.; Hou, R.; Martin, L.; Rungta, R.; Sankararaman, K.A.; Oguz, B.; et al. Effective long-context scaling of foundation models. arXiv 2023, arXiv:2309.16039. [Google Scholar] [CrossRef]
- Chen, S.; Wong, S.; Chen, L.; Tian, Y. Extending context window of large language models via positional interpolation. arXiv 2023, arXiv:2306.15595. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. touvron2023llama. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Yang, A.; Li, A.; Yang, B.; Zhang, B.; Hui, B.; Zheng, B.; Yu, B.; Gao, C.; Huang, C.; Lv, C.; et al. Qwen3 technical report. arXiv 2025, arXiv:2505.09388. [Google Scholar] [CrossRef]
| Layer | Qasper | MultiFieldQA-en | 2WikiMultihopQA |
|---|---|---|---|
| 3 | 38.5 | 28.5 | 42.0 |
| 6 | 44.0 | 34.0 | 48.5 |
| 9 | 46.5 | 35.5 | 50.0 |
| 12 | 47.0 | 37.0 | 51.5 |
| 15 | 48.5 | 38.5 | 53.0 |
| 18 | 47.0 | 39.0 | 52.0 |
| 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | ||
| 4 | 32.8 | 29.3 | 30.7 | 25.6 | 20.3 | 15.8 | 13.5 | 10.2 | |
| 8 | 31.7 | 29.9 | 27.1 | 24.5 | 22.1 | 16.9 | 12.8 | 9.8 | |
| 16 | 33.0 | 32.0 | 28.3 | 22.0 | 21.4 | 15.2 | 11.4 | 9.0 | |
| 32 | 34.6 | 31.8 | 31.8 | 28.2 | 18.0 | 13.3 | 10.0 | 7.6 | |
| 64 | 30.3 | 31.3 | 32.4 | 29.6 | 24.4 | 14.5 | 12.3 | 8.7 | |
| 128 | 29.6 | 30.8 | 32.9 | 26.7 | 25.1 | 19.8 | 11.0 | 9.3 | |
| 256 | 29.5 | 29.9 | 31.7 | 27.1 | 26.3 | 20.0 | 14.2 | 10.8 | |
| 512 | 34.0 | 31.5 | 29.0 | 26.0 | 28.0 | 30.0 | 32.0 | 33.8 | |
| (a) Predicted accuracy on the Single-Doc QA. | |||||||||
| 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | ||
| 4 | 24.1 | 18.5 | 18.7 | 15.3 | 14.6 | 10.7 | 9.8 | 8.1 | |
| 8 | 23.0 | 19.8 | 19.4 | 15.9 | 15.1 | 11.5 | 8.9 | 6.5 | |
| 16 | 23.2 | 22.1 | 20.6 | 17.3 | 16.2 | 12.4 | 10.1 | 7.2 | |
| 32 | 25.1 | 23.7 | 23.5 | 18.8 | 17.5 | 13.3 | 9.5 | 6.8 | |
| 64 | 24.6 | 23.9 | 24.4 | 20.0 | 18.8 | 14.3 | 11.6 | 8.0 | |
| 128 | 24.8 | 24.2 | 25.7 | 21.5 | 19.5 | 16.2 | 12.0 | 9.4 | |
| 256 | 24.9 | 24.3 | 25.9 | 22.0 | 20.3 | 16.8 | 13.5 | 9.5 | |
| 512 | 25.2 | 24.0 | 23.2 | 21.0 | 21.5 | 23.0 | 23.8 | 24.1 | |
| (b) Predicted accuracy on the Multi-Doc QA. | |||||||||
| 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | ||
| 4 | 60.4 | 54.0 | 54.8 | 48.6 | 36.6 | 20.5 | 20.2 | 15.0 | |
| 8 | 65.2 | 55.7 | 54.1 | 48.5 | 39.0 | 26.5 | 15.4 | 10.2 | |
| 16 | 64.4 | 60.9 | 56.0 | 46.8 | 36.8 | 22.6 | 17.0 | 12.1 | |
| 32 | 63.0 | 61.5 | 62.4 | 52.0 | 36.6 | 20.5 | 14.8 | 11.0 | |
| 64 | 62.4 | 62.2 | 62.5 | 55.0 | 47.0 | 26.0 | 21.0 | 15.6 | |
| 128 | 61.8 | 62.4 | 63.7 | 54.7 | 46.0 | 36.8 | 20.2 | 18.5 | |
| 256 | 63.0 | 60.8 | 62.4 | 55.7 | 45.8 | 37.7 | 23.3 | 20.4 | |
| 512 | 65.2 | 62.0 | 60.0 | 54.0 | 55.0 | 58.5 | 61.0 | 65.4 | |
| (c) Predicted accuracy for Few-Shot Learning. | |||||||||
| Method | SDI | BSD | |
|---|---|---|---|
| Baseline | 0.13 | 0.10 | 0.065 |
| TAI only | 0.12 | 0.10 | 0.048 |
| TAI + Boundary Reg. | 0.11 | 0.08 | 0.041 |
| Configuration | (ms) | (GB) | E (J/1k Tokens) | |
|---|---|---|---|---|
| Uncompressed | 38.5 | 46 | 118 | |
| 3.9 | 6.1 | 15 | 1208 | |
| 5.6 | 8.7 | 21 | 1357 |
| Avg | I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|---|
| GLM-4-9B-Chat | 30.2 | 30.9 | 27.2 | 33.3 | 38.5 | 28.0 | 24.2 |
| GLM-4-Plus | 44.3 | 41.7 | 42.4 | 46.9 | 51.3 | 46.0 | 48.5 |
| Qwen2.5-72B-Inst. | 39.4 | 40.6 | 35.2 | 42.0 | 25.6 | 50.0 | 42.4 |
| GPT-4o | 50.1 | 48.6 | 44.0 | 58.0 | 46.2 | 56.0 | 51.5 |
| Llama-3.1-8B-Inst. | 30.0 | 34.9 | 30.4 | 23.5 | 17.9 | 32.0 | 30.3 |
| Our method(Llama-3.1-8B-Inst.) | 35.6 | 35.8 | 36.1 | 38.2 | 37.4 | 39.3 | 28.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Hu, B. Distance-Based Compression Method for Large Language Models. Appl. Sci. 2025, 15, 9482. https://doi.org/10.3390/app15179482
Shen H, Hu B. Distance-Based Compression Method for Large Language Models. Applied Sciences. 2025; 15(17):9482. https://doi.org/10.3390/app15179482
Chicago/Turabian StyleShen, Hongxin, and Baokun Hu. 2025. "Distance-Based Compression Method for Large Language Models" Applied Sciences 15, no. 17: 9482. https://doi.org/10.3390/app15179482
APA StyleShen, H., & Hu, B. (2025). Distance-Based Compression Method for Large Language Models. Applied Sciences, 15(17), 9482. https://doi.org/10.3390/app15179482






