A Review of Methods for Assessing the Quality of Measurement Systems and Results
Abstract
1. Introduction
- (i)
- compare how key metrological concepts (accuracy, precision, repeatability, reproducibility, trueness, bias, and measurement uncertainty) are defined and applied in major frameworks (MSA, ISO 5725, GUM, ISO 21748, etc.);
- (ii)
- illustrate their application through real or literature-based data examples;
- (iii)
- identify key terminological inconsistencies that may lead to misinterpretation;
- (iv)
- offer guidelines for method selection and harmonization, including the integration of digital and AI-based tools.
2. Comparison of Terminology, Standards, and Methodologies
3. Methods in Practice
3.1. Example of Gage R&R Study Using and R Method
3.2. Example of a Gage R&R Study Using Attribute Agreement Analysis
3.3. Example of the Application of ISO 5725
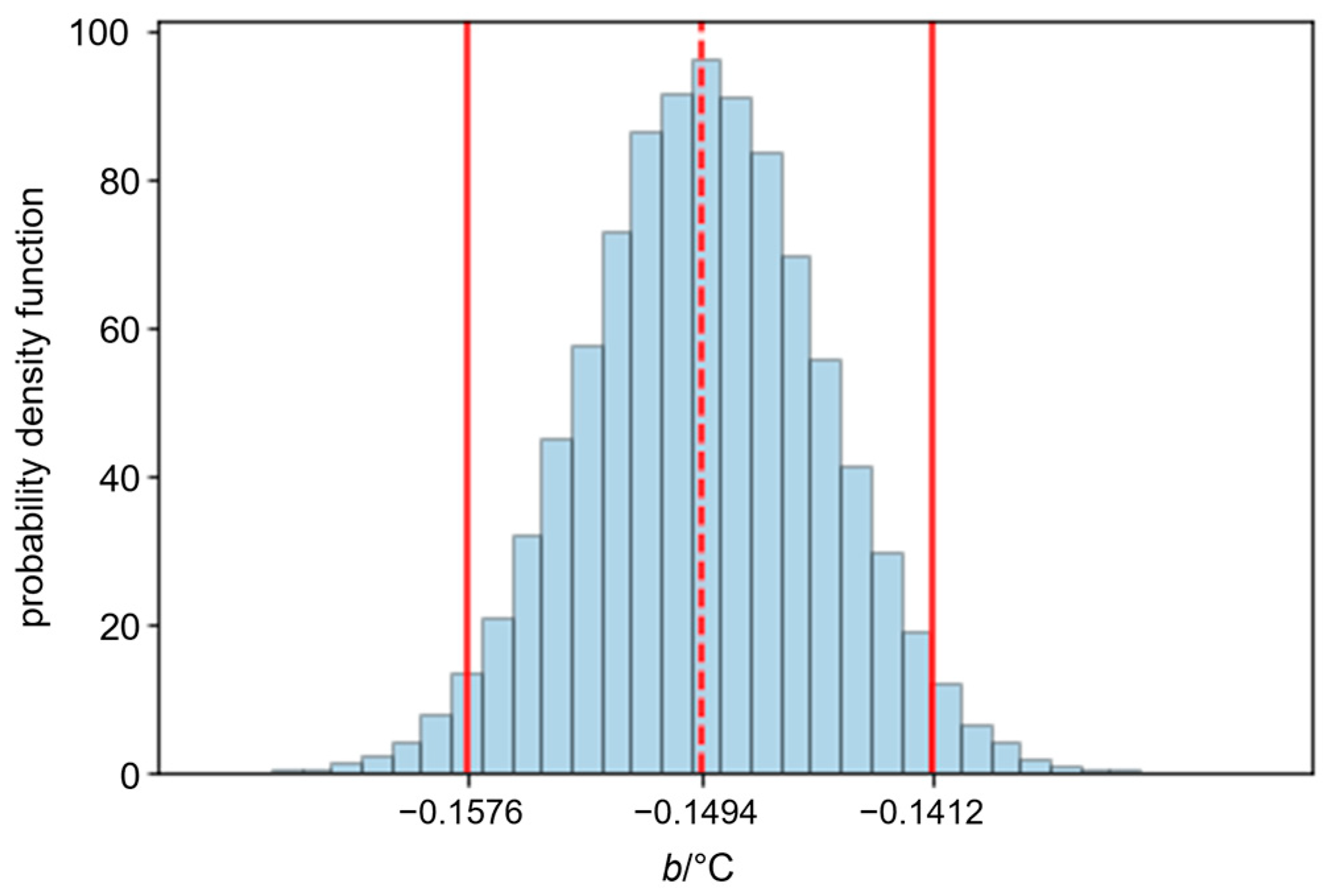
3.4. Example of Measurement Uncertainty Evaluation Using the GUM Method
- b(t) is the predicted value of the thermometer correction at temperature t, expressed in °C;
- y1 = −0.1712 °C is the intercept of the calibration curve, with an associated standard uncertainty of s(y1) = 0.0029 °C;
- y2 = 0.00218 °C is the slope of the calibration curve, with an associated standard uncertainty of s(y2) = 0.00067 °C;
- r(y1, y2) = −0.930 is the estimated correlation coefficient between y1 and y2;
- s = 0.0035 °C is the estimated standard deviation of the fit residuals;
- t is the temperature at which the correction is to be predicted, expressed in °C;
- t0 is the chosen reference temperature, an exactly known fixed value, expressed in °C.
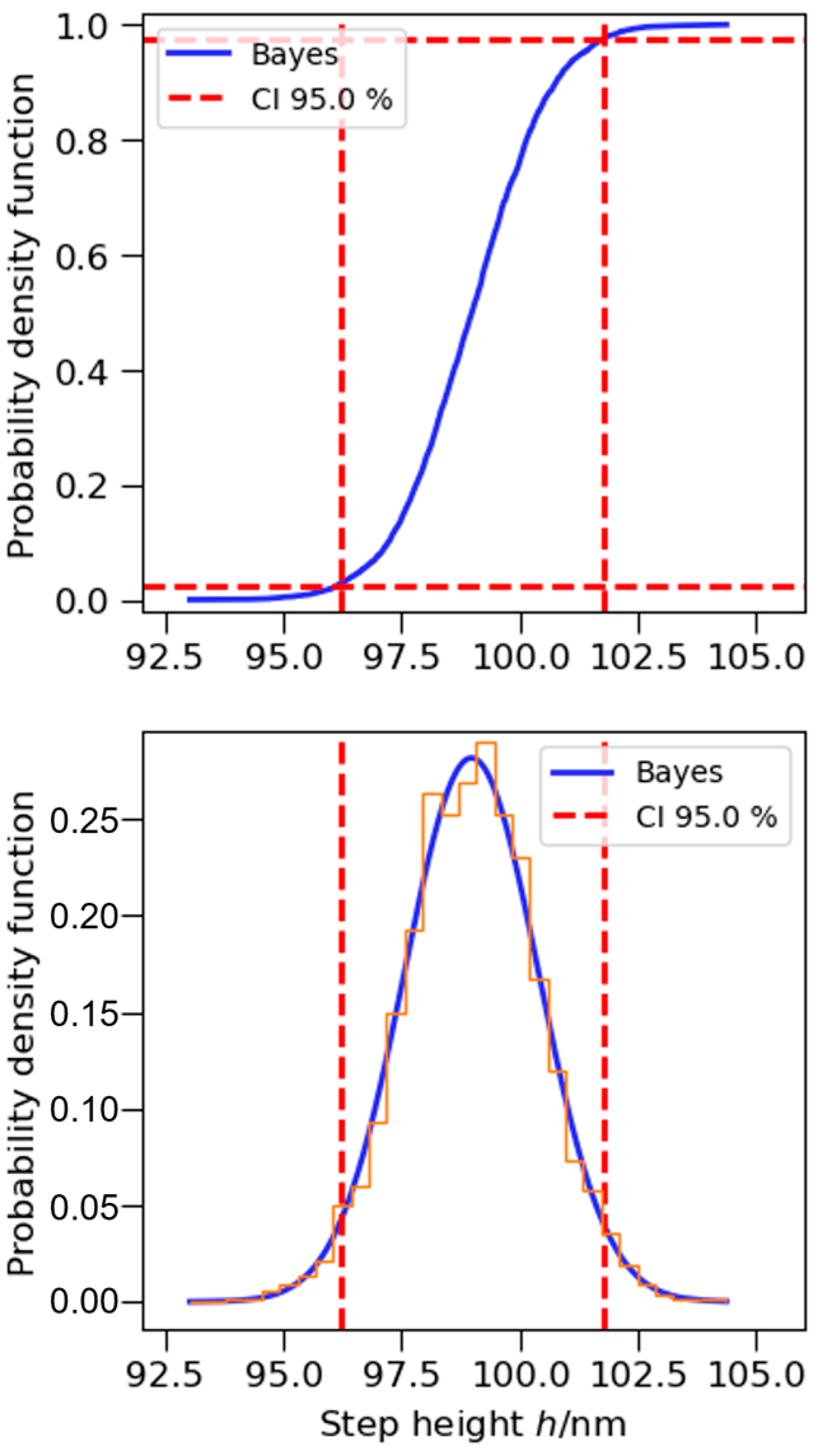
3.5. Example of Measurement Uncertainty Evaluation Using the Monte Carlo Simulation Method
3.6. Example of Measurement Uncertainty Evaluation Using the Bayesian Approach
4. Discussion: Strengths, Limitations, and Method Selection
4.1. Applicability and Scope of Measurement System Analysis (MSA)
- To assess the quality of measurement systems in order to understand how much of the variation in results is caused by the measurement system compared to the actual product variation.
- To analyze components within the measurement system (gauge, operator, and interactions).
- When introducing new measurement systems, to verify their suitability before use.
- In the context of quality control when measuring or verifying product compliance with requirements.
- In situations where discrete decisions are made (e.g., during inspection or visual examination).
- Multiple operators evaluate the same set of parts (e.g., pass/fail) multiple times, and the results are compared with each other and with a known “gold standard”. The following aspects are analyzed: accuracy relative to the reference (how often the operator agrees with the correct answer), internal consistency of the operator (repeatability), and consistency among operators (reproducibility).
- To assess inter-rater agreement, especially in situations where multiple rating levels are possible (e.g., low/medium/high defect severity). The kappa coefficient indicates the degree of agreement beyond chance.
4.2. Advantages and Limitations of the MSA
- It is ideal for quick, operational verification of measurement capability within industrial production.
- It clearly links the measurement system to process control and decision-making—for example, whether a result can be used to accept or reject a part.
- It provides clear thresholds and acceptability criteria.
- MSA is an integrated part of quality management systems and tools such as SPC (Statistical Process Control), PPAP (Production Part Approval Process), and APQP (Advanced Product Quality Planning).
- The focus is on the measurement system as a whole, not just the measurement result.
- It is tailored to specific industrial processes and is less applicable in scientific or research environments.
- It requires multiple operators to repeat measurements on the same sample, which is often not feasible in practice.
- It does not provide a systematic evaluation of measurement uncertainty.
- It is limited to production environments and intra-laboratory assessments.
4.3. Applicability and Scope of the ISO 5725 Series of Standards
- For designing and conducting interlaboratory studies aimed at determining the repeatability (within-laboratory) and reproducibility (between-laboratories) of measurement results.
- For evaluating the trueness of measurement methods based on experimental data obtained from multiple laboratories.
- For internal quality control of measurement methods within a single laboratory, especially when the same method is applied continuously over time.
- For assessing the accuracy (i.e., trueness and precision) of a method in research settings where the number of available samples is small, measurement conditions are not standardized, or the method is applied in a non-standard context.
- ISO 5725 covers a wide range of measurement situations, allowing for the analysis of results obtained under different conditions, from various laboratories and methods.
- The approach is internationally standardized, meaning that the results and procedures are globally recognized and accepted, especially in the scientific community, in industry, and by regulatory bodies.
- The standards distinguish between different sources of variability, including repeatability, intermediate precision, and reproducibility, enabling a detailed analysis of method performance under varying conditions.
- The approach can be adapted to different levels of complexity, from simple laboratory tests to full interlaboratory studies, depending on the user’s needs.
- It requires a solid understanding of statistics (e.g., ANOVA, variance analysis, and outlier tests), which can be a barrier for use in small laboratories or in industrial settings without data specialists.
- It does not provide numerical values of measurement uncertainty directly but focuses on estimates of precision and trueness as components of accuracy. As a result, results often need to be further converted into uncertainty estimates for accreditation purposes.
- It is not designed for rapid evaluation of measurement systems on production lines, where quick detection of operator or instrument deviations is crucial.
- The standards were originally developed for analytical and laboratory methods (e.g., chemical and microbiological), making them more difficult to apply directly to methods involving complex image processing (e.g., AFM, 3D optical measurements, and Computed Tomography).
- They are not designed to systematically analyze and control all digital and software-related factors that may influence the measurement result.
4.4. Applicability and Scope of Measurement Uncertainty Evaluation
4.5. Advantages and Limitations of GUM, Monte Carlo, and Bayesian Methods
4.5.1. Advantages of the GUM, Monte Carlo, and Bayesian Approaches
4.5.2. Limitations of the GUM, Monte Carlo, and Bayesian Approaches
4.6. Limitations and Sources of Uncertainty
5. Conclusions
6. Future Directions and Recommendations
- Continued education of engineers and measurement system users on the importance of expressing and interpreting measurement uncertainty;
- Promotion of the integration of advanced numerical and probabilistic methods into everyday practice;
- Exploration of the potential of AI and ML in metrology;
- Standardization of uncertainty evaluation procedures for automated production environments;
- Development of modular tools and systems for quality assessment, enabling the flexible application of different methods (GUM, MCS, and Bayesian) according to user needs.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pendrill, L.R. Using Measurement Uncertainty in Decision-Making and Conformity Assessment. Metrologia 2014, 51, S206. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPA; OIML. Evaluation of Measurement Data—The Role of Measurement Uncertainty in Conformity Assessment; JCGM: Sèvres, France, 2012. [Google Scholar]
- AIAG. Measurement Systems Analysis: Reference Manual, 4th ed.; Automotive Industry Action Group: Southfield, MI, USA, 2010. [Google Scholar]
- ISO 5725-1:2023; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 1: General Principles and Definitions. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 5725-2:2019; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 2: Basic Method for the Determination of Repeatability and Reproducibility of a Standard Measurement Method. International Organization for Standardization: Geneva, Switzerland, 2019.
- ISO 5725-3:2023; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 3: Intermediate Precision and Alternative Designs for Collaborative Studies. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 5725-4:2020; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 4: Basic Methods for the Determination of the Trueness of a Standard Measurement Method. International Organization for Standardization: Geneva, Switzerland, 2020.
- ISO/DIS 5725-5; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 5: Alternative Methods for the Determination of the Precision of a Standard Measurement Method. International Organization for Standardization: Geneva, Switzerland, 1998.
- ISO 5725-6:1994; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 6: Use in Practice of Accuracy Values. International Organization for Standardization: Geneva, Switzerland, 1994.
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. International Organization for Standardization: Geneva, Switzerland, 2008.
- JCGM 101:2008; Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method. International Organization for Standardization: Geneva, Switzerland, 2008.
- Cox, M.; Shirono, K. Informative Bayesian Type A Uncertainty Evaluation, Especially Applicable to a Small Number of Observations. Metrologia 2017, 54, 642–652. [Google Scholar] [CrossRef]
- Van Der Veen, A.M.H. Bayesian Methods for Type A Evaluation of Standard Uncertainty. Metrologia 2018, 55, 670–684. [Google Scholar] [CrossRef]
- Lira, I.; Grientschnig, D. Bayesian Assessment of Uncertainty in Metrology: A Tutorial. Metrologia 2010, 47, R1–R14. [Google Scholar] [CrossRef]
- ISO 21748:2017; Guidance for the Use of Repeatability, Reproducibility and Trueness Estimates in Measurement Uncertainty Evaluation. International Organization for Standardization: Geneva, Switzerland, 2017.
- Bich, W.; Cox, M.G.; Dybkaer, R.; Elster, C.; Estler, W.T.; Hibbert, B.; Imai, H.; Kool, W.; Michotte, C.; Nielsen, L.; et al. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Metrologia 2012, 49, 702–705. [Google Scholar] [CrossRef]
- Arendacká, B.; Täubner, A.; Eichstädt, S.; Bruns, T.; Elster, C. Linear Mixed Models: Gum and Beyond. Meas. Sci. Rev. 2014, 14, 52–61. [Google Scholar] [CrossRef]
- Runje, B.; Novak, A.H.; Razumić, A.; Piljek, P.; Štrbac, B.; Orosnjak, M. Evaluation of Consumer and Producer Risk in Conformity Assessment Decisions. In Proceedings of the 30th Daaam International Symposium on Inteligent Manufacturing and Automation, Zadar, Croatia, 23–26 October 2019; Danube Adria Association for Automation and Manufacturing, DAAAM: Vienna, Austria, 2019. [Google Scholar]
- Cox, M.G.; Harris, P.M. Software Support for Metrology Best Practice Guide No. 6. Uncertainty Evaluation. Available online: https://eprintspublications.npl.co.uk/4655/ (accessed on 24 July 2025).
- Kacker, R.N. Bayesian Alternative to the ISO-GUM’s Use of the Welch–Satterthwaite Formula. Metrologia 2005, 43, 1. [Google Scholar] [CrossRef]
- Aggogeri, F.; Barbato, G.; Barini, E.M.; Genta, G.; Levi, R. Measurement Uncertainty Assessment of Coordinate Measuring Machines by Simulation and Planned Experimentation. CIRP J. Manuf. Sci. Technol. 2011, 4, 51–56. [Google Scholar] [CrossRef]
- Božić, D.; Runje, B.; Razumić, A. Risk Assessment for Linear Regression Models in Metrology. Appl. Sci. 2024, 14, 2605. [Google Scholar] [CrossRef]
- Forbes, A. Traceable Measurements Using Sensor Networks. Trans. Mach. Learn. Data Min. 2015, 8, 77–100. [Google Scholar]
- Bell, S.A. A Beginner’s Guide to Uncertainty of Measurement; National Physical Laboratory: Teddington, UK, 2001. [Google Scholar]
- ISO-ISO/IEC 17025; Testing and Calibration Laboratories. International Organization for Standardization: Geneva, Switzerland, 2017.
- Forbes, A.B. Measurement Uncertainty and Optimized Conformance Assessment. Measurement 2006, 39, 808–814. [Google Scholar] [CrossRef]
- Allard, A.; Fischer, N.; Smith, I.; Harris, P.; Pendrill, L. Risk Calculations for Conformity Assessment in Practice. In Proceedings of the 19th International Congress of Metrology (CIM2019), Paris, France, 24–26 September 2019; EDP Sciences: Les Ulis, France, 2019; p. 16001. [Google Scholar]
- Ellison, S.L.R.; Williams, A. Quantifying Uncertainty in Analytical Measurement, 3rd ed.; Eurachem/CITAC: Teddington, UK, 2012. [Google Scholar]
- Burdick, R.K.; Borror, C.M.; Montgomery, D.C. A Review of Methods for Measurement Systems Capability Analysis. J. Qual. Technol. 2003, 35, 342–354. [Google Scholar] [CrossRef]
- Zanobini, A.; Sereni, B.; Catelani, M.; Ciani, L. Repeatability and Reproducibility Techniques for the Analysis of Measurement Systems. Measurement 2016, 86, 125–132. [Google Scholar] [CrossRef]
- Simion, C. Assessing Bias and Linearity of a Measurement System. Appl. Mech. Mater. 2015, 760, 621–626. [Google Scholar] [CrossRef]
- Pai, F.-Y.; Yeh, T.-M.; Hung, Y.-H. Analysis on Accuracy of Bias, Linearity and Stability of Measurement System in Ball Screw Processes by Simulation. Sustainability 2015, 7, 15464–15486. [Google Scholar] [CrossRef]
- Abdelgadir, M.; Gerling, C.; Dobson, J. Variable Data Measurement Systems Analysis: Advances in Gage Bias and Linearity Referencing and Acceptability. Int. J. Metrol. Qual. Eng. 2020, 11, 16. [Google Scholar] [CrossRef]
- Sahay, C.; Ghosh, S.; Haja Mohideen, S.M. Effects of Within Part Variation on Measurement System Analysis. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 45196, pp. 1827–1836. [Google Scholar]
- Runje, B.; Novak, A.H.; Razumić, A. Measurement System Analysis in Production Process. In Proceedings of the XVII International Scientific Conference on Industrial Systems (IS’17), Novi Sad, Serbia, 4–6 October 2017; pp. 274–277. [Google Scholar]
- Wang, Y.; Zhang, D.; Zhang, S.; Jia, Q.; Zhang, H. Quality Confirmation of Electrical Measurement Data for Space Parts Based on MSA Method. In Signal and Information Processing, Networking and Computers, Proceedings of the 7th International Conference on Signal and Information Processing, Networking and Computers (ICSINC), Rizhao, China, 21–23 September 2020; Wang, Y., Fu, M., Xu, L., Zou, J., Eds.; Springer: Singapore, 2020; pp. 344–351. [Google Scholar]
- Paneva, V.I. Evaluation of Adequacy of Quantitative Laboratory Chemical Analysis Techniques. Inorg. Mater. 2009, 45, 1652–1657. [Google Scholar] [CrossRef]
- Cosmi, F.; Dal Maso, A. BES TESTTM Accuracy Evaluation by Means of 3D-Printed Phantoms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 1783–1792. [Google Scholar] [CrossRef]
- Garcia, O.; Di Giorgio, M.; Vallerga, M.B.; Radl, A.; Taja, M.R.; Seoane, A.; De Luca, J.; Stuck Oliveira, M.; Valdivia, P.; Lamadrid, A.I. Interlaboratory Comparison of Dicentric Chromosome Assay Using Electronically Transmitted Images. Radiat. Prot. Dosim. 2013, 154, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Klauenberg, K.; Martens, S.; Bošnjaković, A.; Cox, M.G.; van der Veen, A.M.; Elster, C. The GUM Perspective on Straight-Line Errors-in-Variables Regression. Measurement 2022, 187, 110340. [Google Scholar] [CrossRef]
- Bich, W.; Callegaro, L.; Pennecchi, F. Non-Linear Models and Best Estimates in the GUM. Metrologia 2006, 43, S196. [Google Scholar] [CrossRef]
- Carmona, J.A.; Ramírez, P.; García, M.C.; Santos, J.; Muñoz, J. Linear and Non-Linear Flow Behavior of Welan Gum Solutions. Rheol. Acta 2019, 58, 1–8. [Google Scholar] [CrossRef]
- Bodnar, O.; Wübbeler, G.; Elster, C. On the Application of Supplement 1 to the GUM to Non-Linear Problems. Metrologia 2011, 48, 333. [Google Scholar] [CrossRef]
- Cox, M.; Harris, P.; Siebert, B.R.-L. Evaluation of Measurement Uncertainty Based on the Propagation of Distributions Using Monte Carlo Simulation. Meas. Tech. 2003, 46, 824–833. [Google Scholar] [CrossRef]
- Chen, A.; Chen, C. Comparison of GUM and Monte Carlo Methods for Evaluating Measurement Uncertainty of Perspiration Measurement Systems. Measurement 2016, 87, 27–37. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Hegazy, R.S. Comparison of GUM and Monte Carlo Methods for the Uncertainty Estimation in Hardness Measurements. Int. J. Metrol. Qual. Eng. 2017, 8, 14. [Google Scholar] [CrossRef]
- Niemeier, W.; Tengen, D. Uncertainty Assessment in Geodetic Network Adjustment by Combining GUM and Monte-Carlo-Simulations. J. Appl. Geod. 2017, 11, 67–76. [Google Scholar] [CrossRef]
- Papadopoulos, C.E.; Yeung, H. Uncertainty Estimation and Monte Carlo Simulation Method. Flow Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- Garg, N.; Yadav, S.; Aswal, D.K. Monte Carlo Simulation in Uncertainty Evaluation: Strategy, Implications and Future Prospects. MAPAN 2019, 34, 299–304. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, T.; Liu, S.; Zhang, W.; Yang, B.; Chen, L. Quantification of Model Uncertainty and Variability for Landslide Displacement Prediction Based on Monte Carlo Simulation. Gondwana Res. 2023, 123, 27–40. [Google Scholar] [CrossRef]
- Possolo, A.; Merkatas, C.; Bodnar, O. Asymmetrical Uncertainties. Metrologia 2019, 56, 45009. [Google Scholar] [CrossRef]
- Honarvar, A. Modeling of Asymmetry between Gasoline and Crude Oil Prices: A Monte Carlo Comparison. Comput. Econ. 2010, 36, 237–262. [Google Scholar] [CrossRef]
- Huang, H. A Propensity-Based Framework for Measurement Uncertainty Analysis. Measurement 2023, 213, 112693. [Google Scholar] [CrossRef]
- Rashki, M. The Soft Monte Carlo Method. Appl. Math. Model. 2021, 94, 558–575. [Google Scholar] [CrossRef]
- Sengupta, A.; Mondal, S.; Das, A.; Guler, S.I. A Bayesian Approach to Quantifying Uncertainties and Improving Generalizability in Traffic Prediction Models. Transp. Res. Part C Emerg. Technol. 2024, 162, 104585. [Google Scholar] [CrossRef]
- Meija, J.; Bodnar, O.; Possolo, A. Ode to Bayesian Methods in Metrology. Metrologia 2023, 60, 52001. [Google Scholar] [CrossRef]
- Bardsley, J.M. MCMC-Based Image Reconstruction with Uncertainty Quantification. SIAM J. Sci. Comput. 2012, 34, A1316–A1332. [Google Scholar] [CrossRef]
- Green, P.L.; Worden, K. Bayesian and Markov Chain Monte Carlo Methods for Identifying Nonlinear Systems in the Presence of Uncertainty. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140405. [Google Scholar] [CrossRef] [PubMed]
- Chandra, R.; Simmons, J. Bayesian Neural Networks via MCMC: A Python-Based Tutorial. IEEE Access 2024, 12, 70519–70549. [Google Scholar] [CrossRef]
- Carobbi, C.; Pennecchi, F. Bayesian Conformity Assessment in Presence of Systematic Measurement Errors. Metrologia 2016, 53, S74. [Google Scholar] [CrossRef]
- Elster, C. Calculation of Uncertainty in the Presence of Prior Knowledge. Metrologia 2007, 44, 111–116. [Google Scholar] [CrossRef]
- Stephan, K.E.; Penny, W.D.; Daunizeau, J.; Moran, R.J.; Friston, K.J. Bayesian Model Selection for Group Studies. NeuroImage 2009, 46, 1004–1017. [Google Scholar] [CrossRef] [PubMed]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian Statistics and Modelling. Nat. Rev. Methods Primers 2021, 1, 1–26. [Google Scholar] [CrossRef]
- Demeyer, S.; Fischer, N.; Elster, C. Guidance on Bayesian Uncertainty Evaluation for a Class of GUM Measurement Models. Metrologia 2020, 58, 14001. [Google Scholar] [CrossRef]
- Abduljaleel, M.; Midi, H.; Karimi, M. Outlier Detection in the Analysis of Nested Gage R&R, Random Effect Model. Stat. Transit. New Ser. 2019, 20, 31–56. [Google Scholar] [CrossRef]
- Al-Qudah, S.K. A Study of the AIAG Measurement System Analysis (MSA) Method for Quality Control. J. Manag. Eng. Integr. 2017, 10, 68–80. [Google Scholar]
- Al-Refaie, A.; Bata, N. Evaluating Measurement and Process Capabilities by GR&R with Four Quality Measures. Measurement 2010, 43, 842–851. [Google Scholar] [CrossRef]
- Aquila, G.; Peruchi, R.S.; Junior, P.R.; Rocha, L.C.S.; de Queiroz, A.R.; de Oliveira Pamplona, E.; Balestrassi, P.P. Analysis of the Wind Average Speed in Different Brazilian States Using the Nested GR&R Measurement System. Measurement 2018, 115, 217–222. [Google Scholar] [CrossRef]
- Cepova, L.; Kovacikova, A.; Cep, R.; Klaput, P.; Mizera, O. Measurement System Analyses–Gauge Repeatability and Reproducibility Methods. Meas. Sci. Rev. 2018, 18, 20–27. [Google Scholar] [CrossRef]
- Kooshan, F. Implementation of Measurement System Analysis System (MSA): In the Piston Ring Company Case Study. Int. J. Sci. Technol. 2012, 2, 749–761. [Google Scholar]
- Marques, R.A.M.; Pereira, R.B.D.; Peruchi, R.S.; Brandao, L.C.; Ferreira, J.R.; Davim, J.P. Multivariate GR&R through Factor Analysis. Measurement 2020, 151, 107107. [Google Scholar] [CrossRef]
- Peruchi, R.S.; Balestrassi, P.P.; de Paiva, A.P.; Ferreira, J.R.; de Santana Carmelossi, M. A New Multivariate Gage R&R Method for Correlated Characteristics. Int. J. Prod. Econ. 2013, 144, 301–315. [Google Scholar] [CrossRef]
- Razumić, A.; Runje, B.; Keran, Z.; Trzun, Z.; Pugar, D. Reproducibility of Areal Topography Parameters Obtained by Atomic Force Microscope. Teh. Glas. 2025, 19, 1–6. [Google Scholar] [CrossRef]
- Bontempi, M.; Cardinale, U.; Bragonzoni, L.; Muccioli, G.M.M.; Alesi, D.; di Matteo, B.; Marcacci, M.; Zaffagnini, S. A Computer Simulation Protocol to Assess the Accuracy of a Radio Stereometric Analysis (RSA) Image Processor According to the ISO-5725. arXiv 2020, arXiv:2006.03913. [Google Scholar]
- D’Aucelli, G.M.; Giaquinto, N.; Mannatrizio, S.; Savino, M. A Fully Customizable MATLAB Framework for MSA Based on ISO 5725 Standard. Meas. Sci. Technol. 2017, 28, 44007. [Google Scholar] [CrossRef]
- Stöckl, D.; Van Uytfanghe, K.; Cabaleiro, D.; Thienpont, L. Calculation of Measurement Uncertainty in Clinical Chemistry. Clin. Chem. 2005, 51, 276–277. [Google Scholar] [CrossRef] [PubMed]
- Feinberg, M. Basics of Interlaboratory Studies: The Trends in the New ISO 5725 Standard Edition. TrAC Trends Anal. Chem. 1995, 14, 450–457. [Google Scholar] [CrossRef]
- Razumić, A. Procjena Mjerne Nesigurnosti Rezultata Mjerenja na Području Mikroskopije Atomskih Sila u Dimenzijskom Nanomjeriteljstvu. Ph.D. Thesis, Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Zagreb, Croatia, 2024. [Google Scholar]
- Alar, V.; Razumić, A.; Runje, B.; Stojanović, I.; Kurtela, M.; Štrbac, B. Application of Areal Topography Parameters in Surface Characterization. Appl. Sci. 2025, 15, 6573. [Google Scholar] [CrossRef]
- Razumić, A.; Runje, B.; Lisjak, D.; Kolar, D.; Horvatić Novak, A.; Štrbac, B.; Savković, B. Atomic Force Microscopy: Step Height Measurement Uncertainty Evaluation. Teh. Glas. 2024, 18, 209–214. [Google Scholar] [CrossRef]
- van der Veen, A.; Cox, M.; Greenwood, J.; Bošnjaković, A.; Karahodžić, V.; Martens, S.; Klauenberg, K.; Elster, C.; Demeyer, S.; Fischer, N.; et al. Good Practice in Evaluating Measurement Uncertainty—Compendium of Examples; EURAMET: Teddington, UK, 2021. [Google Scholar]
- Cox, M.G.; Greenwood, J.; Bošnjaković, A.; Karahodžić, V. Two-point and Multipoint Calibration. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 57–68. [Google Scholar]
- Ribeiro, A.S.; Cox, M.G.; Almeida, M.C.; Sousa, J.A.; Martins, L.L.; Simoes, C.; Brito, R.; Loureiro, D.; Silva, M.A.; Soares, A.C. Evaluation of Measurement Uncertainty in Average Areal Rainfall—Uncertainty Propagation for Three Methods. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 205–218. [Google Scholar]
- Martins, L.L.; Ribeiro, A.S.; Cox, M.G.; Sousa, J.A.; Loureiro, D.; Almeida, M.C.; Silva, M.A.; Brito, R.; Soares, A.C. Evaluation of Measurement Uncertainty in SBI—Single Burning Item Reaction to Fire Test. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 77–90. [Google Scholar]
- Cox, M.G.; Gardiner, T.; Robinson, R.; Smith, T.; Ellison, S.L.R.; Van der Veen, A.M.H. Greenhouse Gas Emission Inventories. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 269–282. [Google Scholar]
- Demeyer, S.; Fischer, N.; Cox, M.G.; Van der Veen, A.M.H.; Sousa, J.A.; Pellegrino, O.; Bošnjaković, A.; Karahodžić, V.; Elster, C. Bayesian Approach Applied to the Mass Calibration Example in JCGM 101:2008. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 71–76. [Google Scholar]
- Caebergs, T.; De Boeck, B.; Pétry, J.; Sebaïhi, N.; Cox, M.G.; Fischer, N.; Greenwood, J. Uncertainty Evaluation of Nanoparticle Size by AFM, by Means of an Optimised Design of Experiment for a Hierarchical Mixed Model in a Bayesian Framework Approach. In Good Practice in Evaluating Measurement Uncertainty; EURAMET: Teddington, UK, 2021; pp. 171–188. [Google Scholar]
- ISO 15189:2022; Medical Laboratories—Requirements for Quality and Competence. International Organization for Standardization: Geneva, Switzerland, 2022.
- ISO/IEC 17020:2012; Conformity Assessment—Requirements for the Operation of Various Types of Bodies Performing Inspection. International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO 10012:2003; Measurement Management Systems—Requirements for Measurement Processes and Measuring Equipment. International Organization for Standardization: Geneva, Switzerland, 2003.
- ISO 14253-1:2017; Geometrical Product Specifications (GPS)—Inspection by Measurement of Workpieces and Measuring Equipment Part 1: Decision Rules for Verifying Conformity or Nonconformity with Specifications. International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 9001:2015; Quality Management Systems—Requirements. International Organization for Standardization: Geneva, Switzerland, 2015.
- Keran, Z.; Runje, B.; Piljek, P.; Razumić, A. Roboforming in ISF—Characteristics, Development, and the Step Towards Industry 5.0. Sustainability 2025, 17, 2562. [Google Scholar] [CrossRef]
- Shankar, R.; Gupta, L. Modelling Risks in Transition from Industry 4.0 to Industry 5.0. Ann. Oper. Res. 2024, 342, 1275–1320. [Google Scholar] [CrossRef]
- Zio, E.; Guarnieri, F. Industry 5.0: Do Risk Assessment and Risk Management Need to Update? And If Yes, How? Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2025, 239, 389–396. [Google Scholar] [CrossRef]
- Begoli, E.; Bhattacharya, T.; Kusnezov, D. The Need for Uncertainty Quantification in Machine-Assisted Medical Decision Making. Nat. Mach. Intell. 2019, 1, 20–23. [Google Scholar] [CrossRef]
- Nagel, C.; Pilia, N.; Loewe, A.; Dössel, O. Quantification of Interpatient 12-Lead ECG Variabilities within a Healthy Cohort. Curr. Dir. Biomed. Eng. 2020, 6, 493–496. [Google Scholar] [CrossRef]
- Aston, P.J.; Mehari, T.; Bosnjakovic, A.; Harris, P.M.; Sundar, A.; Williams, S.E.; Dössel, O.; Loewe, A.; Nagel, C.; Strodthoff, N. Multi-Class ECG Feature Importance Rankings: Cardiologists vs Algorithms. In Proceedings of the 2022 Computing in Cardiology (CinC), Tampere, Finland, 4–7 September 2022; Volume 498, pp. 1–4. [Google Scholar]
- Mehari, T.; Sundar, A.; Bosnjakovic, A.; Harris, P.; Williams, S.E.; Loewe, A.; Doessel, O.; Nagel, C.; Strodthoff, N.; Aston, P.J. Ecg Feature Importance Rankings: Cardiologists vs. Algorithms. IEEE J. Biomed. Health Inform. 2024, 28, 2014–2024. [Google Scholar] [CrossRef] [PubMed]
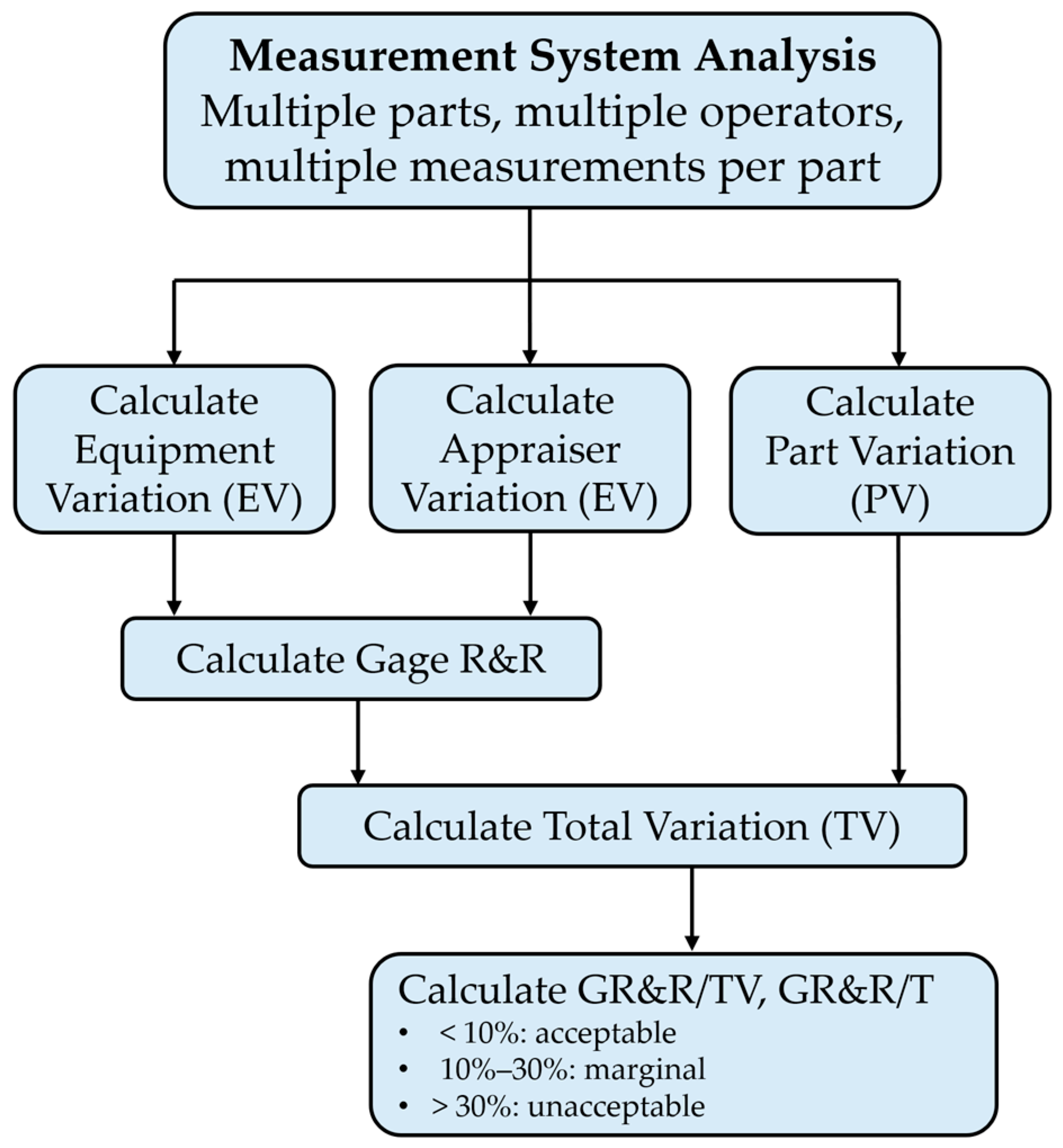
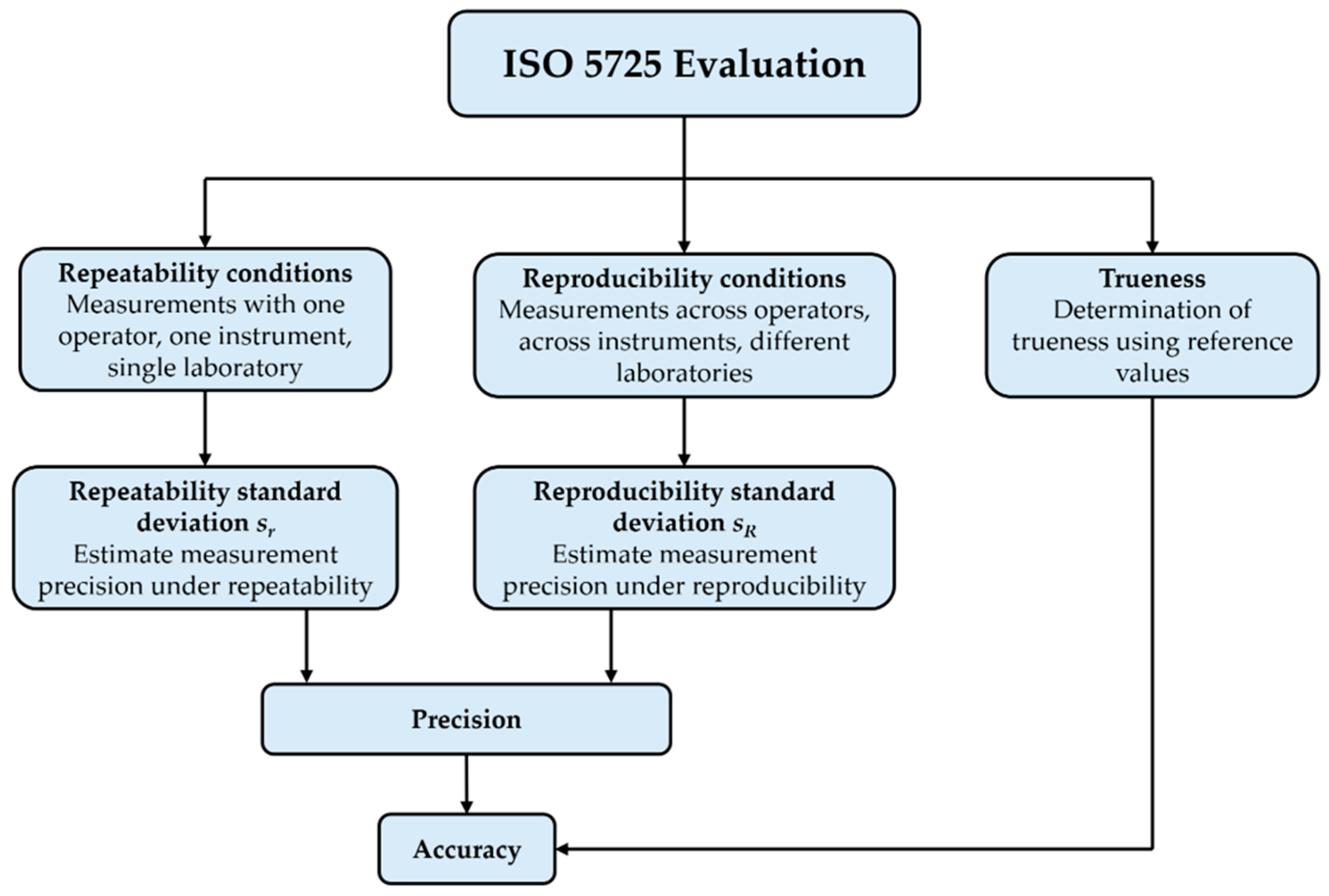
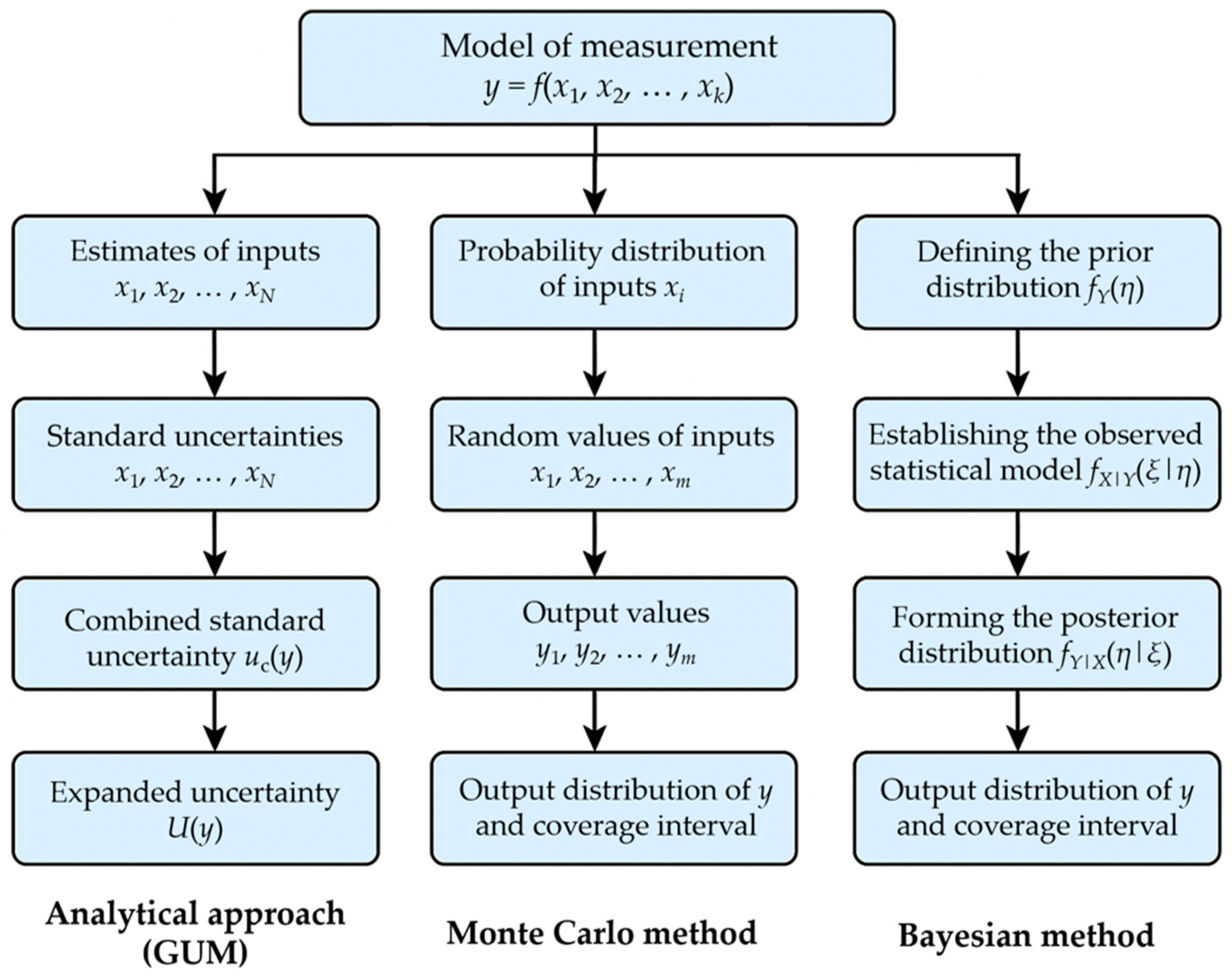
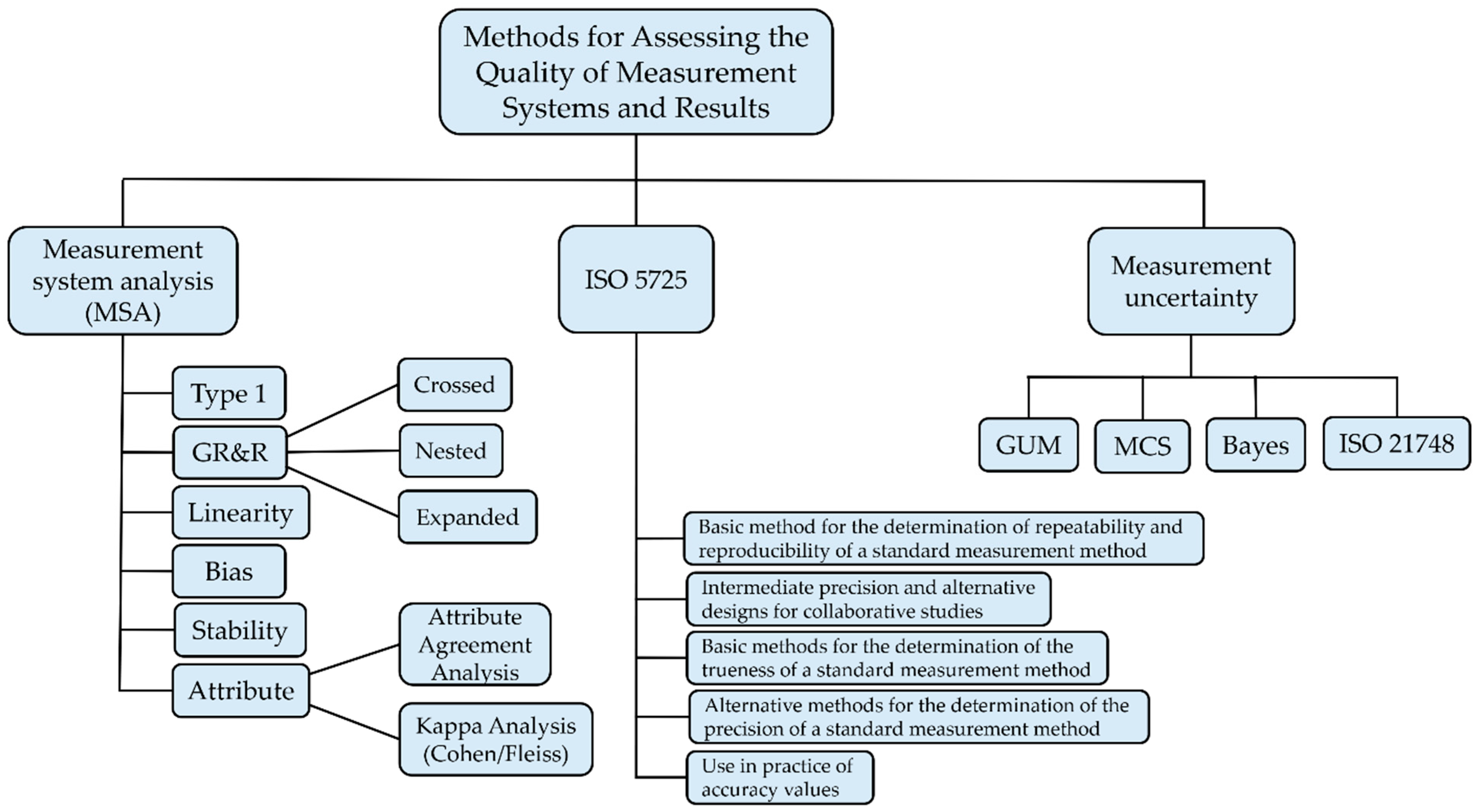
| Concept | Definition VIM | Definition GUM (JCGM 100) | Definition ISO 5725:2023 | Definition MSA (Reference Manual Fourth Edition) |
|---|---|---|---|---|
| Measurement result | Set of quantity values attributed to a measurand along with relevant information. | An estimate of the value of a measurand accompanied by a statement of uncertainty. | Value obtained by applying a measurement procedure according to a test method. | Result of the measurement process involving the system, operator, and environment. |
| Measurement error | Difference between a measured quantity value and a reference quantity value; includes systematic and random components. | Not directly defined; discussed in the context of uncertainty. Error is a concept underlying uncertainty. | Overall error defined as a combination of trueness and precision. | Difference between the average result and the reference value (bias). |
| Precision | Closeness of agreement between indications or measured values obtained under specified conditions. | Quantified by standard deviation of measured values under repeatability or reproducibility conditions. | Based on the standard deviation in results under defined conditions. | Variability expressed as Equipment Variation (EV). |
| Trueness | Closeness of the mean of measured values to the reference value; inversely related to systematic error. | Discussed indirectly; related to the concept of systematic error. | Closeness of the mean result to the accepted reference value. | Not directly used; focus is on bias as an expression of trueness. |
| Accuracy | Combination of trueness and precision; not a quantity and not expressed numerically. | Sometimes used informally to mean closeness to true value, but not defined as a quantity. | Accuracy = trueness + precision. Quantified experimentally. | Often incorrectly used as a synonym for bias. |
| Bias | Estimate of a systematic measurement error, i.e., the difference between the expectation of test results and a reference value. | Systematic effect on a measurement result, often corrected or accounted for through uncertainty. | Difference between the expected result and the reference value. | Systematic error expressed as deviation from the reference value. |
| Repeatability and Reproducibility | Repeatability: same conditions. Reproducibility: different conditions across labs/operators. | Used as input in uncertainty models; considered under standard uncertainty estimates. | Repeatability: same conditions. Reproducibility: different labs, equipment, and operators. | EV (repeatability) and AV (reproducibility) via Gage R&R studies. |
| Measurement uncertainty | Non-negative parameter characterizing the dispersion of quantity values attributed to a measurand. | Parameter associated with the result of a measurement, characterizing dispersion of values that could be reasonably attributed to the measurand (uncertainty means doubt, and therefore in its broadest sense, uncertainty of measurement means doubt about the validity of the result of a measurement). | Is not explicitly defined (but it is clearly implied that repeatability, reproducibility, and trueness constitute experimental input data that can be used in the evaluation of measurement uncertainty, for example, in accordance with the GUM or ISO 21748, and bias (as an expression of trueness) should be corrected for if known, and the remaining uncertainty of the correction can be included in the overall measurement uncertainty). | Estimate of the range within which the true value is believed to lie. |
| MSA Method | Data Type | Purpose | Recommended Illustration | Acceptance Criteria |
|---|---|---|---|---|
| Gage R&R (Average & Range) | Variable | Basic assessment of repeatability and reproducibility of the measurement system | Scatter plot by parts and appraisers | GRR < 10%: acceptable, 10–30%: marginal, >30%: unacceptable |
| Gage R&R (ANOVA) | Variable | Detailed statistical analysis of variability components | Variance components chart, interaction plot | Same as above but includes significance tests for sources of variation |
| Gage R&R (Nested) | Variable | Used when the same parts are not available for all appraisers (e.g., destructive testing) | Box plot by appraiser | Interpret based on % contribution of nested sources; GRR guidelines apply |
| Expanded Gage R&R | Variable | Extended analysis including additional factors (e.g., time, device, and location) | Multifactor plot, interaction diagram | Acceptability depends on total variation explained; no fixed % thresholds |
| Type 1 Gage Study | Variable | Quick check of bias and repeatability of a single device | Histogram and control chart | Cg ≥ 1.33; Cgk ≥ 1.33 (capability indices) |
| Linearity Study | Variable | Assessment of measurement bias across the measurement range | Scatter plot with regression line | Linearity slope ≈ 0; R2 > 0.9; individual biases within limits |
| Bias Study | Variable | Assessment of deviation from known reference value | Bar chart (bias) | Bias within tolerance limits or statistically non-significant |
| Stability Study | Variable | Check of measurement system consistency over time | and R control chart | No significant trend; all points within control limits |
| Attribute Agreement Analysis | Attribute | Assessment of rater consistency and agreement with standard | Accuracy matrix, agreement table | ≥90% agreement recommended; ≥70% for marginal acceptability |
| Kappa Analysis (Cohen/Fleiss) | Attribute | Statistical measure of inter-rater agreement (multiple raters) | Kappa heatmap | Kappa > 0.75: strong agreement; 0.4–0.75: moderate; <0.4: weak |
| Part | Purpose | Typical Application | Recommended Illustration | Acceptance Criteria |
|---|---|---|---|---|
| ISO 5725-1:2004 | Introduces general principles for evaluating the accuracy of measurement methods and results, including definitions and framework. | Reference for terminology, planning accuracy studies, and understanding components of accuracy. | Concept diagrams showing relationship between accuracy, trueness, and precision. | No specific criteria; foundational concepts and definitions. |
| ISO 5725-2:2020 | Provides basic methods for estimating repeatability and reproducibility through interlaboratory studies. | Evaluation of precision in collaborative tests; standard design for reproducibility studies. | Standard deviation charts, Youden plots, repeatability vs. reproducibility plots. | Repeatability and reproducibility standard deviations should be within limits relevant to the method or product specification. |
| ISO 5725-3:2024 | Describes designs for obtaining intermediate precision and provides alternatives to designs in Part 2. | Used when variability due to operator, time, or equipment must be evaluated within the same lab. | Box plots, control charts stratified by operator or day. | Intermediate precision variability should be assessed in context of long-term method performance. |
| ISO 5725-4:2020 | Provides basic methods for the determination of trueness using reference values. | Used to assess bias in measurement methods through comparison with reference materials. | Bias plots, difference plots, histograms comparing measurement and reference values. | Bias should be statistically insignificant or within acceptable limits of the method. |
| ISO 5725-5:2004/corr2009 | Presents alternative methods for determining trueness and precision under specific conditions. | Applied in cases with limited data, non-standard conditions, or specific method constraints. | Simulation plots, adaptive model visualizations. | Acceptance depends on context-specific statistical validation; no fixed universal limits. |
| ISO 5725-6:2004 | Provides practical examples of applications of the trueness and precision concepts. | Training, guidance for implementation, and case studies of statistical evaluations. | Applied case study charts, visual summaries of study outcomes. | Illustrative only; no acceptance criteria defined. |
| Source of Variation | %Contribution | %Study Var | %Tolerance |
|---|---|---|---|
| Total Gage R&R | 0.32 | 5.68 | 12.90 |
| Repeatability | 0.26 | 5.10 | 11.58 |
| Reproducibility | 0.06 | 2.50 | 5.69 |
| Part-To-Part | 99.68 | 99.84 | 226.90 |
| Total Variation | 100.00 | 100.00 | 227.27 |
| %Contribution Refers to how much variation is caused by the measurement system itself, in comparison to total variation. | %Study Variation Reflects the proportion of variation due to the measurement system relative to overall process variation. | %Tolerance Compares the variability of the measurement system to the full specification tolerance of the part or product. |
| ≤1% The measurement system is considered acceptable. | <10% Acceptable. | |
| 1–9% May be acceptable, depending on the application. | 10–30% Marginally acceptable. | |
| >9% Unacceptable. | >30% Unacceptable. | |
| Appraiser | Number of Samples | Matched Ratings | Agreement Rate | 95% CI |
|---|---|---|---|---|
| A | 30 | 30 | 100.00% | (90.50, 100.00) |
| B | 30 | 29 | 96.67% | (82.78, 99.92) |
| C | 30 | 30 | 100.00% | (90.50, 100.00) |
| Appraiser | Number of Samples | Matched Ratings | Agreement Rate | 95% CI |
|---|---|---|---|---|
| A | 30 | 29 | 96.67% | (82.78, 99.92) |
| B | 30 | 29 | 96.67% | (82.78, 99.92) |
| C | 30 | 28 | 93.33% | (77.93, 99.18) |
| Appraiser | Incorrect Reject/Accept (%) | Incorrect Accept/Reject (%) | Mixed Ratings (%) |
|---|---|---|---|
| A | 0.00 | 12.50 | 0.00 |
| B | 0.00 | 0.00 | 3.33 |
| C | 0.00 | 25.00 | 0.00 |
| Number of Samples | Matched Ratings | Agreement Rate | 95% CI |
|---|---|---|---|
| 30 | 26 | 86.67% | (69.28; 96.24) |
| Sa/nm | Sz/nm | Sq/nm | ||||
|---|---|---|---|---|---|---|
| Year 2021 | Measurement series | Measurement series | Measurement series | |||
| 1 | 2 | 1 | 2 | 1 | 2 | |
| 50.849 | 50.157 | 174.521 | 175.914 | 54.646 | 54.385 | |
| 0.151 | 0.224 | 1.395 | 1.590 | 0.468 | 0.202 | |
| 50.503 | 175.218 | 54.515 | ||||
| 0.191 | 1.495 | 0.360 | ||||
| 0.346 | 0.697 | 0.130 | ||||
| 0.342 | 0.580 | 0.091 | ||||
| 0.392 | 1.604 | 0.372 | ||||
| 0.528 | 4.133 | 0.995 | ||||
| 1.083 | 4.433 | 1.027 | ||||
| Year 2025 | Measurement series | Measurement series | Measurement series | |||
| 1 | 2 | 1 | 2 | 1 | 2 | |
| 50.24 | 51.24 | 182.50 | 176.63 | 51.812 | 53.71 | |
| 0.16 | 0.19 | 2.03 | 1.63 | 0.174 | 0.244 | |
| 50.74 | 179.63 | 52.76 | ||||
| 0.177 | 1.843 | 0.212 | ||||
| 0.503 | 2.064 | 0.947 | ||||
| 0.122 | 0.240 | 0.238 | ||||
| 0.215 | 1.859 | 0.319 | ||||
| 0.489 | 5.094 | 0.586 | ||||
| 0.593 | 5.394 | 0.881 | ||||
| Quantity | Symbol | Distribution | Value |
|---|---|---|---|
| Temperature | t | Fixed value | 30 °C |
| Reference temperature | t0 | Constant | 24.0085 °C |
| Intercept (calibration curve) | y1 | Normal | (M, −0.1625, 0.0011) |
| Slope (calibration curve) | y2 | Normal | (M, 0.00218, 0.00067) |
| Method | h | u(h) | Coverage Interval (95%) |
|---|---|---|---|
| nm | nm | nm | |
| MCS | 98.9 | 1.45 | [96.0, 101.8] |
| Bayes | 98.3 | 1.41 | [96.1, 101.7] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razumić, A.; Runje, B.; Alar, V.; Štrbac, B.; Trzun, Z. A Review of Methods for Assessing the Quality of Measurement Systems and Results. Appl. Sci. 2025, 15, 9393. https://doi.org/10.3390/app15179393
Razumić A, Runje B, Alar V, Štrbac B, Trzun Z. A Review of Methods for Assessing the Quality of Measurement Systems and Results. Applied Sciences. 2025; 15(17):9393. https://doi.org/10.3390/app15179393
Chicago/Turabian StyleRazumić, Andrej, Biserka Runje, Vesna Alar, Branko Štrbac, and Zvonko Trzun. 2025. "A Review of Methods for Assessing the Quality of Measurement Systems and Results" Applied Sciences 15, no. 17: 9393. https://doi.org/10.3390/app15179393
APA StyleRazumić, A., Runje, B., Alar, V., Štrbac, B., & Trzun, Z. (2025). A Review of Methods for Assessing the Quality of Measurement Systems and Results. Applied Sciences, 15(17), 9393. https://doi.org/10.3390/app15179393







