Dynamical Neural Models in Experimental Identification of Helicopter Educational Model—Methodology Proposal

Abstract

A design of methodology for experimental identification of nonlinear dynamical systems using feed-forward MLP neural networks as dynamical neural models is presented in this paper. The proposed methodology consists of four modules and makes use of already existing models of the nonlinear dynamical system. The methodology is verified in the case study, which is dedicated to the experimental identification of the modified helicopter educational plant CE 150 from Humusoft company. The previously created gray-box model of the helicopter educational model is used to estimate optimal neural network structure. The obtained black-box helicopter model, represented by a dynamical neural model, captures interactions between elevation and azimuth subsystems. The dynamical neural model is used to design three control algorithms without subsystem decoupling that are verified in the simulation environment and on the real helicopter educational model.

1. Introduction

The CE 150 educational helicopter model shown in Figure 1 represents a benchmark system often used in nonlinear dynamical system identification. It is a nonlinear dynamical system with two degrees of freedom—elevation and azimuth angle. The helicopter educational model consists of five subsystems, main and tail rotor, elevation, azimuth, and balancing weight, which allows for adjusting the center of gravity of the elevation subsystem [1]. Interactions between elevation and azimuth subsystems, unstable and relatively fast dynamics, and a MIMO system make identification of the educational helicopter model challenging. The model is also considered as a benchmark system, as it covers a wide variety of real system dynamics. Experiences and skills gained from modeling and controlling the educational helicopter model find practical applications, for example, in autonomous flying drone control.

Modeling of the education helicopter model was previously performed using analytical or experimental identification. Parameters of the analytically derived mathematical model were fitted using genetic algorithms [2], the Nelder–Mead method [3], or the nonlinear least squares method [4]. Mathematical modeling was completely omitted in [5], where the authors used a set of linear regression models to approximate the dynamics of the helicopter educational model. An MLP neural network was used by the authors in [6]. The resulting black-box model of the helicopter educational model was validated indirectly using a PID control algorithm. Different controller types have been used to stabilize and control a helicopter educational model. The mathematical model of the helicopter educational plant was linearized in multiple operating points in [7] to design a set of robust control algorithms with smooth transitions between them. An experimentally tuned fuzzy control algorithm was used in [2] to control elevation and azimuth subsystems separately. In [8], the designed fuzzy control algorithm was compared to the PID control algorithm. Authors in [9] designed a control structure with the super-twisting sliding mode controller in the inner loop and the composite nonlinear feedback controller in the outer loop. PID, adaptive gain scheduling, and fuzzy control algorithms were used in [10] to gather data to train a neural network for direct control of the helicopter educational model. In [11], the neural network controller was trained online using a training algorithm based on the extended Kalman filter. Authors in [12] trained an MLP neural network to approximate the dynamics of the helicopter educational model. This network was used to train an inverse neural network that was used directly in the control structure to track the reference signal.

Different types of neural networks can be used to approximate the dynamics of a nonlinear dynamical system. In [13], the authors used a radial basis function network (RBFN) to capture the nonlinear dynamics of SISO systems and designed an RBFN-based controller. Application of recurrent neural networks (RNNs) in SISO and MIMO dynamical system identification was presented in [14]. The primary advantage of RNNs compared to MLP networks is that system dynamics is handled internally, eliminating the need to determine system order by hand. A black-box model of a nonlinear SISO system based on the long-short term memory (LSTM) neural network is presented in [15]. The authors used the obtained black-box model to design an MPC control algorithm with a verification on the real system. In [16], the authors compared MLP, RNN, LSTM, and GRU neural networks in a system identification task. On the selected benchmark system, the MLP network required the least amount of resources to train while offering relatively low prediction error. Authors in [17] utilized temporal convolutional neural networks (TCNNs) to identify the Silverbox benchmark system and compared prediction results with other system identification methods. Authors highlighted that TCNNs are more suitable for systems with longer memory requirements. In this paper, the MLP neural network is used to approximate the dynamics of the helicopter educational model. The main reason for choosing the MLP neural network over other neural network types is the ability to utilize instantaneous linearization. Instantaneous linearization allows the design of computationally efficient control algorithms using classical synthesis methods, which is presented in this paper.

The CE 150 helicopter educational model was used in the Center of Modern Control Techniques and Industrial Informatics (CMCT&II) at the Faculty of Electrical Engineering and Informatics (FEEI) at the Technical University of Košice, which the authors of this paper are part of. A model predictive control algorithm was designed in [18]. This model predictive control algorithm was designed based on a set of experimentally identified models, and the obtained results were evaluated graphically. The design of model predictive control algorithms was generalized in [19] with an example based on the helicopter educational model. In the dissertation thesis [20], the author was focused primarily on the experimental identification of nonlinear dynamical systems using classical and intelligent methods. Classical methods were used in the design of the methodology for gray-box model identification. The proposed methodology was used in the identification of SISO system of the aerodynamic levitation plant in [21]. Finally, the methodology was formulated and validated on MIMO system of helicopter educational model in [4]. A methodology for black-box model identification using neural networks alongside a case study for its verification was also presented in the dissertation thesis [20]. This methodology and case study together form the research basis of this paper, the aim of which is to qualitatively compare control algorithms synthesized from the black-box model.

In Section 2, a proposed methodology for experimental identification of nonlinear dynamical systems using the feed-forward neural network as a dynamical neural model is presented. Here, the proposed methodology is divided into four modules with corresponding description. Section 3 presents the overview of the helicopter educational model and the verification of the proposed methodology in a case study. This case study demonstrates Dynamic Neural Models in Experimental Identification of Helicopter Educational Model. The validated dynamical neural model captures interactions between helicopter subsystems and represents a digital twin of the helicopter educational model. The digital twin is used in Section 4 to design and verify various control algorithms whose performance is verified using the real helicopter educational model.

2. Design of Methodology for Experimental Identification Using Feed-Forward Neural Networks

The proposed methodology is based on the methodology formulated in [4,20], where also a gray-box model of the helicopter educational plant was created, and the general experimental identification loop [22], which is modified to accommodate the use of MLP (multilayer perceptron) feed-forward neural networks as dynamical neural models in dynamics approximation. The resulting model is considered to be a black-box model of the real system. Using traditional MLP networks instead of more modern networks like recurrent and LSTM networks is advantageous in the availability of methods for nonlinear controller and estimator synthesis [22]. The advantage of the proposed methodology compared to the general experimental identification loop is that it can use an existing model to tune the hyperparameters of the neural network. Another advantage is that data obtained from an existing model have known noise characteristics, which is not possible to achieve with data from the real system. 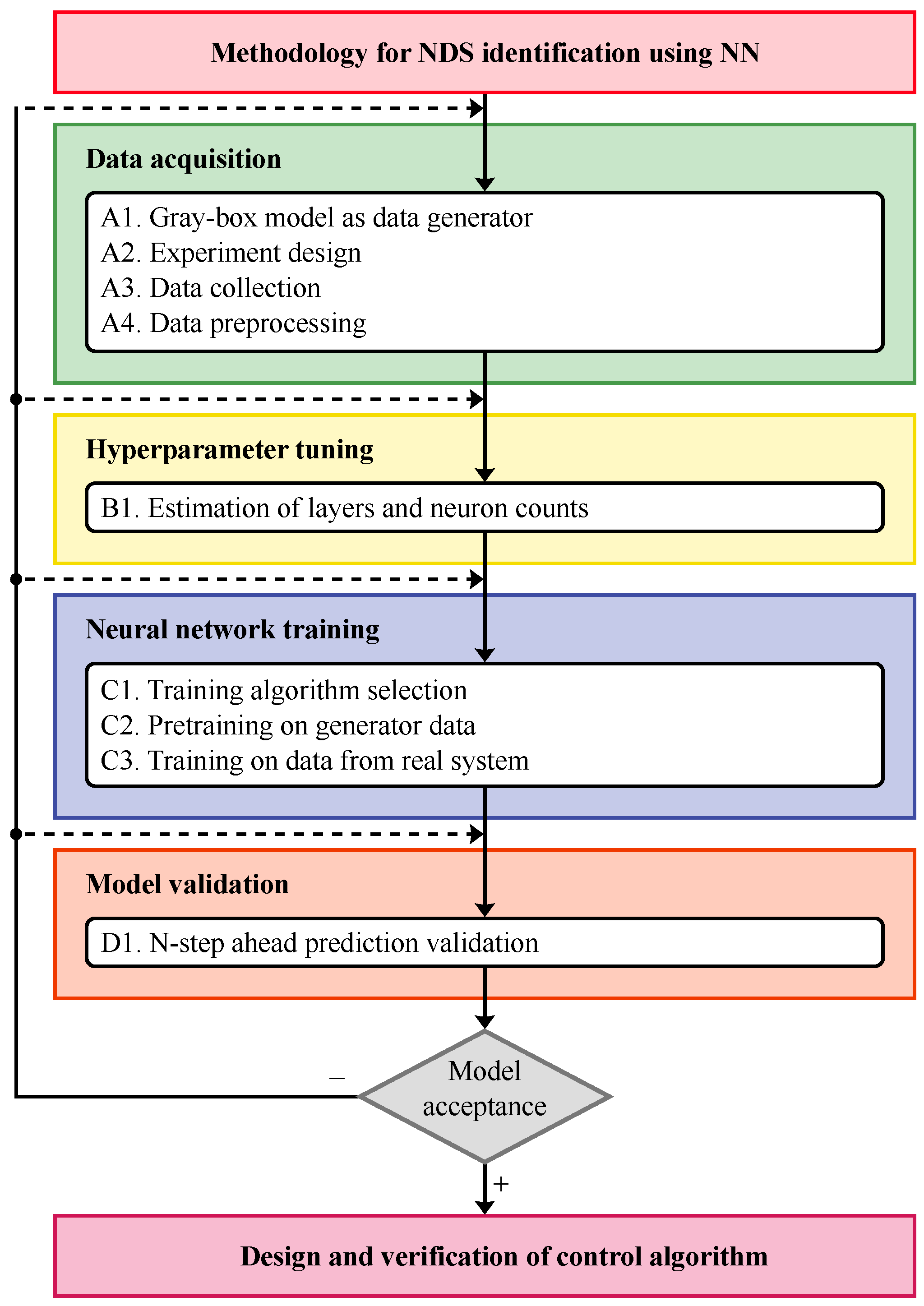The proposed methodology is illustrated in Figure 2.

The proposed methodology consists of four modules: Data acquisition, Hyperparameter tuning, Neural network training, and Model validation. Each module is further divided into submodules as necessary. The Data acquisition module is used to obtain and process data from the real system. It consists of the following submodules:

• A1. Gray-box model as data generator—a gray-box model of the identified system (if it exists) is used to obtain data for neural network training;
• A2. Experiment design—a series of experiments is designed to obtain experimental data from the real system;
• A3. Data collection—multiple realizations of designed experiments are performed, and data from the real system are recorded with a selected sampling period;
• A4. Data preprocessing—recorded data are preprocessed to reduce noise, normalize data, and create training and testing datasets.

The Hyperparameter tuning module consists of a single submodule B1. Estimation of layers and neuron counts. In this submodule, hyperparameters such as the number of layers, number of neurons per layer, types of activation functions, etc., of the neural network are tuned. Data from the gray-box model could be used to estimate optimal hyperparameter values.

The Neural network training module is divided into the following submodules:

• C1. Training algorithm selection—the training algorithm is selected from available algorithms implemented by the neural network training library or framework;
• C2. Pretraining on generator data—data from the gray-box model could be used to pretrain a designed neural network, thus speeding up neural network convergence;
• C3. Training on data from real system—final training of the neural network is performed on the data from the real system, so that the neural network can approximate its dynamics.

The Model validation module consists of submodule D1. N-step ahead prediction validation. In this submodule, an n-step ahead nonlinear recurrent predictor is created from the dynamical neural model. The overall performance of the dynamical neural model is evaluated in terms of its capability to predict system behavior n-steps forward.

The validated model can be used in state estimation, nonlinear control design, diagnostics, analyses, and more. In this paper, the nonlinear black-box model based on the dynamical neural model is used to design a state estimator and various nonlinear controllers. If validation reveals unsatisfactory performance of the black-box model, individual modules of the proposed methodology are repeated as needed.

3. Verification of Proposed Methodology on the Educational Helicopter Model—Case Study

The CE 150 helicopter educational model is an unstable 2 DOF educational model designed as a benchmark system for dynamical system identification and control [1]. It consists of four subsystems—main and tail rotors as well as elevation and azimuth subsystems. The main and tail rotors are directly powered by DC motors, whose speed is controlled by a PWM signal. The elevation and azimuth subsystems can move freely in the range of $\left[-45°;45°\right]$ and $\left[-130°;130°\right]$, respectively. The position of elevation and azimuth subsystems is sensed using an incremental rotary encoder. 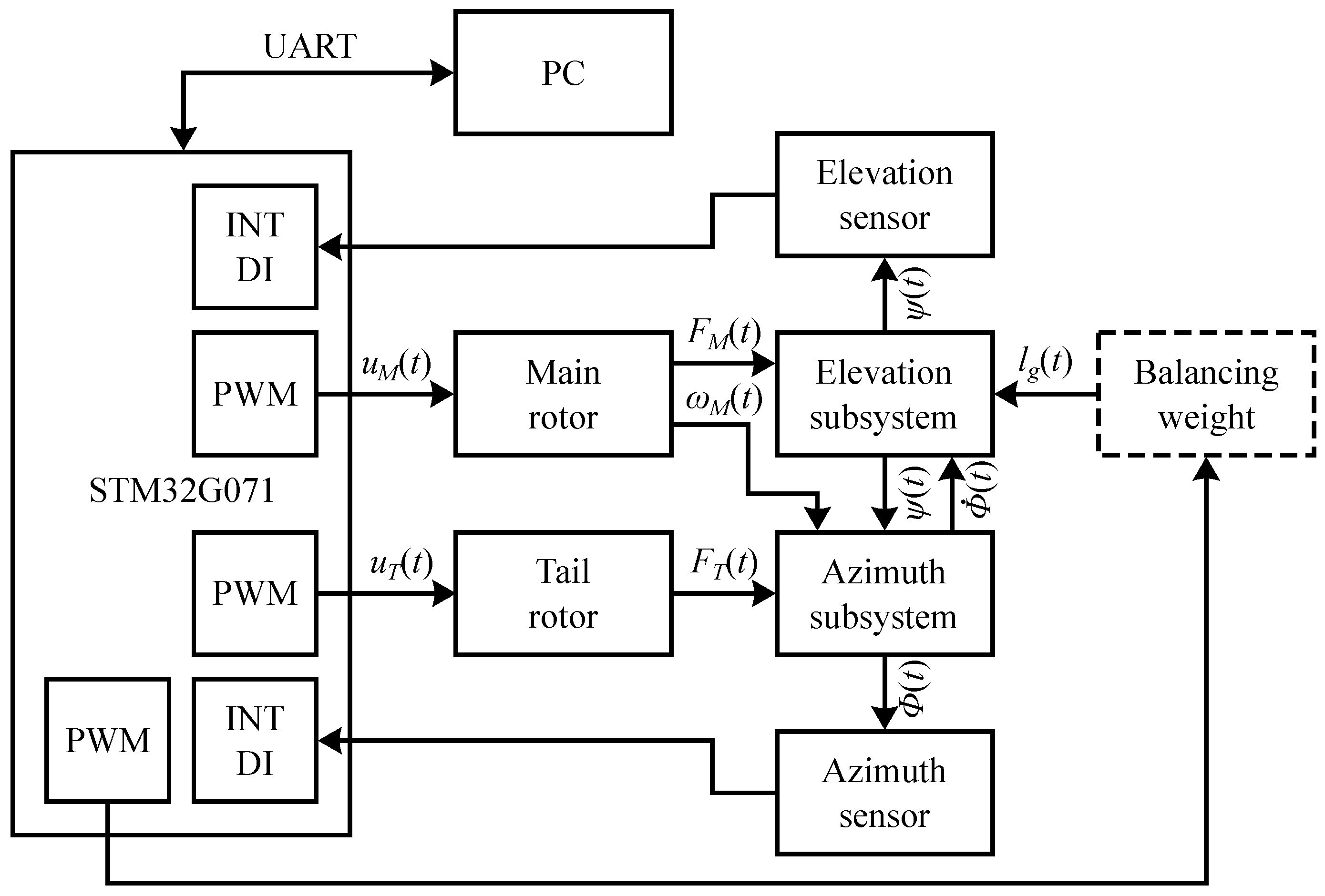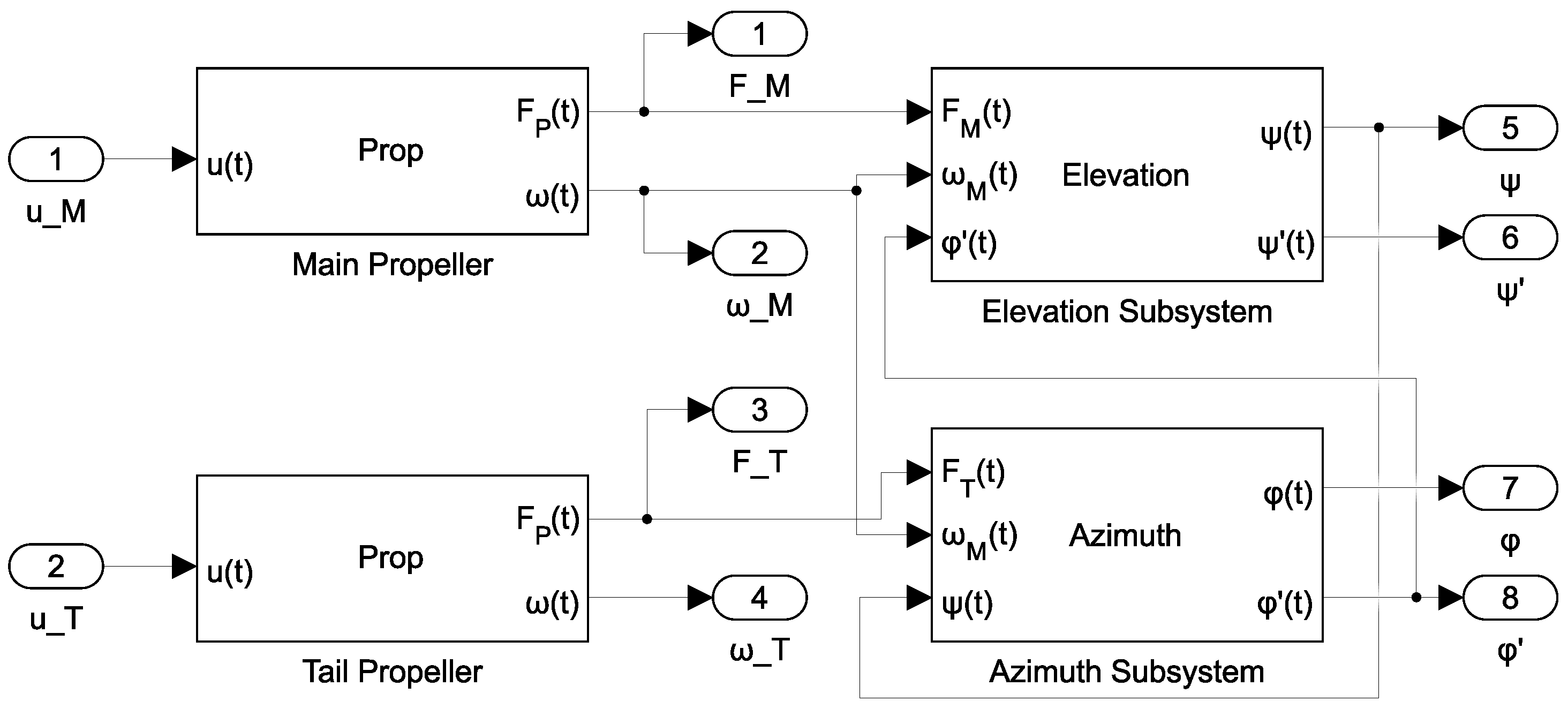The original CE 150 helicopter educational model used an MF624 IO expansion card, which was replaced by the STM32 microcontroller [20]. The subsystem block diagram of the helicopter educational model, including analytically determined interactions between subsystems, is shown in Figure 3. The adjustable balancing weight is not considered in this paper.

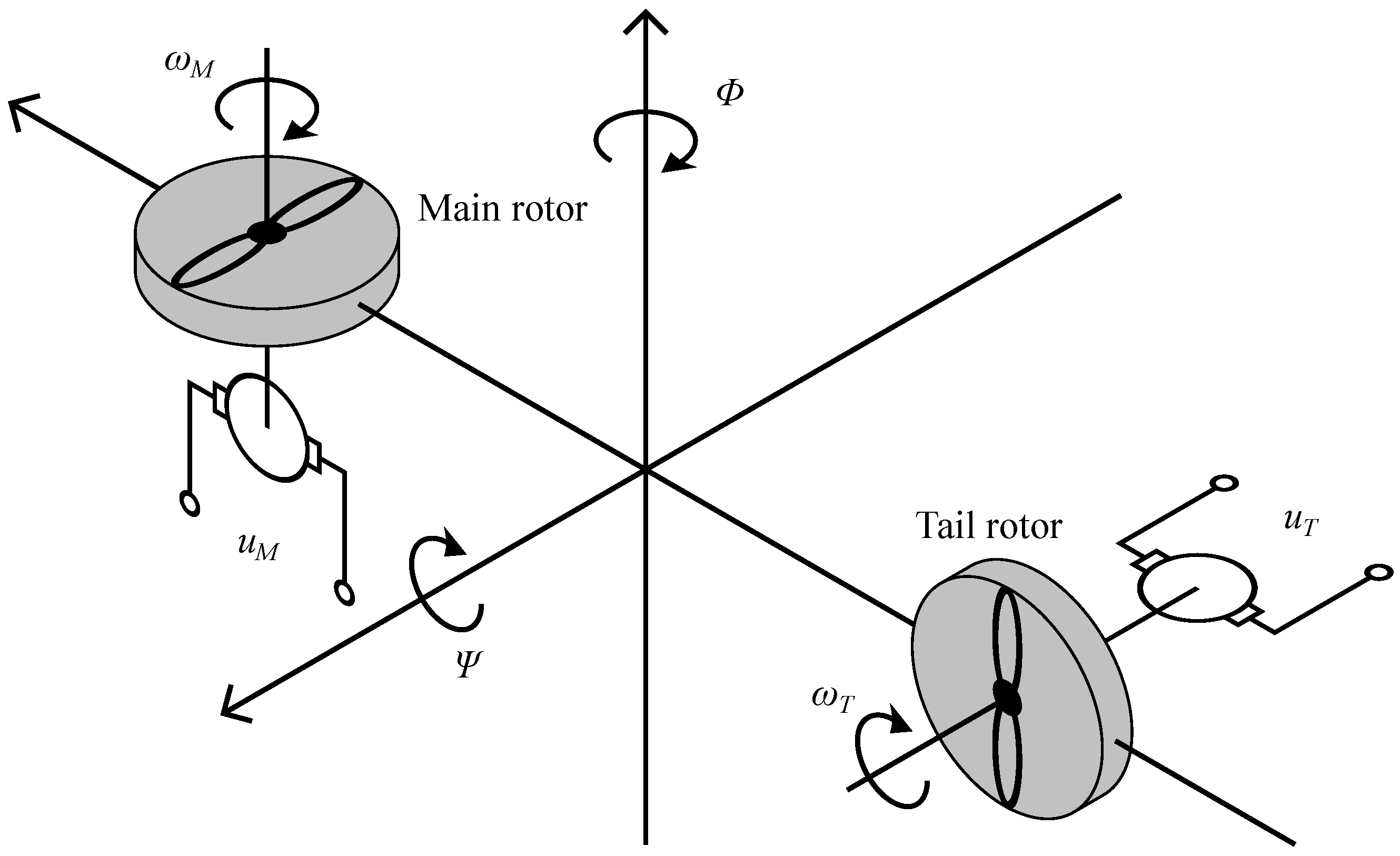
Figure 4 shows the schematic overview of the helicopter educational model, including the orientation of main rotor speed ${\omega }_M\left(t\right)$, tail rotor speed ${\omega }_T\left(t\right)$, elevation angle $\Psi \left(t\right)$, and azimuth angle $\Phi \left(t\right)$. These variables, alongside elevation speed $\dot{\Psi }\left(t\right)$ and azimuth speed $\dot{\Phi }\left(t\right)$, form a state vector $\mathit{x}\left(t\right)=\left[{\omega }_M\left(t\right),\Psi \left(t\right),\dot{\Psi }\left(t\right),{\omega }_T\left(t\right),\Phi \left(t\right),\dot{\Phi }\left(t\right)\right]$. Main rotor input voltage $u_M\left(t\right)$ and tail rotor input voltage $u_T\left(t\right)$ form an input vector $\mathit{u}\left(t\right)=\left[u_M\left(t\right),u_T\left(t\right)\right]$.

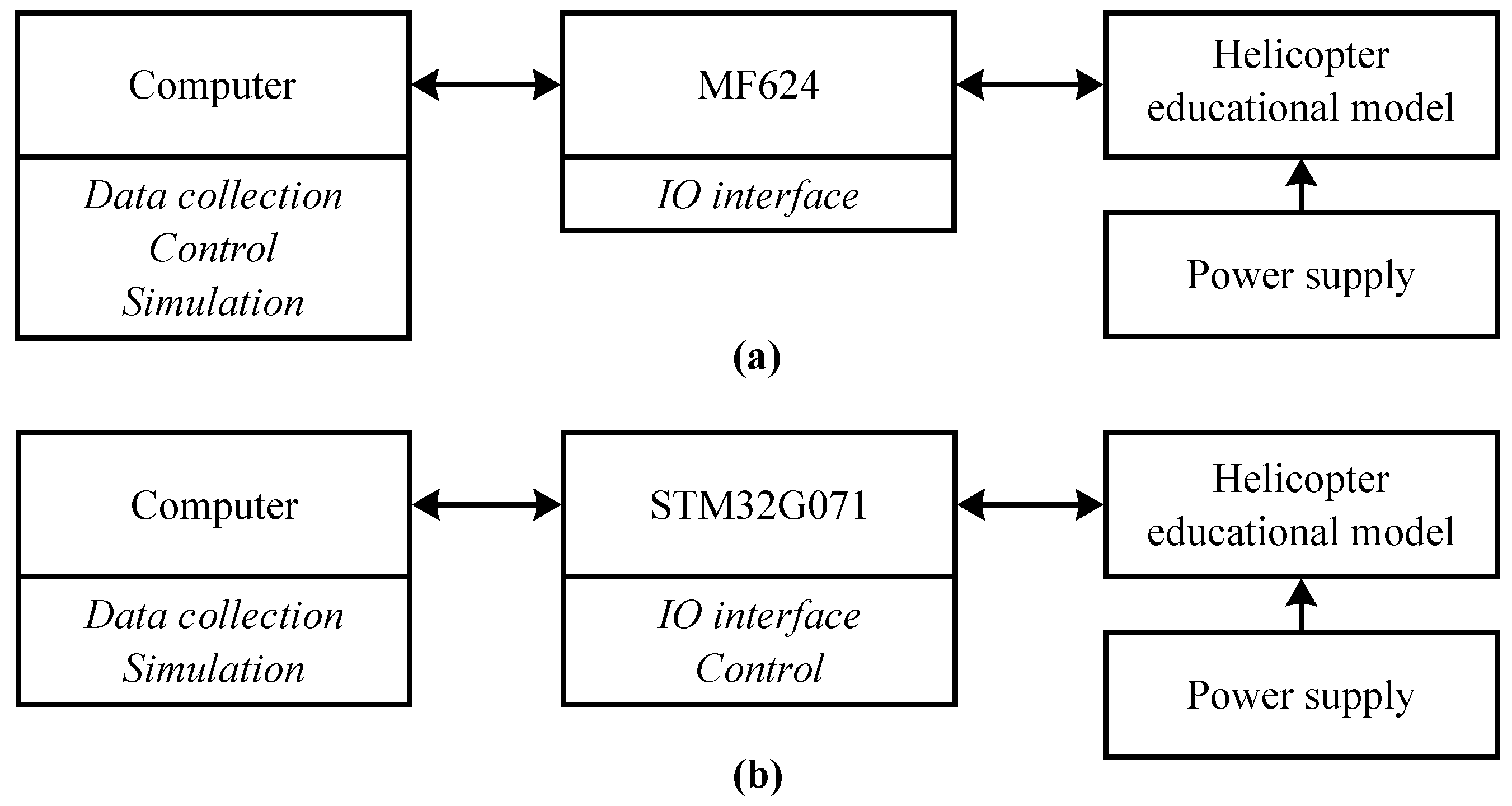
The modified helicopter educational model is used in this paper to demonstrate and validate the presented methodology. The modification of the original CE 150 helicopter educational model is based on replacing the MF624 input/output laboratory card with a development board based on the STM32 microcontroller. This modification allows the implementation of real-time control algorithms without the influence of the task scheduler present in modern desktop operating systems. The STM32 is connected to the computer using a widely adopted USB interface, as opposed to the outdated PCI interface of the MF264 IO laboratory card. Comparison of the original and modified helicopter educational model is shown in Figure 5.

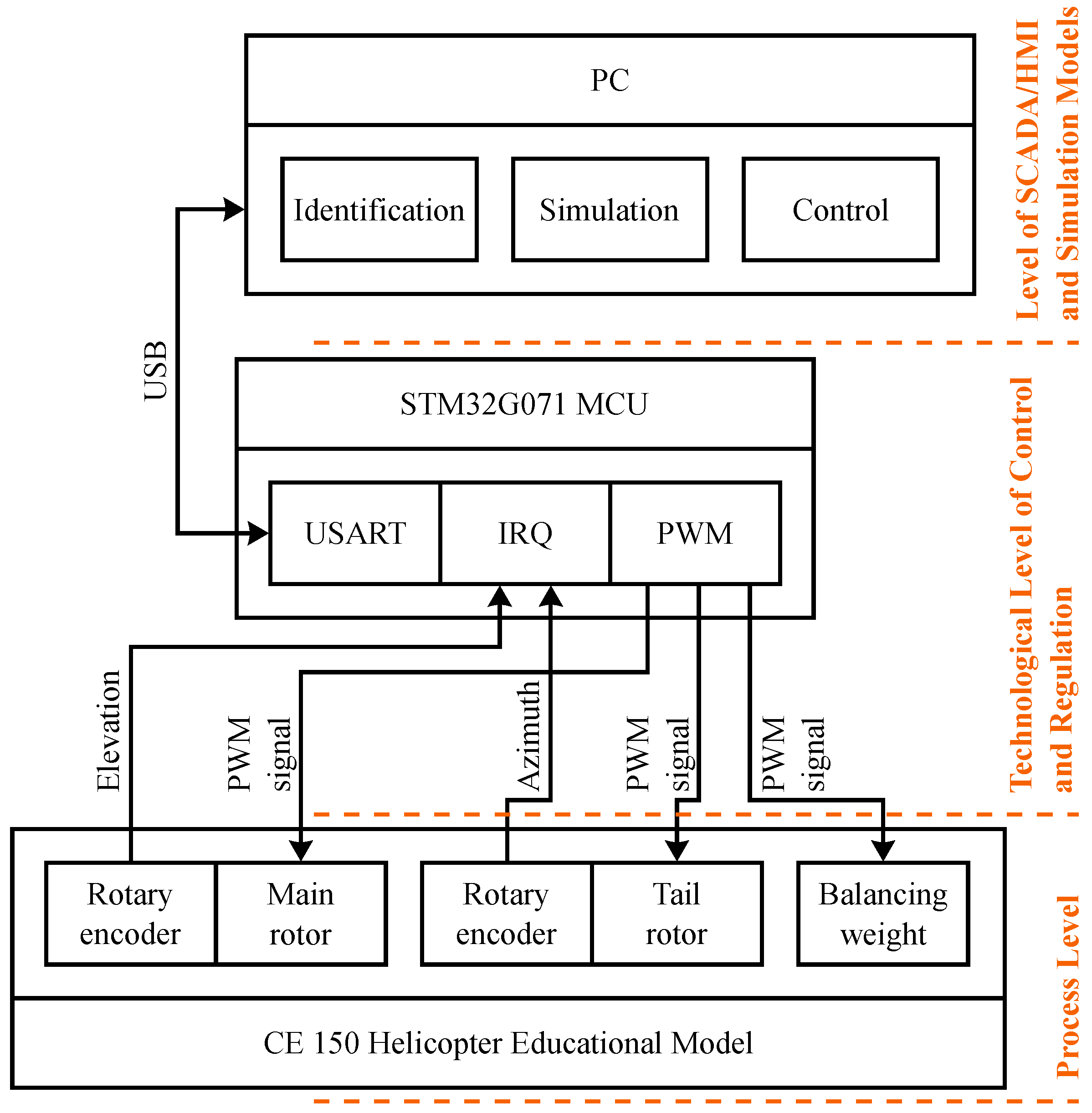
The modified helicopter educational model is implemented in the first three levels of the distributed control system (DCS) architecture in CMCT&II [23]. Helicopter skeleton, main and tail rotors, elevation and azimuth incremental rotary sensors, and balancing weight are present on the Process Level. The STM32 microcontroller and implemented control algorithms are present on the Technological Level of Control and Regulation. Finally, the simulation model, identification and control synthesis algorithms, and visualization tools are present on the Level of SCADA/HMI and Simulation Models. Implementation of the modified helicopter educational model into the remaining two levels (Information Level of Control and Management Control Level) is reserved for future research. The implementation of the modified helicopter educational model into DCS architecture in CMCT&II is illustrated in Figure 6.

In case study [4], a gray-box model of the educational helicopter model was obtained by combining the means of analytical and experimental identification in a complex methodology for gray-box modeling of nonlinear dynamical systems. The modified mathematical model was derived from the educational manual [1]; nine experiments were realized on the real system to obtain experimental data, unknown values of parameters were estimated using the combination of local and global nonlinear optimization methods, the gray-box model was indirectly validated in a control structure, and various control algorithms were designed and verified on the real system. Derived differential equations and experimentally identified parameters form a digital twin of the helicopter educational model, which is implemented as a custom subsystem in the MATLAB (R2023b) Simulink environment, as shown in Figure 7.

The case study presented in this paper builds on the gray-box model obtained in [4]. The gray-box model is used as a data generator to estimate the optimal structure of the neural network and speed up the training process. This case study validates the proposed methodology for experimental identification of nonlinear dynamical systems using feed-forward MLP neural networks.

3.1. Data Acquisition from the Helicopter Educational Model

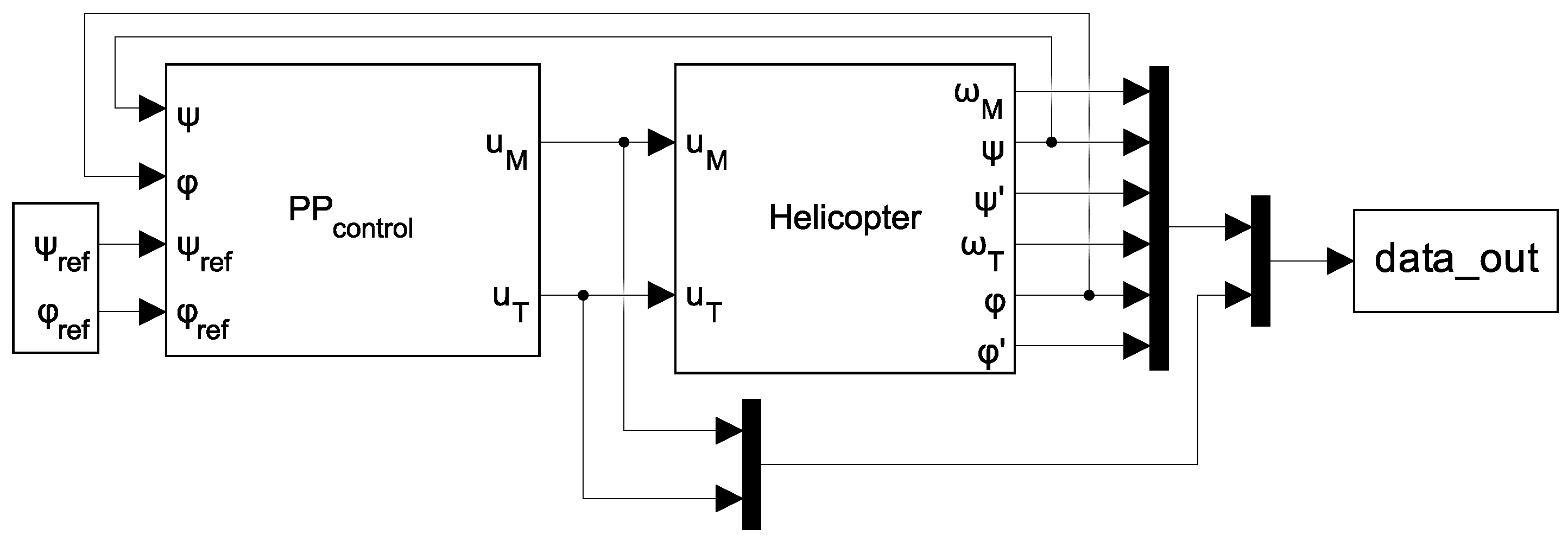
The Data acquisition is the first module of the proposed methodology consisting of four submodules. In the Gray-box model as data generator (A1) submodule, the gray-box model of the helicopter educational model is first used to determine a suitable operational area of the helicopter educational model while considering physical and practical limits. Then, the gray-box model is used to generate experimental data for the neural network training in the control structure shown in Figure 8. The elevation and the azimuth subsystems are controlled simultaneously using a modified polynomial controller [4]. A trapezoidal signal with random period and amplitude is selected as a reference signal for both subsystems. The output of the gray-box model is distorted by the white noise to improve the robustness and prevent overfitting of the final dynamical neural model [22]. Data collected from the gray-box model are shown in Figure 9.

In the Experiment design (A2) submodule, three experiments on the real helicopter educational model are designed to capture its dynamics. The first experiment is similar to the experiment conducted on the gray-box model, as both the elevation and the azimuth subsystems are controlled simultaneously using a modified polynomial controller to capture interactions between subsystems. The additive white noise is not used to distort the system output in this case. In the second experiment, the azimuth subsystem is locked, and the tail rotor is excited with a constant input $u_{T0}$. The elevation subsystem is controlled by the modified polynomial controller from [4], and the random trapezoidal signal is used as an elevation angle reference signal ${\Psi }_{ref}\left(t\right)$. In the third experiment, the elevation subsystem is locked, and the main rotor is excited with a constant input $u_{M0}$. The azimuth subsystem is controlled by the modified polynomial controller, and a random trapezoidal signal is used as an azimuth angle reference ${\Phi }_{ref}\left(t\right)$. As the dynamics of the azimuth subsystem is highly dependent on the elevation angle $\Psi \left(t\right)$, the experiment is repeated for different elevation angles $\Psi \left(t\right)$. 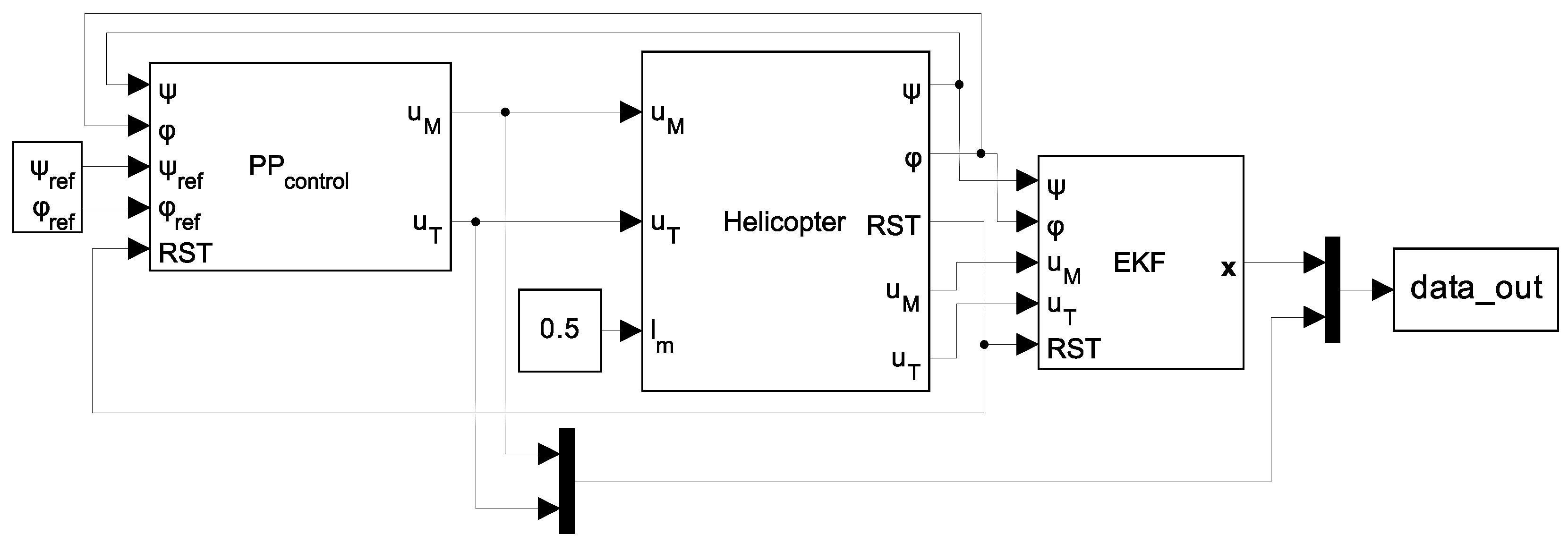Experimental data from all three experiments are collected using the hardware in the loop control structure shown in Figure 10.

Data from multiple realizations of designed experiments are collected in the Data collection (A3) submodule. All experiments are conducted on the real helicopter educational model. Data are sampled at the selected sampling period $T_s=0.05\left[\mathrm{s}\right]$. Although the educational manual [1] recommended a sampling period $T_s=0.01\left[\mathrm{s}\right]$, the results in [4] prove that the chosen sampling period is sufficient to control the helicopter educational model. The longer sampling period allows the use of more computationally demanding control and estimation algorithms.

Collected data from the gray-box model and the real helicopter educational model are processed in the Data preprocessing (A4) submodule. This involves estimating state variables from measured data using a designed extended Kalman filter [24] and splitting the data into training and testing datasets. A sample of data collected from the real helicopter educational model is shown in Figure 11.

Experimental data prepared in the Data acquisition module can be used to estimate the optimal neural network structure, train the neural network, and validate the dynamical neural model, approximating the dynamics of the real helicopter educational model.

3.2. Hyperparameter Tuning of Dynamical Neural Model

Data collected from the helicopter gray-box model are used in the Hyperparameter tuning module to find the optimal structure of the neural network and the parameters involved in the neural network training. This module consists of a single submodule, Estimation of layers and neuron counts (B1), whose goal is to estimate optimal neural network structure. Hyperparameters of interest with corresponding values or intervals are listed in

Table 1. Hyperparameter values considered in the Estimation of layers and neuron counts submodule.

Parameters	Values
number of hidden layers	$[1;3]$
neurons per hidden layer(s) 1	$[36;200]$ $[36;128]$ and $[12;48]$ $[36;100]$, $[22;96]$ and $[10;32]$
activation function	$sig\left(x\right)$2 or $tanh\left(x\right)$
number of training epochs	$[250;900]$ with 50 epoch increments
training dataset	(a) with interactions (1st experiment) (b) without interactions (2nd and 3rd experiment)

¹ The number of neurons per hidden layer is ordered in descending order from the input to the output of the neural network. ² Sigmoid function.

. Provided parameter intervals are selected empirically while taking into account previous experiences [19].

A random search method is utilized to tune the selected hyperparameters. This involves training multiple neural networks with different combinations of hyperparameters and evaluating prediction accuracy. The overall neural network error is defined as a weighted sum of normalized prediction error (90%) and normalized network complexity (10%; measured in number of weights). Tuning hyperparameters using the data from the gray-box model allows to design structure of the neural network with similar complexity as the validated gray-box model. This strategy prevents the neural network from underfitting and overfitting.

Optimal hyperparameter values are selected from roughly 10,000 neural networks trained on the data from the gray-box model. The average time to train and evaluate a single neural network is roughly 1 min using an NVIDIA RTX 4070 Ti graphics card. The best performing neural network, chosen as a balance between the number of weights and accuracy, has one hidden layer with 132 neurons, a sigmoidal activation function, 800 training epochs, and a training dataset with interactions. The structure of the proposed neural network is extended with a trigonometric function layer to preprocess the elevation angle $\Psi \left(t\right)$ and internal normalization layers to allow the use of inputs and outputs without rescaling. The proposed neural network represents a nonlinear state-space black-box model (a dynamical neural model), whose structure is illustrated in Figure 12.

The proposed dynamical neural model with weights adopted in the optimal hyperparameter tuning process allows to approximate dynamics of the gray-box model. To create an approximator of the real educational helicopter model, it is necessary to train the neural network on the data collected from the real system.

3.3. Neural Network Training

In the Neural network training module, the proposed neural network is trained offline on the data from the real helicopter educational model. The module consists of three submodules, out of which the first is the Training algorithm selection (C1) submodule. This submodule aims to select an optimal training algorithm used in neural network weight optimization. For this task, an Adam training algorithm is selected for its fast convergence in various applications [25]. A weighted mean squared error (MSE) is used as the loss function during training and validation to account for the varying scales of the state prediction vector $\widehat{\mathit{x}}\left(k+1\right)$ elements. The TensorFlow neural network library is used for dynamical neural network training.

In the Pretraining on generator data (C2) submodule, the proposed neural network should be trained on the data from the generator. Because hyperparameter tuning is perfomed by training multiple neural networks, the best performing neural network model is already trained on the data from the generator. Therefore, the output of this submodule is the neural network pretrained on the data from the gray-box model of the helicopter education model.

Training the proposed neural network on the data from the real helicopter education model is carried out in the Training on data from real system (C3) submodule. To avoid data overfitting, an early stopping strategy is adopted. This strategy stops neural network training in case the validation accuracy does not improve in five consecutive epochs. In the training process on the data from the real system, the training is stopped early after 713 epochs.

As the proposed neural network consists of custom layers, the trained model cannot be directly imported into MATLAB. Therefore, a conversion function is created that converts a TensorFlow neural network into a MATLAB function, including all weights and transformations. The advantage of direct conversion into a MATLAB function instead of implementing custom layers in MATLAB is the ability to use MATLAB’s automatic code generation to speed up simulations. The dynamical neural model trained on the data from the real helicopter educational model needs to be validated before it can be used to design stabilizing control algorithms.

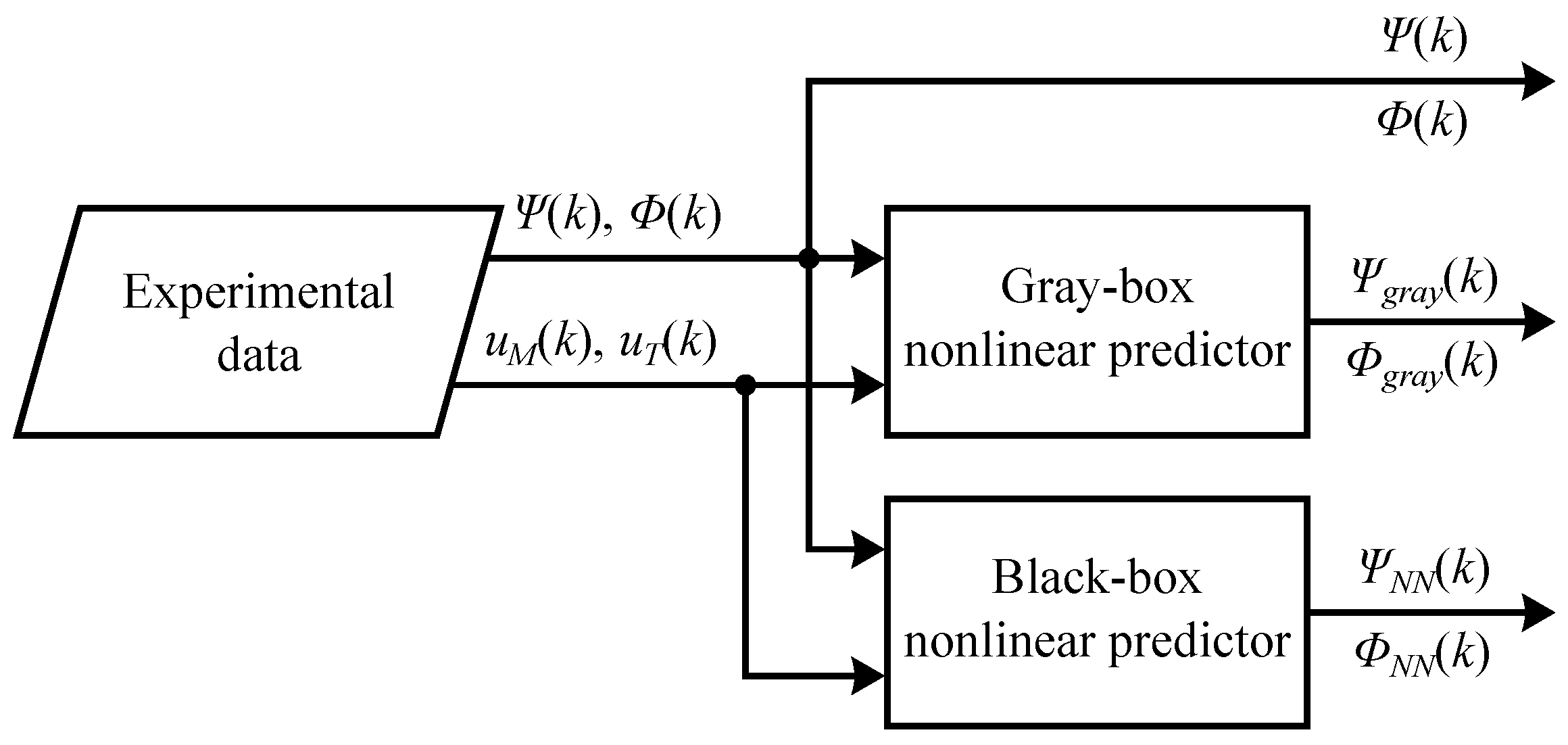
3.4. Dynamical Neural Model Validation

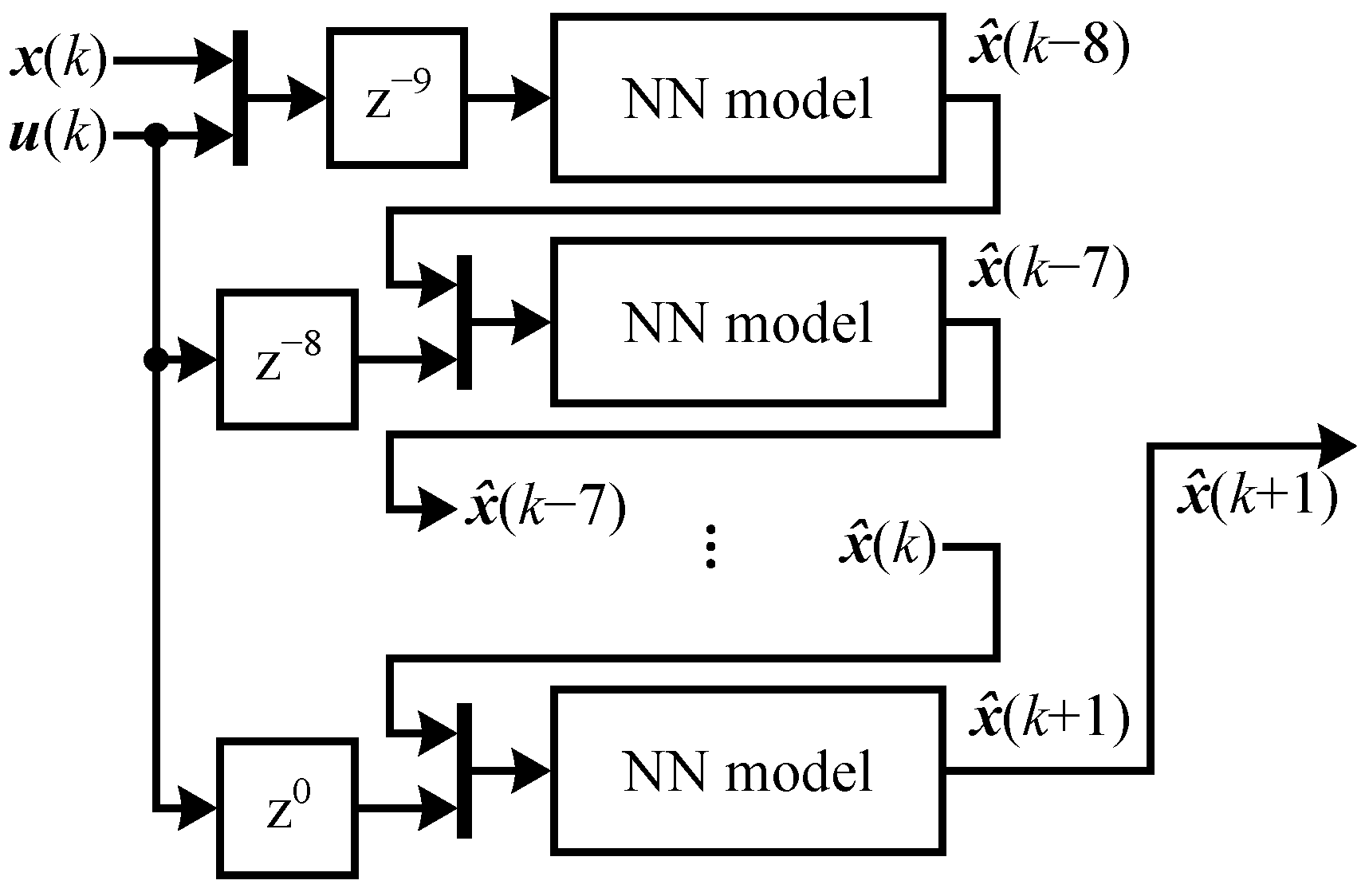
In the Model validation module, the helicopter educational model dynamics prediction of the dynamical neural model is validated in the N-step ahead prediction validation submodule. First, the 10-step ahead nonlinear black-box predictor is constructed from the dynamical neural model as shown in Figure 13. The nonlinear predictor is later compared to the output of the real helicopter educational model and the nonlinear gray-box predictor from [4]. The direct validation is performed in structure shown in Figure 14.

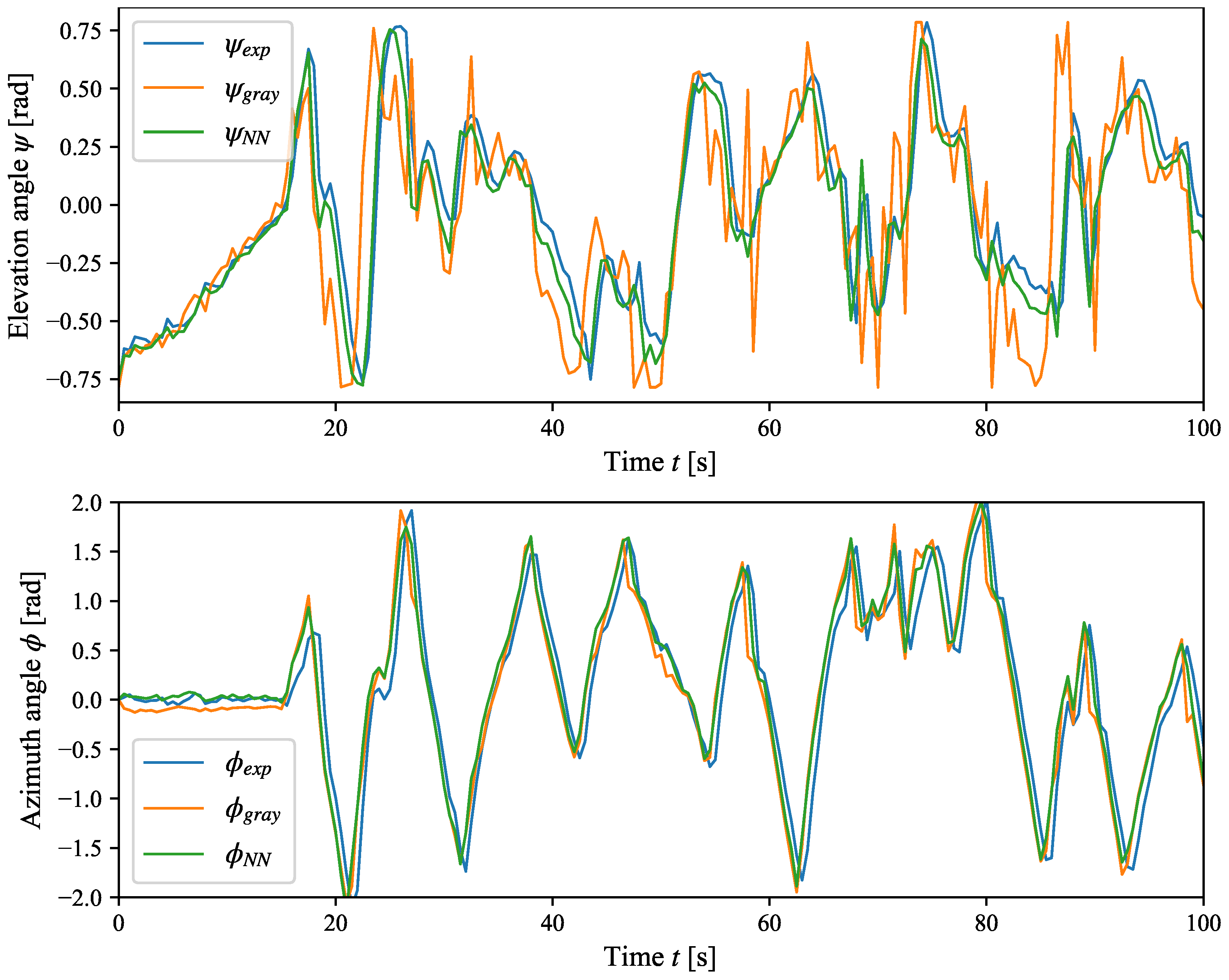
The validation results are shown in Figure 15 and

Table 2. Quantitative comparison of gray-box and black-box predictors.

Model	MSE ($\mathit{\Psi }$)	MSE ($\mathit{\Phi }$)
gray-box	$0.097460$	$0.121542$
black-box	$0.011128$	$0.083265$

. The azimuth subsystem dynamics approximation capabilities of the black-box predictor are slightly better compared to the gray-box predictor. In the case of the elevation subsystem dynamics approximation, the proposed black-box predictor performs much better, i.e., prediction error against the output of the real elevation subsystem is much smaller. The obtained results prove that the dynamical neural model can approximate the dynamics of the real helicopter educational model. A successfully validated dynamical neural model can be used to design stabilizing control algorithms and state estimators. The structure of the dynamical neural model and trained weights form the basis of the digital twin of the helicopter educational model.

4. Design of Stabilizing Controllers Based on the Dynamical Neural Model of the Helicopter Educational Model

The design of polynomial, LQI, and MPC control algorithms is presented in this section. The design of all three control algorithms is based on the dynamical neural model of the helicopter educational model. The motivation for choosing this set of control algorithms is to demonstrate the versatility of the dynamical neural model in the design of input–output, optimal state-space, and model predictive controllers. The dynamical neural model of the educational helicopter model is a one-step-ahead state-space predictor generalized as

$$\begin{array}{c}\hfill \widehat{\mathit{x}}\left(k+1\right)={\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k\right),\mathit{u}\left(k\right)\right)\end{array}$$

(1)

where $\mathit{x}\left(k\right)$ is a state vector, $\mathit{u}\left(k\right)$ is an input vector, and ${\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(·\right)$ is the dynamical neural model. This model is used in the design of all three selected control algorithms.

Synthesis of a polynomial control algorithm requires linearizing (1) at the selected operational point $\mathit{OP}=\left[{\mathit{x}}_{\mathbf{0}},{\mathit{u}}_{\mathbf{0}}\right]$. The steady state vector ${\mathit{x}}_{\mathbf{0}}$ and steady input vector ${\mathit{u}}_{\mathbf{0}}$ are calculated numerically using the nonlinear least squares method by minimizing residuals

$$\begin{array}{c}\hfill r_{OP}={\mathit{q}}_{\mathit{OP}}\left({\mathit{x}}_{\mathbf{0}}-{\widehat{\mathit{f}}}_{\mathit{NNSS}}\left({\mathit{x}}_{\mathbf{0}},{\mathit{u}}_{\mathbf{0}}\right)\right)\end{array}$$

(2)

where ${\mathit{q}}_{\mathit{OP}}$ is a row vector that normalizes steady state vector ${\mathit{x}}_{\mathbf{0}}$ elements. The dynamical neural model (1) is then linearized in the selected operational point $\mathit{OP}$ using the Symbolic Toolbox by calculating Jacobians symbolically:

$$\begin{array}{c}\hfill \widehat{\mathit{A}}={\left.{\displaystyle \frac{\partial {\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k\right),\mathit{u}\left(k\right)\right)}{\partial \mathit{x}\left(k\right)}}\right|}_{\mathit{OP}};\widehat{\mathit{B}}={\left.{\displaystyle \frac{\partial {\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k\right),\mathit{u}\left(k\right)\right)}{\partial \mathit{u}\left(k\right)}}\right|}_{\mathit{OP}}\end{array}$$

(3)

Finally, the linearized state-space deviation model is obtained,

$$\begin{array}{c}\hfill \mathsf{\Delta }\mathit{x}\left(k+1\right)=\widehat{\mathit{A}}\mathsf{\Delta }\mathit{x}\left(k\right)+\widehat{\mathit{B}}\mathsf{\Delta }\mathit{u}\left(k\right)\end{array}$$

(4)

where $\mathsf{\Delta }\mathit{x}\left(k\right)=\mathit{x}\left(k\right)-{\mathit{x}}_{\mathbf{0}}$ and $\mathsf{\Delta }\mathit{u}\left(k\right)=\mathit{u}\left(k\right)-{\mathit{u}}_{\mathbf{0}}$. The linearized state-space model (4) is used as an input of the ss2tf function to convert the state-space model into transfer functions of the elevation $F_{\Psi /U_M}\left(z\right)$ and azimuth $F_{\Phi /U_T}\left(z\right)$ subsystems

$$\begin{array}{c}\hfill F_{\Psi /U_M}\left(z\right)={\displaystyle \frac{B_{el}\left(z\right)}{A_{el}\left(z\right)}};F_{\Phi /U_T}\left(z\right)={\displaystyle \frac{B_{az}\left(z\right)}{A_{az}\left(z\right)}}\end{array}$$

(5)

These transfer functions, alongside transfer functions of polynomial controllers for elevation $F_{U_M/E_{\Psi }}\left(z\right)$ and azimuth $F_{U_T/E_{\Phi }}\left(z\right)$ subsystems,

$$\begin{array}{c}\hfill F_{U_M/E_{\Psi }}\left(z\right)={\displaystyle \frac{Q_{el}\left(z\right)}{P_{el}\left(z\right)}};F_{U_T/E_{\Phi }}\left(z\right)={\displaystyle \frac{Q_{az}\left(z\right)}{P_{az}\left(z\right)}}\end{array}$$

(6)

are used to formulate transfer functions of the closed-loop control structure for the elevation subsystem

$$\begin{array}{c}\hfill F_{\Psi /{\Psi }_{ref}}\left(z\right)={\displaystyle \frac{F_{\Psi /U_M}\left(z\right)F_{U_M/E_{\Psi }}\left(z\right)}{1+F_{\Psi /U_M}\left(z\right)F_{U_M/E_{\Psi }}\left(z\right)}}={\displaystyle \frac{B_{el}\left(z\right)Q_{el}\left(z\right)}{A_{el}\left(z\right)P_{el}\left(z\right)+B_{el}\left(z\right)Q_{el}\left(z\right)}}\end{array}$$

(7)

and for the azimuth subsystem

$$\begin{array}{c}\hfill F_{\Phi /{\Phi }_{ref}}\left(z\right)={\displaystyle \frac{F_{\Phi /U_T}\left(z\right)F_{U_T/E_{\Phi }}\left(z\right)}{1+F_{\Phi /U_T}\left(z\right)F_{U_T/E_{\Phi }}\left(z\right)}}={\displaystyle \frac{B_{az}\left(z\right)Q_{az}\left(z\right)}{A_{az}\left(z\right)P_{az}\left(z\right)+B_{az}\left(z\right)Q_{az}\left(z\right)}}\end{array}$$

(8)

The characteristic polynomial of the elevation subsystem control structure is

$$\begin{array}{c}\hfill P_{elcl}\left(z\right)=A_{el}\left(z\right)P_{el}\left(z\right)+B_{el}\left(z\right)Q_{el}\left(z\right)\end{array}$$

(9)

and the characteristic polynomial of the azimuth subsystem control structure is

$$\begin{array}{c}\hfill P_{azcl}\left(z\right)=A_{az}\left(z\right)P_{az}\left(z\right)+B_{az}\left(z\right)Q_{az}\left(z\right)\end{array}$$

(10)

The reference characteristic polynomials $P_{elcl}^{\ast }\left(z\right)$ and $P_{azcl}^{\ast }\left(z\right)$ are constructed from the desired close-loop control structure poles ${\mathit{z}}_{\mathit{el}}^{\ast }$ and ${\mathit{z}}_{\mathit{az}}^{\ast }$. The polynomial control algorithm is designed by comparing characteristic polynomials to reference polynomials $P_{elcl}\left(z\right)=P_{elcl}^{\ast }\left(z\right)$ and $P_{azcl}\left(z\right)=P_{azcl}^{\ast }\left(z\right)$. The feedback control law for the elevation subsystem is

$$\begin{array}{c}\hfill u_{Mfb}\left(k\right)=\sum _{i=0}^3\left(q_{eli}\left(k-i\right)e_{\Psi }\left(k-i\right)\right)-\sum _{i=1}^3\left(p_{eli}\left(k-i\right)u_M\left(k-i\right)\right)\end{array}$$

(11)

and for the azimuth subsystem, it is

$$\begin{array}{c}\hfill u_{Tfb}\left(k\right)=\sum _{i=0}^3\left(q_{azi}\left(k-i\right)e_{\Phi }\left(k-i\right)\right)-\sum _{i=1}^3\left(p_{azi}\left(k-i\right)u_T\left(k-i\right)\right)\end{array}$$

(12)

Multiple feedback control algorithms are designed for different operational points $\mathit{OP}$ and are smoothly switched between based on the elevation angle $\Psi \left(k\right)$. The feedforward control algorithm is designed based on the steady input vector ${\mathit{u}}_{\mathbf{0}}$. It approximates the input vector $\mathit{u}\left(k\right)$ based on the elevation angle $\Psi \left(k\right)$ using second-order polynomials. The final control law for the elevation and azimuth subsystems is formulated as

$$\begin{array}{c}\hfill \mathit{u}\left(k\right)=\left[\begin{array}{c}{u}_M\left(k\right)\\ u_T\left(k\right)\end{array}\right]=\left[\begin{array}{c}{u}_{Mfb}\left(k\right)+u_{Mff}\left(k\right)\\ u_{Tfb}\left(k\right)+u_{Tff}\left(k\right)\end{array}\right]\end{array}$$

(13)

and is implemented into the control structure shown in Figure 16.

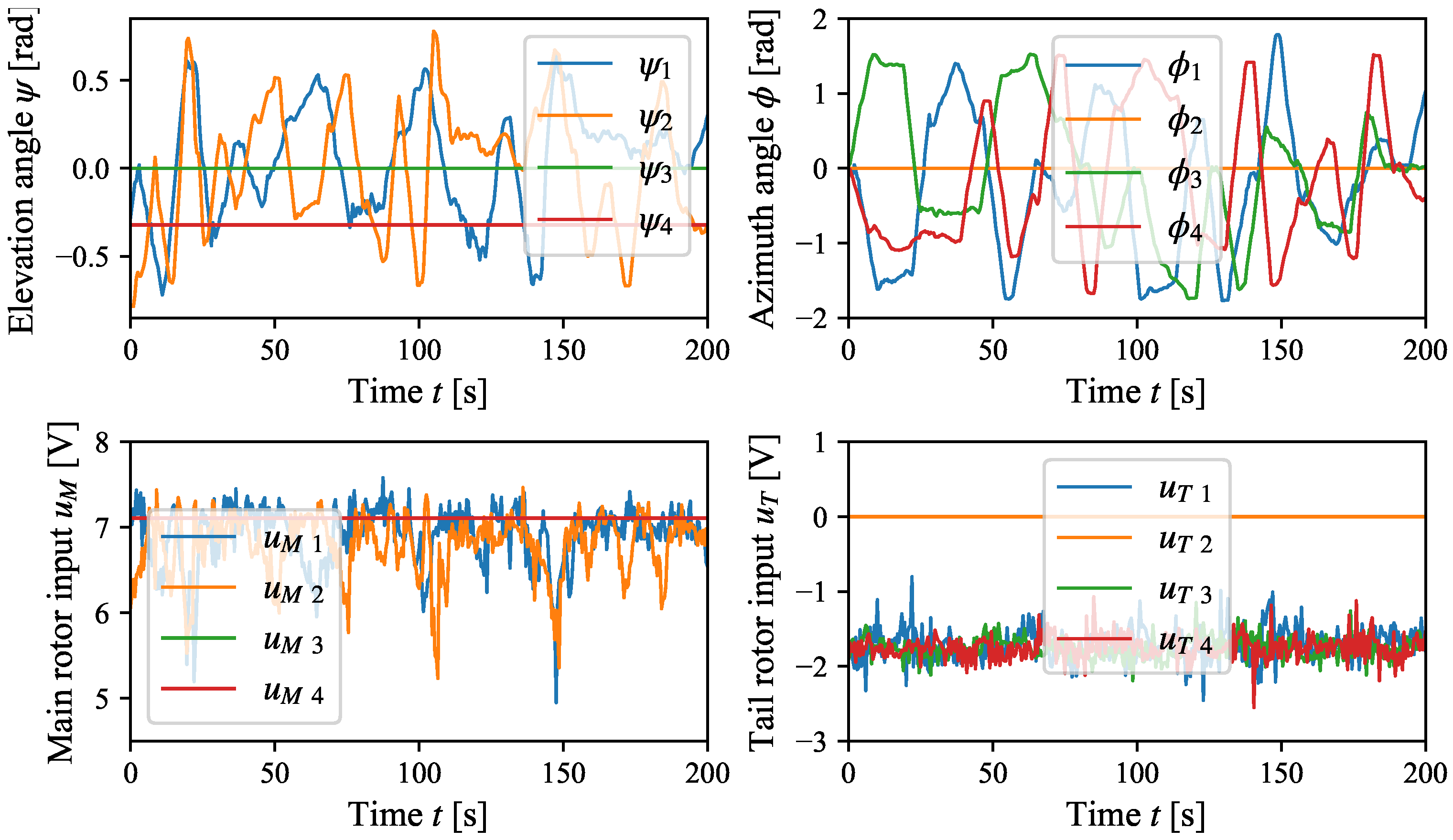
The designed polynomial feedback and feedforward control algorithm is verified using the real helicopter educational model and helicopter gray box model. Verification results shown in Figure 17 prove that the control algorithm designed from the dynamical neural model of the helicopter educational model can track the elevation ${\Psi }_{ref}\left(t\right)$ and azimuth ${\Phi }_{ref}\left(t\right)$ reference angle. Main rotor $u_M\left(t\right)$ and tail rotor $u_T\left(t\right)$ inputs are slightly distorted by noise. The designed polynomial pole-placement feedback and feedforward control algorithm is computationally efficient such that it can run on the STM32 microcontroller while maintaining the selected sampling period $T_s$.

The designed polynomial pole-placement control algorithm is quantitatively evaluated in

Table 3. Quantitative evaluation of polynomial pole-placement feedback and feedforward control algorithm.

Environment	MSE ($\mathit{\Psi }$)	MSE ($\mathit{\Phi }$)	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{M}}\right)$	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{T}}\right)$
simulation	$1.31782\times {10}^{-5}$	$1.68658\times {10}^{-4}$	$0.006538$	$0.004694$
real	$4.15319\times {10}^{-4}$	$1.70688\times {10}^{-2}$	$1.330930$	$0.110878$

. The energy requirement ${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }\mathit{u}\right)$ of the control algorithm is calculated as

$$\begin{array}{c}\hfill V_E\left(u\right)={\displaystyle \frac{1}{N-1}}\sum _{k=2}^N{\left(u\left(k\right)-u(k-1)\right)}^2\end{array}$$

(14)

The design of the LQI control algorithm is based on the linearized state-space model (4), which is transformed into an extended form. The extended state vector ${\mathit{x}}_{\mathit{i}}\left(k\right)$ contains also the sum of the control error ${\mathit{e}}_{\mathit{i}}\left(k\right)$. By minimizing the quadratic criteria

$$\begin{array}{c}\hfill V_{LQI}\left({\mathit{x}}_{\mathit{i}},\mathit{u}\right)=\sum _{k=0}^{\infty }\left({\mathit{x}}_{\mathit{i}}^T\left(k\right){\mathit{Q}}_{\mathit{LQI}}{\mathit{x}}_{\mathit{i}}\left(k\right)+{\mathit{u}}^T\left(k\right){\mathit{R}}_{\mathit{LQI}}\mathit{u}\left(k\right)\right)\end{array}$$

(15)

where ${\mathit{Q}}_{\mathit{LQI}}$ and ${\mathit{R}}_{\mathit{LQI}}$ are positive definite weighting matrices, the control law

$$\begin{array}{c}\hfill \mathit{u}\left(k\right)=-{\mathit{K}}_{\mathit{LQI}}{\mathit{x}}_{\mathit{i}}\left(k\right)\end{array}$$

(16)

is obtained, where ${\mathit{K}}_{\mathit{LQI}}$ is the feedback gain. The matrix ${\mathit{K}}_{\mathit{LQI}}$ is calculated by solving the Riccati algebraic equation. Alternatively, the MATLAB function lqi can be used to synthesize feedback gain ${\mathit{K}}_{\mathit{LQI}}$. Values of ${\mathit{Q}}_{\mathit{LQI}}$ and ${\mathit{R}}_{\mathit{LQI}}$ matrices are determined experimentally. Multiple feedback gain matrices are designed for different operational points $\mathit{OP}$ and are smoothly switched between based on the elevation angle $\Psi \left(k\right)$.

The practical implementation of the LQI control algorithm requires the entire state vector $\mathit{x}\left(k\right)$ to be measurable, which is not the case for the helicopter educational model. Therefore, an extended Kalman filter based on the dynamical neural model (1) was created. The system noise covariance matrix ${\sigma }_{\mathit{d}}^2$ and the sensory noise covariance matrix ${\sigma }_{\mathit{v}}^2$ are determined experimentally. 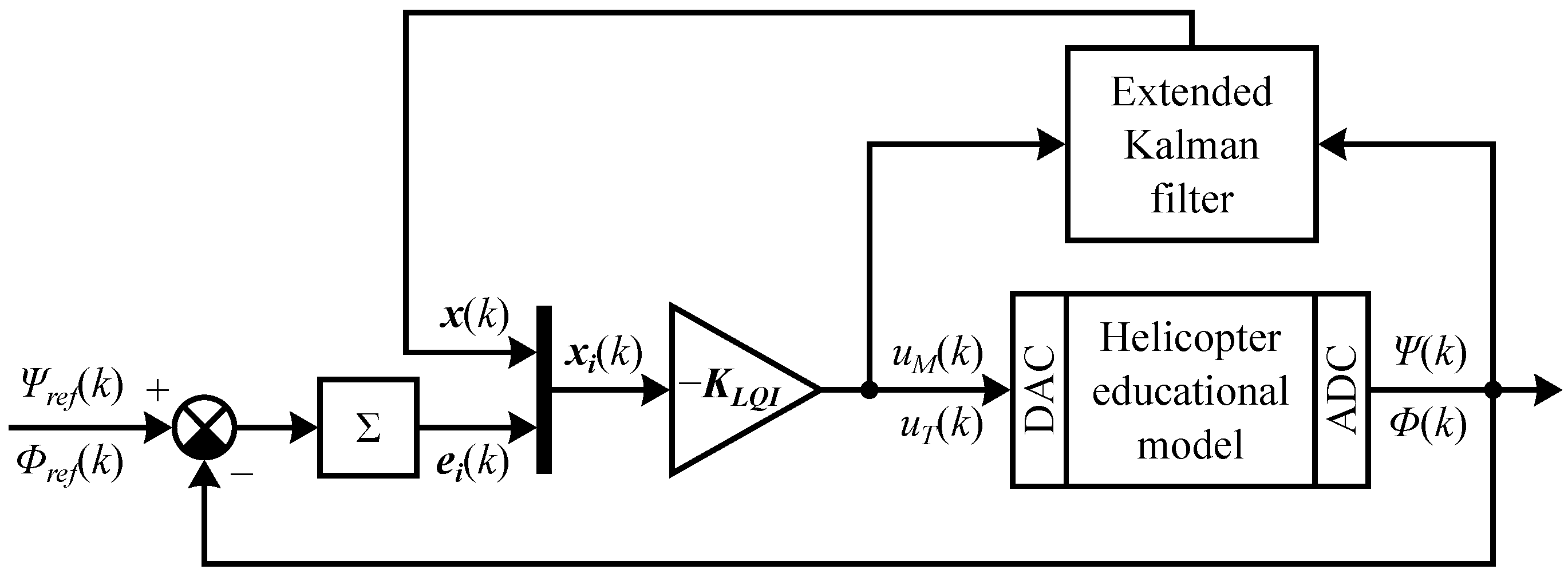The control structure implementing the LQI control algorithm with the designed extended Kalman filter is shown in Figure 18.

The results shown in Figure 19 and

Table 4. Quantitative evaluation of LQI control algorithm.

Environment	MSE ($\mathit{\Psi }$)	MSE ($\mathit{\Phi }$)	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{M}}\right)$	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{T}}\right)$
simulation	$1.06076\times {10}^{-4}$	$2.73762\times {10}^{-4}$	$0.082883$	$0.026343$
real	$7.42957\times {10}^{-4}$	$1.45276\times {10}^{-2}$	$17.6894$	$3.34448$

demonstrate the application of the LQI control algorithm and the extended Kalman filter designed from the dynamical neural model. The presented results are obtained from the real helicopter educational model and the helicopter gray-box model. The reference angle (${\Psi }_{ref}\left(t\right)$ and ${\Phi }_{ref}\left(t\right)$) tracking capability of the designed LQI control algorithm is decent. Due to the high noise sensitivity of the LQI control algorithm, the main rotor $u_M\left(t\right)$ and tail rotor $u_T\left(t\right)$ input ranges are limited. The Kalman filter based on the black-box model is computationally too demanding for the STM32 microcontroller to maintain a constant sampling period $T_s$. Therefore, state estimation and control run on an attached computer.

The model predictive control algorithm (MPC) is designed based on the nonlinear state-space dynamical neural model (1), which is a single-step nonlinear predictor. A recurrent multi-step predictor is constructed from (1) as

$$\begin{array}{cc}\hfill \widehat{\mathit{x}}\left(k+1\right)& ={\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k\right),{\mathit{u}}_{\mathit{opt}}\left(k\right)\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill \widehat{\mathit{x}}\left(k+n_u+1\right)& ={\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k+n_u\right),{\mathit{u}}_{\mathit{opt}}\left(k+n_u\right)\right)\hfill \\ \hfill & ⋮\hfill \\ \hfill \widehat{\mathit{x}}\left(k+n_p\right)& ={\widehat{\mathit{f}}}_{\mathit{NNSS}}\left(\mathit{x}\left(k+n_p-1\right),{\mathit{u}}_{\mathit{opt}}\left(k+n_u\right)\right)\hfill \end{array}$$

(17)

where $n_p$ is the prediction horizon, $n_u$ is the control horizon, and ${\mathit{u}}_{\mathit{opt}}\left(·\right)$ is the optimal input vector sequence

$$\begin{array}{c}\hfill {\mathit{u}}_{\mathit{opt}}=\left[{\mathit{u}}_{\mathit{opt}}\left(1\right),\dots ,{\mathit{u}}_{\mathit{opt}}\left(n_u\right)\right]\end{array}$$

(18)

The optimal input sequence ${\mathit{u}}_{\mathit{opt}}$ minimizes the MPC cost function

$$\begin{array}{cc}\hfill V_{MPC}& =\sum _{i=1}^{n_p}\left({\widehat{\mathit{e}}}^T\left(k+i\right){\mathit{Q}}_{\mathit{MPC}}\widehat{\mathit{e}}\left(k+i\right)\right)+\hfill \\ \hfill & +\sum _{i=1}^{n_u}\left({\widehat{\mathit{u}}}^T\left(k+i-1\right){\mathit{R}}_{\mathit{MPC}}\widehat{\mathit{u}}\left(k+i-1\right)\right)\hfill \end{array}$$

(19)

where ${\mathit{Q}}_{\mathit{MPC}}$ and ${\mathit{R}}_{\mathit{MPC}}$ are experimentally determined weighting matrices, and $\widehat{\mathit{e}}\left(k\right)={\mathit{y}}_{\mathit{ref}}\left(k\right)-\mathit{C}\widehat{\mathit{x}}\left(k\right)$ is the error prediction. The MPC control law

$$\begin{array}{c}\hfill \mathit{u}\left(k\right)=\underset{V_{MPC}}{min}{\mathit{u}}_{\mathit{opt}}\left(k\right)\end{array}$$

(20)

applies the first element of the optimal input sequence ${\mathit{u}}_{\mathit{opt}}\left(k\right)$ to the system input $\mathit{u}\left(k\right)$.

The practical implementation of the proposed MPC control algorithm based on the predictor (17) requires that all elements of the state vector $\mathit{x}\left(k\right)$ are measurable. As the helicopter educational model does not allow measuring all states, the extended Kalman filter designed for the LQI control algorithm is utilized to estimate state vector values $\widehat{\mathit{x}}\left(k\right)$. 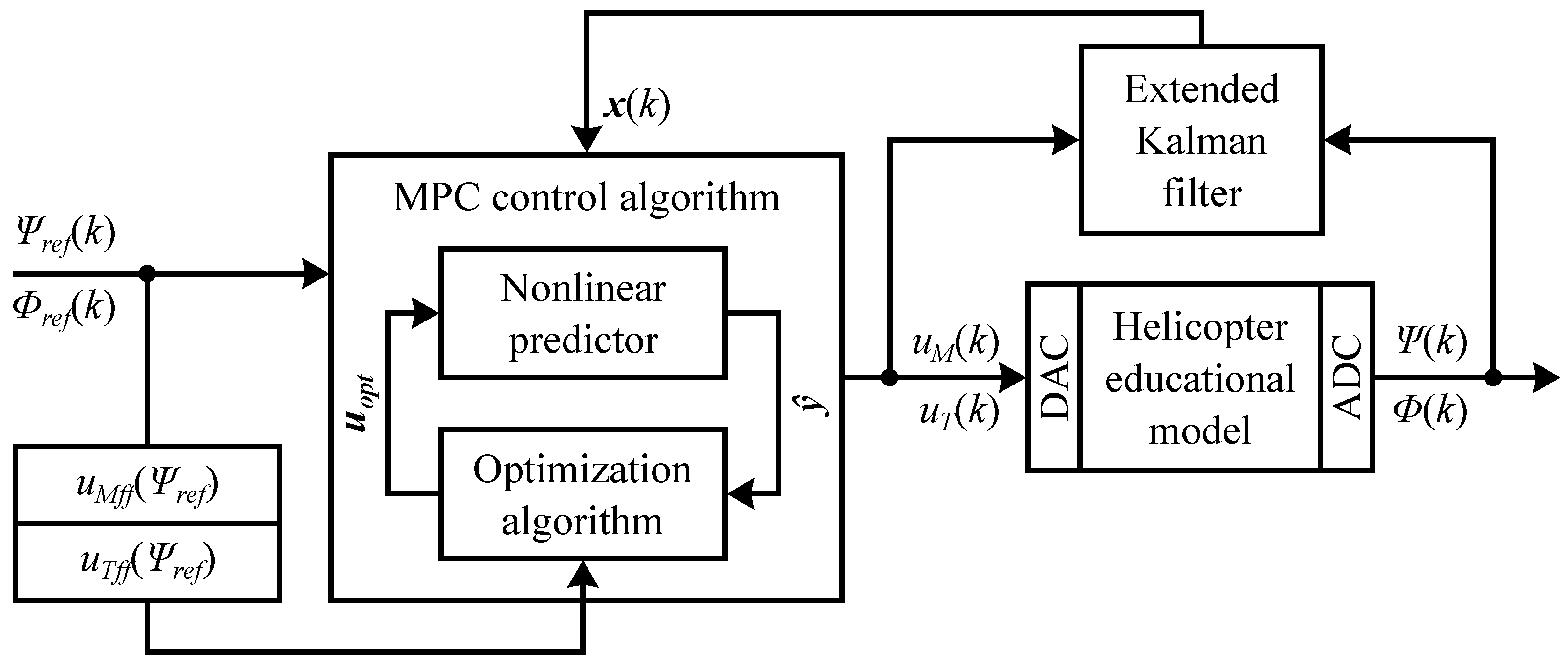The final control structure for the MPC control algorithm is shown in Figure 20.

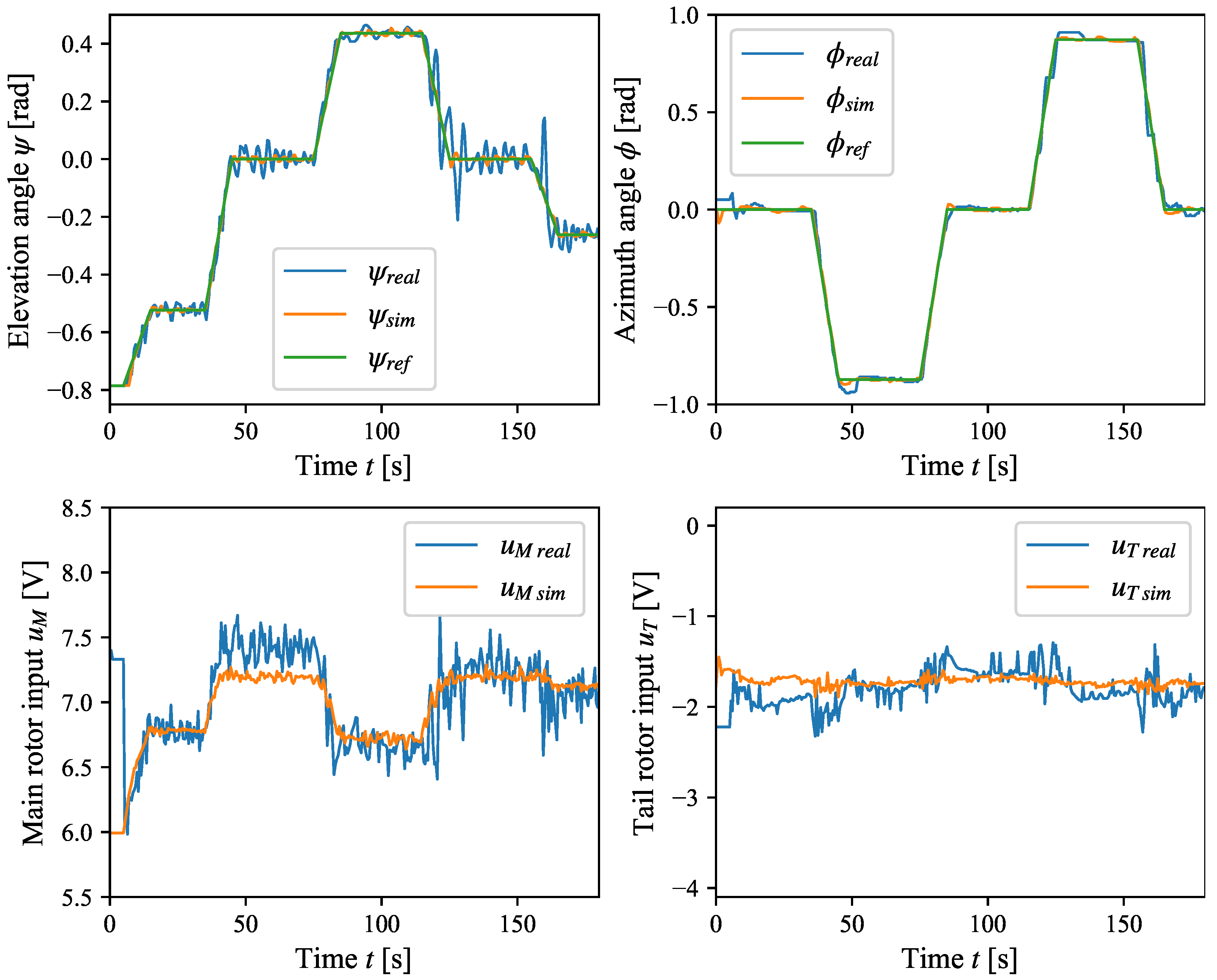
The MPC control algorithm with the extended Kalman filter is verified using the real helicopter educational model and helicopter gray-box model. The verification results are shown in Figure 21 and

Table 5. Quantitative evaluation of MPC control algorithm.

Environment	MSE ($\mathit{\Psi }$)	MSE ($\mathit{\Phi }$)	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{M}}\right)$	${\mathit{V}}_{\mathit{E}}\left(\mathsf{\Delta }{\mathit{u}}_{\mathit{T}}\right)$
simulation	$7.12309\times {10}^{-5}$	$1.26564\times {10}^{-4}$	$0.001276$	$0.001845$
real	$2.28379\times {10}^{-3}$	$1.65455\times {10}^{-2}$	$0.069124$	$0.053830$

. The designed MPC control algorithm induces minor oscillations of the elevation angle $\Psi \left(t\right)$. Azimuth angle $\Phi \left(t\right)$ tracks the azimuth reference angle ${\Phi }_{ref}\left(t\right)$ well with minor overshoots. Both main rotor $u_M\left(t\right)$ and tail rotor $u_T\left(t\right)$ inputs are mostly unaffected by noise. The MPC control algorithm with prediction horizon $n_p=10$ and black-box predictor requires on average $1.19\mathrm{ms}$ of calculation time per sample in the Simulink environment with an AMD Ryzen 7 5800U processor, which makes it possible to run the control loop in real time.

All three designed control algorithms, designed from a dynamical neural model, can stabilize a real helicopter educational model. Further improvements can be made by tuning synthesis parameters. In this paper, the same synthesis parameters are used as in [4] to make results comparable.

5. Conclusions

In this paper, a methodology based on neural networks for experimental nonlinear dynamical system identification is proposed. The proposed methodology uses the data obtained from the gray-box model, which allows to determine optimal neural network structure and speeds up the training process. The verification of the proposed methodology is presented in a case study of the experimental identification of the helicopter educational model using feed-forward MLP neural networks. Data from the helicopter gray-box model are used to fine-tune the neural network structure and pre-train the neural network on the data with known noise properties. Later, data from the real helicopter educational model, which also capture interactions between elevation and azimuth subsystems, are used to train the neural network. The dynamical neural model is directly validated in a 10-step ahead prediction task and compared to the nonlinear predictor based on the gray-box model. Prediction error of the proposed nonlinear predictor based on the dynamical neural model is significantly smaller than that of the nonlinear predictor based on the gray-box model. The validated dynamical neural model represents a digital twin of the real helicopter educational model as it matches its dynamics. The digital twin is used to design polynomial, LQI, and MPC control algorithms that are evaluated using qualitative and quantitative comparison. The design of stabilizing control algorithms from the dynamical neural model indirectly validates that the dynamical neural model is a digital twin of the helicopter educational model. Although the dynamical neural model captures interactions between subsystems, it can be further improved by considering the effect of the electronically adjustable balancing weight on the elevation subsystem. Also, different control synthesis parameters can be used to enhance the performance of the designed control algorithms. The particular synthesis parameters are selected for direct comparison with results obtained in [4]. The proposed methodology can be used to create digital twins of various components used in the ALICE experiment at CERN.