A Q-Learning-Assisted Evolutionary Optimization Method for Solving the Capacitated Vehicle Routing Problem

Abstract

The Capacitated Vehicle Routing Problem (CVRP) is a classic combinatorial optimization problem in logistics and distribution, with significant theoretical and practical importance. To address the limitations of traditional evolutionary algorithms—particularly their use of fixed operator selection and simplistic search strategies—this paper proposes a Q-learning-based evolutionary algorithm (QEA). By incorporating a reinforcement learning mechanism, the QEA adaptively selects among multiple neighborhood search operators, effectively balancing global exploration and local exploitation. In addition, a novel insertion-based crossover operator and a set of diverse neighborhood search strategies are designed to further enhance solution quality and search efficiency. Experimental results on a variety of standard CVRP benchmark instances show that the QEA demonstrates a superior performance and strong robustness, significantly outperforming several representative state-of-the-art algorithms for solving the CVRP. These results confirm the effectiveness and practical value of the proposed method.

1. Introduction

With the rapid development of logistics distribution, intelligent transportation, and warehouse management, how to efficiently plan vehicle routing has become an increasingly important issue [1]. The Capacitated Vehicle Routing Problem (CVRP) is representative of this challenge. Its objective is to design routes for multiple vehicles originating from a central depot to serve a set of customers, while minimizing the total travel distance and ensuring that each vehicle’s load does not exceed its capacity [2]. As a well-known NP-hard problem [3], the complexity of the CVRP grows rapidly with the problem size, making it difficult to obtain optimal solutions within an acceptable computational time. To address this, a Q-learning-assisted evolutionary algorithm is proposed to enhance the solution quality for the CVRP by adaptively selecting effective search operators.

To tackle the CVRP, a wide range of heuristic and metaheuristic methods have been proposed. Classical heuristic algorithms such as the savings algorithm [4], nearest neighbor [5], and sweep algorithm [6] are capable of generating feasible solutions quickly, but often suffer from local optima. In recent years, evolutionary algorithms (EAs) have been widely applied to the CVRP due to their powerful global search capabilities. Typical approaches include Genetic Algorithms [7], Differential Evolution [8], Ant Colony Optimization (ACO) [9], and Particle Swarm Optimization [10]. To further improve performance, many studies have integrated mechanisms such as Large Neighborhood Search (LNS) [11] and adaptive search [12], leading to sophisticated hybrid intelligent algorithms.

İlhan et al. [13] proposed an Improved Simulated Annealing algorithm for the CVRP, which incorporates crossover operators from Genetic Algorithms and employs a hybrid selection strategy to enhance convergence speed. Li et al. [14] developed an Adaptive Genetic Algorithm with self-adaptive crossover and mutation operators, achieving a promising performance on CVRP instances. Altabeeb et al. [15] addressed the local optimum issue of the Firefly Algorithm (FA) by integrating two local search strategies and genetic components, resulting in a hybrid method named CVRP-FA with an enhanced solution quality. Souza et al. [16] introduced novel mutation operators within a discrete DE framework, augmented with multiple local search operators to solve the CVRP effectively. Xiao et al. [17] proposed a Variable Neighborhood Simulated Annealing algorithm by combining Variable Neighborhood Search and Simulated Annealing, which performs well on large-scale CVRP instances. Akpinar [18] hybridized LNS and ACO to develop LNS-ACO, leveraging ACO’s solution construction mechanism to improve LNS’s performance. Additionally, Queiroga et al. [19] proposed a partial optimization metaheuristic under special intensification conditions for the CVRP, which combines neighborhood enumeration with mathematical programming to achieve high-quality solutions, particularly on large-scale instances.

Recent research has also focused on fuzzy and uncertain demand variants of the CVRP. Zacharia et al. [20] studied the Vehicle Routing Problem with Fuzzy Payloads considering fuel consumption, emphasizing energy consumption. Yang et al. [21] and Abdulatif et al. [22] investigated fuzzy demand VRPs with soft time windows, addressing uncertainty and temporal flexibility in delivery scheduling.

However, traditional EAs often rely on fixed or randomly selected operators, which limits their ability to adapt search strategies based on the current solution state or search stage. This can result in a low search efficiency and slow convergence. In recent years, reinforcement learning (RL) mechanisms have been introduced into evolutionary frameworks [23,24], enabling adaptive operator scheduling. For example, Q-learning-based local search scheduling methods [25,26] have shown potential in enhancing search intelligence. Irtiza et al. [27] incorporated Q-learning into an evolutionary algorithm (EA) to schedule local search operators, demonstrating an improved performance on CVRP with Time Windows (CVRPTW) instances. Costa et al. [28] employed deep reinforcement learning to intelligently guide two-opt operations, enabling general local search strategies to adapt automatically to specific routing problems such as the CVRP. Kalatzantonakis et al. [29] developed a reinforcement learning–variable neighborhood search method for the CVRP, achieving superior adaptability. Zong et al. [30] proposed an RL-based framework for solving multiple vehicle routing problems with time windows. Zhang et al. [31] integrated RL into multi-objective evolutionary algorithms for assembly line balancing under uncertain demand, demonstrating RL’s broader applicability. A comprehensive survey by Song et al. [32] reviews reinforcement learning-assisted evolutionary algorithms and highlights future research directions. Xu et al. [33] presented a learning-to-search approach for VRP with multiple time windows, further proving RL’s potential in routing problems.

Motivated by these developments, the objective of this study is to develop and evaluate a Q-learning-based Evolutionary Algorithm (QEA) for solving the CVRP, with the aim of improving the solution quality and adaptability through intelligent operator scheduling. The core idea of the QEA is to combine the global search ability of evolutionary algorithms with the adaptive learning capability of Q-learning. By dynamically adjusting the selection of neighborhood search operators based on individual fitness states, the QEA achieves an intelligent balancing of search direction and resource allocation, while preserving population diversity. The main contributions of this work are as follows:

(1)

A Q-learning-based evolutionary framework is proposed to solve the CVRP. By introducing a reinforcement learning mechanism for operator scheduling, the algorithm overcomes the limitations of traditional fixed operator selection, enabling adaptive strategy evolution.

(2)

A novel insertion crossover operator is designed specifically for the CVRP evolutionary framework to generate high-quality offspring. Instead of recombining individual nodes, it operates on complete route segments, allowing better preservation of feasible structures and encouraging diverse yet valid route combinations.

(3)

Three neighborhood search operators targeting different search stages were designed, focusing, respectively, on global perturbation, accelerated convergence, and local optimization. By adaptively adjusting the search scope and direction, and dynamically allocating search resources based on individual fitness, these operators enable intelligent control of the search strategy, effectively enhancing the overall search efficiency and solution quality of the algorithm.

The rest of this paper is organized as follows. Section 2 introduces the definition and mathematical model of the CVRP. Section 3 presents the detailed design of the QEA, including the encoding scheme, evolutionary framework, Q-learning-based operator selection, and algorithm components. Section 4 reports the experimental setup and numerical results, followed by performance comparisons with existing methods. Finally, Section 5 concludes this paper and outlines directions for future research.

2. Problem Background

The Capacitated Vehicle Routing Problem (CVRP) is one of the most classic and important variants of routing optimization problems, with broad theoretical significance and practical applications [34]. The problem involves a set of customers to be served by a fleet of homogeneous vehicles departing from a common depot, each vehicle having the same capacity constraint. The objective is to design delivery routes for each vehicle such that all customer demands are satisfied while minimizing the total travel distance of all vehicles.

The CVRP can be represented by a graph G = (N, E), where the node set N = {0, 1, …, n} and the edge set E = {(i, j): i, j∈N} connect these nodes. Here, node 0 denotes the depot, and nodes {1, 2, …, n} represent the customers. Each customer i ∈ N’(N − {0}) has a demand m_i, and each edge has an associated cost d_ij, which corresponds to the travel distance from node i to node j. The mathematical model of the CVRP is formulated as follows [35].

The objective function:

$$Minimize {\displaystyle \sum _{i=0}^N{\displaystyle \sum _{j=0}^N{\displaystyle \sum _{k=1}^K{d}_{ij}{x}_{ij}^k}}}$$

(1)

Subject to

$${\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=0}^N{x}_{ij}^k=1 j\in \{1,\dots ,N\}:i\ne j}}$$

(2)

$${\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j=0}^N{x}_{ij}^k=1 j\in \{1,\dots ,N\}:i\ne j}}$$

(3)

$${\displaystyle \sum _{i=0}^N{\displaystyle \sum _{j=0}^N{x}_{ij}^{k}dij\le Qk k\in \{1,\dots ,K\}}}$$

(4)

$${\displaystyle \sum _{j=1}^N{x}_{ij}^k={\displaystyle \sum _{j=1}^N{x}_{ij}^k\le 1} i=}0 and k\in \{1,\dots ,K\}$$

(5)

$${\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j=1}^N{x}_{ij}^k\le K} i=0}$$

(6)

The variable $x_{ij}^k$ represents a decision variable: it takes the value 1 if vehicle k travels from node i to node j, and 0 otherwise. Equation (1) is the objective function, aiming to minimize the total travel distance of all vehicles. Constraints (2) and (3) ensure that each customer node is visited exactly once by a single vehicle. Constraint (4) guarantees that the total demand of customer nodes assigned to a route does not exceed the vehicle’s capacity. Constraint (5) ensures that each vehicle starts and ends its route at the depot after serving its assigned customers. Constraint (6) limits the number of routes used to serve customers to a maximum of K, corresponding to the total number of available vehicles.

3. QEA for CVRP

This section systematically presents the structure and key components of the QEA. First, the overall framework of the QEA is outlined. Then, the encoding and decoding strategies for individuals, along with the initialization method for the population, are described. Subsequently, the selection, crossover, and mutation operators are introduced. This is followed by a detailed explanation of the Q-learning-driven operator selection strategy and three specially designed neighborhood search operators. Through the seamless integration of these components, QEA effectively balances solution quality and search efficiency, demonstrating strong global exploration and local exploitation capabilities.

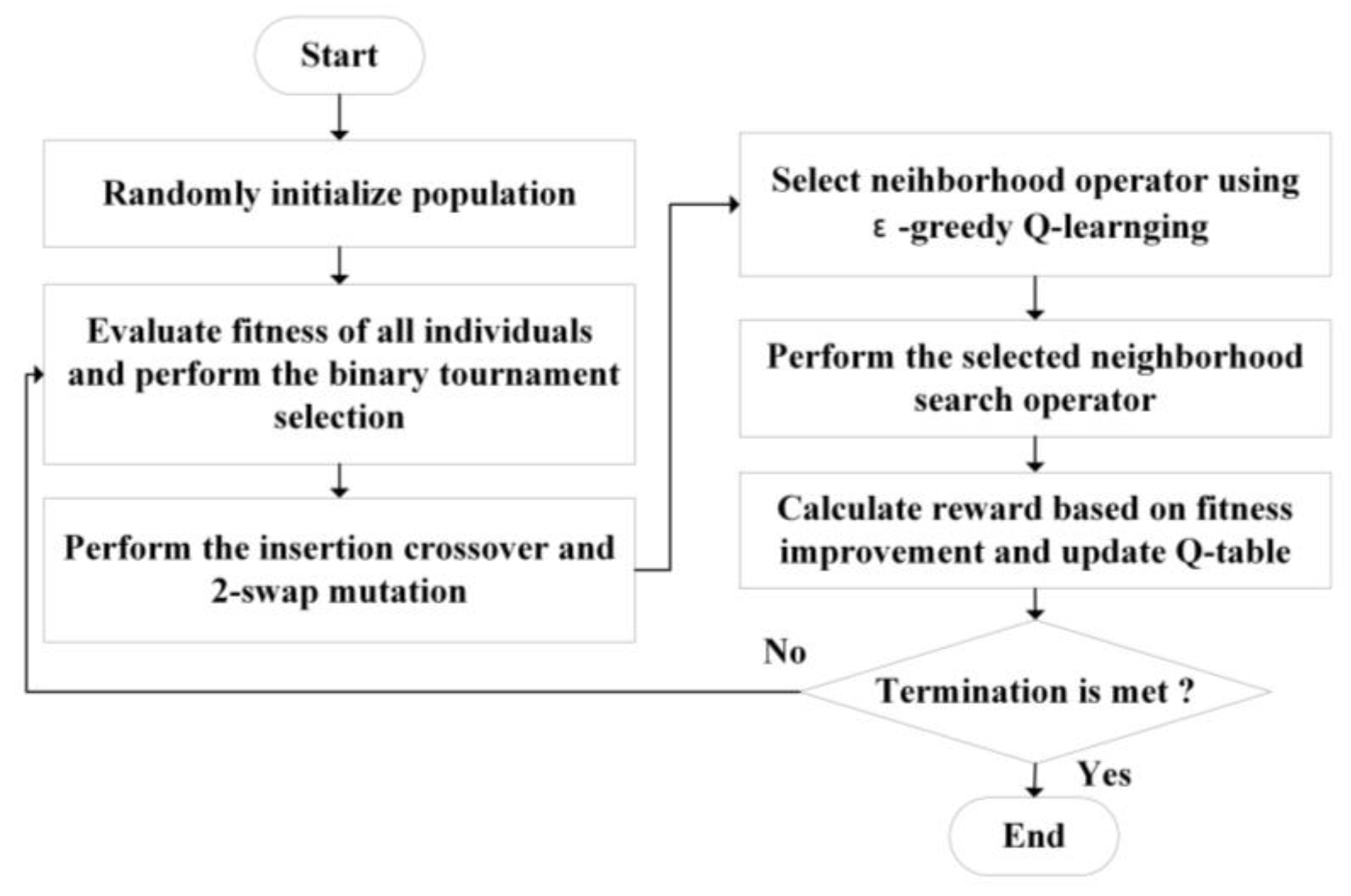
3.1. QEA Framework Overview

As illustrated in Figure 1, the QEA integrates the global search capability of evolutionary algorithms with the adaptive learning mechanism of reinforcement learning, aiming to efficiently solve the CVRP. The QEA represents solutions using a path-based encoding scheme, and it evolves high-quality solutions through population initialization, insertion crossover, neighborhood search, and a Q-learning-driven operator selection strategy. The core idea is to leverage the Q-learning mechanism during each local search step to adaptively select the most appropriate neighborhood search operator, thereby dynamically adjusting the search strategy and enhancing the algorithm’s robustness and adaptability.

3.2. Individual Encoding and Decoding

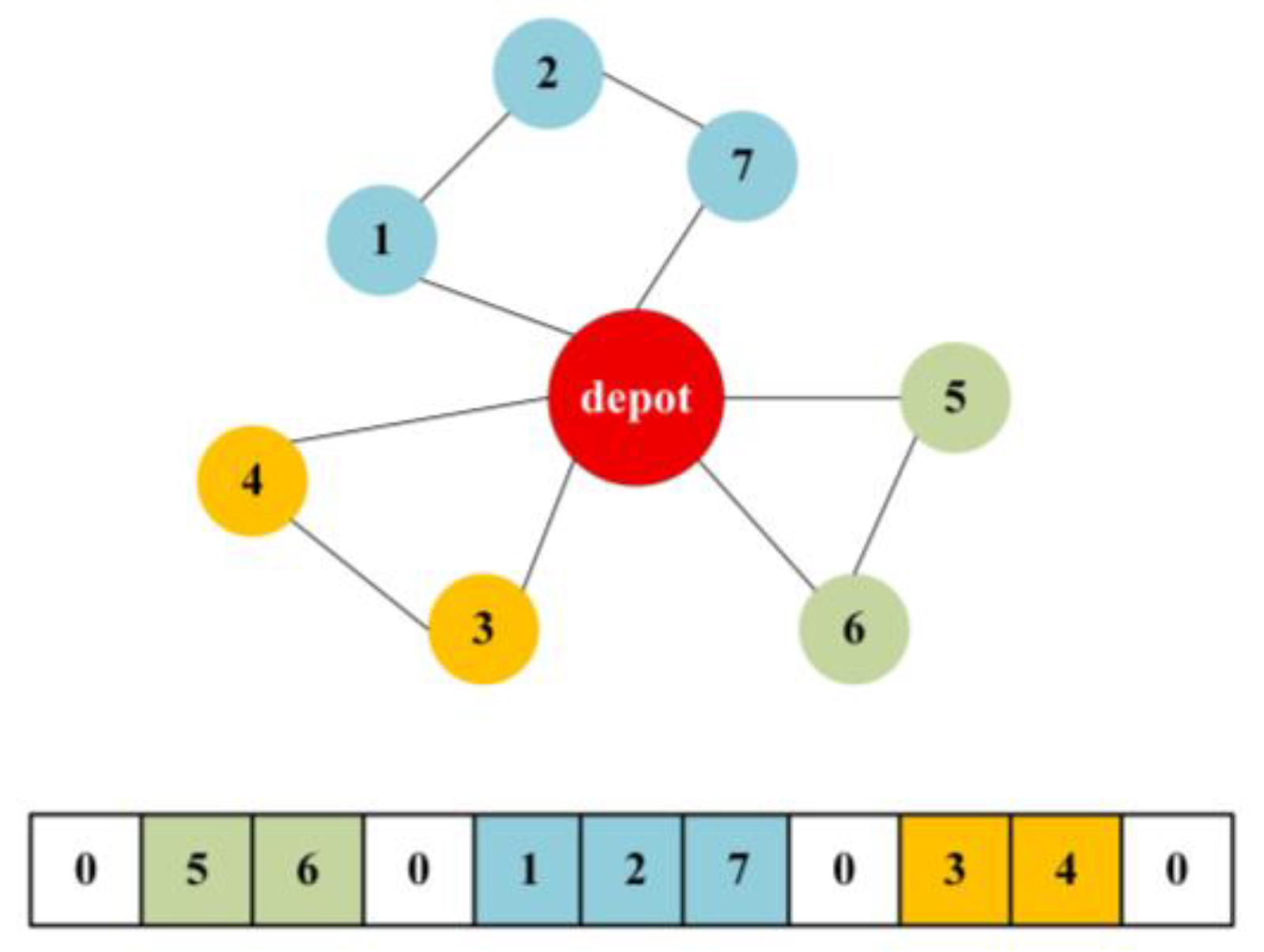
Encoding: In the QEA, a solution is represented using serial number coding, which offers a compact structure, ease of manipulation, and compatibility with crossover and mutation operations. Each individual is encoded as an integer sequence that includes all customer node indices, interspersed with several separators (represented by the depot index, set as 0 to divide the routes among multiple vehicles. For example, a sample individual {0, 5, 6, 0, 1, 2, 7, 0, 3, 4, 0} can be illustrated in Figure 2, which indicates that the depot dispatches three vehicles to serve seven customer nodes.

Decoding: For each individual, the sequence is read from left to right, starting from the depot. Each occurrence of the depot marks the end of a vehicle route. The customer nodes between two depot entries are assigned to a vehicle, and the route load is updated in real time to ensure capacity constraints are considered. For example, the individual can be decoded into three vehicle routes as follows: Vehicle 1: 0–5–6–0, Vehicle 2: 0–1–2–7–0, Vehicle 3: 0–3–4–0. These three routes together form a feasible solution to CVRP instance.

3.3. Initialization Phase

In the initialization phase of the QEA, a set of individuals is randomly generated, each representing a feasible or partially feasible solution to the CVRP. The generation process is based on a random permutation of customer nodes, followed by capacity-constrained route segmentation. The procedure is as follows:

First, all customer nodes are randomly shuffled. The algorithm then sequentially scans this shuffled sequence, adding each customer to the current route until adding another customer would violate the vehicle’s capacity constraint. At that point, the depot 0 is inserted at the beginning and end of the route. A new route is then initiated, and the process continues until all customers have been assigned.

If all customer nodes are successfully assigned to routes that respect capacity limits, the individual is considered feasible. However, in some cases, a subset of customers may remain unassigned due to insufficient remaining capacity. These remaining nodes are grouped into the final route, which may violate capacity constraints. In this case, the individual is treated as an infeasible solution, and a penalty term is introduced into the fitness function to penalize the total overload in the violated routes. The fitness of an individual is defined as

$$fitness=\left\{\begin{array}{l}F+\tau Penalty, if Penalty > 0 \hfill \\ F, otherwise\hfill \end{array}\right.$$

(7)

where F is the total travel distance of all routes, Penalty is the total overload across all routes violating the capacity constraint, τ is the penalty coefficient, set to 20 in our experiments to effectively distinguish infeasible individuals, and we will analyze the influence of τ on the performance of QEA in the following section.

3.4. Evolution Phase

3.4.1. Binary Tournament Selection

To select high-quality individuals from the current population for crossover and subsequent search operations, the QEA adopts the classical Binary Tournament Selection operator [36]. This method maintains an appropriate selection pressure while preserving population diversity. Specifically, in each iteration, two distinct individuals are randomly selected from the population. Their fitness values are compared, and the individual with the better fitness is selected to enter the next-generation population. This process is repeated until a new population of the predefined size is generated.

3.4.2. Insertion Crossover

Traditional crossover operators, such as Order Crossover (OX) [37] and Cycle Crossover (CX) [38], were originally designed for the Traveling Salesman Problem (TSP) [39]. However, these operators are not well suited to solving the CVRP due to the inherent differences in problem structure and constraints. Additionally, while OX has been adapted in some CVRP variants, such as those involving fuzzy constraints [1], it does not inherently preserve the feasibility of capacity-constrained solutions. In the CVRP, capacity limits must be strictly satisfied, and using OX or CX directly may lead to infeasible solutions. To address this issue, we propose a novel Insertion Crossover operator tailored specifically for the CVRP.

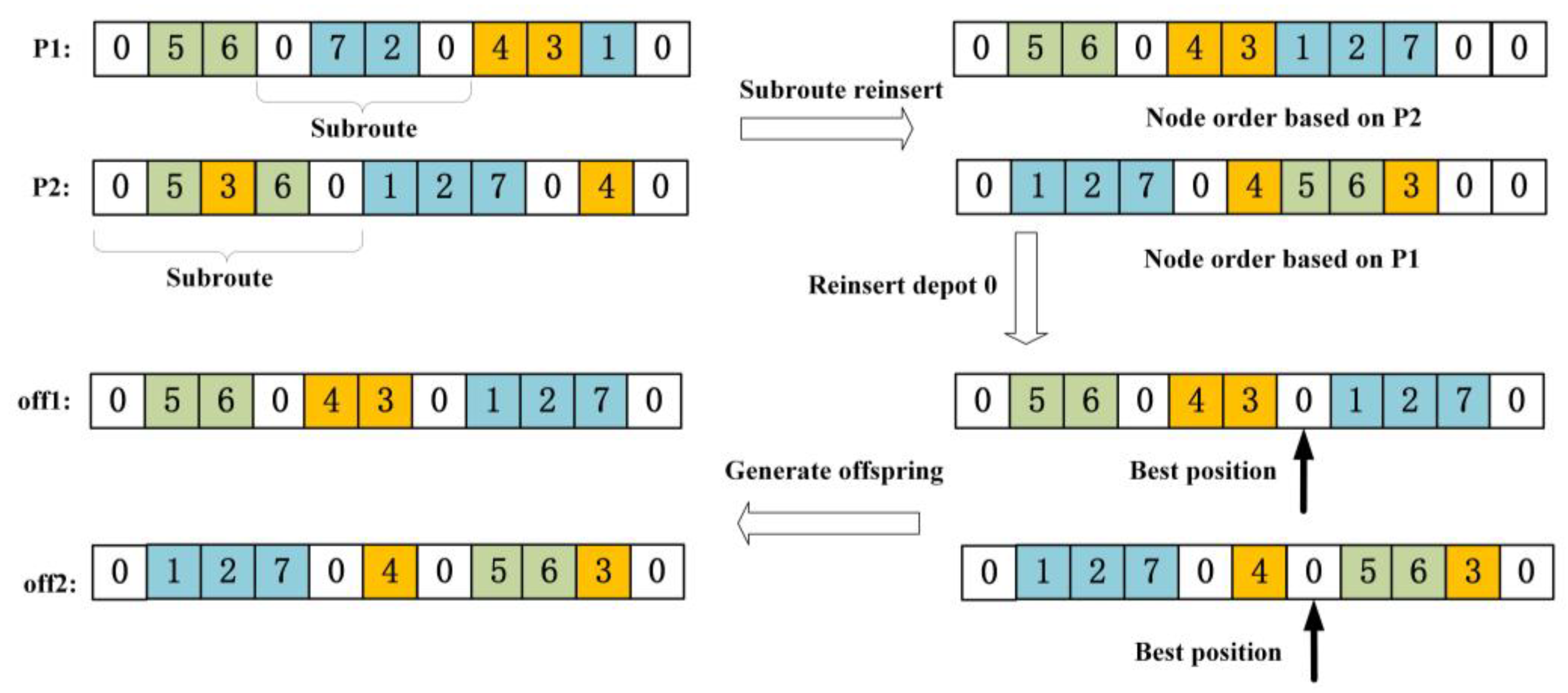
The proposed operator not only preserves useful path information from parent individuals but also enhances the global exploration ability of the algorithm. Specifically, it begins by randomly selecting two parent individuals and extracting a subroute (i.e., a sequence between two depots) from one parent. This subroute is then inserted into the end of the second parent’s chromosome while maintaining the node order of the receiving parent. After constructing a new chromosome, the penultimate depot 0 is reinserted at every possible location within the last two routes to reconstruct feasible solutions. Among all resulting candidates, the one with the best fitness is selected as the final offspring. The entire procedure is illustrated in Figure 3.

This strategy guarantees that all generated offspring remain feasible without requiring repair operations, which is a critical advantage over traditional operators. It effectively combines promising substructures from both parents and explores diverse path organizations, leading to an improved solution quality and search efficiency. The detailed procedure is illustrated in Algorithm 1.

Algorithm 1 Insertion Crossover

Input: two parent individuals p1 and p2. Output: two offspring individuals.

1: Begin 2:   For each (P_from, P_to) in [(p1, p2), (p2, p1)] do 3:     randomly select one sub-path s from P_from 4:     remove all customers in s from P_to → get base sequence B 5:     insert sub-path s at the end of B → form extended sequence E 6:     remove second-to-last depot 0 from E 7:     For each possible position i to reinsert the depot: 8:       insert 0 at position i → form candidate sequence Ei 9:       decode Ei and evaluate fitness Fi 10:    select each sequence E_best with minimal Fi 11:    assig E_best as one offspring

12:    End for 13: End

3.4.3. Two-Swap Mutation

To enhance population diversity and avoid premature convergence, this study employs a two-swap mutation operator. For each individual, the mutation process randomly selects two customer nodes within the chromosome and exchanges their positions. This swapping procedure is repeated five times to generate a mutated individual. After mutation, if the fitness of the new individual is better than that of the original parent, the mutated individual is accepted into the next generation; otherwise, the original parent is retained. This simple yet effective operator facilitates a local search around the current solution and introduces beneficial variations while maintaining the feasibility of routes.

3.5. Q-Learning-Based Operator Selection

Q-learning is a reinforcement learning (RL) method [40] that gradually improves decision-making by learning a state–action value function, known as the Q-function, to select the optimal action in a given state. Due to its scalability and ability to update decision policies through accumulated experience, Q-learning is well-suited to adaptively selecting among multiple neighborhood search operators.

In this study, each neighborhood search operator (NS) is treated as a distinct action. The action set is defined as A = {NS1, NS2, NS3}. The state space is simplified and defined as the index of the previously chosen operator,

$$S=\{0, 1, 2\}$$

(8)

where each state corresponds to the last action taken. This concise state representation focuses learning on operator effectiveness transitions.

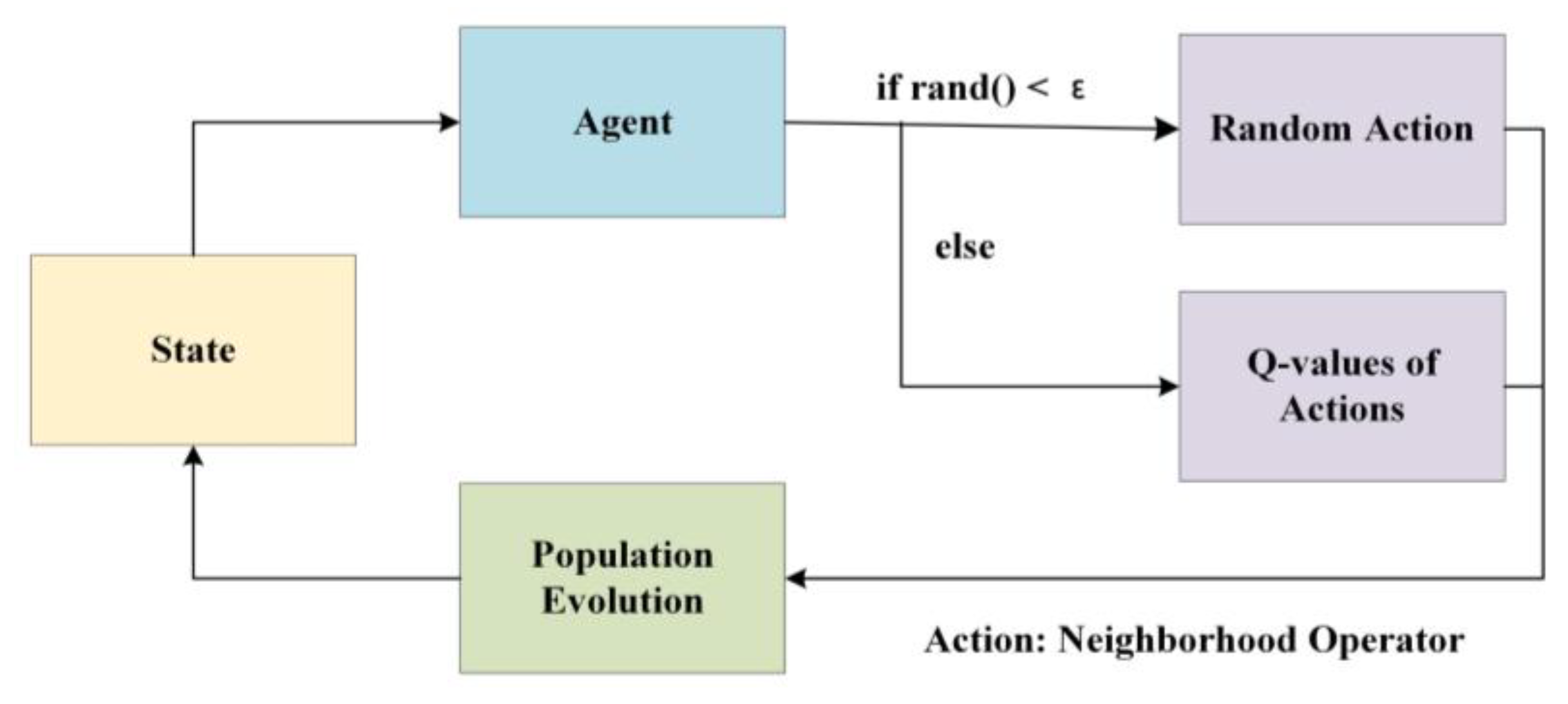
During each iteration, the Q-learning algorithm employs an ε-greedy strategy to select an action (a neighborhood operator) for local search perturbation, as shown in (9):

$$a_t=\left\{\begin{array}{l}random action, with probability \epsilon \hfill \\ \arg {\max }_{a}Q(s_t,a), with probability 1-\epsilon \hfill \end{array}\right.$$

(9)

If the Q-table is uninitialized or contains all zeros, the action is selected randomly to encourage exploration. After executing the selected operator on all individuals in the population (see algorithm implementation below), a cumulative reward is computed as the total fitness improvement:

$$r_t={\displaystyle \sum _{i = 1}^N(f_{before}^{(i)}-f_{after}^{(i)})}$$

(10)

where $f_{before}^{(i)}$ and $f_{after}^{(i)}$ represent the fitness values of the i-th individual before and after applying the operator, respectively.

The environment then transitions to the next state s_t+1 = a_t, and the Q-table is updated using the classic Q-learning update rule (11):

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma \max Q(s_t+1,a^{\prime })-Q(s_t,a_t)]$$

(11)

where α is the learning rate and γ is the discount factor that controls the importance of future rewards. Through this iterative learning and updating process, the Q-learning mechanism adaptively adjusts the probabilities of selecting each neighborhood operator, favoring those that consistently yield better solution improvements. The procedure is illustrated in Figure 4.

3.6. Neighborhood Search

To improve both search efficiency and solution quality of the QEA across different search stages, three targeted neighborhood search operators are designed, each focusing on a distinct objective: global diversification, accelerated convergence, and local exploitation. These operators dynamically allocate search resources based on individual fitness values and guide the search direction by modifying path structures, thus enhancing the QEA’s overall performance. The pseudo-code of the QEA is shown in Algorithm 2.

Neighborhood Operator 1 (Global Perturbation):

This operator is designed to enhance the global search capability. It begins by randomly deleting r nodes from the solution, where t is computed using (12):

$$t=\min (indFit/\min Fit\times cusNum\times 0.1, cusNum\times 0.4)$$

(12)

Here, indFit denotes the fitness of the current individual, minFit is the best fitness in the population, and cusNum is the total number of customers. The key idea is to assign more search resources to lower-quality individuals. After removing the nodes, they are reinserted into positions that minimally increase the total fitness.

Algorithm 2 QEA

Input: problem instances, α, γ, ε, population size N, MaxGeneration Output: best solution.

1: Begin 2:   initialize population P with N individuals 3:   evaluate fitness of each individual in P 4:   initialize Q(st, at) with values 0 5:   set Q-learning parameters: α, γ, ε 6:   for generation = 1 to MaxGeneration do 7:     p’← Φ 8:      while |P’| < N do 9:        select two parents p1, p2 from p using binary tournament 10:        offspring ← Insertion Crossover(p1, p2) 11:        offspring ← 2-swap mutation

12:        s ← discretize state of offspring 13:        choose neighborhood operator using ε-greedy strategy 14:        offspring’← apply neighborhood search to offspring 15:        evaluate fitness of offspring’ 16:        compute reward rt based on fitness improvement 17:        update Q(st, at) using:               Q(st, at) ← Q(st, at) +α[rt + γmax Q(st+1, a’)- Q(st, at)] 18:        add offspring’ to P’ 19:      end while 20:      P ← P’ 21:   end for 22: End

Neighborhood Operator 2 (Accelerated Convergence):

This operator aims to speed up convergence by focusing on critical nodes. It deletes t nodes with the largest travel distances in the current solution (t is also calculated via Equation (11), assuming that these nodes have the greatest impact on fitness). The deleted nodes are then reinserted at positions that incur the smallest increase in total cost.

Neighborhood Operator 3 (Local Exploitation):

This operator focuses on intensifying the local search. It randomly selects a reference node and deletes t nodes that are most correlated with it, also based on Equation (12). Correlation is calculated using (13):

$$cor=1/(d_{ij}+r_{ij})$$

(13)

where d_ij is the distance between nodes i and j. After removing the most related nodes, they are reinserted into positions that minimally affect fitness.

3.7. Computational Complexity

Before the evolution process begins, the initialization of the Q-table and the population requires a time complexity of O(N), where N is the population size. In each generation, the QEA consists of several main components: fitness evaluation, binary tournament selection, insertion-based crossover, two-swap mutation, and Q-learning-guided neighborhood search.

For each individual, the fitness evaluation’s complexity is O(n), binary tournament selection is O(1), insertion crossover is O(n²), two-swap mutation is O(n), Q-learning-guided neighborhood search is O(n²), and Q-table update is O(1). Therefore, the total computational complexity for all individuals in one generation is O(N×n²), which is dominated by the crossover and neighborhood search operations.

4. Experiments

4.1. Problem Instances and Performance Metric

To evaluate the performance of the proposed QEA, this study adopts the standard CVRP benchmark instances proposed by Augerat et al. [41]. These benchmark instances are widely recognized in the literature and cover a diverse range of problem scales and complexities, making them suitable for comprehensive performance assessment. The instances differ in the number of customers, customer locations, number of vehicles, and vehicle capacity constraints. Such diversity allows for testing the algorithm’s robustness and adaptability across different types of scenarios. All datasets are publicly available at http://vrp.atd-lab.inf.puc-rio.br/index.php/en/, accessed on 13 September 2024.

To assess algorithmic performance, we use the Relative Deviation (RD) between the Obtained Solution (OS) and the Current Best Known Solution (CS), calculated using Equation (14) as follows:

$$RD={\displaystyle \frac{OS-CS}{CS}}\times 100$$

(14)

A lower RD value indicates that the algorithm produces solutions closer to the best-known results, thereby reflecting a superior optimization performance. By evaluating RD across various instances, we can assess not only the average effectiveness of the proposed method but also its consistency and stability in solving the CVRP under different levels of difficulty.

4.2. Parameter Setting of QEA

The configuration of algorithm parameters significantly affects the performance and convergence behavior of the solution process. In the proposed QEA, three key hyperparameters play crucial roles in controlling the learning dynamics and the exploration–exploitation balance:

(1)

Learning rate α: which determines how quickly the Q-values are updated based on new experiences;

(2)

Discount factor γ: which controls the importance of future rewards relative to immediate ones;

(3)

Greedy factor ε: which balances the trade-off between exploration and exploitation.

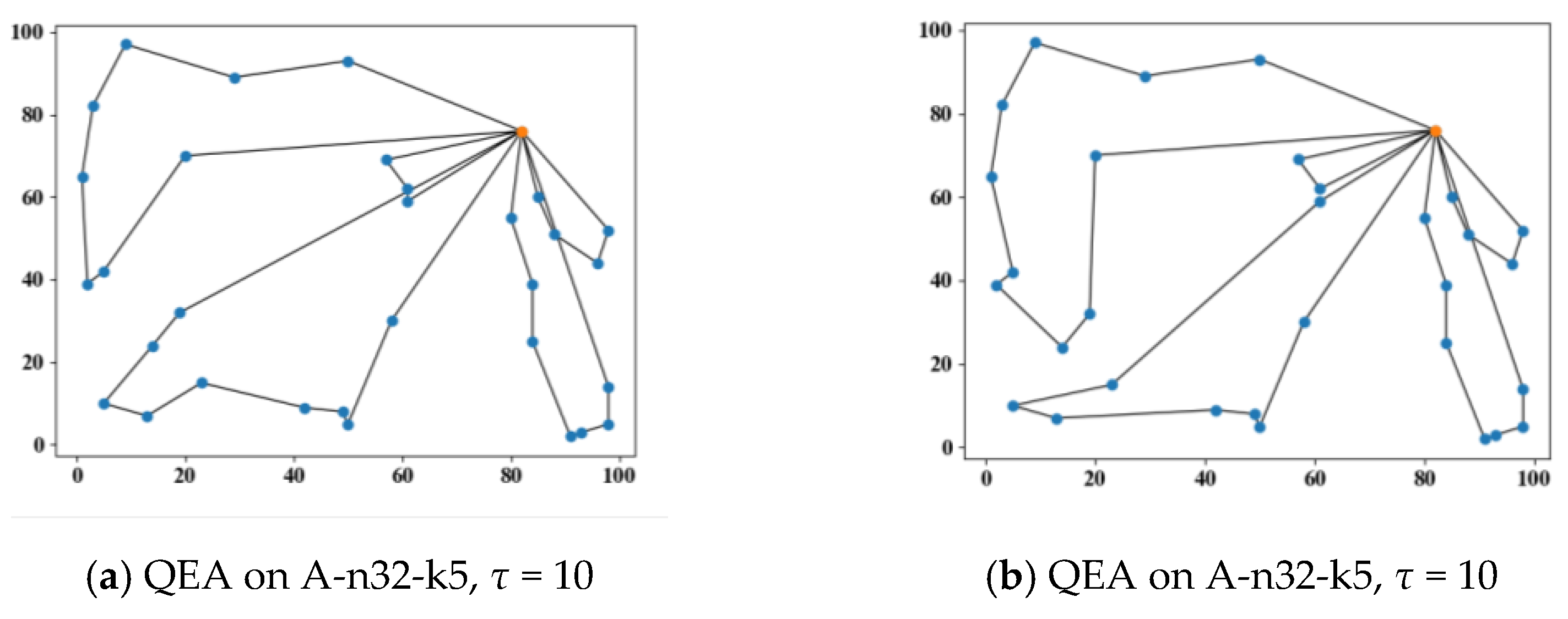
In addition to these hyperparameters, the QEA introduces a fixed penalty coefficient τ to penalize infeasible solutions that violate vehicle capacity constraints. To evaluate the impact of this parameter, a case study is conducted on the A-n32-k5 instance. As shown in Figure 5, when τ = 10, the QEA generates routes with a slightly shorter total distance, but one of the routes exceeds the vehicle’s capacity limit, violating the constraint. In contrast, when τ = 20, all routes strictly adhere to the capacity constraint. This demonstrates that a small penalty fails to sufficiently discourage infeasible solutions, while a larger penalty effectively enforces feasibility. Furthermore, we have verified that setting τ = 20, enables the QEA to consistently produce feasible solutions that satisfy capacity constraints across all tested CVRP benchmark instances. Therefore, τ = 20, is adopted as the fixed penalty coefficient in all experiments.

To identify the optimal combination of α, γ, and ε, the Taguchi method [42] is adopted as an efficient experimental design approach. This method systematically reduces the number of experimental trials while ensuring that the main effects of each parameter are thoroughly explored. As shown in

Table 1. Parameters and their levels.

Parameter	Level 1	Level 2	Level 3
α	0.1	0.2	0.3
γ	0.7	0.8	0.9
ε	0.05	0.1	0.2

, each parameter is assigned three representative levels, and a series of controlled experiments are conducted.

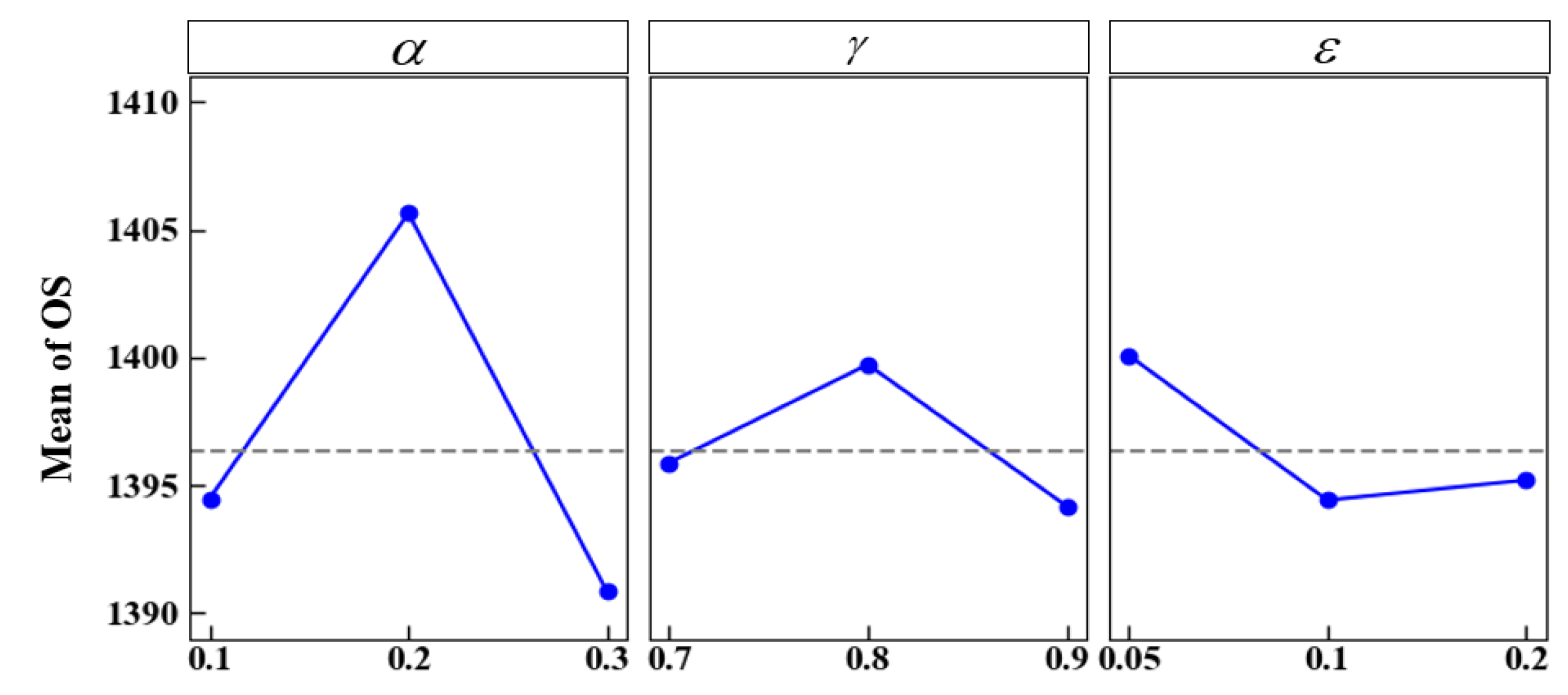
For each combination of parameter values, the QEA is independently executed ten times on representative CVRP instances. The average best solution value across the runs is then recorded to mitigate the impact of stochastic variation and provide a reliable basis for comparison. Figure 6 illustrates the main effect plots for the three key parameters. Based on the experimental results and a comprehensive analysis, the optimal parameter configuration is determined to be α = 0.3, γ = 0.9, ε = 0.1.

Furthermore, the Q-table is initialized to zero for all state–action pairs, indicating that the algorithm starts without any prior knowledge of the utility of different neighborhood search operators. The initial state is defined by selecting a random action (one of the neighborhood search operators is randomly chosen at the beginning of each run). The population size in the QEA is set to 100, and the maximum number of fitness evaluations is set to 1 × 10⁵ for all benchmark datasets.

Table 2. QEA hyperparameters and initialization settings.

Parameter	Value
Q(s, a)	0
α	0.3
γ	0.9
ε	0.1
τ	20
population size	100
max fitness evaluations	1 × 105

summarizes all initialization settings and hyperparameters used in the implementation of the QEA.

4.3. Compared Algorithms and Experimental Setting

For performance evaluation, a comparative analysis was conducted against four representative algorithms that have demonstrated competitive results in solving the CVRP, including LNSi [18], a large neighborhood search algorithm that only accepts improving solutions; LNSa, which applies an acceptance criterion similar to that proposed by Ropke and Pisinger [43]; LNS-ACO [18], which combines Ant Colony Optimization with neighborhood search mechanisms; and CVRP-FA [15], a novel hybrid metaheuristic integrating two local search operators with the Firefly Algorithm.

To ensure a fair comparison, all algorithms were configured with the same population size of 100 and executed independently five times on each benchmark instance to reduce statistical bias. In each run, the maximum number of fitness evaluations was set to 1×10⁵, and the other algorithm-specific parameters were configured according to their respective original studies. Furthermore, the Wilcoxon rank-sum test with a significance level of α = 0.05 was used to evaluate the statistical significance of performance differences between algorithms.

4.4. Experimental Results

As shown in

Table 3. The comparison between QEA and the other four algorithms (bold values indicate the optimal solutions for the test instances).

		LNSi		LNSa		LNS-ACO		CVRP-FA		QEA
Instance	CS	OS	RD	OS	RD	OS	RD	OS	RD	OS	RD
A-n32-k5	784	784	0.00	784	0.00	784	0.00	796	1.53	784	0.00
A-n36-k5	799	805	0.70	799	0.00	799	0.00	799	0.00	799	0.00
A-n44-k6	937	952	1.49	940	0.32	937	0.00	937	0.00	937	0.00
A-n60-k9	1354	1380	1.92	1360	0.44	1355	0.07	1355	0.07	1354	0.00
A-n61-k9	1034	1085	4.93	1072	3.68	1067	3.19	1045	1.06	1039	1.37
A-n69-k9	1159	1194	3.02	1179	1.81	1172	0.96	1168	0.78	1166	0.60
A-n80-k10	1763	1846	4.71	1823	3.40	1815	2.95	1773	0.57	1796	1.87
B-n31-k5	672	672	0.00	672	0.00	672	0.00	672	0.00	672	0.00
B-n34-k5	788	788	0.00	788	0.00	788	0.00	788	0.00	788	0.00
B-n50-k8	1312	1335	1.75	1320	0.61	1319	0.53	1318	0.45	1314	0.15
B-n63-k10	1496	1532	2.41	1520	1.60	1514	1.20	1518	1.47	1514	1.20
B-n64-k9	861	892	3.60	880	2.21	874	1.51	862	0.12	861	0.00
B-n66-k9	1316	1348	2.43	1336	1.52	1330	1.06	1324	0.61	1322	0.45
B-n78-k10	1221	1241	1.64	1234	1.06	1228	0.57	1234	1.06	1235	1.15
P-n16-k8	450	450	0.00	450	0.00	450	0.00	450	0.00	450	0.00
P-n22-k2	216	216	0.00	216	0.00	216	0.00	216	0.00	216	0.00
P-n50-k7	554	569	2.71	561	1.26	559	0.90	557	0.54	554	0.00
P-n51-k10	741	761	2.70	752	1.48	747	0.81	750	1.21	744	0.40
P-n55-k10	694	708	2.02	696	0.29	696	0.29	698	0.58	695	0.14
P-n101-k4	681	735	7.93	731	7.34	722	6.02	685	0.59	714	4.85
+/-/=	-	15/0/5		14/0/6		11/1/8		11/3/6		-

, the proposed QEA achieves a performance that is either equal to or closer to the best-known solutions in the majority of benchmark instances. Notably, in instances such as A-n32-k5, B-n31-k5, and P-n50-k7, the QEA is capable of reaching or maintaining the current best-known solution, indicating the algorithm’s strong global search ability and effective convergence behavior. Moreover, across most B-class datasets and medium-scale P-class instances, QEA exhibits consistently low RD values. This outcome reflects the algorithm’s high level of robustness, as well as its ability to generalize across different problem characteristics.

However, in a few complex or large-scale instances, specifically A-n80-k10, B-n78-k10, and P-n101-k4, the QEA’s performance is slightly surpassed by certain comparison algorithms, most notably the CVRP-FA. This discrepancy may stem from the substantial increase in the search space and the structural complexity of large-scale CVRP instances. In such scenarios, the QEA’s Q-learning-driven operator scheduling mechanism might face difficulty in rapidly adapting to diverse and intricate local search landscapes, which can hinder the full exploitation of promising solution regions. This limitation underscores the need for more dynamic or hierarchical control strategies to maintain efficient exploration and exploitation under scaling complexity.

Despite these minor limitations, the QEA demonstrates strong overall competitiveness. Out of 20 benchmark instances, the QEA achieves a superior performance compared to LNSi in 15 instances, LNSa in 14, LNS-ACO in 11, and CVRP-FA in 11 cases. These statistics not only highlight the algorithm’s broad applicability but also reinforce its effectiveness across a wide range of CVRP scenarios.

Furthermore, the Wilcoxon signed-rank test results, as reported in

Table 4. Wilcoxon rank-sum test results between QEA and the other four algorithms.

Statistical Item	LNSi	LNSa	LNS-ACO	CVRP-FA
p-value	0.0050	0.0013	0.0120	0.1394
Significance (α = 0.05)	Significant	Significant	Significant	Not Significant

, reveal that the QEA’s performance advantages over the baseline methods are statistically significant at the 5% confidence level in most cases. This suggests that the observed performance gains are not due to random chance, but rather stem from the effectiveness of the algorithm’s design, including its adaptive operator selection strategy, insertion crossover mechanism, and diversified neighborhood search operators.

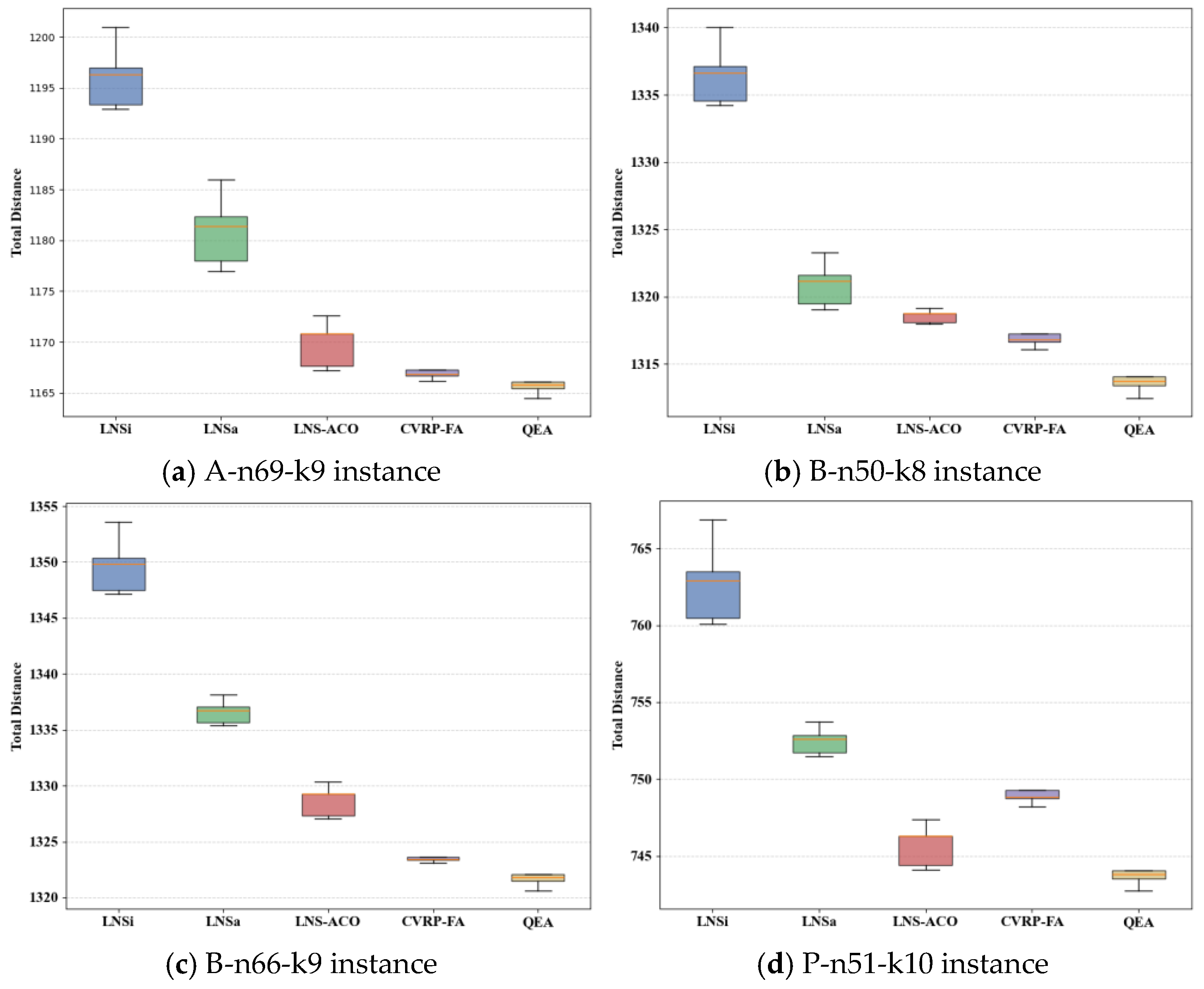
To better illustrate the stability and distribution of algorithmic performance, we additionally computed standard deviations from 10 independent runs and generated boxplots for representative benchmark instances. Figure 7 presents these boxplots, which visually depict the distribution of solution quality for the QEA and competing algorithms. The boxplots highlight the median performance, variability, and presence of outliers, providing further insights into the robustness and consistency of the compared methods. Overall, the QEA demonstrates relatively lower variance and fewer extreme deviations, confirming its stable search behavior across diverse test cases. Corresponding standard deviation values are also summarized in

Table 5. Algorithm performance comparison based on standard deviation metrics on selected CVRP instances. (The bold font indicates the value of the standard deviation for the algorithm that performs optimally across different instances).

Algorithm	A-n69-k9	B-n50-k8	B-n66-k9	P-n51-k10
LNSi	4.59	3.31	3.68	3.86
LNSa	4.39	2.09	1.35	1.10
LNS-ACO	2.53	0.53	1.55	1.51
CVRP-FA	1.29	1.34	0.67	1.26
QEA	1.06	1.07	0.97	0.87

to complement these graphical analyses.

In summary, the QEA demonstrates a superior search efficiency, robustness, and solution quality in small- and medium-sized CVRP instances. While it already competes favorably with advanced metaheuristic algorithms, its performance on large-scale problems can be further enhanced. Future work could explore the incorporation of dynamic depth adjustment mechanisms, hierarchical reinforcement learning frameworks, or hybrid memory-based strategies to strengthen the algorithm’s scalability and convergence in high-dimensional solution spaces.

4.5. Component Analysis

To comprehensively assess the contribution of each core component within the proposed QEA framework, four algorithmic variants were constructed and tested: QEA-RND, QEA-SR, QEA-wo-IC, and QEA-wo-NS. Each variant was designed to isolate and examine the impact of a specific module in the QEA.

To evaluate the effectiveness of the Q-learning-based adaptive operator selection strategy, two variants were developed. QEA-RND randomly selects neighborhood search operators without any learning guidance, serving as a baseline for non-adaptive operator scheduling. QEA-SR employs a deterministic strategy based on the historical success rate of each operator, defined as the frequency with which an operator improves the best solution in the current population.

In addition, QEA-wo-IC refers to the version in which the proposed insertion crossover operator is omitted, and QEA-wo-NS disables all neighborhood search operations. These ablation variants were designed to investigate the role of each operator class in driving search quality, convergence speed, and solution diversity. To ensure a fair comparison, all QEA variants share the same parameter configuration and initialization strategy as the original QEA, as described in Section 4.2.

Table 6. Comparisons between QEA variants based on hypervolume for component analysis across all benchmark instances.

Statistical Item	QEA-RND	QEA-SR	QEA-wo-IC	QEA-wo-NS
QEA is significantly better	14	12	16	16
Two algorithms are similar	6	8	4	4
QEA is significantly worse	0	0	0	0

summarizes the comparative performance of the QEA and its four variants across all benchmark instances. The Wilcoxon signed-rank test, conducted at a significance level of α = 0.05, reveals that the QEA significantly outperforms QEA-RND, QEA-SR, QEA-wo-IC, and QEA-wo-NS on 14, 12, 16, and 16 problem instances. In all test cases, the QEA demonstrates a superior or equal performance compared to its simplified counterparts.

These results clearly validate the necessity and effectiveness of each component integrated into the QEA. The adaptive operator selection mechanism enabled by Q-learning contributes to smarter decision-making during the search, while the insertion crossover and neighborhood search modules collectively enhance the algorithm’s ability to explore the solution space and refine high-quality routes. The consistent advantage over all variants confirms that the synergy among these components is critical to achieving a high performance and robustness when solving the Capacitated Vehicle Routing Problem.

5. Conclusions

This paper proposes a Q-learning-assisted evolutionary algorithm to solve the CVRP, called the QEA. Firstly, the QEA integrates a reinforcement learning mechanism into the evolutionary framework to adaptively schedule search operators according to the fitness of individuals, effectively overcoming the limitations of fixed operator strategies. Secondly, a novel insertion crossover operator is developed, which recombines complete route segments instead of individual nodes, thereby preserving feasible route structures and enhancing population diversity. Thirdly, the QEA designs three neighborhood search operators that target global exploration, convergence acceleration, and local refinement, respectively. These operators dynamically adjust their behaviors based on individual fitness to improve search efficiency. The experimental results show that the QEA achieves a competitive performance on standard CVRP benchmark instances and performs particularly well on small- and medium-scale problems.

Despite its promising performance, the proposed approach also has certain limitations. Specifically, the QEA shows a relatively slower convergence on large-scale and highly complex instances, indicating a limited search depth under certain configurations. Furthermore, the current Q-learning design relies on relatively simple state features, which may restrict the learning granularity. To address these issues, future work will explore more expressive representations of the state space and integrate deep reinforcement learning techniques to enable better generalization and scalability. We also plan to extend the QEA to handle multi-objective and dynamic variants of the CVRP, and we will investigate its applicability to other combinatorial optimization problems.