Feature Extractor for Damage Localization on Composite-Overwrapped Pressure Vessel Based on Signal Similarity Using Ultrasonic Guided Waves
Abstract
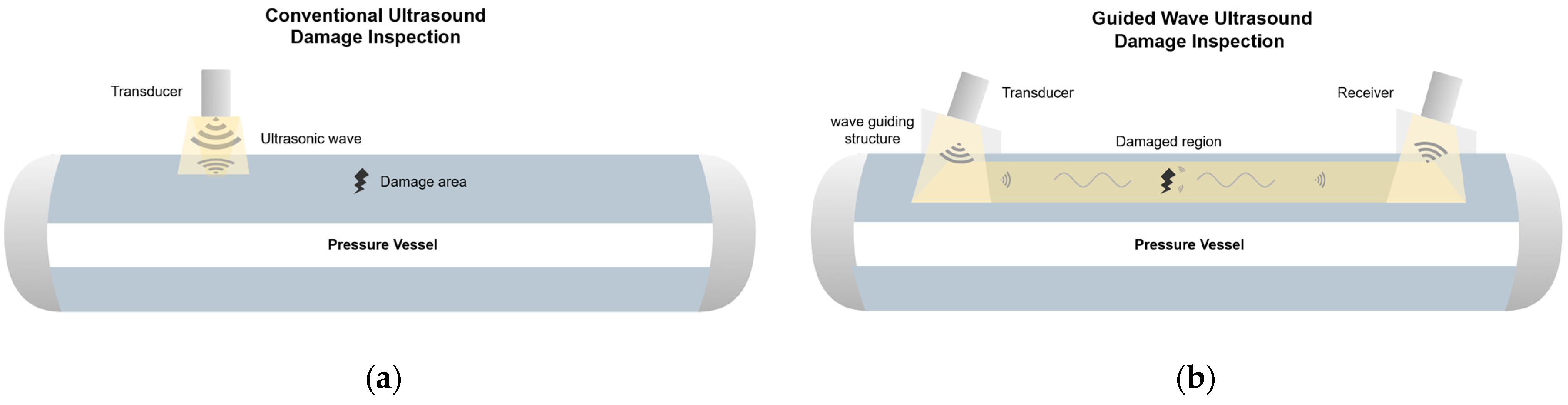
1. Introduction
2. Materials and Methods
2.1. Design of Experiments
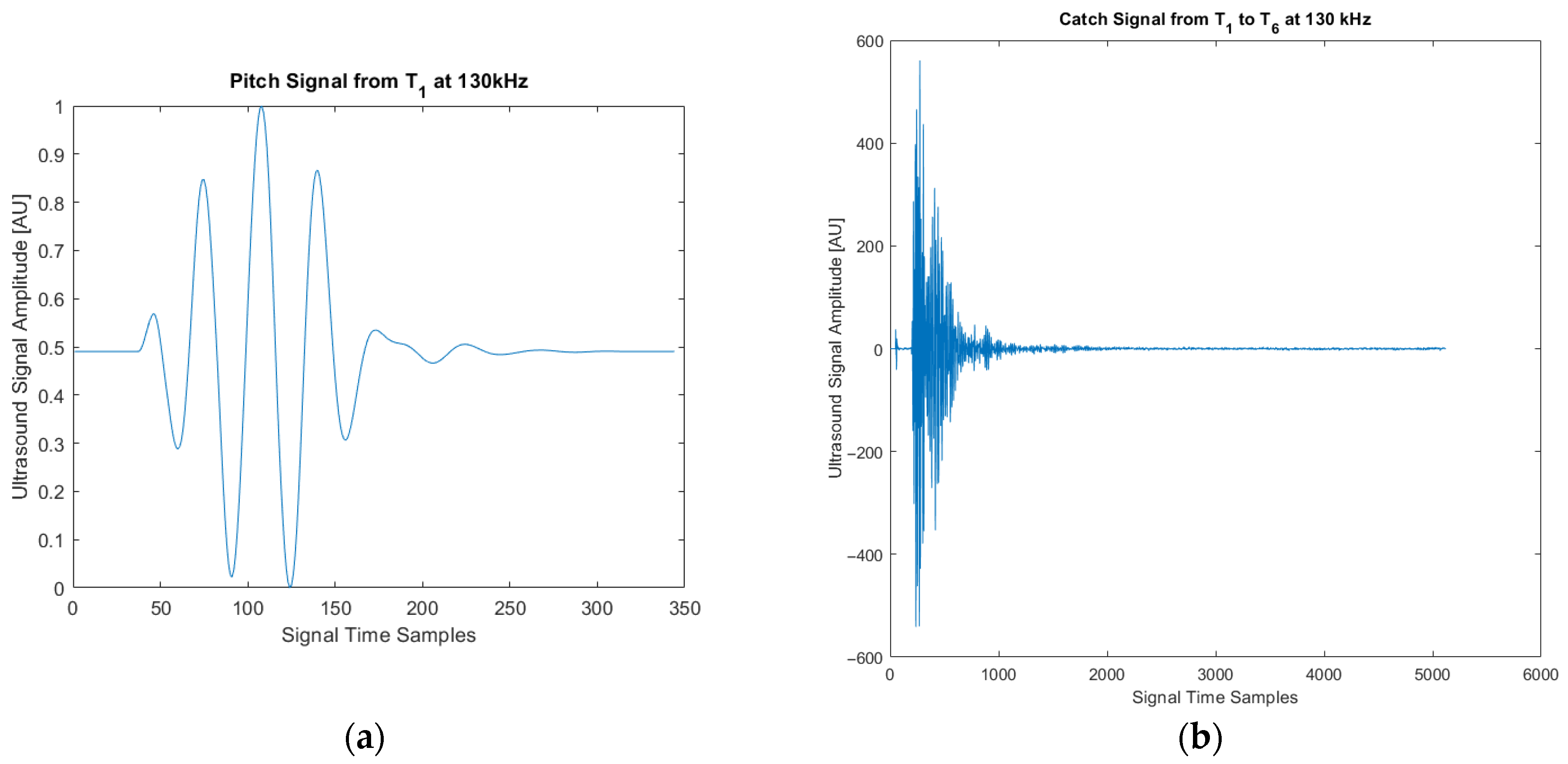
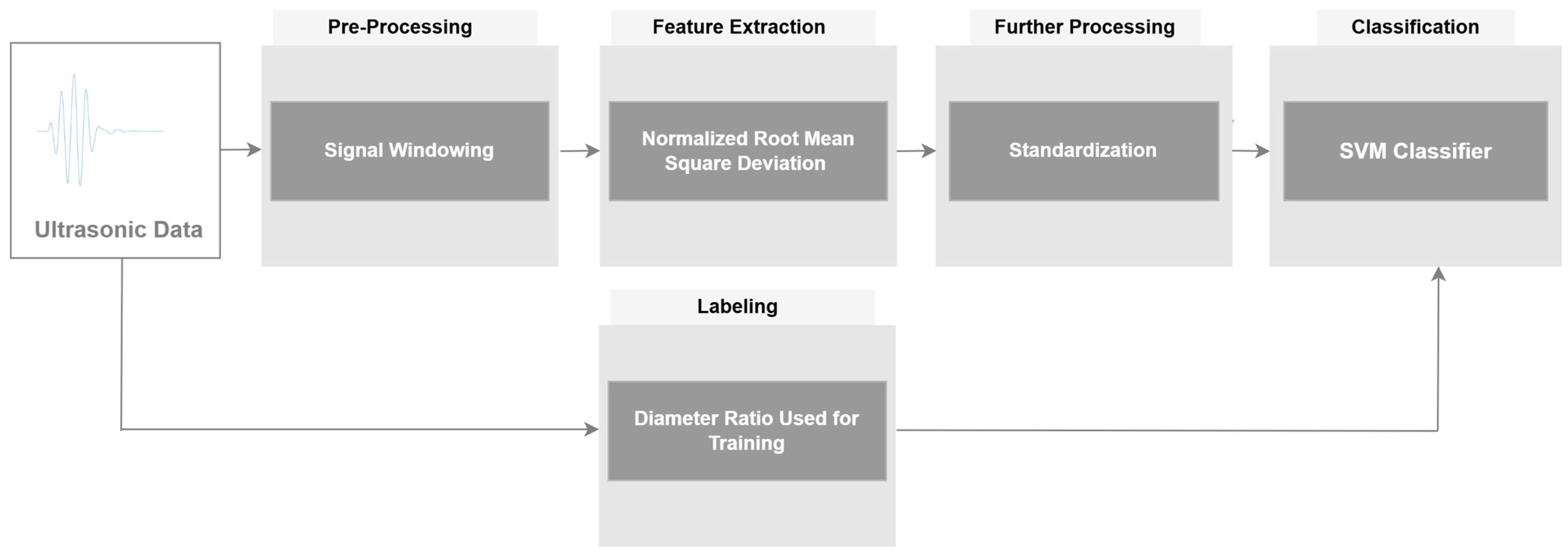
2.2. Signal Evaluation Methods

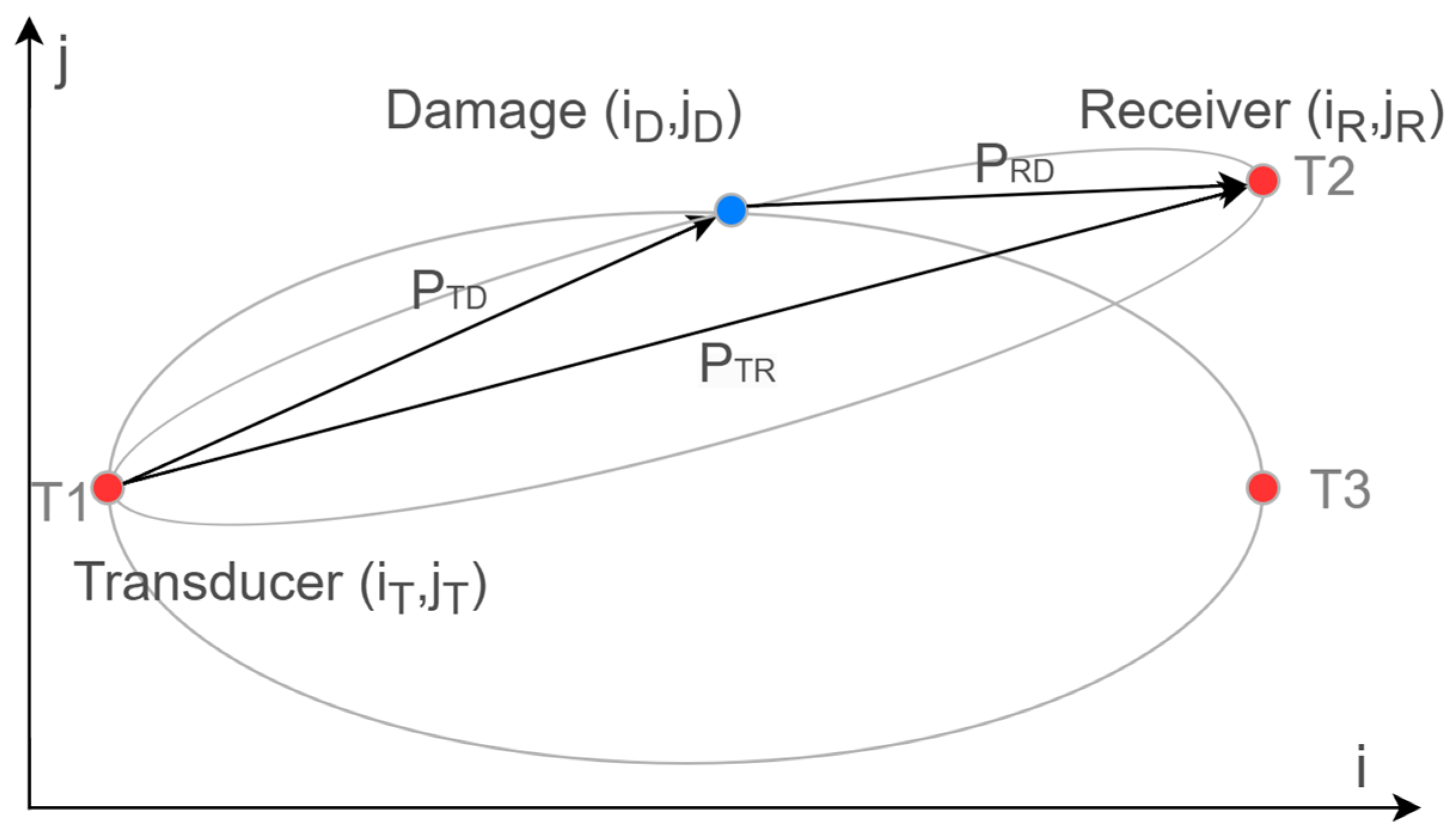
3. Results
3.1. Binary Classification Results
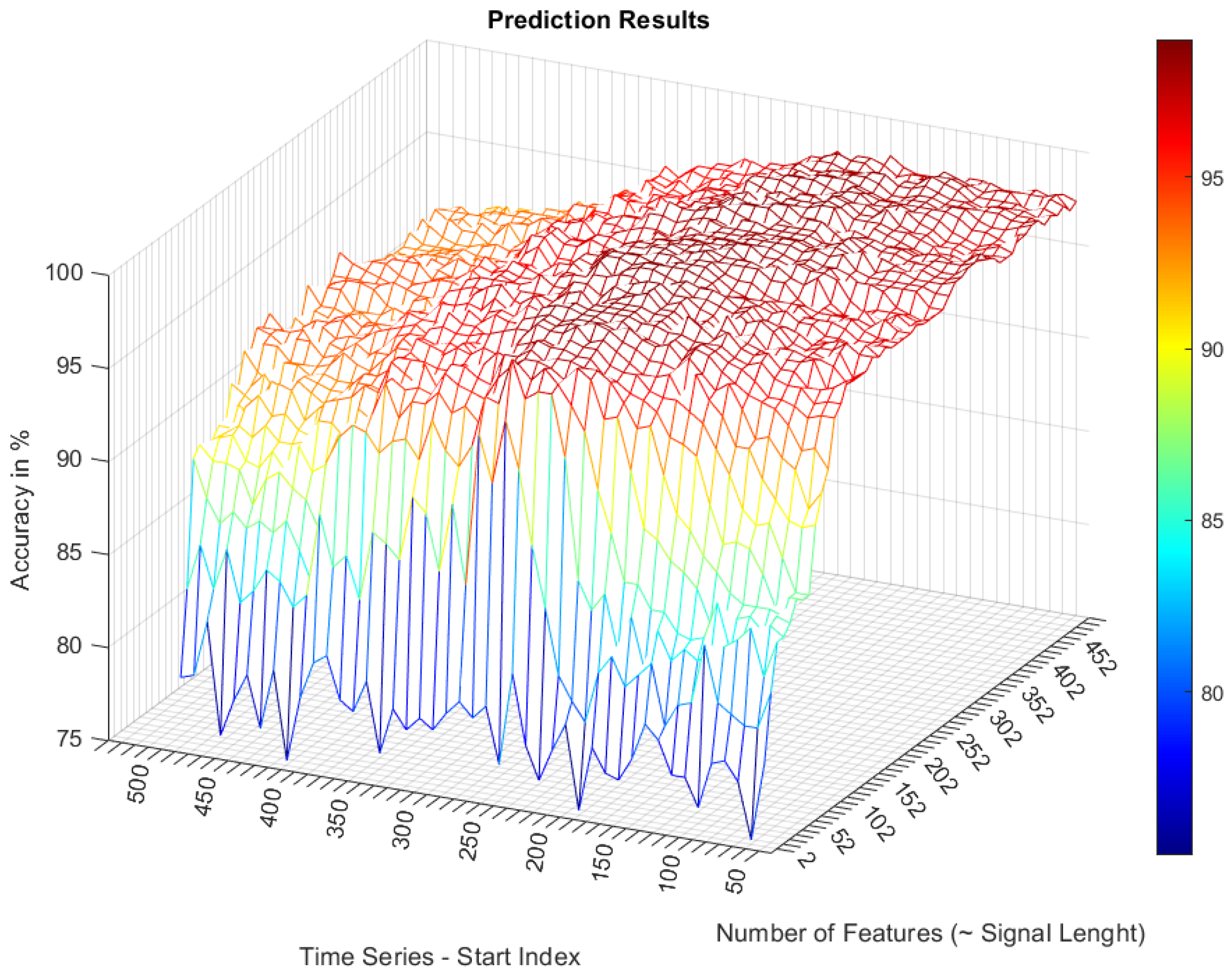
3.1.1. Windowing Selection
3.1.2. Best Diameter Ratio Cutoff
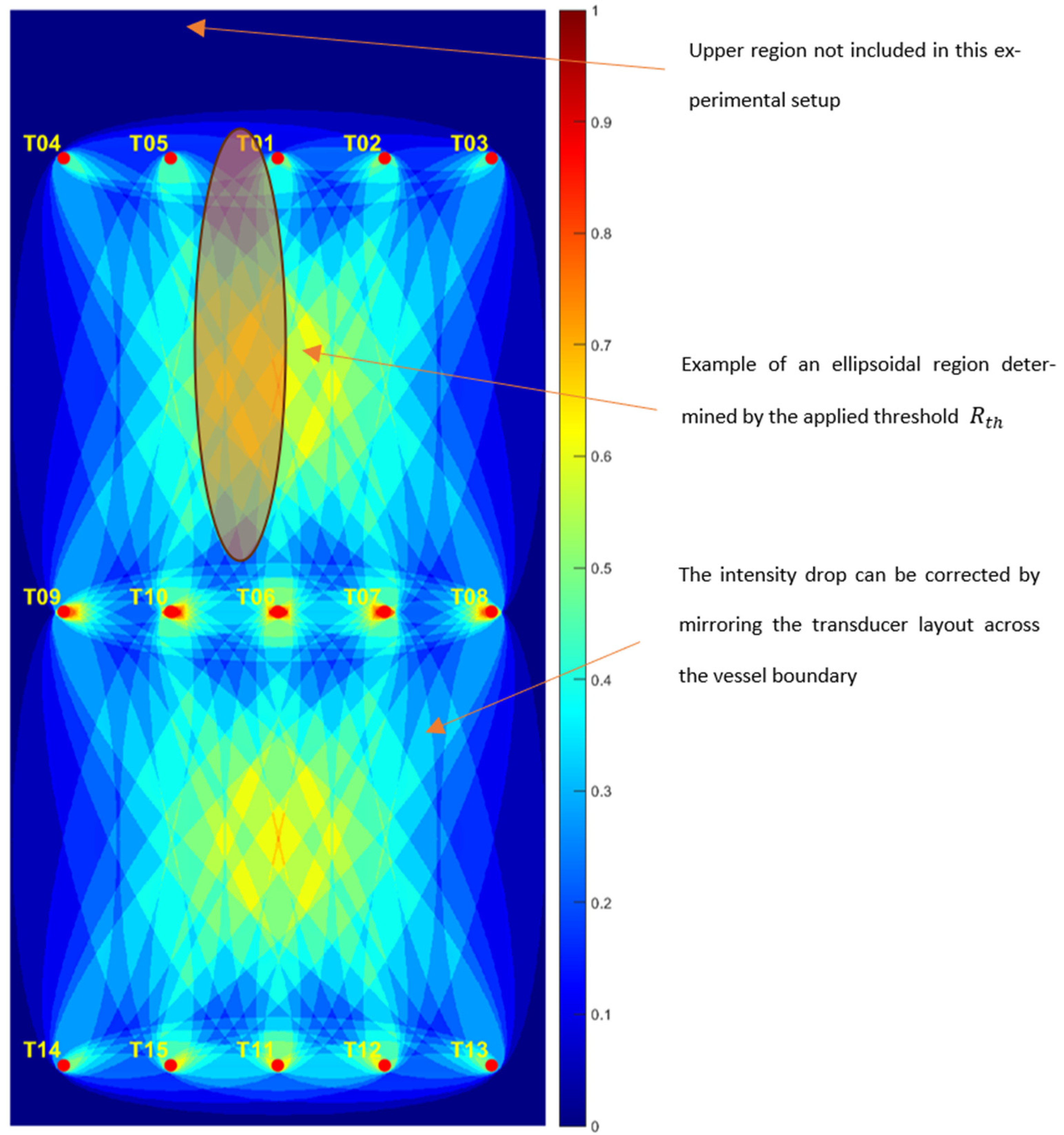
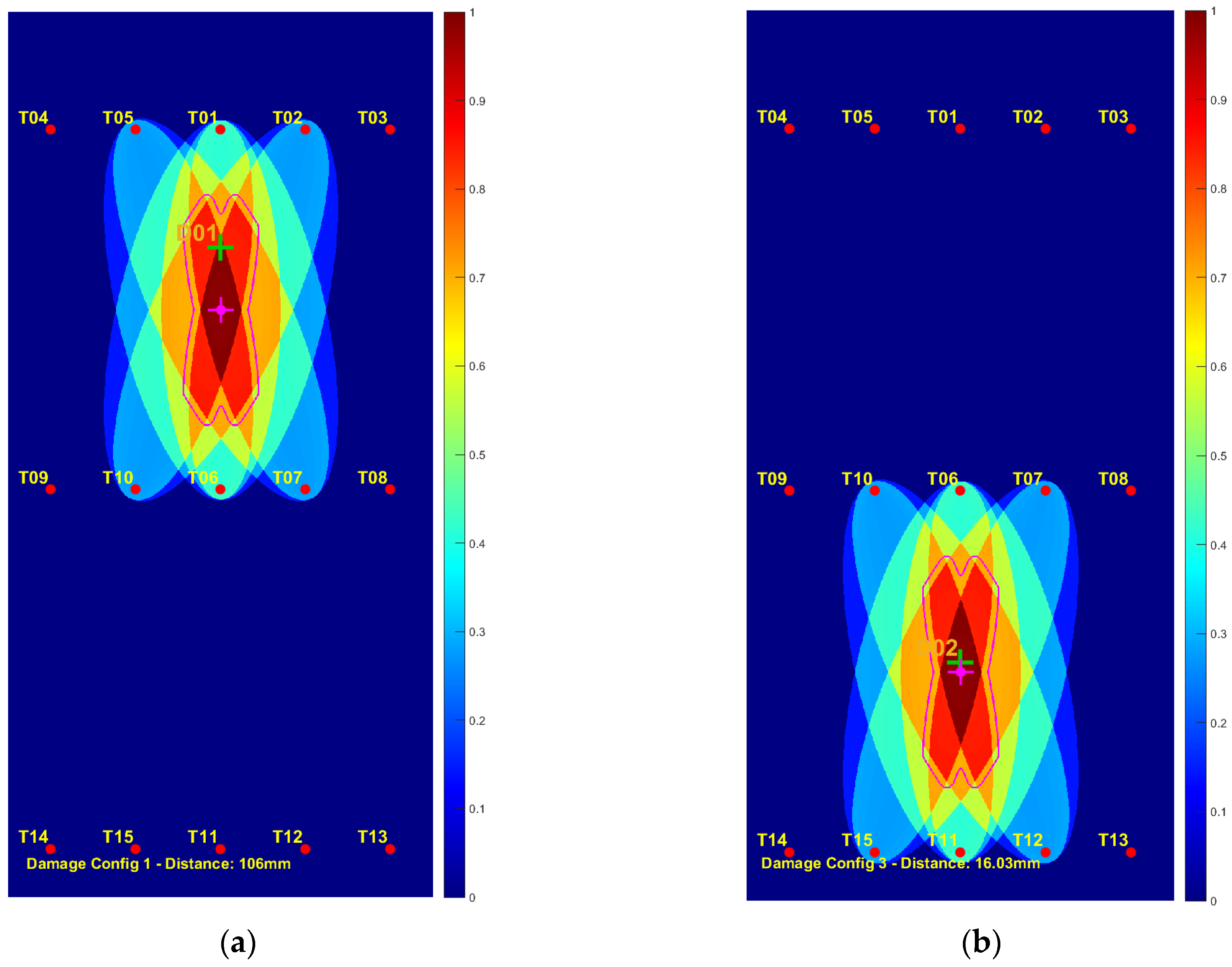
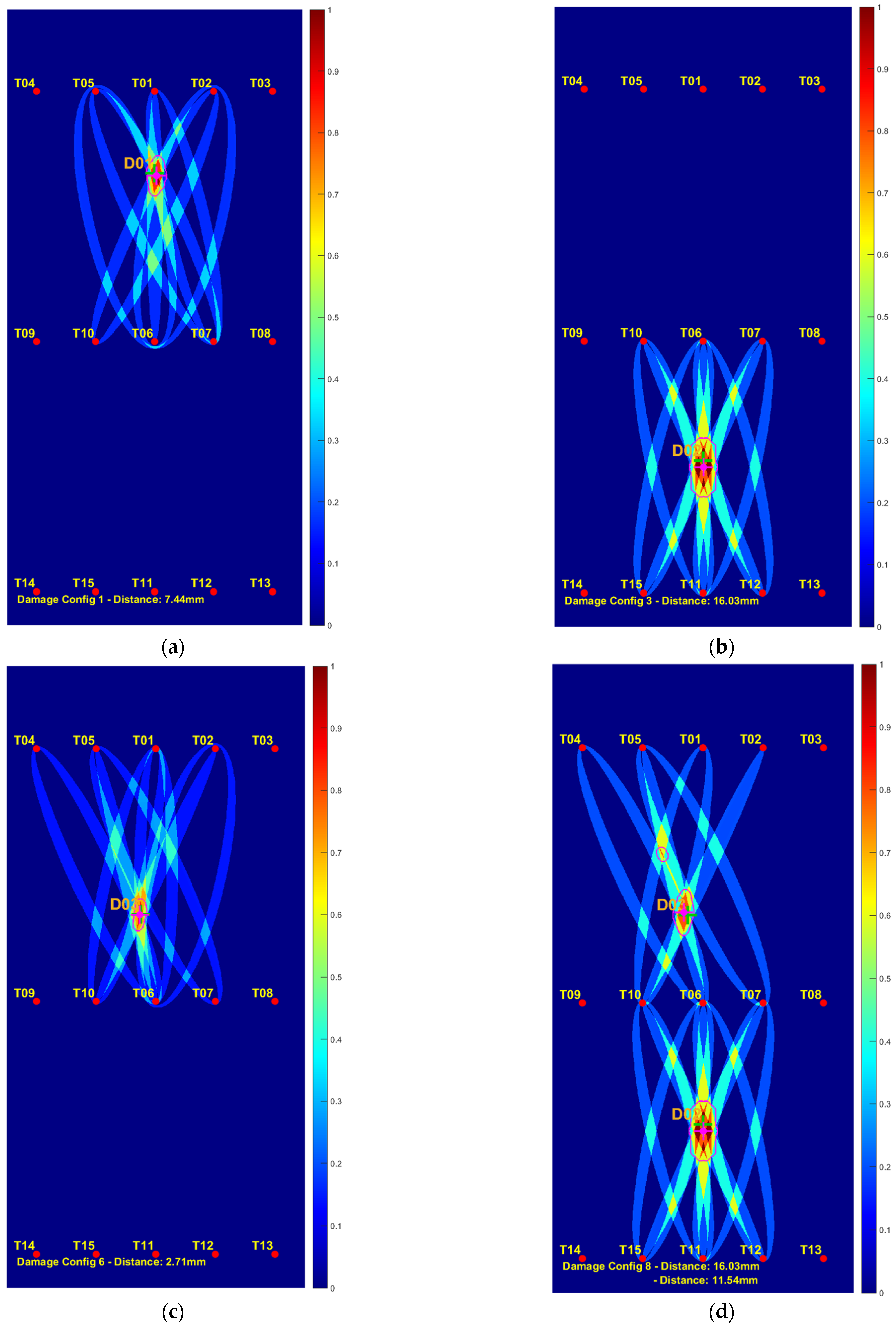
3.1.3. Visualization of Binarized Classification
3.2. Quantized Classification Results
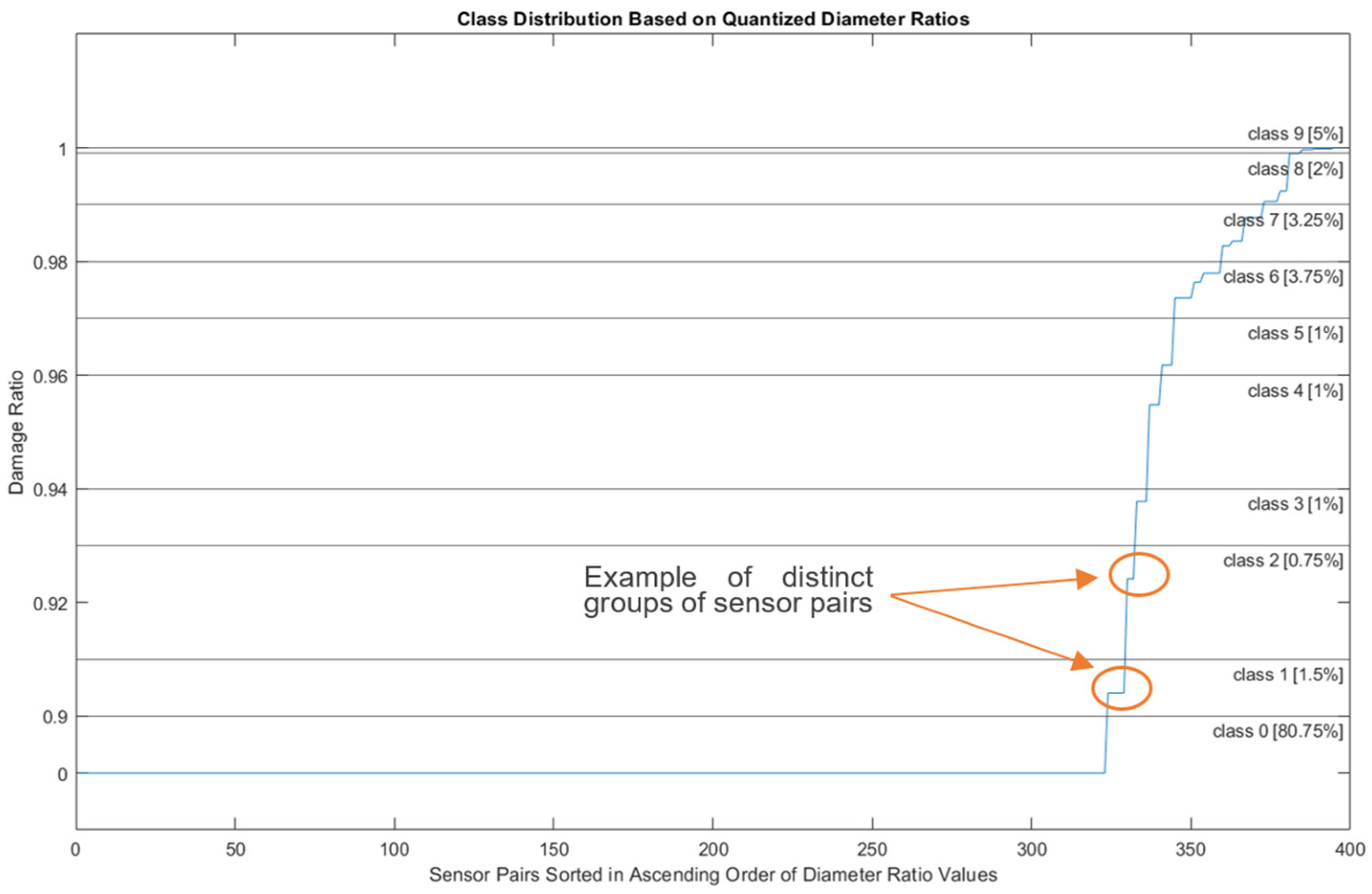
3.2.1. Diameter Ratio Quantization
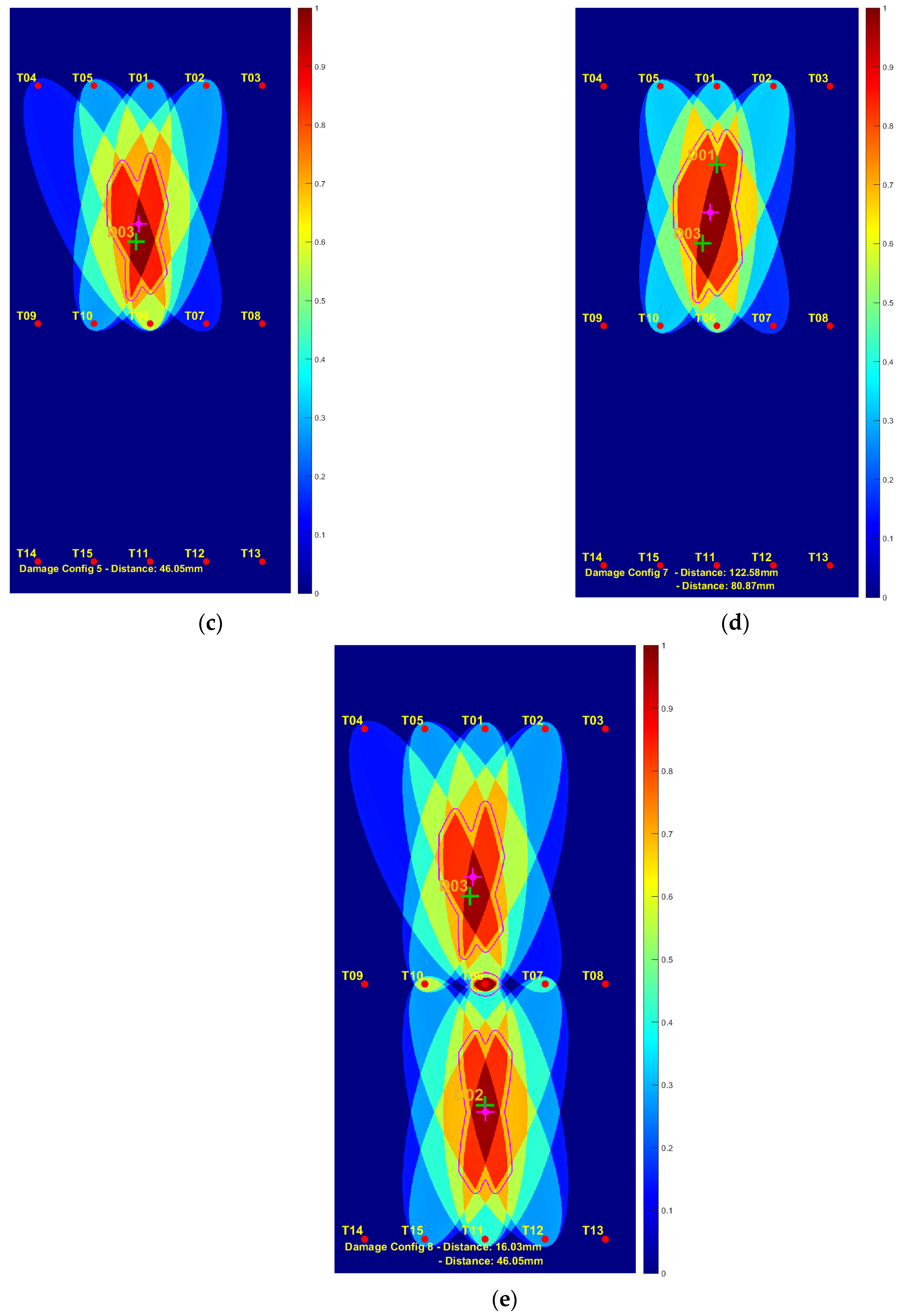
3.2.2. Results and Visualization of Quantized Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| COPV | Composite-Overwrapped Pressure Vessel |
| SHM | Structural Health Monitoring |
| UGW | Ultrasonic Guided Waves |
| ML | Machine Learning |
| RAPID | Reconstruction Algorithm For Probabilistic Inspection |
| FESC | Feature Extraction, Feature Selection and Classification |
| NRMSD | Normalized Root Mean Square Deviation |
| SVM | Support Vector Machine |
| PCA | Principle Component Analysis |
| LOGO-CV | Leave-One-Group-Out Cross-Validation |
References
- Zhai, S.; Zhou, S.; Chen, S.; Yang, B.; Li, Y. Novel Defect Location Method for Pressure Vessel by Using L (0, 2) Mode Guided Wave. J. Press. Vessel Technol. 2019, 141, 010910. [Google Scholar] [CrossRef]
- Zatar, W.A.; Nguyen, H.D.; Nghiem, H.M. Ultrasonic pitch and catch technique for non-destructive testing of reinforced concrete slabs. J. Infrastruct. Preserv. Resil. 2020, 1, 12. [Google Scholar] [CrossRef]
- Zima, B.; Moll, J. Theoretical and experimental analysis of guided wave propagation in plate-like structures with sinusoidal thickness variations. Arch. Civ. Mech. Eng. 2023, 23, 34. [Google Scholar] [CrossRef]
- El Moutaouakil, H.; Prager, J.; Schütze, A.; Schneider, T. Machine Learning Model Based on Signal Difference Features for Damage Localization on Hydrogen Pressure Vessel Using Ultrasonic Guided Waves. Sensoren Und Messsyst. 2024, 130–136. [Google Scholar] [CrossRef]
- Capineri, L.; Bulletti, A. Ultrasonic Guided-Waves Sensors and Integrated Structural Health Monitoring Systems for Im-pact Detection and Localization: A Review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Li, K.; Zhang, D.; Xu, W. Security Risks in Deep Learning Implementations. In Proceedings of the 2018 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 24 May 2018; pp. 123–128. [Google Scholar] [CrossRef]
- Goodarzi, P.; Schütze, A.; Schneider, T. Comparison of different ML methods concerning prediction quality, domain adaptation and robustness. Tech. Mess. 2022, 89, 224–239. [Google Scholar] [CrossRef]
- Tabatabaeipour, M.; Hettler, J.; Delrue, S.; Van Den Abeele, K. Reconstruction Algorithm for Probabilistic Inspection of Damage (RAPID) in Composites. In Proceedings of the 11th European Conference on Non-Destructive Testing (ECNDT 2014), Prague, Czech Republic, 6–11 October 2014; e-Journal of Nondestructive Testing. Volume 19. Available online: https://www.ndt.net/?id=16842 (accessed on 2 December 2024).
- Hua, J.; Lin, J.; Zeng, L. High-resolution damage detection based on local signal difference coefficient model. Struct. Health Monit. 2015, 14, 20–34. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W.; Shen, Y.; Liu, Y.; Jiang, S. Influence of the PZT Sensor Array Configuration on Lamb Wave Tomography Imaging with the RAPID Algorithm for Hole and Crack Detection. Sensors 2020, 20, 860. [Google Scholar] [CrossRef]
- Bai, L.; Velichko, A.; Drinkwater, B.W. Ultrasonic characterization of crack-like defects using scattering matrix similarity metrics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015, 62, 545–559. [Google Scholar] [CrossRef]
- El Moutaouakil, H.; Memmolo, V.; Schauer, J.; Payman, G.; Schneider, T.; Schütze, A. Feature Extraction Based On Signal Similarity for Damage Detection with Ultrasonic Guided Waves. In Proceedings of the IEEE I2MTC—International In-stru-mentation and Measurement Technology Conference, Chemnitz, Germany, 19–22 May 2025. [Google Scholar]
- Goodarzi, P.; Schütze, A.; Schneider, T. Domain shifts in industrial condition monitoring: A comparative analysis of au-tomated machine learning models. J. Sens. Sens. Syst. 2025, 14, 119–132. [Google Scholar] [CrossRef]
- El Moutaouakil, H.; Fuchs, C.; Savli, E.; Heimann, J.; Prager, J.; Moll, J.; Tschöke, K.; Márquez Reyes, O.; Schackmann, O.; Memmolo, V.; et al. Acquiring a Machine Learning Data Set for Structural Health Monitoring of Hydrogen Pressure Vessels at Operating Conditions using Guided Ultrasonic Waves. In Proceedings of the 10th European Workshop on Structural Health Monitoring (EWSHM 2024), Potsdam, Germany, 10–13 June 2024; Available online: https://www.ndt.net/?id=29754 (accessed on 10 December 2024).
- Schnur, C.; Goodarzi, P.; Lugovtsova, Y.; Bulling, J.; Prager, J.; Tschöke, K.; Moll, J.; Schütze, A.; Schneider, T. Towards Interpretable Machine Learning for Automated Damage Detection Based on Ultrasonic Guided Waves. Sensors 2022, 22, 406. [Google Scholar] [CrossRef]
- McKeon, P.; Yaacoubi, S.; Declercq, N.F.; Ramadan, S.; Yaacoubi, W.K. Baseline subtraction technique in the fre-quen-cy-wavenumber domain for high sensitivity damage detection. Ultrasonics 2014, 54, 592–603. [Google Scholar] [CrossRef]
- Masserey, B.; Raemy, C.; Fromme, P. High-frequency guided ultrasonic waves for hidden defect detection in multi-layered aircraft structures. Ultrasonics 2014, 54, 1720–1728. [Google Scholar] [CrossRef]
- Voß, J.; Wittkowski, R. On the shape-dependent propulsion of nano- and microparticles by traveling ultrasound waves. Nanoscale Adv. 2020, 2, 3890–3899. [Google Scholar] [CrossRef]
- Alleyne, D.N.; Cawley, P. The interaction of Lamb waves with defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Saadatmorad, M.; Jafari-Talookolaei, R.-A.; Pashaei, M.-H.; Khatir, S. Damage detection on rectangular laminated com-posite plates using wavelet based convolutional neural network technique. Compos. Struct. 2021, 278, 114656. [Google Scholar] [CrossRef]
- Dorst, T.; Schneider, T.; Eichstädt, S.; Schütze, A. Uncertainty-aware automated machine learning toolbox. Tech. Mess. 2023, 90, 141–153. [Google Scholar] [CrossRef]
- Spuler, M.; Sarasola-Sanz, A.; Birbaumer, N.; Rosenstiel, W.; Ramos-Murguialday, A. Comparing metrics to evaluate performance of regression methods for decoding of neural signals. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015. [Google Scholar] [CrossRef] [PubMed]
- Carrizosa, E.; Nogales-Gómez, A.; Romero Morales, D. Heuristic approaches for support vector machines with the ramp loss. Optim. Lett. 2013, 8, 1125–1135. [Google Scholar] [CrossRef]
- MathWorks: Support Vector Machines for Binary Classification. Version R2024a. Available online: http://www.mpi-forum.org (accessed on 15 May 2024).
- Guo, J.; Zeng, X.; Liu, Q.; Qing, X. Lamb Wave-Based Damage Localization and Quantification in Composites Using Probabilistic Imaging Algorithm and Statistical Method. Sensors 2022, 22, 4810. [Google Scholar] [CrossRef]
- Nerlikar, V.; Mesnil, O.; Miorelli, R.; D’Almeida, O. Damage detection with ultrasonic guided waves using machine learning and aggregated baselines. Struct. Health Monit. 2023, 23, 443–462. [Google Scholar] [CrossRef]
- Lawley, D.N. XIII. A Statistical Examination of the Centroid Method. Proc. R. Soc. Edinb. Sect. A Math. Phys. Sci. 1954, 64, 175–189. [Google Scholar] [CrossRef]
- Bayoumi, A.B.M.; Savli, E.; Mueller, I.; Tschöke, K.; Memmolo, V.; Moll, J. Reliability Assessment of Damage Localization Techniques for Guided Wave-based Structural Health Monitoring Systems in Composite Stiffened Structures. In Proceedings of the 11th European Workshop on Structural Health Monitoring (EWSHM 2024), Potsdam, Germany, 10–13 June 2024; Volume 29. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Y.; Zhao, H.; Yi, L.; Guo, T.; Li, A. Mixed Skewness Probability Modeling and Extreme Value Predicting for Physical System Input–Output Based on Full Bayesian Generalized Maximum-Likelihood Estimation. IEEE Trans. Instrum. Meas. 2023, 73, 2504516. [Google Scholar] [CrossRef]


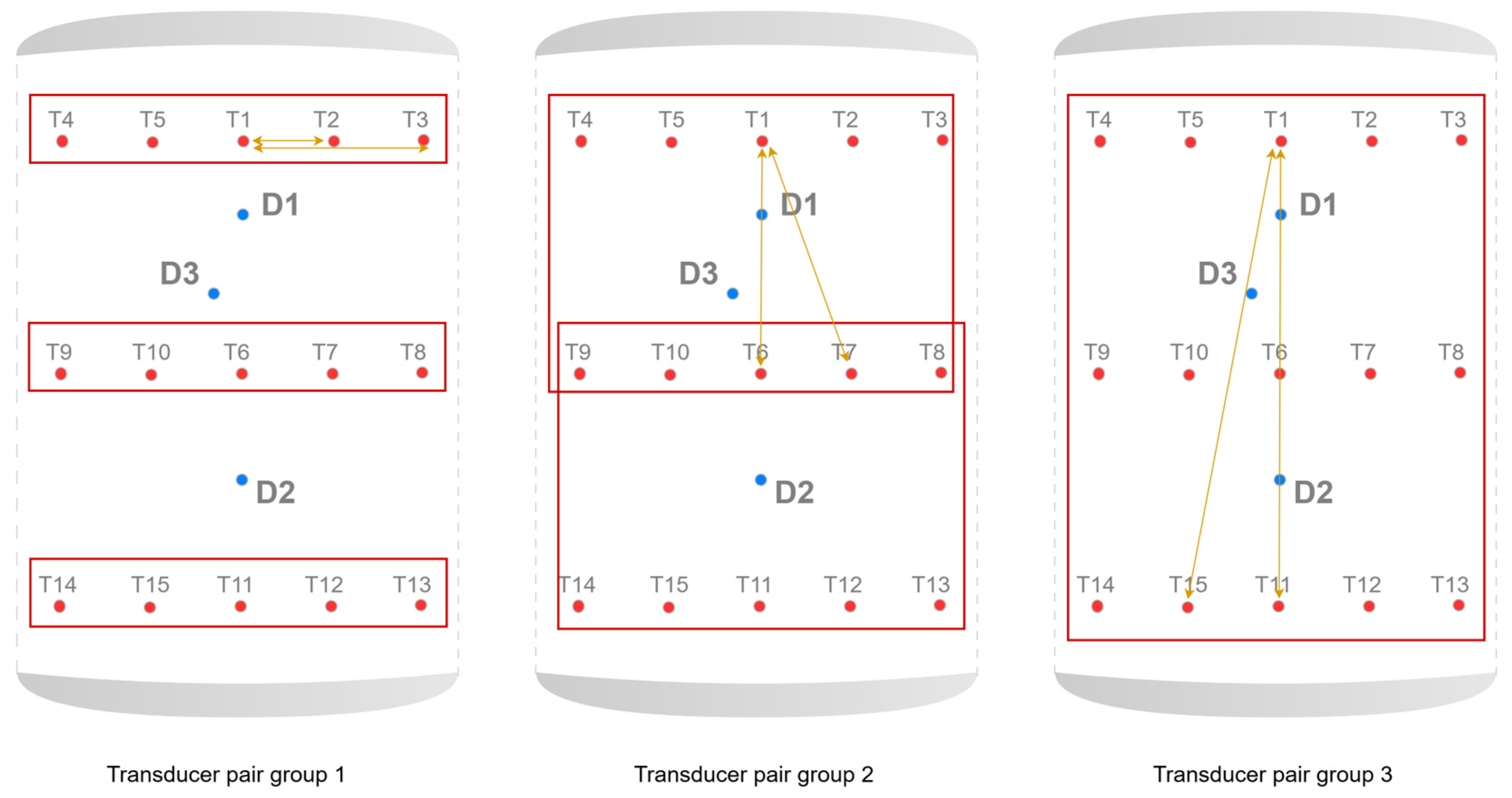
| Damage ID | Damage Configuration |
|---|---|
| 1 | 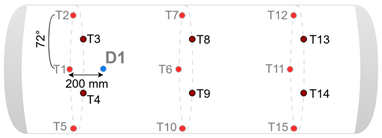 |
| 2 | 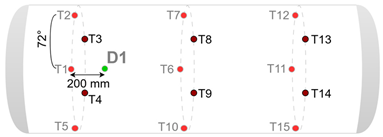 |
| 3 | 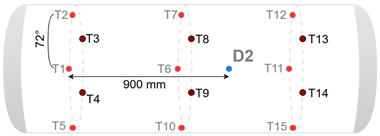 |
| 4 | 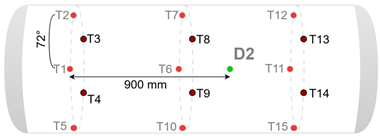 |
| 5 | 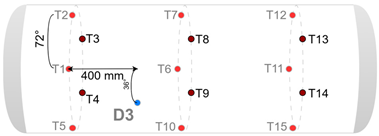 |
| 6 | 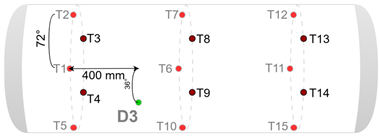 |
| 7 | 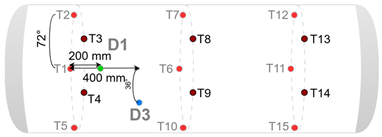 |
| 8 |  |
| Accuracy in % | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Damage Ratio | Damage Config 1 | Damage Config 2 | Damage Config 3 | Damage Config 4 | Damage Config 5 | Damage Config 6 | Damage Config 7 | Damage Config 8 | Average |
| 0.90 | 100 | 100 | 100 | 100 | 96 | 100 | 96 | 100 | 98.75 |
| 0.91 | 100 | 98 | 100 | 100 | 98 | 100 | 94 | 100 | 98.25 |
| 0.92 | 100 | 98 | 100 | 100 | 98 | 100 | 94 | 100 | 98.25 |
| 0.93 | 100 | 98 | 100 | 100 | 98 | 100 | 94 | 100 | 98.25 |
| 0.94 | 100 | 100 | 100 | 100 | 100 | 100 | 96 | 100 | 99.50 |
| 0.95 | 100 | 100 | 100 | 100 | 100 | 100 | 94 | 100 | 99.25 |
| 0.96 | 100 | 100 | 100 | 100 | 100 | 100 | 94 | 100 | 99.25 |
| 0.97 | 100 | 100 | 100 | 100 | 100 | 100 | 92 | 100 | 99.00 |
| 0.98 | 100 | 100 | 100 | 98 | 98 | 100 | 90 | 100 | 98.00 |
| 0.99 | 100 | 100 | 100 | 100 | 98 | 100 | 94 | 100 | 98.75 |
| Predicted Class | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ellipsoid Diameter Ratio Recovered | 0 | 0.90 | 0.925 | 0.945 | 0.95 | 0.96 | 0.975 | 0.98 | 0.985 | 0.999 |
| Accuracy in % | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Damage Ratio | Damage Config 1 | Damage Config 2 | Damage Config 3 | Damage Config 4 | Damage Config 5 | Damage Config 6 | Damage Config 7 | Damage Config 8 | Average | Localization Error in mm |
| 0.90 | 96 | 100 | 98 | 92 | 92 | 96 | 84 | 88 | 93.75 | 30 |
| 0.91 | 96 | 100 | 100 | 98 | 92 | 98 | 84 | 94 | 95.00 | 29 |
| 0.93 | 94 | 100 | 100 | 98 | 92 | 98 | 84 | 94 | 95.00 | 26 |
| 0.94 | 96 | 100 | 100 | 98 | 96 | 100 | 86 | 96 | 96.50 | 21 |
| 0.96 | 94 | 100 | 98 | 100 | 96 | 100 | 86 | 96 | 96.25 | 23 |
| 0.97 | 96 | 100 | 100 | 98 | 96 | 100 | 88 | 98 | 97.00 | 25 |
| 0.98 | 96 | 100 | 100 | 100 | 98 | 98 | 88 | 98 | 97.25 | 20 |
| 0.99 | 98 | 100 | 98 | 100 | 98 | 98 | 94 | 98 | 98.00 | 29 |
| 0.999 | 100 | 100 | 100 | 98 | 98 | 100 | 94 | 100 | 98.75 | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Moutaouakil, H.; Heimann, J.; Lozano, D.; Memmolo, V.; Schütze, A. Feature Extractor for Damage Localization on Composite-Overwrapped Pressure Vessel Based on Signal Similarity Using Ultrasonic Guided Waves. Appl. Sci. 2025, 15, 9288. https://doi.org/10.3390/app15179288
El Moutaouakil H, Heimann J, Lozano D, Memmolo V, Schütze A. Feature Extractor for Damage Localization on Composite-Overwrapped Pressure Vessel Based on Signal Similarity Using Ultrasonic Guided Waves. Applied Sciences. 2025; 15(17):9288. https://doi.org/10.3390/app15179288
Chicago/Turabian StyleEl Moutaouakil, Houssam, Jan Heimann, Daniel Lozano, Vittorio Memmolo, and Andreas Schütze. 2025. "Feature Extractor for Damage Localization on Composite-Overwrapped Pressure Vessel Based on Signal Similarity Using Ultrasonic Guided Waves" Applied Sciences 15, no. 17: 9288. https://doi.org/10.3390/app15179288
APA StyleEl Moutaouakil, H., Heimann, J., Lozano, D., Memmolo, V., & Schütze, A. (2025). Feature Extractor for Damage Localization on Composite-Overwrapped Pressure Vessel Based on Signal Similarity Using Ultrasonic Guided Waves. Applied Sciences, 15(17), 9288. https://doi.org/10.3390/app15179288







