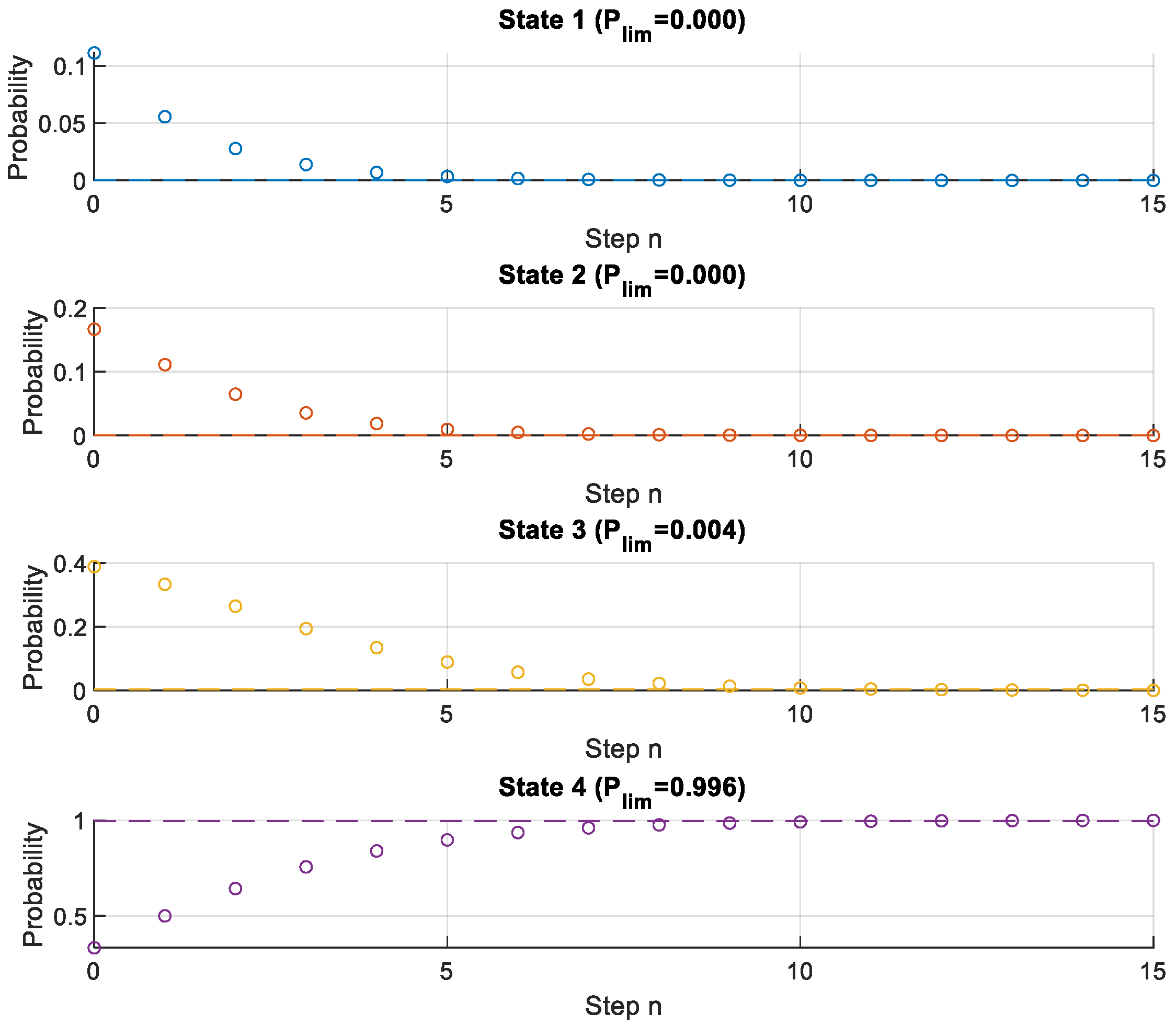1. Introduction
Effective lifecycle management of buildings and structural components has increasingly become a priority in contemporary construction practice. Decisions related to maintenance, refurbishment, and replacement directly impact the economic efficiency, safety, and sustainability of constructed assets. To facilitate informed decision-making, accurate prediction of building performance and degradation over time is essential. However, uncertainty in environmental conditions, material properties, and operational loads complicates precise forecasting of deterioration processes. Thus, there is a growing demand for reliable probabilistic models that can effectively capture the inherent randomness in the lifecycle behavior of buildings.
One promising approach for addressing this challenge involves the application of Markov chain models, which offer a structured method for modeling state transitions over discrete time intervals. Markov chains allow researchers and asset managers to quantify the probability of transitions between various condition states—from initial, optimal conditions to intermediate stages of progressive deterioration, ultimately culminating in structural failure. The simplicity and flexibility of these probabilistic models make them particularly useful for lifecycle analysis, enabling consistent incorporation of empirical inspection data, expert judgment, or theoretical predictions.
Therefore, this paper aims to demonstrate a practical application of discrete-time Markov chains for predicting the service life of buildings and their structural components. The analysis emphasizes how transition probabilities and associated metrics such as absorption times and fundamental matrices can inform proactive lifecycle management strategies. Furthermore, simulation results and graphical visualizations included in this study clearly illustrate deterioration patterns, underscoring the inevitability of structural failure in the absence of appropriate maintenance interventions. Ultimately, this approach provides building owners, facility managers, and engineers with robust analytical tools to optimize the timing of interventions, allocate resources efficiently, and significantly enhance the sustainability of constructed assets.
2. Literature Review
Effective lifecycle management of constructed assets has gained significant attention, driven by the increasing emphasis on sustainability, economic optimization, and enhanced reliability of infrastructure systems [
1,
2]. Numerous studies have focused on methodologies aimed at predicting the service life of buildings and structural components [
3,
4,
5], incorporating both deterministic and probabilistic frameworks [
6,
7]. Traditional deterministic approaches generally involve defining degradation pathways based on standardized conditions and typical environmental exposures but often neglect inherent uncertainties related to materials, environmental variability, and operational demands [
2,
8].
Recently, lifecycle planning methodologies have increasingly shifted towards probabilistic modeling to better account for uncertainties in predicting building degradation [
9,
10]. Within this context, Markov chain modeling has emerged as a robust and widely accepted probabilistic method due to its mathematical clarity and adaptability in capturing state-dependent deterioration processes [
11,
12]. Specifically, discrete-time Markov chains have proven effective in modeling progressive deterioration, enabling quantifiable predictions of asset conditions as they evolve through discrete performance states [
6,
13].
In parallel, recent studies have explored hybrid approaches that combine Markov modeling with deep learning techniques to improve predictive capability and interpretability [
14,
15,
16]. Physics-guided deep Markov models integrate physical state space structure with deep generative networks to enable accurate learning of nonlinear dynamical systems under uncertainty [
14]. Hybrid hidden Markov LSTM architectures have been applied to short-term traffic flow prediction, leveraging regime switching dynamics together with sequence learning to capture temporal dependencies more effectively [
15]. Deep learning methods have also been developed to decompose macromolecules into independent Markovian domains, providing a data-driven way to extract interpretable kinetic models from high-dimensional molecular simulations [
16]. These advances illustrate the potential of combining probabilistic structure with neural architectures, a direction that could be considered in future extensions of the fuzzy Markov framework presented in this study.
Fundamentally, Markov chain models rely on the Markovian assumption, stating that future state transitions depend solely on the current state, independent of previous system states [
17]. While this assumption simplifies mathematical analysis, its validity in structural deterioration modeling has been widely supported by empirical observations and monitoring data, confirming its practical utility in various engineering applications [
18,
19]. Successful implementations have been extensively documented, particularly in infrastructure management, including bridge deterioration modeling [
19,
20], pavement condition assessments [
11,
18,
21], and building component lifecycle analysis [
10,
22].
To further improve the predictive accuracy of Markov models, several studies have integrated expert judgment, inspection data, and Bayesian updating techniques into transition probability estimation [
13,
23]. Additionally, combining Markov chain modeling with Monte Carlo simulations and optimization methods has provided advanced frameworks for asset management decision-making [
10,
18]. Although such approaches are not implemented in this study, they represent valuable extensions for future research aiming to enhance predictive accuracy and decision support. Despite significant advancements, the adoption and demonstration of Markov chain methodologies specifically for the lifecycle management of buildings remain relatively limited, highlighting the need for further practical investigations [
7,
9].
Therefore, this study addresses this gap by illustrating how discrete-time Markov chain models can be effectively employed to support building lifecycle management decisions. Such models enable asset managers and engineers to better predict deterioration, optimize maintenance planning, and enhance the sustainability and economic efficiency of constructed assets.
3. Service Life Planning and Markov Chain Modeling
Effective service life planning for buildings and structural components requires accurate modeling of deterioration processes and prediction of their long-term performance. Given inherent uncertainties related to material characteristics, environmental conditions, and operational usage, probabilistic modeling techniques typically provide more realistic predictions compared to deterministic methods. One particularly effective and transparent probabilistic method for representing the progression of structural deterioration is discrete-time Markov chain modeling.
A discrete-time Markov chain describes stochastic transitions between discrete condition states, operating under the core assumption known as the Markovian property. This property states that the probability of transitioning to any future state depends solely on the current state, without regard to prior states or events. Formally, the Markovian property can be expressed mathematically using the following conditional probability relationship:
Here, denotes the state of the system at discrete time step .
The state transitions within a Markov chain are captured by a transition probability matrix
, whose elements represent the probability of moving from one state to another in a single time step. The transition matrix is defined as follows:
The elements of the transition matrix satisfy the fundamental condition that the sum of transition probabilities from any given state equals one:
To initiate the analysis, an initial state probability distribution is established as the vector
:
The probability distribution at any future time step
can then be computed iteratively from the initial distribution and the transition probability matrix:
Within Markov chain theory, states are classified as either transient or absorbing. Absorbing states are defined as states from which no further transitions to other states occur, mathematically represented by the following:
In Markov chains that contain absorbing states, the transition matrix can be partitioned into submatrices that separately describe transient and absorbing states:
Here, describes transition probabilities between transient states; denotes transition probabilities from transient states to absorbing states; and is the identity matrix representing the absorbing states.
To assess transitions among transient states and to compute the expected duration before absorption, the fundamental matrix
is introduced and defined as follows:
Each entry
of the fundamental matrix
represents the expected number of visits to transient state
, given that the chain started from transient state
, prior to eventual absorption. The expected time to absorption, starting from transient state
, is then calculated using the sum:
Over an extended number of steps, a Markov chain typically converges toward a stationary (steady-state) distribution, represented by the vector
. This stationary distribution describes the long-term behavior of state probabilities and satisfies the equilibrium condition:
Practically, the stationary distribution
can be computed through eigenvector decomposition of the transition matrix:
The stationary distribution corresponds to the eigenvector associated with an eigenvalue equal to one, normalized so that its components sum to unity.
The application of Markov chain modeling in the context of service life planning for buildings and structural components enables probabilistic forecasting of deterioration, providing valuable quantitative insight that can significantly improve maintenance scheduling, resource allocation, and asset sustainability decisions.
4. Application to Service Life Planning
The empirical data used in this study to analyze state transitions of structural deterioration were derived from systematic inspections and expert evaluations of building conditions over consecutive observation periods. These observations were structured into discrete condition states, categorizing structural integrity from optimal condition to complete failure.
In practice, evaluation criteria are used with varying degrees of detail resulting from the percentage wear of the element [
10,
24,
25,
26,
27,
28,
29].
In the present case, a four-point grading system was applied:
State 1: Very good, corresponding to element wear 0–15%;
State 2: Medium, corresponding to element wear 16–30%;
State 3: Satisfactory, corresponding to element wear 31–50%;
State 4: Poor, corresponding to element wear 51–70%.
It is clear that above 70% wear an additional criterion will correspond to a critical condition qualifying the object for demolition. This threshold reflects expert-based assessment practices used in Poland during technical inspections and aligns with recommendations found in national guidelines on building diagnostics and refurbishment planning [
24,
25,
26]. The following verbal evaluation criteria can be assigned to the various states of wear and tear:
The building element (or type of construction, finishing, or equipment) is well maintained, maintained and shows no wear and damage. The characteristics and properties of the incorporated materials meet the requirements of the standard.
The building element is properly maintained. It is expedient to carry out current repairs consisting of minor repairs, additions, maintenance, and waterproofing.
There are minor damages and cavities in the building elements that do not threaten public safety. Partial major renovation is advisable.
There is significant damage, cavities in the building elements. Features and properties of built-in materials are of a reduced class. Comprehensive major renovation or replacement required.
Table 1 presents the evaluation results showing the condition states assigned to each structural and building element during inspection periods in 2020 and 2025. These data are essential for determining observed transitions between condition states and subsequently constructing the frequency (count) matrix [
30]. The frequency matrix serves as the foundation from which the transition probability matrix is derived by normalizing each row, reflecting realistic deterioration patterns and informing probabilistic predictions of structural performance and service life.
In this study, one step in the discrete-time Markov chain corresponds to the period between two consecutive technical inspections of the building. Based on the available dataset, this interval is five years and is used consistently throughout the discrete and continuous model analyses.
The MATLAB 2024b code provided clearly illustrates these theoretical concepts, offering a numerical framework for practical implementation of Markovian analysis in lifecycle modeling of constructed assets. In the subsequent section, we present numerical results obtained from computational simulations performed using an original program developed in MATLAB 2024b with the Econometrics Toolbox.
5. Analysis of Markov Chain Results
The Markov chain analysis performed in this study provides detailed probabilistic insights into the deterioration process of buildings, explicitly capturing the progression of asset conditions over time. Initially, the process involved defining a frequency matrix, often referred to as the count matrix , which represents observed or estimated transitions between discrete condition states of the structure.
The empirical data regarding observed transitions between discrete states of structural deterioration, collected from inspections or expert evaluations, is presented in
Table 1. Based on these observations, the frequency (count) matrix
is constructed as follows:
From this count matrix, a transition probability matrix
was computed by normalizing each row, resulting in the following probability representation:
Each entry in this matrix represents the probability of transitioning from state to state in a single discrete time step. For instance, the probability of remaining in State 1 is 50%, whereas the probability of deteriorating from State 2 to State 3 is 67%. Importantly, State 4 is identified as an absorbing state since no transitions occur from this state to any other state.
An initial state probability distribution
was established based on the count data, and is represented by the following:
After one discrete time step, the updated state probability distribution
was computed using the relation
, yielding the following:
This shift clearly illustrates the progression of structural degradation, as probabilities gradually move toward more deteriorated states.
Further analysis involved identifying transient and absorbing states, which is critical for determining the expected remaining service life of the structure. The fundamental matrix
was computed by isolating transient states (States 1 to 3), using Equation (8):
Each element in this fundamental matrix indicates the expected number of visits to transient state , given that the system started in transient state before eventually reaching absorption. Utilizing the fundamental matrix, the average times to reach the absorbing state from each transient state were determined as follows:
Starting from State 1: 5.8333 steps;
Starting from State 2: 3.8333 steps;
Starting from State 3: 2.3333 steps.
These results highlight the necessity of early maintenance interventions, as structures initially in healthier states have significantly longer expected lifetimes before reaching failure. Although the presented average times to absorption provide useful insight into the expected progression of deterioration, they are based on a relatively small dataset. Consequently, these estimates are subject to sampling variability, and confidence intervals could not be reliably determined within the scope of this study.
The long-term behavior of the Markov chain was further explored using multistep simulations. After an extended number of time steps (e.g., 15 steps), the probability distribution
was observed to converge almost entirely to the absorbing state, indicating inevitable structural failure:
The eigenvalue analysis also reinforced this finding, showing one eigenvalue equal to one, a characteristic of absorbing Markov chains. The stationary distribution derived from eigen decomposition methods confirmed the inevitability of the absorbing state, represented by the vector:
In practical terms, the certainty of eventually reaching the absorbing state highlights the need for timely inspections and preventive interventions. For example, if the average time to absorption suggests a remaining service life of about 4–6 inspection cycles, planning inspections more frequently would help detect accelerated deterioration early and allow corrective actions before failure.
These numerical findings were complemented by graphical interpretations, which visually demonstrated the rapid convergence of probabilities toward the absorbing state, further supporting the analysis results.
Overall, the Markov chain approach demonstrated in this study provides an effective and rigorous framework for quantifying and predicting the deterioration process of buildings. Such probabilistic modeling is instrumental in supporting lifecycle management decisions, particularly in planning optimal timing for maintenance and refurbishment interventions, ultimately contributing to improved structural sustainability and resource efficiency.
6. Graphical Results from the Markov Chain Model
The graphical outcomes obtained through simulation provide valuable insight into the Markov chain dynamics, clearly illustrating the probabilistic evolution of structural states and long-term performance predictions for constructed assets.
Figure 1 depicts the evolution of state probabilities across 15 discrete time steps, demonstrating how structural conditions transition over the lifecycle. Initially, State 1, representing an optimal or “very good” structural condition, exhibits the highest probability. However, this probability rapidly declines toward zero within the first five steps, signifying that remaining indefinitely in a pristine condition is improbable without maintenance interventions.
In contrast, the probability associated with State 4—the absorbing failure state—increases consistently over time, approaching nearly unity (~0.996) after 15 steps. The dashed line denoting the limiting probability reinforces the inevitability of eventual structural failure if no corrective actions are implemented.
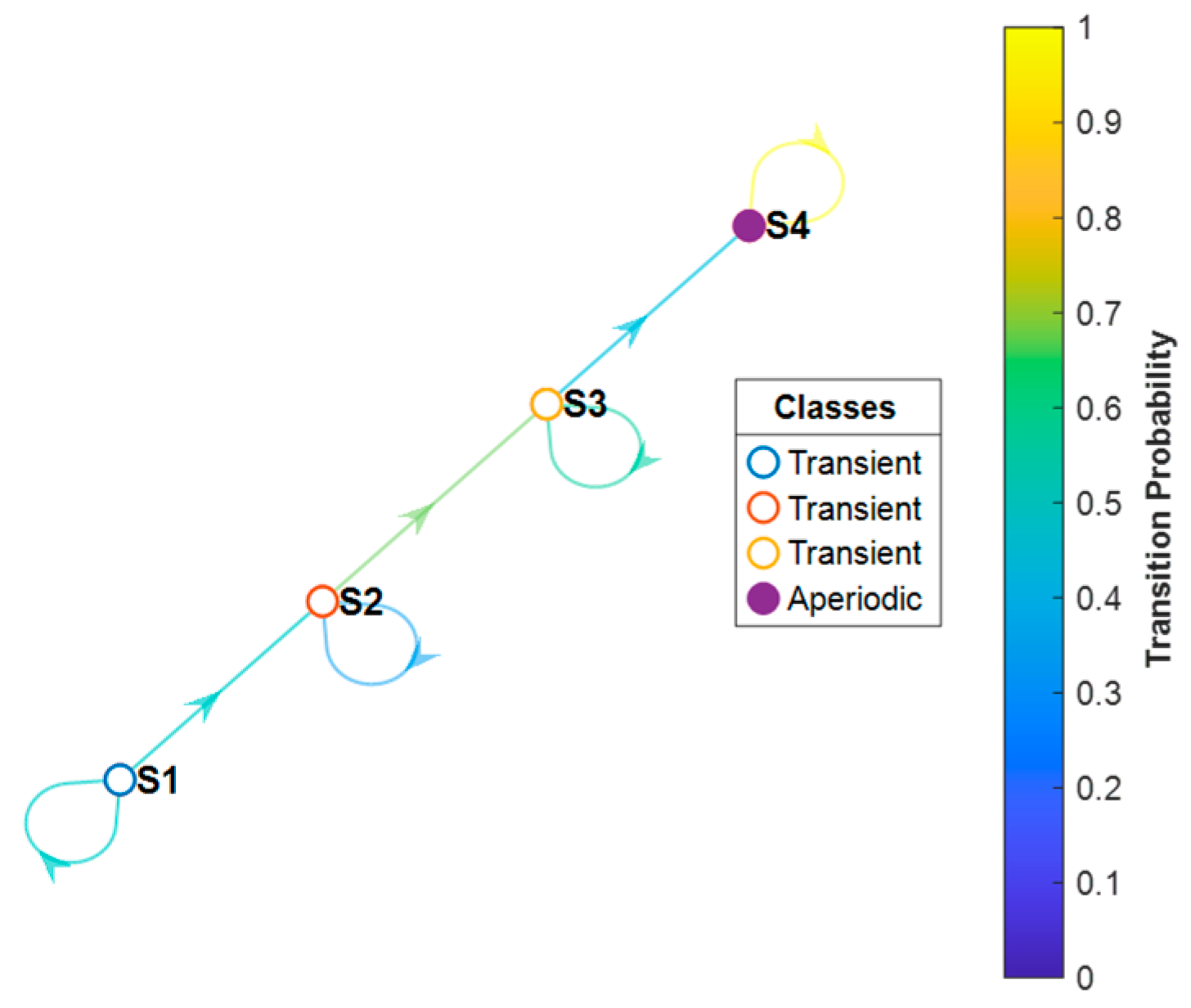
Complementing these temporal dynamics,
Figure 2 presents a clear visualization of the Markov chain structure in the form of a state transition graph. Here, each state is depicted as a node, and the directional edges illustrate transition pathways. The three initial states (S1, S2, and S3) are categorized as transient, implying eventual progression toward absorption. State S4, distinctly identified as an absorbing, aperiodic state, is a terminal condition from which the structure does not recover. The color gradient employed, spanning from blue (low probability) to yellow (high probability), graphically conveys transition probabilities, facilitating intuitive understanding. Arrows between states confirm the linear progression from initial optimal conditions toward ultimate structural failure, consistent with real-world deterioration processes.
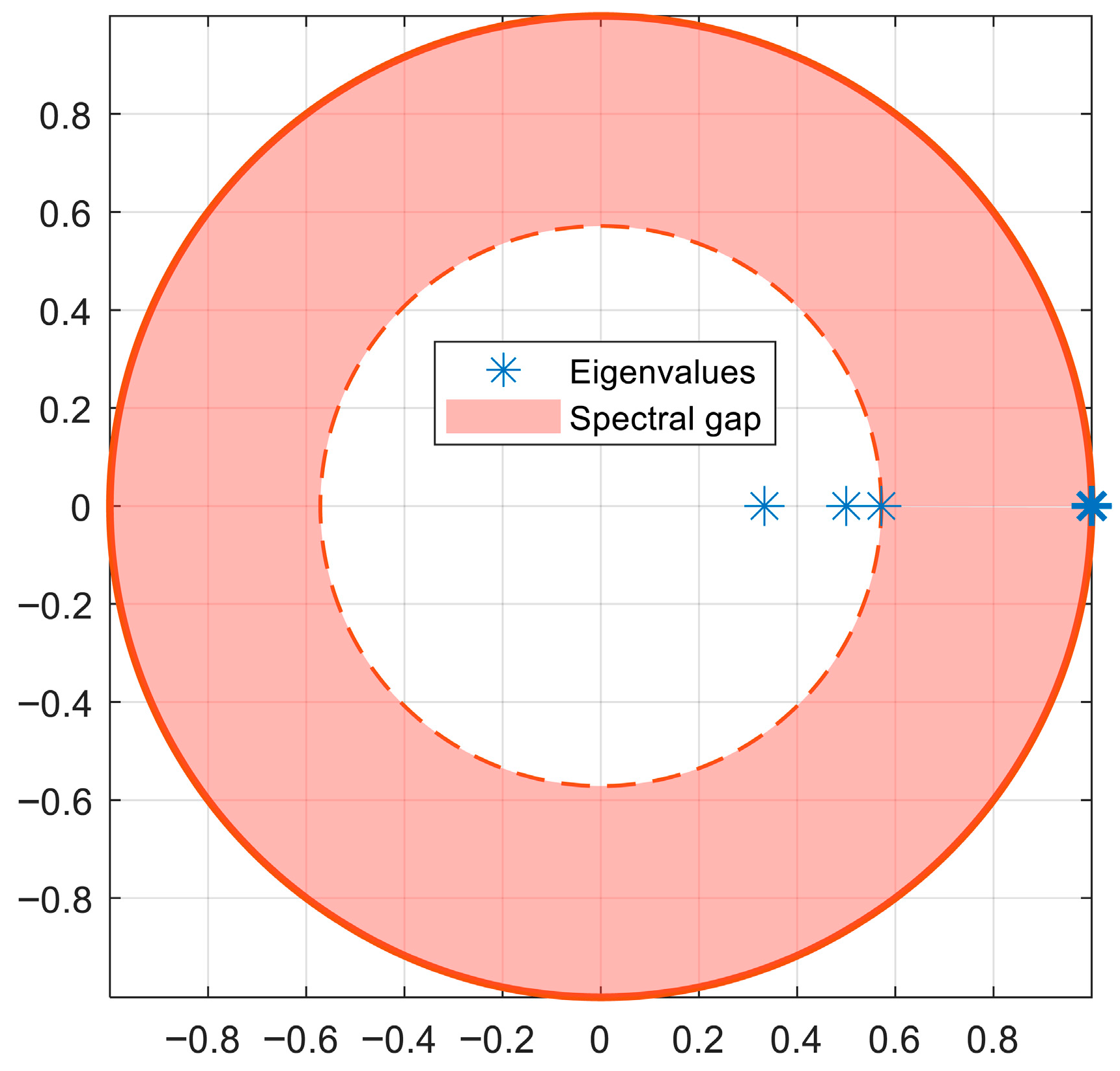
Further insights are provided by
Figure 3, which displays the eigenvalues of the Markov chain’s transition matrix within the complex plane. In Markov chain theory, eigenvalue analysis is fundamental for understanding convergence behaviors and the stability of states. Here, eigenvalues are represented by blue markers and reside within or exactly on the unit circle boundary, with one eigenvalue precisely located at unity. This eigenvalue at one is a hallmark of absorbing Markov chains, reflecting the presence of a stable absorbing state. Additionally, the depicted spectral gap highlighted as a shaded annulus indicates a clear separation between the eigenvalue at unity and other eigenvalues, confirming the rapid convergence of transient state probabilities toward the absorbing condition. The presence of this spectral gap emphasizes efficient and predictable long-term convergence to structural failure, further validating the numerical results.
In summary, these graphical analyses substantiate and vividly illustrate the theoretical and numerical findings derived from Markov chain modeling. They confirm the progressive and irreversible nature of structural deterioration under consideration, highlighting State 4 as an inevitable outcome in the absence of maintenance interventions. Consequently, these insights offer a rigorous probabilistic foundation for lifecycle management decisions, enabling asset managers and engineers to better anticipate structural performance, optimize maintenance planning, and effectively allocate resources.
7. Fuzzy Markov Chain Results
Fuzzy set theory, originally introduced by [
31], allows the explicit incorporation of uncertainty and imprecision into mathematical modeling. The MATLAB 2024b code analyzed in this part expands the traditional discrete-time Markov chain modeling approach presented in the previous part by integrating fuzzy set theory, thereby enabling explicit consideration of uncertainty in lifecycle assessments of buildings. Initially, crisp counts representing state transitions were transformed into fuzzy numbers using triangular membership functions [
32,
33]. The triangular form was selected due to its simplicity, interpretability, and minimal data requirements. It can be fully defined by three intuitive parameters (lower bound, most probable value, and upper bound), which are easily derived from empirical inspections and expert judgment. This choice is also supported by its widespread use in engineering applications where datasets are limited, ensuring computational efficiency while maintaining compatibility with the α-cut analysis employed in this study. Specifically, each crisp entry
in the count matrix
was converted into a triangular fuzzy number
, defined by the following triple [
34]:
The resulting fuzzy count matrix
thus contained triangular fuzzy numbers for all state transitions. Subsequently, a fuzzy transition probability matrix
was derived by normalizing each fuzzy count entry row-wise, yielding fuzzy probabilities:
To quantify uncertainty explicitly, the alpha-cut approach was applied. The alpha-cut method decomposes each fuzzy number into interval subsets at different confidence levels α ∈ [0, 1] [
35]. Formally, an alpha-cut for a fuzzy number
is represented as follows:
where
and
are lower and upper bounds of the fuzzy number at confidence level α. Analysis at different alpha levels provides a structured representation of uncertainty propagation in the Markovian lifecycle process.
Starting from an initial crisp probability distribution
, the fuzzy probability distribution after
steps,
, is computed through iterative multiplication with the fuzzy transition matrix:
For interpretability, the fuzzy distributions obtained at each step can be defuzzified via the centroid method. Finally, the fuzzy analysis included the calculation of the expected time to absorption for transient states, represented as fuzzy numbers. This fuzzy expected absorption time is computed through the fundamental matrix
, derived separately for each alpha-level scenario:
where
denotes the fuzzy sub-matrix of transient state transitions. Each fuzzy element of the resulting matrix
quantifies the uncertainty in the expected number of steps before absorption.
Overall, incorporating fuzzy set theory and alpha-cut analysis into Markovian lifecycle modeling significantly enhances the ability to manage and interpret uncertainty, providing robust and practical support for maintenance decisions in building lifecycle management.
Based on the MATLAB calculations presented, the defuzzified one-step probability distribution is as follows:
In addition to these point estimates, the analysis also produced full uncertainty bounds using the α-cut method.
Table 2 and
Table 3 present the lower and upper limits of the results for selected α levels (0.0, 0.5, and 1.0). These bounds show the range of possible outcomes consistent with the uncertainty in the inspection data and expert judgements, allowing the reader to assess both the central tendency and the spread of predictions.
The presented α-cut bounds clearly show how the level of assumed uncertainty affects the model outputs. At α = 1.0, the results coincide with the crisp case, giving a single deterministic value for each quantity. Reducing α widens the bounds, as more variation in the input transition counts is allowed. For the expected time to absorption, wider intervals for α = 0.0 indicate a greater range of possible lifespans, particularly for assets starting in better condition (State 1). Similarly, the probability distributions after 15 steps reveal that with high uncertainty (low α), there is still a small but non-zero chance of being in a non-absorbing state, while for α = 1.0 the outcome is almost entirely concentrated in the absorbing failure state. This representation complements the defuzzified values and provides a transparent picture of how uncertainty propagates through the fuzzy Markov chain model.
The fuzzy analysis was meaningful because it provided uncertainty intervals at different α levels, which cannot be obtained from a purely crisp analysis. The fact that defuzzified values match the crisp results (compare Equation (25) to Equation (17)) is a consequence of the symmetry of the adopted triangular fuzzy numbers, not an indication of identical analyses. The key added value lies in the α-cut ranges, which show how widely the predictions may vary depending on the uncertainty in the input data.
After 15 simulation steps, the defuzzified fuzzy distribution of states converged to the following:
Furthermore, the fuzzy analysis of average times to absorption yielded the following defuzzified estimates for transient states:
State 1: 4.25 steps;
State 2: 3.75 steps;
State 3: 2.44 steps.
Compared to the crisp Markov chain results, the defuzzified fuzzy estimates indicate slightly shorter expected times to absorption for States 1 and 2 and a marginally longer time for State 3. These differences reflect the influence of uncertainty in the transition probabilities, which in the fuzzy approach results in a more conservative prediction for better condition states and a slightly more optimistic estimate for more deteriorated states. This comparison confirms that incorporating fuzzy modeling can help capture uncertainty effects that may not be visible in purely crisp analyses, thereby supporting more robust maintenance planning decisions.
These computational results demonstrate the practical utility of fuzzy Markov modeling in quantifying and interpreting lifecycle uncertainties for built assets.
8. Continuous Markov Chain
While discrete-time Markov chains provide a robust and straightforward method for modeling deterioration processes at fixed intervals, continuous-time Markov chains (CTMCs) allow transitions between states to be modeled at any instant in time. For consistency with the discrete-time formulation, one step corresponds to the five-year interval between two consecutive inspections in the dataset. This additional flexibility more accurately reflects real-world scenarios, such as the deterioration processes of buildings and structural components, where state changes occur continuously rather than at discrete time steps.
In a continuous-time Markov chain, the system’s evolution is described by an intensity matrix
, whose off-diagonal elements
(for
) represent instantaneous transition rates from state
to state
. The diagonal elements
are defined to ensure that the rows of
sum to zero:
The behavior of a CTMC can be described by a system of differential equations known as the Kolmogorov forward equations [
17]:
Here,
is the state probability distribution at time
, represented as a row vector. Given an initial probability distribution
, the solution to this system of differential equations can be expressed through the matrix exponential
This solution provides the probability distribution of the states at any future time
[
6].
Motivation for employing continuous-time Markov chains stems from their capacity to capture the dynamic and continuous nature of structural degradation. Unlike discrete-time models, CTMCs allow for predicting state probabilities at arbitrary future times, which facilitates precise and flexible scheduling of maintenance interventions and optimizes resource allocation [
19].
The numerical simulation performed using MATLAB effectively illustrates this concept. Initially, a discrete transition matrix
(Equation (13)) was derived from empirical count data over a specified interval
years (see
Table 1). From this discrete matrix, the intensity matrix
was computed using the matrix logarithm relation:
The matrix logarithm was computed using MATLAB’s dedicated function, which applies advanced numerical algorithms to maintain stability even when eigenvalues are close together. In our case, the matrix is small, contains only non-negative values, and has eigenvalues inside the unit circle, which avoids typical instability issues. The result was verified by converting it back to the original transition matrix and by cross-checking with an independent method. Both checks confirmed full numerical consistency, ensuring that the procedure is reliable for the data used in this study.
The logarithm in Equation (29) refers explicitly to the natural logarithm, and the operation involves the complex mathematical task of computing the matrix logarithm. MATLAB achieves this by employing a function that calculates the matrix logarithm through eigen decomposition. Specifically, the matrix is diagonalized, the logarithm of each eigenvalue is computed individually, and then the matrix is reconstructed using the eigenvectors and these logarithms of eigenvalues. This method is numerically robust and is particularly well-suited for analyzing continuous-time Markov chains. In practical terms, the negative values on the diagonal of the intensity matrix represent the total rate at which the system leaves a given state. Their magnitude reflects how quickly deterioration is expected to progress from that state to any other state in the model.
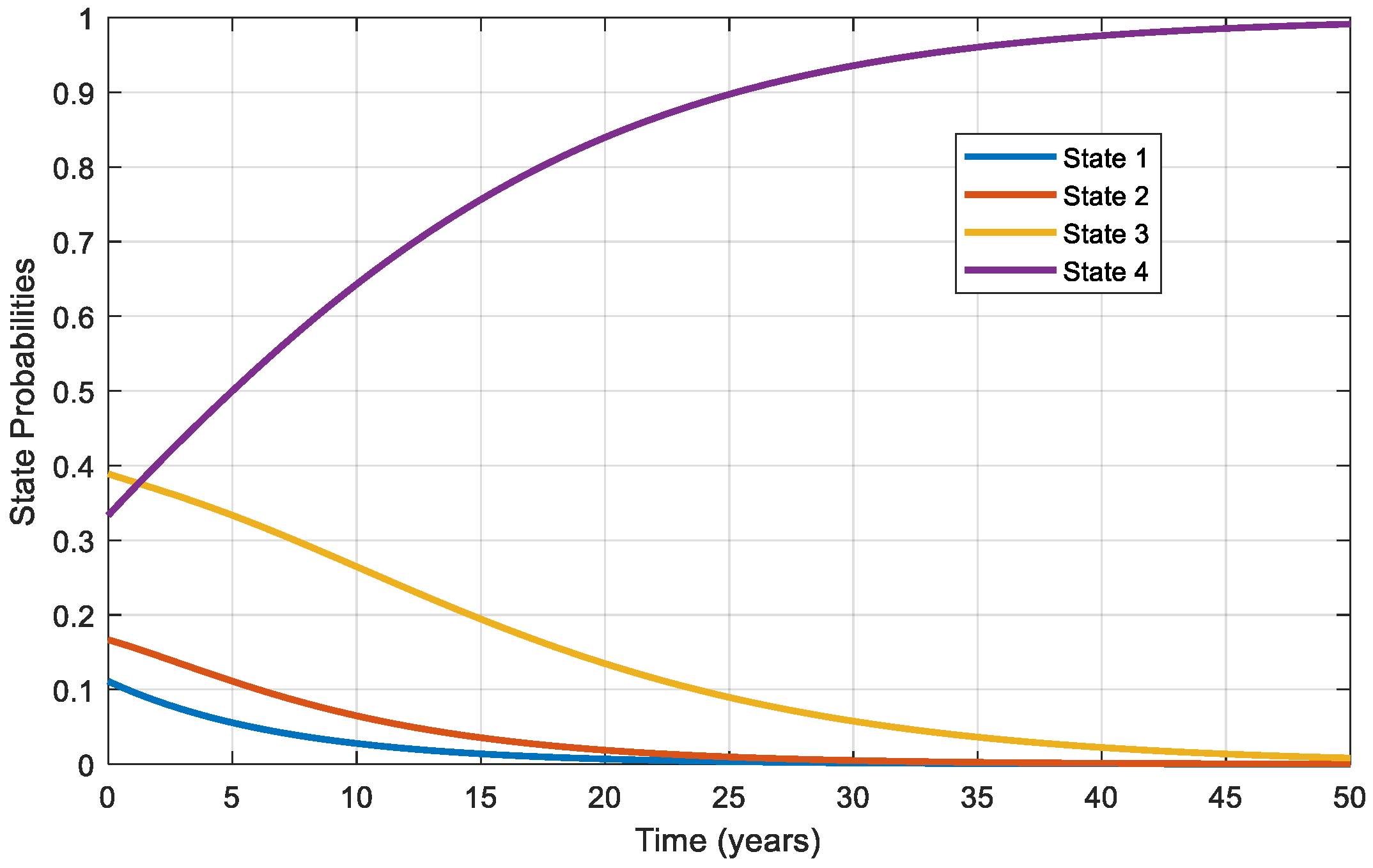
Subsequently, the continuous-time evolution of probabilities was obtained by evaluating Equation (28) across desired time points. The results visualized in
Figure 4 demonstrate a smooth probability transition reflecting gradual and continuous deterioration, emphasizing the accuracy and utility of the continuous-time approach. Specifically,
Figure 4 demonstrates how state probabilities evolve over time, with State 4 probability steadily increasing towards unity, confirming structural failure as inevitable without maintenance interventions. These graphical results align closely with the previously computed discrete-time Markov chain outcomes, reinforcing the validity and reliability of the continuous-time modeling approach (compare
Figure 1).
Further analysis involves determining the stationary distribution of the continuous Markov chain by solving the equilibrium condition:
This stationary distribution describes the long-term equilibrium state of the system, indicating the likelihood of structural states remaining constant under steady deterioration dynamics [
13].
A direct numerical comparison between the discrete-time and continuous-time models shows close agreement. For the same initial state distribution and empirical data, the probability of reaching the absorbing state after 15 years is 0.9994 in the discrete model and 0.9993 in the continuous model. The corresponding mean times to absorption from States 1, 2, and 3 differ by less than 1.5%. These results indicate that, under the present inspection interval of five years, both models produce consistent predictions, with the continuous formulation offering the additional advantage of computing state probabilities at any chosen moment in time.
In conclusion, continuous-time Markov chains enrich lifecycle analysis by accurately representing deterioration processes over continuous intervals, enabling refined predictions and strategic maintenance decisions. Their use enhances durability, reliability, and economic efficiency in the management of buildings and structural assets.
9. Conclusions
This paper presented a probabilistic approach based on discrete-time Markov chain modeling for predicting the service life and deterioration processes of buildings and structural components. The analysis illustrated clearly how constructed assets transition progressively from optimal structural conditions through intermediate states of degradation, ultimately reaching an absorbing state representing structural failure. By utilizing empirical transition matrices and fundamental Markovian computations—including the fundamental matrix, absorption times, and stationary distributions—the model provided robust quantitative insights into the expected lifecycle of buildings.
A notable novelty of the proposed formulation lies in the explicit integration of systematic expert evaluations and structured empirical data, ensuring realistic modeling of deterioration patterns and significantly enhancing the predictive accuracy and practical applicability of the Markovian approach.
Numerical simulations emphasized that structural deterioration is both predictable and inevitable when no preventive maintenance interventions are implemented. The calculated average times to absorption highlighted the importance of early and timely maintenance interventions, as initial healthier states significantly extended expected asset lifetimes. Graphical analyses and eigenvalue studies further supported these numerical findings, clearly demonstrating the model’s reliability in capturing the progression toward structural failure.
Overall, the presented Markov chain methodology serves as a powerful analytical tool for lifecycle management, allowing building managers, engineers, and decision-makers to optimize maintenance planning, allocate resources efficiently, and enhance the sustainability and economic efficiency of construction assets. Future research may focus on integrating inspection data, condition monitoring, and Bayesian updating approaches to refine the transition probability estimates and further enhance predictive accuracy. Additionally, expanding this model to include cost–benefit analysis or decision optimization techniques could significantly strengthen its applicability in practical asset management scenarios. In particular, cost–benefit analysis could be directly integrated into the Markov framework by associating transition probabilities and expected times to absorption with maintenance and intervention costs, as well as with the economic consequences of failure. Such integration would enable decision-makers to optimize maintenance schedules not only for technical performance but also for economic efficiency, further enhancing the practical value of the approach.
It is important to note that the numerical results in this study are based on a small dataset: 18 building elements observed over a five-year period (2020–2025). This is not sufficient to fully capture the long-term nature of structural deterioration. As a result, some transition probabilities may be statistically unreliable due to sparse observations and zero entries in the count matrix. These limitations do not affect the methodological validity of the proposed approach but should be considered when interpreting the results. We recommend applying the framework to larger and longer-term datasets in future studies, potentially supported by expert assessments or Bayesian updating to improve reliability in the early stages of modeling.