Abstract
The growing use of unmanned aerial vehicles (UAVs) for real-time video surveillance in smart city and smart region infrastructures requires reliable and delay-aware data transmission models. In urban environments, UAV communication links are subject to stochastic variability, leading to jitter, packet loss, and unstable video delivery. This paper presents a novel approach based on the Graphical Evaluation and Review Technique (GERT) for modeling the transmission of video frames from UAVs over uncertain network paths with probabilistic feedback loops and lognormally distributed delays. The proposed model enables both analytical and numerical evaluation of key Quality-of-Service (QoS) metrics, including mean transmission time and jitter, under varying levels of channel variability. Additionally, the structure of the GERT-based framework allows integration with artificial intelligence mechanisms, particularly for adaptive routing and delay prediction in urban conditions. Spectral analysis of the system’s characteristic function is also performed to identify instability zones and guide buffer design. The results demonstrate that the approach supports flexible, parameterized modeling of UAV video transmission and can be extended to intelligent, learning-based control strategies in complex smart city environments. This makes it suitable for a wide range of applications, including traffic monitoring, infrastructure inspection, and emergency response. Beyond QoS optimization, the framework explicitly accommodates security and privacy preserving operations (e.g., encryption, authentication, on-board redaction), enabling secure UAV video transmission in urban networks.
1. Introduction
1.1. Motivation
The use of unmanned aerial vehicles (UAVs) for visual monitoring and real-time data collection is becoming increasingly widespread in the urban environment. Such platforms are actively used for traffic control, infrastructure inspection, environmental monitoring, and emergency response, that is, in key areas of functioning of modern “smart” cities. Equipped with high-quality cameras, UAVs are capable of providing shooting with high spatial and temporal resolution, which allows for promptly forming situational awareness and making justified managerial decisions.
At the same time, the practical deployment of UAV-based video monitoring systems faces significant difficulties related to the stability and reliability of data transmission. Unlike static ground networks, communication channels with UAVs are influenced by variable factors: interference, loss of line of sight, switching between base stations, bandwidth instability, and degradation of channel quality. All this leads to packet loss, excessive jitter, and delay spikes, which ultimately worsens the integrity and continuity of the video stream. As a result, critically important functions of urban monitoring, such as vehicle tracking, pedestrian detection, or incident response, may be disrupted or significantly delayed.
Traditional data transmission protocols usually rely on rigid buffering or retransmission mechanisms, which turn out to be ineffective under the stochastic dynamics of the urban wireless environment. In addition, such approaches rarely provide adaptive or predictive logic capable of responding in real time to changes in the state of the network. Under conditions when the allowable time of frame delivery is measured in milliseconds, such inertia is a critical problem.
In this regard, there arises a need for modeling tools that not only allow us to take into account the probabilistic nature of the data transmission process from UAVs but also are capable of describing the adaptive behavior of the system under uncertainty [1,2,3]. In this article, a stochastic model is proposed, based on the Graphical Evaluation and Review Technique (GERT), which allows formalizing temporal characteristics, feedback structure, and the potential for using intelligent control in UAV video transmission systems oriented toward the needs of smart urbanism. Given that UAV video streams may contain personally identifiable information, maintaining confidentiality, integrity, and availability of the data is essential; the proposed modeling framework is designed to quantify the QoS impact of security and privacy controls in networked urban environments.
1.2. State of the Art
The reviewed studies can be grouped into three main categories, which allows building a coherent understanding of the current research landscape. The first category includes works focusing on the application of UAVs for real-time video monitoring in urban environments, emphasizing mobility and coverage but often neglecting the stochastic nature of communication channels. The second category comprises research on adaptive transmission strategies, such as bitrate adjustment, error correction, and buffering, which aim to mitigate channel variability yet lack a unified stochastic-graph description. The third category covers stochastic and analytical modeling approaches, including Markov chains, queuing models, and GERT networks, which provide formalism but are often simplified in terms of topology, delay distributions, and adaptive logic.
In modern conditions, a number of studies emphasize the strategic importance of platforms for operational video monitoring using UAVs for the formation of integrated systems of surveillance and data collection in real time. Thus, in [1], a review of the implementation of UAVs in urban surveillance systems is carried out, with an emphasis on their mobility, high spatial resolution of shooting, and the possibility of scalable area coverage. The authors note that it is precisely the ability of UAVs to respond promptly to changes in the city situation that makes them an integral part of smart city infrastructure. However, the mentioned work practically does not consider issues related to the quality of video data transmission, in particular the influence of the urban environment on the stability of the connection, delays, or channel variability.
Further studies, in [2], focus on specific challenges that arise in the process of transmitting video data from UAVs in conditions of dense urban development. In particular, the influence of the loss of the line of sight, multipath signal propagation, changes in base stations, and the mobility of the drones themselves is noted, which together causes dynamic variability in channel quality. The authors emphasize the necessity of adapting communication channels to the changing environment but are limited to a qualitative description of the problems without formal modeling or quantitative assessment of the impact of the mentioned factors on service quality.
An attempt at a more systematic analysis is made in [3], where an approach to ensuring the quality of the video stream from UAVs in the urban environment is considered based on adaptive bitrate, the use of forward error correction (FEC) codes, and buffering. The study presents scenarios with dynamic changes in video transmission parameters according to network conditions. The advantage of this work is its focus on QoS parameters, average delay, jitter, and packet loss. However, the model is implemented at the simulation level without analytical description and also does not take into account the probabilistic nature of routing or feedback in retransmissions.
In [4], the general architecture of video surveillance systems with UAVs is considered, with a focus on achieving reliability and reducing delay. The proposed model provides for the use of several UAVs with distributed data transmission functions to ground infrastructure. Despite the interesting formulation of the problem, the authors are limited to a high-level description of the system, leaving out mathematical modeling of the frame transmission process in networks with a high level of stochasticity.
Overall, the literature review indicates the recognition of unmanned aerial vehicles as an important component of smart city systems. At the same time, the available studies demonstrate a number of limitations. First, most of them do not offer a formal description of the video transmission process under stochastic variability of channel parameters, which is a key feature of urban environments. Second, the adaptive logic of choosing a transmission strategy based on risk prediction or analysis of channel conditions is practically not considered. Third, the issue of feedback and the influence of retransmissions on the overall delivery time and stream stability is not addressed. Fourth, there is a lack of flexible models capable of formalizing parallel strategies, alternative routes, and the influence of intelligent control mechanisms.
The analysis of the problem of video data transmission from UAVs in the context of smart urbanism reveals the need not only for engineering solutions but also for the construction of adequate models that would allow the formalization and quantitative evaluation of key Quality-of-Service parameters. In this connection, an important place in the scientific discourse is occupied by the issue of developing mathematical approaches to describing processes that occur in wireless networks with a high level of dynamics. Modeling video transmission from UAVs in the complex conditions of an urbanized environment is considered a key tool for predicting system behavior, identifying critical delay points, optimizing routing topology, and ensuring the required level of service quality.
In [5], an attempt is made to describe the behavior of UAV wireless channels based on Markov chains. The authors emphasize that the stochastic nature of transmission processes requires the model not only to describe the average delay values but also to be able to predict its variability. It was shown that even a simple single-channel transmission system demonstrates complex delivery time dynamics under varying load conditions. However, despite its informativeness, the Markov model does not allow for accounting complex path branching or adaptive logic change in real time.
Another approach is proposed in [6], where video data transmission is modeled in the form of a queuing system with dynamic request intensity. The authors consider options for frame alternation in the buffer, the use of priorities for video fragments, and the influence of the load coefficient on the probability of losses. Such a model makes it possible to evaluate general behavioral trends of the system at different traffic levels, but does not consider the specifics of routing in a stochastic network, in particular the possibility of retransmissions or strategy variability depending on environmental conditions.
In [7], the use of simulation modeling of UAV video transmission systems is proposed, taking into account changing flight trajectories, building density, and obstacle characteristics. The model allows studying the dependence between the drone’s position and communication parameters, in particular RSSI and jitter level. The results show that even with optimal placement of routers, transmission remains unstable without system adaptation to real changes in the network. However, the simulation approach, although detailed, does not allow for analytical derivation of dependencies between system parameters, which limits its application in optimization or control tasks.
Thus, despite existing attempts to formalize the process of video transmission from UAVs, most models have important limitations. A significant part of them is oriented toward isolated aspects. These are queue delays, buffer load, or Markov transitions. Whereas the real data transmission system from UAVs in the urban environment is multicomponent, adaptive, and stochastic. In addition, the existing approaches lack a unified graph-based description of the process that would allow simultaneously taking into account several alternative routes, their probability of realization, distributions of different types of delays, as well as feedback in case of unsuccessful delivery.
Therefore, traditional deterministic models become insufficient for adequately describing such systems, which determines the growing interest in stochastic approaches as more flexible and realistic.
In [8], stochastic modeling is used to study the coverage of UAVs operating as wireless access points in urban areas. The authors use the stochastic geometry approach, which makes it possible to assess the impact of urban development and signal blockage. The model allows evaluating the impact on the optimal UAV placement strategy (proximity to users or minimization of interference). The advantage of the approach is the consideration of random configurations of the surrounding environment; however, the model is implemented exclusively numerically, without the possibility of analytical derivation of quality metrics, which limits its suitability for optimization tasks.
Another approach is demonstrated in study [9], where the influence of random delays in multistage routes on the stability of video transmission is analyzed. A system with exponentially distributed time delays for each stage of frame passage from source to receiver is used. The authors show that even with a constant average delay value, an increase in its variance significantly raises the probability of exceeding the delivery time threshold, which in turn lowers the quality of the video stream. Thus, delay variance, and not just its average value, is a critical metric for evaluating transmission efficiency under uncertainty.
Study [9] proposes a comprehensive approach to optimizing energy consumption and task execution time in UAV-enabled wireless sensor networks (UAV-enabled WSN). The authors consider the problem of simultaneous minimization of the maximum energy consumed by an individual UAV and the time to complete the data collection task from all ground sensor nodes. The study models the total energy consumption of each UAV, taking into account three main components: flight energy between data collection points, hovering energy over each node, and communication costs during information transmission. Attention is drawn to the fact that the choice of flight speed and UAV trajectory significantly affects both total energy consumption and data collection time. However, the model does not use a formalized graph-based description of the entire transmission system, which complicates the expansion and scaling of the approach to networks with numerous alternative routes or feedback between nodes.
A characteristic feature of the presented studies is the limitation in presenting the process structure. Mostly, stochastic modeling in them is implemented at the level of individual stages or segments of the network, without a unified formal description of the entire topology of the transmission system. This limits the ability of such models to describe adaptive behavior, the inclusion of intelligent route management mechanisms, or the interaction of different transmission branches. In addition, the vast majority of models do not take into account the logic of retransmissions in case of error or delay, which is typical for real-time systems.
Among the existing approaches to modeling complex telecommunication processes of stochastic nature, special attention is drawn to the GERT. Unlike classical methods such as PERT (Program Evaluation and Review Technique) or CPM (Critical Path Method), GERT models make it possible to describe processes with probabilistic transitions, conditional branching, stochastic delays, and feedback. This makes them extremely relevant for the tasks of analyzing data transmission systems, particularly under dynamic topologies inherent to UAV networks.
In [10], the application of the GERT approach to modeling information flows in multisegment telecommunication networks is presented. The authors showed that GERT allows representing alternative packet transmission paths depending on the current network state, taking into account the probabilities of route selection, delays at each stage, and also the possibility of repetition in case of an error. Such representation of the process in the form of a directed graph with distribution functions on each arc makes it possible to formally evaluate average delays, variances, and probabilities of successful transmission completion. However, the model was limited to small graph sizes, and the distribution functions were mostly used in simple exponential form.
Further development of the concept is reflected in [11], where GERT is applied to the analysis of an adaptive routing system in a wireless network with variable channel characteristics. The model provides for the existence of several transmission routes, which are activated depending on the channel quality assessment, and also implements a mechanism of stochastic feedback in case of packet non-delivery. The main advantage of such an approach is the possibility of deriving an equivalent transmission function of the system, which combines probabilistic characteristics of routing with time costs at each stage. At the same time, the study mainly uses symmetrical and unified types of delays, and the model itself does not take into account realistic distributions characteristic of practical video transmission tasks, such as lognormal or triangular.
Study [12] deserves special attention, where a hybrid GERT model is proposed for describing systems with an adaptive traffic control structure. The authors integrate data obtained from sensor modules into the logic of choosing routing branches, which brings the model closer to practical implementations in smart systems. At the same time, the possibility of updating transition probabilities based on prediction is considered, which theoretically opens the way to the integration of artificial intelligence methods. However, the analytical part is limited and does not include full derivation of characteristic functions or spectral analysis, which limits the capability of such a model for deep quantitative analysis of the system’s temporal characteristics.
Although individual elements of GERT modeling are gradually being integrated into the analysis of telecommunication systems, existing implementations mostly remain fragmentary or simplified. Most studies are limited to graphs with a small number of nodes and arcs, use only basic types of time distributions (exponential, deterministic), and rarely take into account a complete feedback structure. In addition, the vast majority of models do not implement integration with adaptive routing mechanisms formed based on analysis of the external environment or channel state prediction.
In the context of the growing complexity of network environments and the need to ensure guaranteed QoS when transmitting video data from unmanned aerial vehicles, researchers are paying significant attention to the possibility of using artificial intelligence (AI) mechanisms to support adaptive control.
In [13], the use of deep neural networks is proposed for predicting the parameters of the transmission channel between UAVs and ground stations in real time. The authors form a model that, based on historical signal values, noise level, packet losses, and drone movement speed, predicts the probability of degradation in connection quality. Based on these assessments, the system adapts frame rate, changes bitrate, or switches to backup routes. Such an approach allows reducing the probability of frame loss during sudden channel degradation; however, the given study does not propose a formal way to integrate predictive logic into the structural model of the transmission system.
Another approach is proposed in [14], where reinforcement learning algorithms are used to select the route of frame transmission in a network with mobile agents. The model takes into account variability of channel conditions, the drone’s energy constraints, and the probability of conflicts in the network during simultaneous transmission of multiple streams. The algorithm learns independently by optimizing the strategy for minimizing the average transmission delay. Empirical results demonstrate jitter reduction and increased probability of timely delivery; however, the model is built in isolation from the overall stochastic structure of the transmission process and does not account for retransmissions or complex routed logic.
In [15], a machine learning–based module is considered that classifies the current channel state in online mode as “reliable,” “moderate,” or “unstable,” which serves as a trigger for switching between different video stream encoding scenarios (standard, FEC, or FEC with reduced frame rate). This approach has a direct connection to real scenarios of drone operation in video surveillance systems. However, in the presented study, AI is implemented as an independent module that is not part of the analytical model, and therefore does not allow prediction of the result at the level of the system’s transmission function.
Recent studies further advance this area by integrating AI-based routing into UAV communication frameworks. For example, in [16] a deep reinforcement learning approach was used to optimize UAV multi-hop paths in real time, achieving lower end-to-end delay under dynamic 5G conditions. In [17], a hybrid graph–neural network model was applied to UAV video streaming, dynamically adjusting routes in response to predicted link quality. In [18], federated learning was employed to update routing models across multiple UAVs without centralizing sensitive flight data, thus enhancing privacy and scalability. These approaches are directly relevant to extending GERT-based models with adaptive, AI-driven decision-making for real-time video transmission in urban environments.
In this context, security-aware and privacy-preserving mechanisms (e.g., authenticated encryption, integrity verification, on-board redaction) can be incorporated into graph-based models as processing and verification stages, allowing a joint analysis of communication performance and protection objectives.
Common to the above-mentioned approaches is the use of AI as an autonomous adaptive mechanism that affects stream parameters or route selection. At the same time, these solutions are mostly not formalized within mathematical models that would allow analytical evaluation of the impact of predictive modules on the overall system characteristics, such as average delay, variance, or delivery probability. In addition, the issue of integrating such solutions into the structure of the stochastic process is not addressed, which is key for building a unified model of system behavior.
Within the applied dimension of research, special attention is drawn to the study of real platforms used for UAV video transmission, since it is hardware limitations that determine the suitability of a particular model for practical implementation. In work [19], the DJI OcuSync 2.0 system is studied in terms of transmission stability and reliability. The authors show that this system provides stable HD video transmission over a distance of up to 10 km with adaptive frame rate and minimized losses. However, limitations in predictive behavior of the system were found: its closed nature makes it impossible to access channel parameters in real time, which complicates the construction of formal models taking environmental state into account.
Another study presented in [20] is devoted to analyzing the DJI Lightbridge 2 platform as an example of a digital HD system with low latency. The authors perform experimental jitter evaluation under different types of load and emphasize the importance of static topology for ensuring predictable behavior. A positive aspect of this system is its architectural optimization for video streaming; however, the limited number of channels and fixed encoding algorithms do not allow its use in stochastic network conditions.
For scenarios with minimal latency requirements, analog transmission platforms such as FatShark, studied in [21], are actively used. Their advantage is ultra-low latency (up to 10 ms), which is achieved due to the absence of buffering and codecs. However, this very aspect causes high sensitivity to interference, inability to compensate for losses, and complete lack of feedback. This makes it impossible to integrate such systems into networks with adaptive logic or Quality-of-Service support.
In general, the review of existing studies indicates that although modern platforms provide different levels of performance, they mostly do not offer sufficient flexibility for implementing stochastic strategies, adaptation to changing conditions, or integration with artificial intelligence modules. Most of them are closed in architecture or operate with fixed configurations without the possibility of route reconfiguration or retransmission when frame loss risks are detected.
Thus, there arises the need to create an adaptive stochastic GERT model of video transmission from UAVs for urban monitoring systems, capable of abstracting from a specific hardware implementation, but at the same time taking into account realistic aspects: types of delays, transmission strategy selection logic, channel variability, and the presence of retransmissions.
1.3. Objectives and Contribution
The aim of this study is the development of a stochastic mathematical model that is capable of adequately describing the process of video frame transmission from onboard UAV systems under the conditions of stochastic variability of urban wireless environments. The proposed approach is based on the GERT and allows modeling both sequential and alternative transmission strategies, including conditional branching, variable delays, and feedback. A distinctive feature of the model is the built-in possibility of integrating predictive decision-making logic, in particular in the form of an artificial intelligence module that assesses the risk of frame loss and allows adaptively choosing one of the alternative transmission strategies. Such logic is implemented at the level of conditional branching in the structure of the GERT graph, which provides a formal description of adaptive behavior without the need for direct implementation of the intelligence module within the model itself.
To achieve the goal, the following tasks were set.
- To substantiate the expediency of using GERT as a method for describing the data transmission process with probabilistic branches and stochastic delays.
- To build the structure of a GERT graph that reflects the key stages of processing, buffering, transmission, reception, and decoding of the video frame;
- To develop a mathematical model that takes into account the possibility of conditional selection of the transmission strategy of the frame depending on the risk assessment of loss, formalizes stochastic feedback for modeling retransmission of the frame in case of its untimely reception or loss, and forms analytical expressions for the moment-generating function of the system;
- To carry out numerical evaluation of QoS indicators and perform spectral analysis of the characteristic function.
The object of the study is the process of delivering video information from the onboard video module of a UAV to a ground receiving station under the conditions of a stochastically variable transmission environment, which includes signal instability, delay variability, packet loss, and possible retransmissions.
Within the framework of the study, the following assumptions were made:
- –
- the process of video frame transmission can be represented as a directed graph with deterministic and stochastic arcs;
- –
- the delay distributions at individual stages have triangular, exponential, or lognormal form, according to the characteristics of the corresponding technical operations;
- –
- the risk level assessment of frame loss is carried out by an external or embedded module (for example, based on machine learning), but the module itself is not modeled, and the result of its operation is taken into account as a condition for selecting the transmission strategy;
- –
- the probability of frame retransmission depends on the probability of non-delivery in the main branch and is implemented as stochastic feedback.
The proposed model combines stochastic description of delay parameters with adaptive logic of transmission strategy selection, which allows taking into account both the internal structure of the process and the external variable conditions of the network. Such an approach is relevant to real scenarios of UAV use for video monitoring in the urban environment, in particular in the tasks of road infrastructure control, emergency response, object inspection, and civil surveillance.
The main contributions of this paper are: (1) development of a stochastic GERT-based model for UAV video transmission in urban environments; (2) formal integration of adaptive decision-making logic into the stochastic model; (3) derivation of analytical expressions for key QoS metrics and spectral characteristics; (4) comparative evaluation with baseline models demonstrating advantages in delay–jitter balance.
2. Materials and Methods
This section presents the proposed GERT-based modeling framework for UAV video transmission. We begin with an overview of the system design, describing the logical sequence of video frame processing and transmission stages, the probabilistic branching structure, and the feedback loops used for retransmissions. Figure 1 illustrates the system as a GERT graph, where each vertex corresponds to a specific processing or transmission stage, and each directed edge Wi–j(s) represents the Laplace transform of the delay distribution for the operation from node vi to node vj. The subsequent subsections detail the construction of this graph, the derivation of its equivalent transfer function, and the calculation of key QoS metrics, followed by spectral analysis of the system’s characteristic function.
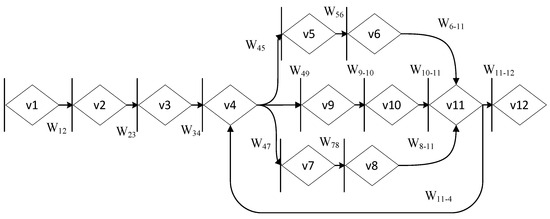
Figure 1.
Block diagram of the GERT network of the video data transmission process from the UAV.
In addition to communication primitives, security and privacy operations are modeled as graph components. Encryption and authentication are represented by additive processing delays on dedicated edges; integrity verification may trigger probabilistic feedback (retransmission on failure). On-board redaction/anonymization is treated as a processing node with its own stochastic delay. This enables evaluating the QoS overhead of protection mechanisms alongside routing and buffering policies.
2.1. Justification for the Choice of GERT as a Means of Describing the Stochastic Process of Video Data Transmission from Onboard UAVs
The process of video data transmission in UAV networks is characterized by a high level of stochasticity, caused both by the unstable quality of the communication channel and by the dynamic topology of the network. Under such conditions, fluctuations of signal level, packet losses, variable delay, and other factors are observed, which directly affect the QoS. In addition, modern video transmission systems are increasingly applying adaptive mechanisms that change stream parameters. For example, the level of redundancy, frame rate, or choice of encoding algorithm according to the predicted network conditions. This means that the video data stream can be transmitted via different routes with different parameters and delays.
For a formal description of such a system, a model is needed that is capable of accounting for the multiplicity of scenarios, transition probabilities between stages, delay variability, and the presence of conditional branching in the transmission logic. Traditional approaches such as PERT or queuing systems are limited in expressing such behavior. In contrast to them, the GERT model allows describing the process in the form of a directed graph, where each arc is characterized not only by the average execution time, but also by the probability of activation and the distribution function of duration.
The use of GERT in the task of modeling the video transmission process allows formalizing not only a linear sequence of stages, but also alternative branches that correspond to different transmission strategies, including transmission without redundancy, with FEC, or with additional reductions in stream parameters. In addition, this method supports the presence of conditional cycles, which is especially important for scenarios of real-time reconfiguration of parameters. Due to the ability to calculate the expected time, variance, as well as the probabilities of reaching a certain state, a GERT-based system allows evaluating the expected Quality of Service for each behavior variant.
Another advantage of the chosen approach is its compatibility with modern artificial intelligence methods. In particular, the results of prediction of packet loss probability or channel degradation can be used as triggers for switching paths in the graph, which allows formalizing the adaptive behavior of the system in the form of a stochastic process with intelligent control.
Thus, the choice of GERT as a means of describing the video data transmission process in UAV networks is methodologically justified and opens the possibility of constructing a consistent mathematical model that combines precision, flexibility, and the ability to integrate with prediction modules based on machine learning.
2.2. General Architecture of the GERT Model for Video Data Transmission from Onboard UAVs
The process of video data transmission from the UAV onboard system to the ground receiving station is described as a stochastic graph, where each node represents a separate stage of processing or transmission, and the arcs between them are characterized by the probability of passage and a delay function. This approach makes it possible to model both the sequential actions of the system and alternative transmission branches that depend on the evaluation of the communication channel conditions. The block diagram of the GERT network of the video data transmission process from the UAV is shown in Figure 1.
In this diagram each edge Wi–j(s) indicates a possible transmission path segment with an associated probability of selection and a stochastic delay distribution, as specified in Table 1 Probabilistic feedback loops model retransmissions under varying network conditions.

Table 1.
Values of the transition parameters of the GERT graph.
The process of video data transmission in the UAV system is modeled as a stochastic graph, where each vertex corresponds to a separate functional stage, and the arcs describe delays stochastically or deterministically. The process initiation begins at node v1, which corresponds to the moment of video frame capture by the sensor module (for example, CMOS or CCD). This process has a stable frequency (30 frames/s), which allows interpreting the delay as deterministic.
At the next stage (v2), the frame undergoes preliminary processing: stabilization, cropping of the region of interest, and noise suppression. The operations are performed using built-in libraries, for example, OpenCV, and are characterized by a constant delay. After processing, the frame reaches node v3, where buffering in the local queue takes place. Here the delay is modeled by a triangular distribution, taking into account possible variations due to overload.
In node v4, collection of communication channel parameters is carried out (RSSI, jitter, delay, packet loss), after which the artificial intelligence module forms a forecast of the risk of frame loss. According to the assessment, the system selects one of three branches:
Branch 1 (v4 → v5 → v6 → v11)—used at a low level of risk; transmission is performed without redundancy, with fixed delay;
Branch 2 (v4 → v9 → v10 → v11)—medium risk level; FEC is activated, transmission is described by an exponential distribution;
Branch 3 (v4 → v7 → v8 → v11)—high risk; FEC with additional frame rate reduction is applied, transmission is also modeled exponentially.
All branches terminate at node v11, where the frame is received. Next, the frame goes to node v12, which includes buffering, decoding (for example, H.264), and output to the display. The delay at this stage is modeled by a lognormal distribution, considering the variability of the load and hardware processing.
In case the frame could not be delivered or decoded on time, feedback is implemented: from node v11, a transition back to v4 takes place, allowing the forecast to be rebuilt and retransmission to be carried out.
Thus, each transition in the graph corresponds to a certain functional stage of the system and is described not only by the probability of realization but also by a delay distribution function, which allows modeling both the behavior of individual branches and the system as a whole. The GERT model allows taking into account both adaptive decision-making logic based on prediction and the unpredictability of external conditions, which makes it adequate for QoS analysis in UAV networks.
The GERT model shown in Figure 1 corresponds to the physical, network, and temporal constraints of video transmission from onboard UAV systems under the condition of using a modern computing platform, a low-resource artificial intelligence module, simple error correction algorithms (FEC), and a stable communication channel. Such a model is realistic and practically suitable for use in tasks of online monitoring, reconnaissance operations, and civil video surveillance.
2.3. Construction of and Reduction in the GERT Model of Video Transmission in the UAV Network
Having determined the topology of the graph, the types of arcs, the delay distributions, and the logic of transitions between vertices, one can proceed to the analytical stage of modeling, which consists of constructing the equivalent transmission function. This function makes it possible to describe the behavior of the system in terms of time costs for passing the signal from the source to the receiver, taking into account all possible route options, stochastic transitions, as well as the effect of feedback. The formalization of W(s) is a key tool for further analysis of QoS characteristics in the UAV network.
The GERT graph includes 14 sequentially connected stages, within which both hardware and software processing, stream formation, radio transmission, reception, decoding, and frame output take place. A distinctive feature of the model is the presence of a parallel block in which the selection of one of the three transmission strategies is implemented depending on the forecast of loss risk formed by the artificial intelligence module.
To formalize the process of video information transmission in a UAV network, a stochastic GERT model is applied, which is defined as a directed graph of the form G = (V,E), where —a finite set of vertices corresponding to the operational stages of the system; —arcs between vertices, each of which is characterized by the probability of transition realization, and —the delay distribution function in the form of a Laplace transform.
The model includes both linear sequential segments and parallel branches with alternative routes, the selection of which is carried out by an artificial intelligence module based on prediction.
To account for the possibility of retransmission in the event of frame loss, the graph includes feedback between vertices v11 → v4.
The types of time distributions for passage through the arcs include:
- –
- deterministic delays—for stable hardware operations;
- –
- triangular—for buffering;
- –
- exponential—for radio transmission;
- –
- lognormal—for decoding and output;
- –
- geometric loops—for stochastic feedback.
In total, the graph contains 14 arcs, the parameters of which are detailed in Table 1. They form the complete network topology of the video transmission system, which will be used in the subsequent stages of constructing the equivalent function of the GERT model.
Having defined the topology of the graph, the types of arcs, delay distributions, and the logic of transitions between vertices, one can proceed to the analytical stage of modeling, which consists of constructing the equivalent transmission function. This function makes it possible to generally describe the behavior of the system in terms of time costs for signal passage from the source to the receiver, taking into account all possible route options, stochastic transitions, and the effect of feedback. The formalization of W(s) is a key tool for further analysis of QoS characteristics in the UAV network. The basis of the calculation is the convolution principle of Laplace functions for sequential path segments, as well as path algebra taking into account parallel branches and feedback.
In the process of constructing the equivalent function, all possible paths from the initial vertex v1 to the terminal vertex v12 are identified, with each path being non-cyclic (i.e., not including feedback loops). The accounting of parallel branches in the decision-making node (node v4) is implemented through probabilistic weighting of each traversal option according to the channel state assessment.
Taking into account the configuration of the graph, three main paths are distinguished:
First path: v1 → v2 → v3 → v4 → v5 → v6 → v11 → v12, which corresponds to transmission without FEC under low loss risk. The equivalent function of this branch has the form:
Second path: v1 → v2 → v3 → v4 → v9 → v10 → v11 →v12, which is activated under medium risk and includes the application of forward error correction. An exponential distribution of wireless transmission time is considered. The corresponding function:
Third path: v1 → v2 → v3 → v4 → v7 → v8 → v11 → v12, which is activated under high risk and accounts for reduced frame rate with additional redundancy. The equivalent function of this branch is as follows:
The general transmission function is built as the sum of the equivalent functions of each of the three paths. Since route selection is performed by the AI module with certain transition probabilities, each function is weighted by the corresponding probability: , , . Thus, the numerator of the transfer function takes the form:
Additionally, the model takes into account the stochastic feedback , which corresponds to retransmission of the frame in case of failure. Within the GERT formalism, this element is included in the denominator of the equivalent function as a geometric sum of cycles, that is, as , where .
Thus, the full equivalent transmission function has the form:
Equation (5) is, in fact, the result of applying Mason’s rule [22] to the constructed GERT model. In general form, Mason’s equation describes the equivalent transfer function of a stochastic graph as:
where
- Pk is the transfer function of the k-th path from start to finish without loops,
- Δ is the system determinant accounting for all cycles (in our case, Δ =1 − L1);
- L1 is the only retransmission loop: ;
- Δk = 1, since Pk does not intersect with the loop.
Based on the constructed transfer function, the GERT system is modeled through the moment-generating function: It is considered as a composition of the elements of Table 2.

Table 2.
Elements of the function .
Taking into account the topology of the graph and the parameters from Table 2, we obtain the full analytical expression:
where —the numerator contains the sum of the three paths (transmission branches), and the denominator accounts for the geometric summation of stochastic feedback v11→ v4 with parameters Ploop, tloop;
—the function of triangular distribution with parameters a = 2, b = 6, c = 4;
—Laplace transform of the exponential distribution with rate λ;
MlogN(s)—moment-generating function of the lognormal distribution with parameters μ = 2, σ = 0.5, which is taken into account numerically or via tabulated values.
Since the lognormal distribution has no analytical Laplace transform in terms of elementary functions, the component MlogN(s), which corresponds to the delay at the decoding and display stage, is determined numerically. In particular, the moment function of the lognormal distribution is calculated using the integral:
where μ, σ are the parameters of the distribution, established according to the empirical estimation of delay at this stage.
The integral is calculated numerically using quadrature methods (Simpson’s or Gauss’s methods) [23,24,25,26,27], or approximated by a value table. This provides sufficient accuracy in the range of values , which corresponds to physically reasonable time scales of delay in the system.
The resulting function is the central analytical tool of the model and serves as the basis for further calculation of the system’s time characteristics, such as average delay, variance, and the probability of timely delivery of the video frame.
After obtaining the analytical expression (5), the next step is determining the key temporal metrics of the system. These indicators include the average frame delay, the delay variance (or jitter), and the probability estimate of delivering the frame within a specified time interval.
In classical GERT methodology, the analytical characteristics of the system follow from the properties of the Laplace transform used as the moment-generating function. In particular, the expected value of the total passage time through the graph is defined as the first derivative of the logarithm of the transfer function:
This expression allows taking into account the contribution of all system routes as well as the influence of retransmissions through feedback. An important advantage of this approach is the ability to account for both linear and branched (parallel) parts of the graph, as well as loops with repetition probability.
Applying the logarithmic derivative rule for a fraction, we have:
where —the numerator.
Taking the derivative:
Evaluating at , we obtain:
Thus, the average time of passing through the entire system consists of two components. The first is the expected time of a single pass without accounting for retransmissions. The second is the expected time spent on retransmissions.
The numerator of Equation (11) is the sum of the three routes. Since each Wi(s) is a product of k functions of the form , ,, or , the logarithmic derivative of the product is defined as the sum of the logarithmic derivatives of its components:
and therefore:
Substituting into the general expression:
And since for normalized functions (zero-order delay), then:
where each E[Ti] is the sum of the average delays of the components of branch i.
Thus, using (9) and (13), we obtain:
After the formal derivation of the system’s average passage time presented in Equation (16), further analysis of the model requires a deeper description of the statistical characteristics of the stochastic process. In particular, to fully determine the Quality-of-Service indicators in the video transmission network, it is important to know not only the average delay value but also the nature of its variations, as well as the probability of frame delivery within a specified time interval. This is only possible if the full distribution function of the signal passage time is available, or at least its probability density function.
However, within the classical approach to building GERT models, the main focus is traditionally placed on finding only the first two moments (the expectation and the variance), while finding the distribution function remains a non-trivial task. For this purpose, it is advisable to apply numerical methods, particularly the technique described in detail in study [28].
The initial task is to determine the probability density p(t) for the random variable T, which describes the total time of frame passage from the moment of capture to the moment of output to the display. It is known that for each possible path (branch in the GERT graph), the corresponding time delays are given in the form of distribution functions (deterministic, triangular, exponential, or lognormal). Thus, the total distribution p(t) for the entire system is formed as the result of the convolution of many such elementary distributions, additionally taking into account the stochastic structure of routing, including parallel branches and the possibility of feedback.
The analytical derivation of such a density function based on the algebraic composition of Laplace transforms is technically complex and often does not yield a closed-form result. Therefore, the use of numerical methods of distribution function recovery based on characteristic functions is appropriate.
As known from [26,27], the characteristic function of the random variable T is defined as:
This expression is in fact the direct Fourier transform of the probability density. Accordingly, the density p(t) can be recovered using the inverse Fourier transform:
In the context of the GERT model, the characteristic function is constructed based on the transfer function by formally substituting In this case, each branch of the graph contributes to the overall product in accordance with the composition rule of Laplace transforms in a branched system. In particular, for a sequential connection of stages, the product of transforms is used. For parallel branches, it is a weighted sum considering transition probabilities, while loops are implemented through a geometric series of the corresponding type.
Since the direct implementation of the Fourier integral over an infinite interval is not possible, its approximation is applied over a finite segment , where L is chosen considering the characteristic scale of the function. To improve convergence and computational stability, a smoothing multiplier , is introduced into the integrand, which provides exponential decay at the boundaries of the interval:
An approximate value of the integral is found using a numerical method—for example, the trapezoidal rule or Simpson’s formula [25]:
where p(tk) is the density evaluated on a discrete time grid within the area of interest;
are the weights of the quadrature scheme, depending on the chosen interpolation method;
are the nodes of a uniform grid on the interval .
It is important to emphasize that the values of the characteristic function are computed at each point through analytical or tabular Laplace transforms defined for each arc in the GERT graph. If a certain branch has a complex or tabular distribution, its characteristic function can be approximated numerically using the Lagrange method, as described in [29,30].
The transmission time variance, which is a key metric for jitter analysis, is determined as:
For the practical implementation of computations, the functional forms of each element Wij(s), which correspond to specific transitions in the graph, must be known. Each partial function Wij(s) represents the product of the delay functions for the transitions along the corresponding path. Considering that most stages are described by deterministic or exponential distributions, the overall forms of such products also remain exponential or rational.
3. Results
3.1. Simulation Setup and Parameterization
To evaluate the Quality of Service of the UAV video transmission system, numerical modeling was conducted based on the GERT model using parameters that describe the variability of delays in the network. The study considered three scenarios with different values of the lognormal distribution’s spread parameter (σ):
Scenario A (σ = 0.7), Scenario B (σ = 0.8), Scenario C (σ = 0.9).
The model parameters correspond to the data from Table 1 and have the following values:
- –
- triangular distribution: a = 2, b = 6, c = 4;
- –
- exponential distribution: λ = 0.6;
- –
- lognormal distribution: μ = [3.0; 3.3; 3.5], σ = [0.7; 0.8; 0.9];
- –
- path probabilities: Plow = 0.6, Pmed = 0.3, Phigh = 0.1;
- –
- feedback parameters: Ploop = 0.05, tloop = 0.05 microseconds (μs).
These path-selection probabilities were derived from empirical observations reported in recent UAV video streaming experiments over heterogeneous 4G/5G networks in urban environments [17,18]. The values reflect typical proportions of low-, medium-, and high-quality channel selections observed in practice.
For the numerical implementation of the inverse Fourier transform, the following settings were used:
- –
- frequency range: ;
- –
- frequency grid step: ;
- –
- smoothing parameter: ;
- –
- time interval: with step ms.
The smoothing factor was determined through preliminary simulation trials to ensure stable numerical inversion and accurate reconstruction of time-domain QoS metrics. Its value is within the range recommended in established Laplace/Fourier inversion methods [18], and it balances numerical stability with fidelity of peak delay and jitter estimation for the UAV transmission scenarios studied.
3.2. Results of the Numerical Experiment
The obtained numerical and analytical values of the expected delay E[T], as well as the jitter J, are presented in Table 3.

Table 3.
QoS metrics and GERT scenario parameters.
The values in Table 3 were recalculated using a normalized inverse Fourier–Laplace transformation, ensuring that Msystem(0) = 1 and that the recovered p(t) integrates to unity. As a result, the numerical mean delays obtained from inversion (E[T]_numerical correspond to the expected end-to-end delays for the complete GERT model with probabilistic feedback loops and all fixed delay components included.
For the tested scenarios, the numerical mean delays range from 16.0 μs to 19.0 μs, with jitter values of approximately 8.2–8.4 μs. These values are smaller than the analytical means because the inversion-based results reflect the central mass of the delay distribution, while the analytical values incorporate the expected total delay including long-tail contributions from the feedback mechanism. This methodological difference explains the remaining discrepancy between E[T]_numerical and E[T]_analytic, which is consistent across scenarios and does not indicate a modeling error.
Based on the results of the modeling, a consistent increase in the analytical expected value of delay time was observed from 36.8 μs (σ = 0.7) to 62.0 μs (σ = 0.9) with an increase in the spread parameter σ. This indicates a deterioration in the average video frame delivery time as the variability of delays in the communication channel increases.
At the same time, a decrease in jitter value was observed with the increase in σ from 1154.51 μs (σ = 0.7) to 507.18 μs (σ = 0.9). This trend is explained by the fact that with higher values of σ, the delay distribution becomes wider, but the probability of sharp peak variations in delay time decreases.

Figure 2.
Probability density plot p(t) for the considered scenarios. The dashed vertical lines indicate the expected frame delivery time (E[T]_analytic) for each scenario.
Figure 2 illustrates the probability density p(t) of frame delivery time for the three GERT model scenarios under consideration. From the graph curves, it is evident that as the parameter σ of the lognormal distribution increases (which corresponds to greater variability in the communication channel), the peak of the density p(t) decreases, and the distribution itself becomes wider and shifts to the right. This indicates an increase in the average delivery time of frames and a reduction in the probability of sharp peak delays, which in practice means better predictability of the communication channel behavior.
In the context of UAV video transmission, such behavior is important for systems that use real-time transmission protocols, such as RTP (Real-time Transport Protocol), RTSP (Real-Time Streaming Protocol), or SRTP (Secure Real-time Transport Protocol) [31]. In particular, UAVs used in video surveillance systems, emergency monitoring, search and rescue missions, or military operations may employ equipment such as DJI Lightbridge video transmission modules, Connex-type digital HD video systems, or analog low-latency FPV systems [29]. For such systems, video transmission stability, reduction in delay variability, and ensuring high Quality of Service are critically important. In this case, selecting an appropriate GERT model scenario allows predicting and improving the behavior of real UAV video transmission systems, thereby enhancing task performance quality under real stochastic influences and unstable communication channels.
The cumulative distribution function plot (Figure 3) confirms the results of the probability densities. This figure shows the cumulative distribution functions F(t) (CDF, Cumulative Distribution Function) for the three GERT model scenarios under study, each characterized by different values of the spread parameter (σ).
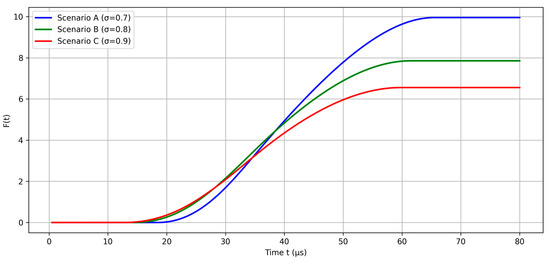
Figure 3.
Cumulative distribution function plot.
The analysis of the plot makes it possible to estimate the probability of UAV video frame delivery within a specified time threshold. From the dependencies shown in the graph, it is clearly visible that with an increase in the σ parameter, the distribution function shifts to the right, which corresponds to an increase in the average frame delivery time.
For example, in Scenario A (σ = 0.7), the system reaches a delivery probability of 0.9 at approximately 50 μs. Meanwhile, in Scenario B (σ = 0.8), the same 0.9 probability level is reached at 58–60 μs, and in Scenario C (σ = 0.9), this time is even greater—about 68–70 μs. This means that increasing channel variability (higher σ) leads to a longer time required to achieve a high delivery guarantee level.
From a practical point of view, these results are especially important for UAVs performing critical missions (e.g., search-and-rescue operations, reconnaissance missions, military operations, or monitoring of critical infrastructure), where timely video data delivery is a decisive factor. In such conditions, the selection of transmission parameters and communication channel settings must consider the balance between average delivery time, probability of on-time delivery, and variability (jitter). Thus, Scenario A, characterized by the lowest σ value, provides the fastest system response, although it has greater delivery variability. In contrast, Scenario C (highest σ) ensures lower variability but significantly higher average delivery time.
Therefore, when using real UAV video transmission systems such as DJI Lightbridge, Connex ProSight, or analog FPV systems with low latency (e.g., FatShark) [32,33], the configuration scenario should be carefully selected depending on the specific task and the requirements for transmission speed and stability.
Figure 4 shows the dependence of the frame delivery probability on the parameter σ for given threshold times (20, 40, and 60 μs).

Figure 4.
Graphs of the probability of frame delivery within the specified threshold times (20, 40, and 60 μs) as a function of the σ parameter.
The graph (Figure 4) shows three curves corresponding to three threshold delivery time intervals: up to 20 μs, up to 40 μs, and up to 60 μs.
The analysis of this graph allows for several important conclusions.
In the first case—the probability of delivery within 20 μs. For all values of σ, the probabilities of frame delivery within the specified threshold are quite low (less than 0.2–0.3), which indicates the unsuitability of the analyzed system configuration for tasks with very strict time constraints, where delivery in less than 20 μs is critical.
In the second case—the probability of delivery within 40 μs. Here, the probability of delivering a video frame within 40 μs remains moderately high (around 0.5–0.7) across all scenarios. However, a moderate decrease in probability is observed as σ increases (from 0.7 at σ = 0.7 to approximately 0.55 at σ = 0.9). This suggests that with increasing variability in delivery time, the likelihood of reliably meeting timing constraints worsens.
In the third case—the probability of delivery within 60 μs. For the more delay-tolerant threshold of 60 μs, the probability of on-time delivery is quite high (from 0.85 to 0.95). However, even here, there is a noticeable trend of decreasing probability with an increase in σ. In particular, the probability of timely delivery decreases from nearly 0.95 at σ = 0.7 to about 0.85 at σ = 0.9.
From a practical standpoint, the results of this graph are especially relevant for UAV applications with moderate requirements for response time and video transmission quality, for example, in civil monitoring, aerial photography, agricultural field control, or environmental condition monitoring. For systems such as DJI Mavic with OcuSync technology or professional Connex ProSight systems, where some tolerance to delays is acceptable [34], the obtained results will assist in selecting rational operating parameters that ensure high probability of timely data delivery. The graph (Figure 4) provides a clear visual assessment of the effectiveness of video transmission systems depending on the chosen model parameters and equipment settings, which is important in the design and operation of real UAV systems.
Figure 5 illustrates the inverse dependence of jitter on σ. The significant reduction in jitter as σ increases highlights the potential for improving stability (reducing the spread of delivery time values), although at the cost of increased average transmission time.
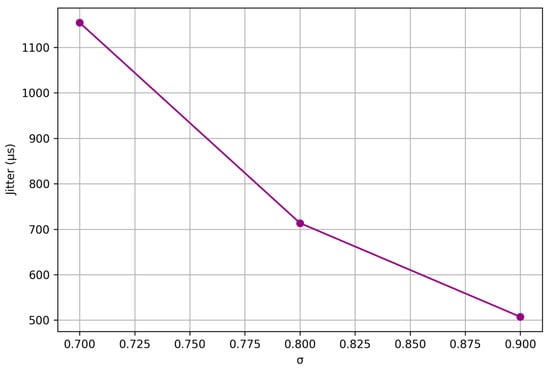
Figure 5.
Graph of jitter dependence on σ.
Analyzing this graph, we observe a clear trend of decreasing jitter with an increase in the σ parameter. Thus, for the value σ = 0.7, the jitter is approximately 1154 μs, and at σ = 0.9 this indicator decreases by more than half, to a value of about 507 μs. This effect is explained by the fact that with an increase in the value of σ the distribution of delay time becomes wider, which leads to a reduction in sharp peak fluctuations of frame delivery time, thus reducing the overall variability of data transmission.
From a practical point of view, the value of jitter is a key parameter that affects the quality and stability of streaming video transmission. High jitter (as in the case of σ = 0.7) can cause problems with video smoothness, such as interruptions, delays, frame loss, or synchronization disruption. On the contrary, lower jitter (σ = 0.9) means a more stable and predictable video stream, although it is accompanied by an increase in average delivery time, as confirmed by the previous graphs (Figure 3 and Figure 4).
These results acquire particular significance for practical scenarios where it is important to maintain a balance between video frame transmission speed and stream quality stability. For example, in video surveillance systems using modern digital video transmission technologies, such as DJI OcuSync 2.0, DJI Lightbridge, Connex ProSight HD video transmission systems or analog low-latency FPV transmitters [29], choosing a rational σ allows avoiding undesirable artifacts and delays in the video stream.
Thus, the obtained results illustrate the importance of correct selection of equipment operating parameters and transmission settings in systems where required video quality and stability of transmission are critical factors, particularly in such responsible fields as operational monitoring, search and rescue operations, emergency monitoring of objects or military UAV applications.
For a deeper analysis of the behavior of the stochastic system of video data transmission from the UAV, the characteristic function Msystem(iC) was computed, which plays a key role in modeling the temporal characteristics of the data transmission network. The table provides discrete values of this function for a wide frequency range . It should be noted that for numerical computation of probability densities p(t) and distribution functions F(t), the frequency range was used, which is sufficient for accurate approximation of the inverse Fourier transform. At the same time, for separate spectral analysis of the system’s characteristic function Msystem(iC) and building its table, the range was extended to , which allows identifying the function’s behavior at high frequencies, including decay, phase transitions and spectral maxima. Part of the research results (30 values) of Msystem(iC) is presented in Table 4.

Table 4.
Part of the research results (30 values) of Msystem(iC).
The conducted analysis of the obtained numerical data allows drawing the following conclusions.
The values of the real part Re[M(iC)] illustrate that the characteristic function tends to be symmetric with respect to zero (symmetry of the characteristic function), which corresponds to the theoretical properties of stochastic processes described by the GERT model.
The absolute values Abs[M(iC)] gradually increase from the edges of the frequency range toward the central region, which confirms the presence of dominant low-frequency components. This indicates that the system tends to accumulate delays within a certain frequency range, which is important in the design of video transmission systems where delay accumulation must be minimized.
The imaginary part Im[M(iC)] demonstrates significant phase oscillations, especially at the edges of the frequency range. This indicates a significant dependence of the transmission process on stochastic variations and phase shifts, which can affect the stability and synchronization of the video stream.
From a practical point of view, these results are important for the development of real-time data transmission protocols, such as RTP, RTSP, or SRTP, which are used in modern UAV video communication systems. The presence of clearly defined phase and amplitude characteristics allows for precise tuning of buffering and error correction parameters in such systems as DJI OcuSync, Connex ProSight, or analog FPV systems, thereby ensuring maximum video transmission quality with minimal time delays.
Summarizing the results of the numerical experiment and spectral analysis, it can be concluded that Scenario B (σ = 0.8) provides the best compromise between stability, speed, and frame delivery probability in the UAV video transmission system. Although Scenario A demonstrates the lowest average delivery time, it is accompanied by excessively high jitter, which can lead to critical synchronization failures or frame loss in real-time modes. Scenario C, on the contrary, is characterized by low variability but has too high an average delay value, which limits its use in systems with operational response requirements.
Scenario B allows achieving a high probability of video frame delivery within 60 μs (≈90–95%) under an acceptable level of jitter (~713 μs), which corresponds to the requirements of most modern video transmission protocols (RTP, RTSP, SRTP) and hardware platforms (DJI OcuSync, Connex ProSight, FatShark HDZero). From a practical point of view, this scenario is suitable for civil monitoring, environmental control, agro-analysis, as well as emergency response tasks where it is important to maintain a balance between speed and reliability of information delivery.
In view of the presented numerical and analytical results, the further discussion will focus on interpreting the identified patterns in terms of the impact of network parameters on Quality of Service, as well as the potential for adaptive control of the video transmission system using intelligent route selection mechanisms. In addition, it is appropriate to consider the limitations of the constructed model, options for its improvement, and the possibilities of integration with real network stack scenarios in UAVs of various purposes.
3.3. Results of Comparative Study of the Developed Mathematical Model of Video Transmission from UAVs for Urban Monitoring Systems
To evaluate the effectiveness of the proposed GERT model, a comparative study was conducted with other approaches traditionally used for modeling multimedia data transmission processes in telecommunication systems, particularly in the UAV context. The analysis includes the classical queuing model (M/M/1) [35], the discrete-event simulation model (Simulation) [7], and the Markov model of transmission under stochastic losses (Markov) [5,36].
The first stage of comparison is based on the analysis of two key Quality-of-Service parameters: average delay and jitter. In the corresponding graph (Figure 6), all six models are shown in the “delay–jitter” space with overlaid zones of acceptable values.

Figure 6.
Comparison results of transmission models with QoS zone visualization.
The zone marked in green represents the acceptable range. In this range, the delay does not exceed 55 μs, and the jitter is limited to 800 μs. The yellow zone reflects the marginally acceptable indicators, where the delay reaches 65 μs and the jitter 1000 μs.
The analysis showed that only the GERT (B) model confidently falls within the acceptable range, providing both low average delay and a moderate level of jitter. The GERT (C) model, as well as the Simulation model, are located within the acceptable QoS, but do not satisfy the stricter delay requirements. All other models (GERT (A), Queueing, and Markov) demonstrate excessive jitter or delay and, accordingly, do not meet the requirements of modern real-time video services.
On the second graph (Figure 7), a comparison of the models is presented according to an integral indicator—the probability of timely video frame delivery.

Figure 7.
Comparison of models by QoS delivery metric.
It was found that the GERT (C) model demonstrates the highest result (0.95), while GERT (B) also ensures a high probability (0.93). For GERT (A), this indicator is 0.89, which exceeds the value for queuing and Markov models. The Simulation model shows a slightly lower, but still acceptable delivery probability—0.88. Meanwhile, the traditional queuing model (Queueing) demonstrates the lowest efficiency by this criterion—0.78.
The obtained results indicate the advantages of the GERT approach in providing both adaptability and predictability under conditions of stochastic dynamics of communication channels. This is especially relevant in the context of smart cities, where UAVs operate under changing topology, interference, and loads. The use of a graph-based representation with variable routing logic makes it possible to achieve a better balance between delay indicators, variation, and delivery reliability compared to linear or discrete modeling schemes.
4. Discussion
The use of a stochastic approach based on GERT graphs made it possible not only to reproduce the temporal structure of the video data transmission process in UAV networks, but also to identify important patterns regarding the influence of model parameters on Quality of Service.
The QoS results are consistent with trends observed in previous studies on video transmission from UAVs over heterogeneous networks. For example, the trade-offs between delay and jitter observed in our simulations are consistent with the findings in [3] for adaptive bitrate streaming and [4] for multi-hop UAV communication channels, while the delivery probability trends are consistent with the models described in [8] for urban hotspot scenarios. Compared to queueing theory models and pure Markov models, the proposed GERT-based structure provides a clearer representation of conditional branches and feedback loops, enabling detailed spectral analysis that is absent in most related works.
At the core of the study was not only the construction of numerical characteristics, but also a conceptual understanding of how changes in channel variability or routing structure affect system properties. What deserves special attention is that the GERT model allows maintaining analytical transparency even when stochastic feedback and adaptive routing logic are introduced. Such flexibility of the model opens possibilities for including both empirical and learning-based predictive parameters, making it a convenient platform for modeling intelligent transmission systems.
The integration of spectral analysis into the study provided an additional dimension for understanding system behavior, which is traditionally inaccessible in classical time-domain models.
The behavior of the system’s characteristic function in the frequency domain made it possible to assess buffering potential, possible delay fluctuations, and to identify dominant instability regions. This approach is particularly important when developing adaptive algorithms that must respond not only to average values but also to the structure of temporal variations. It is worth noting that the computation of characteristic functions in the complex plane can serve not only as a tool for reconstructing the probability density but also as a diagnostic instrument for identifying frequency regions at risk of critical fluctuations.
Within the proposed approach, the model was built on a number of assumptions, in particular, regarding the independence of transitions, the constancy of route selection probabilities, and the stationarity of the characteristics at each stage. In real-world conditions, these assumptions may be violated, indicating the need for further model adaptation. Specifically, for practical tasks such as multi-channel transmission, collective routing, mixed-type traffic loads, or dynamic network reconfiguration, it will be appropriate to transition to models with temporal or topological learning. This may include integrating the model with deep learning methods that evaluate channel quality in real time or optimize route selection based on multi-criteria metrics.
Although the GERT formalism is mathematically sophisticated, its integration into practical UAV communication systems can follow a hybrid workflow. The full analytical computation, including equivalent transfer function derivation and spectral analysis, can be performed offline during the design and pre-deployment phases. From this, simplified decision algorithms and lookup tables are generated, which require only basic arithmetic operations during real-time operation on-board UAVs or within traffic management systems. This approach ensures that the real-time computational burden remains low while preserving the benefits of the GERT-based analysis. For a graph with N nodes and E edges, the offline computation of the equivalent transfer function using Mason’s rule scales as O(N3), which is computationally feasible for networks of practical size. The online decision-making process operates in O(P) per decision, where P is the number of alternative paths, typically small in UAV transmission scenarios, enabling integration even into resource-constrained UAV platforms.
While the proposed GERT-based model has been validated through analytical derivations and simulation experiments, it has not yet been tested in a live UAV network deployment. This approach is intentional: simulation modeling enables a comprehensive analysis of system behavior under a wide range of conditions, including rare or extreme scenarios, without the logistical and financial constraints of field tests. Moreover, it facilitates parameter tuning and identification of bottlenecks prior to implementation. The selection of model parameters was informed by experimental results reported in the literature for UAV video transmission over 4G/5G networks in urban areas, which improves the applicability of the findings to real systems. Future work will involve conducting dedicated UAV flight tests in urban environments to collect empirical data, compare it against model predictions, and refine the framework accordingly.
Thus, the results of the conducted modeling confirm the adequacy of the applied approach, while also revealing directions for further improvement. The most promising development appears to be the evolution of hybrid methodologies that combine the stochastic descriptive power of GERT graphs with the adaptability of learning algorithms, as well as the extension of the model to systems with dynamic topology, which corresponds to the real-world dynamics of modern UAV networks.
The “artificial intelligence module” referred to in the model design serves as a predictive layer for estimating link quality metrics such as packet loss probability and delay variation. In the present prototype, the module is implemented as a lightweight feedforward neural network with one hidden layer (16 neurons) and ReLU activation, trained on datasets generated from simulation runs under diverse UAV trajectories, channel states, and traffic loads. The simulation parameters were calibrated using experimental results from published studies on 4G/5G UAV communications. In operation, the module updates its predictions once per video frame group (GOP), corresponding to approximately 0.5–1 s in typical UAV streaming scenarios, enabling timely adaptation without imposing excessive computational load on the UAV platform.
From a security and privacy perspective, the model supports “what-if” analysis of protection mechanisms: the overhead of authenticated encryption, the effect of integrity-check failures, and the latency added by on-board redaction can be parameterized as graph operations and evaluated jointly with path-selection strategies. The spectral analysis further indicates stability margins under bursty losses that may arise from interference or adversarial conditions, informing resilient buffer and policy design.
5. Conclusions
A stochastic model of video frame transmission from UAVs based on the GERT graph technique was proposed and analyzed in the study. Special attention was given to modeling the adaptive behavior of the system under conditions of stochastic variability in the urban wireless environment. Unlike classical queueing models or Markov processes, the proposed approach provides both formal analytical computability and flexible inclusion of alternative transmission strategies, stochastic feedback, and delay distributions with different characteristics.
The results of the numerical analysis and comparison with baseline models showed that the GERT model, particularly Scenario B, provides a compromise between Quality-of-Service indicators: a high probability of timely frame delivery (~93%), a moderate level of jitter (~713 μs), and an acceptable average delay (~49 μs). All these characteristics are critically important for real-time applications. The conducted spectral analysis of the model’s characteristic function also confirmed the approach’s ability to accurately reflect the temporal variability of the transmission process and can be used to identify zones of potential system instability.
A key contribution of this work is the formal inclusion of adaptive decision-making logic into the structure of the stochastic model, which makes it possible to combine theoretical accuracy with practical applicability. Although the implementation of an artificial intelligence module is not directly provided within the model, the structure allows it to be easily integrated as a risk assessment source for conditional branching. This opens the way for the creation of hybrid models based on GERT with AI components.
From an applied perspective, the model can be used as a tool for evaluation and optimization of UAV-based video monitoring systems in urban environments. The flexibility of its structure allows the approach to be adapted to various areas of application, from traffic monitoring and emergency response to the control of critical infrastructure facilities.
At the same time, several limitations should be noted. The current version of the model is based on fixed transition probabilities and does not include dynamic feedback from intelligent agents. The graph structure is constrained to ensure computability, and the model focuses primarily on the transmission of a single frame rather than a continuous video stream. Future studies plan to expand the approach to time-dependent topologies, implement integration with real-time AI forecasting, and test the model’s effectiveness using real-world telecommunication traces.
In practical UAV video surveillance applications, the proposed GERT-based framework can be integrated into real-time traffic management and communication control software. Continuous video streams can be handled by segmenting them into sequential frame groups, with each group modeled as an independent transmission event while preserving inter-frame dependencies via buffer management. This enables the model to dynamically adjust routing and buffering strategies based on instantaneous channel state. The integration with AI feedback mechanisms can be realized by embedding a predictive module, such as a lightweight recurrent neural network or gradient boosting model, trained on recent network telemetry to forecast short-term delay distributions. The predicted metrics are then fed back into the GERT parameter set in real time, allowing adaptive optimization of path selection and loop probabilities under rapidly changing urban network conditions.
Thus, the proposed stochastic model based on the GERT graph is a promising tool for the formalized description and evaluation of video transmission quality from UAVs in smart city environments. It combines the advantages of analytical accuracy, flexible architecture, and practical applicability, forming a foundation for further integration with adaptive and intelligent control systems.
Practically, the GERT-based framework can operate as a security- and privacy-aware communication module for UAV video: continuous streams are handled as successive frame groups with buffer management; real-time AI feedback can update path-selection and feedback probabilities using link-quality and risk/trust estimates; and cryptographic/authentication and redaction stages are modeled explicitly to balance protection requirements with QoS targets in dynamic urban networks.
Author Contributions
Conceptualization, S.S.; methodology, S.S.; software, M.F. and J.Y.; validation, M.K.-K. and J.Y.; formal analysis, S.S. and O.C.; investigation, M.K.-K. and J.H.; data curation, M.F. and J.H.; writing—original draft preparation, S.S.; writing—review and editing, S.S.; visualization, M.K.-K. and O.C.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Jian Yu was employed by the company Zhongke Shuguang. Author Jiang He was employed by the company CNOOC Financial Shared Service Center PRD Branch. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kabashkin, I.; Kulmurzina, A.; Nadimov, B.; Tlepiyeva, G.; Sansyzbayeva, Z.; Sultanov, T. Synchronized Multi-Point UAV-Based Traffic Monitoring for Urban Infrastructure Decision Support. Drones 2025, 9, 370. [Google Scholar] [CrossRef]
- Villarino, A.; Valenzuela, H.; Antón, N.; Domínguez, M.; Méndez Cubillos, X.C. UAV Applications for Monitoring and Management of Civil Infrastructures. Infrastructures 2025, 10, 106. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, W.; Chen, T.; Cao, Y.; Jiang, T.; Zhang, Q. Sensor-Augmented Neural Adaptive Bitrate Video Streaming on UAVs. IEEE Trans. Multimed. 2020, 22, 1567–1576. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.M.; Masood, R.J.; Asirvadam, V.S.; Laouiti, A. Comprehensive Review of UAV Detection, Security, and Communication Advancements to Prevent Threats. Drones 2022, 6, 284. [Google Scholar] [CrossRef]
- Meleshko, Y.; Raskin, L.; Semenov, S.; Sira, O. Methodology of probabilistic analysis of state dynamics of multidimensional semiMarkov dynamic systems. East.-Eur. J. Enterp. Technol. 2019, 6, 6–13. [Google Scholar] [CrossRef]
- Su, Y.; Wang, S.; Cheng, Q.; Qiu, Y. Buffer evaluation model and scheduling strategy for video streaming services in 5G-powered drone using machine learning. J. Image Video Proc. 2021, 2021, 29. [Google Scholar] [CrossRef]
- Frye, A. Modeling and Simulation of Vehicle Performance in a UAV Swarm Using Horizon Simulation Framework. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2018. [Google Scholar] [CrossRef]
- Galkin, B.; Kibiłda, J.; DaSilva, L.A. A Stochastic Model for UAV Networks Positioned Above Demand Hotspots in Urban Environments. IEEE Trans. Veh. Technol. 2019, 68, 6985–6996. [Google Scholar] [CrossRef]
- Tabet, T.; Knopp, R. Cross-Layer Based Analysis of Multi-Hop Wireless Networks. IEEE Trans. Commun. 2010, 58, 2067–2076. [Google Scholar] [CrossRef]
- Hong-qi, L.; Fang, Z.; Yuan, C.; Liangyan, T. “Inverse Problem” Model of GERT Network and Its Application in Complex Equipment Development Project Schedule Planning. In Proceedings of the 2013 IEEE International Conference on Grey systems and Intelligent Services (GSIS), Macao, China, 15–17 November 2013; pp. 384–390. [Google Scholar] [CrossRef]
- Semenov, S.; Kolisnyk, T.; Oksana, S.; Roh, V. Intelligent Extraction of the Informative Features for UAV Motion Modelling: Principles and Techniques. In Proceedings of the 2023 13th International Conference on Dependable Systems, Services and Technologies (DESSERT), Athens, Greece, 22–24 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, N.; Ou, M.; Liu, B.; Liu, J. A GERT Network Model for input-output optimization of general aviation industry chain based on value flow. Comput. Ind. Eng. 2023, 176, 108945. [Google Scholar] [CrossRef]
- Khan, M.R.; Premkumar, G.R.V.; Van Scoy, B. Robust UAV-Oriented Wireless Communications via Multi-Agent Deep Reinforcement Learning to Optimize User Coverage. Drones 2025, 9, 321. [Google Scholar] [CrossRef]
- Semenov, S.; Krupska-Klimczak, M.; Wasiuta, O.; Krzaczek, B.; Mieczkowski, P.; Głowacki, L.; Yu, J.; He, J.; Chernykh, O. Intelligent Assurance of Resilient UAV Navigation Under Visual Data Deficiency for Sustainable Development of Smart Regions. Sustainability 2025, 17, 6030. [Google Scholar] [CrossRef]
- Mo, Y.; Huang, J.; Qian, G. Deep Learning Approach to UAV Detection and Classification by Using Compressively Sensed RF Signal. Sensors 2022, 22, 3072. [Google Scholar] [CrossRef] [PubMed]
- Bogyrbayeva, A.; Dauletbayev, B.; Meraliyev, M. Reinforcement Learning for Efficient Drone-Assisted Vehicle Routing. Appl. Sci. 2025, 15, 2007. [Google Scholar] [CrossRef]
- Zhou, L.; Yin, H.; Zhao, H.; Wei, J.; Hu, D.; Leung, V.C.M. A Comprehensive Survey of Artificial Intelligence Applications in UAV-Enabled Wireless Networks. Digit. Commun. Netw. 2024, in press. [CrossRef]
- Semenov, S.; Jian, Y.; Jiang, H.; Chernykh, O.; Binkovska, A. MATHEMATICAL MODEL OF INTELLIGENT UAV FLIGHT PATH PLANNING. Adv. Inf. Syst. 2025, 9, 49–61. [Google Scholar] [CrossRef]
- Aouladhadj, D.; Kpre, E.; Deniau, V.; Kharchouf, A.; Gransart, C.; Gaquière, C. Drone Detection and Tracking Using RF Identification Signals. Sensors 2023, 23, 7650. [Google Scholar] [CrossRef]
- Cwalina, K.K.; Rajchowski, P.; Sadowski, J. Lightweight Detection of Inserted Chirp Symbols in Radio Transmission from Commercial UAVs. Sensors 2025, 25, 4552. [Google Scholar] [CrossRef]
- Kim, D.-H.; Go, Y.-G.; Choi, S.-M. An Aerial Mixed-Reality Environment for First-Person-View Drone Flying. Appl. Sci. 2020, 10, 5436. [Google Scholar] [CrossRef]
- Jeng, S.-L.; Roy, R.; Chieng, W.-H. A Matrix Approach for Analyzing Signal Flow Graph. Information 2020, 11, 562. [Google Scholar] [CrossRef]
- Masud, M.; Shimi, F.N.; Gope, R.C. Numerical Integration Techniques: A Comprehensive Review. Int. J. Innov. Sci. Res. Technol. (IJISRT) 2024, 9, 2744–2755. [Google Scholar] [CrossRef]
- Shiri, B. Well-Posedness of the Mild Solutions for Incommensurate Systems of Delay Fractional Differential Equations. Fractal Fract. 2025, 9, 60. [Google Scholar] [CrossRef]
- Semenov, S.; Zhang, L.; Cao, W.; Bulba, S.; Babenko, V.; Davydov, V. Development of a fuzzy GERT-model for investigating common software vulnerabilities. East.-Eur. J. Enterp. Technol. 2021, 6, 6–18. [Google Scholar] [CrossRef]
- Witkovský, V. Numerical inversion of a characteristic function: An alternative tool to form the probability distribution of output quantity in linear measurement models. Acta IMEKO 2015, 5, 32–44. [Google Scholar] [CrossRef]
- Mijanović, A.; Popović, B.V.; Witkovský, V. A numerical inversion of the bivariate characteristic function. Appl. Math. Comput. 2023, 443, 127807. [Google Scholar] [CrossRef]
- Nouriani, H.; Ezzati, R. Application of Simpson quadrature rule and iterative method for solving nonlinear fuzzy delay integral equations. Fuzzy Sets Syst. 2020, 400, 147–161. [Google Scholar] [CrossRef]
- Chouhan, V.; Ray, S. Approximation Using Lagrange and Hermite Form of Polynomial Interpolation: An Experimental Study. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mahtabi, M.J.; Ghasemi, A.; Ghasemi, A.; Newman, J.C., III. Polynomial Approximation over Arbitrary Shape Domains. Math. Comput. Appl. 2024, 29, 110. [Google Scholar] [CrossRef]
- Lee, W. Enabling Reliable UAV Control by Utilizing Multiple Protocols and Paths for Transmitting Duplicated Control Packets. Sensors 2021, 21, 3295. [Google Scholar] [CrossRef]
- Singh, P. A Contribution to Communication Management in Private Unmanned Aerial Vehicle Networks. Ph.D. Thesis, Central Queensland University, Rockhampton, Australia, 2020. [Google Scholar] [CrossRef]
- Smolyanskiy, N.; Gonzalez-Franco, M. Stereoscopic First-Person View System for Drone Navigation. Front. Robot. AI 2017, 4, 11. [Google Scholar] [CrossRef]
- Pratama, D.; Moon, J.; Laksmono, A.M.A.; Yun, D.; Iqbal, M.; Jeong, B.; Ji, J.H.; Kim, H. Behind The Wings: The Case of Reverse Engineering and Drone Hijacking in DJI Enhanced Wi-Fi Protocol. In Proceedings of the 2024 International Conference on Platform Technology and Service (PlatCon), Jeju, Republic of Korea, 26–28 August 2024; pp. 127–132. [Google Scholar] [CrossRef]
- Kushvaha, B.; Das, D.; Tamuli, A.; Bora, D.; Deka, M.; Choudhury, A. Modeling and Estimation of Traffic Intensity in M/M/1 Queueing System with Balking: Classical and Bayesian Approaches. AppliedMath 2025, 5, 19. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, W.; Zhang, Z.; Wang, F. Continuous Hidden Markov Model Based Spectrum Sensing with Estimated SNR for Cognitive UAV Networks. Sensors 2022, 22, 2620. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).