Wake Turbulence Induced by Local Blade Oscillation in a Linear Cascade
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Hot-Wire Anemometry: Principles, Calibration, and Uncertainty Analysis
3. Results and Discussion
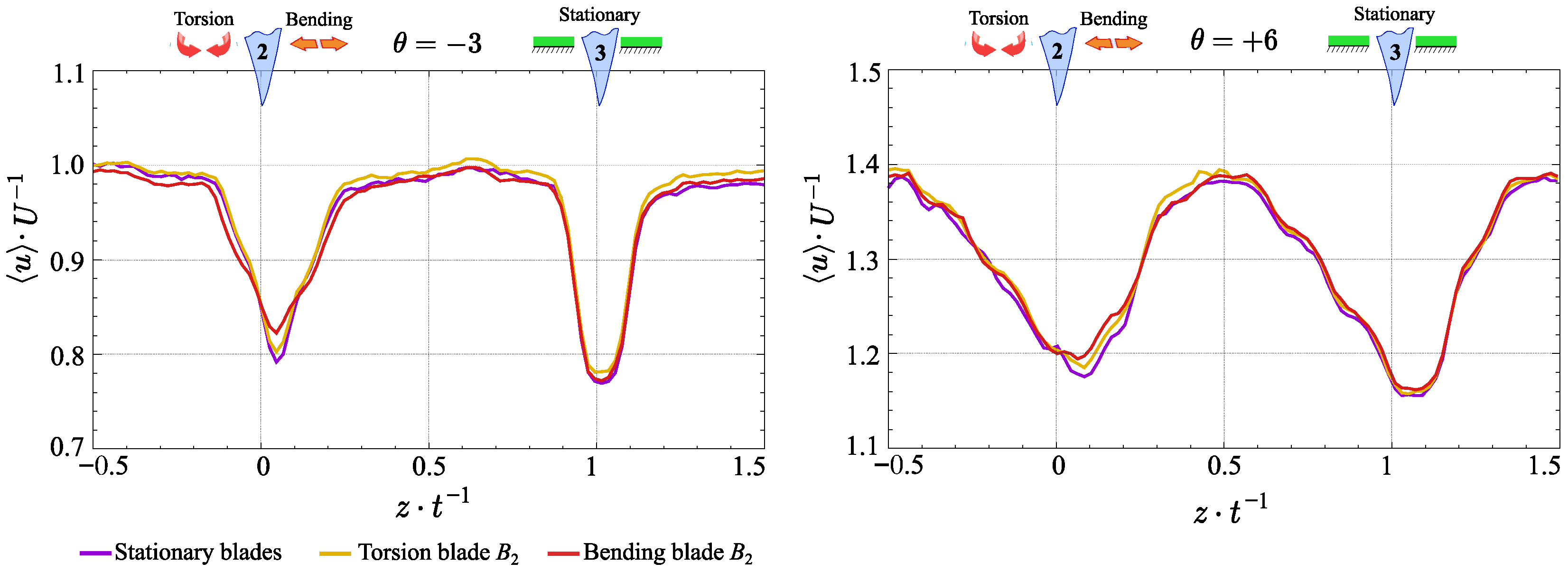
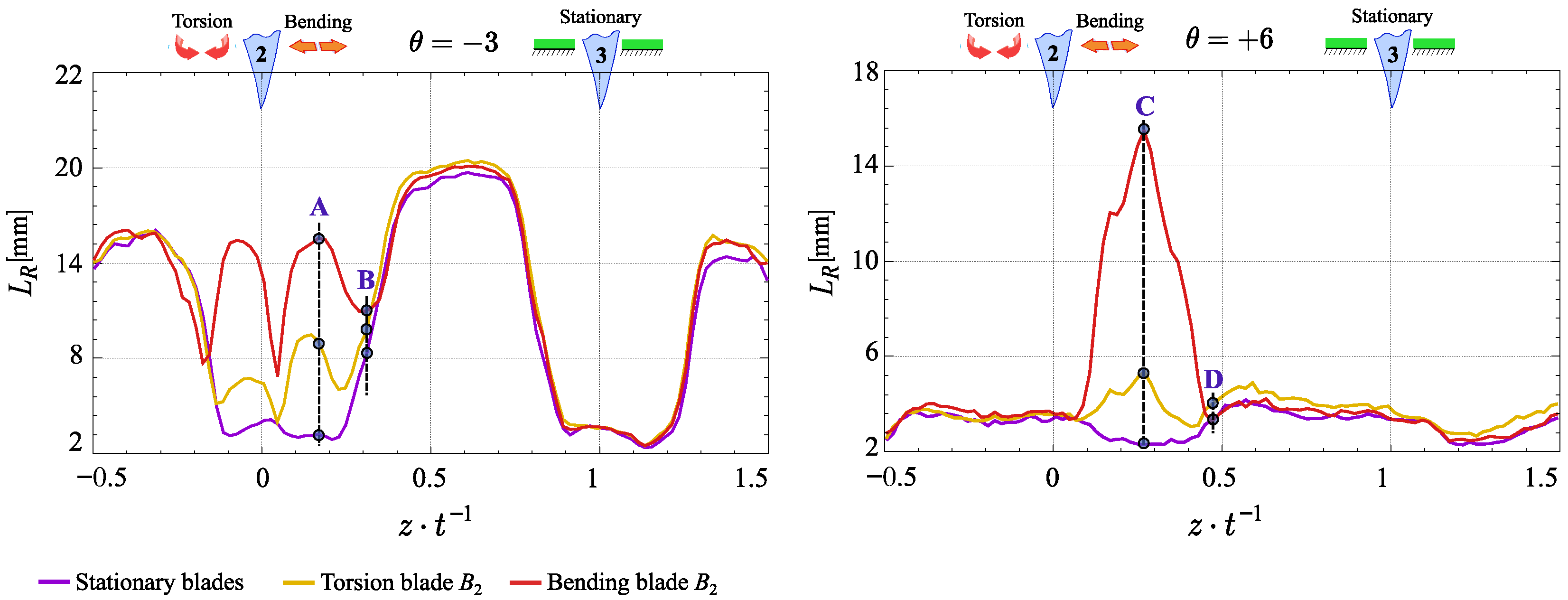
3.1. Wake Topology
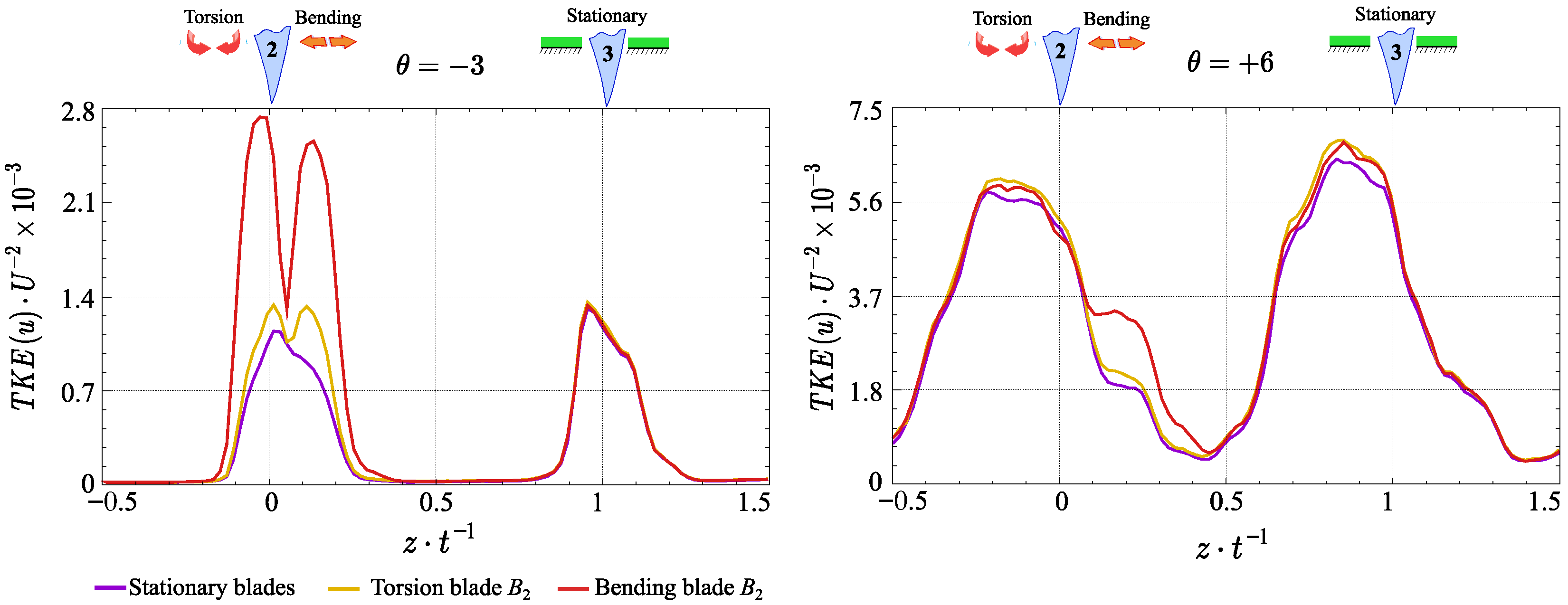
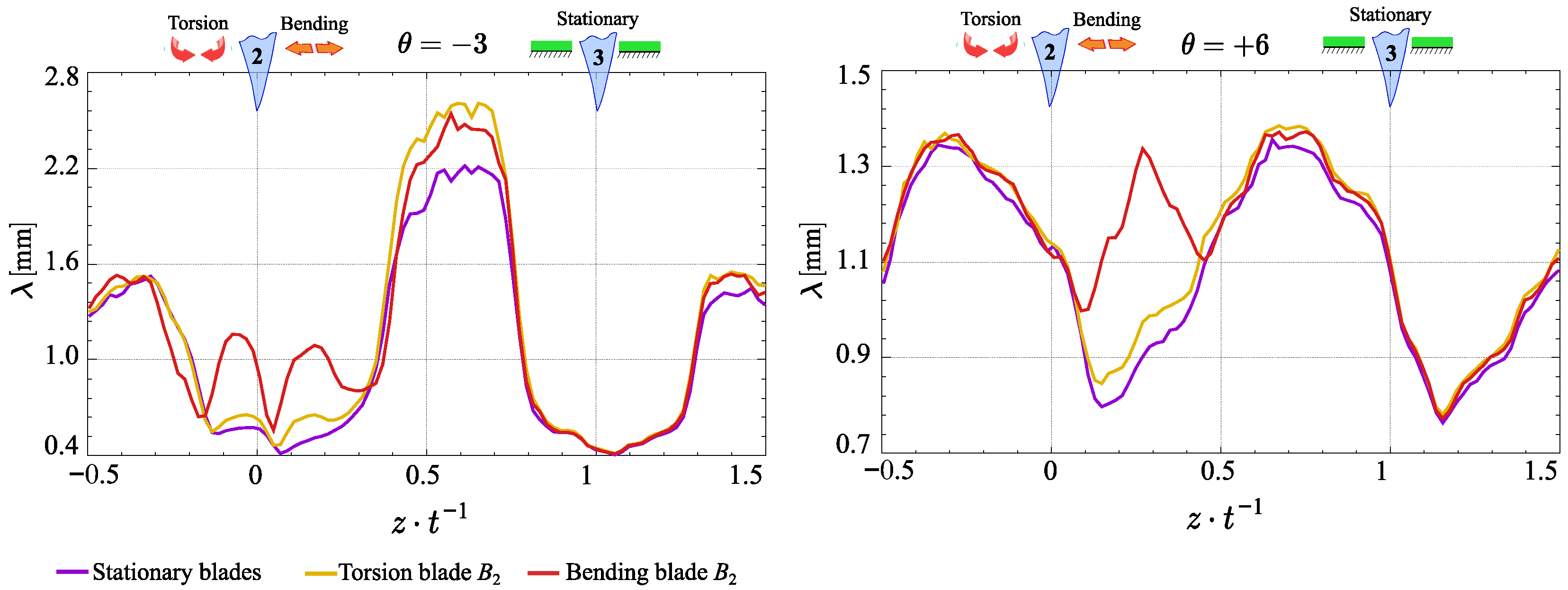
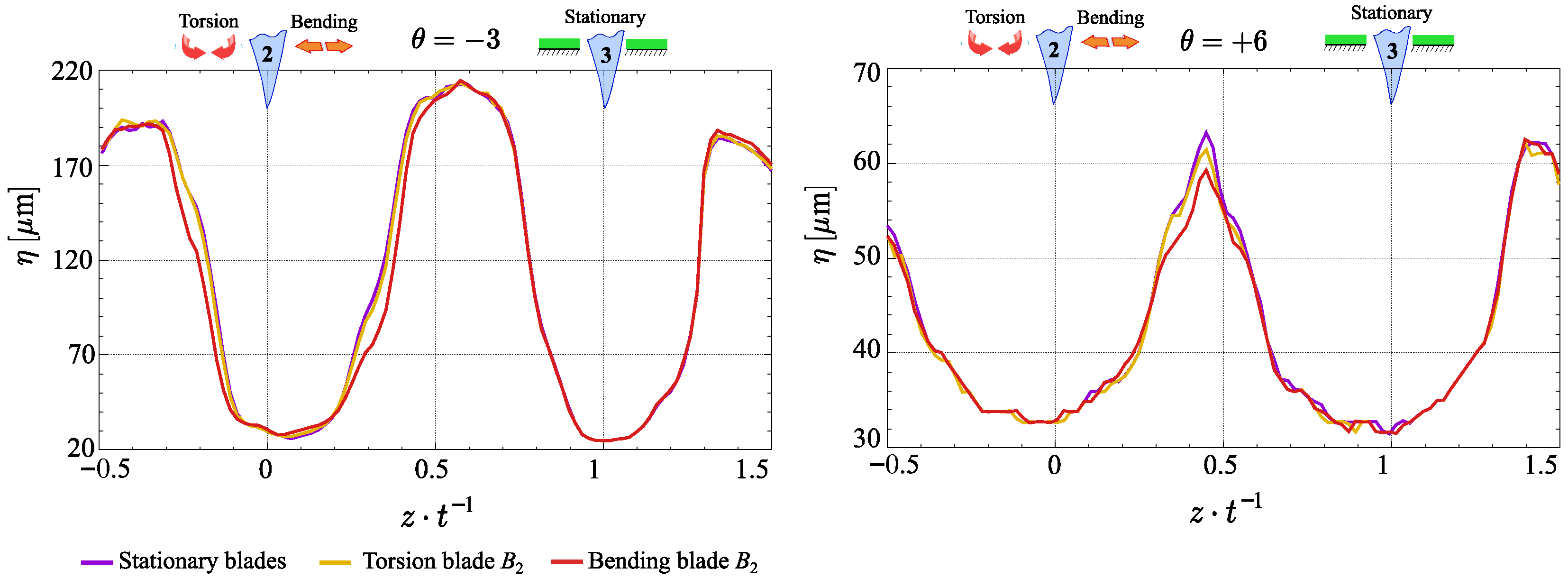
3.2. Turbulence Structure Evaluation
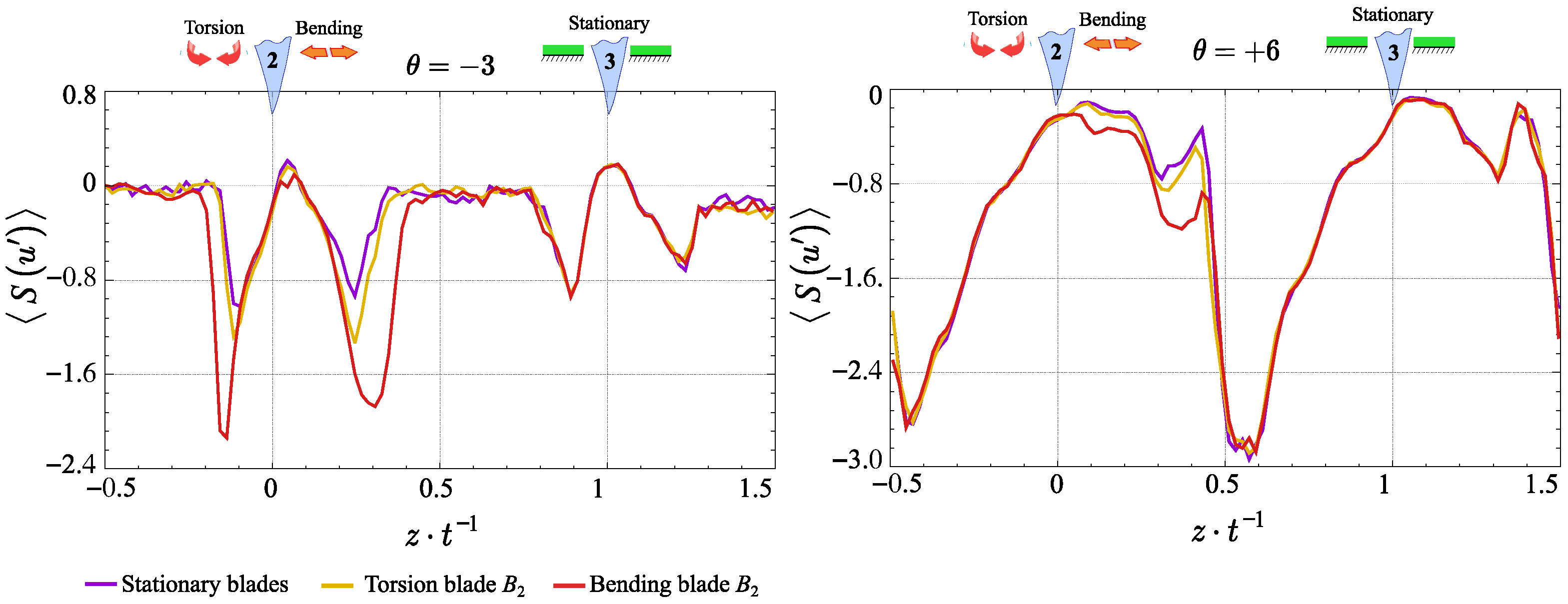
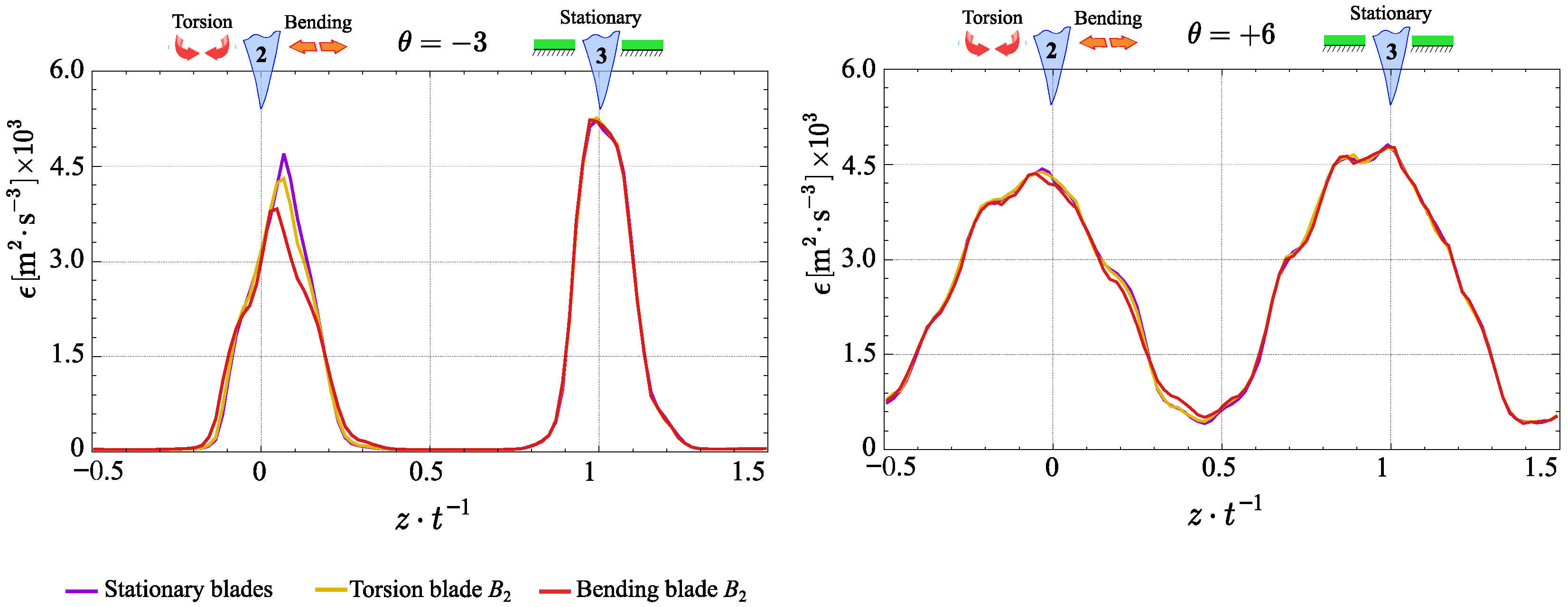
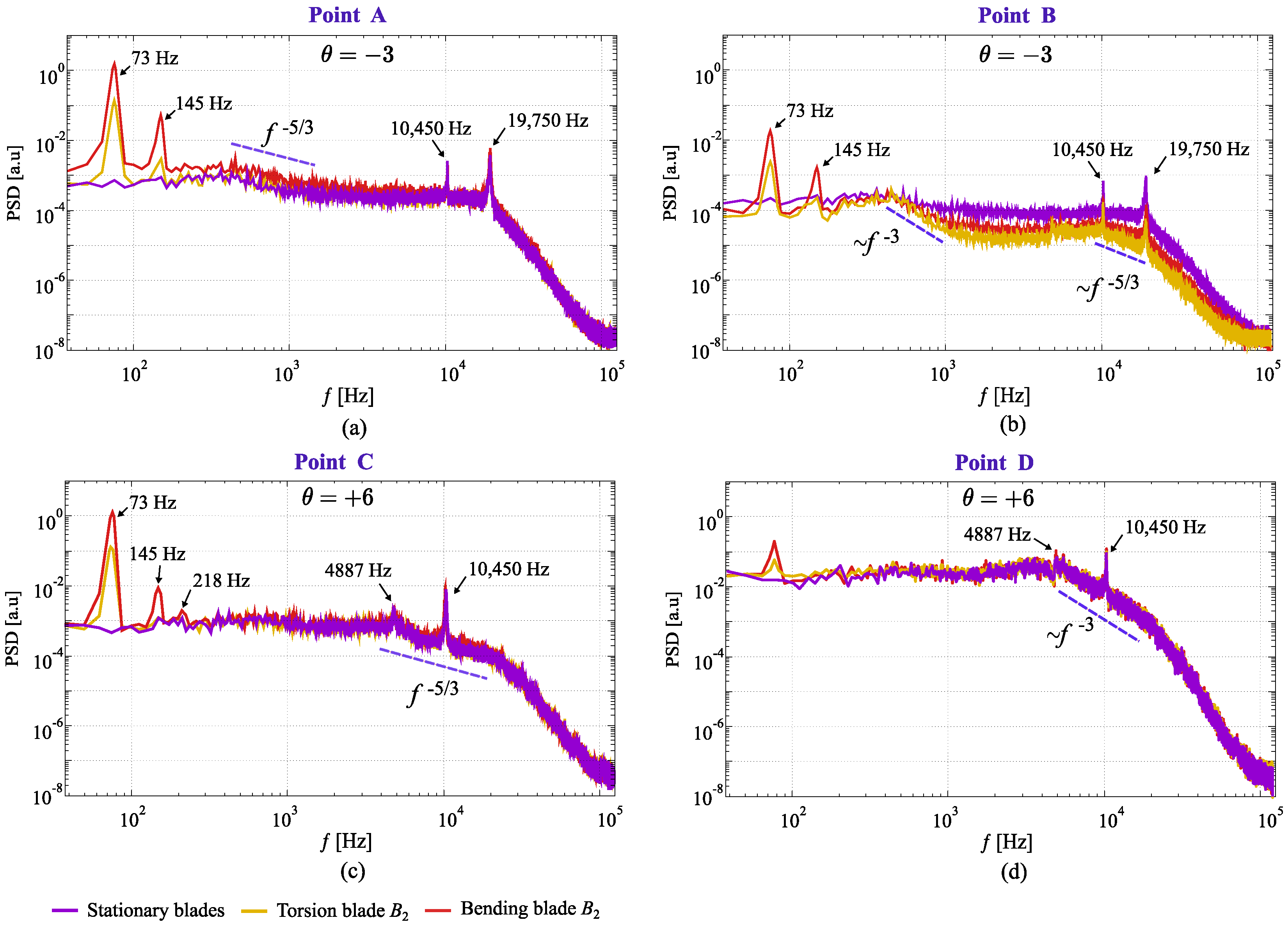
3.3. Spectrum Analyses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eret, P.; Hoznedl, M. Effect of Manufacturing Processes on Blade Throat Size and Position in a Steam Turbine Diaphragm. J. Mach. Eng. 2022, 22, 148–160. [Google Scholar] [CrossRef]
- Tucker, P. Computation of unsteady turbomachinery flows: Part 1—Progress and challenges. Prog. Aerosp. Sci. 2011, 47, 522–545. [Google Scholar] [CrossRef]
- Fürst, J.; Lasota, M.; Lepicovsky, J.; Musil, J.; Pech, J.; Šidlof, P.; Šimurda, D. Effects of a Single Blade Incidence Angle Offset on Adjacent Blades in a Linear Cascade. Processes 2021, 9, 1974. [Google Scholar] [CrossRef]
- Rahmati, M.; He, L.; Wells, R. Interface Treatment for Harmonic Solution in Multi-Row Aeromechanic Analysis. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea and Air, Glasgow, UK, 14–18 June 2010; Volume 6, pp. 1253–1261. [Google Scholar] [CrossRef]
- Erfanian Nakhchi, M.; Win Naung, S.; Rahmati, M. Direct Numerical Simulations of Turbulent Flow over Low-Pressure Turbine Blades with Aeroelastic Vibrations and Inflow Wakes. Energies 2023, 16, 2803. [Google Scholar] [CrossRef]
- Naung, S.W.; Rahmati, M.; Farokhi, H. Direct Numerical Simulation of Interaction between Transient Flow and Blade Structure in a Modern Low-Pressure Turbine. Int. J. Mech. Sci. 2021, 192, 106104. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Y.; Tan, W. Aerodynamic wake oscillator for modeling flow-induced vibration of tandem cylinders with short spans. Int. J. Mech. Sci. 2021, 204, 106–548. [Google Scholar] [CrossRef]
- Wang, X.; Zou, Z. Uncertainty analysis of impact of geometric variations on turbine blade performance. Energy 2019, 176, 67–80. [Google Scholar] [CrossRef]
- Camp, T.R.; Shin, H.W. Turbulence Intensity and Length Scale Measurements in Multistage Compressors. J. Turbomach. 1995, 117, 38–46. [Google Scholar] [CrossRef]
- Oro, J.; Argüelles Díaz, K.; Santolaria, C.; Marigorta, E. On the structure of turbulence in a low-speed axial fan with inlet guide vanes. Exp. Therm. Fluid Sci. 2007, 32, 316–331. [Google Scholar] [CrossRef]
- Maunus, J.; Grace, S.; Sondak, D.; Yakhot, V. Characteristics of Turbulence in a Turbofan Stage. J. Turbomach. 2012, 135, 021024. [Google Scholar] [CrossRef]
- Odier, N.; Duchaine, F.; Gicquel, L.; Staffelbach, G.; Thacker, A.; Rosa, N.; Dufour, G.; Mueller, J.D. Evaluation of Integral Turbulence Scale Through the Fan Stage of a Turbofan Using Hot Wire Anemometry and Large Eddy Simulation. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; p. V02CT42A021. [Google Scholar] [CrossRef]
- Eret, P.; Tsymbalyuk, V. Experimental Subsonic Flutter of a Linear Turbine Blade Cascade with Various Mode Shapes and Chordwise Torsion Axis Locations. J. Turbomach. 2022, 145, 061002. [Google Scholar] [CrossRef]
- Bruun, H. Interpretation of a hot wire signal using a universal calibration law. J. Phys. E Sci. Instrum. 1971, 4, 225–231. [Google Scholar] [CrossRef]
- Bruun, H. Hot wire data corrections in low and in high turbulence intensity flows. J. Phys. E Sci. Instrum. 1972, 5, 812–818. [Google Scholar] [CrossRef]
- Jonás, P. Rotary slanted single wire CTA—A useful tool for 3D flows investigations. EPJ Web Conf. 2013, 45, 01047. [Google Scholar] [CrossRef]
- Nix, A.; Smith, A.; Diller, T.; Ng, W.; Thole, K. High Intensity, Large Length-Scale Freestream Turbulence Generation in a Transonic Turbine Cascade. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; pp. 961–968. [Google Scholar] [CrossRef]
- King, L.V.; Barnes, H.T. On the convection of heat from small cylinders in a stream of fluid: Determination of the convection constants of small platinum wires, with applications to hot-wire anemometry. Proc. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1914, 90, 563–570. [Google Scholar] [CrossRef]
- Andrews, G.E.; Bradley, D.; Hundy, G. Hot wire anemometer calibration for measurements of small gas velocities. Int. J. Heat Mass Transf. 1972, 15, 1765–1786. [Google Scholar] [CrossRef]
- Bruun, H.H. Hot-Wire Anemometry: Principles and Signal Analysis; Oxford University Press: Oxford, UK, 1995; p. 507. [Google Scholar]
- Standard PTC 19.1-2018 (R2018); Test Uncertainty. American Society of Mechanical Engineers: New York, NY, USA, 2018.
- Finn, E. How to Measure Turbulence with Hot-Wire Anemometers—A Practical Guide; Dantec Dynamics A/S: Nozay France, 2002; p. 54. [Google Scholar]
- Duda, D.; Yanovych, V.; Tsymbalyuk, V.; Uruba, V. Effect of Manufacturing Inaccuracies on the Wake Past Asymmetric Airfoil by PIV. Energies 2022, 15, 1227. [Google Scholar] [CrossRef]
- Yanovych, V.; Duda, D.; Uruba, V.; Kosiak, P. The structure of turbulent flow behind the NACA 0012 airfoil at high angles of attack and low Reynolds number. MATEC Web Conf. 2021, 345, 00034. [Google Scholar] [CrossRef]
- Nakhchi, M.; Naung, S.; Rahmati, M. Influence of blade vibrations on aerodynamic performance of axial compressor in gas turbine: Direct numerical simulation. Energy 2022, 242, 122988. [Google Scholar] [CrossRef]
- Dróżdż, A.; Niegodajew, P.; Romańczyk, M.; Elsner, W. Convection velocity in turbulent boundary layers under adverse pressure gradient. Exp. Therm. Fluid Sci. 2023, 145, 110900. [Google Scholar] [CrossRef]
- Berni, C.; Suarez, L.; Michallet, H.; Barthélemy, E. Asymmetry and Skewness in the bottom boundary layer: Small scale experiments and numerical model. Coast. Eng. Proc. 2012, 1, waves.25. [Google Scholar] [CrossRef]
- Jelly, T.; Nardini, M.; Sandberg, R.; Vitt, P.; Sluyter, G. Effects of Localized Non-Gaussian Roughness on High-Pressure Turbine Aerothermal Performance: Convective Heat Transfer, Skin Friction, and the Reynolds’ Analogy. J. Turbomach. 2024, 147, 051017. [Google Scholar] [CrossRef]
- Davies, P. Structure of turbulence. J. Sound Vib. 1973, 28, 513–526. [Google Scholar] [CrossRef]
- Tropea, C.; Yarin, A.; Foss, J. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Pouransari, Z.; Vervisch, L.; Johansson, A. Reynolds Number Effects on Statistics and Structure of an Isothermal Reacting Turbulent Wall-Jet. Flow Turbul. Combust. 2014, 92, 931–945. [Google Scholar] [CrossRef]
- Tennekes, H.; Lumley, J. A First Course in Turbulence, 1st ed.; The MIT Press: Cambridge, MA, USA, 1972; p. 300. [Google Scholar]
- Corrsin, S. The Structure of Turbulent Shear Flow (A. A. Townsend). SIAM Rev. 1979, 21, 581–583. [Google Scholar] [CrossRef]
- Bourgoin, M.; Baudet, C.; Kharche, S.; Mordant, N.; Vandenberghe, T.; Sumbekova, S.; Stelzenmuller, N.; Aliseda, A.; Gibert, M.; Roche, P.E.; et al. Investigation of the small-scale statistics of turbulence in the Modane S1MA wind tunnel. CEAS Aeronaut. J. 2018, 9, 269–281. [Google Scholar] [CrossRef]
- Yanovych, V.; Duda, D.; Uruba, V. Structure turbulent flow behind a square cylinder with an angle of incidence. Eur. J. Mech. B/Fluids 2021, 85, 110–123. [Google Scholar] [CrossRef]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: New York, NY, USA, 1982; p. 197. [Google Scholar]
- Katul, G.G.; Parlange, M.B. Analysis of Land Surface Heat Fluxes Using the Orthonormal Wavelet Approach. Water Resour. Res. 1995, 31, 2743–2749. [Google Scholar] [CrossRef]
- Hinze, J. Turbulence: McGraw-Hill Series in Mechanical Engineering; Cambridge University Press: Newcastle, DE, USA, 1975; p. 790. [Google Scholar]
- Tritton, D. Physical Fluid Dynamics, 2nd ed.; Clarendon Press: Oxford, UK, 1988; p. 346. [Google Scholar]
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Flow 1987, 8, 82–92. [Google Scholar] [CrossRef]
- Pearson, B.; Krogstad, P.Å.; Van De Water, W. Measurements of the turbulent energy dissipation rate. Phys. Fluids 2002, 14, 1288–1290. [Google Scholar] [CrossRef]
- Siebert, H.; Lehmann, K.; Wendisch, M. Observations of small-scale turbulence and energy dissipation rates in the cloudy boundary layer. J. Atmos. Sci. 2006, 63, 1451–1466. [Google Scholar] [CrossRef]
- Muschinski, A.; Frehlich, R.; Balsley, B. Small-scale and large-scale intermittency in the nocturnal boundary layer and the residual layer. J. Fluid Mech. 2004, 515, 319–351. [Google Scholar] [CrossRef]
- Sreenivasan, K. An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 1998, 10, 528–529. [Google Scholar] [CrossRef]
- Kolmogorov, A. Dissipation of Energy in Locally Isotropic Turbulence. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1991, 1890, 15–17. [Google Scholar] [CrossRef]
- Yanovych, V.; Duda, D.; Uruba, V.; Tomášková, T. Hot-Wire Investigation of Turbulence Topology behind Blades at Different Shape Qualities. Processes 2022, 10, 522. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Davidson, P. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Yanovych, V.; Duda, D.; Uruba, V.; Antoš, P. Anisotropy of turbulent flow behind an asymmetric airfoil. SN Appl. Sci. 2021, 3, 885. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Levin, V.; Hunt, J.C.R.; Phillips, O.M.; Williams, D. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Sreenivasan, K. On the universality of the Kolmogorov constant. Phys. Fluids 1995, 7, 2778–2784. [Google Scholar] [CrossRef]
- Dallas, V.; Fauve, S.; Alexakis, A. Statistical Equilibria of Large Scales in Dissipative Hydrodynamic Turbulence. Phys. Rev. Lett. 2015, 115, 204501. [Google Scholar] [CrossRef]
- Cameron, A.; Alexakis, A.; Brachet, M.E. The effect of helicity on the correlation time of large scale turbulent flows. Phys. Rev. Fluids 2017, 2, 114602. [Google Scholar] [CrossRef]
- Cichowlas, C.; Bonaïti, P.; Debbasch, F.; Brachet, M.E. Effective Dissipation and Turbulence in Spectrally Truncated Euler Flows. Phys. Rev. Lett. 2006, 95, 264502. [Google Scholar] [CrossRef]
- Alexakis, A. Quasi-two-dimensional turbulence. Rev. Mod. Plasma Phys. 2023, 7, 31. [Google Scholar] [CrossRef]
- Kraichnan, R.H.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Inertial Ranges in Two-Dimensional Turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef]
- Leith, C.E. Diffusion Approximation for Two-Dimensional Turbulence. Phys. Fluids 1968, 11, 671–672. [Google Scholar] [CrossRef]
- Batchelor, G.K. Computation of the Energy Spectrum in Homogeneous Two-Dimensional Turbulence. Phys. Fluids 1969, 12, 233–239. [Google Scholar] [CrossRef]
- Khatri, H.; Griffies, S.; Uchida, T.; Wang, H.; Menemenlis, D. Role of Mixed-Layer Instabilities in the Seasonal Evolution of Eddy Kinetic Energy Spectra in a Global Submesoscale Permitting Simulation. Geophys. Res. Lett. 2021, 48, e2021GL094777. [Google Scholar] [CrossRef]
- Alexakis, A.; Biferale, L. Cascades and Transitions in Turbulent Flows. Phys. Rep. 2018, 767–769, 1–101. [Google Scholar] [CrossRef]

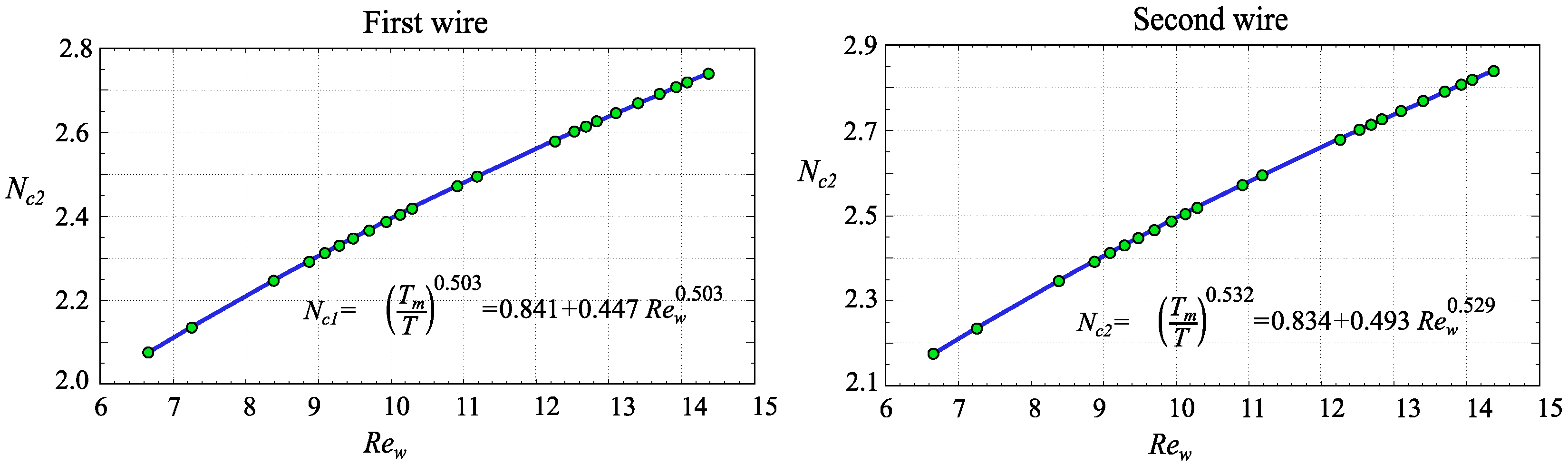
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanovych, V.; Tsymbalyuk, V.; Duda, D.; Uruba, V. Wake Turbulence Induced by Local Blade Oscillation in a Linear Cascade. Appl. Sci. 2025, 15, 9263. https://doi.org/10.3390/app15179263
Yanovych V, Tsymbalyuk V, Duda D, Uruba V. Wake Turbulence Induced by Local Blade Oscillation in a Linear Cascade. Applied Sciences. 2025; 15(17):9263. https://doi.org/10.3390/app15179263
Chicago/Turabian StyleYanovych, Vitalii, Volodymyr Tsymbalyuk, Daniel Duda, and Václav Uruba. 2025. "Wake Turbulence Induced by Local Blade Oscillation in a Linear Cascade" Applied Sciences 15, no. 17: 9263. https://doi.org/10.3390/app15179263
APA StyleYanovych, V., Tsymbalyuk, V., Duda, D., & Uruba, V. (2025). Wake Turbulence Induced by Local Blade Oscillation in a Linear Cascade. Applied Sciences, 15(17), 9263. https://doi.org/10.3390/app15179263








