Experimental and Numerical Research on Non-Coaxial Conical Disk Magnetorheological Fluid Transmission Device
Abstract
1. Introduction
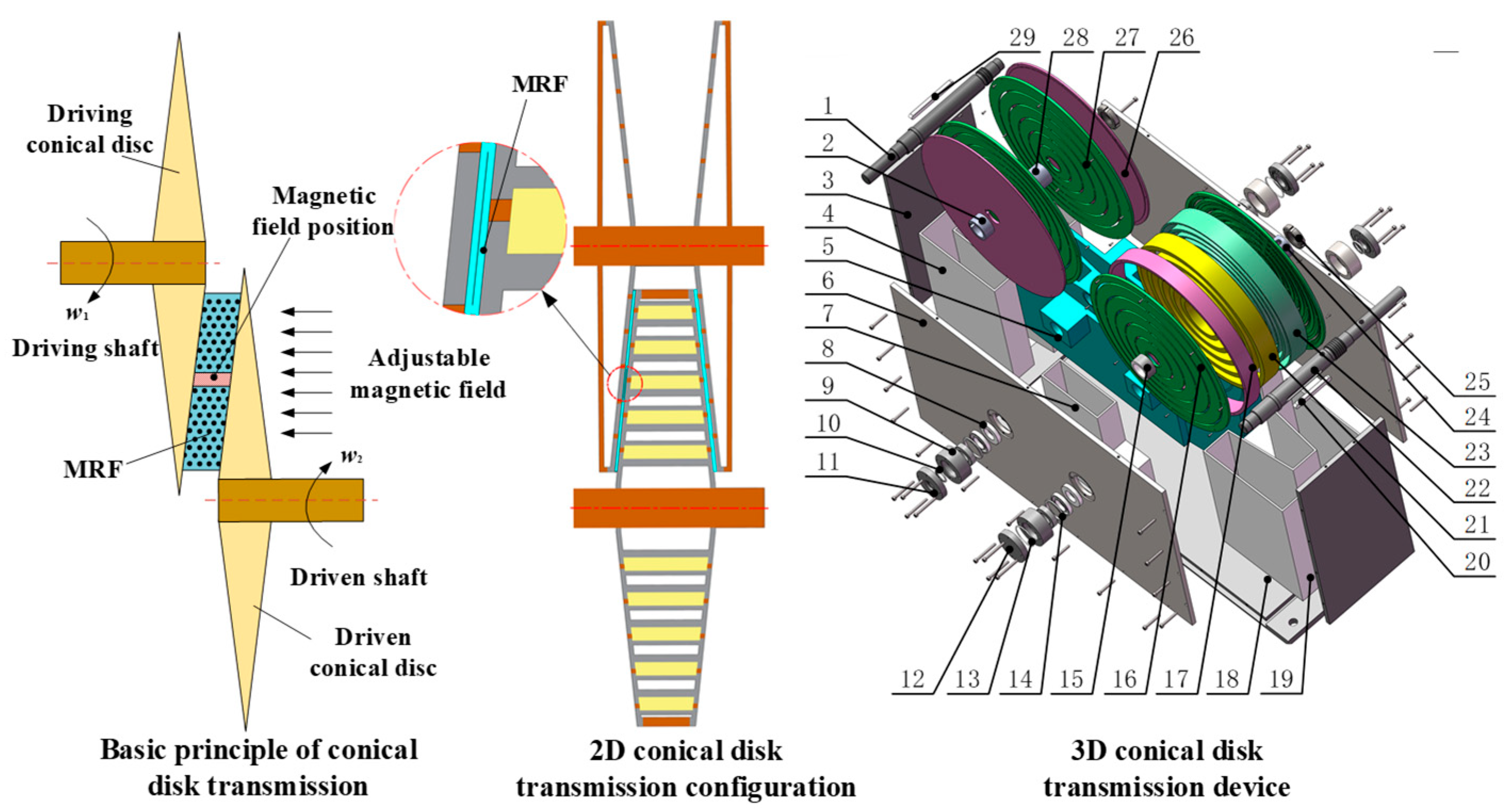
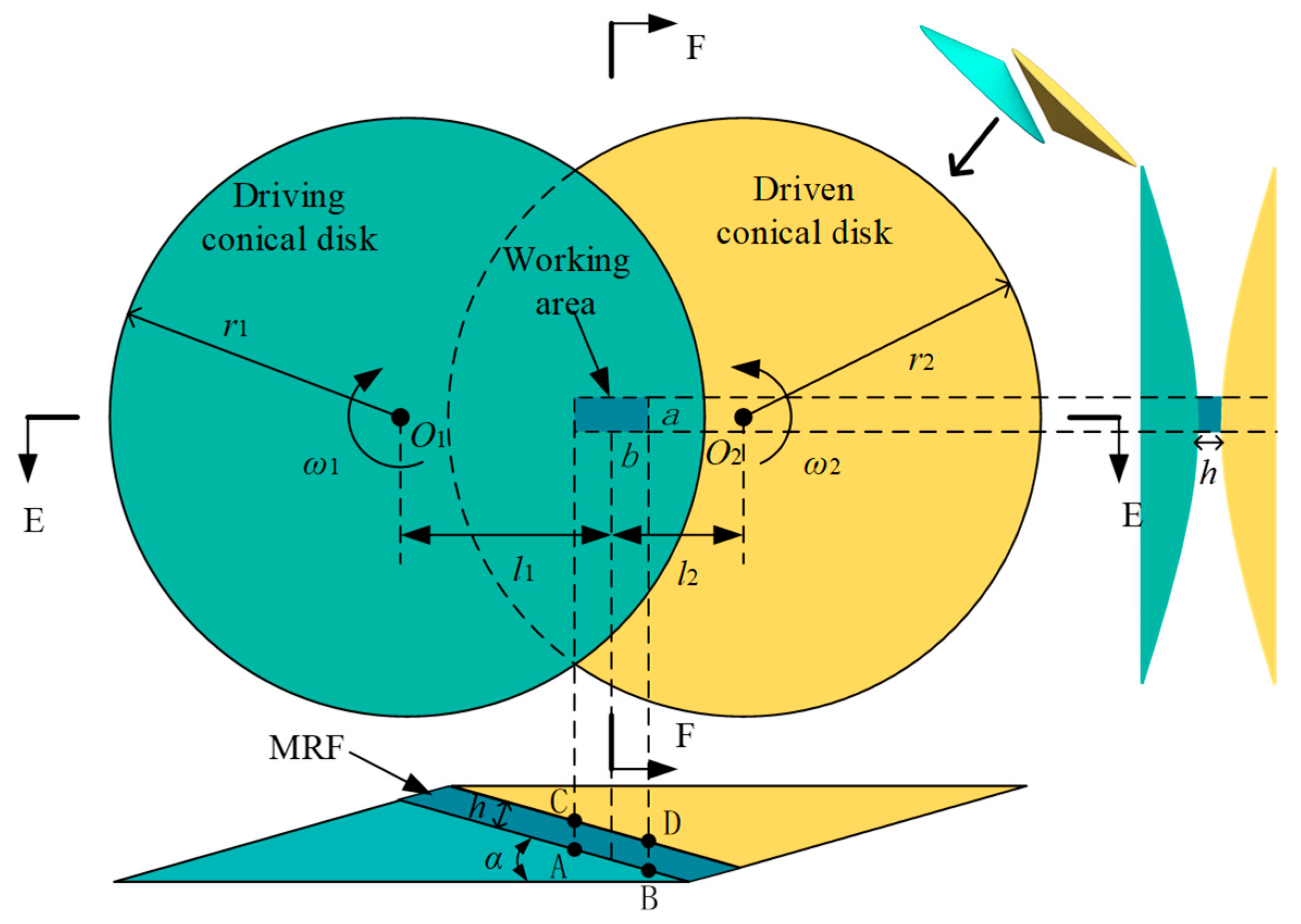
2. Establishment of Transmission Model
3. Transmission Torque of MRFTD
4. Research on Electromagnetic Field of Non-Coaxial Conical Disk MRFTD
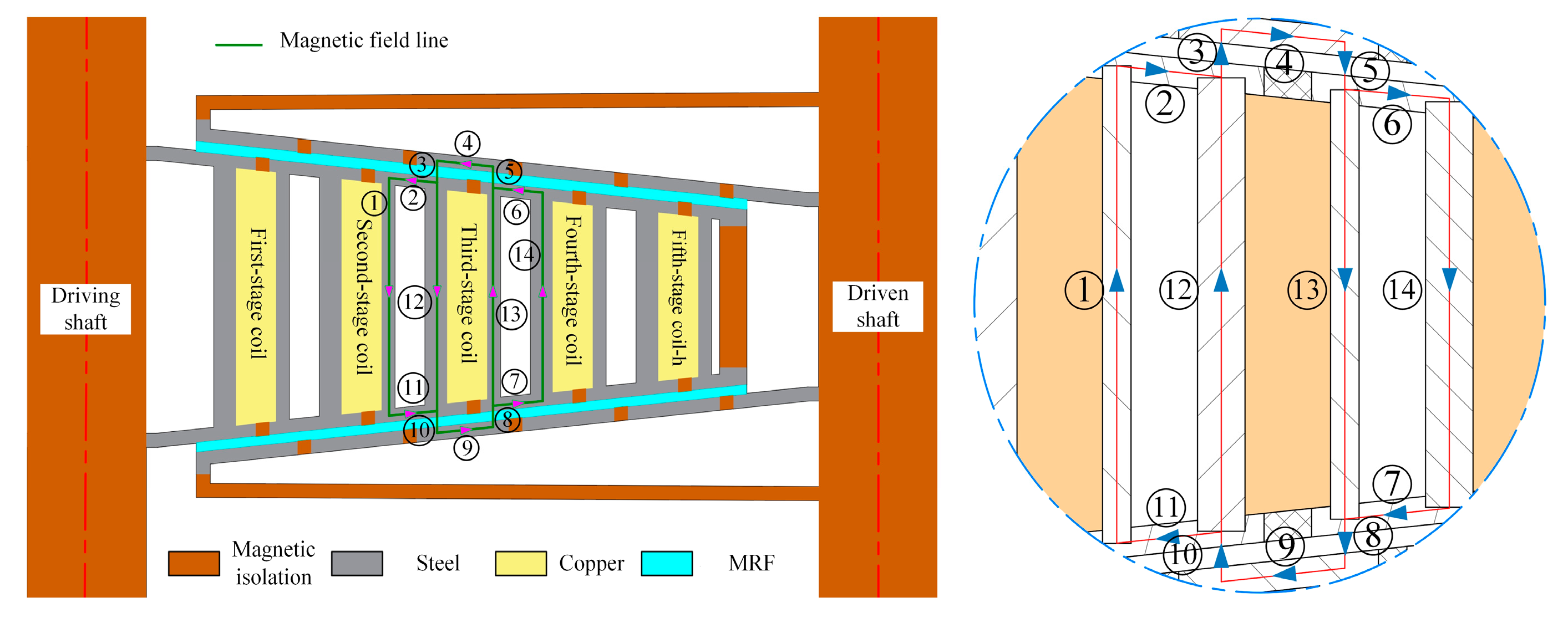
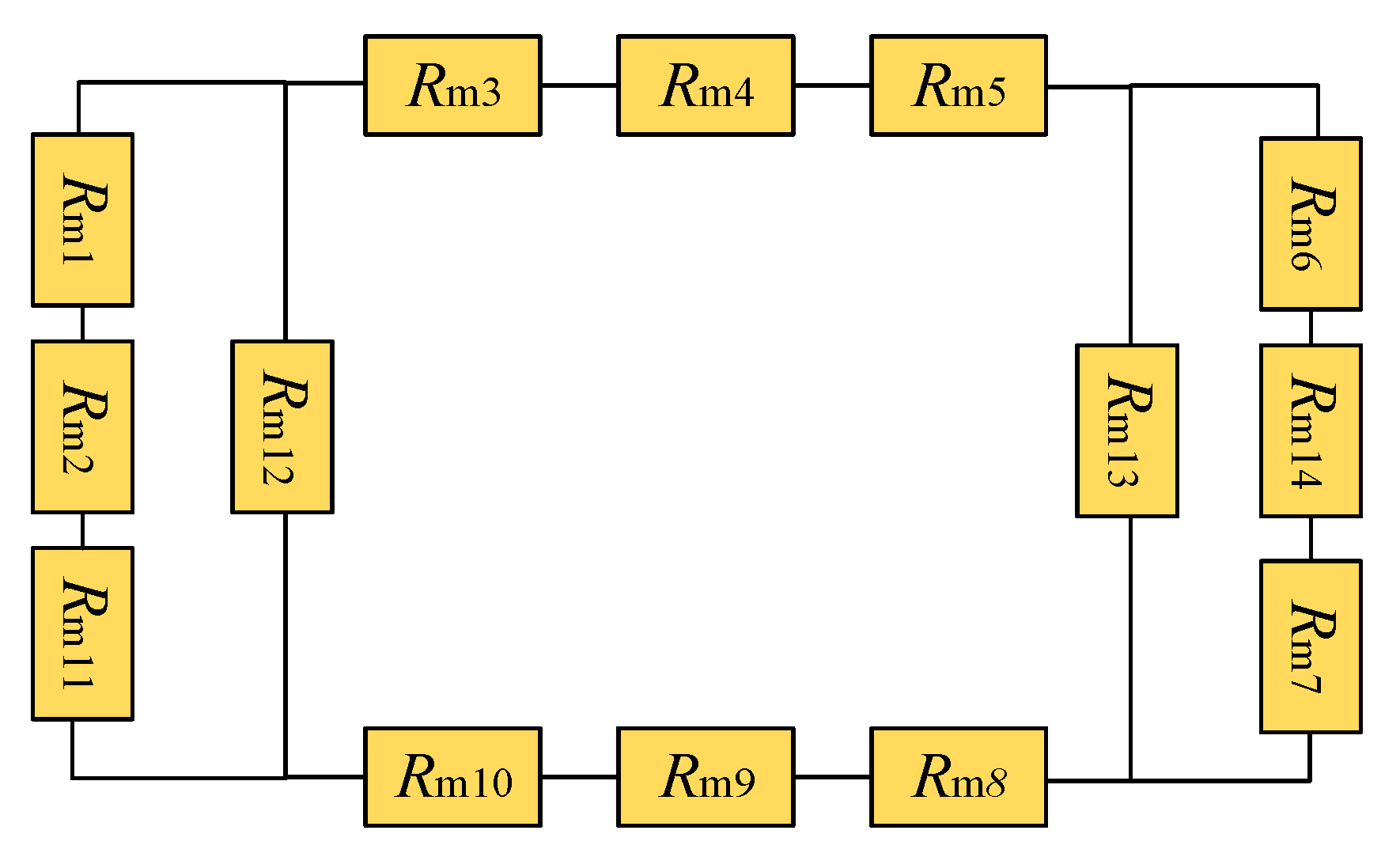
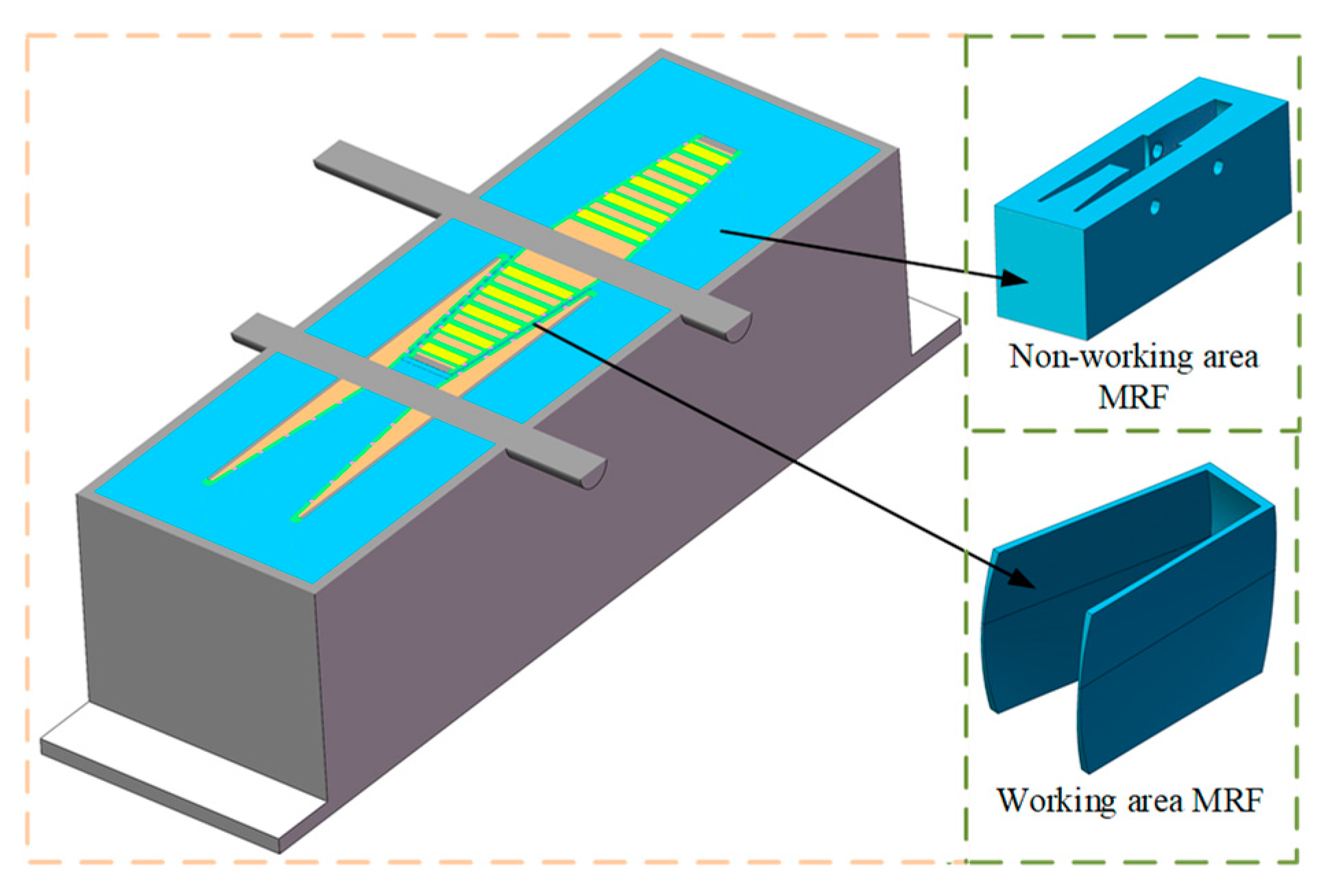
4.1. Magnetic Circuit Design of MRFTD
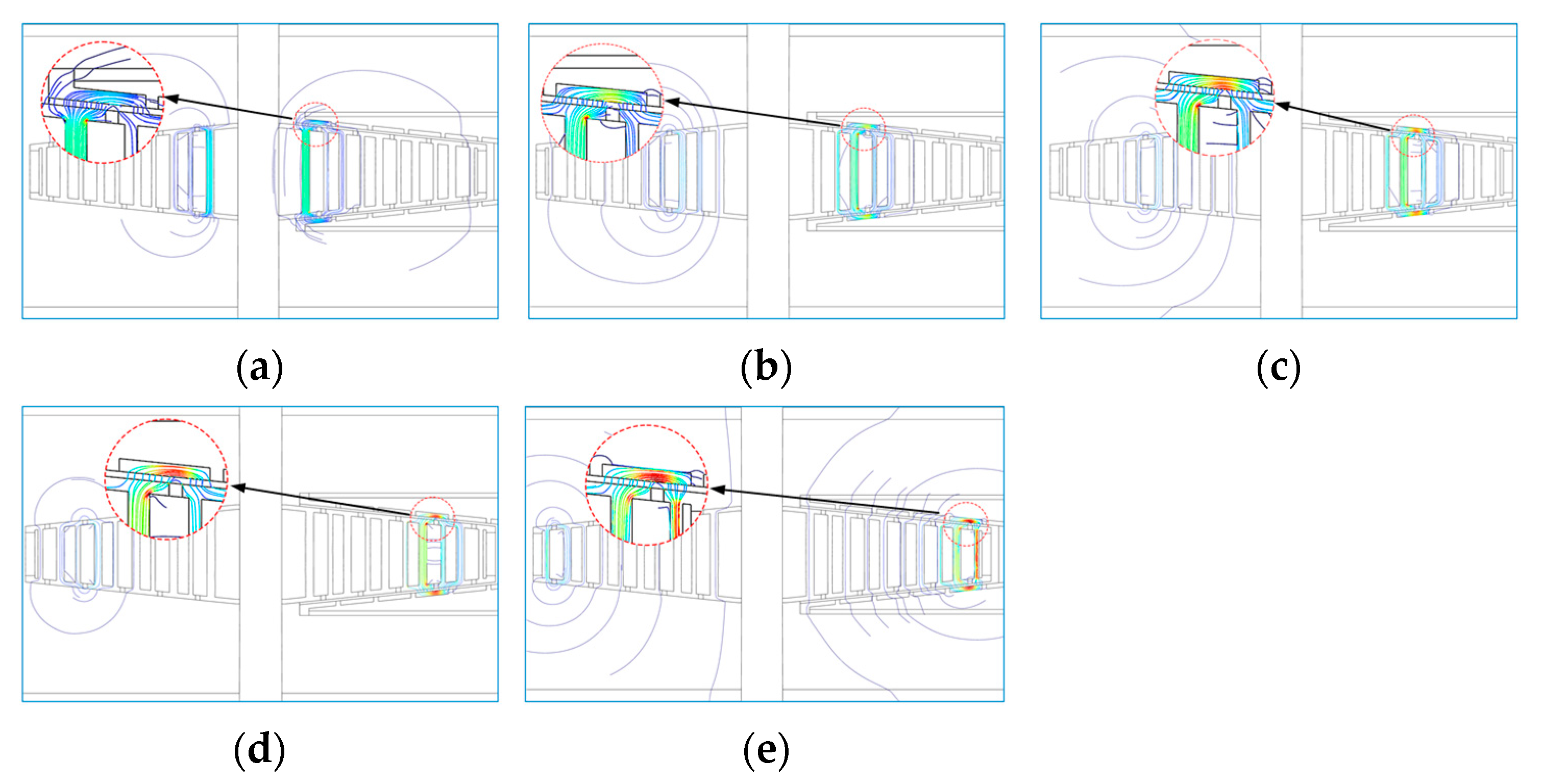
4.2. Electromagnetic Field Analysis
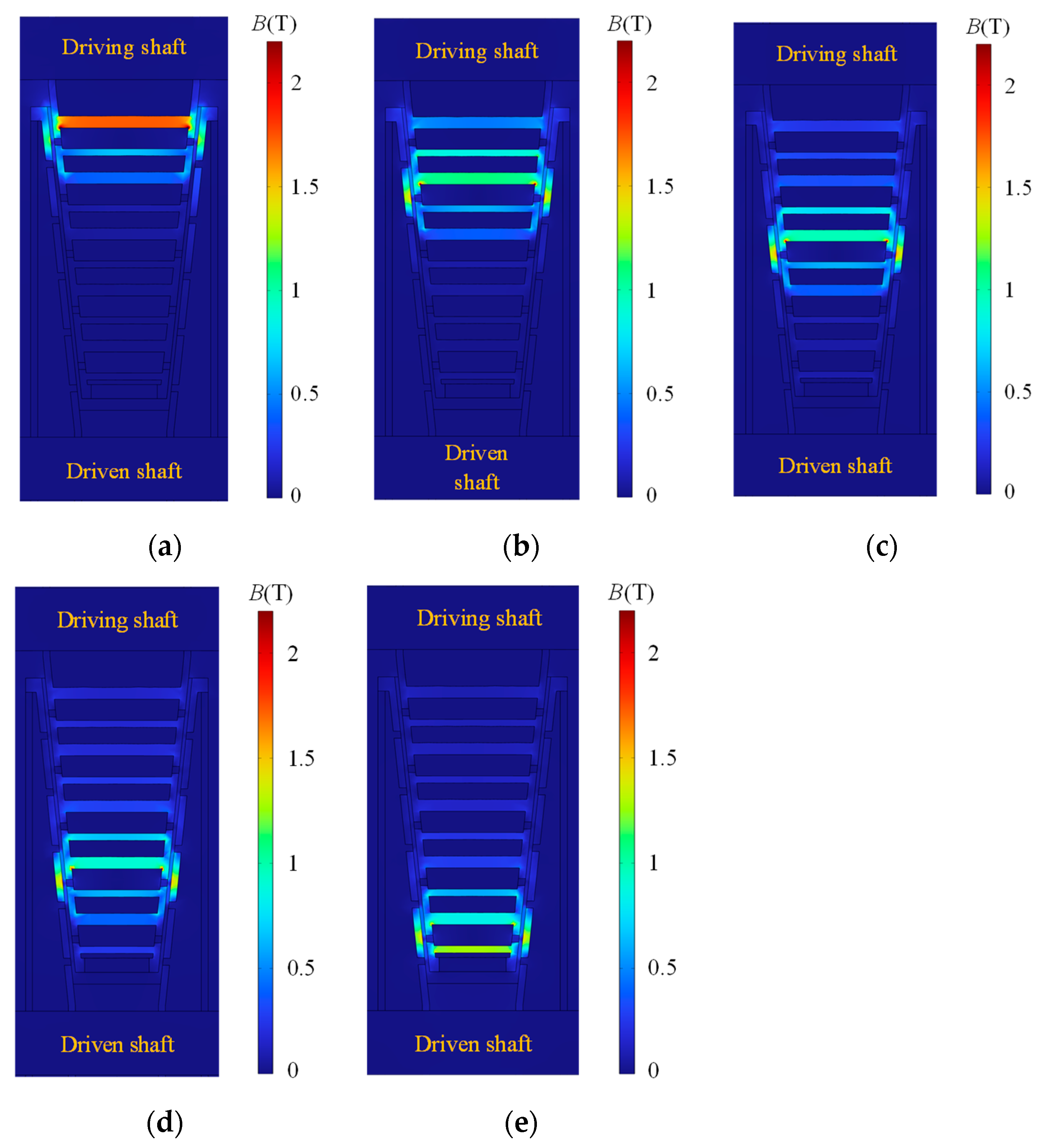
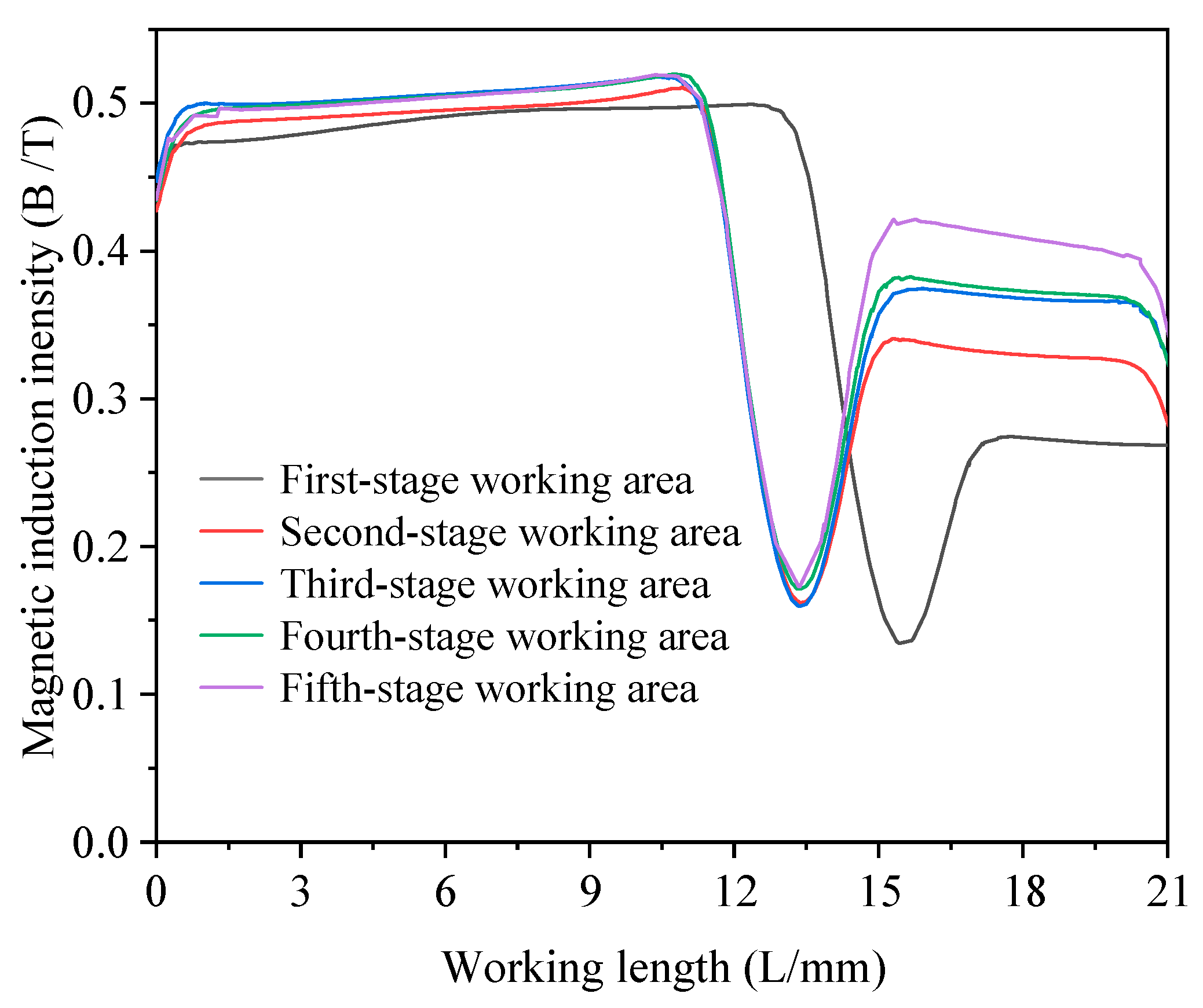
4.3. Influencing Factors of Magnetic Induction
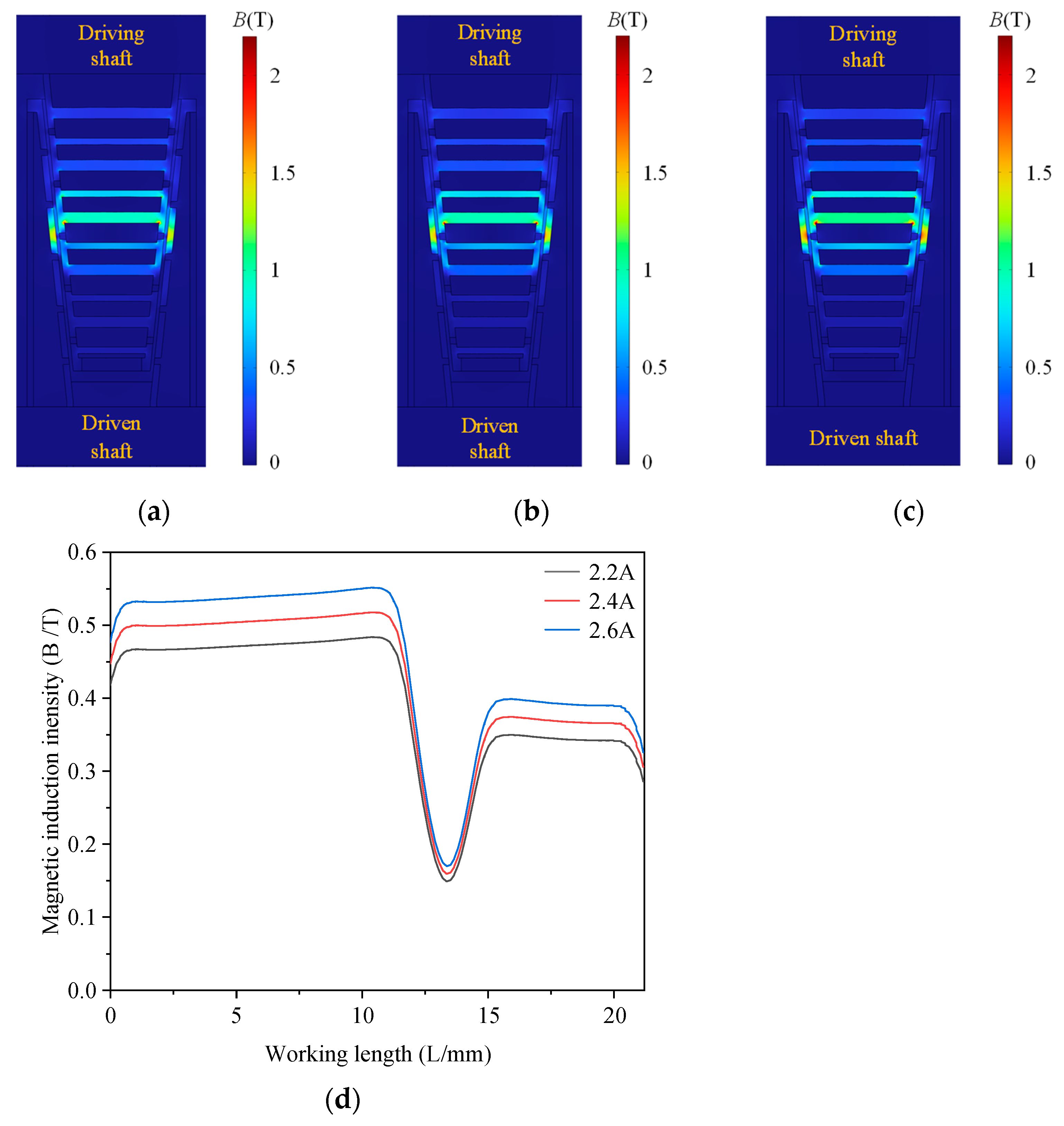
4.3.1. Coil Current
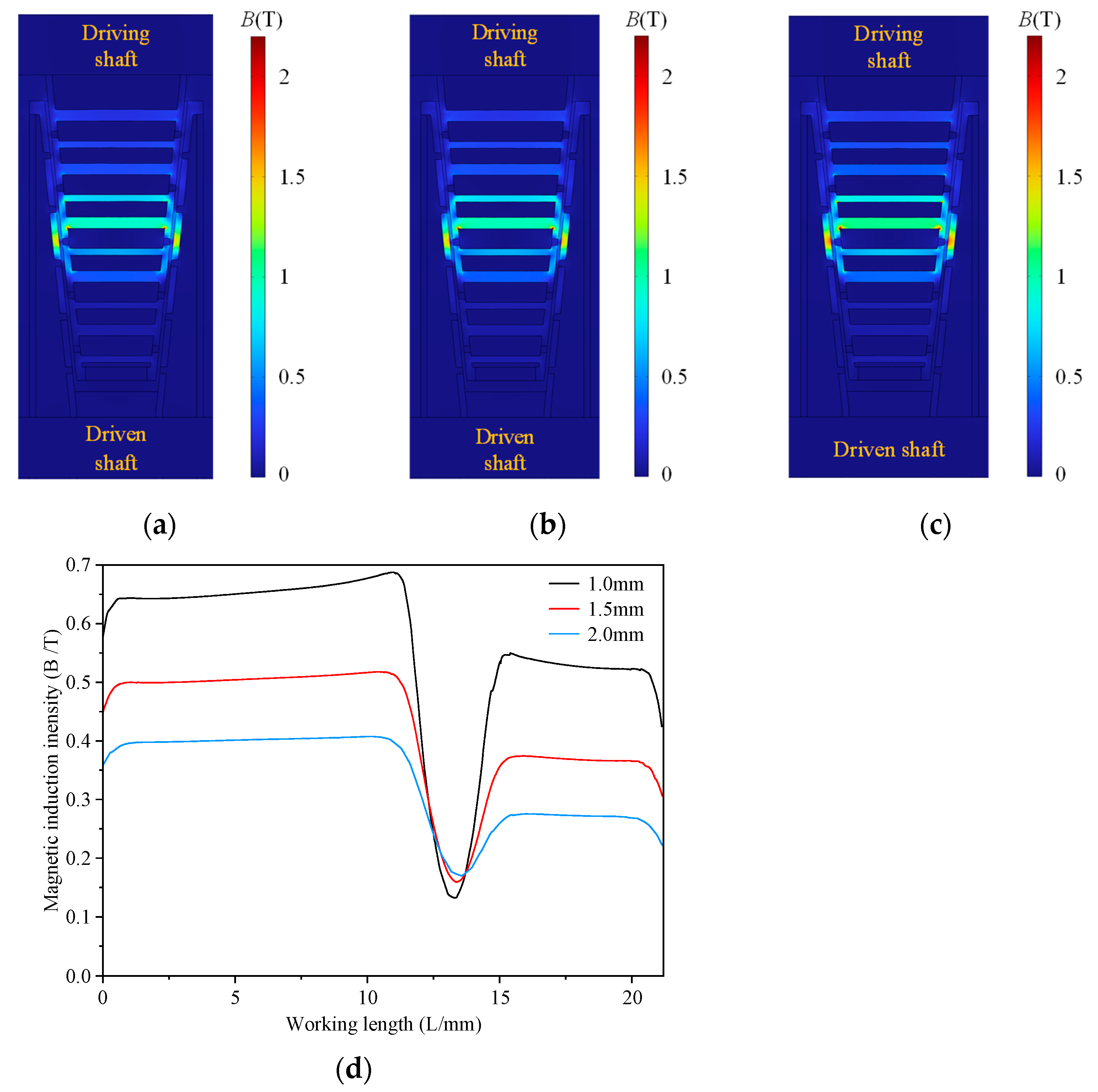
4.3.2. Working Gap
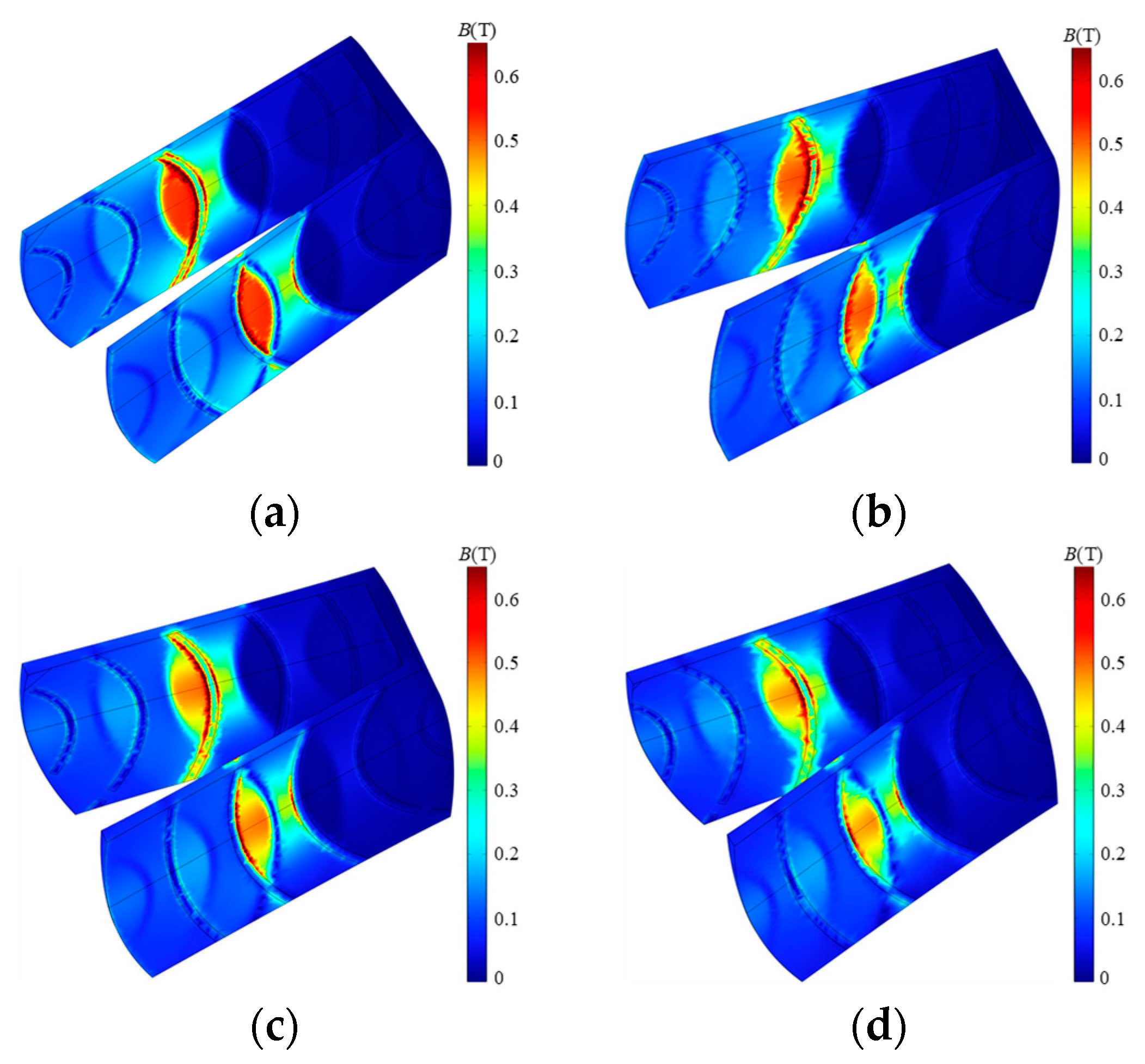
4.3.3. Conical Angle of the Disk
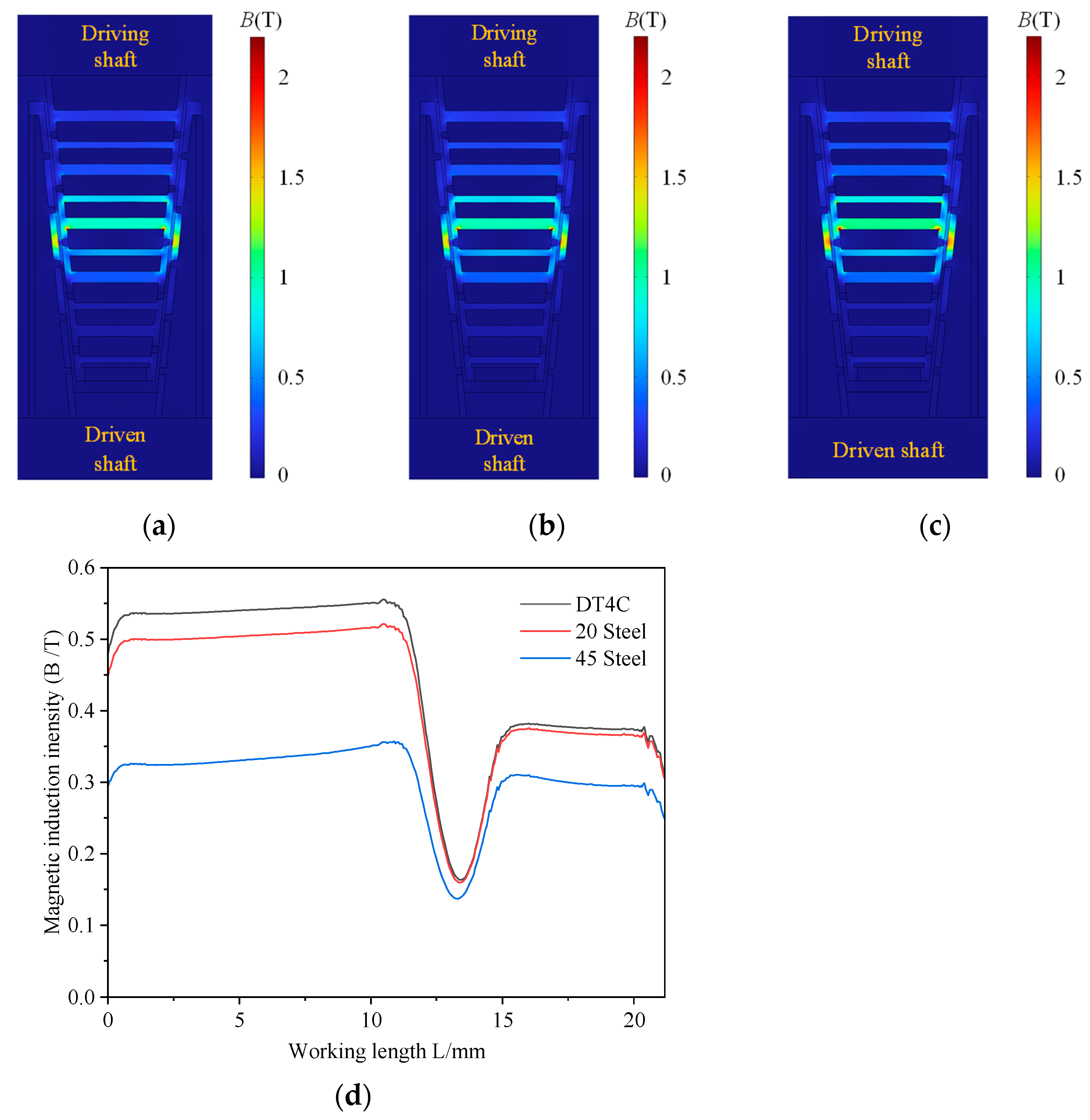
4.3.4. Magnetic Conductive Material
5. Experiments and Discussion
5.1. Experimental System
5.2. Magnetic Field Intensity Characteristics
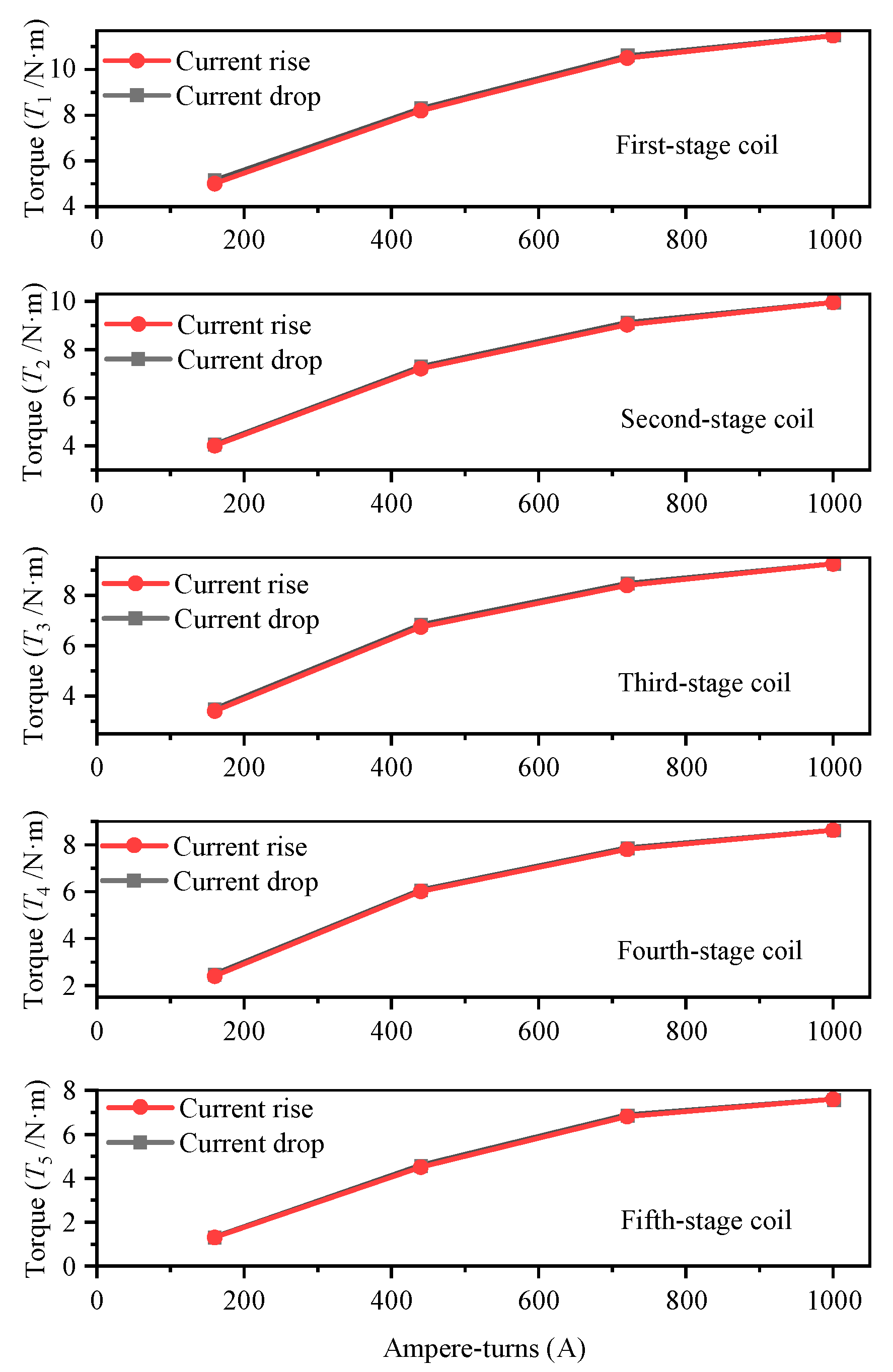
5.3. Transmission Characteristics
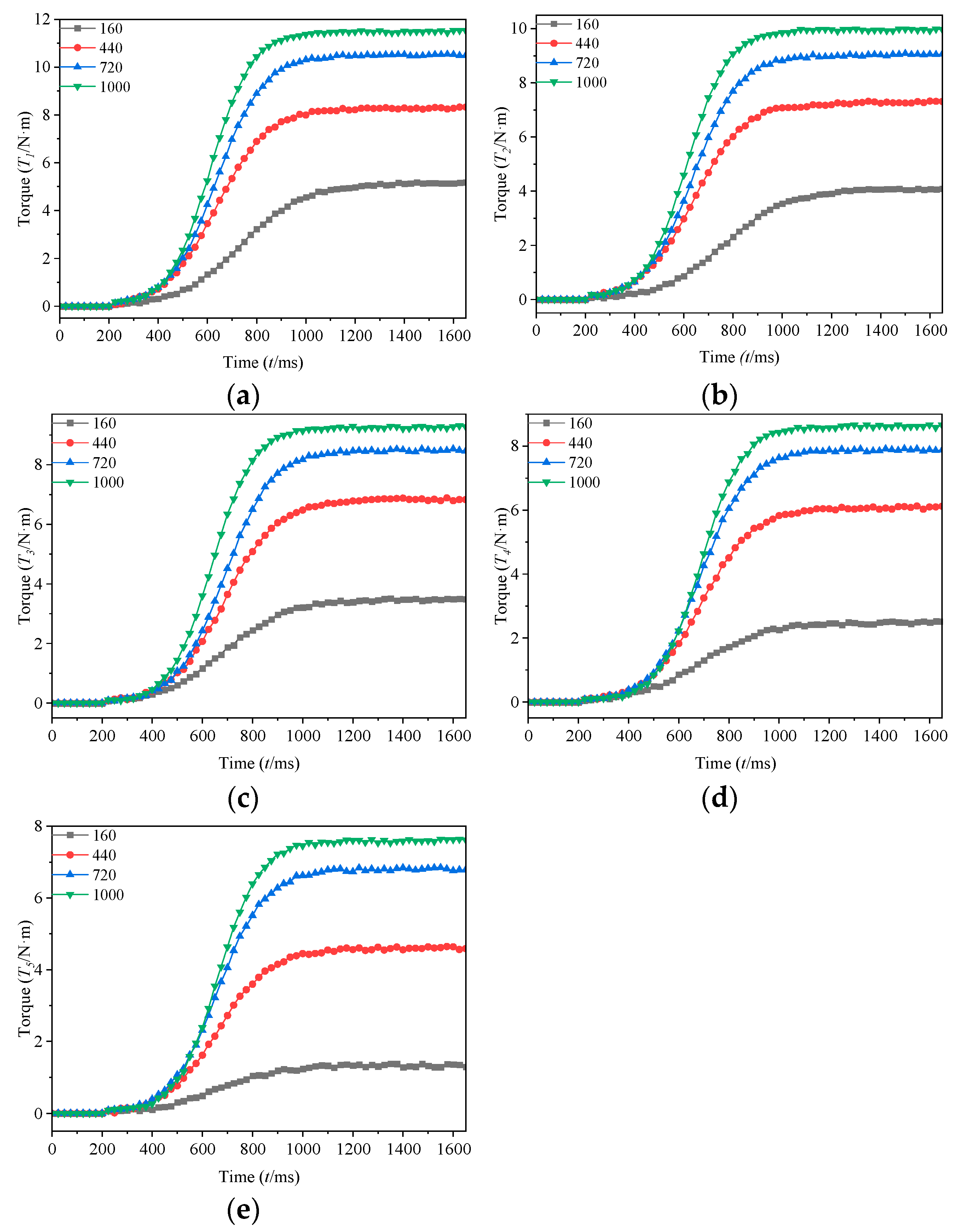
5.4. Torque Response Characteristics
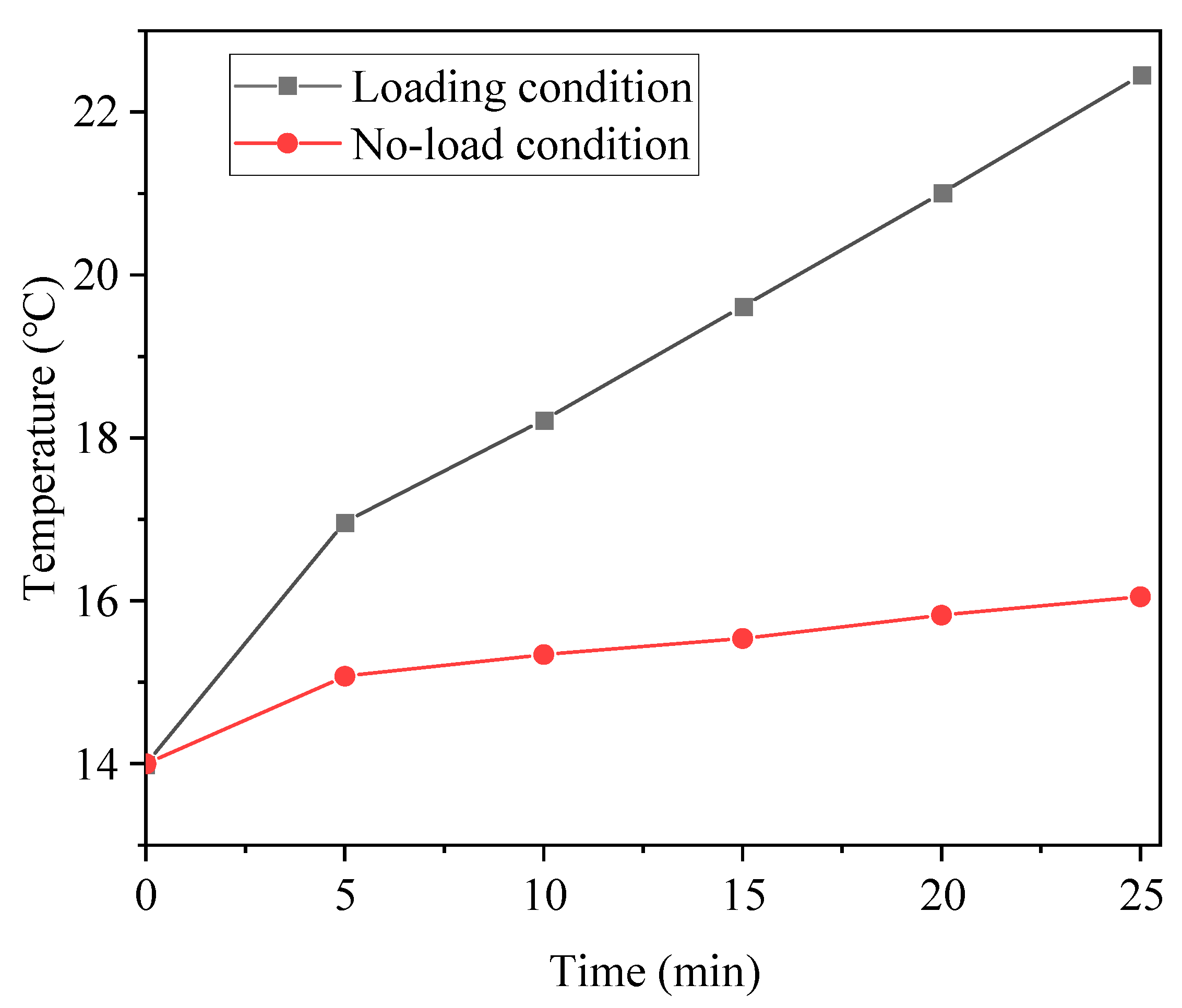
5.5. Temperature Characteristics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ji, J.J.; Wu, X.F.; Tian, Z.Z. Effect on the Sedimentation Stability of Magnetorheological Fluid by Micro-nano Composite System. J. Magn. 2023, 28, 172–180. [Google Scholar] [CrossRef]
- Shiao, Y.; Bollepelly, M. Effect of Pole Head Profile on Torque Performance of a Disc-Type Multipole Magnetorheological Brake. Appl. Sci. 2023, 13, 8327. [Google Scholar] [CrossRef]
- Wu, X.F.; Huang, C.H.; Tian, Z.Z. Development of a novel magnetorheological fluids transmission device for high-power applications. Smart Mater. Struct. 2019, 28, 05502. [Google Scholar] [CrossRef]
- Wu, X.F.; Guo, Y.Y.; Tian, Z.Z.; Xie, F.W.; Ji, J.J.; Li, H.P. Analysis on Flow and Temperature Field of High-Power Magnetorheological Fluid Transmission Device. Appl. Sci. 2022, 12, 5044. [Google Scholar] [CrossRef]
- Kariganaur, A.K.; Kumar, H.; Mahalingam, A. Experimental Investigation on Thermal Stability of Dual Particle Magnetorheological Fluid and Performance. Heat Transfer. Eng. 2024, 45, 1606–1618. [Google Scholar] [CrossRef]
- Park, Y.J.; Choi, S.B. Sensors and Sensing Devices Utilizing Electrorheological Fluids and Magnetorheological Materials—A Review. Sensors 2024, 24, 2842. [Google Scholar] [CrossRef]
- Singh, R.K.; Sarkar, C. Characterization of Magnetorheological Brake in Shear Mode Using High-Strength MWCNTs and Fumed Silica-Based Magnetorheological Fluids at Low Magnetic Fields. J. Tribol.-T. Asme. 2023, 145, 031702. [Google Scholar] [CrossRef]
- Yang, G.X.; Wang, D.M. Application and Torque Stability of the MR Transmission Technology: A Review. J. Magn. 2025, 29, 421–432. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Tian, Z.Z.; Wu, X.F.; Liu, W.; Li, H.P. Research on Magnetic Field Characteristics of Counter-roller Magnetorheological Transmission Device Under Different Coil Arrangements. J. Magn. 2024, 29, 217–225. [Google Scholar] [CrossRef]
- Musialek, K.; Musialek, I.; Osowski, K.; Olszak, A.; Mikulska, A.; Kesy, Z.; Kesy, A.; Choi, S.B. A New Type of Hydraulic Clutch with Magnetorheological Fluid: Theory and Experiment. Micromachines 2024, 15, 572. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Deng, L.; Zhao, J.; Li, W.H.; Du, H.P. Comparative analysis and optimization of nonlinear hysteresis models for a magnetorheological fluid dual-clutch of an electric vehicle transmission. Smart Mater. Struct. 2024, 33, 095045. [Google Scholar] [CrossRef]
- Wu, J.; Kong, W.G.; Liu, Y.H. Structural development of magnetorheological fluid brakes/clutches as typical transmission devices: A review. J. Magn. Magn. Mater. 2024, 614, 172697. [Google Scholar] [CrossRef]
- Wang, S.Y.; Chen, F.; Tian, Z.Z.; Chen, W.X.; Wu, X.F.; Li, A.M. Dynamic Analytical Model Containing Eddy-Current Effects for Response Time of Magnetorheological Clutch. IEEE-Asme. T. Mech. 2023, 28, 3202–3213. [Google Scholar] [CrossRef]
- Park, J.Y.; Jeon, J.H.; Kim, Y.C. A Study on Power Transmission Control for Applying MR Fluid Multi-Plate Clutch to Automobile Power Distribution Device. Appl. Sci. 2024, 14, 3871. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Yang, X.L.; Cao, Z.Q. Effect of temperature on braking performance of the comb-type disc magnetorheological brake. Phys. Scripta 2024, 99, 105024. [Google Scholar] [CrossRef]
- Chen, S.; Huang, J.; Jian, K.L.; Ding, J. Analysis of Influence of Temperature on Magnetorheological Fluid and Transmission Performance. Adv. Mater. Sci. Eng. 2015, 2015, 583076. [Google Scholar] [CrossRef]
- Tian, Z.Z.; Wu, X.F.; Xiao, X.M.; Hao, L. Influence of Temperature on Torque Transmission Stability of Magnetorheological Fluid. J. Magn. 2019, 23, 529–535. [Google Scholar] [CrossRef]
- Wang, S.Y.; Chen, F.; Tian, Z.Z.; Dou, J.; Wu, X.F. Development of water-cooling transmission device for magnetorheological fluid. J. Magn. 2018, 23, 285–292. [Google Scholar] [CrossRef]
- Chen, F.; Wang, X.; Li, H.P.; Li, A.M.; Deng, Y.R.; Tian, Z.Z.; Wu, X.F. A novel water-cooling magnetorheological transmission device. J. Mech. Sci. Technol. 2022, 36, 2309–2319. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, F.; Gu, X.; Li, A.M.; Li, H.P. Research on a novel water-cooling multi-cylinder magnetorheological transmission device. Rev. Sci. Instrum. 2024, 95, 015103. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, Y.H.; Xie, H.Y. Experimental measurement of a multi-pole magnetorheological fluid clutch under air cooling. Rev. Sci. Instrum. 2024, 95, 035109. [Google Scholar] [CrossRef]
- Wang, N.N.; Liu, X.H.; Królczyk, G.; Li, Z.X.; Li, W.H. Effect of temperature on the transmission characteristics of high-torque magnetorheological brakes. Smart Mater. Struct. 2019, 28, 057002. [Google Scholar] [CrossRef]
- Zhang, J.W.; Hu, G.L.; Cheng, Q.; Yu, L.F.; Zhu, W.C. Analysis of braking performance and heat dissipation characteristics of multi-disc magnetorheological brake with an inner water-cooling mechanism. J. Magn. Magn. Mater. 2024, 604, 172313. [Google Scholar] [CrossRef]
- Ji, J.J.; Tian, Z.Z.; Xie, F.W.; Wu, X.F.; Huang, X.K.; Tang, Y.J. The research of a multi-stage roller type magnetorheological transmission device on temperature properties. J. Intell. Mater. Syst. Struct. 2024, 35, 169–180. [Google Scholar] [CrossRef]
- Chen, W.J.; Huang, J.; Yang, Y. Research on the Transmission Performance of a High-Temperature Magnetorheological Fluid and Shape Memory Alloy Composite. Appl. Sci. 2022, 12, 3228. [Google Scholar] [CrossRef]
- Zhang, W.X.; Chen, S.; Huang, J. Analysis of electrothermal shape memory alloy and disc-type magnetorheological fluid combined transmission. Structures 2024, 69, 107345. [Google Scholar] [CrossRef]

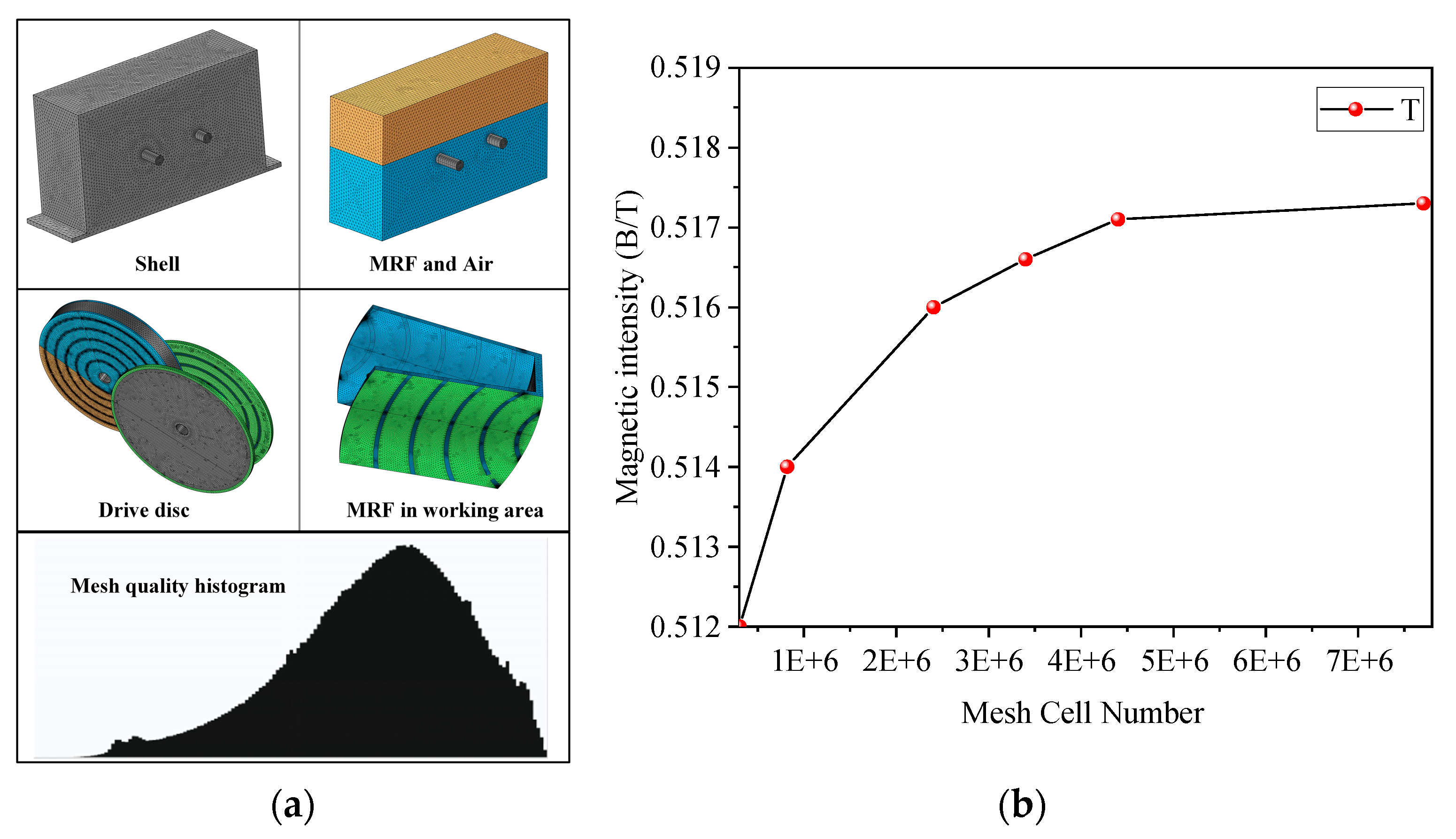





| Component | Parameter |
|---|---|
| Mesh vertex | 820,744 |
| Number of mesh cells | 3,397,902 |
| Minimum mesh cell mass | 0.04918 |
| Average mesh cell mass | 0.6694 |
| Unit volume ratio | 6.465 × 10−5 |
| Mesh volume | 175,900 mm3 |
| Component | Parameter |
|---|---|
| MRF-G28 | Shear yield stress (0.5 T) ≥ 35 kPa |
| Temperature range: −40–140 °C | |
| Zero-field viscosity: 0.28 Pa·s | |
| Torque/speed sensor | Model: JN-DN |
| Accuracy: ±0.3% | |
| Torque range: ±100 N·m | |
| Torque/speed transmitter | Model: BSQ-12-100 NM |
| Output signal: 0–±5 V | |
| Working voltage: 24 VDC | |
| Gaussmeter | Model: CH-1500 |
| Measurement range: 0–3 tons | |
| Resolution: 0.01 mT | |
| NI acquisition | Model: USB-6001 |
| Number of channels: 8 | |
| Output range: ±10 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Liu, W.; Tian, Z.; Guo, Y.; Zhu, M.; Chen, Z. Experimental and Numerical Research on Non-Coaxial Conical Disk Magnetorheological Fluid Transmission Device. Appl. Sci. 2025, 15, 9262. https://doi.org/10.3390/app15179262
Wu X, Liu W, Tian Z, Guo Y, Zhu M, Chen Z. Experimental and Numerical Research on Non-Coaxial Conical Disk Magnetorheological Fluid Transmission Device. Applied Sciences. 2025; 15(17):9262. https://doi.org/10.3390/app15179262
Chicago/Turabian StyleWu, Xiangfan, Wei Liu, Zuzhi Tian, Yangyang Guo, Minjian Zhu, and Zibo Chen. 2025. "Experimental and Numerical Research on Non-Coaxial Conical Disk Magnetorheological Fluid Transmission Device" Applied Sciences 15, no. 17: 9262. https://doi.org/10.3390/app15179262
APA StyleWu, X., Liu, W., Tian, Z., Guo, Y., Zhu, M., & Chen, Z. (2025). Experimental and Numerical Research on Non-Coaxial Conical Disk Magnetorheological Fluid Transmission Device. Applied Sciences, 15(17), 9262. https://doi.org/10.3390/app15179262







