Uniaxial Compressive Mechanical Behavior of Coals with Different Joint Spacing and Angles: A DEM Numerical Simulation Study
Abstract
1. Introduction
2. Numerical Modeling and Micro Parameter Assignment
3. Analysis and Discussion of Results
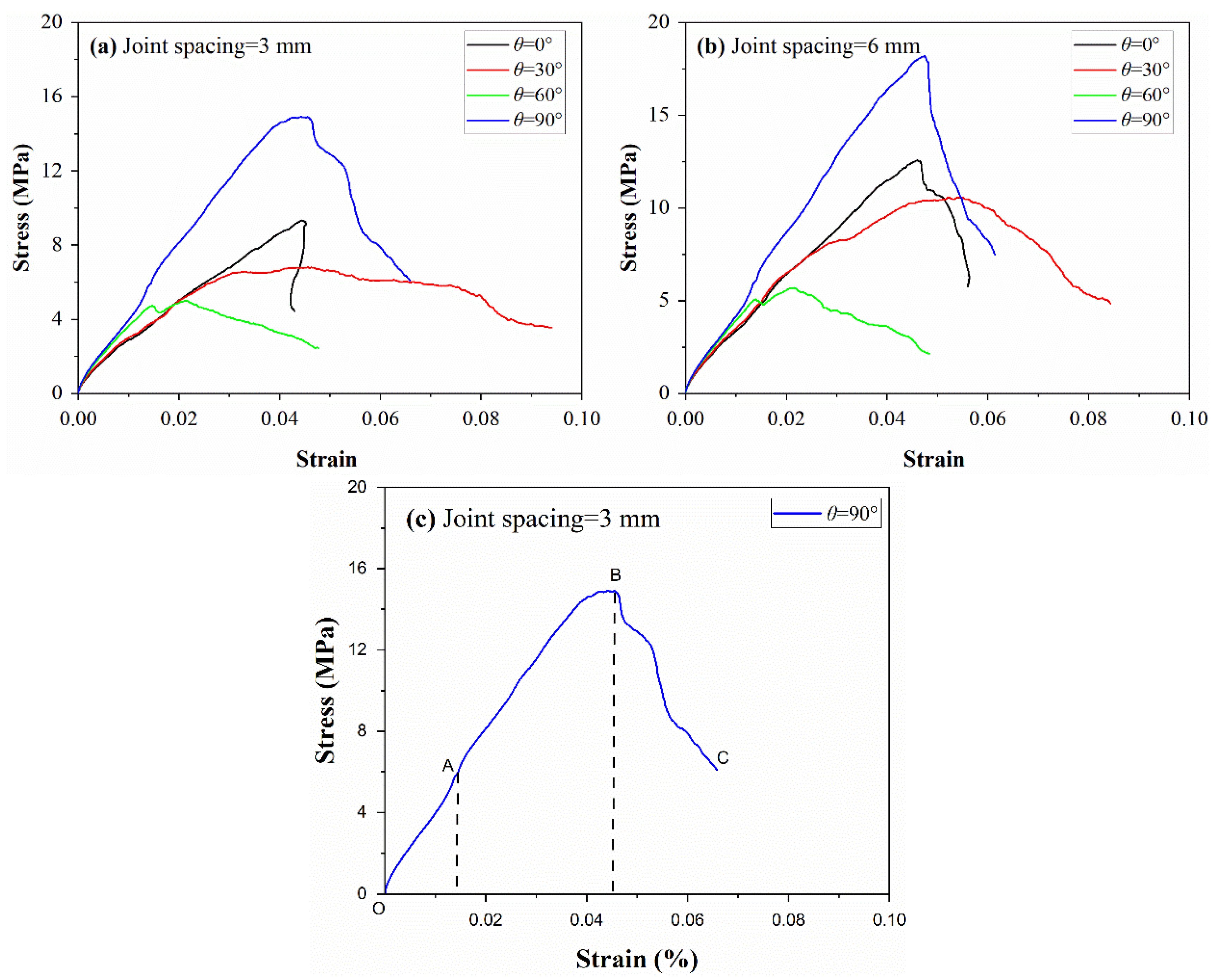
3.1. Stress–Strain Curves and Key Mechanical Parameters
3.2. Failure Mode
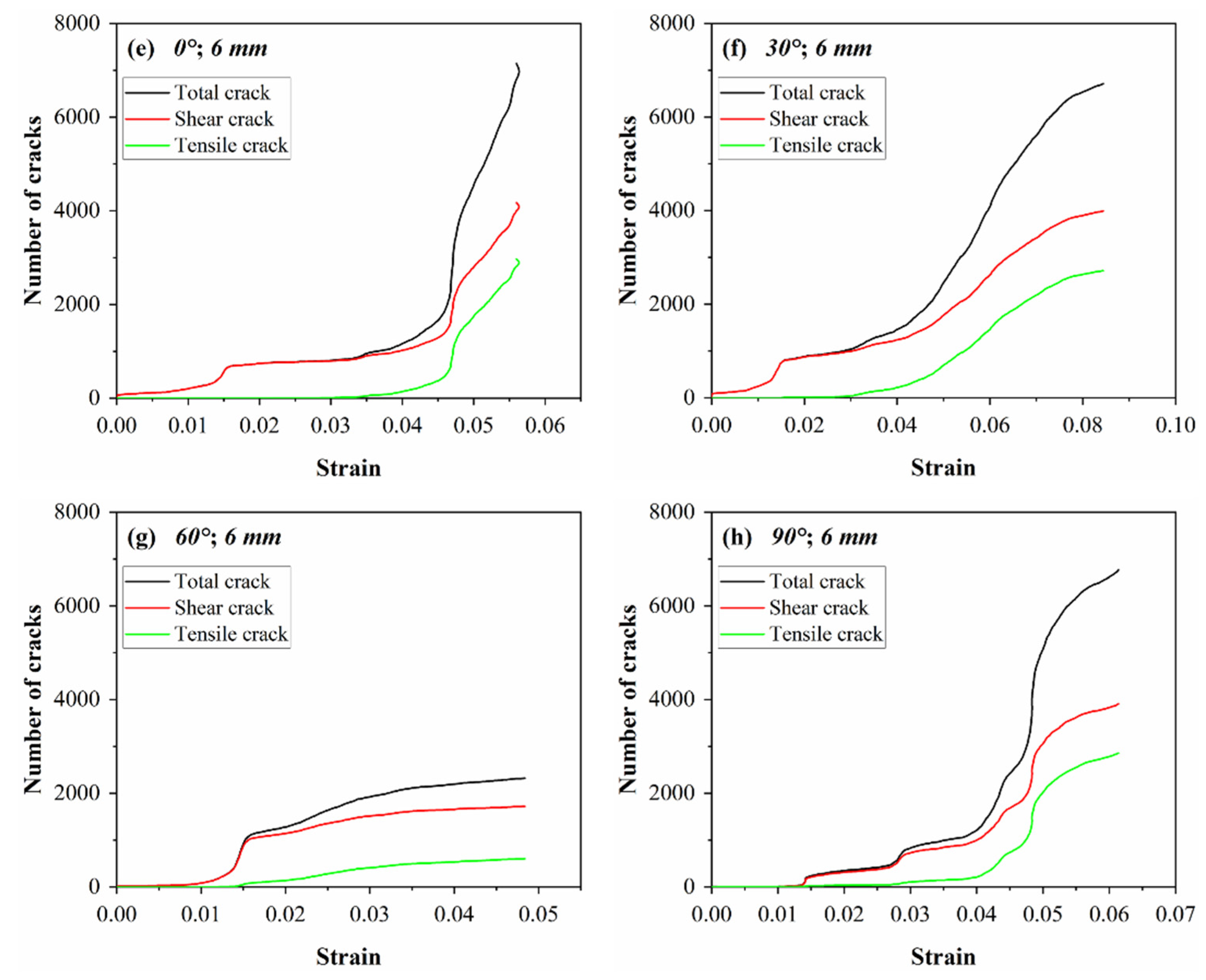
3.3. Microcrack Characteristics
3.4. Force Chain Characteristics
4. Conclusions and Discussions
- (1)
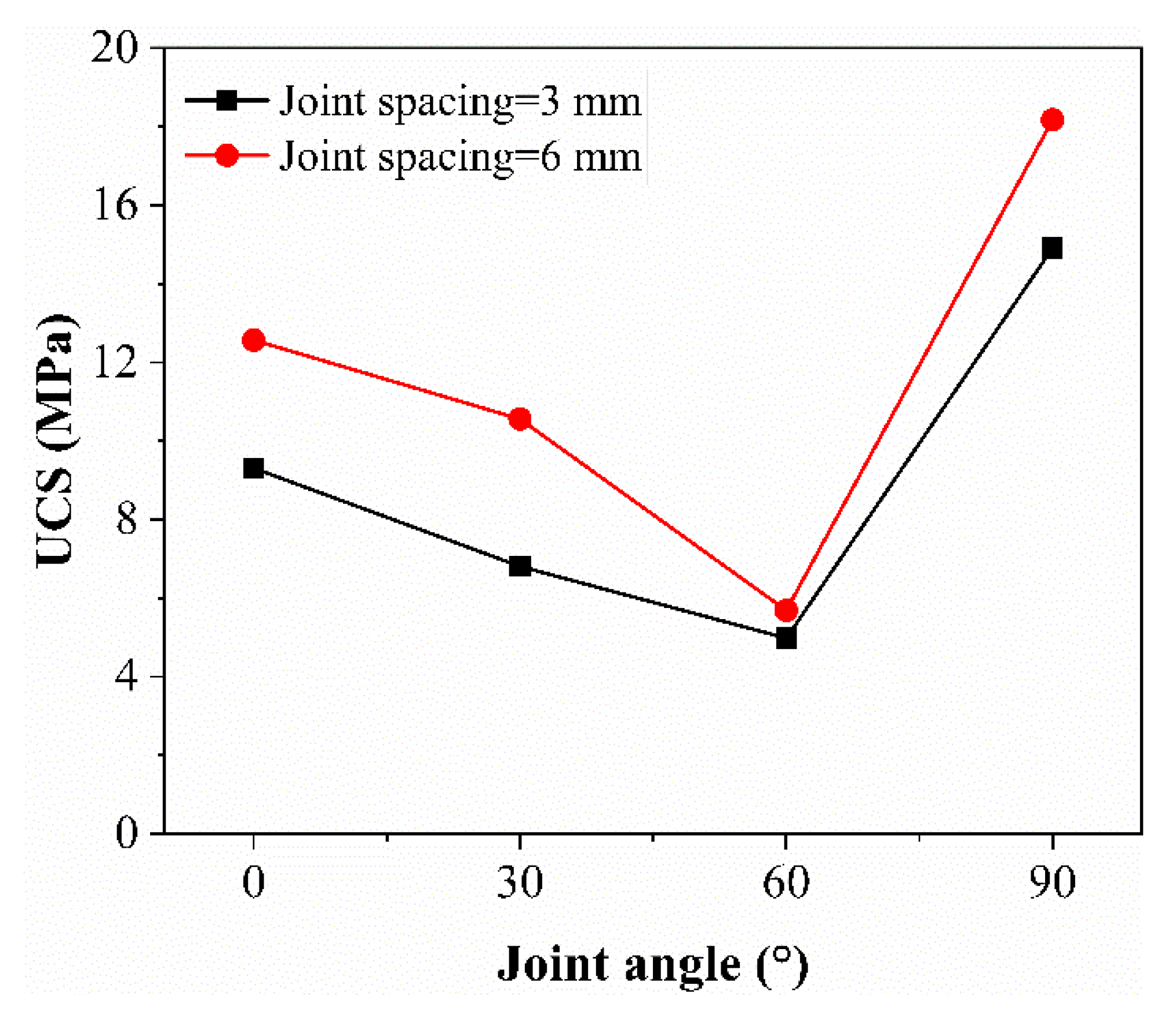
- Under uniaxial compression, the stress–strain curves of the coal sample were divided into three phases, and the increase in JS was beneficial to improve the plasticity of the coal sample. The post-peak plasticity of the sample at JA = 30° and 60° was significantly larger than that of the sample at JA = 0° and 90°. When JS = 3 mm, the UCS decreased and then increased with the increase in JA in a “V”-shape. When JA = 60°, the minimum peak stress is 4.98 MPa. JS = 6 mm has the same law. When JA is the same, JS contributes to the enhancement of UCS in coal sample;
- (2)
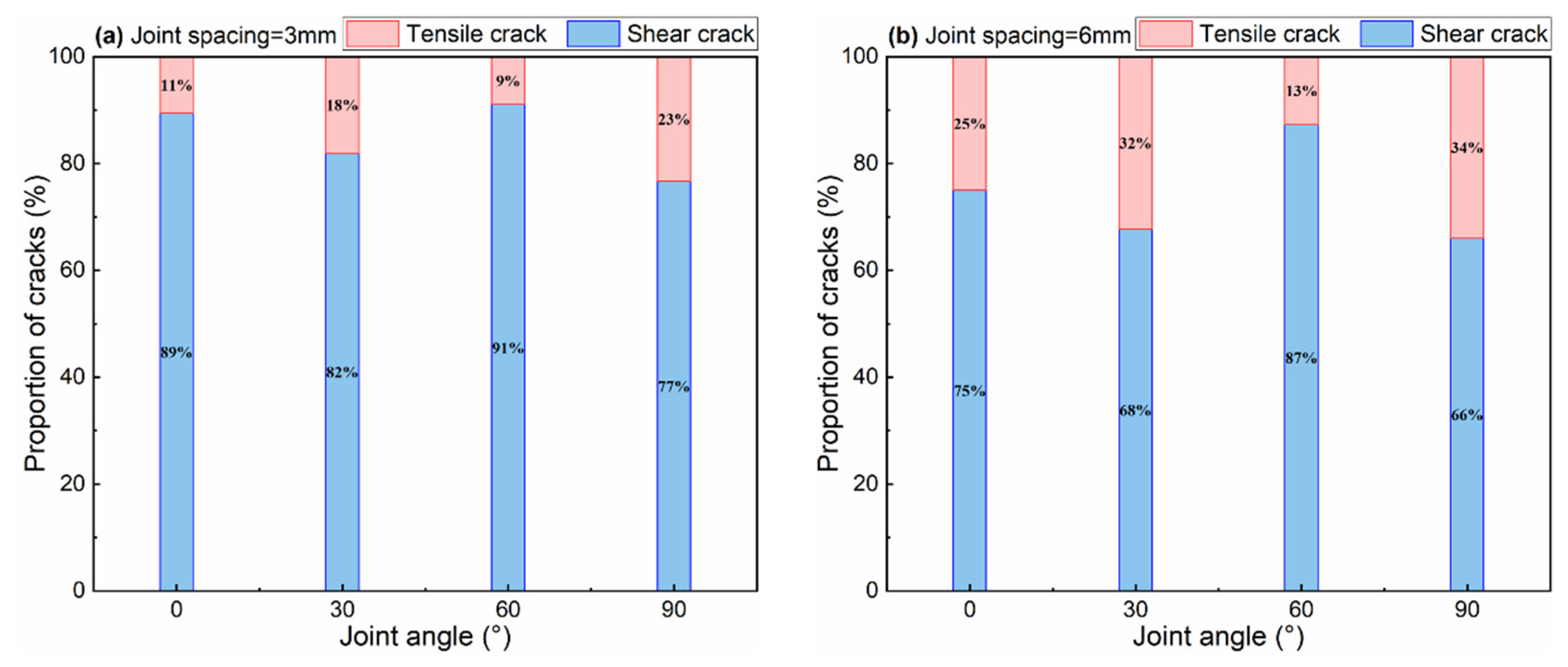
- There are remarkable differences in the rupture modes and crack distributions of coal samples with different JCs and JAs at uniaxial compression conditions. With the increase in JA, the cracks of coal samples transform from “X”-type distribution to “V”-type division, which is dominated by shear cracks. When JA increased from 60° to 90°, the amount of tensile and shear cracks increased to the maximum. With the increase in JC, the crack length increased remarkably, and the crack distribution range expanded;
- (3)
- Tensile crack formation is facilitated at joint angles of 0–60° but suppressed at 60–90°. When JA is the same, the increase in JS benefits tensile crack occurrence. The cracking tendency of coal samples decreased with the increase in JA, then increased and then decreased again, and the cracking tendency converted from centralized distribution to decentralized aggregation and then to centralized distribution. With the increase in JS, the cracking tendency of coal sample is smaller. When JA is 30° and 90°, the microcrack damage tendency is strongly concentrated in the range of 50–110°;
- (4)
- When 0° ≤ JA ≤ 60°, the tensile force chain within the specimen increases and the density of the tensile force chain converges to the end. When 60° ≤ JA ≤ 90°, the tensile force chain within the specimen decreases and the distribution location of the tensile force chain moves from the center to the left and right edges. As JS increases, the distribution range of tensile force chains increases, and the degree of force chain aggregation increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.C.; Ren, F.Q.; Liu, D.Q. Rockburst mechanism research and its control. Int. J. Min. Sci. Technol. 2018, 28, 829–837. [Google Scholar] [CrossRef]
- Hu, J.; He, M.C.; Li, H.R. Rockburst hazard control using the excavation compensation method (ECM): A case study in the Qinling water conveyance tunnel. Engineering 2024, 34, 154–163. [Google Scholar] [CrossRef]
- Li, H.R.; He, M.C.; Qiao, Y.F.; Cheng, T.; Han, Z.Y. Assessing burst proneness and seismogenic process of anisotropic coal via the realistic energy release rate (RERR) index. Rock Mech. Rock Eng. 2024, 58, 2999–3013. [Google Scholar] [CrossRef]
- Akdag, S.; Karakus, M.; Nguyen, G.D.; Taheri, A.; Bruning, T. Evaluation of the propensity of strain burst in brittle granite based on post-peak energy analysis. Undergr. Space 2021, 6, 1–11. [Google Scholar] [CrossRef]
- Li, J.Y.; Liu, D.Q.; He, M.C. Excess energy characteristics of true triaxial multi-faceted rapid unloading rockburst. J. Cent. South Univ. 2024, 31, 1671–1686. [Google Scholar] [CrossRef]
- Sun, J.; Ling, K.; Zhang, S.D. Experimental study on mesoscopic fracture process and weakening mechanism of water on rockbursts. Eng. Fract. Mech. 2025, 318, 110950. [Google Scholar] [CrossRef]
- Hu, J.; He, M.C.; Li, H.R. Control effect of negative poisson’s ratio (NPR) cable on impact-induced rockburst with different strain rates: An experimental investigation. Rock Mech. Rock Eng. 2023, 56, 5167–5180. [Google Scholar] [CrossRef]
- Li, H.R.; He, M.C.; Xiao, Y.M. Granite strainbursts induced by true-triaxial transient unloading at different stress levels: Insights from excess energy ∆E. J. Rock Mech. Geotech. Eng. 2025, in press. [Google Scholar] [CrossRef]
- Ju, F.; Wang, D.; Wang, Z.; Xiao, M.; He, Z.; Ning, P.; Wang, T.; Li, L.; Yan, C.; Zhou, T. Mechanical properties and acoustic emission characteristics of coal sample with a single natural joint of different dip angles. Bull. Eng. Geol. Environ. 2023, 82, 456. [Google Scholar] [CrossRef]
- Ji, P.X.; Viegas, G.; Zhang, Q.B. Mechanical and fracturing characteristics of defected rock-like materials under biaxial compression. Int. J. Rock Mech. Min. Sci. 2024, 176, 105692. [Google Scholar] [CrossRef]
- Yang, S.Q.; Tian, W.T.; Ranjith, P.G. Three-dimensional failure behavior and cracking mechanism of rectangular solid sandstone containing a single fissure under triaxial compression. Rock Mech. Bull. 2022, 1, 100008. [Google Scholar] [CrossRef]
- Ma, G.; He, M.; Hu, J. Mechanical and damage properties study of rocks with different joint inclinations under seepage-stress coupling: Insights based on energy theory. Comput. Part. Mech. 2025. [Google Scholar] [CrossRef]
- Fan, X.; Yu, H.; Deng, Z.Y. Cracking and deformation of cuboidal sandstone with a single nonpenetrating flaw under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 119, 103284. [Google Scholar] [CrossRef]
- Hu, J.H.; Wen, G.P.; Lin, Q.B. Mechanical properties and crack evolution of double-layer composite rocklike specimens with two parallel fissures under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 108, 102610. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Y.M.; Zhao, C.F. Cracking processes and coalescence modes in rock-like specimens with two parallel pre-existing cracks. Rock Mech. Rock Eng. 2018, 51, 3377–3393. [Google Scholar] [CrossRef]
- Lin, H.; Li, S.; Zhang, X. Macro-micro failure and crack coalescence behavior of soft-hard composite rock with three parallel joints under uniaxial compression. J. Mater. Res. Technol. 2024, 29, 2947–2958. [Google Scholar] [CrossRef]
- Mu, H.W.; Song, D.Z.; He, X.Q. Damage and fracture law of coal sample with different joint angles and their characterisation by acoustic emission. Struct. Control Health Monit. 2020, 27, e2639. [Google Scholar] [CrossRef]
- Hu, G.J.; Ma, G.; Liu, J. Size effect of the number of parallel joints on uniaxial compressive strength and characteristic strength. Minerals 2022, 12, 62. [Google Scholar] [CrossRef]
- Lin, Q.B.; Cao, P.; Wen, G.P. Crack coalescence in rock-like specimens with two dissimilar layers and pre-existing double parallel joints under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 139, 104621. [Google Scholar] [CrossRef]
- Xiong, L.X.; Chen, H.J.; Li, T.B. Uniaxial compressive study on mechanical properties of rock mass considering joint spacing and connectivity rate. Arab. J. Geosci. 2019, 12, 642. [Google Scholar] [CrossRef]
- Shan, R.; Liu, N.; Sun, P.; Zhao, Z.; Dong, R.; Dou, H.; Meng, H.; Bai, Y. Experimental and numerical simulation study of rough jointed rock samples under triaxial compression conditions. Eng. Fract. Mech. 2025, 314, 110707. [Google Scholar] [CrossRef]
- Hu, G.J.; Ma, G. Size effect of parallel-joint spacing on uniaxial compressive strength of rock. PLoS ONE 2021, 16, e0257245. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.C.; Yang, W.D.; Duan, K. Mechanical behaviors of the brittle rock-like specimens with multi-nonpersistent joints under uniaxial compression. Constr. Build. Mater. 2019, 220, 426–443. [Google Scholar] [CrossRef]
- Ríos-Bayona, F.; Johansson, F.; Mas-Ivars, D. Using PFC2D to simulate the shear behaviour of joints in hard crystalline rock. Bull. Eng. Geol. Environ. 2022, 81, 381. [Google Scholar] [CrossRef]
- Zheng, Z.; Tang, H.; Zhang, Q. True triaxial test and PFC3D-GBM simulation study on mechanical properties and fracture evolution mechanisms of rock under high stresses. Comput. Geotech. 2023, 154, 105136. [Google Scholar] [CrossRef]
- Yang, S.Q.; Sun, B.W.; Tian, W.L. Discrete element simulation of the mechanical properties of shale with different bedding inclinations under conventional triaxial compression. Chin. J. Eng. 2022, 44, 430–439. [Google Scholar]
- Zhou, Y.; Li, C.; Wang, W.L. A meso-level study on mechanical properties of bedding coal under uniaxial compression. J. Cent. South Univ. 2022, 53, 4036–4047. [Google Scholar]
- Zhao, H.; Hou, J.C.; Zhang, L. Towards concrete-rock interface shear containing similar triangular asperities. Int. J. Rock Mech. Min. 2021, 137, 104547. [Google Scholar] [CrossRef]
- Huang, L.S.; Li, B.; Li, C.; Wu, B.; Wang, J.X. Research on anisotropic characteristics and energy damage evolution mechanism of bedding coal under uniaxial compression. Energy 2024, 301, 131659. [Google Scholar] [CrossRef]
- Li, J.M.; Huang, Y.L.; Pu, H. Influence of block shape on macroscopic deformation response and meso-fabric evolution of crushed gangue under the triaxial compression. Powder Technol. 2021, 384, 112–124. [Google Scholar] [CrossRef]
- Nie, Z.H.; Qi, Q.; Wang, X.; Zhu, Y.G. DEM investigation of strain behaviour and force chain evolution of gravel-sand mixtures subjected to cyclic loading. Particuology 2022, 68, 13–28. [Google Scholar] [CrossRef]
- Li, H.R.; Qiao, Y.F.; Shen, R.X.; He, M.C.; Cheng, T.; Xiao, Y.M.; Tang, J. Effect of water on mechanical behavior and acoustic emission response of sandstone during loading process: Phenomenon and mechanism. Eng. Geol. 2021, 294, 106386. [Google Scholar] [CrossRef]
- Liu, S.K.; Nie, Z.H.; Hu, W.; Gong, J.; Lei, P. Effect of particle type on the shear behaviour of granular materials. Particuology 2021, 56, 124–131. [Google Scholar] [CrossRef]
- Luo, F.; Gao, S.; Xu, Z.; Dong, E.; Diao, Y.; Sang, Y. Mechanical behavior and tension-shear failure mechanism of fractured rock mass under uniaxial condition. Bull. Eng. Geol. Environ. 2023, 82, 314. [Google Scholar] [CrossRef]
- Zhu, K.; Sun, G.; Shi, L.; Lin, S.; Yu, X. Analysis of multi-level force chain network in granite tensile fracture based on 3D-GBM. Eng. Fail. Anal. 2024, 166, 108849. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, L.; Wei, J.; Pu, H.; Zhang, Q.; Hu, L.; Mi, X. Stress evolution in rocks around tunnel under uniaxial loading: Insights from PFC3D-GBM modelling and force chain analysis. Theor. Appl. Fract. Mech. 2024, 134, 104728. [Google Scholar] [CrossRef]



| Particle-Parameters | Values | Contact-Parameters | Values |
|---|---|---|---|
| Minimum radius of the particle, Rmin/mm | 0.28 | Standard deviation of bond tangential strength, τs,dev/MPa | 1.25 |
| Ratio of maximum to minimum of radius, Rrat | 1.66 | Young’s modulus of the parallel bond, /GPa | 2.25 |
| Density of the particle, ρ/(kg·m−3) | 1400 | Ratio of normal to shear stiffness of the parallel bond, | 3.0 |
| Friction coefficient, μ | 0.5 | Average bond normal strength, σn,mean/MPa | 12.5 |
| Young’s modulus of the particle, EC/GPa | 2.25 | Standard deviation of bond normal strength, σn,dev/MPa | 1.25 |
| Ratio of normal to shear stiffness of the particle, kn/ks | 3.0 | Average bond tangential strength, τs,mean/MPa | 12.5 |
| Parallel bonding radius factor, λ | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, E.; Yue, J.; Miao, B.; Xi, D.; Teng, X. Uniaxial Compressive Mechanical Behavior of Coals with Different Joint Spacing and Angles: A DEM Numerical Simulation Study. Appl. Sci. 2025, 15, 9196. https://doi.org/10.3390/app15169196
Zhang H, Wang E, Yue J, Miao B, Xi D, Teng X. Uniaxial Compressive Mechanical Behavior of Coals with Different Joint Spacing and Angles: A DEM Numerical Simulation Study. Applied Sciences. 2025; 15(16):9196. https://doi.org/10.3390/app15169196
Chicago/Turabian StyleZhang, Herui, Enyuan Wang, Jianhua Yue, Bin Miao, Danyang Xi, and Xiaozhen Teng. 2025. "Uniaxial Compressive Mechanical Behavior of Coals with Different Joint Spacing and Angles: A DEM Numerical Simulation Study" Applied Sciences 15, no. 16: 9196. https://doi.org/10.3390/app15169196
APA StyleZhang, H., Wang, E., Yue, J., Miao, B., Xi, D., & Teng, X. (2025). Uniaxial Compressive Mechanical Behavior of Coals with Different Joint Spacing and Angles: A DEM Numerical Simulation Study. Applied Sciences, 15(16), 9196. https://doi.org/10.3390/app15169196






