Acoustic Transmission Characteristics and Model Prediction of Upper and Lower Completion Pipe Strings for Test Production of Natural Gas Hydrate
Abstract
1. Introduction
2. Numerical Analysis of the Acoustic Transmission Characteristics of Pipe Strings
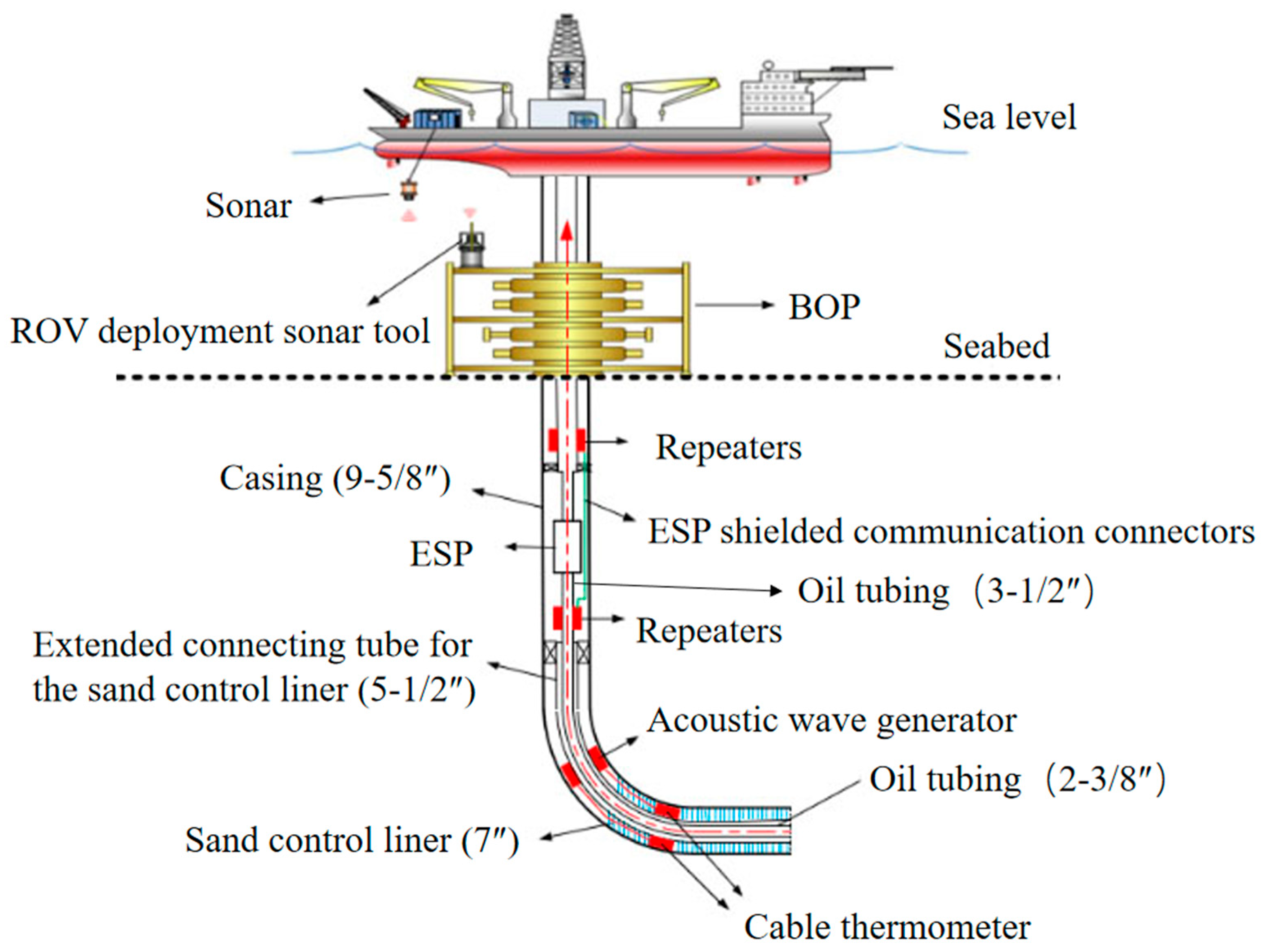
2.1. Overall Program for the Acoustic Transmission of Pipe Strings
2.2. Numerical Simulation of Acoustic Transmission in the Pipe String
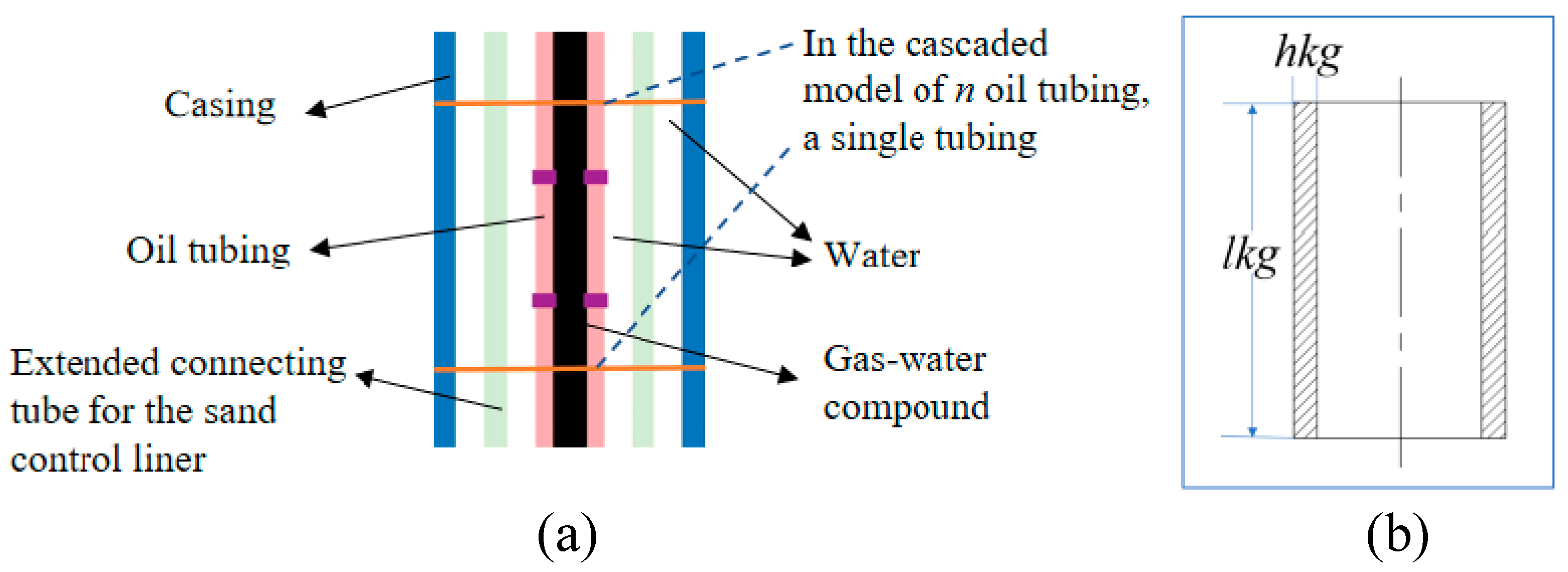
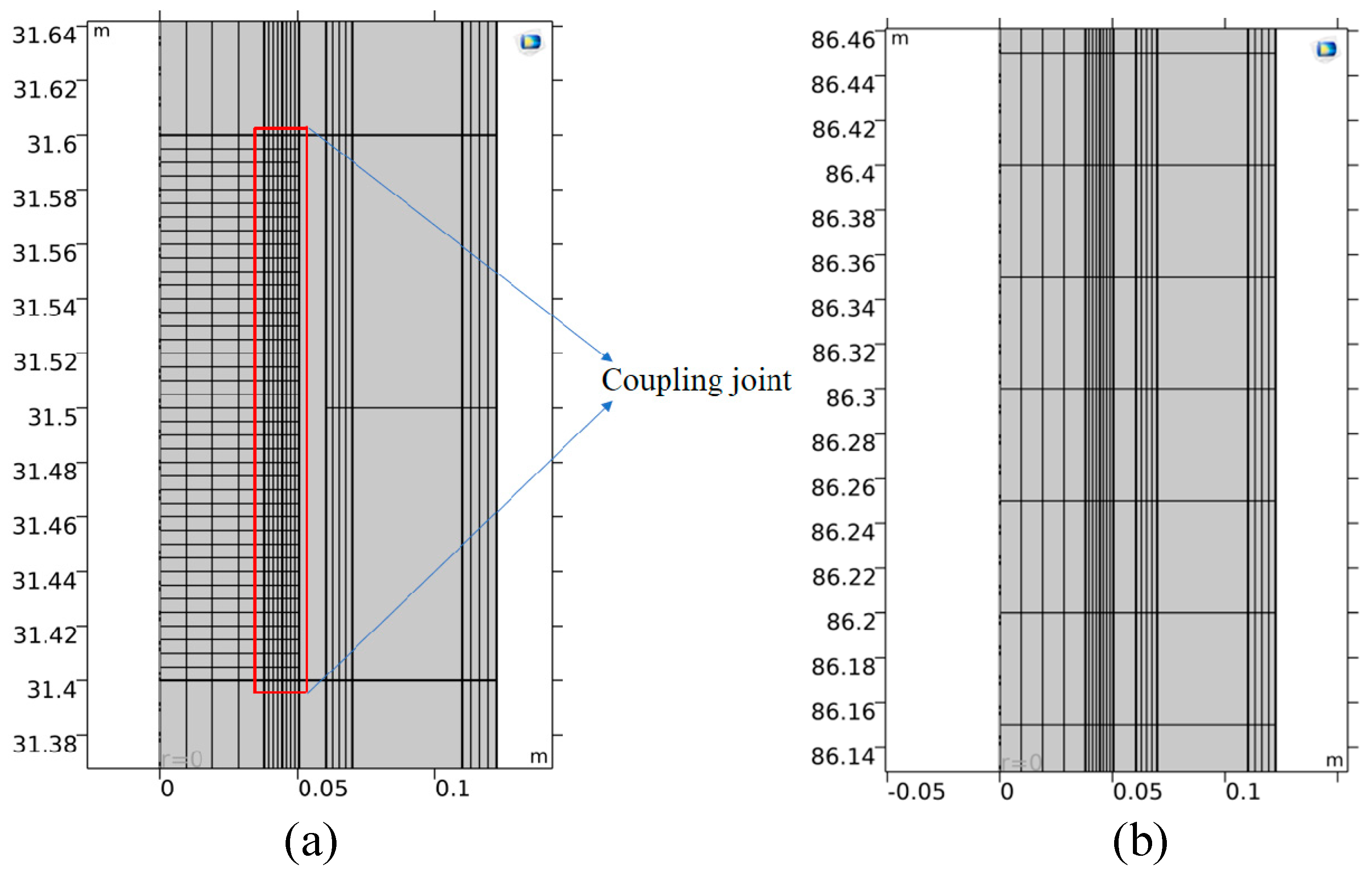
2.2.1. A Finite Element Model for Acoustic Transmission
2.2.2. Evaluation Metrics for the Acoustic Transmission Characteristics
2.3. Parameters for Acoustic Transmission Analysis of Pipe Strings
2.4. Analysis of Pipe String Acoustic Transmission Simulation Results
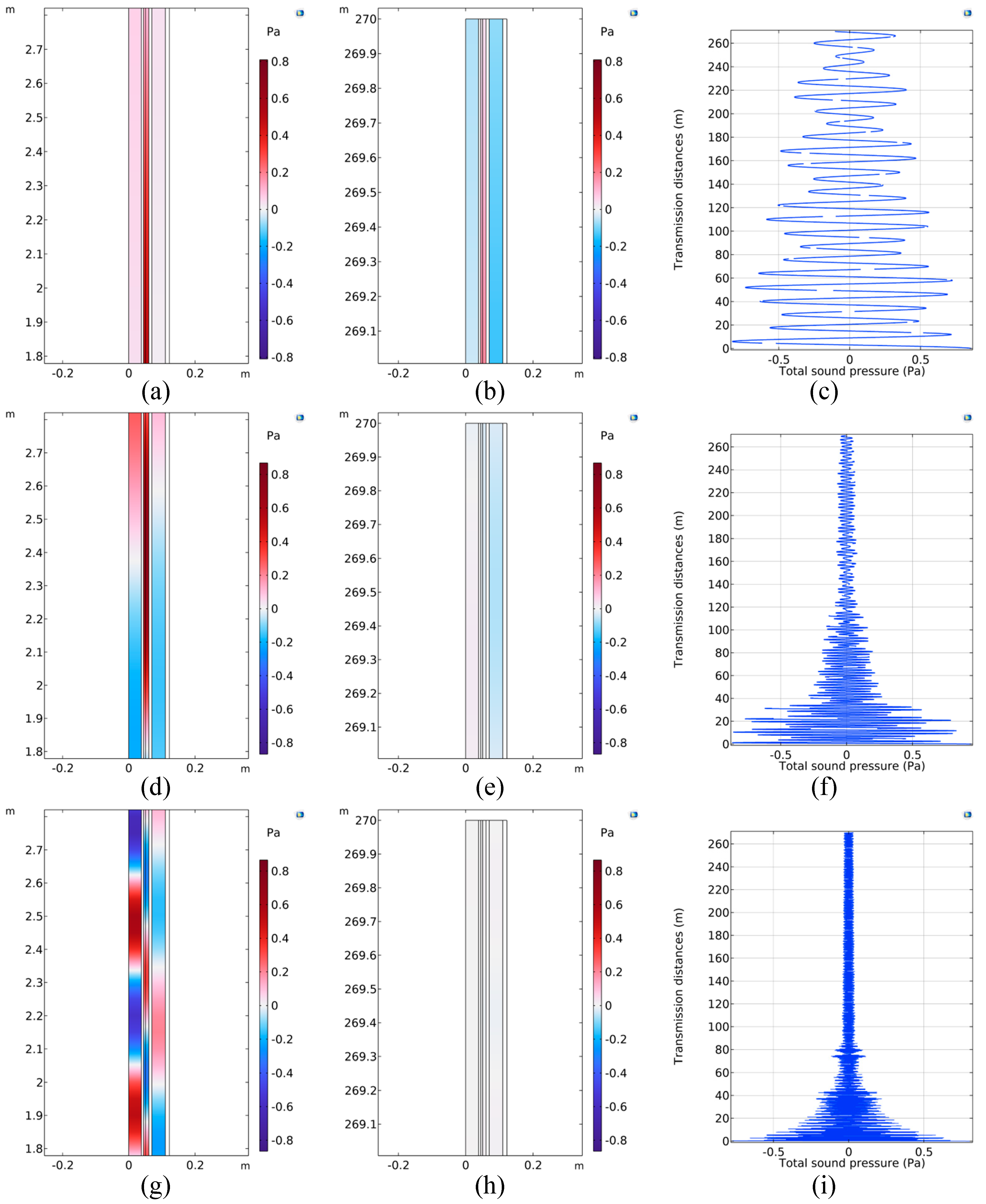
2.4.1. Cloud and Line Plots of the Sound Pressure and Sound Pressure Level in the Pipe String at Different Frequencies
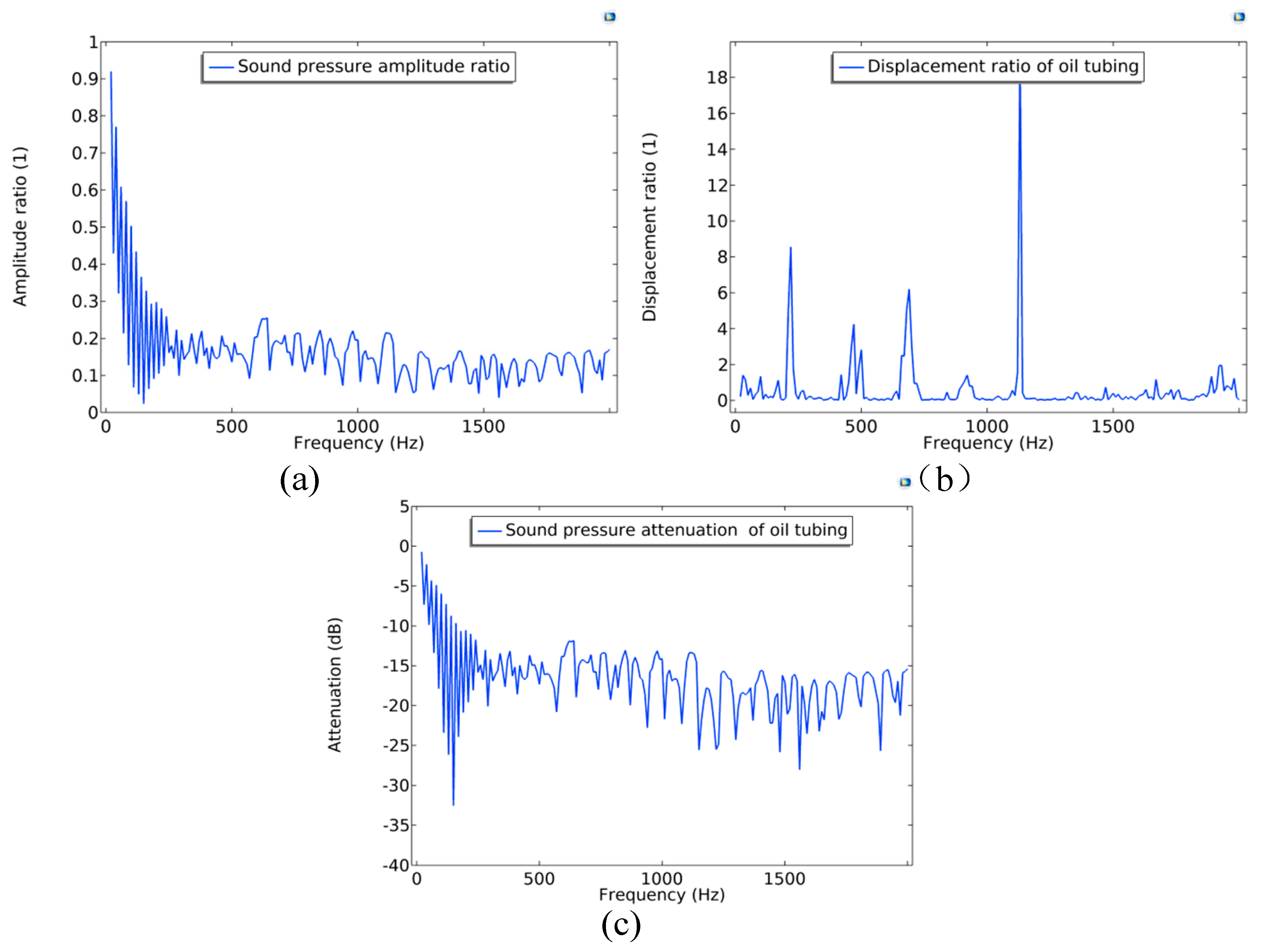
2.4.2. Evaluation Indexes of Acoustic Transmission Characteristics
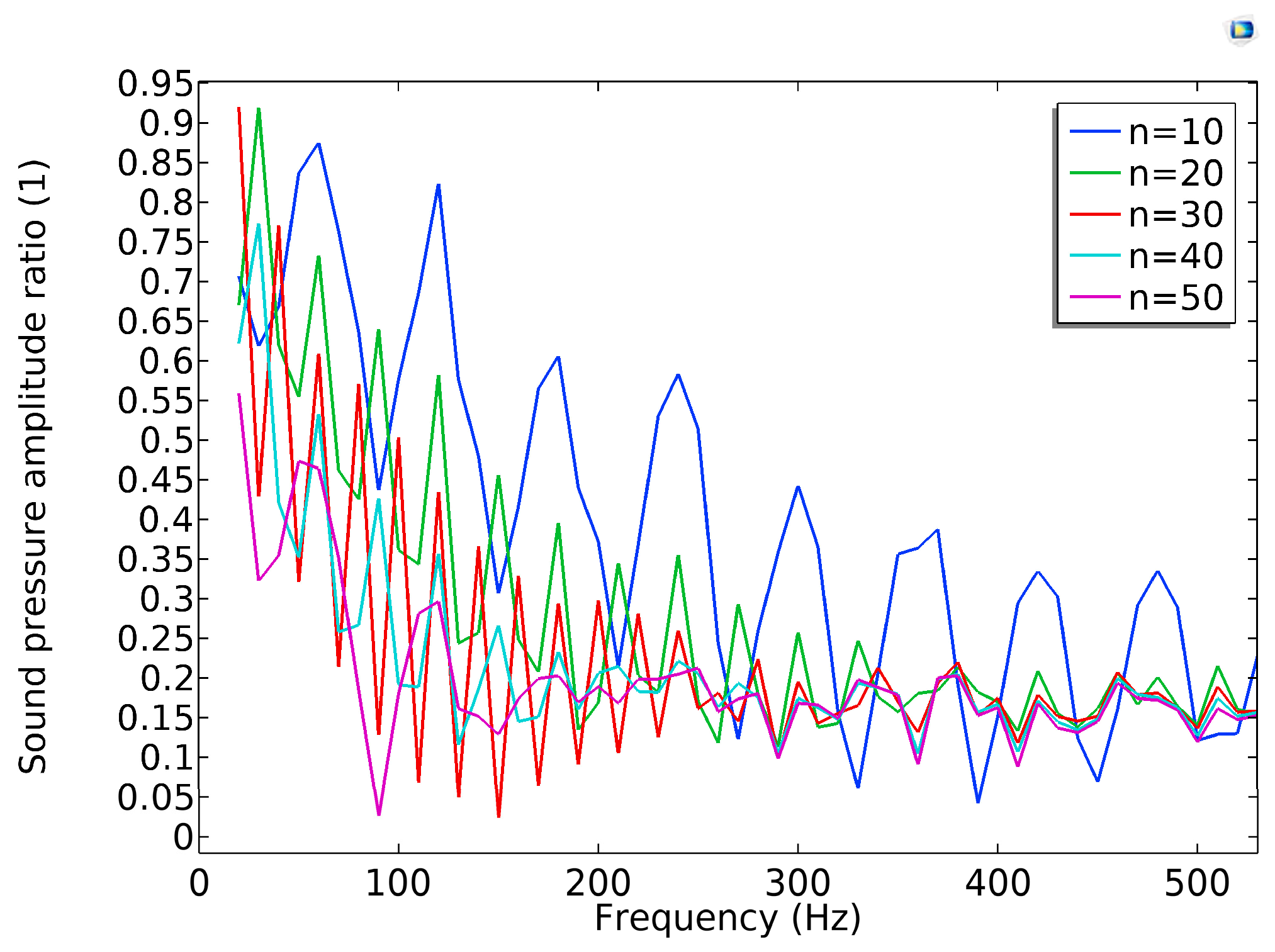
2.4.3. Effects of the Number of Oil Tubing Cascades on Acoustic Transmission Performance
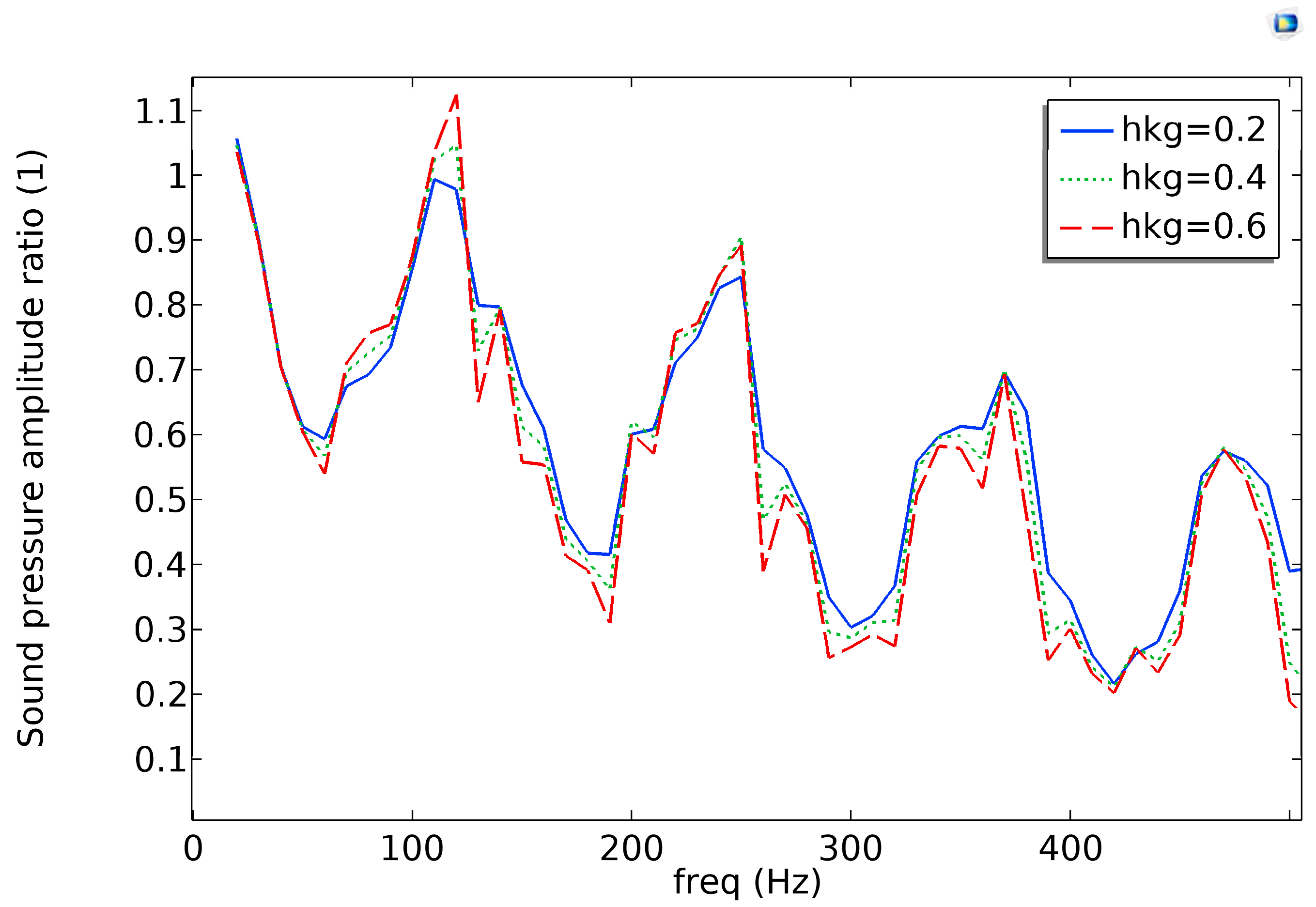
2.4.4. Effects of Hoop Size on Acoustic Transmission Performance
3. Prediction and Parameter Optimization of an Acoustic Transmission Model for Pipe Strings
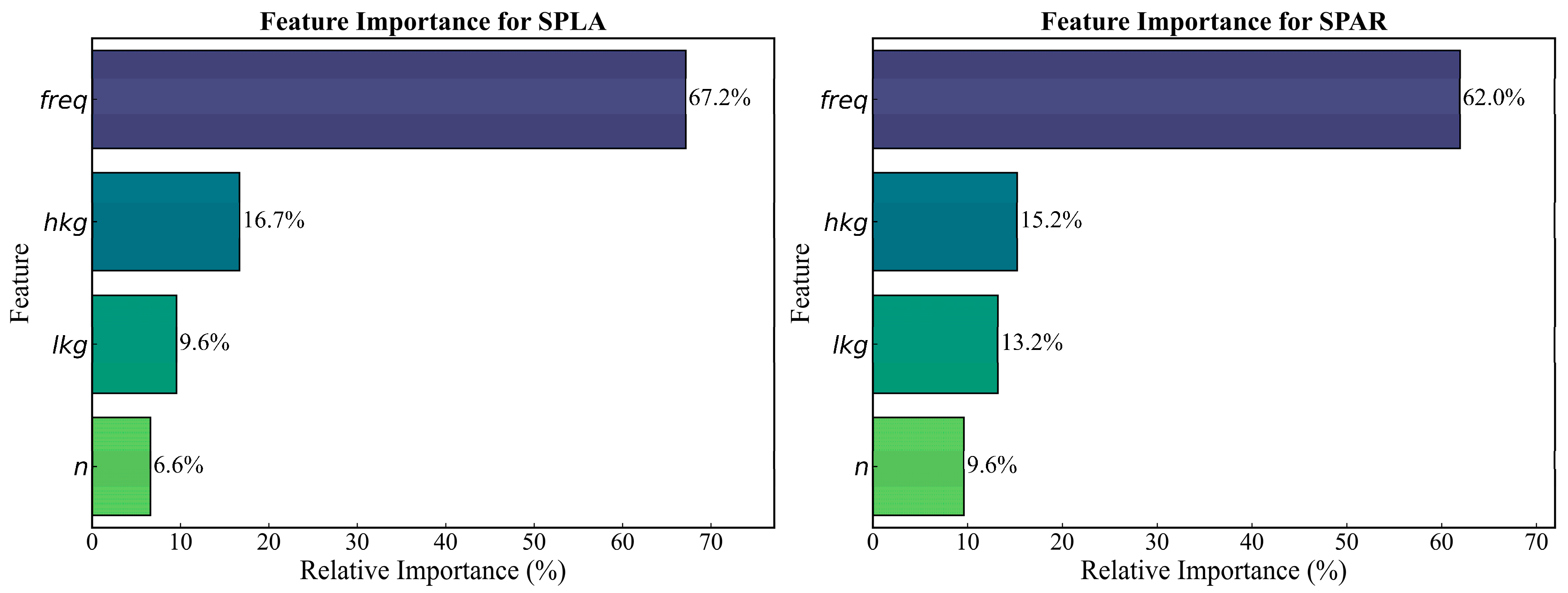
3.1. LightGBM-Based Prediction of the Acoustic Transmission Characteristic Curves of Pipe Strings
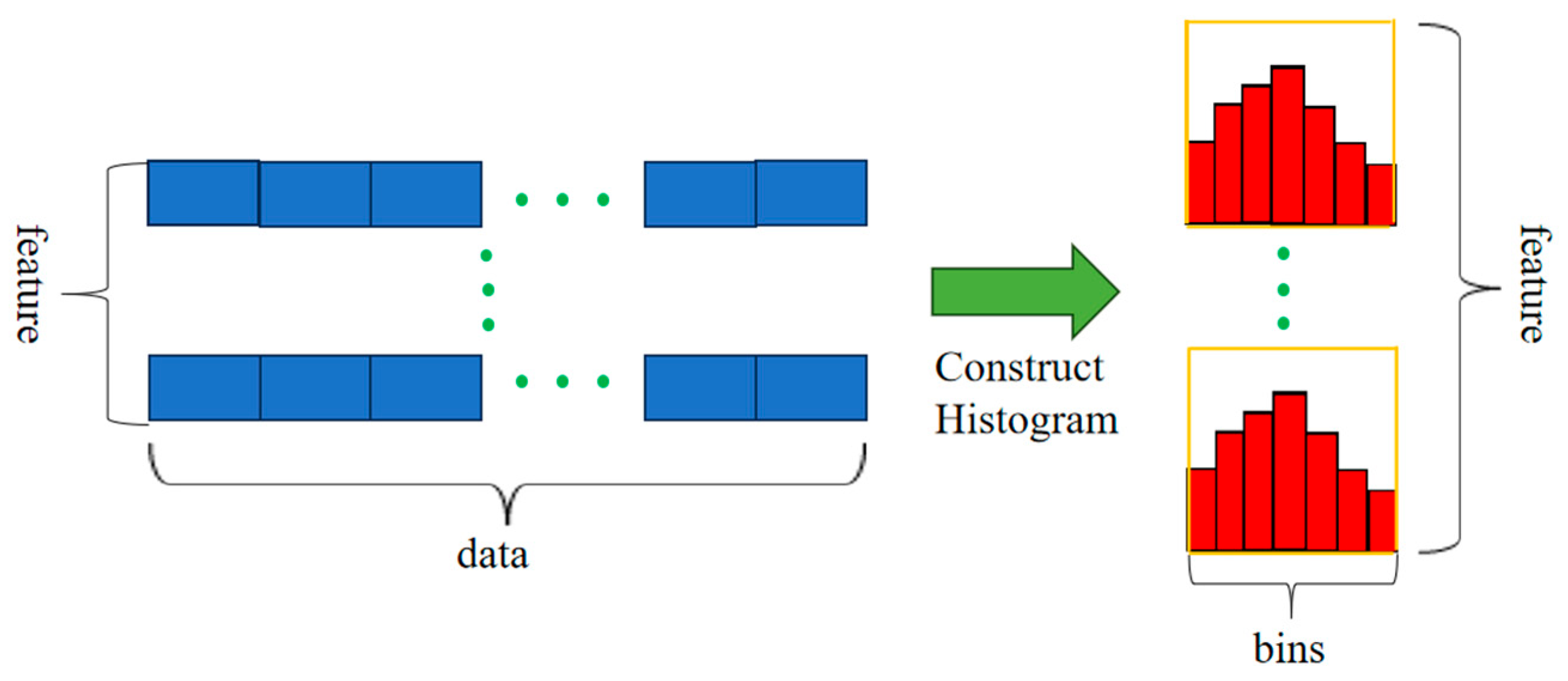
3.1.1. Principles of the LightGBM Algorithm
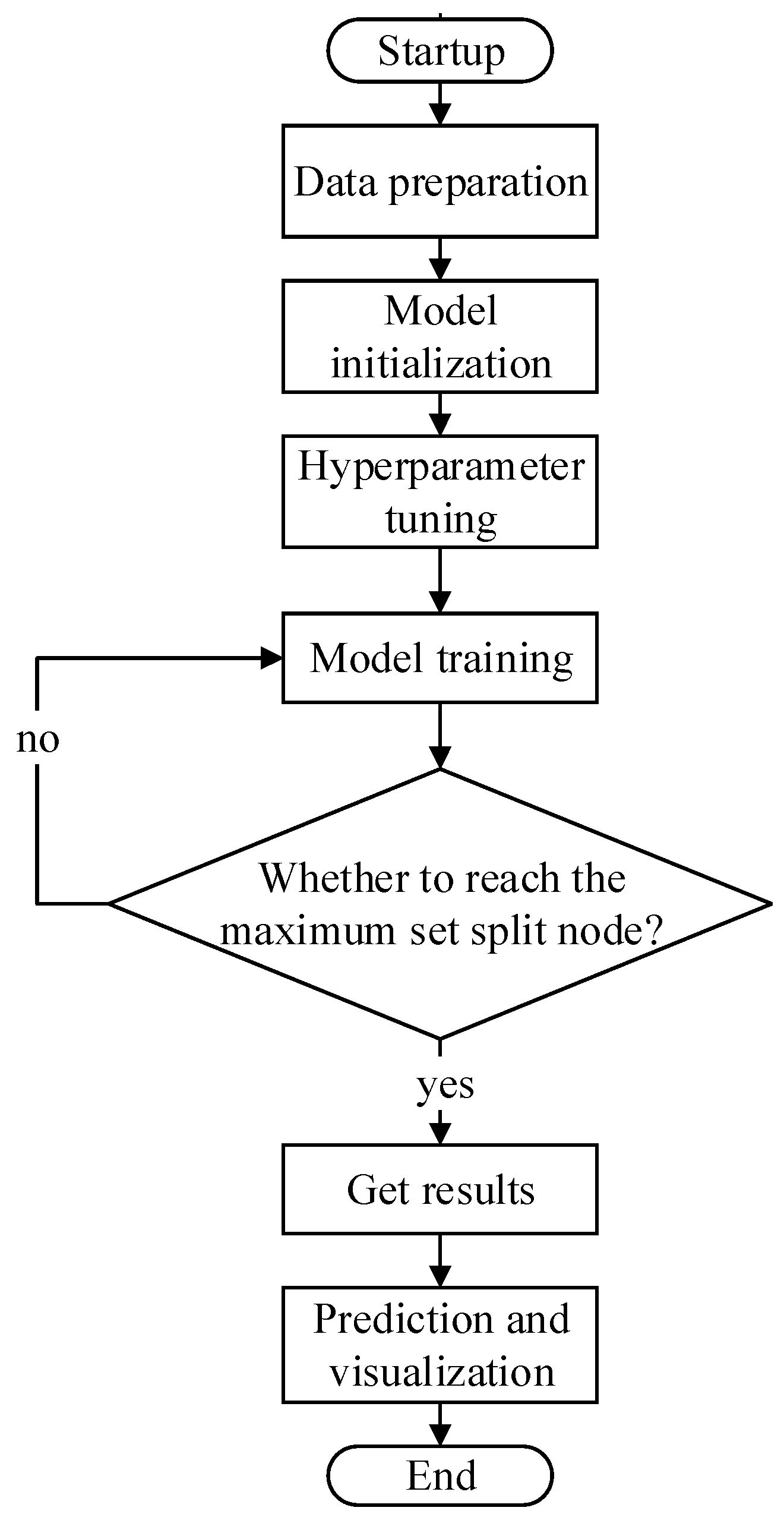
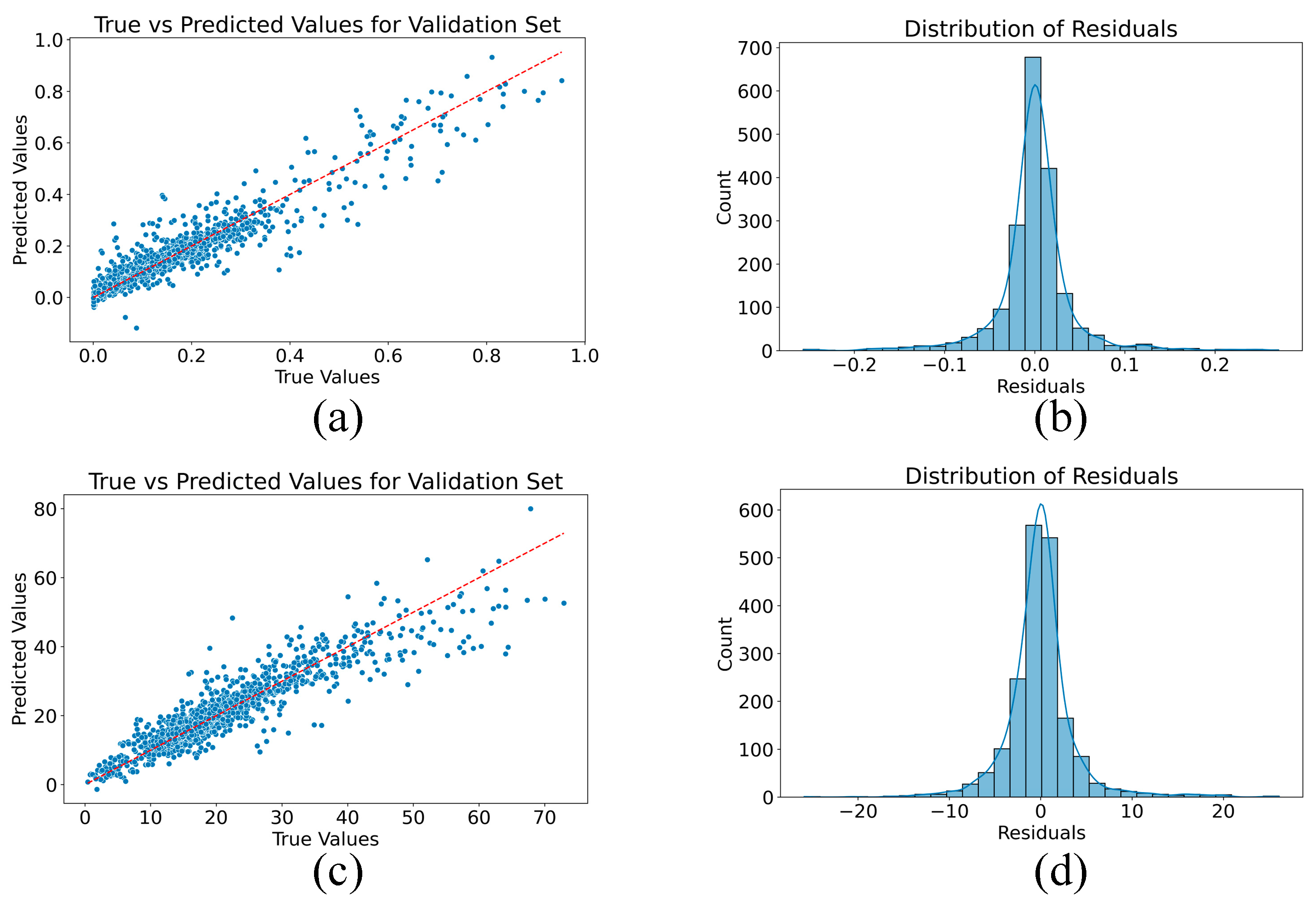
3.1.2. Analysis of Model Prediction Results
3.2. Multi-Objective Optimization of Acoustic Transmission Parameters Based on NSGA-II
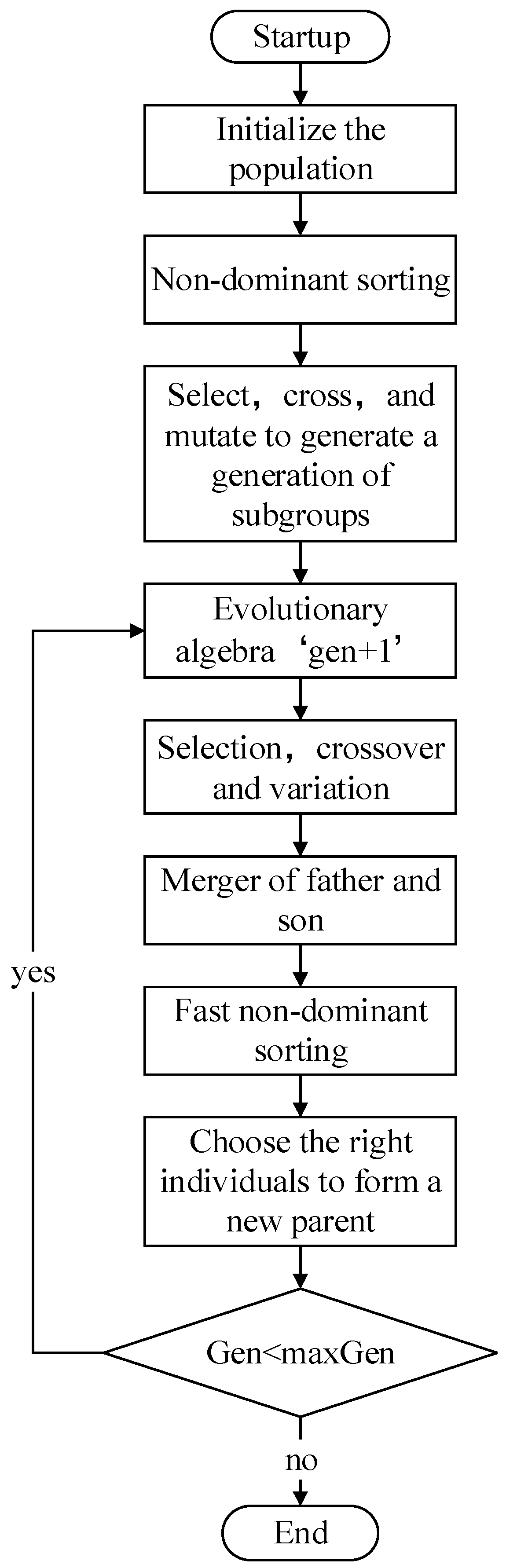
3.2.1. Principles of NSGA-II Algorithm
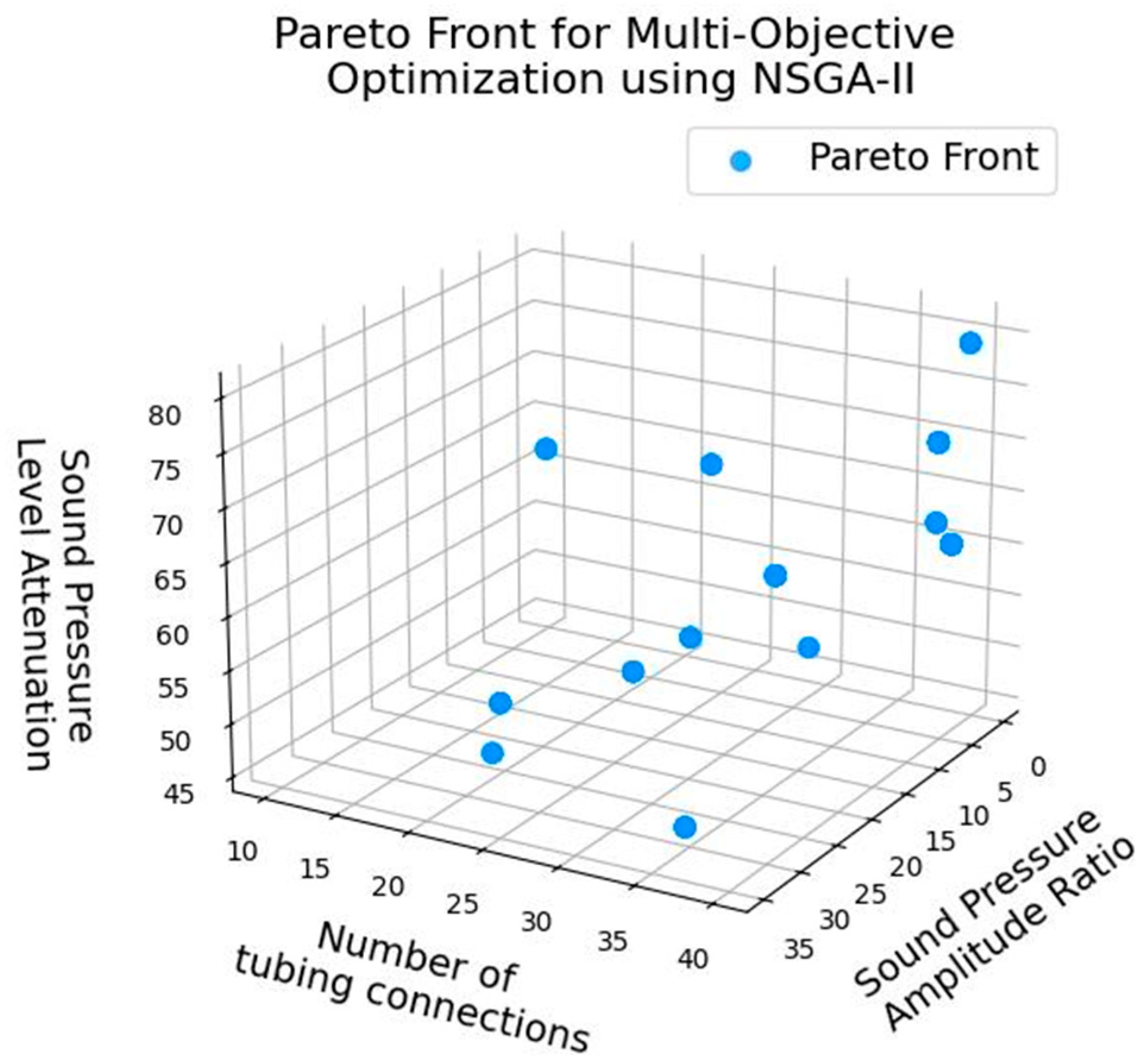
3.2.2. Analysis of Optimization Results
4. Conclusions and Outlook
4.1. Conclusions
4.2. Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Transmission loss (ratio of sound pressure amplitude at the exit to that at the incident end) | |
| Sound pressure at the outlet | |
| Sound pressure at the incident side | |
| Oil tubing displacement ratio (ratio of displacement at the outlet end of the tubing to that at the incident end) | |
| Displacement of the outlet end of the oil tubing | |
| Displacement of the incident end of the oil tubing | |
| Sound pressure attenuation inside the oil tubing | |
| Density of gas–water compounds | |
| Density of liquids | |
| Density of gases | |
| Gas volume fraction | |
| Velocity of sound for gas–water compounds | |
| Velocity of sound in liquids | |
| Speed of sound of gases | |
| Viscosity of gas–water compounds | |
| Viscosity of the liquid | |
| Viscosity of the gas | |
| Sound pressure level in decibels (dB) | |
| The eigenvector of the first sample | |
| Corresponding tags | |
| Value predicted by the model | |
| Predictions from the model for the front wheel | |
| The optimal segmentation point found in the m-th iteration | |
| Features used for optimal segmentation in the m-th iteration | |
| The value is segmented against the feature in the first iteration | |
| Denoting the value of the min. loss function | |
| Loss function, which measures the difference between the predicted value and the actual value | |
| Denoting the model prediction in the first iteration | |
| Denoting the operation of the data segmentation using features and values at points | |
| The operation of segmentation with the best segmentation point, feature, and segmentation value found in the first iteration |
References
- Tong, X.; Zhang, G.; Wang, Z.; Wen, Z.; Tain, Z.; Wang, H.; Feng, M.A.; Wu, Y. Distribution and potential of global oil and gas resources. Pet. Explor. Dev. 2018, 45, 779–789. [Google Scholar] [CrossRef]
- Zhang, C.W.; Zhou, X.G.; Qu, X.C.; Hu, G.F. Transmission design based on sonic drilling parameter. Appl. Mech. Mater. 2014, 528, 328–333. [Google Scholar] [CrossRef]
- Bouldin, B.; Alshmakhy, A.; Bazuhair, A.K.; Alzaabi, M.H.; Fellinghaug, J.A. A Review of Downhole Wireless Technologies and Improvements. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021; SPE: Richardson, TX, USA, 2021. [Google Scholar]
- Wang, Y.; Guang, Z. The new underground positioning system. Acta Pet. Sin. 2002, 23, 77. [Google Scholar]
- Drumheller, D.S.; Kuszmaul, S.S. Acoustic Telemetry; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2003. [Google Scholar]
- Gao, L.; Finley, D.; Gardner, W.; Robbins, C.; Linyaev, E.; Moore, J.; Memarzadeh, M.; Johnson, D. Acoustic telemetry can deliver more real-time downhole data in underbalanced drilling operations. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Mumbai, India, 16–18 October 2006; SPE: Richardson, TX, USA, 2006. [Google Scholar]
- Gao, L.; Gardner, W.; Robbins, C.; Memarzadeh, M.; Johnson, D. Limits on data communication along the drill string using acoustic wave. SPE Reserv. Eval. Eng. 2008, 11, 141–146. [Google Scholar] [CrossRef]
- Filoux, E.; Levassort, F.; Callé, S.; Certon, D.; Lethiecq, M. P2I-9 Modeling of Axisymetrical Transducer Configurations Based on Pseudospectral/Finite-Difference Time-Domain Method. In Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings, New York, NY, USA, 28–31 October 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Ma, H.; Wang, Y. Well-log acoustic velocity prediction based on relevance vector machine. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Che, X.; Qiao, W.; Ju, X.; Lu, J.; Wang, R. Numerical simulations of the reflected P-wave amplitude in azimuthal acoustic reflection logging. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Hawthorn, A.; Aguilar, S. New wireless acoustic telemetry system allows real-time downhole data transmission through regular drillpipe. In Proceedings of the SPE Annual Technical Conference and Exhibition? San Antonio, TX, USA, 9–11 October 2017; SPE: Richardson, TX, USA, 2017. [Google Scholar]
- Liu, X.; Wu, J.; Qiao, H.; Zhao, J.; Li, C.; Zhang, Y.; Wan, L. The real-time acquisition and analysis software system for laser-induced plasma acoustic wave signal. Opto-Electron. Eng. 2019, 46, 180534-1–180534-9. [Google Scholar]
- Ellmauthaler, A.; Seabrook, B.C.; Wilson, G.A.; Maida, J.; Bush, J.; Leblanc, M.; Dupree, J.; Uribe, M. Distributed acoustic sensing of subsea wells. Lead. Edge 2020, 39, 801–807. [Google Scholar] [CrossRef]
- Bachman, H.; Chen, C.; Rufo, J.; Zhao, S.; Yang, S.; Tian, Z.; Nama, N.; Huang, P.; Huang, T.J. An acoustofluidic device for efficient mixing over a wide range of flow rates. Lab. Chip 2020, 20, 1238–1248. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.F.; Jayakody, D.N.K.; Chursin, Y.A.; Affes, S.; Dmitry, S. Recent advances and future directions on underwater wireless communications. Arch. Comput. Method. Eng. 2020, 27, 1379–1412. [Google Scholar] [CrossRef]
- Gao, N.; Lu, K. An underwater metamaterial for broadband acoustic absorption at low frequency. Appl. Acoust. 2020, 169, 107500. [Google Scholar] [CrossRef]
- Marin, J.M.; Ashry, I.; Alkhazragi, O.; Trichili, A.; Khee Ng, T.; Ooi, B.S. Simultaneous distributed acoustic sensing and communication over a two-mode fiber. Opt. Lett. 2022, 47, 6321–6324. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Geng, Y. Wireless Communication System for Drilling Based on OFDM Using Acoustic Wave. In Proceedings of the International Field Exploration and Development Conference, Wuhan, China, 19–21 September 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Wang, C.; Qiao, W.; Zhang, W. Using transfer matrix method to study the acoustic property of drill strings. In Proceedings of the 2006 IEEE International Symposium on Signal Processing and Information Technology, Vancouver, BC, Canada, 27–30 August 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar]
- Shen, Y.Z.; Sheng, L.L. Transmission characteristics of the drilling fluid pressure quadrature phase shift keying signal along a directional wellbore. Acta Pet. Sin. 2011, 32, 340. [Google Scholar]
- Wei, Z.; Yibing, S.; Yanjun, L. Design of acoustic wireless remote transmission system for logging-while-drilling data. In Proceedings of the 2013 IEEE 11th International Conference on Electronic Measurement & Instruments, Harbin, China, 16–19 August 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Hou, Y.; Zhou, R.; Long, X.; Liu, P.; Fu, Y. The design and simulation of new downhole vibration device about acoustic oil recovery technology. Petroleum 2015, 1, 257–263. [Google Scholar] [CrossRef]
- Perez-Arancibia, C.; Godoy, E.; Duran, M. Modeling and simulation of an acoustic well stimulation method. Wave Motion 2018, 77, 214–228. [Google Scholar] [CrossRef]
- Bai, H.; Lin, Q.; Wang, C. Acoustic Communication Signal Recognition Method Based on Discrete Signal Correlation. J. Liaoning Univ. Pet. Chem. Technol. 2021, 41, 87. [Google Scholar]
- Bai, H.; Wang, C.; Lin, Q.; Zhang, L. Acoustic Attenuation Characteristics of Remote Wireless Communication in Oil Wells. J. Liaoning Univ. Pet. Chem. Technol. 2022, 42, 79. [Google Scholar]
- Paillet, F.L.; Cheng, C.H. Acoustic Waves in Boreholes; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Chiantello, D.A. Acoustic Modelling, Data Augmentation and Feature Extraction for In-Pipe Machine Learning Applications; Manchester Metropolitan University: Manchester, UK, 2023. [Google Scholar]
- Ullah, N.; Ahmed, Z.; Kim, J. Pipeline leakage detection using acoustic emission and machine learning algorithms. Sensors 2023, 23, 3226. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Yu, Y.; Wen-wei, X.; Liang, J.; Lu, J.; Xu, B.; Shi, H.; Yu, H.; Qin, R.; Li, X. Design and feasibility analysis of a new completion monitoring technical scheme for natural gas hydrate production tests. China Geol. 2023, 6, 466–475. [Google Scholar] [CrossRef]
- Gutierrez-Estevez, M.A.; Krüger, U.; Krueger, K.A.; Manolakis, K.; Jungnickel, V. Acoustic channel model for adaptive downhole communication over deep drill strings. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 4883–4887. [Google Scholar]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C. The second natural gas hydrate production test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Sojahrood, A.J.; Li, Q.; Haghi, H.; Karshafian, R.; Porter, T.M.; Kolios, M.C. Probing the pressure dependence of sound speed and attenuation in bubbly media: Experimental observations, a theoretical model and numerical calculations. Ultrason. Sonochem 2023, 95, 106319. [Google Scholar] [CrossRef]
- Xin, L.I.; Weihao, L.I.; Jian, S.; Qiang, L.I.; Shaoping, W. Pipelines vibration analysis and control based on clamps’ locations optimization of multi-pump system. Chin. J. Aeronaut. 2022, 35, 352–366. [Google Scholar] [CrossRef]
- Švec, J.G.; Granqvist, S. Tutorial and guidelines on measurement of sound pressure level in voice and speech. J. Speech Lang. Hear. Res. 2018, 61, 441–461. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A model combining convolutional neural network and LightGBM algorithm for ultra-short-term wind power forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 52. [Google Scholar]
- Kadiyala, A.; Kumar, A. Applications of python to evaluate the performance of decision tree-based boosting algorithms. Environ. Prog. Sustain. Energy 2018, 37, 618–623. [Google Scholar] [CrossRef]
- Gurung, R.B.; Lindgren, T.; Boström, H. Learning decision trees from histogram data using multiple subsets of bins. In Proceedings of the The Twenty-Ninth International Flairs Conference, Key Largo, FL, USA, 16–18 May 2016. [Google Scholar]
- Ye, J. A faster drop-in implementation for leaf-wise exact greedy induction of decision tree using pre-sorted deque. arXiv 2017, arXiv:1712.06989. [Google Scholar]
- Li, Z.; Yao, X.; Liu, Z.; Zhang, J. Feature selection algorithm based on LightGBM. J. Northeast. Univ. 2021, 42, 1688. [Google Scholar]
- Afanaseva, O.; Bezyukov, O.; Pervukhin, D.; Tukeev, D. Experimental study results processing method for the marine diesel engines vibration activity caused by the cylinder-piston group operations. Inventions 2023, 8, 71. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]



| Comparison Dimension | Previous Studies | Current Studies |
|---|---|---|
| Research orientation | Acoustic transmission of periodic/single-layer oil pipes | Acoustic transmission of multi-layer pipe strings in hydrate trial production |
| Structural complexity | Single-layer pipe simple model | Multi-layer pipe-fluid coupling model |
| Research method | Theoretical analysis + simple simulation | COMSOL (Version 6.3) simulation + LightGBM prediction + NSGA-II optimization |
| Optimization objective | No clear multi-objective optimization | Max transmission distance, sound pressure ratio, min attenuation |
| Application scenario | Conventional oil and gas downhole monitoring | Natural gas hydrate trial production |
| Innovation summary | Focus on theoretical derivation and single simulation [30] | Construct a multi-layer pipe-fluid coupled acoustic model; establish a “simulation-LightGBM prediction-NSGA-II optimization” closed-loop framework |
| Material properties of structural domains | Structural steel | |
| Isotropic structured loss factor (1) | 0.04 | |
| Density (kg/m3) | 7850 | |
| Young’s modulus (GPa) | 210 | |
| Poisson’s ratio (1) | 0.27 | |
| Material properties of fluid domains | Water | Gas–water compound |
| Intrinsic viscosity (mPa-s) | 0.6 | 0.4 |
| Dynamic viscosity (mPa-s) | 0.8 | 0.5 |
| Density (kg/m3) | 1020 | 600 |
| Speed of sound (m/s) | 1500 | 340 |
| Parametric | Realm | Step Interval | Parameter Description |
|---|---|---|---|
| n | 10–50 (root) | 10 (root) | Number of tubing cascades |
| lkg | 4–12 (mm) | 2 (mm) | Thickness of oil tubing connection clamps |
| hkg | 0.2–1.4 (m) | 0.2 (m) | Width of oil tubing connection clamps |
| freq | 20–2000 (Hz) | 10 (Hz) | source frequency |
| Indicator/Parameter | Model 1 | Model 2 |
|---|---|---|
| Model evaluation metric | ||
| R2 (%) | 88.79 | 85.08 |
| RMSE (dB) | 0.0473 | 4.3955 |
| LightGBM algorithm parameters | ||
| colsample_bytree | [0.6, 0.1, 1.0] | [0.6, 0.1, 1.0] |
| learning_rate | [0.005, 0.005, 0.15] | [0.005, 0.005, 0.15] |
| max_depth | [5, 5, 25] | [5, 5, 25] |
| n_estimators | [200, 200, 1000] | [200, 200, 1000] |
| num_leaves | [20, 20, 60] | [20, 20, 60] |
| subsample | [0.6, 0.1, 1.0] | [0.6, 0.1, 1.0] |
| Extraction of input features (dataset) | hkg, lkg, n, freq | hkg, lkg, n, freq |
| Target variable (validation set) | Sound pressure amplitude ratio | Sound pressure level attenuation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Chen, H.; Yin, G.; Qin, R.; Gao, J.; He, X. Acoustic Transmission Characteristics and Model Prediction of Upper and Lower Completion Pipe Strings for Test Production of Natural Gas Hydrate. Appl. Sci. 2025, 15, 9174. https://doi.org/10.3390/app15169174
Xu B, Chen H, Yin G, Qin R, Gao J, He X. Acoustic Transmission Characteristics and Model Prediction of Upper and Lower Completion Pipe Strings for Test Production of Natural Gas Hydrate. Applied Sciences. 2025; 15(16):9174. https://doi.org/10.3390/app15169174
Chicago/Turabian StyleXu, Benchong, Haowen Chen, Guoyue Yin, Rulei Qin, Jieyun Gao, and Xin He. 2025. "Acoustic Transmission Characteristics and Model Prediction of Upper and Lower Completion Pipe Strings for Test Production of Natural Gas Hydrate" Applied Sciences 15, no. 16: 9174. https://doi.org/10.3390/app15169174
APA StyleXu, B., Chen, H., Yin, G., Qin, R., Gao, J., & He, X. (2025). Acoustic Transmission Characteristics and Model Prediction of Upper and Lower Completion Pipe Strings for Test Production of Natural Gas Hydrate. Applied Sciences, 15(16), 9174. https://doi.org/10.3390/app15169174






