Critical Cluster Mining and Optimal Allocation for Power Grid Projects Based on Complex Networks and Multidimensional Metrics
Abstract
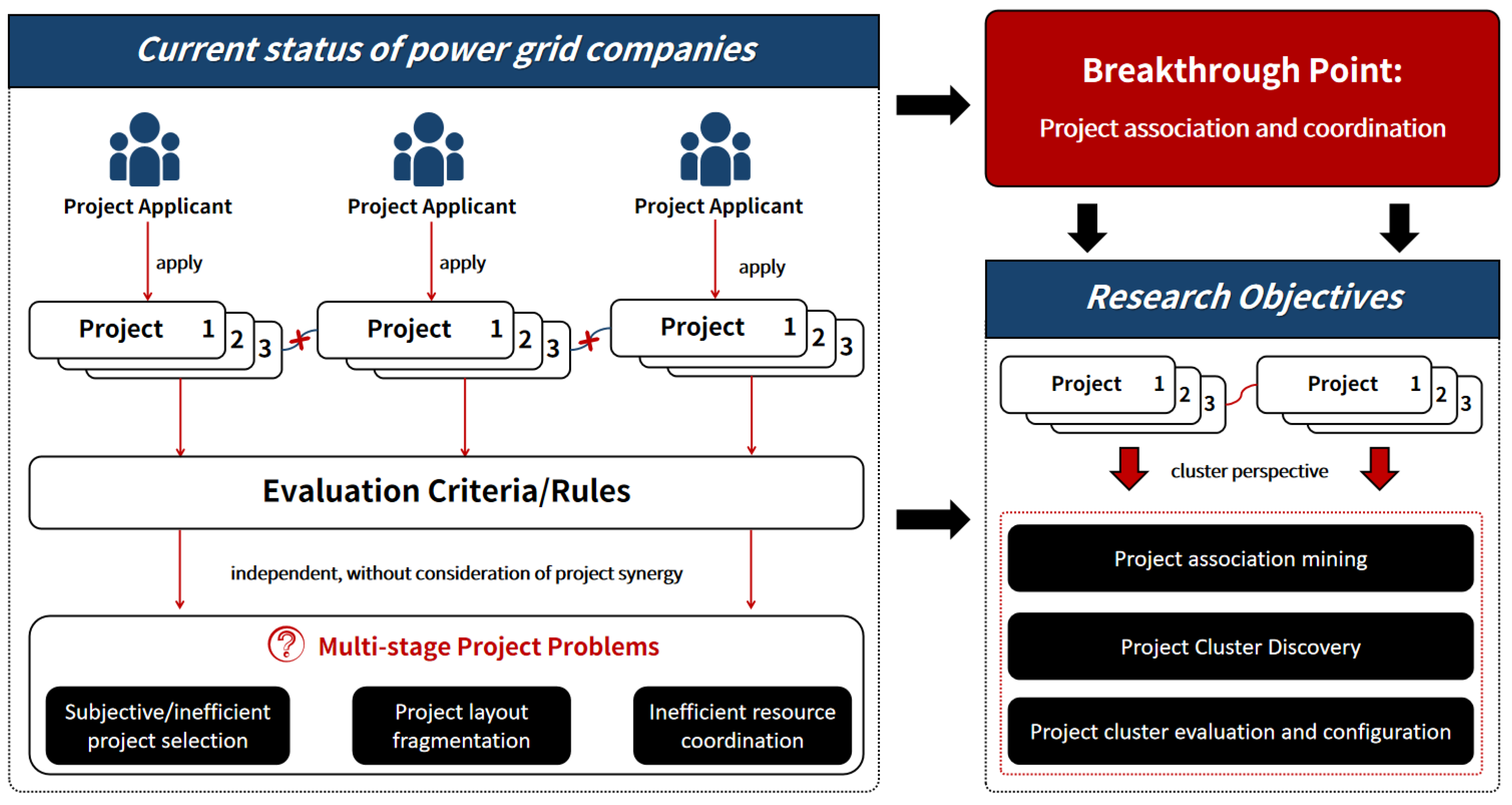
1. Introduction
- (1)
- A project association network is constructed through semantic, geographic, and strategic multidimensional association analysis and the development of fusion strategies. Based on the community detection method, the preliminary preferences of project clusters are successfully realized, which improves upon the single perspective of individual projects and makes up for the existing deficiencies of project management.
- (2)
- An innovative project-cluster-oriented multidimensional evaluation system is proposed that can scientifically and comprehensively assess the management and investment benefits of project clusters, support the configuration optimization of project clusters, provide a quantitative basis for project decision-making, and enhance the scientific nature of project management.
2. Related Work
2.1. Complex Networks
2.2. Community Detection
2.3. Project Portfolio Evaluation and Selection
3. Method
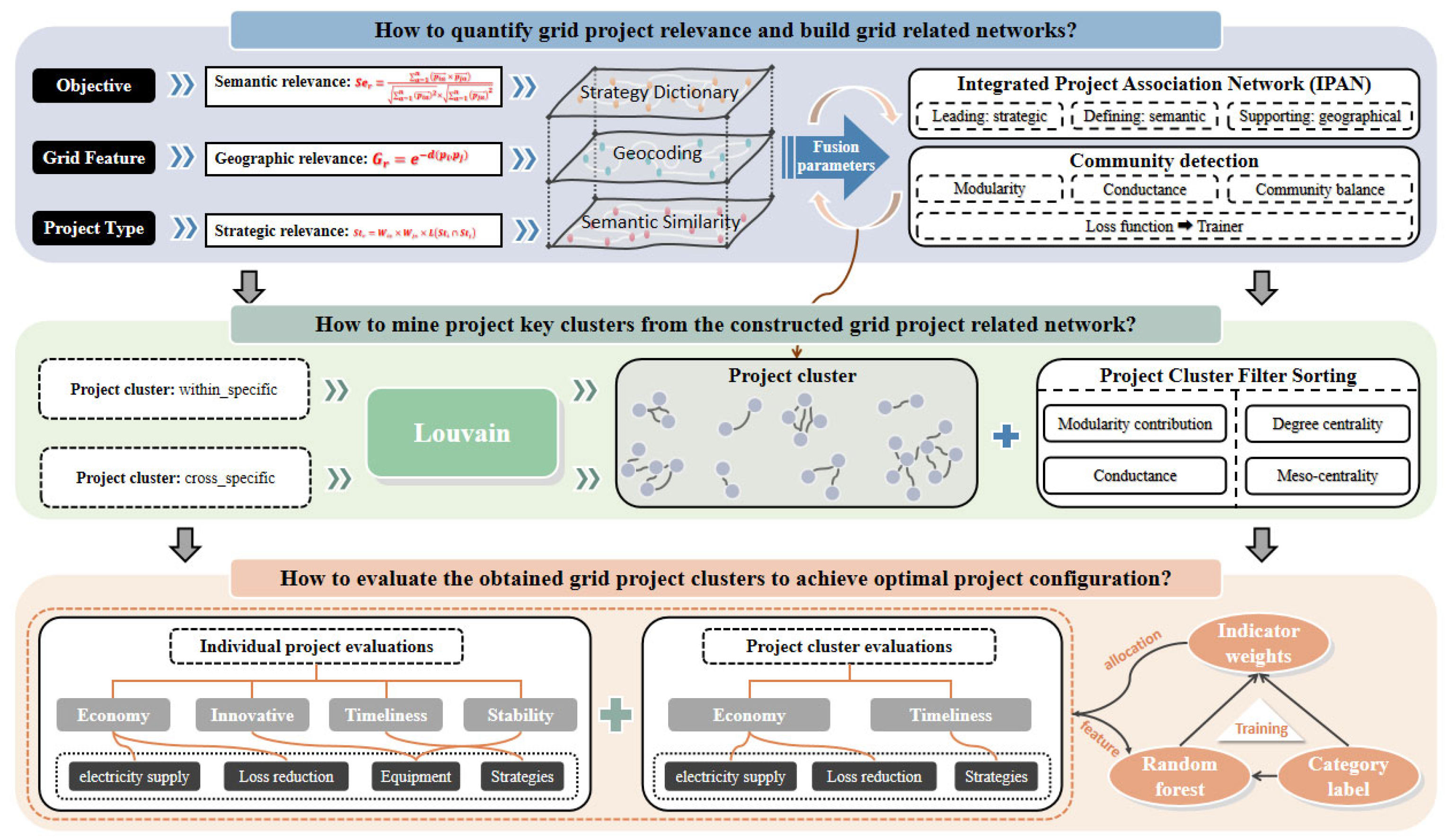
3.1. Question Definition
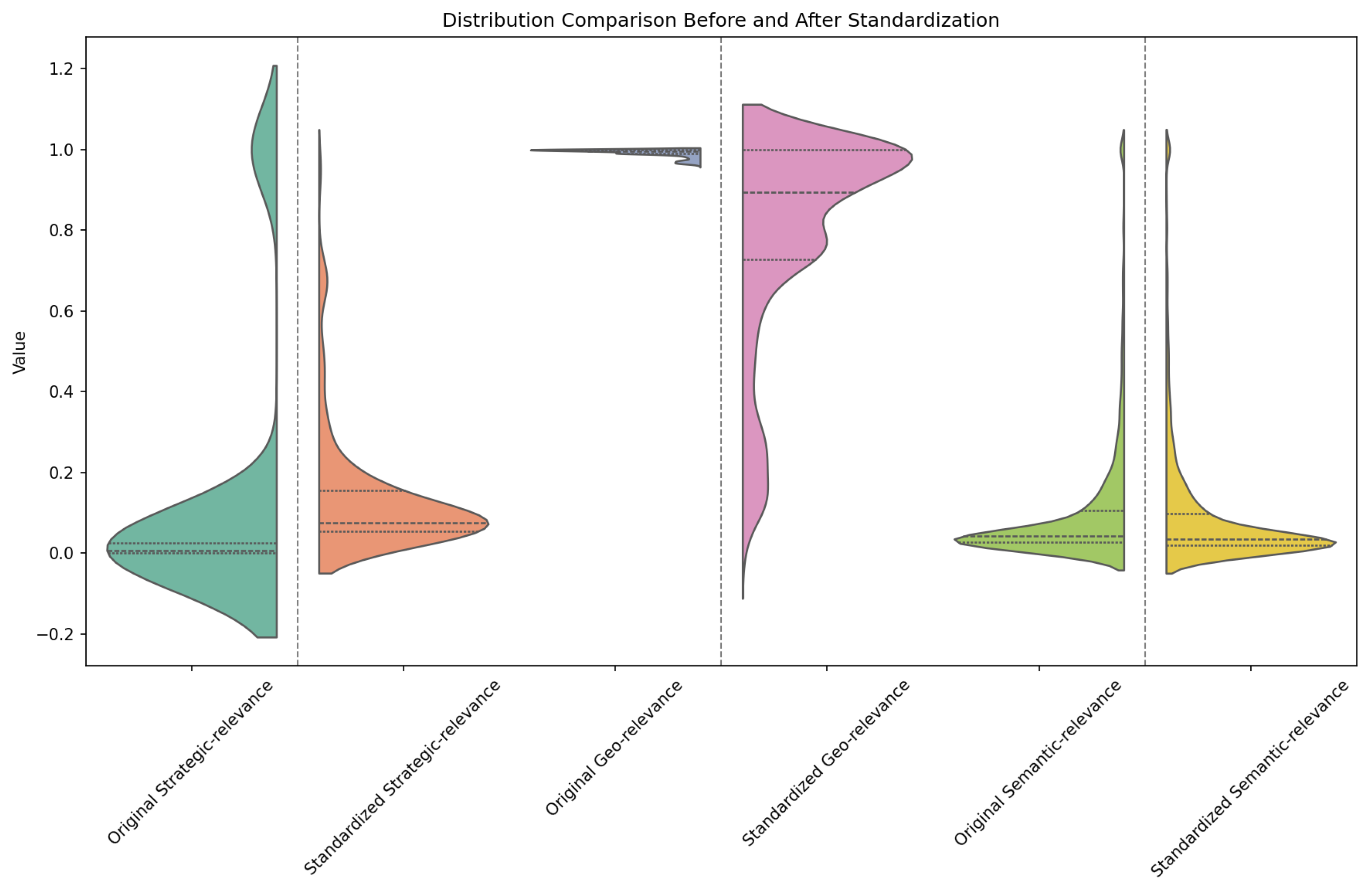
3.2. Complex Network Construction and Fusion
3.3. Project Cluster Mining
- (1)
- Local optimization phase: The algorithm starts from each node and attempts to move it to an adjacent community, calculating the ΔModularity (change in modularity). If the modularity increases after the move, the node is moved into the corresponding community, and this process is repeated until the modularity can no longer be improved.
- (2)
- Network reconstruction phase: Each community is treated as a node, and the weights of the edges connecting communities are the sum of the weights of the edges within the community, forming a new network. The local optimization phase is repeated on the new network until the modularity no longer changes, ultimately yielding the community partitioning results.
3.4. Project Cluster Evaluation
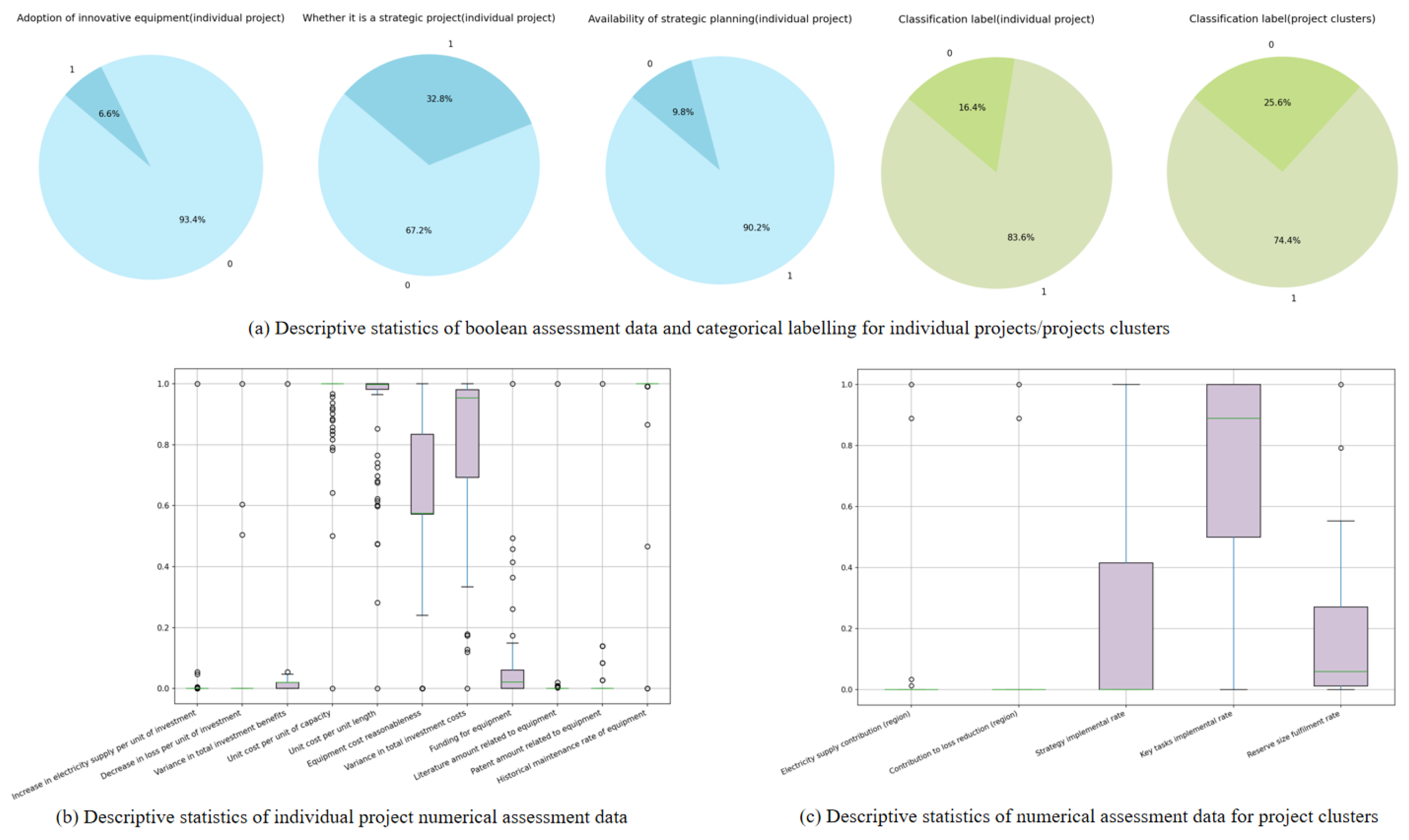
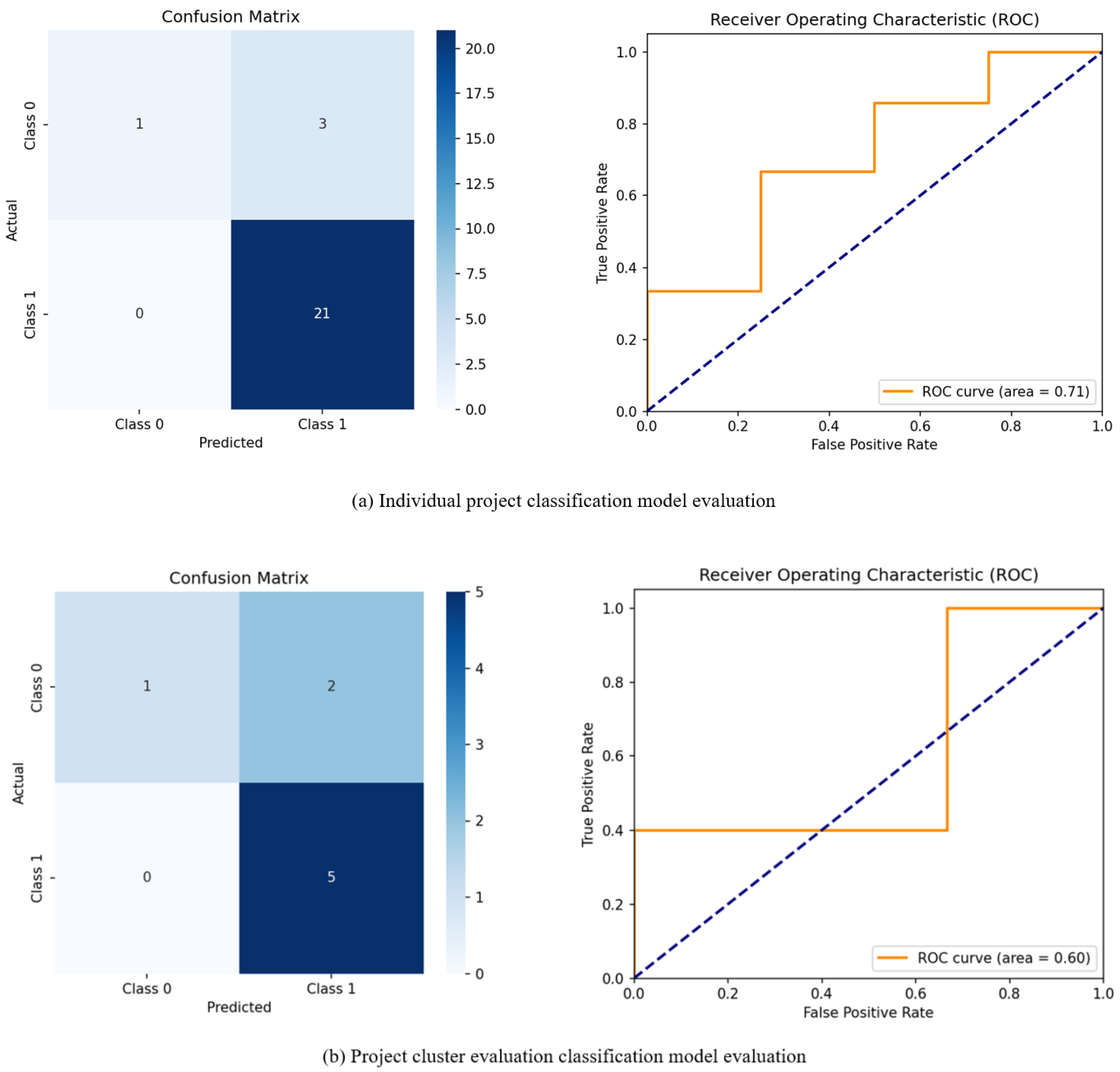
4. Data Validation
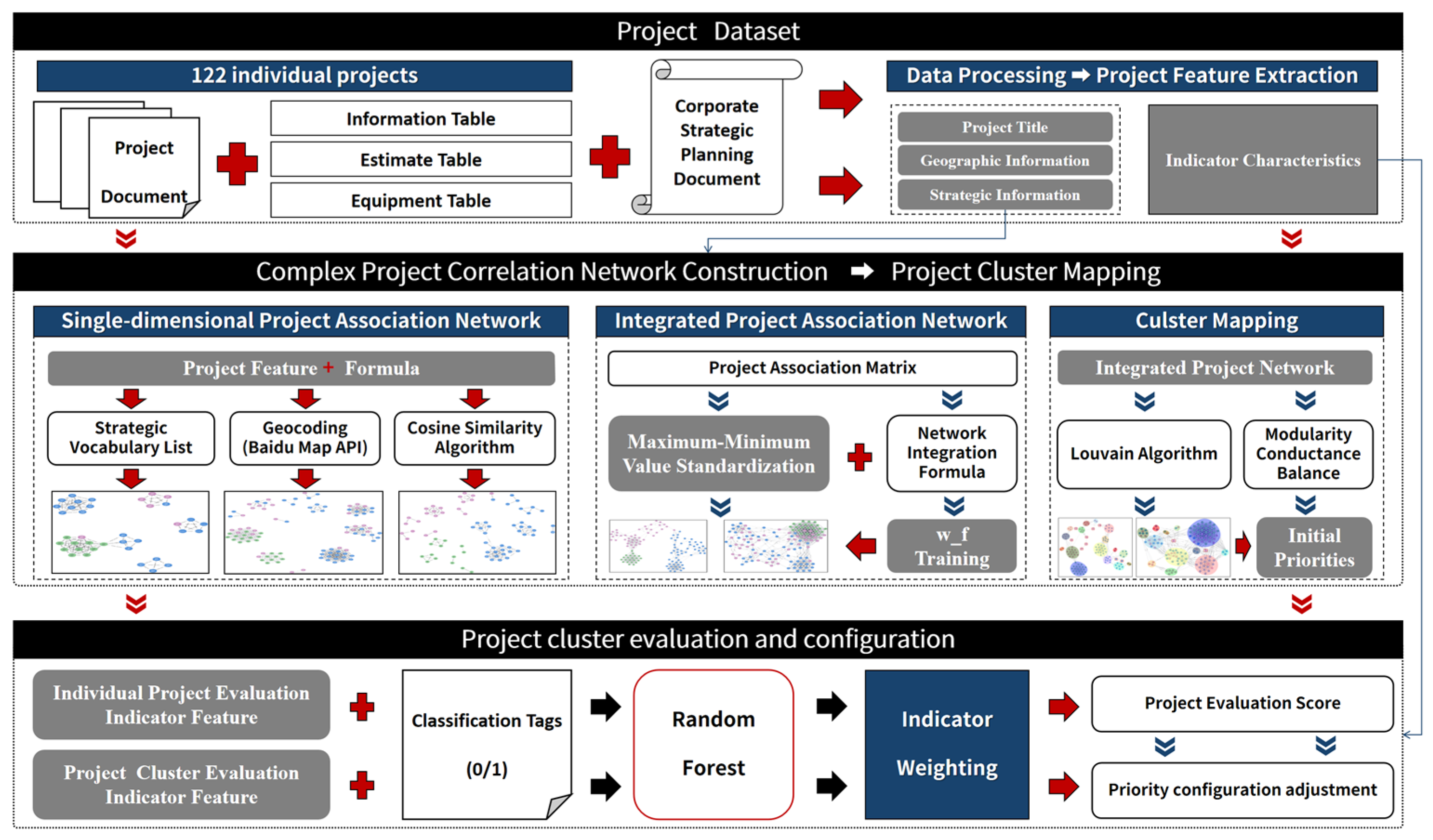
4.1. Dataset
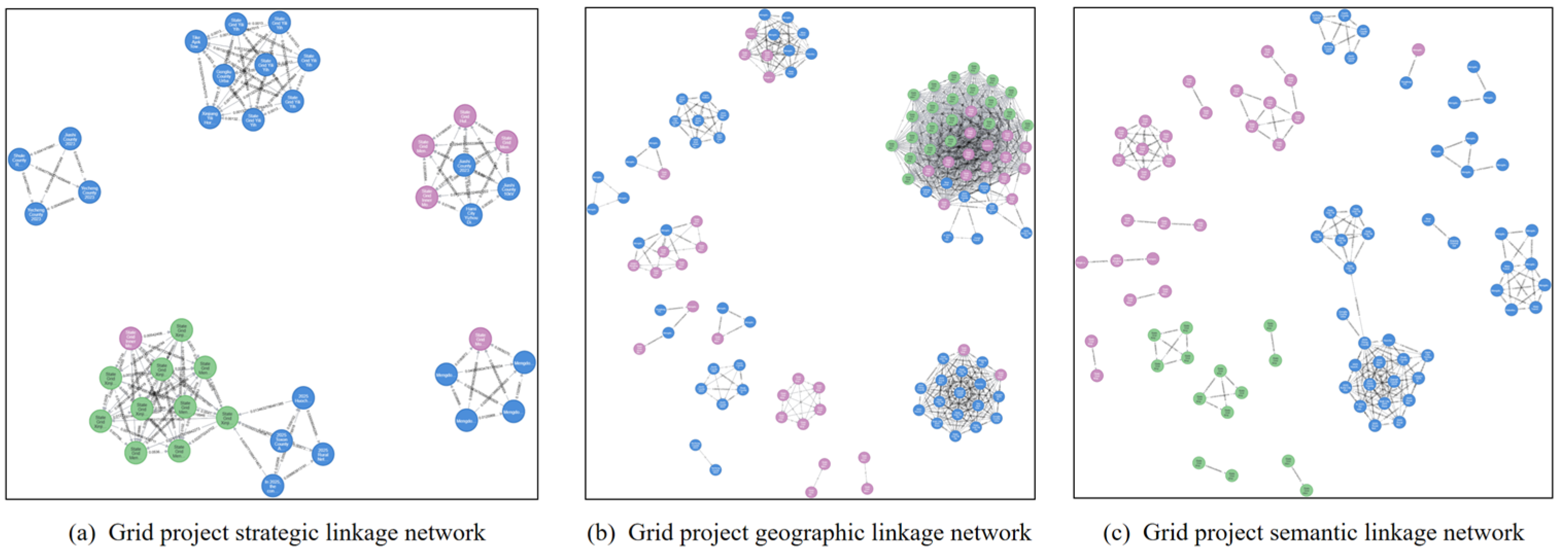
4.2. Complex Project Correlation Network Construction
4.3. Project Cluster Mapping
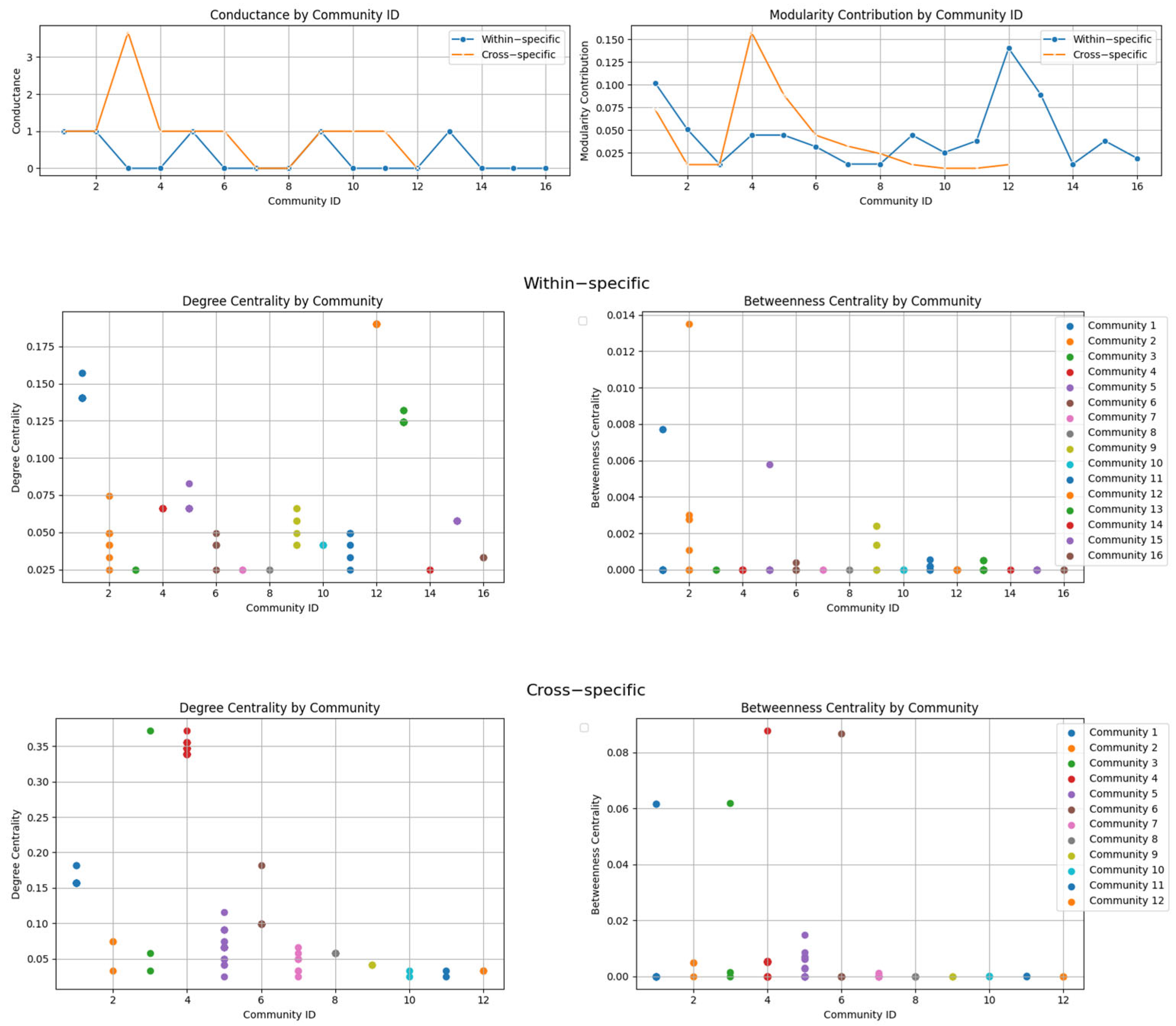
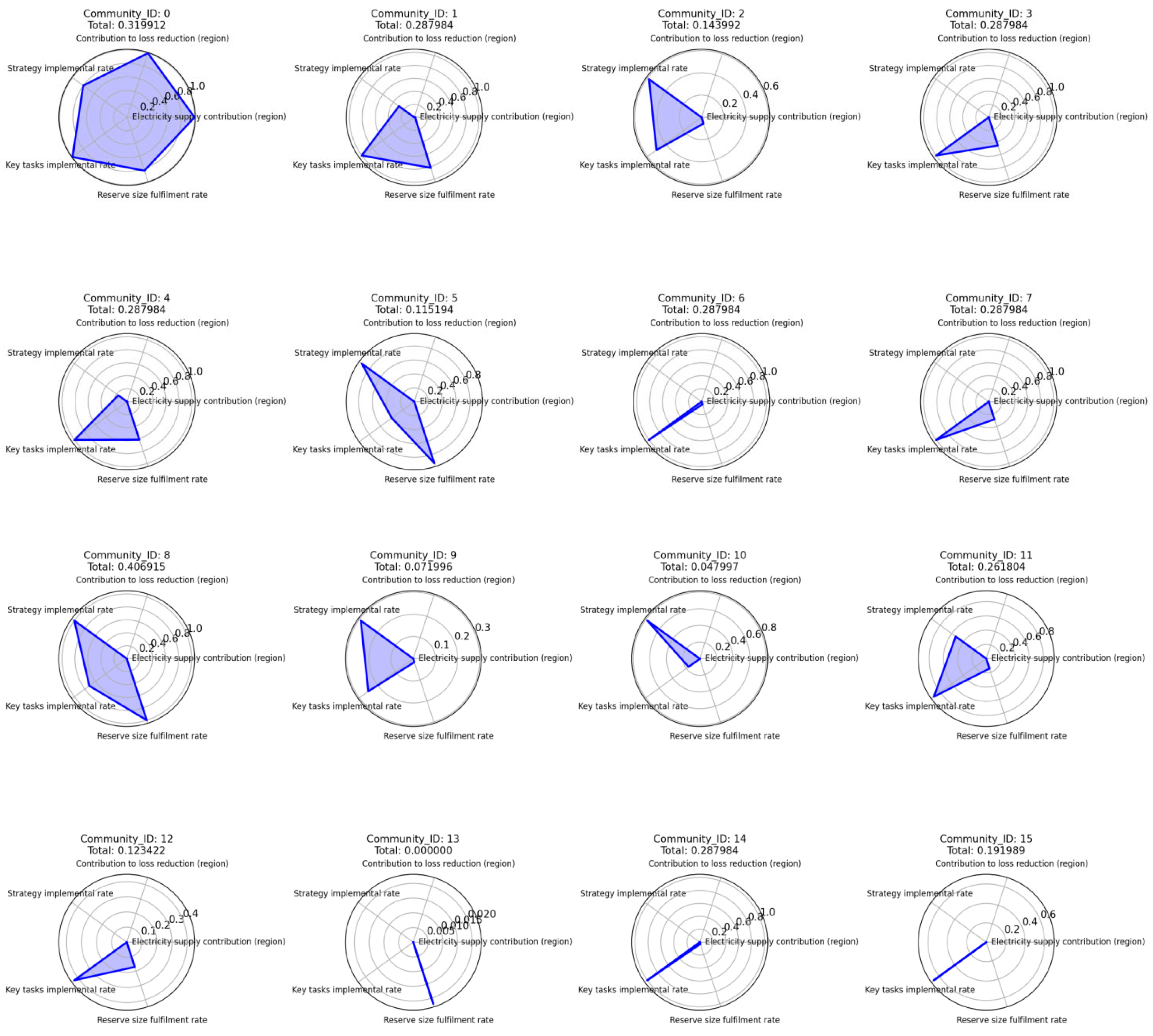
4.4. Project Cluster Evaluation and Configuration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix B.1
| Network Construction and Integration Pseudocode |
|---|
| // ====================== // SINGLE-DIMENSIONAL NETWORK CONSTRUCTION // ====================== // MODULE 1: SEMANTIC NETWORK CONSTRUCTION PROCEDURE build_semantic_network(csv_path, neo4j_config) // Input Processing df ← LOAD_CSV(csv_path) project_names ← EXTRACT_COLUMN(df, 'project_names') // Text Processing tokenized_texts ← APPLY(jieba.cut, project_names) tfidf_matrix ← TFIDF_VECTORIZER(tokenized_texts) // Similarity Calculation similarity_matrix ← COSINE_SIMILARITY(tfidf_matrix) EXPORT_TO_EXCEL(similarity_matrix, 'semantic_relevance.xlsx') // Graph Construction WITH neo4j_driver(neo4j_config) AS driver: driver.EXECUTE(create_nodes, df) driver.EXECUTE(create_relationships, similarity_matrix, threshold=0.4) END PROCEDURE // MODULE 2: GEOGRAPHIC NETWORK CONSTRUCTION PROCEDURE build_geographic_network(csv_path, neo4j_config) // Data Loading df ← LOAD_CSV(csv_path) projects ← EXTRACT_COLUMN(df, 'project_names') addresses ← EXTRACT_COLUMN(df, 'addresses') // Geocoding coordinates ← MAP(geocode, addresses) // Distance Calculation distance_matrix ← PAIRWISE(haversine_distance, coordinates) normalized_distances ← NORMALIZE(distance_matrix) relevance_matrix ← APPLY(exp(-x), normalized_distances) // Graph Construction WITH neo4j_driver(neo4j_config) AS driver: driver.EXECUTE(create_nodes, df) driver.EXECUTE(create_relationships, relevance_matrix, threshold=0.96) END PROCEDURE // MODULE 3: STRATEGIC NETWORK CONSTRUCTION PROCEDURE build_strategic_network(projects_csv, keywords_csv, neo4j_config) // Data Preparation projects_df ← LOAD_CSV(projects_csv) keywords ← LOAD_CSV(keywords_csv) // Feature Engineering tokenized_docs ← APPLY(jieba.cut, projects_df['construction_objectives']) tfidf_matrix, vectorizer ← TFIDF_VECTORIZER(tokenized_docs) // Strategic Relevance keyword_similarity ← COSINE_SIMILARITY(tfidf_matrix, vectorizer.transform(keywords)) strategic_similarity ← MATRIX_PRODUCT(keyword_similarity, keyword_similarity.T) // Graph Construction WITH neo4j_driver(neo4j_config) AS driver: driver.EXECUTE(create_nodes, projects_df) driver.EXECUTE(create_relationships, strategic_similarity) END PROCEDURE // MODULE 4: NETWORK FUSION & COMMUNITY DETECTION PROCEDURE fused_community_detection(semantic_matrix, geo_matrix, strategic_matrix, num_communities) // Tensor Initialization M_sem ← LOAD_MATRIX(semantic_matrix) M_geo ← LOAD_MATRIX(geo_matrix) M_str ← LOAD_MATRIX(strategic_matrix) // Fusion Model w_f ← LEARNABLE_PARAMETER(0.3, bounds=[0.2,0.4]) // Optimization Loop FOR epoch IN 1..100: // Network Fusion fused_adj ← FUSION_FORMULA(M_sem, M_geo, M_str, w_f) // Community Detection graph ← CREATE_GRAPH(fused_adj) communities ← DETECT_COMMUNITIES(graph, num_communities) // Quality Metrics modularity ← CALCULATE_MODULARITY(graph, communities) conductance ← CALCULATE_CONDUCTANCE(graph, communities) // Parameter Update LOSS ← -modularity + conductance UPDATE(w_f, LOSS) RETURN w_f, communities END PROCEDURE // ====================== // SUPPORTING FUNCTIONS // ====================== FUNCTION create_nodes(tx, df): FOR i, (name, category, label) IN ENUMERATE(df): translated ← TRANSLATE([name, category, label]) NODE_TYPE ← CASE category: 'grid_Infrastructure' → 'Grid_Infrastructure' 'production_technology_improvement' → 'Tech_Upgrade' 'grid_digitization' → 'Grid_Digitization' tx.RUN("CREATE (n:{NODE_TYPE} {id: $id, name: $name, ...})", translated) FUNCTION create_relationships(tx, matrix, threshold): FOR i,j IN MATRIX_INDICES(matrix): IF matrix[i,j] > threshold AND i < j: tx.RUN(""" MATCH (a), (b) WHERE a.id = $src AND b.id = $dst CREATE (a)-[:REL_TYPE {weight: $w}]->(b) """, params) FUNCTION fusion_formula(M1, M2, M3, alpha): // Implements the conditional fusion logic RETURN FUSED_MATRIX |
Appendix B.2
| Project Cluster Detection and Evaluation Pseudocode |
|---|
| // ============================================= // COMMUNITY ANALYSIS MODULE - PSEUDOCODE // ============================================= // DATA LOADING PROCEDURE PROCEDURE load_data(adjacency_csv, community_csv) TRY: // Load and validate adjacency matrix adj_df ← READ_CSV(adjacency_csv, index_col=0) IF HAS_MISSING_VALUES(adj_df.values): RAISE ERROR("Missing values detected") IF NOT IS_NUMERIC(adj_df.values): RAISE ERROR("Non-numeric data found") // Load community assignments comm_df ← READ_CSV(community_csv) communities ← GROUP_BY(comm_df, "Community")["NodeID"].AGGREGATE(list) RETURN adj_df.values, communities EXCEPT ERROR AS e: LOG_ERROR(e) TERMINATE END PROCEDURE // NETWORK METRICS CALCULATION FUNCTION calculate_modularity(graph G, community_list C) m ← NUMBER_OF_EDGES(G) Q ← 0 FOR EACH community IN C: subG ← INDUCED_SUBGRAPH(G, community) e ← NUMBER_OF_EDGES(subG) total_degree ← SUM(DEGREE(G, node) FOR node IN community) s ← total_degree / (2*m) Q ← Q + (e/m) - s^2 RETURN Q END FUNCTION FUNCTION calculate_conductance(graph G, community_list C) conductance_values ← [] FOR EACH community IN C: subG ← INDUCED_SUBGRAPH(G, community) internal_edges ← NUMBER_OF_EDGES(subG) boundary_edges ← SUM(DEGREE(G, node) FOR node IN community) - 2*internal_edges denominator ← MIN(2*internal_edges, boundary_edges) IF denominator == 0: conductance ← 0.0 ELSE: conductance ← boundary_edges / denominator APPEND(conductance_values, conductance) RETURN conductance_values END FUNCTION // COMMUNITY STRUCTURE ANALYSIS FUNCTION analyze_community_structure(community_list C) sizes ← [LENGTH(comm) FOR comm IN C] balance ← STANDARD_DEVIATION(sizes) / MEAN(sizes) RETURN sizes, balance END FUNCTION FUNCTION compute_centrality_metrics(graph G, community_list C) degree_cent ← DEGREE_CENTRALITY(G) betweenness_cent ← BETWEENNESS_CENTRALITY(G) centrality_results ← NEW_DICTIONARY() FOR i, comm IN ENUMERATE(C): centrality_results[i] ← NEW_DICTIONARY() FOR node IN comm: centrality_results[i][node] ← { "degree": degree_cent[node], "betweenness": betweenness_cent[node] } RETURN centrality_results END FUNCTION // MAIN ANALYSIS WORKFLOW PROCEDURE main(adjacency_file, community_file, output_file) // Data ingestion adj_matrix, communities ← load_data(adjacency_file, community_file) G ← CONVERT_TO_GRAPH(adj_matrix) // Metric computation modularity ← calculate_modularity(G, communities) conductance ← calculate_conductance(G, communities) sizes, balance ← analyze_community_structure(communities) centralities ← compute_centrality_metrics(G, communities) // Results compilation results ← [] FOR i, comm IN ENUMERATE(communities): results.APPEND({ "CommunityID": i+1, "Size": LENGTH(comm), "Conductance": conductance[i], "ModularityContribution": (LENGTH(comm)/NUMBER_OF_NODES(G)) * modularity, "Nodes": comm, "Centralities": centralities[i] }) // Output generation results_df ← CREATE_DATAFRAME(results) results_df["OverallModularity"] ← modularity results_df["CommunityBalance"] ← balance EXPORT_TO_CSV(results_df, output_file) END PROCEDURE // EXECUTION EXAMPLE IF RUN_AS_MAIN_PROGRAM: adj_path ← "path/to/adjacency_matrix.csv" comm_path ← "path/to/community_assignments.csv" out_path ← "path/to/output_analysis.csv" main(adj_path, comm_path, out_path) END IF |
References
- Seager, G.C. The planning of key fundamentals used in the development of a beneficial project plan. J. Contemp. Manag. 2005, 2, 114–127. [Google Scholar]
- Al-Sumaiti, A.S.; Salama, M.M.A.; Konda, S.R.; Kavousi-Fard, A. A Guided Procedure for Governance Institutions to Regulate Funding Requirements of Solar PV Projects. IEEE Access 2019, 7, 54203–54217. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, M.; Zhang, D.; Goh, H.H.; Ahmad, T.; Liu, H.; Liu, T.; Wang, S.; Wu, T. IntelliSense technology in the new power systems. Renew. Sustain. Energy Rev. 2023, 177, 113229. [Google Scholar] [CrossRef]
- Heymann, F.; Milojevic, T.; Covatariu, A.; Verma, P. Digitalization in decarbonizing electricity systems-Phenomena, regional aspects, stakeholders, use cases, challenges and policy options. Energy 2023, 262, 125521. [Google Scholar] [CrossRef]
- Haque, K.; Mishra, S.; Golias, M.M. Multi-period transportation network investment decision making and policy implications using econometric framework. Res. Transp. Econ. 2021, 89, 101109. [Google Scholar] [CrossRef]
- Zwikael, O.; Meredith, J. Evaluating the Success of a Project and the Performance of Its Leaders. IEEE Trans. Eng. Manag. 2021, 68, 1745–1757. [Google Scholar] [CrossRef]
- Shen, Z.; Li, X. An extended model of dynamic project portfolio selection problem considering synergies between projects. Comput. Ind. Eng. 2023, 179, 109175. [Google Scholar] [CrossRef]
- Bob-Milliar, G.K.; Alagidede, I.P. Fragmentation of Projects and the Symbolism of Development Aid in Northern Ghana. Voluntas 2024, 35, 1143–1153. [Google Scholar] [CrossRef]
- Carminati, L.; Pirola, F.; Lagorio, A.; Cimini, C.; Jurczuk, A.; Boucher, X. Skills, Technical and Organizational Support Needed for Collaborative Networks 5.0. In Navigating Unpredictability: Collaborative Networks in Non-Linear Worlds; Springer International Publishing Ag: Cham, Switzerland, 2024; Volume 726, pp. 380–396. [Google Scholar]
- Killen, C.P.; Kjaer, C. Understanding project interdependencies: The role of visual representation, culture and process. Int. J. Proj. Manag. 2012, 30, 554–566. [Google Scholar] [CrossRef]
- Benissa, T.; Patil, A. Drivers for Clustering and Inter-Project Collaboration—A Case of Horizon Europe Projects. Adm. Sci. 2024, 14, 104. [Google Scholar] [CrossRef]
- Martinsuo, M. Project portfolio management in practice and in context. Int. J. Proj. Manag. 2013, 31, 794–803. [Google Scholar] [CrossRef]
- Davis, K. Different stakeholder groups and their perceptions of project success. Int. J. Proj. Manag. 2014, 32, 189–201. [Google Scholar] [CrossRef]
- Kudratova, S.; Huang, X.; Kudratov, K.; Qudratov, S. Corporate sustainability and stakeholder value trade-offs in project selection through optimization modeling: Application of investment banking. Corp. Soc. Responsib. Environ. Manag. 2020, 27, 815–824. [Google Scholar] [CrossRef]
- Harrison, K.R.; Elsayed, S.M.; Weir, T.; Garanovich, I.L.; Boswell, S.G.; Sarker, R.A. A Novel Multi-Objective Project Portfolio Selection and Scheduling Problem. In Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence 2022, Singapore, 4–7 December 2022; pp. 480–487. [Google Scholar]
- Zhai, S.-L.; Wu, X.-L.; Wang, S.-Y.; Zhao, T. Application of Interaction Effect Multichoice Goal Programming in Project Portfolio Analysis. Math. Probl. Eng. 2021, 2021, 1863632. [Google Scholar] [CrossRef]
- Bai, L.; Bai, J.; An, M. A methodology for strategy-oriented project portfolio selection taking dynamic synergy into considerations. Alex. Eng. J. 2022, 61, 6357–6369. [Google Scholar] [CrossRef]
- Loperfido, N.; Shushi, T. Optimal Portfolio Projections for Skew-Elliptically Distributed Portfolio Returns. J. Optim. Theory Appl. 2023, 199, 143–166. [Google Scholar] [CrossRef]
- Lukas, C.; Neubert, M.-F.; Schöndube, J.R. Exploring decision-making: Experimental observations on project selection and the impact of justification pressure. J. Manag. Gov. 2024, 29, 735–775. [Google Scholar] [CrossRef]
- Olgun, N.; Ozkaynak, E. A novel approach to detecting epileptic patients: Complex network-based EEG classification. J. Complex Netw. 2024, 12, cnae044. [Google Scholar] [CrossRef]
- Wang, X. What can we learn from multimorbidity? A deep dive from its risk patterns to the corresponding patient profiles. Decis. Support Syst. 2024, 186, 114313. [Google Scholar] [CrossRef]
- Moussa, A.; El-Dakhakhni, W. Managing Interdependence-Induced Systemic Risks in Infrastructure Projects. J. Manag. Eng. 2022, 38, 04022048. [Google Scholar] [CrossRef]
- Feng, J.R.; Zhao, M.; Yu, G.; Zhang, J.; Lu, S. Dynamic risk analysis of accidents chain and system protection strategy based on complex network and node structure importance. Reliab. Eng. Syst. Saf. 2023, 238, 109413. [Google Scholar] [CrossRef]
- Li, X.; Ning, X.; Ma, J.; Han, Z. Investigating the Evolution Path of Urban Natural Gas Pipeline Accidents Using a Complex Network Approach. Asce-Asme J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2024, 10, 06024005. [Google Scholar] [CrossRef]
- Lan, Z.; Chen, X.; Liu, Y.; Chen, D.; Li, W. Complex Network Construction and Pattern Recognition of China’s Provincial Low-Carbon Economic Development with Long Time Series: Based on the Detailed Spatial Relationship. Pol. J. Environ. Stud. 2022, 31, 2131–2148. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X. The time-frequency evolution of multidimensional relations between global oil prices and China’s general price level. Energy 2022, 244, 122579. [Google Scholar] [CrossRef]
- Jiang, X.; Xie, Y. Investigation of Urban–Canal–Rural Integration Characteristics Based on Multidimensional Connectivity Network Analysis: A Case Study of the Canal in Jiangsu Province, China. J. Urban Plan. Dev. 2024, 150, 04024049. [Google Scholar] [CrossRef]
- Ding, J.; Zheng, Y.; Wang, H.; Cannistraci, C.V.; Gao, J.; Li, Y.; Shi, C. Artificial Intelligence for Complex Network: Potential, Methodology and Application. In Companion Proceedings of the ACM on Web Conference 2025; Association for Computing Machinery: New York, NY, USA, 2024; pp. 5–8. [Google Scholar]
- Peng, N.; Zhu, X.; Liu, Y.; Nie, B.; Cui, Y.; Geng, Q.; Yu, C. Complex network dynamics of the topological structure in a geochemical field from the Nanling area in South China. Sci. Rep. 2020, 10, 19826. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.-J.; Xu, C.; Li, J.; Sun, J.; Xie, J.; Feng, L.; Zhou, T.; Hu, Y. Reconstructing the evolution history of networked complex systems. Nat. Commun. 2024, 15, 2849. [Google Scholar] [CrossRef]
- Li, J.; Lai, S.; Shuai, Z.; Tan, Y.; Jia, Y.; Yu, M.; Song, Z.; Peng, X.; Xu, Z.; Ni, Y.; et al. A comprehensive review of community detection in graphs. Neurocomputing 2024, 600, 128169. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Zarezade, M.; Nourani, E.; Bouyer, A. Community Detection using a New Node Scoring and Synchronous Label Updating of Boundary Nodes in Social Networks. J. Ai Data Min. 2020, 8, 201–212. [Google Scholar]
- Zhang, W.; Shang, R.; Jiao, L. Large-scale community detection based on core node and layer-by-layer label propagation. Inf. Sci. 2023, 632, 1–18. [Google Scholar] [CrossRef]
- Yao, J.; Liu, B. Community-Detection Method of Complex Network Based on Node Influence Analysis. Symmetry 2024, 16, 754. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, N.; Xie, J.; Hu, A.; Liu, X.; Yan, R.; Wan, L.; Sun, Y. Detecting network communities based on central node selection and expansion. Chaos Solitons Fractals 2024, 188, 115482. [Google Scholar] [CrossRef]
- Sheykhzadeh, J.; Zarei, B.; Soleimanian Gharehchopogh, F. Community Detection in Social Networks Using a Local Approach Based on Node Ranking. IEEE Access 2024, 12, 92892–92905. [Google Scholar] [CrossRef]
- Zhang, B.; Mi, Y.; Zhang, L.; Zhang, Y.; Li, M.; Zhai, Q.; Li, M. Dynamic Community Detection Method of a Social Network Based on Node Embedding Representation. Mathematics 2022, 10, 4738. [Google Scholar] [CrossRef]
- Jeon, H.; Ko, H.-K.; Jo, J.; Kim, Y.; Seo, J. Measuring and Explaining the Inter-Cluster Reliability of Multidimensional Projections. IEEE Trans. Vis. Comput. Graph. 2022, 28, 551–561. [Google Scholar] [CrossRef]
- Ni, L.; Xu, H.; Zhang, Y.; Luo, W. Spatial-Aware Local Community Detection Guided by Dominance Relation. IEEE Trans. Comput. Soc. Syst. 2023, 10, 686–699. [Google Scholar] [CrossRef]
- Ni, L.; Li, Q.; Zhang, Y.; Luo, W.; Sheng, V.S. LSADEN: Local Spatial-Aware Community Detection in Evolving Geo-Social Networks. IEEE Trans. Knowl. Data Eng. 2024, 36, 3265–3280. [Google Scholar] [CrossRef]
- Akachar, E.; Bougteb, Y.; Ouhbi, B.; Frikh, B. LeaDCD: Leadership concept-based method for community detection in social networks. Inf. Sci. 2025, 686, 121341. [Google Scholar] [CrossRef]
- Wu, X.; Teng, D.; Zhang, H.; Hu, J.; Quan, Y.; Miao, Q.; Sun, P.G. Graph reconstruction and attraction method for community detection. Appl. Intell. 2025, 55, 357. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M. A new multi-period optimization model for resilient-sustainable project portfolio evaluation under interval-valued Pythagorean fuzzy sets with a case study. Int. J. Mach. Learn. Cybern. 2021, 12, 3541–3560. [Google Scholar] [CrossRef]
- Zarjou, M.; Khalilzadeh, M. Optimal project portfolio selection with reinvestment strategy considering sustainability in an uncertain environment: A multi-objective optimization approach. Kybernetes 2022, 51, 2437–2460. [Google Scholar] [CrossRef]
- Alexandrova, M. Evaluation of Project Portfolio Management Performance: Long and Short-Term Perspective. Hradec Econ. Days 2021, 11, 11–21. [Google Scholar]
- Bai, L.; Qu, X.; Liu, J.; Han, X. Analysis of factors influencing project portfolio benefits with synergy considerations. Eng. Constr. Archit. Manag. 2023, 30, 2691–2715. [Google Scholar] [CrossRef]
- Zaidouni, A.; Idrissi, M.A.J.; Bellabdaoui, A. Towards a Methodological Approach for Intelligent IS/IT Project Portfolio Dashboard. In International Conference on Digital Technologies and Applications; Springer Nature: Cham, Switzerland, 2024; Volume 1099, pp. 326–335. [Google Scholar]
- Qian, L.; Dou, Y.; Gong, C.; Xu, X.; Tan, Y. Project Group Program Generation and Decision Making Method Integrating Coupling Network and Hesitant Fuzzy. Mathematics 2023, 11, 4010. [Google Scholar] [CrossRef]
- ForouzeshNejad, A. A hybrid data-driven model for project portfolio selection problem based on sustainability and strategic dimensions: A case study of the telecommunication industry. Soft Comput. 2023, 28, 2409–2429. [Google Scholar] [CrossRef]
- Han, R.; Li, X.; Shen, Z.; Jia, D. A framework of robust project portfolio selection problem under strategic objectives considering the risk propagation. Eng. Constr. Archit. Manag. 2023, 31, 4872–4896. [Google Scholar] [CrossRef]
- Pinones, P.; Derpich, I.; Venegas, R. Circular Economy 4.0 Evaluation Model for Urban Road Infrastructure Projects, Ciroad. Sustainability 2023, 15, 3205. [Google Scholar] [CrossRef]
- Pilat, D.; Jecmen, K.; Teichmann, D.; Mertlova, O. Transport Infrastructure Investment Project Portfolio Optimization Using a Cascade Approach to Solving the Min-Max Problem. In Proceedings of the 40th International Conference Mathematical Methods in Economics 2022, Jihlava, Czech Republic, 7–9 September 2022; pp. 280–285. [Google Scholar]
- Ramedani, A.M.; Mehrabian, A.; Didehkhani, H. A two-stage sustainable uncertain multi-objective portfolio selection and scheduling considering conflicting criteria. Eng. Appl. Artif. Intell. 2024, 132, 107942. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech.-Theory Exp. 2008, 10, P10008. [Google Scholar] [CrossRef]
- Leskovec, J.; Lang, K.J.; Mahoney, M.W. Empirical comparison of algorithms for network community detection. arXiv 2010, arXiv:1004.3539. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]


| Object | Dimension | Level-1 Metrics | Level 2-Metrics | Type |
|---|---|---|---|---|
| Single project | Economics | Benefit | Increase in the electricity supply per unit of investment | numeric |
| Decrease in the loss per unit of investment | numeric | |||
| Variance in the total investment benefits | numeric | |||
| Cost | Unit cost per unit of capacity | numeric | ||
| Unit cost per unit length | numeric | |||
| Equipment cost reasonableness | numeric | |||
| Variance in the total investment cost | numeric | |||
| Innovation | Equipment innovation | Adoption of innovative equipment | Boolean | |
| Weight of innovative equipment | numeric | |||
| Funding for equipment | numeric | |||
| Amount of literature related to equipment | numeric | |||
| Number of patents related to equipment | numeric | |||
| Timeliness | Strategic timeliness | Whether it is a strategic project | Boolean | |
| Availability of strategic planning | Boolean | |||
| Stability | Equipment stability | Historical maintenance rate of equipment | numeric | |
| Project cluster | Economics | Benefit | Electricity supply contribution (region) | numeric |
| Contribution to loss reduction (region) | numeric | |||
| Timeliness | Strategic timeliness | Strategy implementation rate | numeric | |
| Timeliness of reserve planning | Key task implementation rate | numeric | ||
| Reserve size fulfillment rate | numeric |
| Strategic Vocabulary |
|---|
| Project Attack |
| Qinghai Huatugou Tong Construction |
| Qinghai Huatugou |
| Reducing Power Losses |
| Aral, Bachu, and other 750 kV projects |
| Finance |
| Hami North-Chongqing UHV Tributary Supporting Power Delivery |
| Major scientific research project research and development |
| Major science and technology public relations |
| Community ID (Postsorting) | Subproject ID (Postsorting) |
|---|---|
| 11 | (101~121) |
| 0 | 4, (0, 6, 7, 35, 36, 38~46) |
| 12 | (62, 94, 96), (59, 61, 62, 66, 67, 92, 93, 95, 97~99) |
| 3 | (8, 20, 23~27) |
| 14 | (68, 70~74) |
| 1 | 2, (13, 14), 3, 12, 32, 7, 1 |
| 8 | (49, 52), (51, 53), 50, (54, 55) |
| 12 | 88, (78, 79), 58, 80, 87 |
| 4 | 34, (9~11, 33, 47, 48) |
| 5 | 15, (16~18), 19 |
| 9 | 57, (81~83) |
| 15 | (74~76) |
| 2 | (84, 85) |
| 6 | (21, 22) |
| 7 | (30, 31) |
| 13 | (64, 65) |
| Object | Dimension | Weights (Dimensions) | Level 1 Metrics | Weights (Level 1) | Level 2 Metrics | Weights (Level 2) |
|---|---|---|---|---|---|---|
| Single project | Economics | 0.73 | Benefit | 0.05 | Increase in the electricity supply per unit of investment | 0.02 |
| Decrease in the loss per unit of investment | 0.00 | |||||
| Variance in the total investment benefits | 0.04 | |||||
| Cost | 0.68 | Unit cost per unit of capacity | 0.04 | |||
| Unit cost per unit length | 0.18 | |||||
| Equipment cost reasonableness | 0.16 | |||||
| Variance in the total investment cost | 0.30 | |||||
| Innovation | 0.14 | Equipment innovation | 0.14 | Adoption of innovative equipment | 0.00 | |
| Weight of innovative equipment | 0.00 | |||||
| Funding for equipment | 0.14 | |||||
| Amount of literature related to equipment | 0.00 | |||||
| Number of patents related to equipment | 0.00 | |||||
| Timeliness | 0.06 | Strategic timeliness | 0.06 | Whether it is a strategic project | 0.05 | |
| Availability of strategic planning | 0.01 | |||||
| Stability | 0.07 | Equipment stability | 0.07 | Historical maintenance rate of equipment | 0.07 | |
| Project cluster | Economics | 0.03 | Benefit | 0.03 | Electricity supply contribution (region) | 0.02 |
| Contribution to loss reduction (region) | 0.01 | |||||
| Timeliness | 0.97 | Strategic timeliness | 0.20 | Strategy implementation rate | 0.20 | |
| Timeliness of reserve planning | 0.77 | Key task implementation rate | 0.29 | |||
| Reserve size fulfillment rate | 0.48 |
| Community ID (Postsorting) | Subproject ID (Postsorting) |
|---|---|
| 11 | (101~121) |
| 0 | 4, (0, 6, 7, 35, 36, 38~46) |
| 12 | (62, 94, 96), (59, 61, 62, 66, 67, 92, 93, 95, 97~99) |
| 3 | (8, 20, 23~27) |
| 14 | (68, 70~74) |
| 1 | 2, (13, 14), 3, 12, 32, 7, 1 |
| 8 | (49, 52), (51, 53), 50, (54, 55) |
| 12 | 88, (78, 79), 58, 80, 87 |
| 4 | 34, (9~11, 33, 47, 48) |
| 5 | 15, (16~18), 19 |
| 9 | 57, (81~83) |
| 15 | (74~76) |
| 2 | (84, 85) |
| 6 | (21, 22) |
| 7 | (30, 31) |
| 13 | (64, 65) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Chen, S.; Jin, X.; Mu, W.; Zhang, H. Critical Cluster Mining and Optimal Allocation for Power Grid Projects Based on Complex Networks and Multidimensional Metrics. Appl. Sci. 2025, 15, 9166. https://doi.org/10.3390/app15169166
Liu M, Chen S, Jin X, Mu W, Zhang H. Critical Cluster Mining and Optimal Allocation for Power Grid Projects Based on Complex Networks and Multidimensional Metrics. Applied Sciences. 2025; 15(16):9166. https://doi.org/10.3390/app15169166
Chicago/Turabian StyleLiu, Minghong, Shuxu Chen, Xianing Jin, Wenxin Mu, and Huan Zhang. 2025. "Critical Cluster Mining and Optimal Allocation for Power Grid Projects Based on Complex Networks and Multidimensional Metrics" Applied Sciences 15, no. 16: 9166. https://doi.org/10.3390/app15169166
APA StyleLiu, M., Chen, S., Jin, X., Mu, W., & Zhang, H. (2025). Critical Cluster Mining and Optimal Allocation for Power Grid Projects Based on Complex Networks and Multidimensional Metrics. Applied Sciences, 15(16), 9166. https://doi.org/10.3390/app15169166






