Spectroscopy of ITO Films in Optical and Terahertz Spectral Ranges
Abstract
1. Introduction
2. Samples and Experimental Technique
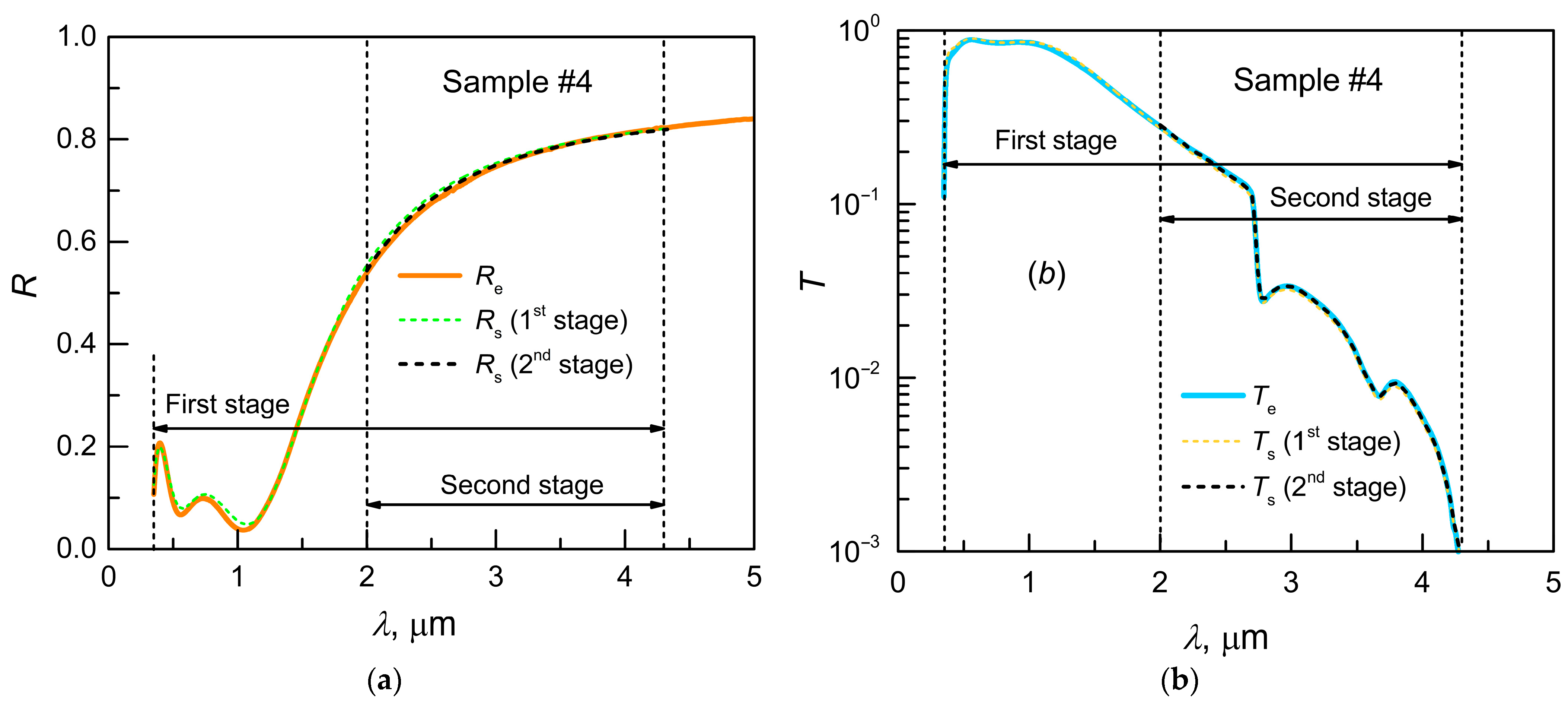
3. Transmittance and Reflectivity Spectra: Experimental Results
4. Theoretical Modeling of the Transmittance and Reflectivity Spectra
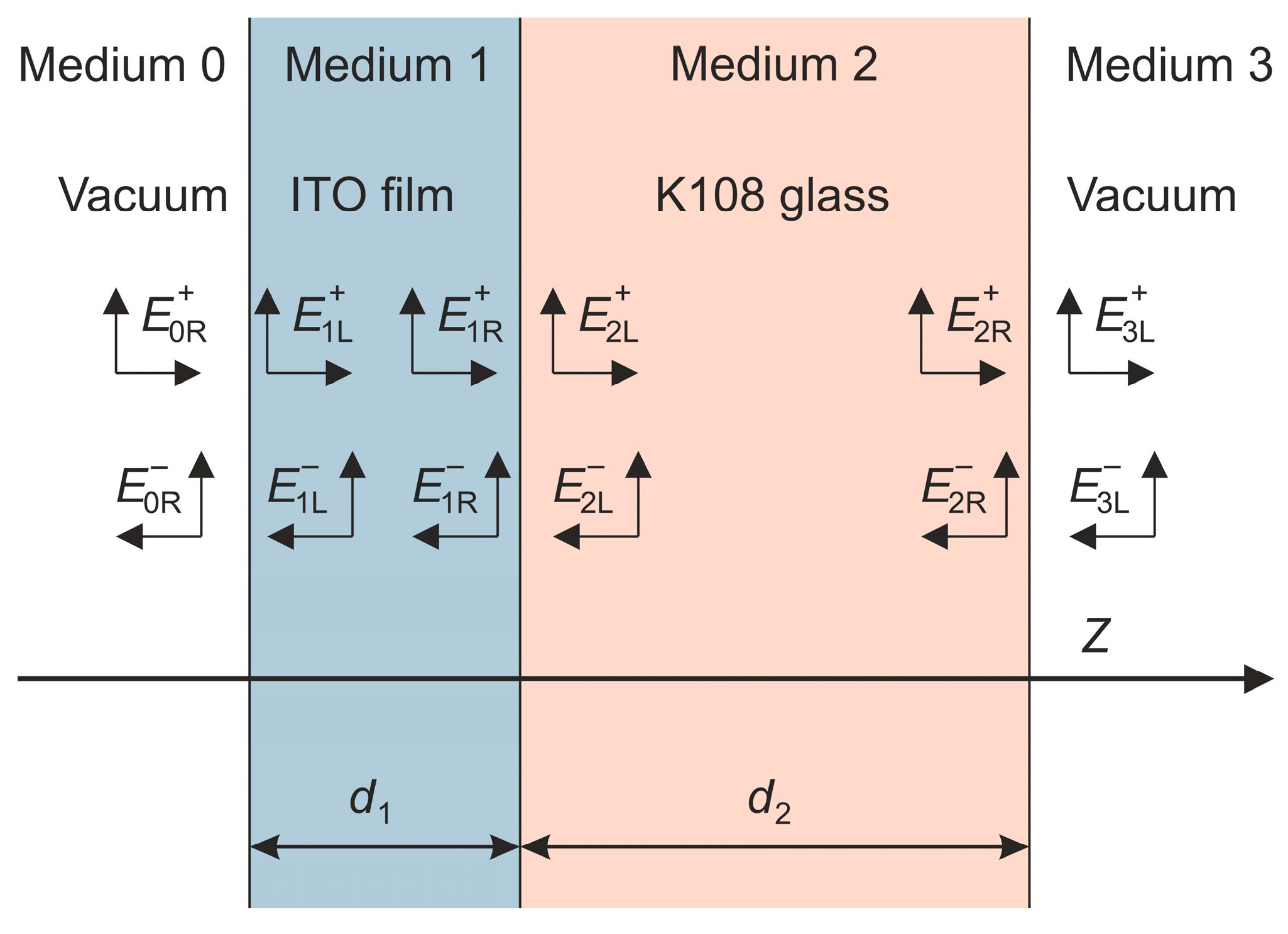
4.1. Free-Standing ITO Film
4.2. The ITO Film on a Glass Substrate
5. Determination of ITO Film Parameters
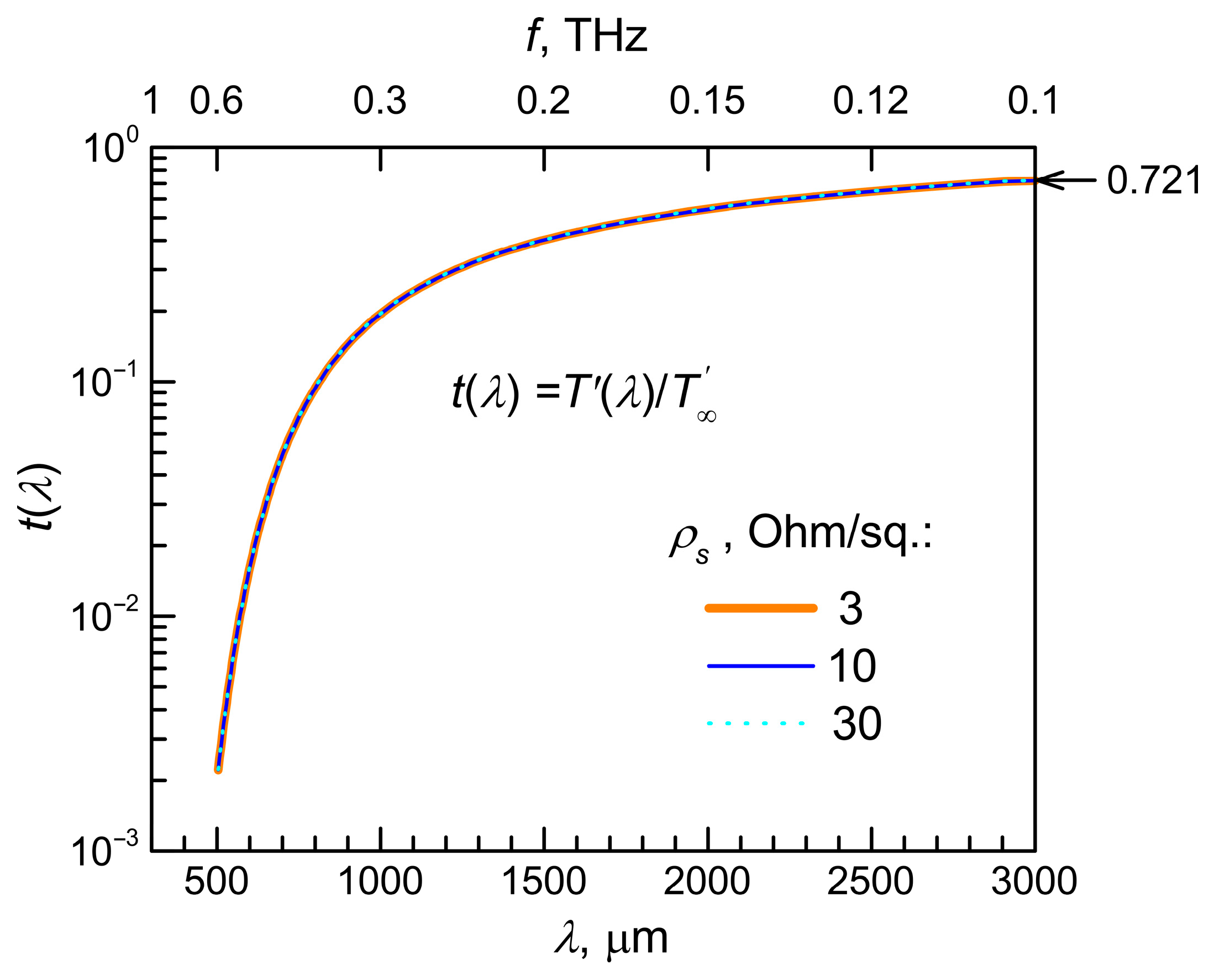
5.1. Determination of DC Sheet Resistivity

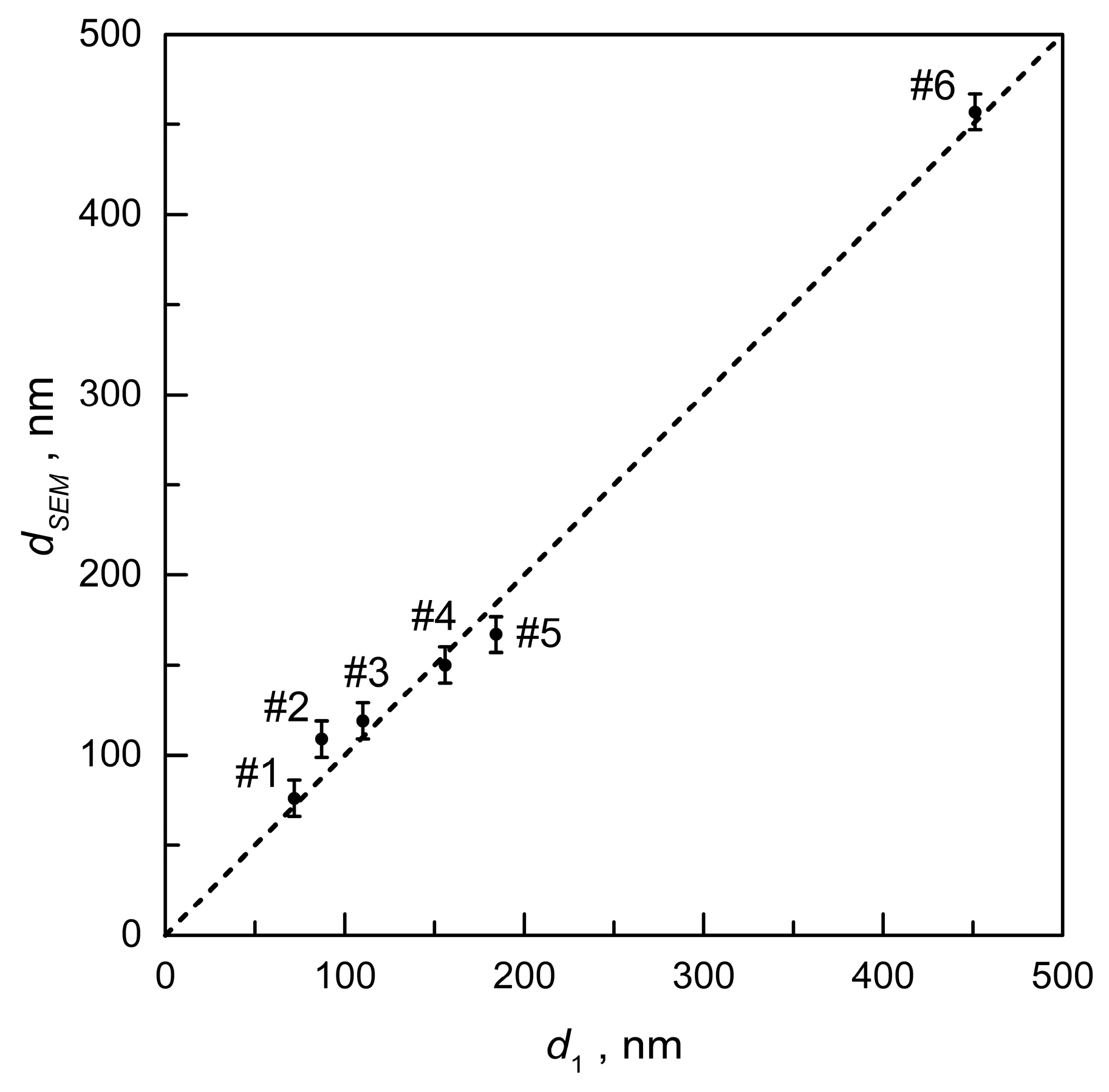
5.2. Determination of ITO Film Thickness, Free Electron Concentration and Mobility
6. Discussion of the Results
7. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DC | Direct Current |
| FIR | Far Infra-Red |
| ITO | Indium Tin Oxide |
| MIR | Mid Infra-Red |
| NIR | Near Infra-Red |
| SEM | Scanning Electron Microscope |
| TDS | Time Domain Spectroscopy |
References
- Khodzitsky, M.K.; Bassarab, V.V.; Shakhmin, A.A.; Sokolov, V.S.; Kropotov, G.I. The Electromagnetic Shielding of Optoelectronic Devices by Mesh Structures. Appl. Sci. 2021, 11, 9841. [Google Scholar] [CrossRef]
- Batrakov, K.; Kuzhir, P.; Maksimenko, S.; Paddubskaya, A.; Voronovich, S.; Kaplas, T.; Svirko, Y. Enhanced microwave shielding effectiveness of ultrathin pyrolytic carbon films. Appl. Phys. Lett. 2013, 103, 073117. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Zhang, C.; Zhang, Y.; Zhang, Z.; Lu, Z.; Tan, J.; Guo, L.J. Transparent ultrathin doped silver film for broadband electromagnetic interference shielding. In Proceedings of the IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Ann Arbor, MI, USA, 16–18 July 2018; pp. 1–3. [Google Scholar]
- Klein, C.A. Microwave shielding effectiveness of EC-coated dielectric slabs. IEEE Trans. Microw. Theory Tech. 1990, 38, 321–324. [Google Scholar] [CrossRef]
- Erdogan, N.; Erden, F.; Astarlioglu, A.T.; Ozdemir, M.; Ozbay, S.; Aygun, G.; Ozyuzer, L. ITO/Au/ITO multilayer thin films on transparent polycarbonate with enhanced EMI shielding properties. Curr. Appl Phys. 2020, 20, 489–497. [Google Scholar] [CrossRef]
- González, M.; Pozuelo, J.; Baselga, J. Electromagnetic shielding materials in GHz range. Chem. Rec. 2018, 18, 1000–1009. [Google Scholar] [CrossRef]
- Huang, J.-C. EMI shielding plastics: A review. Adv. Polym. Technol. 1995, 14, 137–150. [Google Scholar] [CrossRef]
- Stadler, A. Transparent Conducting Oxides—An Up-To-Date Overview. Materials 2012, 5, 661–683. [Google Scholar] [CrossRef] [PubMed]
- Granqvist, C.G.; Hultåker, A. Transparent and conducting ITO films: New developments and applications. Thin Solid Films 2002, 411, 1–5. [Google Scholar] [CrossRef]
- Kwak, D.-J.; Moon, B.H.; Lee, D.K.; Park, C.S.; Sung, Y.M. Comparison of transparent conductive indium tin oxide, titanium-doped indium oxide, and fluorine-doped tin oxide films for dye-sensitized solar cell application. J. Electr. Eng. Technol. 2011, 6, 684–687. [Google Scholar] [CrossRef]
- Yan, X.; Mont, F.W.; Poxson, D.J.; Schubert, M.F.; Kim, J.K.; Cho, J.; Schubert, E.F. Refractive-Index-Matched Indium–Tin-Oxide Electrodes for Liquid Crystal Displays. Jpn. J. Appl. Phys. 2009, 48, 120203. [Google Scholar] [CrossRef]
- Li, S.; Tian, M.; Gao, Q.; Wang, M.; Li, T.; Hu, Q.; Li, X.; Wu, Y. Nanometer-thin indium tin oxide for advanced high-performance electronics. Nat. Mater. 2019, 18, 1091–1097. [Google Scholar] [CrossRef]
- Pasquarelli, R.M.; Ginley, D.S.; O’Hayre, R. Solution processing of transparent conductors: From flask to film. Chem. Soc. Rev. 2011, 40, 5406. [Google Scholar] [CrossRef] [PubMed]
- Si, M.; Andler, J.; Lyu, X.; Niu, C.; Datta, S.; Agrawal, R.; Ye, P.D. Indium–tin-oxide transistors with one nanometer thick channel and ferroelectric gating. ACS Nano 2020, 14, 11542–11547. [Google Scholar] [CrossRef] [PubMed]
- Yi, F.; Shim, E.; Zhu, A.Y.; Zhu, H.; Reed, J.C.; Cubukcu, E. Voltage tuning of plasmonic absorbers by indium tin oxide. Appl. Phys. Lett. 2013, 102, 221102. [Google Scholar] [CrossRef]
- Zhu, M.; Xiong, C.; Lee, Q. Research on ITO transparent electromagnetic shielding coatings for E-O system. In Proceedings of the 3rd International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Chengdu, China, 14 November 2007; Volume 6722, pp. 875–881. [Google Scholar]
- Huang, J.L.; Yau, B.S.; Chen, C.Y.; Lo, W.T.; Lii, D.F. The electromagnetic shielding effectiveness of indium tin oxide films. Ceram. Int. 2001, 27, 363–365. [Google Scholar] [CrossRef]
- Osipkov, A.; Makeev, M.; Garsiya, E.; Filyaev, A.; Sinyagaeva, K.; Kirillov, D.; Ryzhenko, D.; Yurkov, G. Radio-Shielding metamaterials transparent in the visible spectrum: Approaches to creation. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Wrexham, UK, 22–26 June 2020; p. 012007. [Google Scholar]
- Kropotov, G.I.; Bassarab, V.V.; Shakhmin, A.A.; Sokolov, V.S.; Shalygin, V.A. Spectroscopy of ITO coatings in optical and microwave ranges. In Proceedings of the 49th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Perth, Australia, 1–6 September 2024; pp. 1–3. [Google Scholar]
- Zhao, H.; Ma, X.; Song, X.; Zheng, H.; Yan, H. Study on the optimization of wave absorption of glass substrate indium tin oxide film composite building materials. J. Mater. Sci. Mater. Electron. 2024, 35, 335. [Google Scholar] [CrossRef]
- Choi, Y.J.; Gong, S.C.; Johnson, D.C.; Golledge, S.; Yeom, G.Y.; Park, H.H. Characteristics of the electromagnetic interference shielding effectiveness of Al-doped ZnO thin films deposited by atomic layer deposition. Appl. Surf. Sci. 2013, 269, 92–97. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kang, K.M.; Lee, H.S.; Park, H.H. Electromagnetic interference shielding behaviors of Zn-based conducting oxide films prepared by atomic layer deposition. Thin Solid Films 2015, 583, 226–232. [Google Scholar] [CrossRef]
- Kim, W.M.; Ku, D.Y.; Lee, I.K.; Seo, Y.W.; Cheong, B.K.; Lee, T.S.; Kim, I.; Lee, K.S. The electromagnetic interference shielding effect of indium–zinc oxide/silver alloy multilayered thin films. Thin Solid Films 2005, 473, 315–320. [Google Scholar] [CrossRef]
- Chen, Z.; Zhuo, Y.; Tu, W.; Li, Z.; Ma, X.; Pei, Y.; Wang, G. High mobility indium tin oxide thin film and its application at infrared wavelengths: Model and experiment. Opt. Express 2018, 26, 22123. [Google Scholar] [CrossRef]
- Maniyara, R.A.; Graham, C.; Paulillo, B.; Bi, Y.; Chen, Y.; Herranz, G.; Baker, D.E.; Mazumder, P.; Konstantatos, G.; Pruneri, V. Highly transparent and conductive ITO substrates for near infrared applications. APL Mater. 2021, 9, 021121. [Google Scholar] [CrossRef]
- Thirumoorthi, M.; Prakash, J.T.J. Structure, optical and electrical properties of indium tin oxide ultra thin films prepared by jet nebulizer spray pyrolysis technique. J. Asian Ceram. Soc. 2016, 4, 124–132. [Google Scholar] [CrossRef]
- Askari, H.; Fallah, H.; Askari, M.; Mohmmadieyh, M.C. Electrical and optical properties of ITO thin films prepared by DC magnetron sputtering for low-emitting coatings. Mater. Sci. 2014. [Google Scholar] [CrossRef]
- Ananthanarayanan, D.; Leon, J.J.D.; Wong, J.; Nicolay, S.; Aberle, A.G.; Ho, J.W. Mid-infrared characterization and modelling of transparent conductive oxides. Sol. Energy 2020, 209, 424–430. [Google Scholar] [CrossRef]
- Kim, J.; Shrestha, S.; Souri, M.; Connell, J.G.; Park, S.; Seo, A. High-temperature optical properties of indium tin oxide thin-films. Sci. Rep. 2020, 10, 12486. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N.M.; Sabah, F.A.; Abdulgafour, H.I.; Alsadig, A.; Sulieman, A.; Alkhoaryef, M. The effect of post annealing temperature on grain size of indium-tin-oxide for optical and electrical properties improvement. Results Phys. 2019, 13, 102159. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Au, W.-C.; Pan, C.-L. Characterization of Indium Tin Oxide (ITO) Thin Films towards Terahertz (THz) Functional Device Applications. Coatings 2024, 14, 895. [Google Scholar] [CrossRef]
- Bassarab, V.V.; Shalygin, V.A.; Shakhmin, A.A.; Sokolov, V.S.; Kropotov, G.I. Spectroscopy of a borosilicate crown glass in the wavelength range of 0.2 µm–15 cm. J. Opt. 2023, 25, 065401. [Google Scholar] [CrossRef]
- Kropotov, G.I.; Shakhmin, A.A.; Kaplunov, I.A.; Rogalin, V.E. Application of Spectral Devices in the Optical Engineering and Scientific Research. Photonics Russ. 2023, 5, 378–392. [Google Scholar] [CrossRef]
- Seeger, K. Semiconductor Physics: An Introduction, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 35–46. ISBN 978-3-642-06023-6. [Google Scholar]
- Qiao, Z.; Latz, R.; Mergel, D. Thickness dependence of In2O3:Sn film growth. Thin Solid Films 2004, 466, 250–258. [Google Scholar] [CrossRef]
- Ukhanov, Y.I. Optical Properties of Semiconductors; Nauka: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Hamberg, I.; Granqvist, C.; Berggren, K.; Sernelius, B.; Engström, L. Bandgap Widening in Heavily Sn-Doped In2O3. Phys. Rev. B. 1984, 30, 3240–3249. [Google Scholar] [CrossRef]
- Hillier, J.A.; Camelio, S.; Cranton, W.; Nabok, A.V.; Mellor, C.J.; Koutsogeorgis, D.C.; Kalfagiannis, N. When ellipsometry works best: A case study with transparent conductive oxides. ACS Photonics 2020, 7, 2692–2702. [Google Scholar] [CrossRef]
- Cleary, J.W.; Smith, E.M.; Leedy, K.D.; Grzybowski, G.; Guo, J. Optical and electrical properties of ultra-thin indium tin oxide nanofilms on silicon for infrared photonics. Opt. Mater. Express 2018, 8, 1231–1245. [Google Scholar] [CrossRef]
- Shalygin, V.A.; Moldavskaya, M.D.; Panevin, V.Y.; Galimov, A.I.; Melentev, G.A.; Artemyev, A.A.; Firsov, D.A.; Vorobjev, L.E.; Klimko, G.V.; Usikova, A.A.; et al. Interaction of surface plasmon-phonon polaritons with terahertz radiation in heavily doped GaAs epilayers. J. Phys. Condens. Matter 2019, 31, 105002. [Google Scholar] [CrossRef] [PubMed]
- Uprety, P.; Junda, M.M.; Salmon, H.; Podraza, N.J. Understanding near Infrared Absorption in Tin Doped Indium Oxide Thin Films. J. Phys. D Appl. Phys. 2018, 51, 295302. [Google Scholar] [CrossRef]
- Katsidis, C.C.; Siapkas, D.I. General transfer-matrix method for optical multilayer systems with coherent, partially coherent, and incoherent interference. Appl. Opt. 2002, 41, 3978. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Jung, S.; Jeong, I. Optical modeling for polarization-dependent optical power dissipation of thin-film organic solar cells at oblique incidence. J. Opt. Soc. Korea 2012, 16, 6–12. [Google Scholar] [CrossRef]
- Adamov, R.B.; Pashnev, D.; Shalygin, V.A.; Moldavskaya, M.D.; Vinnichenko, M.Y.; Janonis, V.; Jorudas, J.; Tumėnas, S.; Prystawko, P.; Krysko, M.; et al. Optical performance of two dimensional electron gas and GaN:C buffer layers in AlGaN/AlN/GaN heterostructures on SiC substrate. Appl. Sci. 2021, 11, 6053. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259. [Google Scholar] [CrossRef]
- Liu, X.; Kang, J.H.; Yuan, H.; Park, J.; Cui, Y.; Hwang, H.Y.; Brongersma, M.L. Tuning of plasmons in transparent conductive oxides by carrier accumulation. ACS Photonics 2018, 5, 1493–1498. [Google Scholar] [CrossRef]
- Gui, Y.; Miscuglio, M.; Ma, Z.; Tahersima, M.H.; Sun, S.; Amin, R.; Dalir, H.; Sorger, V.J. Towards integrated metatronics: A holistic approach on precise optical and electrical properties of Indium Tin Oxide. Sci. Rep. 2019, 9, 11279. [Google Scholar] [CrossRef]
- Inritsapong, Y.; Chindaudom, P.; Nuntawong, N.; Patthanasetthakul, V.; Horphathum, M.; Eiamchai, P.; Pokaipisit, A.; Limsuwan, P. Post-annealing effects on the structural, optical and electrical properties of ito films studied by spectroscopic ellipsometry. Mod. Phys. Lett. B 2010, 24, 595–605. [Google Scholar] [CrossRef]
- Hinrichs, K.; Furchner, A.; Rappich, J.; Oates, T.W. Polarization-dependent and ellipsometric infrared microscopy for analysis of anisotropic thin films. J. Phys. Chem. C 2013, 117, 13557–13563. [Google Scholar] [CrossRef]
- Rasheed, M.; Barillé, R. Optical constants of DC sputtering derived ITO, TiO2 and TiO2: Nb thin films characterized by spectrophotometry and spectroscopic ellipsometry for optoelectronic devices. J. Non Cryst. Solids 2017, 476, 1–14. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kondo, M. Effects of carrier concentration on the dielectric function of ZnO: Ga and In2O3:Sn studied by spectroscopic ellipsometry: Analysis of free-carrier and band-edge absorption. Phys. Rev. B Condens. Matter 2005, 71, 075109. [Google Scholar] [CrossRef]
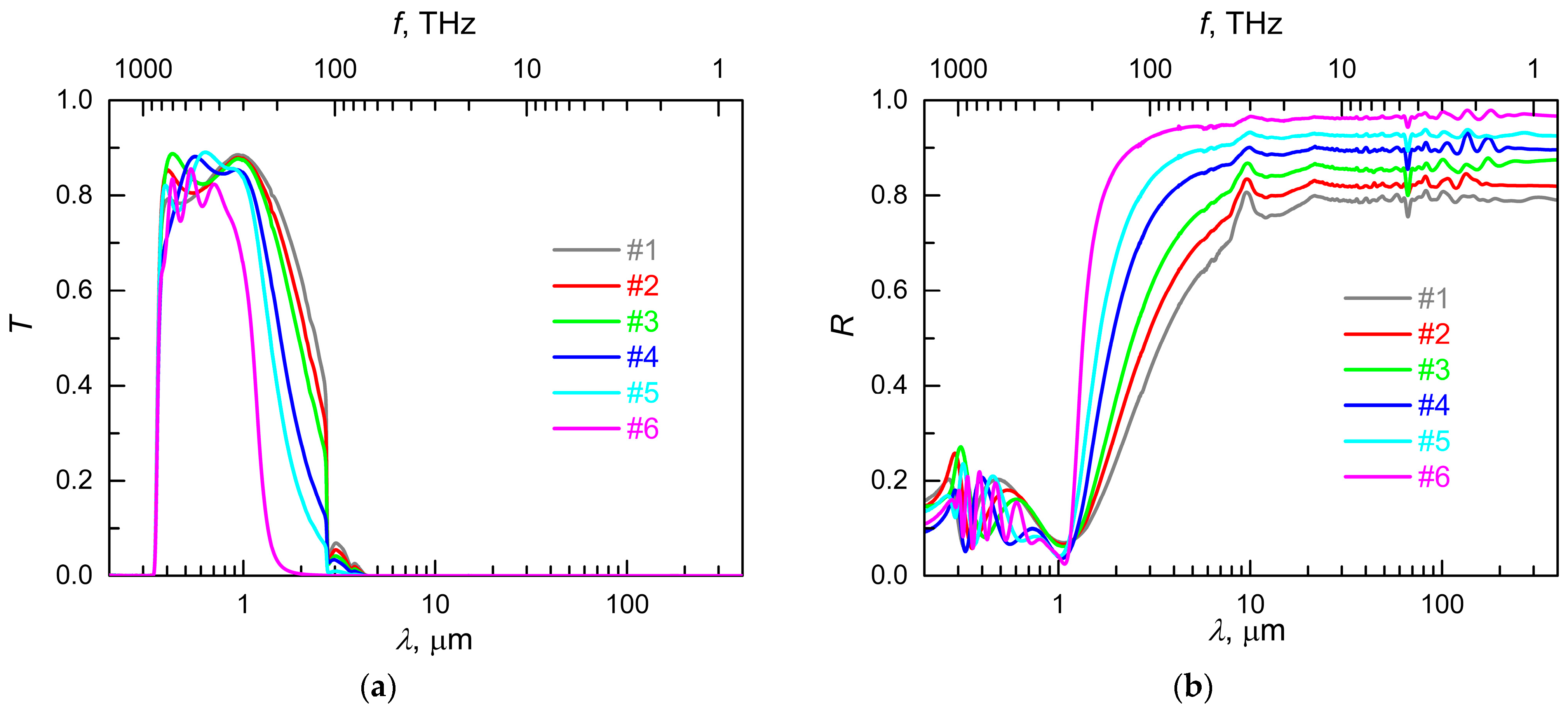
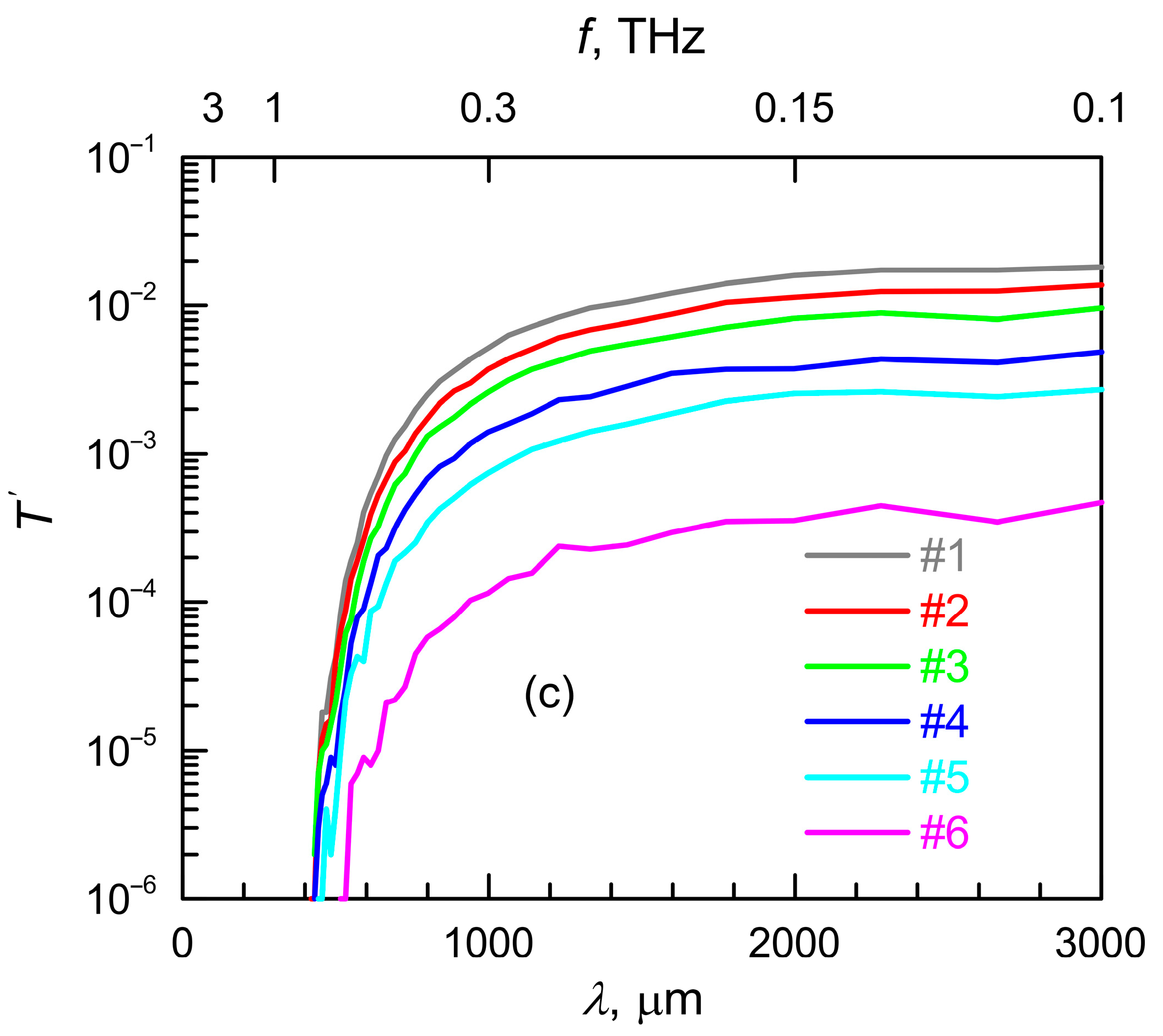
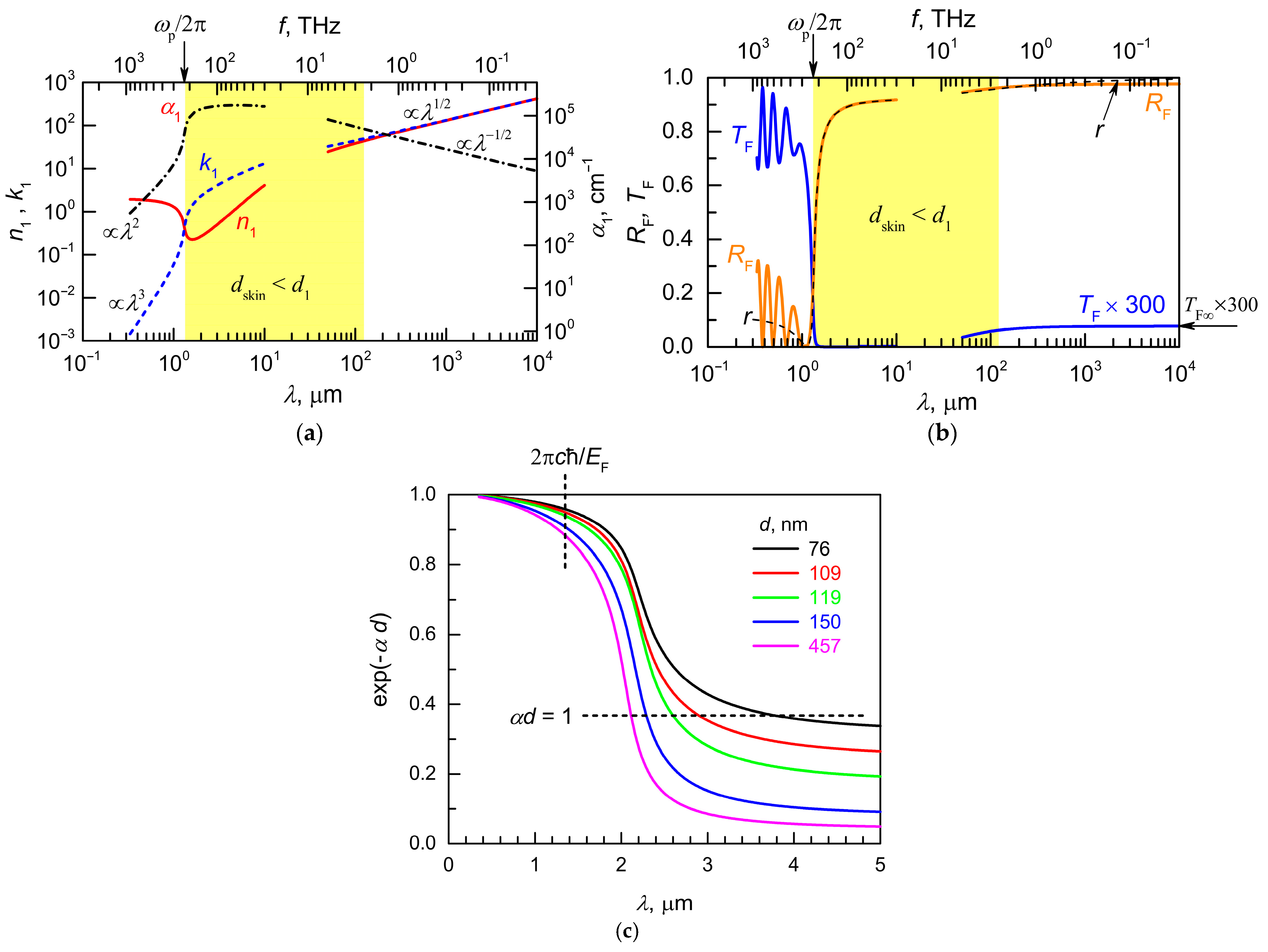
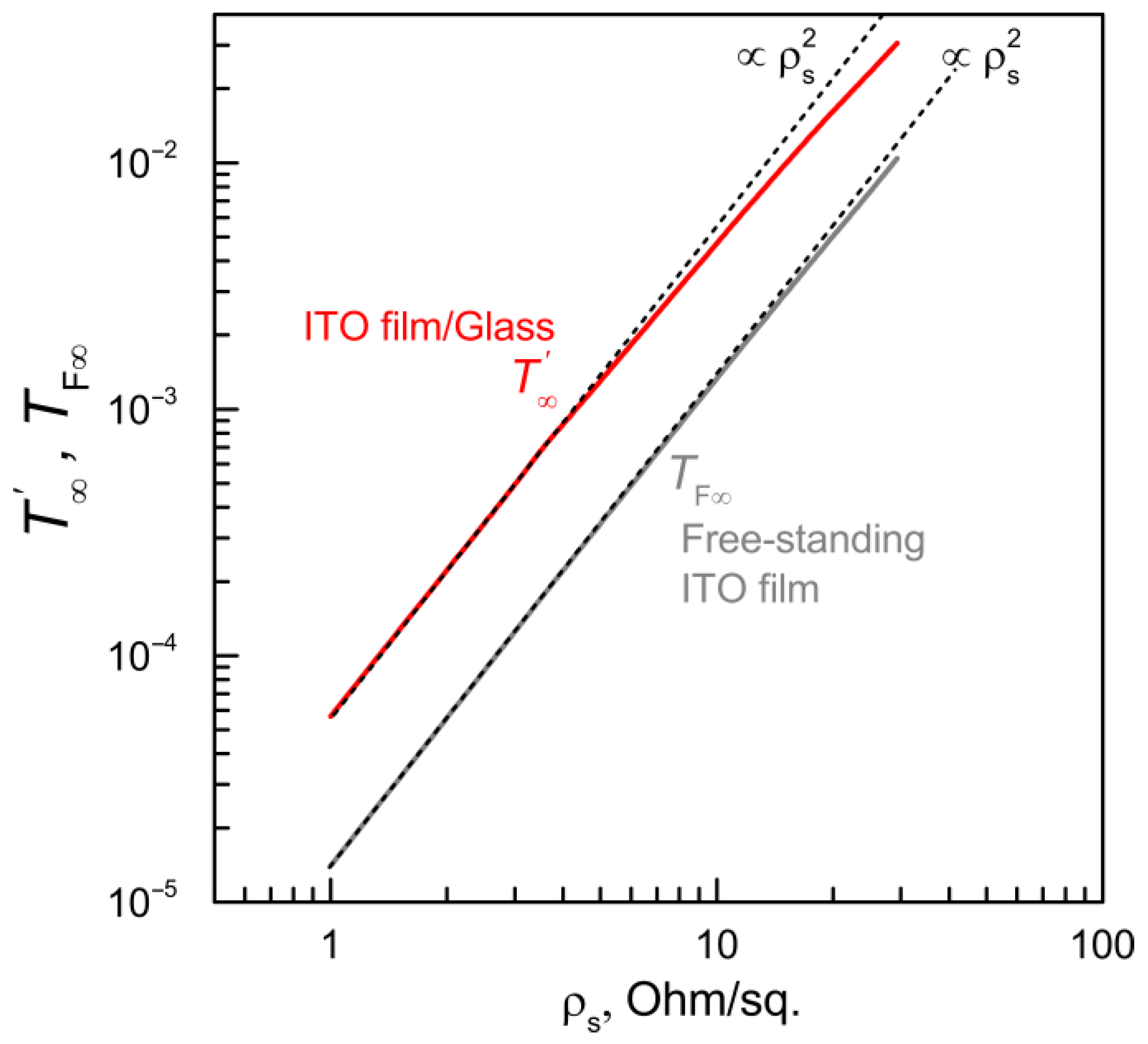
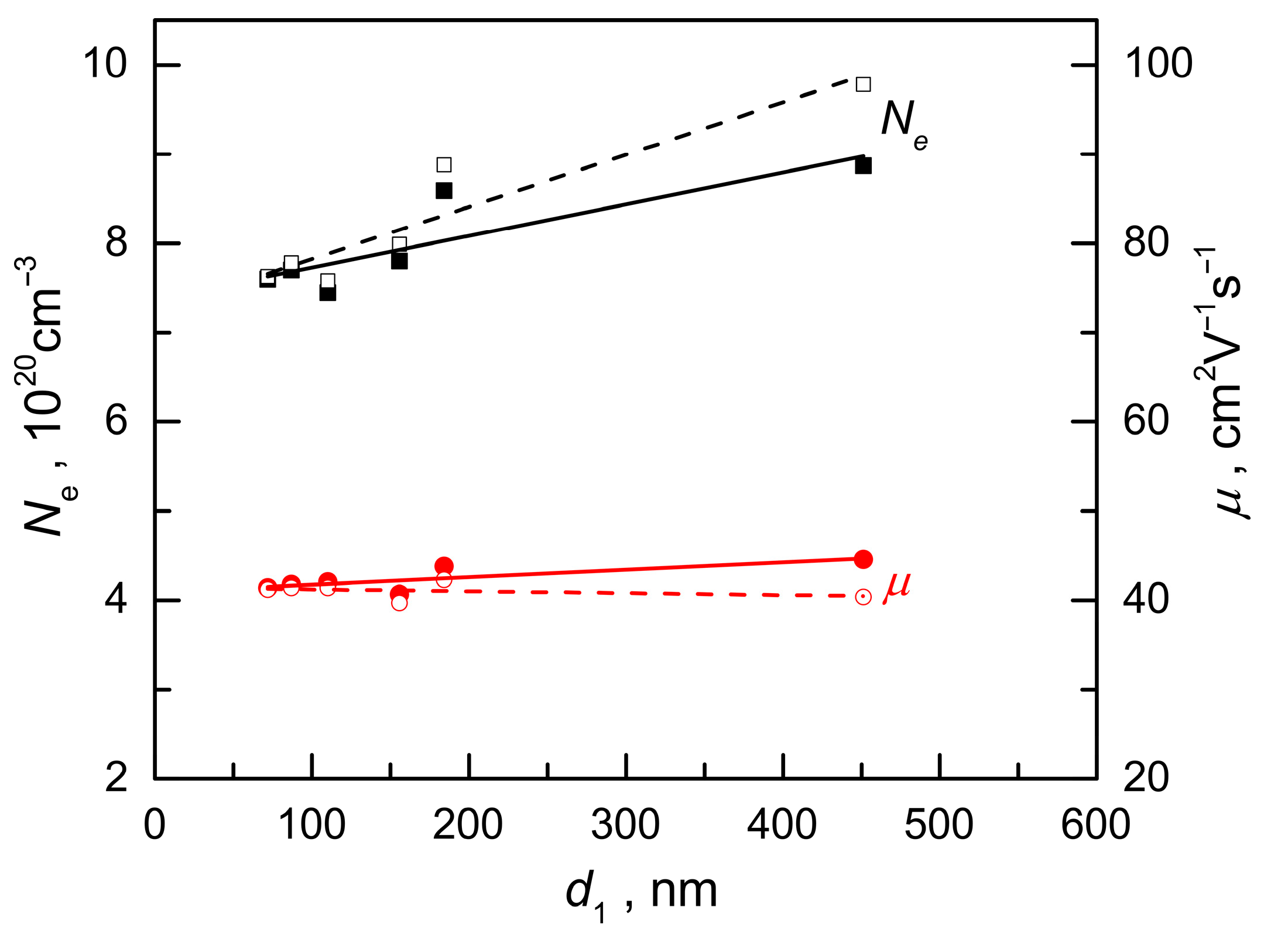
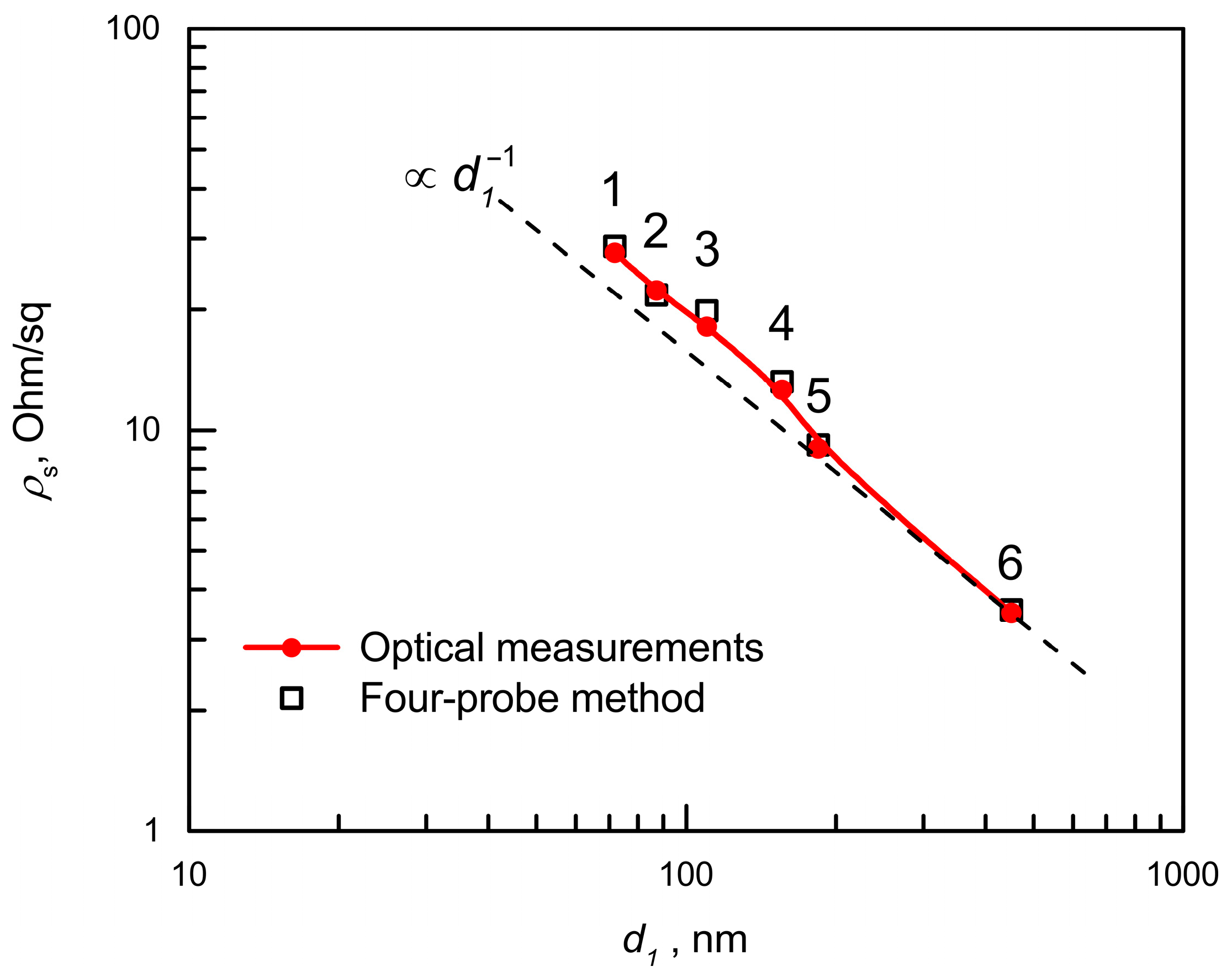
| Sample Number | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| ITO film thickness , nm | 76 ± 10 | 109 ± 10 | 119 ± 10 | 150 ± 10 | 167 ± 10 | 457 ± 10 |
| DC sheet resistivity , Ohm/sq | 28.7 ± 1.2 | 21.7 ± 0.6 | 19.8 ± 0.7 | 13.2 ± 0.5 | 9.18 ± 0.26 | 3.56 ± 0.02 |
| DC volume resistivity , 10−4 Ohm × cm | 2.19 | 2.37 | 2.36 | 1.98 | 1.53 | 1.63 |
| Spectrometer | Spectral Range | Operating Wavelengths | Operating Frequencies |
|---|---|---|---|
| Photon RT | UV/VIS | 0.185–1.65 μm | 182–1622 THz |
| FTIR spectrometer Vertex 70 | NIR | 0.667–8.34 μm | 36–450 THz |
| MIR | 1.3–27 μm | 11.1–231 THz | |
| FIR | 14–335 μm | 0.9–21.4 THz | |
| TERA K8 THz TDS system | THz | 150–3000 μm | 0.1–2 THz |
| Sample Number | (Ohm/Sq.) | (Ohm/Sq.) | ||
|---|---|---|---|---|
| #1 | 0.0279 | 27.7 | 0.7 | 0.025 |
| #2 | 0.0197 | 22.3 | 0.6 | 0.027 |
| #3 | 0.0138 | 18.1 | 0.8 | 0.044 |
| #4 | 0.0074 | 12.6 | 0.6 | 0.048 |
| #5 | 0.0040 | 9.0 | 0.6 | 0.067 |
| #6 | 0.00067 | 3.5 | 0.3 | 0.086 |
| Sample Number | (nm) | , (nm) | |||
|---|---|---|---|---|---|
| #1 | 71.9 | 1.2 | 0.017 | 7.63 | 41.2 |
| #2 | 87.1 | 1.1 | 0.013 | 7.78 | 41.4 |
| #3 | 110.1 | 1.7 | 0.015 | 7.58 | 41.4 |
| #4 | 155.9 | 1.8 | 0.012 | 7.99 | 39.7 |
| #5 | 184.3 | 1.9 | 0.010 | 8.88 | 42.3 |
| #6 | 451.2 | 2.8 | 0.006 | 9.78 | 40.4 |
| Sample Number | ) | ) | ||||
|---|---|---|---|---|---|---|
| #1 | 7.60 | 0.05 | 0.006 | 41.4 | 2.0 | 0.048 |
| #2 | 7.70 | 0.05 | 0.007 | 41.8 | 2.0 | 0.047 |
| #3 | 7.45 | 0.04 | 0.005 | 42.1 | 2.7 | 0.064 |
| #4 | 7.80 | 0.05 | 0.006 | 40.7 | 2.7 | 0.066 |
| #5 | 8.59 | 0.06 | 0.007 | 43.8 | 3.7 | 0.084 |
| #6 | 8.87 | 0.45 | 0.050 | 44.6 | 6.3 | 0.142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassarab, V.V.; Shalygin, V.A.; Shakhmin, A.A.; Kropotov, G.I. Spectroscopy of ITO Films in Optical and Terahertz Spectral Ranges. Appl. Sci. 2025, 15, 9121. https://doi.org/10.3390/app15169121
Bassarab VV, Shalygin VA, Shakhmin AA, Kropotov GI. Spectroscopy of ITO Films in Optical and Terahertz Spectral Ranges. Applied Sciences. 2025; 15(16):9121. https://doi.org/10.3390/app15169121
Chicago/Turabian StyleBassarab, Vladimir V., Vadim A. Shalygin, Alexey A. Shakhmin, and Grigory I. Kropotov. 2025. "Spectroscopy of ITO Films in Optical and Terahertz Spectral Ranges" Applied Sciences 15, no. 16: 9121. https://doi.org/10.3390/app15169121
APA StyleBassarab, V. V., Shalygin, V. A., Shakhmin, A. A., & Kropotov, G. I. (2025). Spectroscopy of ITO Films in Optical and Terahertz Spectral Ranges. Applied Sciences, 15(16), 9121. https://doi.org/10.3390/app15169121





