Using Neural Networks to Predict the Frequency of Traffic Accidents by Province in Poland
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
| Lower Silesia | Kuyavia–Pomerania | Lublin Province | Lubusz Province | Lodz Province | Lesser Poland | Masovia | Opole Province | |
| 2001 | 2,909,622 | 2,069,747 | 2,201,720 | 1,008,983 | 2,617,318 | 3,236,268 | 5,121,681 | 1,066,438 |
| 2002 | 2,904,694 | 2,069,166 | 2,196,992 | 1,008,196 | 2,607,380 | 3,237,217 | 5,128,623 | 1,061,009 |
| 2003 | 2,898,313 | 2,068,142 | 2,191,172 | 1,008,786 | 2,597,094 | 3,252,949 | 5,135,732 | 1,055,667 |
| 2004 | 2,893,055 | 2,068,258 | 2,185,156 | 1,009,168 | 2,587,702 | 3,260,201 | 5,145,997 | 1,051,531 |
| 2005 | 2,888,232 | 2,068,253 | 2,179,611 | 1,009,198 | 2,577,465 | 3,266,187 | 5,157,729 | 1,047,407 |
| 2006 | 2,882,317 | 2,066,371 | 2,172,766 | 1,008,520 | 2,566,198 | 3,271,206 | 5,171,702 | 1,041,941 |
| 2007 | 2,878,410 | 2,066,136 | 2,166,213 | 1,008,481 | 2,555,898 | 3,279,036 | 5,188,488 | 1,037,088 |
| 2008 | 2,877,059 | 2,067,918 | 2,161,832 | 1,008,962 | 2,548,861 | 3,287,136 | 5,204,495 | 1,033,040 |
| 2009 | 2,876,627 | 2,069,083 | 2,157,202 | 1,010,047 | 2,541,832 | 3,298,270 | 5,222,167 | 1,031,097 |
| 2010 | 2,917,242 | 2,098,711 | 2,178,611 | 1,023,215 | 2,542,436 | 3,336,699 | 5,267,072 | 1,017,241 |
| 2011 | 2,916,577 | 2,098,370 | 2,171,857 | 1,023,158 | 2,533,681 | 3,346,796 | 5,285,604 | 1,013,950 |
| 2012 | 2,914,362 | 2,096,404 | 2,165,651 | 1,023,317 | 2,524,651 | 3,354,077 | 5,301,760 | 1,010,203 |
| 2013 | 2,909,997 | 2,092,564 | 2,156,150 | 1,021,470 | 2,513,093 | 3,360,581 | 5,316,840 | 1,004,416 |
| 2014 | 2,908,457 | 2,089,992 | 2,147,746 | 1,020,307 | 2,504,136 | 3,368,336 | 5,334,511 | 1,000,858 |
| 2015 | 2,904,207 | 2,086,210 | 2,139,726 | 1,018,075 | 2,493,603 | 3,372,618 | 5,349,114 | 996,011 |
| 2016 | 2,903,710 | 2,083,927 | 2,133,340 | 1,017,376 | 2,485,323 | 3,382,260 | 5,365,898 | 993,036 |
| 2017 | 2,902,547 | 2,082,944 | 2,126,317 | 1,016,832 | 2,476,315 | 3,391,380 | 5,384,617 | 990,069 |
| 2018 | 2,901,225 | 2,077,775 | 2,117,619 | 1,014,548 | 2,466,322 | 3,400,577 | 5,403,412 | 986,506 |
| 2019 | 2,900,163 | 2,072,373 | 2,108,270 | 1,011,592 | 2,454,779 | 3,410,901 | 5,423,168 | 982,626 |
| 2020 | 2,891,321 | 2,061,942 | 2,095,258 | 1,007,145 | 2,437,970 | 3,410,441 | 5,425,028 | 976,774 |
| Subcarpathia | Podlaskie Province | Pomerania | Silesia | Holy Cross | Warmia-Masuria | Greater Poland | West Pomerania | |
| 2001 | 2,104,138 | 1,209,439 | 2,178,337 | 4,741,816 | 1,299,382 | 1,428,469 | 3,350,437 | 1,698,402 |
| 2002 | 2,105,050 | 1,207,704 | 2,183,636 | 4,731,533 | 1,295,885 | 1,428,449 | 3,355,279 | 1,697,718 |
| 2003 | 2,097,248 | 1,205,117 | 2,188,918 | 4,714,982 | 1,291,598 | 1,428,885 | 3,359,932 | 1,696,073 |
| 2004 | 2,097,975 | 1,202,425 | 2,194,041 | 4,700,771 | 1,288,693 | 1,428,714 | 3,365,283 | 1,694,865 |
| 2005 | 2,098,263 | 1,199,689 | 2,199,043 | 4,685,775 | 1,285,007 | 1,428,601 | 3,372,417 | 1,694,178 |
| 2006 | 2,097,564 | 1,196,101 | 2,203,595 | 4,669,137 | 1,279,838 | 1,426,883 | 3,378,502 | 1,692,838 |
| 2007 | 2,097,338 | 1,192,660 | 2,210,920 | 4,654,115 | 1,275,550 | 1,426,155 | 3,386,882 | 1,692,271 |
| 2008 | 2,099,495 | 1,191,470 | 2,219,512 | 4,645,665 | 1,272,784 | 1,427,073 | 3,397,617 | 1,692,957 |
| 2009 | 2,101,732 | 1,189,731 | 2,230,099 | 4,640,725 | 1,270,120 | 1,427,118 | 3,408,281 | 1,693,198 |
| 2010 | 2,127,948 | 1,203,448 | 2,275,494 | 4,634,935 | 1,282,546 | 1,453,782 | 3,446,745 | 1,723,741 |
| 2011 | 2,128,687 | 1,200,982 | 2,283,500 | 4,626,357 | 1,278,116 | 1,452,596 | 3,455,477 | 1,722,739 |
| 2012 | 2,129,951 | 1,198,690 | 2,290,070 | 4,615,870 | 1,273,995 | 1,450,697 | 3,462,196 | 1,721,405 |
| 2013 | 2,129,294 | 1,194,965 | 2,295,811 | 4,599,447 | 1,268,239 | 1,446,915 | 3,467,016 | 1,718,861 |
| 2014 | 2,129,187 | 1,191,918 | 2,302,077 | 4,585,924 | 1,263,176 | 1,443,967 | 3,472,579 | 1,715,431 |
| 2015 | 2,127,657 | 1,188,800 | 2,307,710 | 4,570,849 | 1,257,179 | 1,439,675 | 3,475,323 | 1,710,482 |
| 2016 | 2,127,656 | 1,186,625 | 2,315,611 | 4,559,164 | 1,252,900 | 1,436,367 | 3,481,625 | 1,708,174 |
| 2017 | 2,129,138 | 1,184,548 | 2,324,251 | 4,548,180 | 1,247,732 | 1,433,945 | 3,489,210 | 1,705,533 |
| 2018 | 2,129,015 | 1,181,533 | 2,333,523 | 4,533,565 | 1,241,546 | 1,428,983 | 3,493,969 | 1,701,030 |
| 2019 | 2,127,164 | 1,178,353 | 2,343,928 | 4,517,635 | 1,233,961 | 1,422,737 | 3,498,733 | 1,696,193 |
| 2020 | 2,121,229 | 1,173,286 | 2,346,671 | 4,492,330 | 1,224,626 | 1,416,495 | 3,496,450 | 1,688,047 |
| Province | Area | Population | ||
|---|---|---|---|---|
| in ha | in km2 | Total | per 1 km2 | |
| Poland | 31,270,525 | 312,705 | 38,265,013 | 122 |
| Lower Silesia | 1,994,670 | 19,947 | 2,891,321 | 145 |
| Kuyavia–Pomerania | 1,797,134 | 17,971 | 2,061,942 | 115 |
| Lublin Province | 2,512,246 | 25,123 | 2,095,258 | 83 |
| Lubusz Province | 1,398,793 | 13,988 | 1,007,145 | 72 |
| Łodz Province | 1,821,895 | 18,219 | 2,437,970 | 134 |
| Lesser Poland | 1,518,279 | 15,183 | 3,410,441 | 225 |
| Masovia | 3,555,847 | 35,559 | 5,425,028 | 153 |
| Opole Province | 941,187 | 9412 | 976,774 | 104 |
| Subcarpathia | 1,784,576 | 17,846 | 2,121,229 | 119 |
| Podlaskie Province | 2,018,702 | 20,187 | 1,173,286 | 58 |
| Pomerania | 1,832,368 | 18,323 | 2,346,671 | 128 |
| Silesia | 1,233,309 | 12,333 | 4,492,330 | 364 |
| Holy Cross | 1,171,050 | 11,710 | 1,224,626 | 105 |
| Warmia-Masuria | 2,417,347 | 24,173 | 1,416,495 | 59 |
| Greater Poland | 2,982,650 | 29,826 | 3,496,450 | 117 |
| West Pomerania | 2,290,472 | 22,905 | 1,688,047 | 74 |


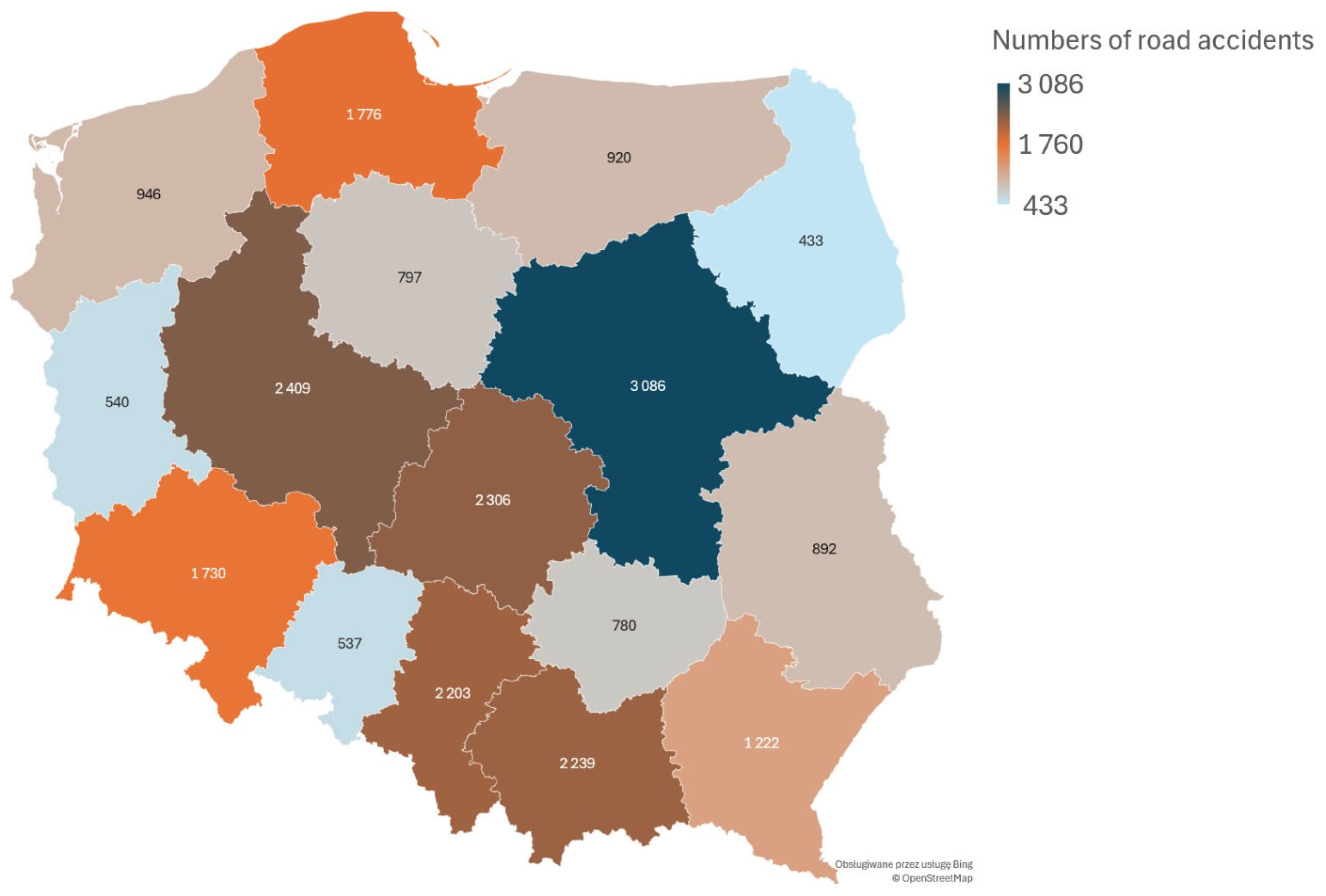
- Demographic and infrastructural differences between provinces influence the historical accident rates and are thus implicitly embedded in the model.
- Legislative changes, such as increased penalties for violations introduced in 2022, and external shocks like the COVID-19 pandemic, are represented through fluctuations in the time series.
- Temporal patterns, including long-term trends and seasonal variations, are captured during model training.
- ME—mean error
- MAE—mean absolute error
- MPE—mean percentage error
- MAPE—mean absolute percentage error
- SSE—mean square error
4. Results
Road Accident Forecasting
- -
- Teaching 70%, testing 15%, and validation 15%;
- -
- Teaching 80%, testing 10%, and validation 10%.
5. Discussion
6. Conclusions
- Collect historical road accident data by region for a minimum of 10 consecutive years.
- Preprocess the data to ensure completeness and consistency.
- Adapt the neural network architecture to match the data scope (e.g., number of input neurons = number of years).
- Train multiple MLP models with varying hidden layer sizes and activation functions.
- Validate the model using a holdout dataset or cross-validation and select the best-performing version based on MAPE or MAE.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- WHO. The Global Status on Road Safety 2018; WHO: Geneva, Switzerland, 2018; 403p, ISBN 9789241565684. Available online: https://iris.who.int/bitstream/handle/10665/276462/9789241565684-eng.pdf?sequence=1 (accessed on 17 April 2022).
- Žuraulis, V.; Sokolovskij, E. Vehicle velocity relation to slipping trajectory change: An option for traffic accident reconstruction. Promet—Traffic Transp. 2018, 30, 395–406. [Google Scholar] [CrossRef]
- Stepanović, N.; Tubić, V.; Milenković, M.; Halaj, K. The impact of basic traffic flow characteristics on traffic accident occurrence on 2-lane rural roads in Serbia. Transport 2025, 40, 64–73. [Google Scholar] [CrossRef]
- Pečeliūnas, R.; Žuraulis, V.; Droździel, P.; Pukalskas, S. Prediction of road accident risk for vehicle fleet based on statistically processed tire wear model. Promet—Traffic Transp. 2022, 34, 619–630. [Google Scholar] [CrossRef]
- Lyashuk, O.; Mironov, D.; Martyniuk, V.; Aulin, V.; Tson, O.; Maruschak, P. Risk analysis of road traffic accidents in Ukraine. Transport 2024, 39, 350–359. [Google Scholar] [CrossRef]
- Gorzelańczyk, P.; Sokolovskij, E. Using neural networks to forecast the amount of traffic accidents in Poland and Lithuania. Sustainability 2025, 17, 1846. [Google Scholar] [CrossRef]
- Helgason, A. Fractional integration methods and short Time series: Evidence from asimulation study. Polit. Anal. 2016, 24, 59–68. [Google Scholar] [CrossRef]
- Forecasting Based on Time Series. 2022. Available online: http://pis.rezolwenta.eu.org/Materialy/PiS-W-5.pdf (accessed on 17 April 2022).
- Procházka, J.; Flimmel, S.; Čamaj, M.; Bašta, M. Modelling the Number of Road Accidents. In Applications of Mathematics and Statistics in Economics. International Scientific Conference, Szklarska Poręba, 30 August–3 September 2017; Publishing House of the University of Economics in Wrocław: Wrocław, Poland, 2017. [Google Scholar] [CrossRef]
- Sunny, C.M.; Nithya, S.; Sinshi, K.S.; Vinodini, V.M.D.; Lakshmi, A.K.G.; Anjana, S.; Manojkumar, T.K. Forecasting of Road Accident in Kerala: A Case Study. In Proceedings of the 2018 International Conference on Data Science and Engineering (ICDSE), Kochi, India, 7–9 August 2018. [Google Scholar] [CrossRef]
- Dudek, G. Forecasting Time Series with Multiple Seasonal Cycles Using Neural Networks with Local Learning. In Artificial Intelligence and Soft Computing ICAISC 2013; Lecture Notes in Computer Science; Rutkowski, L., Korytkowski, M., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; p. 7894. [Google Scholar] [CrossRef]
- Szmuksta-Zawadzka, M.; Zawadzki, J. Forecasting on the Basis of Holt-Winters Models for Complete and Incomplete Data. Research Papers of the Wrocław University of Economics 2009, No. 38. Available online: http://bazekon.icm.edu.pl/bazekon/element/bwmeta1.element.ekon-element-000164937729 (accessed on 17 April 2022).
- Lavrenz, S.; Vlahogianni, E.; Gkritza, K.; Ke, Y. Time series modeling in traffic safety research. Accid. Anal. Prev. 2018, 117, 368–380. [Google Scholar] [CrossRef] [PubMed]
- Al-Madani, H. Global road fatality trends’estimations based on country-wise microlevel data. Accid. Anal. Prev. 2018, 111, 297–310. [Google Scholar] [CrossRef] [PubMed]
- Chudy-Laskowska, K.; Pisula, T. Prognozowanie liczby wypadków drogowych na Podkarpaciu. Logistics 2015, 4, 2782–2796. [Google Scholar]
- Gorzelanczyk, P. Application of neural networks to forecast the number of road accidents in provinces in Poland. Heliyon 2023, 9, e12767. [Google Scholar] [CrossRef] [PubMed]
- Jurkovic, M.; Gorzelanczyk, P.; Kalina, T.; Jaros, J.; Mohanty, M. Impact of the COVID-19 pandemic on road traffic accident forecasting in Poland and Slovakia. Open Eng. 2022, 12, 578–589. [Google Scholar] [CrossRef]
- Central Statistical Office. Available online: www.gus.pl (accessed on 17 April 2022).
- Province Names in English. Available online: https://polandtravel.agency/regions-of-poland/ (accessed on 17 April 2022).
- Statistic Road Accident. Available online: https://statystyka.policja.pl/ (accessed on 17 April 2022).
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building machines that learn and think like people. Behav. Brain Sci. 2017, 40, e253. [Google Scholar] [CrossRef] [PubMed]
- Becoming Human. How Netflix Uses AI, Data Science, and Machine Learning—From a Product Perspective. Available online: www.becominghuman.ai (accessed on 10 August 2019).
- Forbes. The Amazing Ways eBay Is Using Artificial Intelligence to Boost Business Success. Available online: www.forbes.com (accessed on 12 September 2020).
- Wu, Y.; Schuster, M.; Chen, Z.; Le, Q.V.; Norouzi, M.; Macherey, W.; Krikun, M.; Cao, Y.; Gao, Q.; Macherey, K.; et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv 2020, arXiv:1609.08144. [Google Scholar]
- Oronowicz-Jaśkowiak, W. The application of neural networks in the work of forensic experts in child abuse cases. Adv. Psychiatry Neurol. 2019, 28, 273–282. [Google Scholar] [CrossRef]
- Wójcik, A. Autoregressive Vector Models as a Response to the Critique of Multi-Equation Structural Econometric Models; Publishing House of the University of Economics in Katowice: Katowice, Poland, 2014; Volume 193. [Google Scholar]
- Baron, B.; Pasierbek, A. Comparison of the performance of coupled gradient and quasi-Newtonian BFGS algorithms in the problem of optimizing power distribution in a power system. Electrics 2009, 3, 211. [Google Scholar]
- Gorzelańczyk, P. Change in the Mobility of Polish Residents during the COVID-19 Pandemic. Commun.-Sci. Lett. Univ. Zilina 2022, 24, A100–A111. [Google Scholar] [CrossRef]

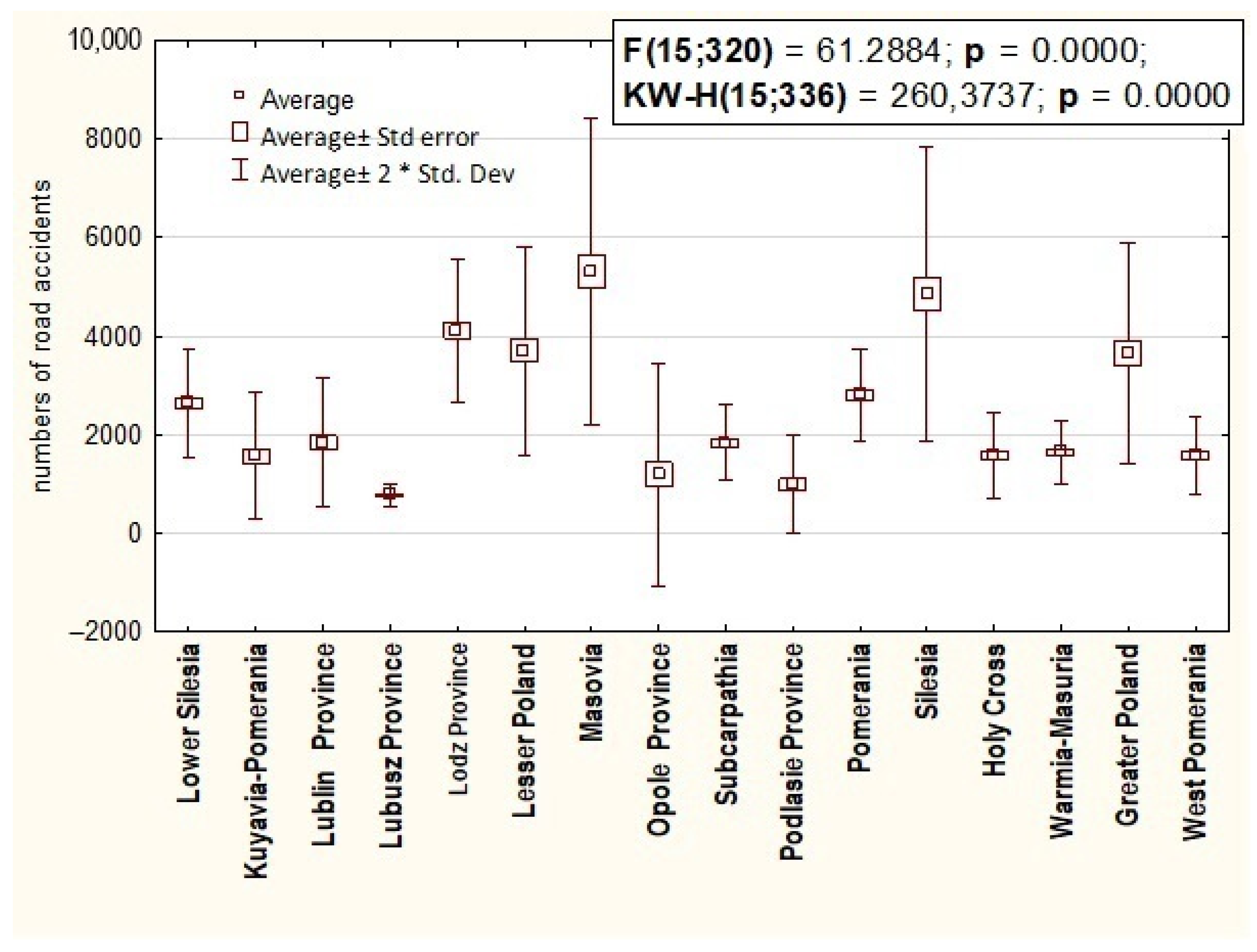

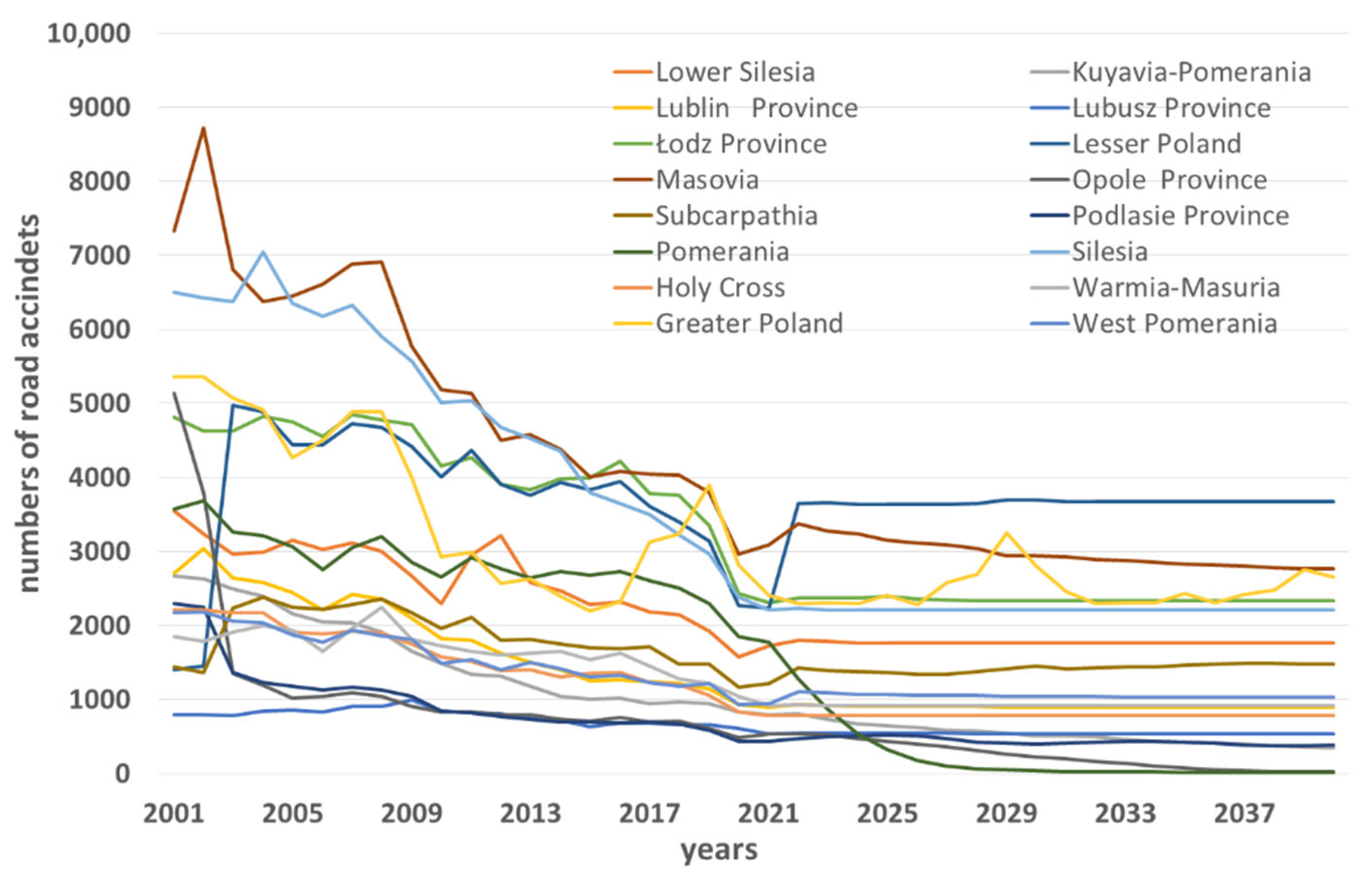
| Province | Network Number | Network Name | Learning Algorithm | Activation (Hidden) | Activation (Output) | Errors | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ME | MAE | MPE | MAPE | SSE | ||||||
| Lower Silesia | 20 | MLP 10-3-1 | BFGS 8 | Exponential | Linear | 22.06 | 105.58 | 0.23% | 4.48% | 199.39 |
| Kuyavia–Pomerania | 200 | MLP 10-2-1 | BFGS 4 | Tanh | Tanh | 6.39 | 64.20 | 0.19% | 5.83% | 79.33 |
| Lublin Province | 20 | MLP 10-6-1 | BFGS 4 | Tanh | Tanh | 15.71 | 63.21 | 0.95% | 4.81% | 78.17 |
| Lubusz Province | 60 | MLP 10-6-1 | BFGS 5 | Tanh | Logistics | 1.70 | 29.54 | 0.18% | 4.69% | 38.85 |
| Łodz Province | 80 | MLP 10-2-1 | BFGS 11 | Logistics | Tanh | 72.07 | 134.71 | 2.92% | 4.54% | 190.24 |
| Lesser Poland | 40 | MLP 10-7-1 | BFGS 33 | Logistics | Exponential | 115.52 | 138.82 | 4.51% | 5.15% | 276.59 |
| Masovia | 40 | MLP 10-3-1 | BFGS 6 | Exponential | Linear | 72.14 | 186.35 | 2.43% | 5.21% | 248.13 |
| Opole Province | 40 | MLP 10-6-1 | BFGS 10 | Linear | Linear | 3.58 | 45.73 | 1.69% | 7.28% | 60.00 |
| Subcarpathia | 80 | MLP 10-8-1 | BFGS 14 | Exponential | Tanh | 24.55 | 363.96 | 2.23% | 20.76% | 674.90 |
| Podlaskie Province | 40 | MLP 10-6-1 | BFGS 19 | Logistics | Tanh | 8.49 | 31.52 | 2.81% | 6.16% | 47.92 |
| Pomerania | 20 | MLP 10-4-1 | BFGS 21 | Logistics | Tanh | 40.84 | 70.60 | 2.29% | 3.47% | 139.26 |
| Silesia | 60 | MLP 10-4-1 | BFGS 7 | Logistics | Linear | 29.29 | 122.23 | 0.24% | 3.24% | 152.45 |
| Holy Cross | 100 | MLP 10-8-1 | BFGS 7 | Logistics | Tanh | 17.02 | 48.83 | 2.18% | 4.55% | 61.91 |
| Warmia-Masuria | 200 | MLP 10-6-1 | BFGS 9 | Logistics | Tanh | 0.52 | 36.85 | 0.18% | 3.10% | 52.19 |
| Greater Poland | 60 | MLP 10-4-1 | BFGS 1 | Exponential | Exponential | 9.98 | 392.95 | 3.07% | 14.06% | 477.32 |
| West Pomerania | 100 | MLP 10-2-1 | BFGS 7 | Logistics | Linear | 15.13 | 59.73 | 1.87% | 5.09% | 70.69 |
| Average | 28.44 | 118.43 | 1.75% | 6.40% | 177.96 | |||||
| Province | Network Number | Network Name | Learning Algorithm | Activation (Hidden) | Activation (Output) | Errors | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ME | MAE | MPE | MAPE | SSE | ||||||
| Lower Silesia | 200 | MLP 10-2-1 | BFGS 0 | Linear | Exponential | 29.65 | 97.51 | 0.02% | 4.10% | 207.57 |
| Kuyavia–Pomerania | 100 | MLP 10-6-1 | BFGS 13 | Logistics | Linear | 2.25 | 28.07 | 0.06% | 2.82% | 34.20 |
| Lublin Province | 20 | MLP 10-4-1 | BFGS 10 | Tanh | Logistics | 2.72 | 71.71 | 0.50% | 5.81% | 80.54 |
| Lubusz Province | 60 | MLP 10-8-1 | BFGS 24 | Tanh | Exponential | 0.47 | 10.55 | 0.00% | 1.65% | 12.90 |
| Łodz Province | 40 | MLP 10-2-1 | BFGS 5 | Tanh | Logistics | 43.99 | 197.34 | 0.06% | 5.94% | 272.65 |
| Lesser Poland | 20 | MLP 10-2-1 | BFGS 5 | Logistics | Logistics | 94.48 | 467.44 | 0.87% | 15.28% | 540.21 |
| Masovia | 80 | MLP 10-8-1 | BFGS 3 | Tanh | Linear | 25.07 | 202.75 | 1.54% | 5.56% | 261.11 |
| Opole Province | 100 | MLP 10-6-1 | BFGS 18 | Tanh | Linear | 6.19 | 24.53 | 1.63% | 4.08% | 37.95 |
| Subcarpathia | 80 | MLP 10-2-1 | BFGS 4 | Logistics | Linear | 5.06 | 114.15 | 1.68% | 7.69% | 141.80 |
| Podlaskie Province | 20 | MLP 10-4-1 | BFGS 16 | Linear | Linear | 1.51 | 30.69 | 0.86% | 5.47% | 42.34 |
| Pomerania | 60 | MLP 10-3-1 | BFGS 7 | Logistics | Tanh | 5.38 | 87.26 | 0.57% | 3.97% | 123.00 |
| Silesia | 200 | MLP 10-4-1 | BFGS 46 | Logistics | Exponential | 17.85 | 41.76 | 0.82% | 1.56% | 64.00 |
| Holy Cross | 80 | MLP 10-4-1 | BFGS 14 | Tanh | Exponential | 4.95 | 26.67 | 0.26% | 2.19% | 33.00 |
| Warmia-Masuria | 80 | MLP 10-4-1 | BFGS 20 | Tanh | Exponential | 0.60 | 7.58 | 0.10% | 0.56% | 10.00 |
| Greater Poland | 40 | MLP 10-8-1 | BFGS 19 | Tanh | Exponential | 8.16 | 131.72 | 0.17% | 5.01% | 181.00 |
| West Pomerania | 100 | MLP 10-5-1 | BFGS 3 | Exponential | Exponential | 7.21 | 87.72 | 0.93% | 7.55% | 114.22 |
| Average: | 15.97 | 101.72 | 0.63% | 4.95% | 134.81 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorzelańczyk, P.; Zabel, J.; Sokolovskij, E. Using Neural Networks to Predict the Frequency of Traffic Accidents by Province in Poland. Appl. Sci. 2025, 15, 9108. https://doi.org/10.3390/app15169108
Gorzelańczyk P, Zabel J, Sokolovskij E. Using Neural Networks to Predict the Frequency of Traffic Accidents by Province in Poland. Applied Sciences. 2025; 15(16):9108. https://doi.org/10.3390/app15169108
Chicago/Turabian StyleGorzelańczyk, Piotr, Jacek Zabel, and Edgar Sokolovskij. 2025. "Using Neural Networks to Predict the Frequency of Traffic Accidents by Province in Poland" Applied Sciences 15, no. 16: 9108. https://doi.org/10.3390/app15169108
APA StyleGorzelańczyk, P., Zabel, J., & Sokolovskij, E. (2025). Using Neural Networks to Predict the Frequency of Traffic Accidents by Province in Poland. Applied Sciences, 15(16), 9108. https://doi.org/10.3390/app15169108










